Abstract
Ensuring high reliability and low latency poses challenges for numerous applications that require rigid performance guarantees, such as industrial automation and autonomous vehicles. Our research primarily concentrates on addressing the real-time requirements of ultra-reliable low-latency communication (URLLC). Specifically, we tackle the challenge of hard delay constraints in real-time transmission systems, overcoming this obstacle through a finite blocklength coding scheme. In the physical layer, we encode randomly arriving packets using a variable-length coding scheme and transmit the encoded symbols by truncated channel inversion over parallel channels. In the network layer, we model the encoding and transmission processes as tandem queues. These queues backlog the data bits waiting to be encoded and the encoded symbols to be transmitted, respectively. This way, we represent the system as a two-dimensional Markov chain. By focusing on instances when the symbol queue is empty, we simplify the Markov chain into a one-dimensional Markov chain, with the packet queue being the system state. This approach allows us to analytically express power consumption and formulate a power minimization problem under hard delay constraints. Finally, we propose a heuristic algorithm to solve the problem and provide an extensive evaluation of the trade-offs between the hard delay constraint and power consumption.
1. Introduction
In the 6G era [1], ultra-reliable low-latency communication (URLLC) scenarios impose stringent delay constraints, encompassing applications such as autonomous driving and industrial automation. The principal objective of URLLC, which is to ensure real-time requirements with hard delay constraints, has attracted widespread attention in academia [2]. It is worth noting that finite blocklength coding with a short-frame structure exhibits an excellent low-latency performance [3]. Accordingly, this work proposes a variable-length finite blocklength coding scheme to satisfy the hard latency constraint over time-varying wireless channel fading. Meanwhile, we customize the corresponding dynamic framing and power allocation to suit the variable-length channel coding.
Hard delay constraints play a crucial role in URLLC scenarios, as they ensure timely and reliable data delivery [2]. In light of this, academia has embarked on comprehensive studies of both transmission designs and network structures relevant to hard delay constraints. Most research has primarily targeted transmission designs, such as [4,5,6,7,8,9,10,11,12]. For instance, Ref. [4] explored network communications under stringent timeliness constraints, demonstrating the superior performance of network coding over routing in delay-constrained unicast settings. The authors of [5] addressed the challenges of delay-constrained scheduling for point-to-point communications over time-varying channels using a channel-threshold policy. Ref. [6] ensured adherence to hard delay constraints by exploiting frequency and spatial diversity techniques. The authors of [7] proposed an optimal power control policy to minimize the probability of violating delay bounds. In [8], an optimal dynamic coding-window selection policy was proposed for delay-constrained communications. Kumar investigated a framework of hard delay constraints for real-time communication from a queueing perspective in [9,10]. The authors of [11] consider the delay-constrained scheduling problem of point-to-point communication, while the authors of [12] consider the hard deadline constraints of multichannel systems in a cognitive radio scenario. Subsequent works have investigated many network structures, such as [13,14,15,16]. For instance, the authors of [13] explored optimal forwarding for real-time communication over multi-hop wireless lossy networks under strict latency constraints. In [14], the scheduling of delay constrained transmissions were investigated for coded caching. Ref. [15] optimized user offloading and resource allocation in a mobile cloud computing system with delay constraints. Likewise, Ref. [16] focused on maximizing delay-constrained coverage in vehicular networks through optimal base station deployment.
The maximal achievable coding rate of finite blocklength coding was investigated in [17], which provided significant insights into how low latency requirements can be effectively met using a short frame structure. Consequently, academia has pursued research concerning the maximal achievable coding rate of finite blocklength coding and its applicable network structures. Most of this research has primarily focused on the maximal achievable coding rate, as seen in [18,19,20,21]. For instance, the authors in [18] characterized the maximal achievable rate in block fading channels using the channel-side information at the receiver (CSIR). The authors of [19] investigated the maximal achievable rate over quasi-static multiple-input multiple-output fading channels. Ref. [20] investigated the finite blocklength limits in multi-antenna AWGN channels, shedding light on channel dispersion and its impact on coding delay and optimal coding schemes. The maximal achievable rate was investigated in parallel complex AWGN channels in [21]. Subsequent studies have investigated applicable network structures, such as [3,22,23,24]. The study in [3] reviewed the advances in information theory related to finite blocklength coding in short-packet transmissions system. The authors in [22] re-evaluated frame design principles involving finite blocklength coding in cellular wireless systems. In [23], the scheduling of downlink non-orthogonal multiple access (NOMA) was examined in the context of short-packet communications. The work in [24] proposed a fast HARQ protocol, substantially improving throughput, delay, and error probability with finite blocklength coding.
Numerous studies have implemented finite blocklength coding in low-latency communication systems. As demonstrated in [25], there exists a significant disparity between the current channel coding for URLLC and the standard approximation of finite blocklength coding [26]. Extensive research efforts have examined the design of low-latency transmission using finite blocklength coding in single-user systems. For instance, Ref. [27] proposed an adaptive blocklength transmission framework and two novel schemes to optimize the end-to-end delay in 6G networks. Refs. [28,29] have investigated finite blocklength coding in low-latency transmission systems. The exploration of low-latency transmission design using finite blocklength coding has extended to multiple access systems as well. A multi-access transmission design utilizing finite blocklength coding has been examined in low-latency vehicular communications, rate-splitting multiple access, and Internet of Things systems [30,31,32,33,34]. Furthermore, the authors in [35,36] have investigated the variable coding policy used in low-latency communications.
The aforementioned work [4,5,6,7,8,13,14,15,16] adopts an common assumption that the transmission power and rate analysis is based on the classical Shannon capacity formula. This assumption is valid only when the channel coding adopts an extremely long blocklength [17]. Nonetheless, the future 6G system is expected to support a wide range of services for emerging applications, such as autonomous driving and industrial automation, where the blocklength is short and sometimes subject to hard delay and reliability constraints [3]. This implies that the long codewords required by the Shannon capacity formula may become impractical. Consequently, the previous designs in [4,5,6,7,8,13,14,15,16] are unsuitable for these 6G applications. In the previously mentioned research [3,22,23,24], although finite blocklength coding is utilized, its application to the scheduling of communications with stringent delay constraints is not considered. While [25,26,27,28,29,30,31,32,33,34,35,36] have investigated the use of finite blocklength coding in low-latency communications, they do not adequately address the enforcement of hard delay constraints. These oversights render the aforementioned studies ill-suited for real-time communication systems.
In our previous work [37], we focused on optimizing the average delay in short-packet transmission systems. However, in URLLC, we not only consider the average delay but also ensure that all data packets do not exceed a hard delay constraint [38]. Therefore, in this paper, we delve into hard-delay-constrained communication in short-packet transmission systems, utilizing variable-length coding. In conventional URLLC systems, the focus has primarily been placed on minimizing the average delay or outage probability. However, these studies have not addressed the issues pertaining to hard delay constraints and finite blocklength coding. To this end, we propose a cross-layer design policy tailored to short-packet transmission systems with hard delay constraints. In particular, we encode randomly arriving packets via variable-length coding and transmit the encoded symbols by truncated channel inversion over parallel channels, with the channel-side information at the transmitter (CSIT). Furthermore, we model the data queue and symbol queue as a two-dimensional Markov chain. By adopting the embedded Markov chain and focusing on instances when the symbol queue is empty, we simplify our derived Markov chain into a one-dimensional Markov chain, with the data queue length being the system state. We investigate the analytic expression of average power consumption per slot in the embedded Markov chain. To derive the hard-delay-constrained policy, two heuristic algorithms are proposed. We utilize gradient descent, based on the policies obtained from these heuristic algorithms, to achieve an enhanced hard-delay-constrained policy that effectively strikes a balance between delay constraint and power consumption. Through simulations, we have also verified that our presented policy outperforms the traditional on-demand transmission policy and CSIR policy.
The rest of this paper is organized as follows: Section 2 illustrates the system model. The finite blocklength coding with a cross-layer approach is investigated in Section 3. In Section 4, a heuristic algorithm is proposed to obtain the hard delay constraint policy. Numerical results and concluding remarks are presented in Section 5 and Section 6, respectively. The research flow chart of this paper is shown in Figure 1.
Figure 1.
Research flow chart.
2. System Model
This paper considers a real-time transmission system, such as that depicted in Figure 2. Specifically, the system is designed to transmit packets via parallel fading channels within a hard delay constraint. Time is discretized into time slots, with each slot spanning a duration of T seconds. Meanwhile, we suppose that the transmitter has perfect knowledge of the channel state information. This assumption facilitates transmit power adaptation, which partially mitigates the detrimental impact of channel fades.
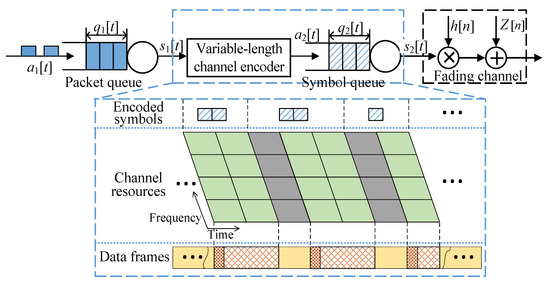
Figure 2.
System model.
2.1. Physical Layer of the Channel Model
In the physical layer, we denote the transmitted signal during the t-th time slot as , while the corresponding received signal at the receiver is denoted as . Let denote the channel coefficient. The relationship between the transmitted and received signals is expressed as
Herein, denotes an additive white Gaussian noise process with a noise spectral density of . Meanwhile, denotes the channel gain.
In practical systems with limited transmit power, the deep fading phenomena inherent to wireless channels pose significant challenges for achieving the low latency and high reliability requirements of URLLC. To address these challenges, we propose the use of parallel channels to ensure more reliable transmission. For the convenience of our theoretical analysis, we adopt a transmission scheme that selects the best among these parallel channels. However, to achieve hard delay constraints, it is necessary to employ parallel channels to enhance reliability.
Let M denote the number of parallel channels, with the channel gain denoted as . We assume that these parallel channels follow an independent and identically distributed () Rayleigh distribution over time. That is, the probability density function () of the channel gain is . Furthermore, the cumulative distribution function () of the channel gain is denoted as .
In the interest of analytical representation, we turn to utilize the maximal channel gain, expressed as
The corresponding to this maximal channel gain is given by
Subsequently, associated with the maximal channel gain is derived as
It is worth noting that our framework remains accommodating to diverse channel distribution and multiplexing schemes. The emphasis on maximal channel gain is strictly a matter of analytical convenience. The system model we propose is suitable for various wireless communication systems that require meeting hard delay constraints, where factors like interference and mobility can be normalized into the channel gain. Our proposed approach is applicable to different channel models.
2.2. Finite Blocklength Coding in the Physical Layer
In practice, a short frame structure is utilized to achieve ultra-low-latency transmission. Thus, the system is obligated to implement channel coding with a finite blocklength over parallel channels. The coding rate and the blocklength for finite blocklength coding are denoted by and , respectively. Given the block error probability and the received signal to noise ratio , we know that [17]
where is the inverse of the Gaussian Q-function. Adjusting the coding rate is similar to adaptive modulation and coding in information theory. However, in finite blocklength coding, new challenges arise. The coding length is finite, and the codewords generated together need to be transmitted at a constant signal-to-noise ratio.
In the finite blocklength coding regime, maintaining a consistent signal-to-noise ratio across the symbols that are collectively encoded is critical. Thus, power adaptation should ensure a consistent signal-to-noise ratio over the symbols, where B and denote the channel bandwidth and the power consumption, respectively. To mitigate the high levels of power consumption caused by poor channel conditions, we considered implementing truncated channel inversion. To ensure a constant signal-to-noise ratio at the receiver, the power consumption at the transmitter is
Our objective is to optimize the threshold of the truncated channel inversion in order to minimize the average power consumption while achieving a hard delay constraint in the system.
2.3. The Queueing Model in the Network Layer
As shown in Figure 2, we characterize the packet transmission dynamics in the network layer using a packet queuing model. Queuing effects arise due to the fact that the coding’s blocklength may require multiple time slots for transmission. Consequently, the transmission process is conceptualized as the symbol queue. The packet queue and symbol queue together form a tandem queue.
To begin with, let us introduce the packet queue. Suppose that data packets of size A bits arrive deterministically at the transmitter in each time slot. We define queue length, , in terms of the number of packets waiting in the queue. In particular, evolves as
where , and K is the maximum queue length constrained by the buffer size. Moreover, denotes the service rate in terms of the number of data packets transmitted in time slot t.
Considering Equation (5), the achievable channel coding rate in finite blocklength coding increases with the coding blocklength. Consequently, it is more power-efficient to accumulate a sufficient number of packets before the coding process. We propose a greedy framing policy, where all packets in the packet queue undergo finite blocklength coding when the symbol queue is empty. Consequently, the service rate of the packet queue is given by
Subsequently, a detailed introduction to the symbol queue is provided. Throughout the finite blocklength coding process, the data packets transmitted by the packet queue , each encompassing A bits, are encoded into symbols. The relationship between the service rate of the packet queue and the coding blocklength is given by
The encoded symbols are buffered in a symbol queue and transmitted over a time-varying fading channel across multiple time slots. The symbol queue’s length is defined as the number of symbol blocks backlogged in the symbol queue in the t-th time slot. Each symbol block spans T s and B Hz in the time and spectral domains, respectively. Subsequently, the arrival rate of the symbol queue is defined as the number of symbol blocks that arrive. The service rate of the symbol queue is defined as the number of symbol blocks transmitted in the t-th time slot. Consequently, the evolution of the symbol queue is defined as
During the encoding process, the data packets can be encoded into multiple symbols. The number of symbols that can be transmitted in each time slot is generally multiple and contingent upon the available channel resources. When the system is allocated T s and B Hz as its channel resources, we set . Subsequently, the coding blocklength can be quantified as the number of symbol blocks . Then, is formulated as
The ceiling function has been utilized in Equation (11) to account for the symbol blocks being discrete units. The use of variable-length coding introduces variability in the transmission time. The constructed symbol queue is designed to indicate the transmission process of symbols. Consequently, communication signalling based on the symbol queue can prompt the receiver to commence decoding.
2.4. The Hard-Delay Constraint
In this real-time transmission system, the delay of data packets in the system consists of two components: the queueing delay of the packet queue and the transmission delay of the symbol queue. The maximum waiting time of a data packet in the system, defined as W, is given by
where and represent the maximum queueing delay in the packet queue and the maximum transmission delay in the symbol queue, respectively. To satisfy the hard delay constraint, it is necessary to limit the waiting time of data packets within the system. This indicates that the waiting time of the data packets in both the packet queue and the symbol queue should be limited. In the following, we separately consider the maximum waiting time of the data packets in these two queues.
In light of Equation (7), the hard delay constraint in the packet queue is characterized by an integer K. Notably, K represents the maximal number of time slots that a packet is allowed to be backlogged in the packet queue, with . The nature of the deterministic packet arrival process leads us to the fact that if , it indicates that the earliest packets have been in the queue for more than K time slots. Consequently, these initial packets violate the hard delay constraint and should be dropped. In real-time communication systems, it is necessary to design policies to ensure that all data packets are transmitted within their designated time limits to achieve a packet loss rate of zero.
The delay-violation probability is defined as the proportion of data packets that violate the hard delay constraint. We use to denote the delay-violation probability, which is given by
As long as the packet queue does not exceed the maximum queue length, the symbol queue will necessarily have the maximum length, according to Equations (8)–(10). Therefore, as long as the overflow of the packet queue is constrained, this tandem queuing system will not experience overflow. Then, we do not need to incorporate the symbol dropping mechanism. Therefore, the condition implies that all packets obey the hard delay constraint.
For the symbol queue, it is also necessary to restrict the maximum waiting time of the symbol blocks. In the next section, we will provide a detailed explanation of how to limit the maximum waiting time in the symbol queue using embedded Markov chains.
Our aim is to obtain a variable-length coding policy that minimizes the transmission power while ensuring the hard delay constraint. The explicit design of our variable-length coding policy is addressed in the next section.
3. Cross-Layer Design for Finite Blocklength Coding
In this section, we generate a variable-length coding policy to satisfy the hard delay constraint. In particular, we consider implementing truncated channel inversion to determine the service rate. Based on this, we prove that the hard delay constraint can be satisfied with finite average power. Then, we formulate the system as an embedded Markov chain. Based on this, we consider the packet queue length as the only system state, while the evolution of the symbol queue length is embedded into the transition probabilities. Moreover, we demonstrate that the variable-length coding policy is capable of achieving this hard delay constraint by guaranteeing a limitation on both the maximum queuing delay and transmission delay.
3.1. Achieving the Hard Delay Constraint with Finite Average Power
We use to denote the number of symbol blocks corresponding to data packets. Subsequently, we have under conditions where and . Let k and l represent the number of time slots and the number of symbol blocks that have been successfully transmitted after a finite blocklength coding process, respectively. Then, we have
Considering that the transmission in a deep fading channel requires infinite power, we should suspend symbol transmission during deep fading to save power, particularly when the remaining number of symbol blocks is less than the number of the remaining time slots. To satisfy the hard delay constraint, it is necessary to transmit the symbol block when the remaining number of symbol blocks is equal to the remaining number of time slots, regardless of the channel quality. As such, the service rate of the symbol queue is given by
In each time slot, the threshold of the truncated channel inversion is intrinsically related to three parameters: , defined as the number of data packets concurrently encoded; k; and l. For a more concise expression, we abbreviate to .
Let denote the fixed receiver power. The average power for in a single time slot is defined as
The average power consumption of the system is given by
Based on Equations (4) and (17), the average power for in a single time slot is defined as
We assume in this equation without a loss of generality. To facilitate the computation of Equation (19), we propose the following two lemmas.
Lemma 1.
The integral expression satisfies
where we have
Proof.
Firstly, we consider the following integral expression:
Secondly, we prove the convergence of Equation (22) by considering two cases, i.e., and . For the case when ,
which proves there is convergence. When , we have
Therefore, the lemma is proved. ☐
Lemma 2.
The following equality holds, i.e.,
Here, is an arbitrary function of i.
Proof.
In this proof, we consider the following expression, which is equivalent to Equation (25):
Therefore, the lemma is proved. ☐
Theorem 1.
The average power across the optimal subchannel of parallel fading channels is expressed as
Remarkably, even when .
Proof.
Initially, we employ integration by parts to reshape the integral subject. Following this, the higher-order polynomial is expanded through the implementation of the binomial theorem, thereby facilitating its integration. Subsequently, Lemma 1 is invoked to substitute the associated integral expression. The ensuing expression post-integration is simplified utilizing Lemma 2. Finally, we utilize Lemma 1 to prove the convergence of Theorem 1.
Leveraging Equation (19), the average power over the optimal subchannel of parallel fading channels is expressed as
Next, we employ Lemma 2, where we define
In this way, we have
According to Lemma 1, we prove the convergence of Equation (30). At this point, the theorem is proved. ☐
By using Lemmas 1 and 2, the average power consumption is given in Theorem 1, which demonstrates that the average power consumption of a parallel fading channel is finite. Then, using Theorem 1, we show that the system can meet the hard delay constraint with finite power consumption with a Markov chain.
3.2. Embedded Markov Chain Model
In this finite blocklength coding system, we model the packet and symbol queues as a two-dimensional Markov chain, denoting the system state as . The transition probability of the two-dimensional Markov chain is derived from Equations (7) and (10). Fortunately, we observe that the evolution of the symbol queue, i.e., the transmission process of encoded symbols, is determined by the packet queue length, i.e., , when a new variable-length encoding process starts. Consequently, the two-dimensional Markov chain is transformed into an embedded Markov chain. In this embedded Markov chain, the packet queue length at the beginning of an encoding process becomes the sole system state, with the transmission process of encoded symbols embedded into the transition probabilities. In our previous work [37], we utilized a two-dimensional Markov chain as it was necessary to calculate the average delay of the system. However, in a system with a hard delay constraint, we only need to ensure that the maximum delay does not exceed the threshold. Therefore, we utilized a one-dimensional embedded Markov chain.
To facilitate understanding, Figure 3 illustrates the process of the embedded Markov chain. From a global perspective, incorporating all time slots, the system operates in a two-dimensional paradigm, constituted by the packet queue and the symbol queue. In Figure 3, the blue line represents the change in the packet queue, while the red line represents the change in the symbol queue. However, our focus is selectively directed towards time slots where the symbol queue is empty, as indicated by the red arrow. Then, we treat the packet queue as an embedded Markov chain. With the derived one-dimensional Markov chain, we can significantly reduce the complexity for the steady-state analysis and system performance optimization.
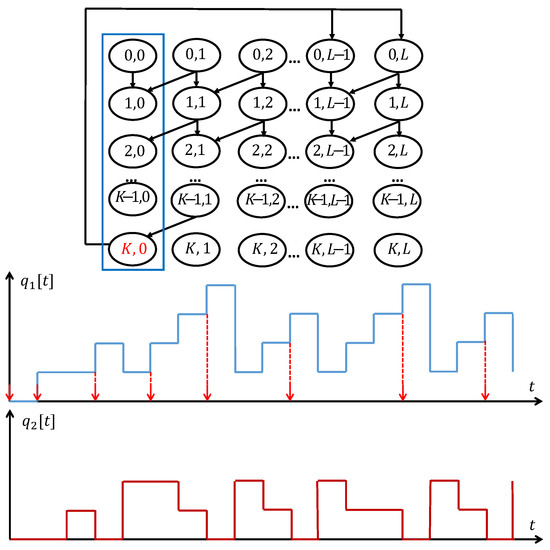
Figure 3.
Transition diagram of . The other queue states are similar to the transition diagram. The diagram also depicts the evolution of the system state over time slots. In the embedded Markov chain, we focus exclusively on the time slots indicated by the red arrows.
Theorem 2.
The packet queue having a maximum queue length and a delay-violation probability is a necessary and sufficient condition for satisfying the hard delay constraint in the system, defined as .
Proof.
Firstly, we demonstrate the sufficiency of the theorem. The given maximum length K of the packet queue and the delay-violation probability ensure that data packets can wait for at most K time slots in the packet queue. Additionally, the condition in the packet queue guarantees the transmission of symbols in the symbol queue within the specified delay constraint. Consequently, the hard delay constraint is satisfied, affirming the sufficiency of the theorem.
Subsequently, we establish the necessity of this through a proof by contradiction. To derive a contradiction, let us assume that the transmission of the symbol queue requires time slots while adhering to the hard delay constraint D. In this scenario, the accumulation of data packets in the packet queue surpasses the prescribed maximum length K, resulting in packet loss and a violation of the hard delay constraint. This contradiction highlights the necessity of the theorem. Therefore, the theorem is proved. ☐
Given the policy , we have . The steady-state distribution of this Markov chain is denoted as , which is expressed as
To ensure the normalization condition, the following equation holds:
where signifies the steady-state probability distribution of the embedded Markov chain and represents a -dimensional vector with all entries equal to one. Subsequently, we will derive the balance equation.
Lemma 3.
At the beginning of the k-th time slot, the probability distribution of the number of symbol blocks already transmitted, denoted by l, which are coded by ζ packets, is expressed as
where we have
Additionally, is defined as the set that contains all vectors obtained by selecting l positions in a k-dimensional all-zero vector and setting them to 1.
Proof.
This proof is conducted through induction on k. The primary approach involves deriving the probability distribution for each time slot sequentially, followed by mathematical induction to establish a general expression.
We define as the transmission probability in the k-th time slot, which represents the probability of successfully transmitting l symbols before the k-th time slot. These symbols are encoded from a set of data packets. The transmission probability is given by
We now proceed by induction. In the first time slot, we have
In the second time slot, we have
In the third time slot, we have
We define as the set that contains all vectors obtained by selecting l positions in a k-dimensional all-zero vector and setting them to 1, assuming the following equation holds for :
Based on Equation (42), we can derive the following expression
At this point, the mathematical induction proof is complete. As such, this lemma is proved. ☐
Theorem 3.
The transition probability is defined as
Then, the transition probability is calculated as
Proof.
In a finite blocklength coding system, data packets are encoded into symbol blocks. The probability of having transmitted symbol blocks within time slots is expressed as . The probability of transmitting the last symbol block in the -th time slot is expressed as . By multiplying these two probabilities, the lemma is then proven. ☐
Based on the transition probability presented in Theorem 3, we can derive the corresponding balance equation for the packet queue state . Thus, we obtain
where represents the transition matrix.
Our objective is to minimize the average power consumption of the system while adhering to hard delay constraints. To achieve this, we introduce the following theorem, which derives the average power consumption from the perspective of an embedded Markov chain.
Theorem 4.
The average power in the finite blocklength coding system is
Proof.
The average power consumption on the embedded Markov chain is given by
The average number of packets that appear on the embedded Markov chain is expressed as
In this finite blocklength coding system, there is one packet per time slot. Consequently, the average power consumption per packet is equal to the average power consumption per time slot. Through the division of the average power consumption across the embedded Markov chain by the corresponding average number of packets in this chain, we derive the average power consumption per time slot. ☐
In this section, we demonstrated the feasibility of achieving hard delay constraints with limited power. The embedded Markov chain is utilized to ensure the hard delay constraints are met. Furthermore, we also present the average power consumption.
4. A Heuristic Algorithm to Obtain the Hard Delay Constraint Policy
This section aims to achieve minimized power consumption while adhering to hard delay constraints.
4.1. Cross-Layer Optimization Problem
To design a truncated channel inversion policy, we formulate an optimization problem that aims to minimize the average power while satisfying the hard delay constraint. The problem is expressed as
where the vector is defined as a vector with all elements equal to one. In our previous work [37], we optimized the transmission rate and code blocklength. In this study, we focus on optimizing the transmission threshold of the fading channel.
The optimization problem (50) is a non-convex problem with multiple constraints, which makes it a significant challenge to solve. To overcome this, we transform the problem into an unconstrained optimization problem.
Theorem 5.
The problem (50) is equivalent to
where we have
In this equation, represents the cofactor of the i-th row and j-th column. If has no solution or any of its elements are less than zero, then the optimization problem has no solution.
Proof.
By introducing a matrix entirely composed of ones, we have
Subsequently, the following equation is derived:
We define
Then, we have
where represents the cofactor of the i-th row and j-th column. Then, we have
Up to this point, can be expressed as a function of . Consequently, the problem can be formulated as an unconstrained optimization problem. Then, the theorem is proved. ☐
4.2. The Heuristic Algorithm
The optimization variable in optimization problem (51) spans a total of dimensions. Given the non-convex nature of this high-dimensional optimization problem, finding an optimal solution poses a significant challenge with no readily available standard algorithm. To address this, we introduce a suboptimal heuristic algorithm to explore solutions to the truncated channel inversion policy. Subsequently, we leverage gradient descent, initializing the process with the suboptimal policy solution to iteratively refine and approach an optimal policy. Specifically, we propose the first heuristic algorithm, setting
Following this, we employ a one-dimensional exhaustive search policy to obtain a suboptimal solution to optimization problem (51). Utilizing this suboptimal policy as the initial point, we iteratively resolve the problem by employing both gradient descent and an exact line search method, as shown in Algorithm 1.
| Algorithm 1 Algorithm combining a heuristic algorithm and gradient descent approach |
|
When using the gradient descent algorithm, it is necessary to compute the derivative of with respect to . As such, we define
Based on this, we next formulate
where is the objective function of problem (51), i.e., the average transmission power in Theorem 4.
Next, we compute the derivative of with respect to . Firstly, the derivative of is
Secondly, we note that
under which we have
Thirdly, according to Equations (57) and (58), we can re-write as
where (excluding ) represents a sequence generated by permuting the order of elements v times. The set of all possible orderings of (excluding ) is denoted as . Similarly, (excluding ) denotes a sequence obtained by permuting the order of elements k times, and represents the set of all possible orderings of (excluding ). In this way,
Here, is the indicator function. Meanwhile, we have
where represents . As such, the derivative of with respect to is given by
Furthermore, the derivative of with respect to is given by
Consequently, we obtain the derivative of , i.e., the average power , as
Although the proposed algorithm is heuristic in nature, the simulation results demonstrate its superior performance. The algorithm shows a noticeable improvement over conventional transmission policies.
We introduce an improved policy for the proposed heuristic algorithm by considering different channel thresholds for different numbers of encoded data packets . Specifically, we propose the second heuristic algorithm, setting
Subsequently, we formulate a series of subproblems aimed at minimizing the average power components corresponding to different values of :
Using a similar method to Algorithm 1, we initialize the thresholds based on the solutions of the subproblems (76) and iteratively solve problem (51). In terms of numerical results, the proposed algorithm demonstrates a superior performance compared to other algorithms, especially when operating at a lower complexity.
The complexity of the first heuristic algorithm depends on the granularity of search, denoted as . Assuming as the search granularity, the complexity of the first heuristic algorithm is . The complexity of the second heuristic algorithm relates to the maximum length of the coded data packets and the search granularity, with the complexity . Algorithm 1 combines the complexities of either the first or second heuristic algorithm, plus the complexity of gradient descent. Assuming as the number of search steps in gradient descent, its complexity is . If Algorithm 1 starts from the solution obtained by the first heuristic algorithm, its complexity is .
5. Simulation Results
This section presents both theoretical and simulation results to validate our theoretical analysis and emphasize the effectiveness of the proposed policy for hard-delay-constrained communication. We examine a practical scenario in URLLC that leverages finite blocklength coding. For this scenario, we set the packet size to bits, the block error probability to , the power consumption per symbol to W, the channel bandwidth to Hz, the coherence time to s, and the noise spectral density of the Gaussian noise process to dBm.
Figure 4 illustrates the changes in average power consumption corresponding to the changes in the hard delay constraints. The red line represents the policy of Algorithm 1, which integrates both heuristic algorithms and gradient descent. The blue line corresponds to the first heuristic algorithm, while the pink line depicts the second heuristic algorithm. The black line signifies the maximum coding blocklength policy, which selectively initiates transmissions that are in proximity to the hard delay constraint, thereby maximizing the coding blocklength. The on-demand transmission policy, with a channel threshold set to zero, is denoted by the grey line. Both the heuristic algorithms and the maximum coding blocklength policy display non-smooth characteristics owing to inaccuracies in symbol block quantization. Notably, Algorithm 1 exhibits the best performance, substantiating the superiority of our proposed policy over baseline policies. Additionally, the excellent match between the theoretical and simulation results in the figure is noteworthy. It is important to highlight that as the hard delay constraint increases gradually, the average power consumption decreases. This is attributed to a larger hard delay constraint providing more flexibility in selecting transmission opportunities, allowing for the identification of time slots with superior channel quality for transmission and consequently leading to reduced power consumption.
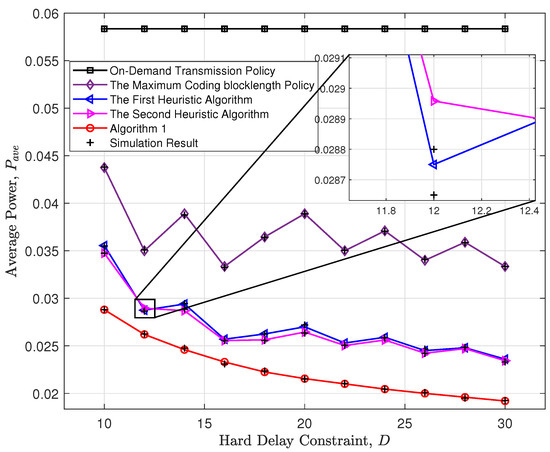
Figure 4.
The average power of the hard-delay-constrained policy, which changes with the hard delay constraint.
Figure 5 delineates the power consumption trend, using the first heuristic algorithm as the channel gain varies. We observe that as the channel gain threshold increases, the average power consumption first decreases and then increases. The declining trend arises as an increasing channel gain threshold in poor-quality channels allows for the avoidance of transmission, consequently saving power. However, as the channel gain threshold increases, the symbol block is eventually forced to transmit through any channel when reaching the upper limit of the hard delay constraint, disregarding channel quality. It is noteworthy that power consumption at a channel threshold of zero is higher than when the channel threshold is extremely high. A channel threshold equal to zero implies immediate transmission once symbols are encoded, resulting in a shorter coding blocklength. On the contrary, a high channel threshold demands waiting, potentially until the upper limit imposed by the hard delay constraint, before initiating transmission. In such cases, the coding blocklength is longer. Therefore, based on Equation (5), the power consumption at a zero channel threshold is higher than that at an extremely high channel threshold.
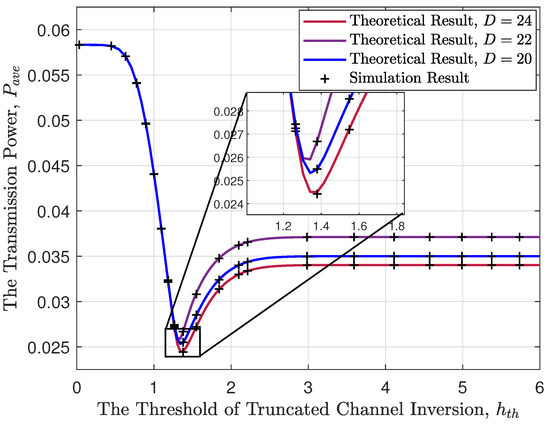
Figure 5.
The transmission power changes with the threshold of truncated inversion.
Figure 6 illustrates the performance of two heuristic algorithms as the upper limit of the hard delay constraint varies. With an increase in the hard delay constraint, the number of system states also increases, thereby slowing down the convergence of the gradient descent method. Thus, only the results of the heuristic algorithms are displayed. As observed, when the upper limit of the hard delay constraint increases, the average power consumption decreases. This phenomenon can be explained from two perspectives. Firstly, a higher hard delay constraint provides more time slots for transmission, enabling the selection of better-quality channels and, consequently, reducing power consumption. Secondly, with a high hard delay constraint, more data packets can be accumulated for transmission, resulting in a longer coding blocklength, further contributing to the reduction in power consumption.
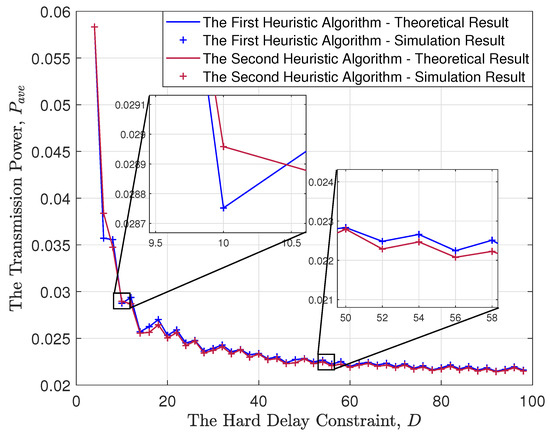
Figure 6.
A comparison between the first heuristic algorithm and the second heuristic algorithm.
Figure 7 depicts the change in average power consumption as a function of the iteration number of the gradient descent policy. As the iteration number increases, a deceleration in descent speed is observed, pointing to an eventual convergence. Notably, the rate of convergence of the gradient descent policy slows down with increases in the hard delay constraint. This slowdown can be attributed to the scale of the Markov chain states and the scale of the channel truncation threshold parameters. The increased number of parameters leads to a slower convergence rate. Consistent with the observations in Figure 4, Figure 7 also illustrates a gradual decrease in average power consumption with an increase in the hard delay constraint.
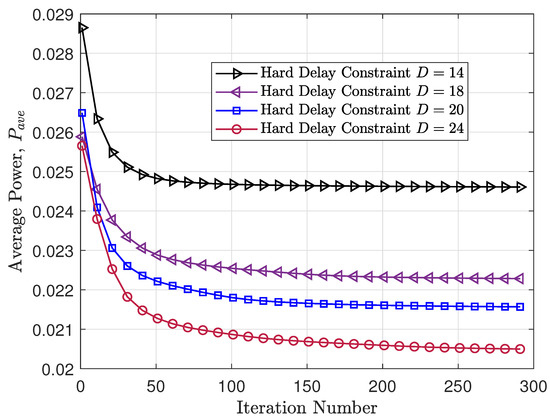
Figure 7.
The numerical result of the gradient descent policy, which changes with the iteration number.
Figure 8 illustrates the comparison of our presented scheme with the CSIT and the CSIR scheme in [18]. To clearly demonstrate the comparison between the two policies, we modified some simulation parameters. Here, we set the packet size to bits, the channel bandwidth to Hz, and the coherence time to s. Additionally, we showcase the performance of the CSIT scheme and the CSIR scheme under different block error probabilities. It is worth noting that in the CSIR scheme, channel inversion truncation is not required. Therefore, in this simulation, we set the maximum queue length equal to the maximum coding blocklength. In Figure 8, we observe that our presented CSIT scheme performs better when the hard delay constraint is relatively small. For instance, when the block error probability and the hard delay constraint , our presented CSIT scheme outperforms the CSIR scheme. Similarly, when the block error probability and the hard delay constraint , our presented CSIT scheme outperforms the CSIR scheme. Therefore, we find that as the block error probability decreases, the advantage interval of our presented CSIT scheme increases.
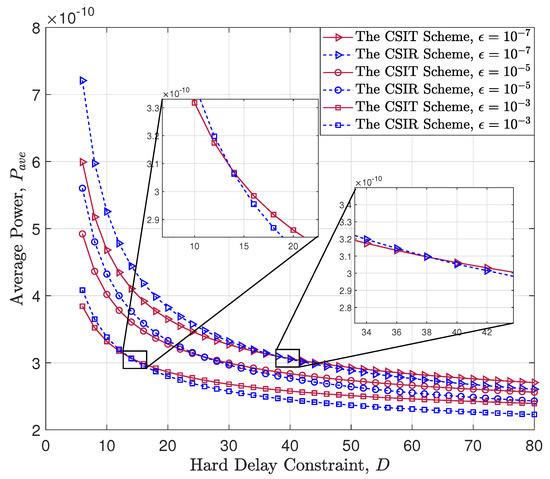
Figure 8.
A comparison of the CSIT and CSIR schemes.
6. Conclusions
Real-time transmissions in URLLC require the system to meet hard delay constraints. To address this, we put forth a cross-layer transmission leveraging variable-length coding and truncated channel inversion over parallel channels. In this way, we formulate the system as a two-dimensional Markov chain, where we have packet queue buffering bits poised for encoding and a symbol queue buffering encoded symbols set for transmission. By adopting the embedded Markov chain and focusing on instances when the symbol queue is empty, we simplify our derived Markov chain into a one-dimensional Markov chain, with the data queue length being the system state. Then, we propose an effective gradient descent-based algorithm to reduce the average power consumption, where a well-performing initial point is obtained by a heuristic algorithm. Moreover, a trade-off between the average power and the hard delay constraint is obtained. The numerical results show that our algorithm can meet the hard delay constraint and outperforms conventional algorithms.
Author Contributions
Conceptualization, W.C. and Y.-J.A.Z.; formal analysis, Y.L.; methodology, Y.L. and X.Z.; software, Y.L.; writing—original draft, Y.L.; writing—review and editing, X.Z., W.C., and Y.-J.A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant No. 62401140.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
References
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2019, 34, 134–142. [Google Scholar] [CrossRef]
- Popovski, P.; Chiariotti, F.; Huang, K.; Kalør, A.E.; Kountouris, M.; Pappas, N.; Soret, B. A Perspective on Time Toward Wireless 6G. Proc. IEEE 2022, 110, 1116–1146. [Google Scholar] [CrossRef]
- Durisi, G.; Koch, T.; Popovski, P. Toward Massive, Ultrareliable, and Low-Latency Wireless Communication With Short Packets. Proc. IEEE 2016, 104, 1711–1726. [Google Scholar] [CrossRef]
- Wang, C.C.; Chen, M. Sending Perishable Information: Coding Improves Delay-Constrained Throughput Even for Single Unicast. IEEE Trans. Inf. Theory 2017, 63, 252–279. [Google Scholar] [CrossRef]
- Lee, J.; Jindal, N. Energy-efficient scheduling of delay constrained traffic over fading channels. IEEE Trans. Wirel. Commun. 2009, 8, 1866–1875. [Google Scholar] [CrossRef]
- Li, C.; Chen, W.; Poor, H.V. Diversity Enabled Low-Latency Wireless Communications with Hard Delay Constraints. IEEE J. Sel. Areas Commun. 2023, 41, 2107–2122. [Google Scholar] [CrossRef]
- Li, X.; Dong, X.; Wu, D. On Optimal Power Control for Delay-Constrained Communication over Fading Channels. IEEE Trans. Inf. Theory 2011, 57, 3371–3389. [Google Scholar] [CrossRef]
- Li, R.; Gangammanavar, H.; Eryilmaz, A. Optimal Dynamic Coding-Window Selection for Serving Deadline-Constrained Traffic over Time-Varying Channels. IEEE Trans. Inf. Theory 2012, 58, 6556–6571. [Google Scholar] [CrossRef]
- Hou, I.H.; Kumar, P. Queueing systems with hard delay constraints: A framework for real-time communication over unreliable wireless channels. Queueing Syst. 2012, 71, 151–177. [Google Scholar] [CrossRef]
- Singh, R.; Hou, I.H.; Kumar, P.R. Fluctuation analysis of debt based policies for wireless networks with hard delay constraints. In Proceedings of the IEEE INFOCOM 2014—IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 2400–2408. [Google Scholar] [CrossRef]
- Zheng, Q.; Shin, K. On the ability of establishing real-time channels in point-to-point packet-switched networks. IEEE Trans. Commun. 1994, 42, 1096–1105. [Google Scholar] [CrossRef]
- Ewaisha, A.E.; Tepedelenlioğlu, C. Throughput Optimization in Multichannel Cognitive Radios With Hard-Deadline Constraints. IEEE Trans. Veh. Technol. 2016, 65, 2355–2368. [Google Scholar] [CrossRef]
- Zou, Z.; Soldati, P.; Zhang, H.; Johansson, M. Energy-Efficient Deadline-Constrained Maximum Reliability Forwarding in Lossy Networks. IEEE Trans. Wirel. Commun. 2012, 11, 3474–3483. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, A.; Wang, X. Joint Scheduling and Power Optimization for Delay Constrained Transmissions in Coded Caching over Wireless Fading Channels. IEEE Trans. Wirel. Commun. 2021, 21, 2093–2106. [Google Scholar] [CrossRef]
- Chen, M.H.; Dong, M.; Liang, B. Resource Sharing of a Computing Access Point for Multi-User Mobile Cloud Offloading with Delay Constraints. IEEE Trans. Mob. Comput. 2018, 17, 2868–2881. [Google Scholar] [CrossRef]
- Zhu, Y.; Bao, Y.; Li, B. On Maximizing Delay-Constrained Coverage of Urban Vehicular Networks. IEEE J. Sel. Areas Commun. 2012, 30, 804–817. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Poor, H.V.; Verdu, S. Channel Coding Rate in the Finite Blocklength Regime. IEEE Trans. Inf. Theory 2010, 56, 2307–2359. [Google Scholar] [CrossRef]
- Yang, W.; Durisi, G.; Koch, T.; Polyanskiy, Y. Block-Fading Channels at Finite Blocklength. In Proceedings of the IEEE International Symposium on Wireless Communication Systems, Ilmenau, Germany, 27–30 August 2013; pp. 1–4. [Google Scholar]
- Yang, W.; Durisi, G.; Koch, T.; Polyanskiy, Y. Quasi-Static Multiple-Antenna Fading Channels at Finite Blocklength. IEEE Trans. Inf. Theory 2014, 60, 4232–4265. [Google Scholar] [CrossRef]
- Collins, A.; Polyanskiy, Y. Coherent Multiple-Antenna Block-Fading Channels at Finite Blocklength. IEEE Trans. Inf. Theory 2018, 65, 380–405. [Google Scholar] [CrossRef]
- Ghanem, W.R.; Jamali, V.; Sun, Y.; Schober, R. Resource Allocation for Multi-User Downlink MISO OFDMA-URLLC Systems. IEEE Trans. Commun. 2020, 68, 7184–7200. [Google Scholar] [CrossRef]
- Trillingsgaard, K.F.; Popovski, P. Downlink Transmission of Short Packets: Framing and Control Information Revisited. IEEE Trans. Commun. 2017, 65, 2048–2061. [Google Scholar] [CrossRef]
- Sun, X.; Yan, S.; Yang, N.; Ding, Z.; Shen, C.; Zhong, Z. Short-Packet Downlink Transmission with Non-Orthogonal Multiple Access. IEEE Trans. Wirel. Commun. 2018, 17, 4550–4564. [Google Scholar] [CrossRef]
- Makki, B.; Svensson, T.; Caire, G.; Zorzi, M. Fast HARQ over Finite Blocklength Codes: A Technique for Low-Latency Reliable Communication. IEEE Trans. Wirel. Commun. 2018, 18, 194–209. [Google Scholar] [CrossRef]
- Shirvanimoghaddam, M.; Mohammadi, M.S.; Abbas, R.; Minja, A.; Yue, C.; Matuz, B.; Han, G.; Lin, Z.; Liu, W.; Li, Y.; et al. Short Block-Length Codes for Ultra-Reliable Low Latency Communications. IEEE Commun. Mag. 2018, 57, 130–137. [Google Scholar] [CrossRef]
- Erseghe, T. Coding in the Finite-Blocklength Regime: Bounds Based on Laplace Integrals and Their Asymptotic Approximations. IEEE Trans. Inf. Theory 2016, 62, 6854–6883. [Google Scholar] [CrossRef]
- Cheng, W.; Xiao, Y.; Zhang, S.; Wang, J. Adaptive Finite Blocklength for Ultra-Low Latency in Wireless Communications. IEEE Trans. Wirel. Commun. 2021, 21, 4450–4463. [Google Scholar] [CrossRef]
- Qiao, D.; Gursoy, M.C.; Velipasalar, S. Throughput-Delay Tradeoffs with Finite Blocklength Coding over Multiple Coherence Blocks. IEEE Trans. Commun. 2019, 67, 5892–5904. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Y.; Gursoy, M.C.; Velipasalar, S.; Schmeink, A. Throughput Analysis of Low-Latency IoT Systems with QoS Constraints and Finite Blocklength Codes. IEEE Trans. Veh. Technol. 2020, 69, 3093–3104. [Google Scholar] [CrossRef]
- Fu, X.; Guo, C.; Qu, Y.; Lin, X.H. Resource Allocation and Blocklength Selection for Low-Latency Vehicular Communications. IEEE Wirel. Commun. Lett. 2021, 10, 914–918. [Google Scholar] [CrossRef]
- Xu, Y.; Mao, Y.; Dizdar, O.; Clerckx, B. Rate-Splitting Multiple Access with Finite Blocklength for Short-Packet and Low-Latency Downlink Communications. IEEE Trans. Veh. Technol. 2022, 71, 12333–12337. [Google Scholar] [CrossRef]
- He, Q.; Zhu, Y.; Zheng, P.; Hu, Y.; Schmeink, A. Multi-Device Low-Latency IoT Networks with Blind Retransmissions in the Finite Blocklength Regime. IEEE Trans. Veh. Technol. 2021, 70, 12782–12795. [Google Scholar] [CrossRef]
- Makki, B.; Svensson, T.; Coldrey, M.; Alouini, M.S. Finite Block-Length Analysis of Large-But-Finite MIMO Systems. IEEE Wirel. Commun. Lett. 2019, 8, 113–116. [Google Scholar] [CrossRef]
- Kourtellaris, C.K.; Psomas, C.; Krikidis, I. Finite Blocklength Analysis of Multiple Access Channels with/without Cooperation. IEEE Trans. Commun. 2020, 68, 6317–6330. [Google Scholar] [CrossRef]
- Ozcan, G.; Gursoy, M.C. Throughput of Cognitive Radio Systems with Finite Blocklength Codes. IEEE J. Sel. Areas Commun. 2013, 31, 2541–2554. [Google Scholar] [CrossRef][Green Version]
- Williamson, A.R.; Chen, T.Y.; Wesel, R.D. Variable-Length Convolutional Coding for Short Blocklengths with Decision Feedback. IEEE Trans. Commun. 2015, 63, 2389–2403. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, X.; Chen, W.; Zhang, Y.J.A. A Buffer-Aware Finite Blocklength Coding Scheme for Low-Latency Energy-Efficient Communications. In Proceedings of the GLOBECOM 2022—2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 4734–4739. [Google Scholar] [CrossRef]
- Bennis, M.; Debbah, M.; Poor, H.V. Ultrareliable and Low-Latency Wireless Communication: Tail, Risk, and Scale. Proc. IEEE 2018, 106, 1834–1853. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).