Clustered Distributed Learning Exploiting Node Centrality and Residual Energy (CINE) in WSNs
Abstract
1. Introduction
- A clustering scheme for collaborative learning in WSNs that exploit the gossiping mechanism to exchange model parameters between clusters.
- The consideration of the machine learning capabilities, the residual energy, the centrality information, and the transmission power of the nodes to improve the fairness and speed up the convergence.
- An intelligent scheme to transmit data chunks from cluster heads to cluster members only when it is necessary to reduce the communication load, at the same time enhancing the collaborative learning.
2. Related Work
3. CINE Solution
3.1. Overview of CINE
| Algorithm 1 Protocol-Cluster Management |
|
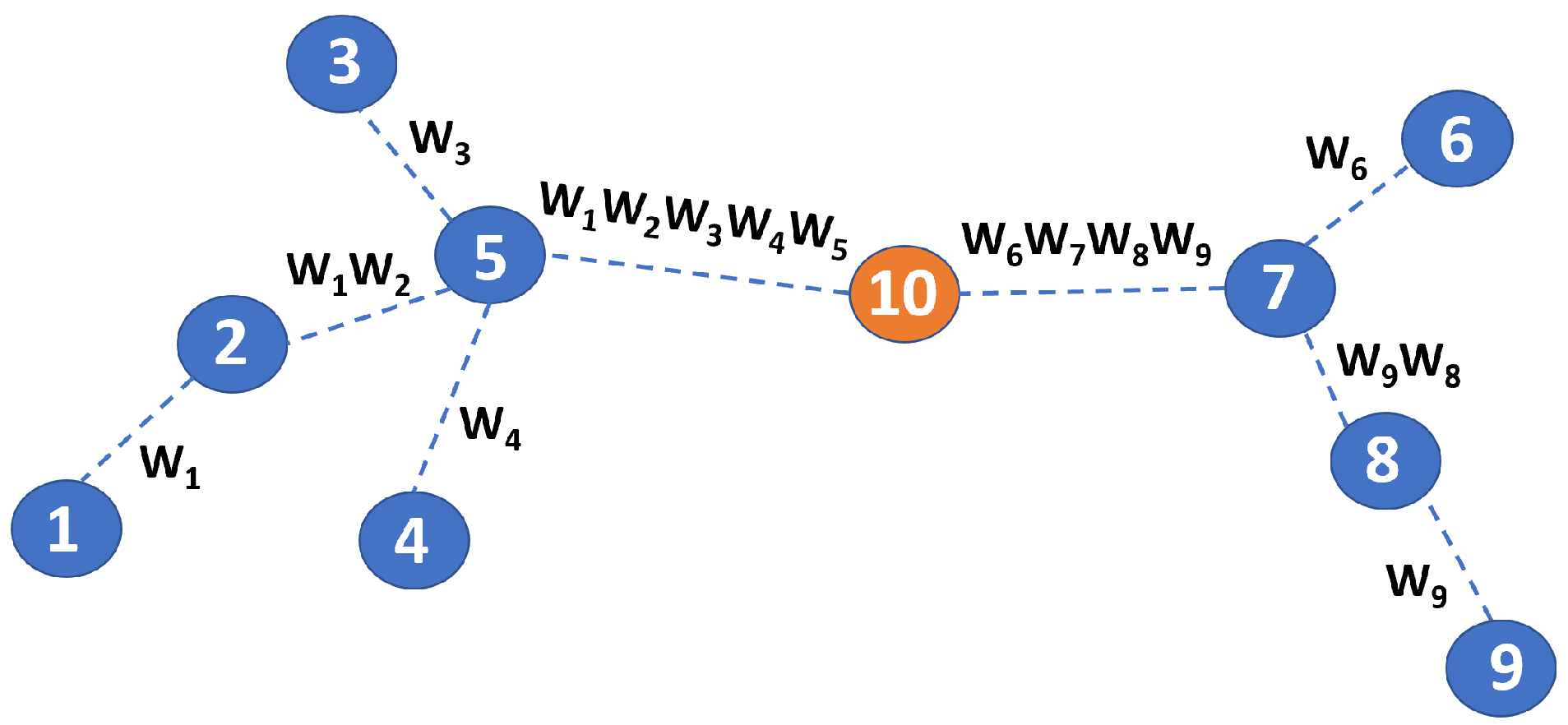
3.2. Centrality
3.3. Distributed Learning and Gossiping
- The low power TX mode, used when a node (either a CH or a simple CM) communicates with other nodes of the same cluster;
- The high power TX mode, used when a CH node communicates with other CH nodes in the CH-network.
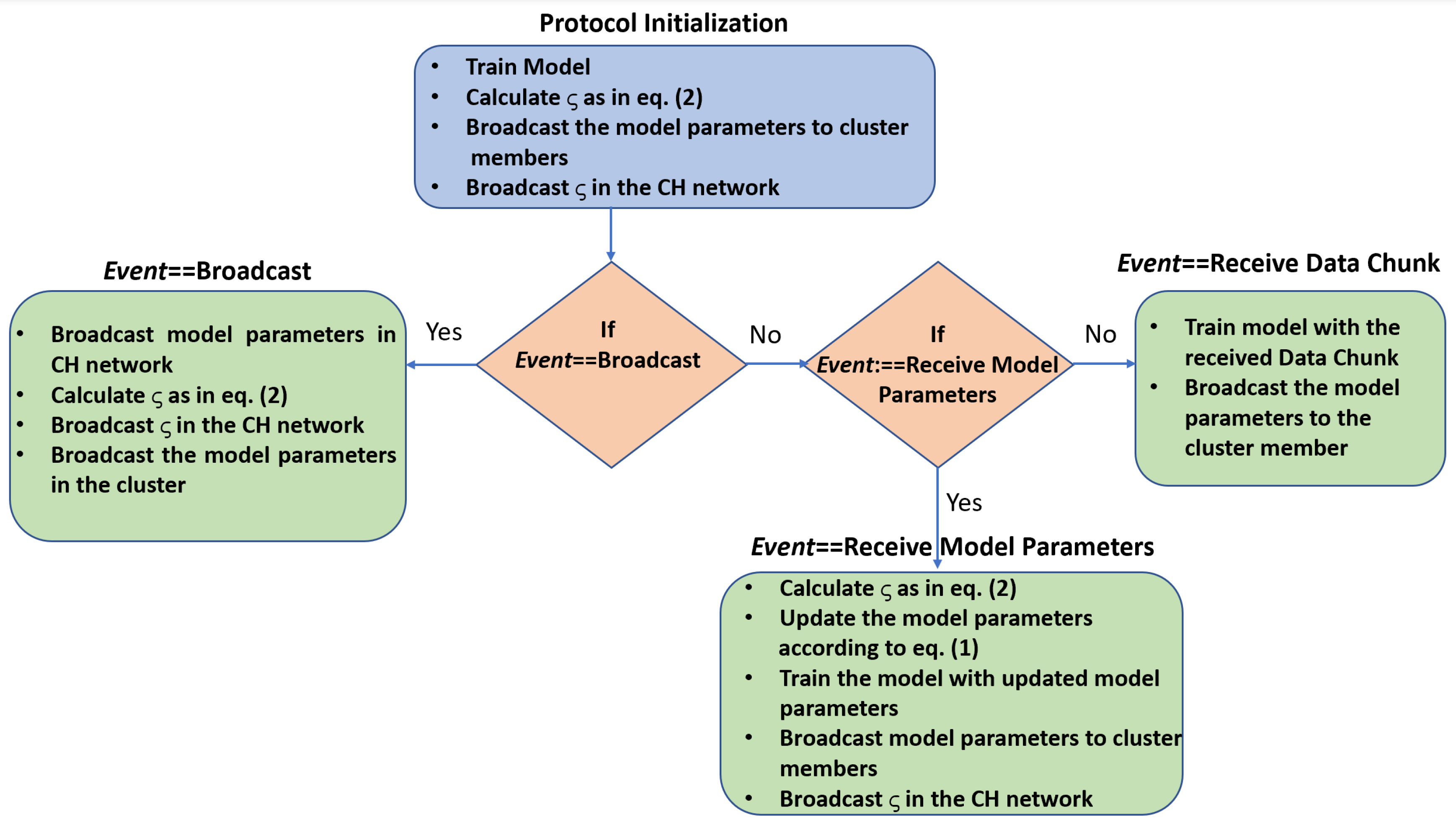
3.4. Protocol Details
| Algorithm 2 CINE Protocol-Cluster Head Functioning |
|
- Broadcast: The cluster head exhibiting the lowest penalty broadcasts its model parameters to both its cluster members and its neighboring CHs.
- Receive Model Parameters: upon receiving the model parameters by another cluster head (i.e., the one exhibiting the lowest penalty), the CH retrains the model.
- Receive Data Chunk: The CH that receives a chunk of data from a CM includes it in its local data set and retrains the model. In this way, the new model is representative of a more comprehensive data set.
4. Performance Evaluation
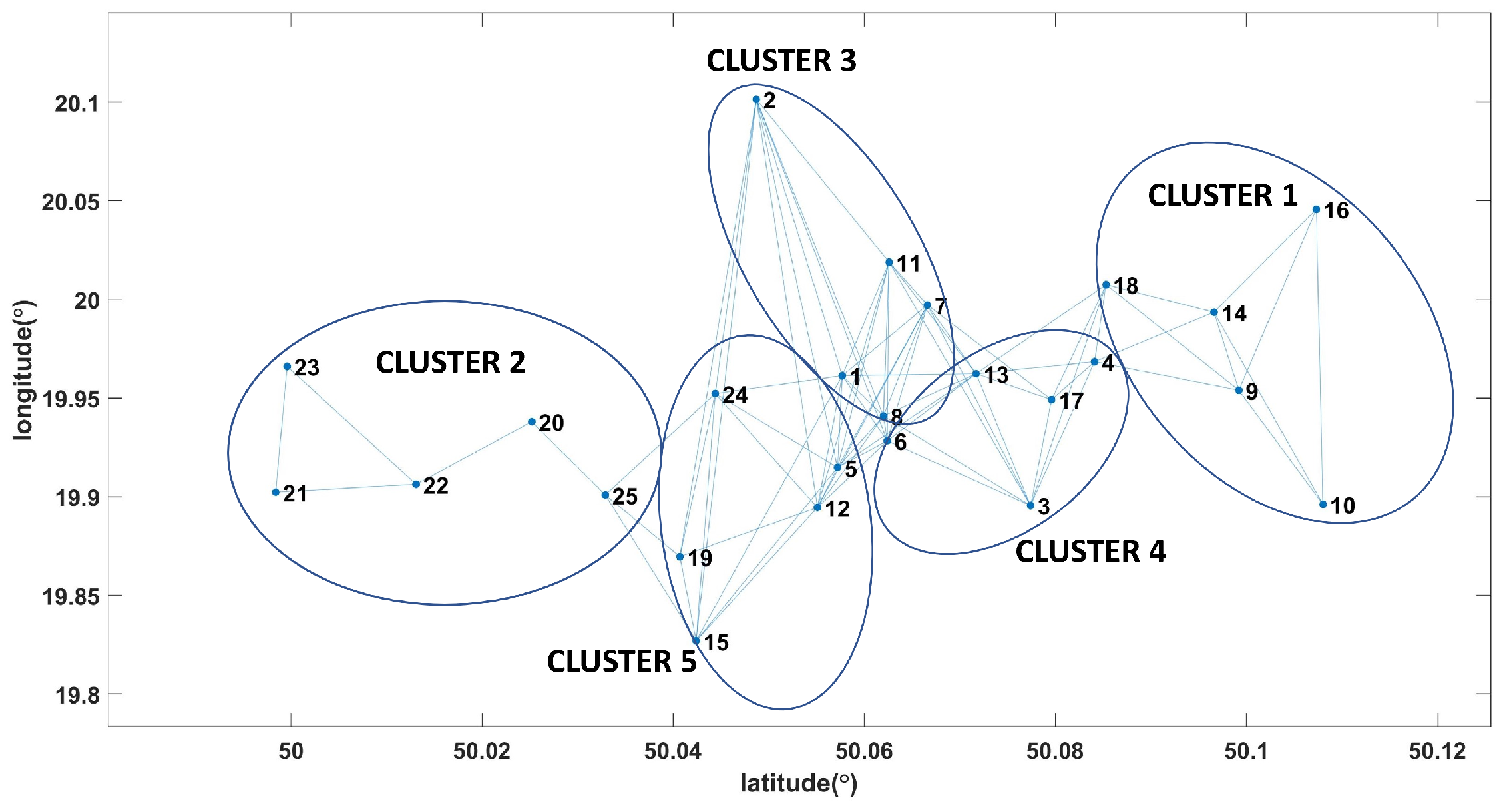
4.1. Simulation Scenario
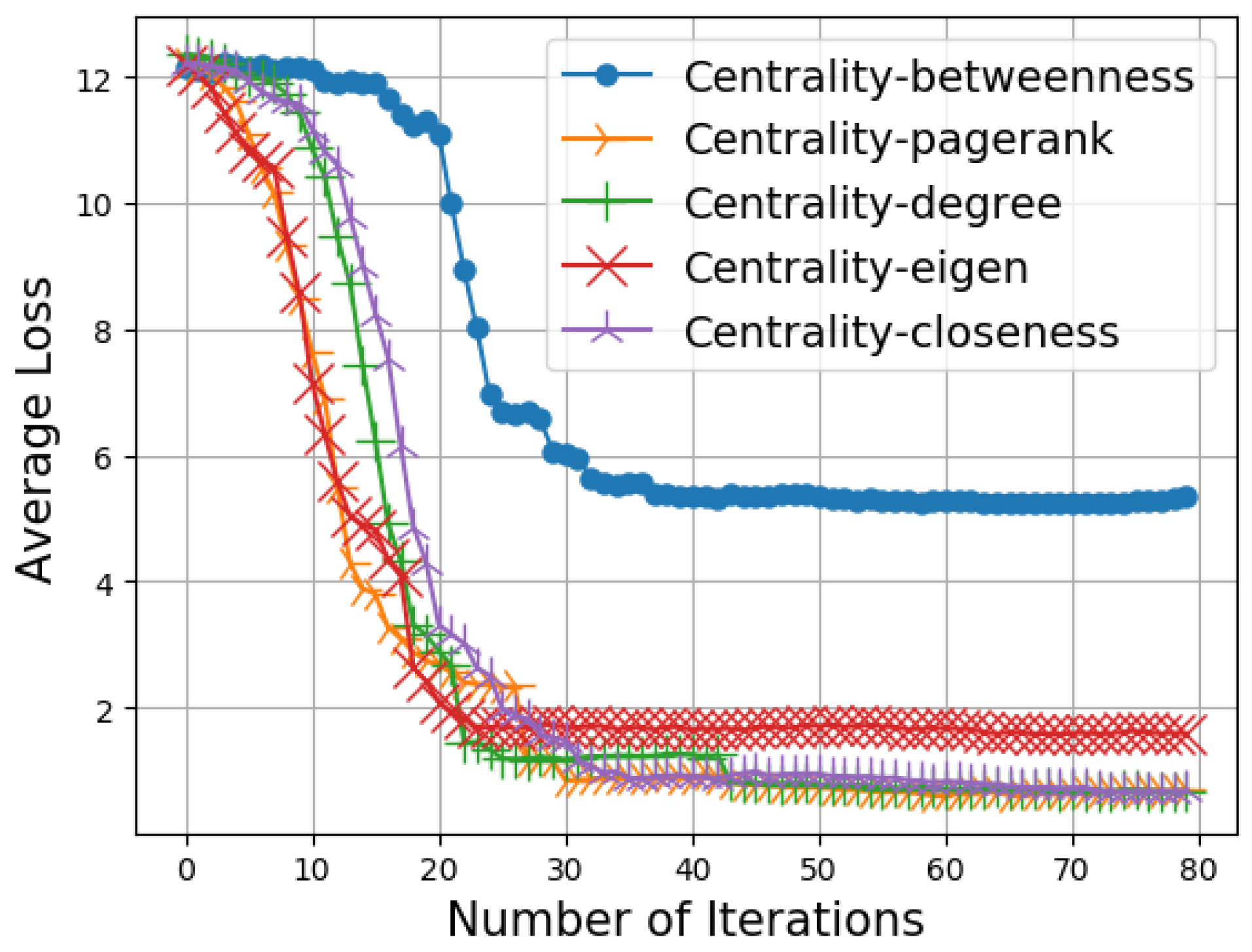
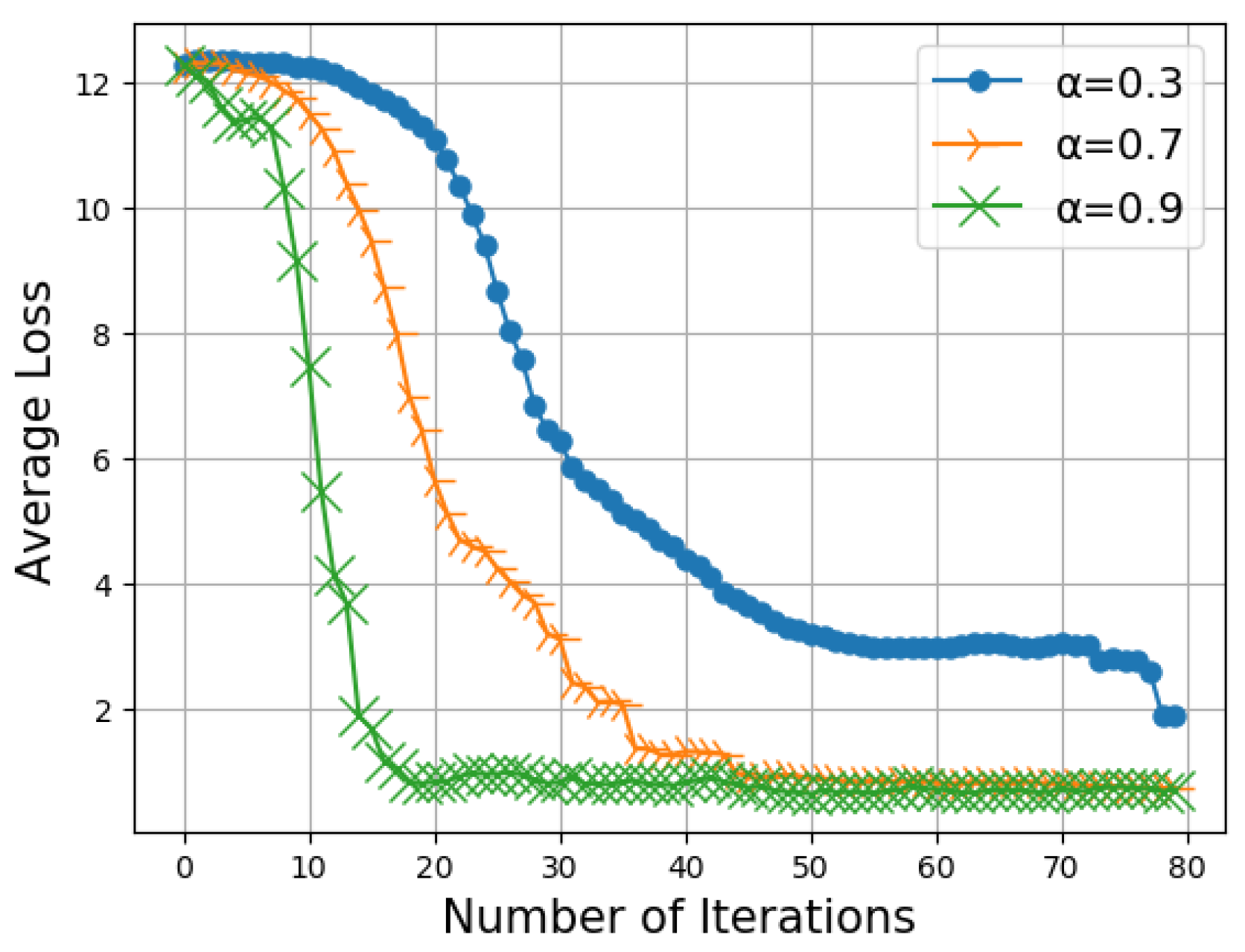
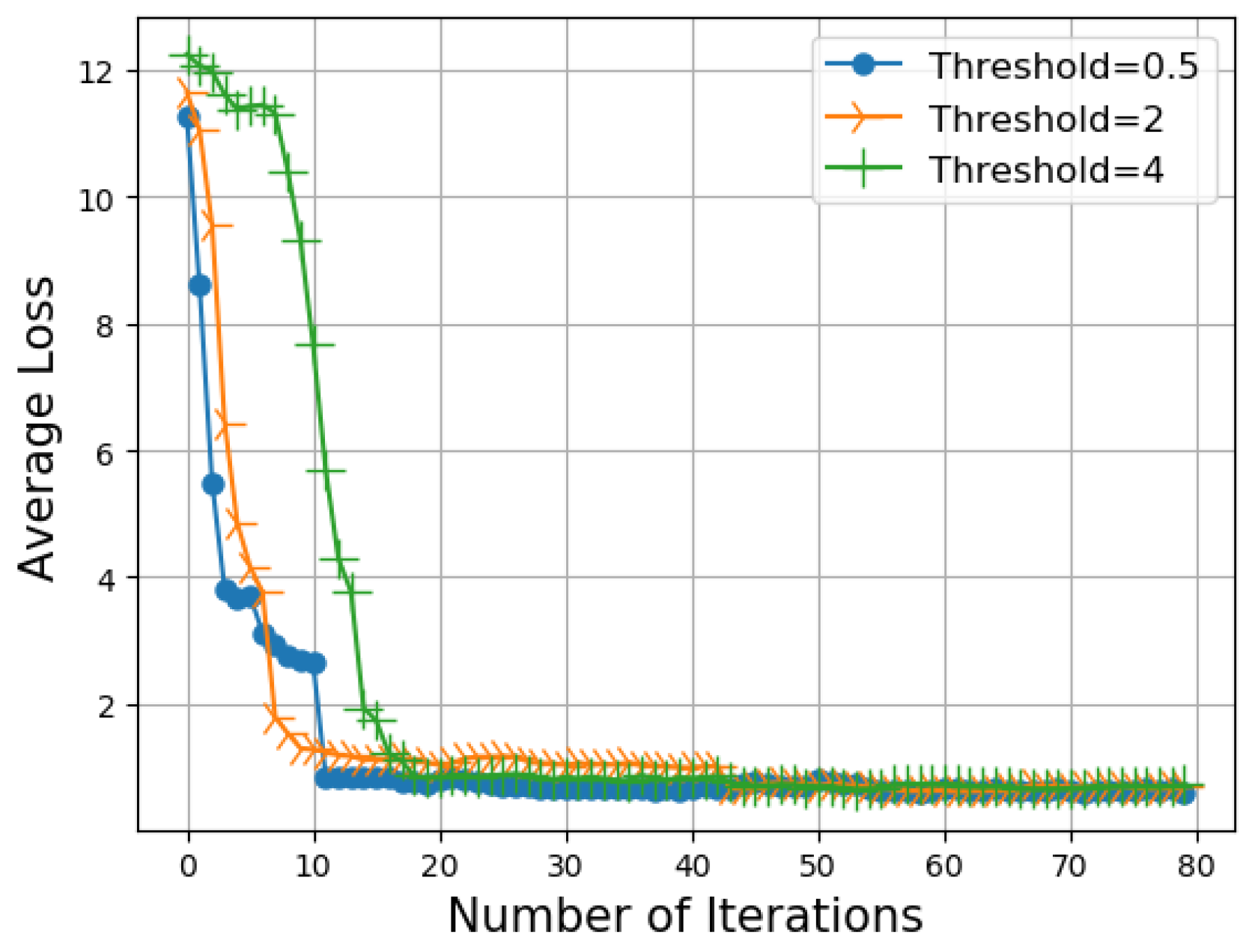
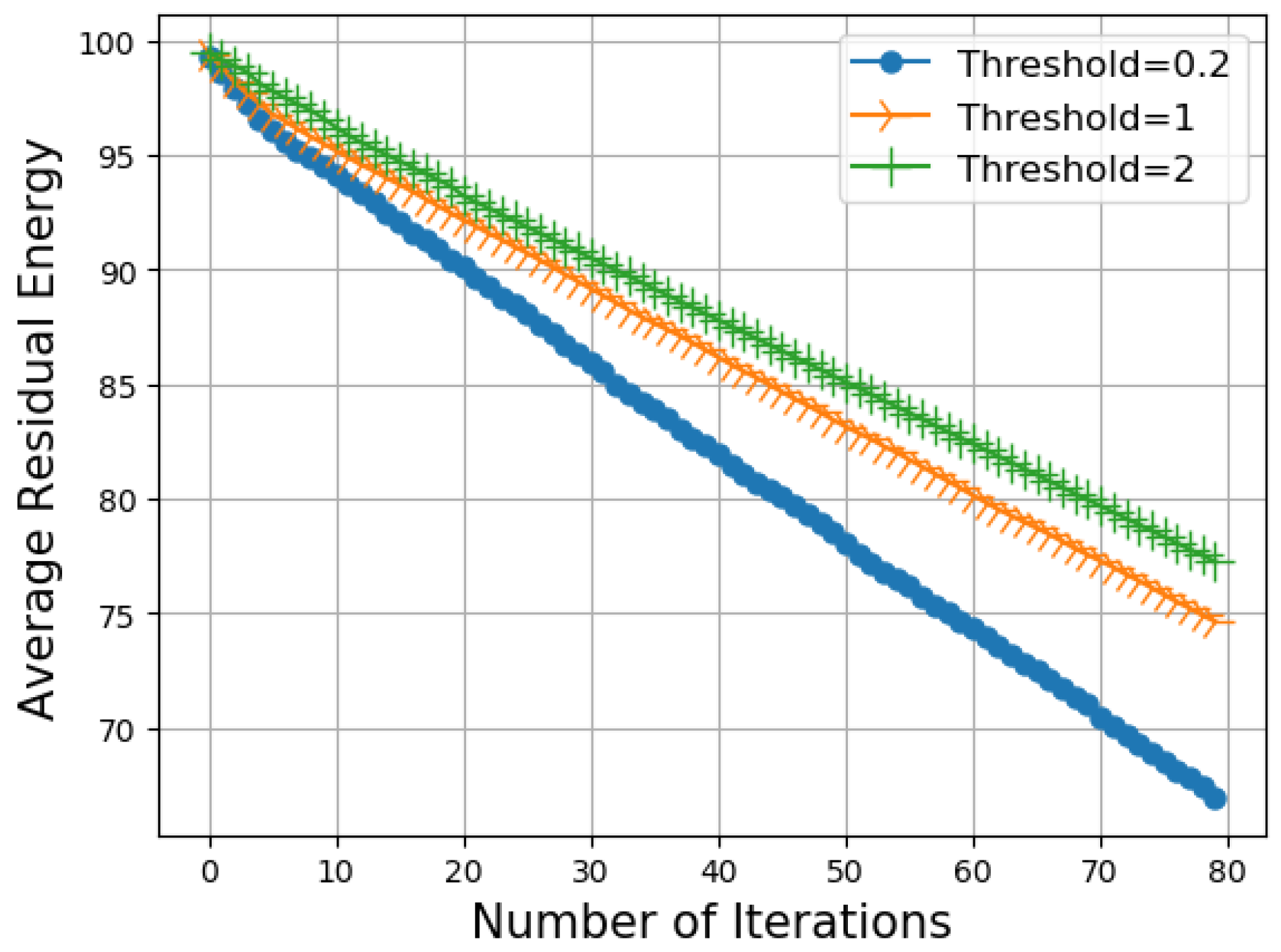
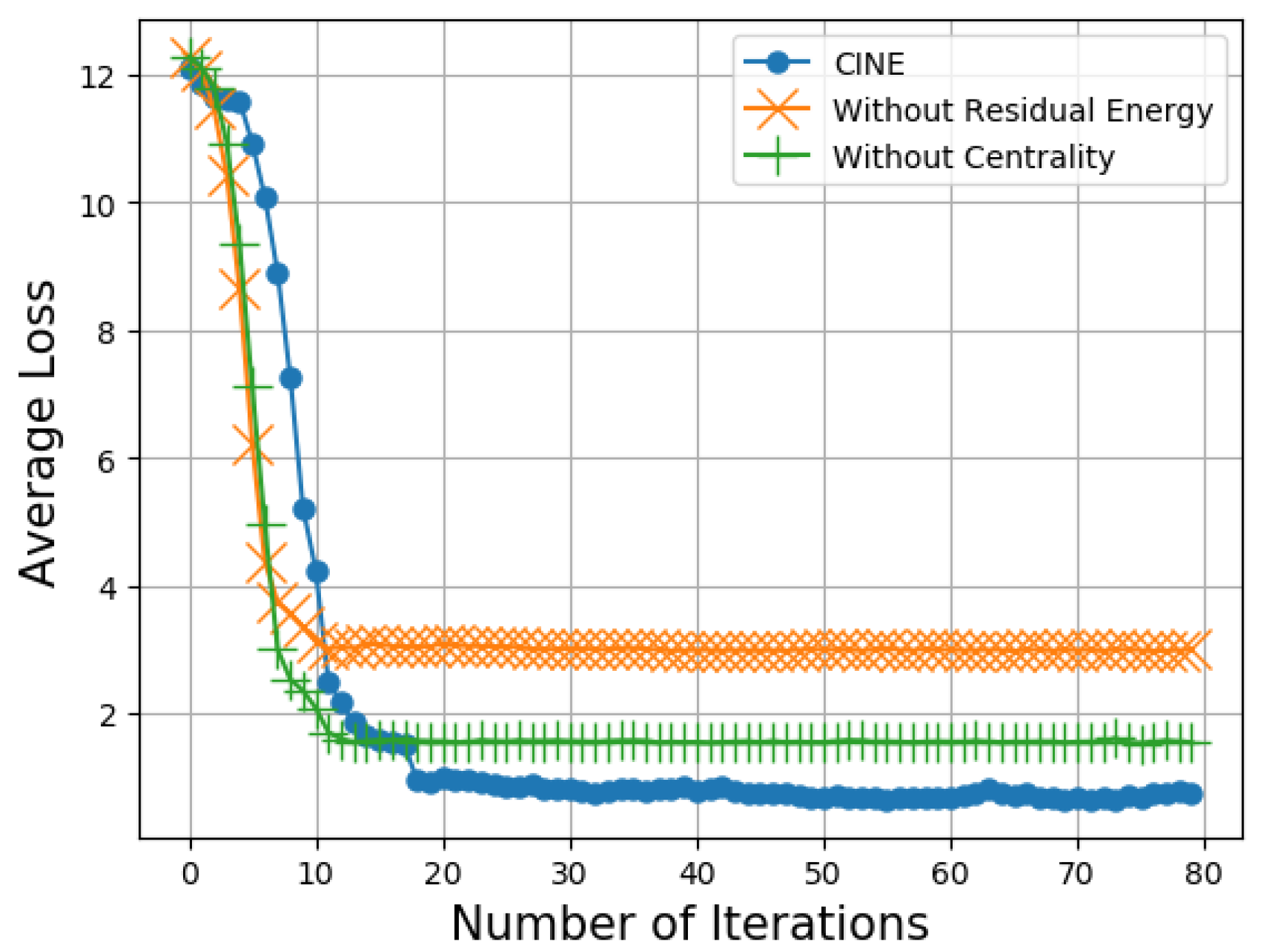
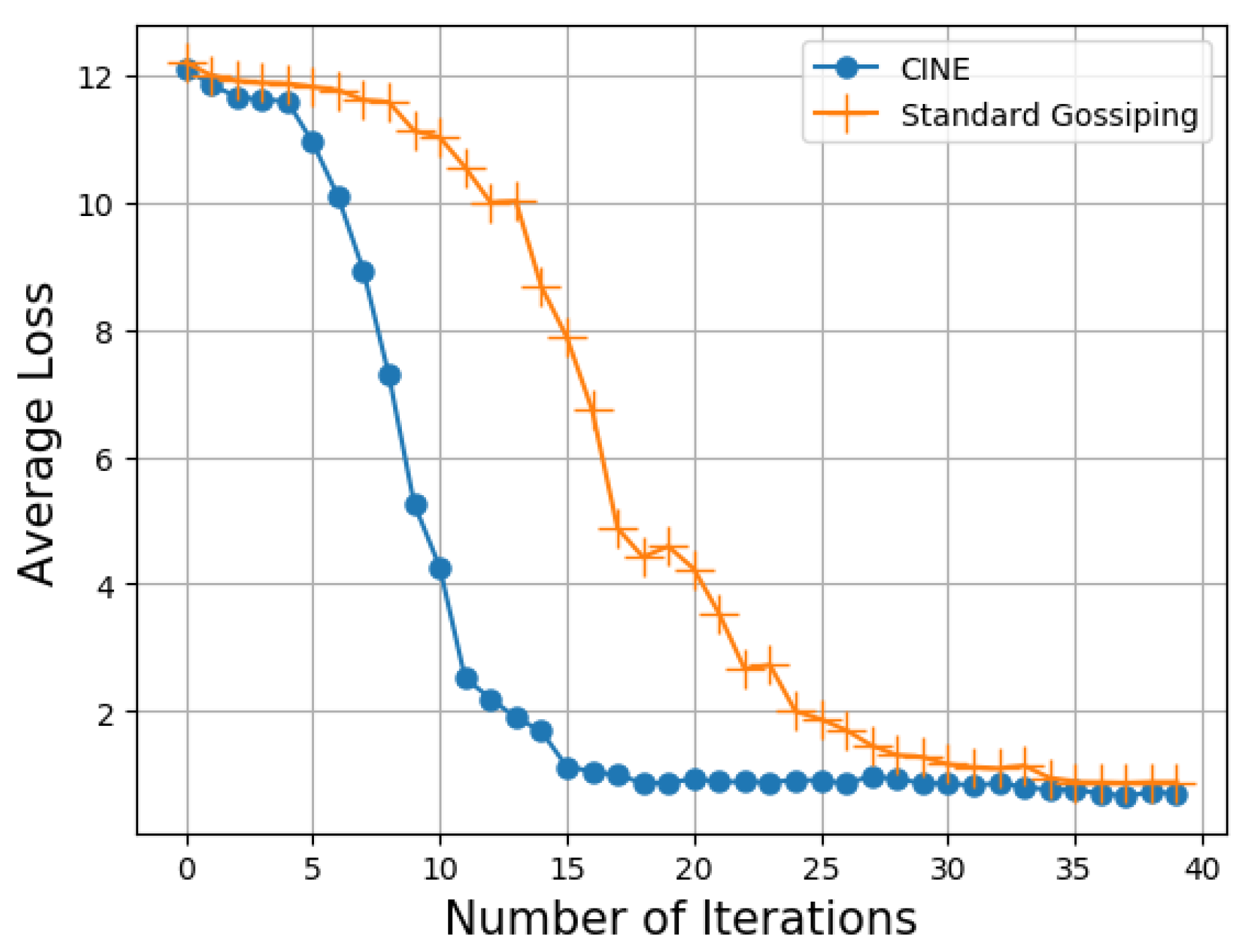
4.2. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alsheikh, M.A.; Lin, S.; Niyato, D.; Tan, H.P. Machine Learning in Wireless Sensor Networks: Algorithms, Strategies, and Applications. IEEE Commun. Surv. Tutor. 2014, 16, 1996–2018. [Google Scholar] [CrossRef]
- Peteiro-Barral, D.; Guijarro-Berdiñas, B. A survey of methods for distributed machine learning. Prog. Artif. Intell. 2013, 2, 1–11. [Google Scholar] [CrossRef]
- Predd, J.B.; Kulkarni, S.B.; Poor, H.V. Distributed learning in wireless sensor networks. IEEE Signal Process. Mag. 2006, 23, 56–69. [Google Scholar] [CrossRef]
- Danaee, A.; de Lamare, R.C.; Nascimento, V.H. Energy-efficient distributed learning with coarsely quantized signals. IEEE Signal Process. Lett. 2021, 28, 329–333. [Google Scholar] [CrossRef]
- Carpentiero, M.; Matta, V.; Sayed, A.H. Distributed Adaptive Learning under Communication Constraints. arXiv 2021, arXiv:2112.02129. [Google Scholar]
- Niknam, S.; Dhillon, H.S.; Reed, J.H. Federated Learning for Wireless Communications: Motivation, Opportunities, and Challenges. IEEE Commun. Mag. 2020, 58, 46–51. [Google Scholar] [CrossRef]
- Luo, B.; Li, X.; Wang, S.; Huang, J.; Tassiulas, L. Cost-Effective Federated Learning Design. arXiv 2020, arXiv:cs.LG/2012.08336. [Google Scholar]
- Sen, P. Funnelling Effect in Networks. In Proceedings of the International Conference on Complex Sciences, Shanghai, China, 23–25 February 2009. [Google Scholar]
- Dimakis, A.G.; Kar, S.; Moura, J.M.F.; Rabbat, M.G.; Scaglione, A. Gossip Algorithms for Distributed Signal Processing. Proc. IEEE 2010, 98, 1847–1864. [Google Scholar] [CrossRef]
- Shah, D. Gossip Algorithms. Found. Trends Netw. 2009, 3, 1–125. [Google Scholar] [CrossRef]
- Boyd, S.; Ghosh, A.; Prabhakar, B.; Shah, D. Randomized gossip algorithms. IEEE Trans. Inf. Theory 2006, 52, 2508–2530. [Google Scholar] [CrossRef]
- Kar, S.; Moura, J. Consensus-based detection in sensor networks: Topology optimization under practical constraints. In Proceedings of the 1st International Workshop on Information Theory in Sensor Networks, Santa Fe, NM, USA, 18–20 June 2007. [Google Scholar]
- Saligrama, V.; Alanyali, M.; Savas, O. Distributed Detection in Sensor Networks with Packet Losses and Finite Capacity Links. IEEE Trans. Signal Process. 2006, 54, 4118–4132. [Google Scholar] [CrossRef]
- Blot, M.; Picard, D.; Cord, M.; Thome, N. Gossip Training for Deep Learning. arXiv 2016, arXiv:cs.CV/1611.09726. Available online: http://xxx.lanl.gov/abs/1611.09726 (accessed on 13 March 2023).
- Daily, J.; Vishnu, A.; Siegel, C.; Warfel, T.; Amatya, V. GossipGraD: Scalable Deep Learning Using Gossip Communication Based Asynchronous Gradient Descent. arXiv 2018, arXiv:cs.DC/1803.05880. [Google Scholar]
- Mertens, J.S.; Galluccio, L.; Morabito, G. Federated learning through model gossiping in wireless sensor networks. In Proceedings of the 2021 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Bucharest, Romania, 24–28 May 2021. [Google Scholar]
- Mertens, J.S.; Galluccio, L.; Morabito, G. MGM-4-FL: Combining federated learning and model gossiping in WSNs. Comput. Netw. 2022, 214, 109144. [Google Scholar] [CrossRef]
- Mertens, J.S.; Galluccio, L.; Morabito, G. Centrality-aware gossiping for distributed learning in wireless sensor networks. In Proceedings of the 2022 IFIP Networking Conference (IFIP Networking), Catania, Italy, 13–16 June 2022. [Google Scholar]
- Lalitha, A.; Kilinc, O.C.; Javidi, T.; Koushanfar, F. Peer-to-Peer Federated Learning on Graphs. arXiv 2019, arXiv:cs.LG/1901.11173. [Google Scholar]
- Savazzi, S.; Nicoli, M.; Rampa, V. Federated Learning With Cooperating Devices: A Consensus Approach for Massive IoT Networks. IEEE Internet Things J. 2020, 7, 4641–4654. [Google Scholar] [CrossRef]
- Dokic, K.; Martinovic, M.; Mandusic, D. Inference Speed and Quantisation of Neural Networks with TensorFlow Lite for Microcontrollers Framework. In Proceedings of the 2020 5th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Corfu, Greece, 25–27 September 2020; pp. 1–6. Available online: https://doi.org/10.1109/SEEDA-CECNSM49515.2020.9221846 (accessed on 12 March 2023).
- Briggs, C.; Fan, Z.; Andras, P. Federated Learning with Hierarchical Clustering of Local Updates to Improve Training on Non-IID Data. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Ouyang, X.; Xie, Z.; Zhou, J.; Huang, J.; Xing, G. ClusterFL: A Similarity-Aware Federated Learning System for Human Activity Recognition. In Proceedings of the MobiSys ’21: 19th Annual International Conference on Mobile Systems, Applications, and Services, Virtual, 24 June–2 July 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 54–66. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Z.; Zhou, Y.; Kailkhura, B. FedCluster: Boosting the Convergence of Federated Learning via Cluster-Cycling. In Proceedings of the 2020 IEEE International Conference on Big Data, Atlanta, GA, USA, 10–13 December 2020; pp. 5017–5026. [Google Scholar] [CrossRef]
- Sattler, F.; Müller, K.R.; Samek, W. Clustered Federated Learning: Model-Agnostic Distributed Multitask Optimization Under Privacy Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3710–3722. [Google Scholar] [CrossRef]
- Al-Sulaifani, A.I.; Al-Sulaifani, B.K.; Biswas, S. Recent trends in clustering algorithms for wireless sensor networks: A comprehensive review. Comput. Commun. 2022, 191, 395–424. [Google Scholar] [CrossRef]
- Jiang, X.; Camp, T. A Review of Geocasting Protocols for a Mobile ad Hoc Network. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=7a515b48994384dd95439cbc4d4584af993b2a49 (accessed on 12 March 2023).
- Gupta, I.; Riordan, D.; Sampalli, S. Cluster-head election using fuzzy logic for wireless sensor networks. In Proceedings of the 3rd Annual Communication Networks and Services Research Conference (CNSR’05), Halifax, NS, Canada, 16–18 May 2005. [Google Scholar] [CrossRef]
- Aditya, V.; Dhuli, S.; Sashrika, P.L.; Shivani, K.K.; Jayanth, T. Closeness centrality Based cluster-head selection Algorithm for Large Scale WSNs. In Proceedings of the 2020 12th International Conference on Computational Intelligence and Communication Networks (CICN), Bhimtal, India, 25–26 September 2020; pp. 107–111. [Google Scholar] [CrossRef]
- Oliveira, E.M.R.; Ramos, H.S.; Loureiro, A.A.F. Centrality-based routing for Wireless Sensor Networks. In Proceedings of the 2010 IFIP Wireless Days, Venice, Italy, 20–22 October 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Jain, A. betweenness centrality Based Connectivity Aware Routing Algorithm for Prolonging Network Lifetime in Wireless Sensor Networks. Wirel. Netw. 2016, 22, 1605–1624. [Google Scholar] [CrossRef]
- Jain, A.; Reddy, B. Node centrality in wireless sensor networks: Importance, applications and advances. In Proceedings of the 2013 3rd IEEE International Advance Computing Conference (IACC), Ghaziabad, India, 22–23 February 2013; pp. 127–131. [Google Scholar] [CrossRef]
- Katz, L. A New Status Index Derived from Sociometric Analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, Y.; Zhao, K.; Tian, Y. A comprehensive survey of loss functions in machine learning. Ann. Data Sci. 2022, 9, 187–212. [Google Scholar] [CrossRef]
- Bonettini, N.; Gonano, C.A.; Bestagini, P.; Marcon, M.; Garavelli, B.; Tubaro, S. Comparing AutoEncoder Variants for Real-Time Denoising of Hyperspectral X-ray. IEEE Sens. J. 2022, 22, 17997–18007. [Google Scholar] [CrossRef]
- Slavic, G.; Baydoun, M.; Campo, D.; Marcenaro, L.; Regazzoni, C. Multilevel Anomaly Detection Through Variational Autoencoders and Bayesian Models for Self-Aware Embodied Agents. IEEE Trans. Multimed. 2022, 24, 1399–1414. [Google Scholar] [CrossRef]
- Aygun, R.C.; Yavuz, A.G. Network Anomaly Detection with Stochastically Improved Autoencoder Based Models. In Proceedings of the 2017 IEEE 4th International Conference on Cyber Security and Cloud Computing (CSCloud), New York, NY, USA, 26–28 June 2017; pp. 193–198. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Chow, J.K.; Su, Z.; Wu, J.; Tan, P.S.; Mao, X.; Wang, Y.H. Anomaly detection of defects on concrete structures with the convolutional autoencoder. Elsevier Adv. Eng. Informatics 2020, 45, 101105. [Google Scholar] [CrossRef]
- Azarang, A.; Manoochehri, H.E.; Kehtarnavaz, N. Convolutional Autoencoder-Based Multispectral Image Fusion. IEEE Access 2019, 7, 35673–35683. [Google Scholar] [CrossRef]
- Chun, C.; Jeon, K.M.; Kim, T.; Choi, W. Drone Noise Reduction using Deep Convolutional Autoencoder for UAV Acoustic Sensor Networks. In Proceedings of the 2019 IEEE 16th International Conference on Mobile Ad Hoc and Sensor Systems Workshops (MASSW), Monterey, CA, USA, 4–7 November 2019; pp. 168–169. [Google Scholar] [CrossRef]
- Lee, H.; Kim, J.; Kim, B.; Kim, S. Convolutional Autoencoder Based Feature Extraction in Radar Data Analysis. In Proceedings of the 2018 Joint 10th International Conference on Soft Computing and Intelligent Systems (SCIS) and 19th International Symposium on Advanced Intelligent Systems (ISIS), Toyama, Japan, 5–8 December 2018; pp. 81–84. [Google Scholar] [CrossRef]
- Ping, Y.H.; Lin, P.C. Cell Outage Detection using Deep Convolutional Autoencoder in Mobile Communication Networks. In Proceedings of the 2020 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Auckland, New Zealand, 7–10 December 2020; pp. 1557–1560. [Google Scholar]
- Øvrebekk, T. The Importance of Average Power Consumption to Battery Life. 2020. Available online: https://blog.nordicsemi.com/getconnected/the-importance-of-average-power-consumption-to-battery-life (accessed on 12 April 2023).
- Liando, J.C.; Gamage, A.; Tengourtius, A.W.; Li, M. Known and Unknown Facts of LoRa: Experiences from a Large-Scale Measurement Study. ACM Trans. Sen. Netw. 2019, 15, 1–35. [Google Scholar] [CrossRef]
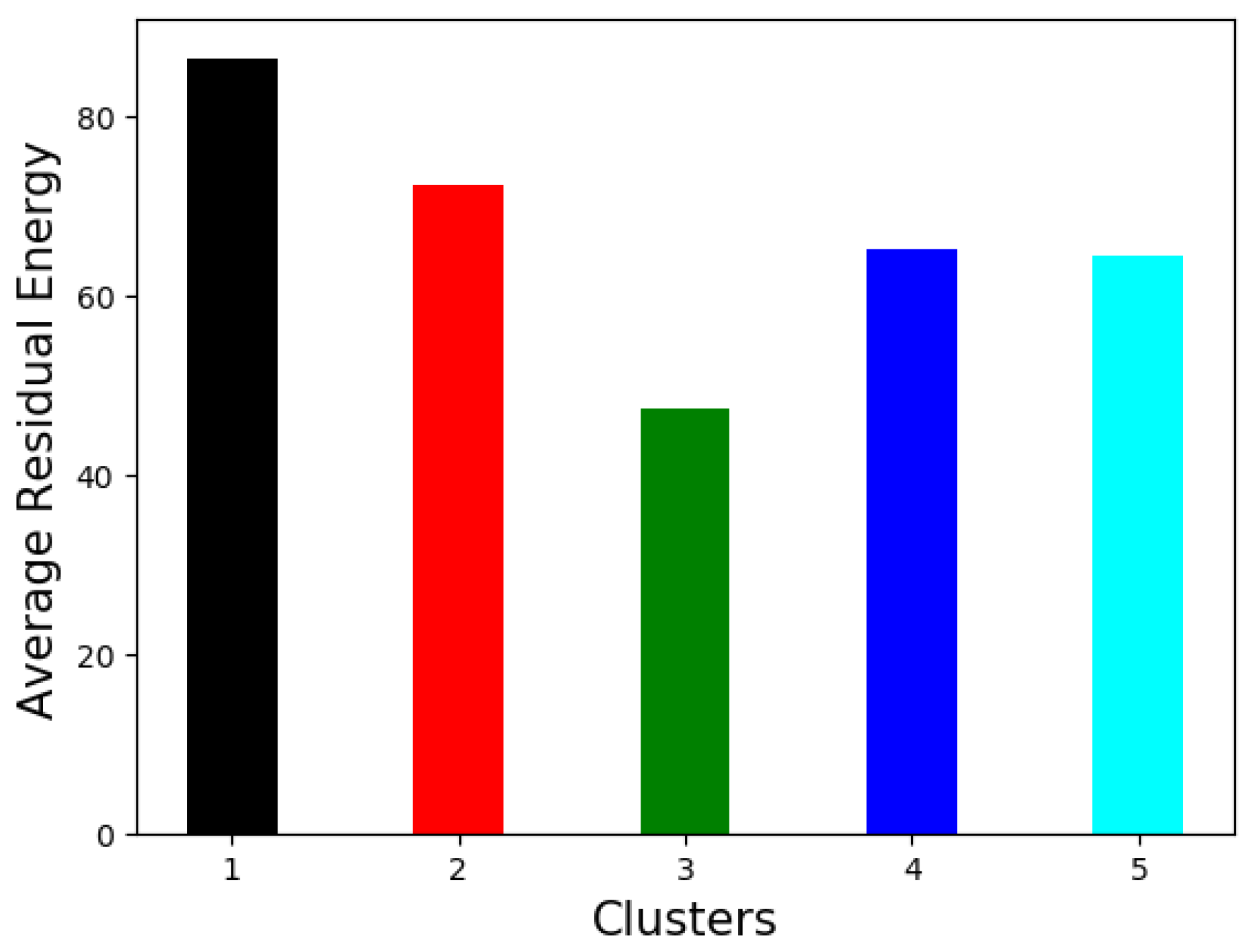

| Cluster | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| avg. | 84.18 | 72.36 | 46.13 | 66.53 | 68.06 |
| std. | 3.31 | 3.62 | 16.52 | 10.09 | 5.18 |
| std. (benchmark) | 4.82 | 7.29 | 20.08 | 16.65 | 8.32 |
| Threshold | Average Data Chunk Transmissions |
|---|---|
| 0.5 | 4.68 |
| 1 | 2.72 |
| 1.5 | 1.92 |
| 2 | 0.32 |
| 2.5 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galluccio, L.; Mertens, J.S.; Morabito, G. Clustered Distributed Learning Exploiting Node Centrality and Residual Energy (CINE) in WSNs. Network 2023, 3, 253-268. https://doi.org/10.3390/network3020013
Galluccio L, Mertens JS, Morabito G. Clustered Distributed Learning Exploiting Node Centrality and Residual Energy (CINE) in WSNs. Network. 2023; 3(2):253-268. https://doi.org/10.3390/network3020013
Chicago/Turabian StyleGalluccio, Laura, Joannes Sam Mertens, and Giacomo Morabito. 2023. "Clustered Distributed Learning Exploiting Node Centrality and Residual Energy (CINE) in WSNs" Network 3, no. 2: 253-268. https://doi.org/10.3390/network3020013
APA StyleGalluccio, L., Mertens, J. S., & Morabito, G. (2023). Clustered Distributed Learning Exploiting Node Centrality and Residual Energy (CINE) in WSNs. Network, 3(2), 253-268. https://doi.org/10.3390/network3020013






