Role of Single-Ion Anisotropy in Stabilizing Higher-Order Skyrmion Crystals in D3d-Symmetric Magnets
Abstract
1. Introduction
2. Model and Method
3. Results
3.1. Zero Magnetic Field
3.2. Nonzero Magnetic Fields
3.2.1. Weak -Type and Easy-Axis Anisotropies
3.2.2. Weak -Type and Easy-Plane Anisotropies
3.2.3. Strong -Type and Easy-Axis Anisotropies
3.2.4. Strong -Type and Easy-Plane Anisotropies
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Skyrme, T.H.R. A non-linear field theory. Proc. R. Soc 1961, 260, 127–138. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals: The mixed state of magnets. Zh. Eksp. Teor. Fiz 1989, 95, 178. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef] [PubMed]
- Kang, W.; Huang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Skyrmion-electronics: An overview and outlook. Proc. IEEE 2016, 104, 2040–2061. [Google Scholar] [CrossRef]
- Finocchio, G.; Büttner, F.; Tomasello, R.; Carpentieri, M.; Kläui, M. Magnetic skyrmions: From fundamental to applications. J. Phys. D Appl. Phys. 2016, 49, 423001. [Google Scholar] [CrossRef]
- Fert, A.; Reyren, N.; Cros, V. Magnetic skyrmions: Advances in physics and potential applications. Nat. Rev. Mater. 2017, 2, 17031. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.; Song, K.M.; Park, T.E.; Xia, J.; Ezawa, M.; Liu, X.; Zhao, W.; Zhao, G.; Woo, S. Skyrmion-electronics: Writing, deleting, reading and processing magnetic skyrmions toward spintronic applications. J. Phys. Condens. Matter 2020, 32, 143001. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Panagopoulos, C. Physical foundations and basic properties of magnetic skyrmions. Nat. Rev. Phys. 2020, 2, 492–498. [Google Scholar] [CrossRef]
- Tokura, Y.; Kanazawa, N. Magnetic Skyrmion Materials. Chem. Rev. 2021, 121, 2857–2897. [Google Scholar] [CrossRef] [PubMed]
- Reichhardt, C.; Reichhardt, C.J.O.; Milošević, M.V. Statics and dynamics of skyrmions interacting with disorder and nanostructures. Rev. Mod. Phys. 2022, 94, 035005. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the Kagomé Lattice: Chiral Spin State Based on A Ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Taguchi, Y.; Oohara, Y.; Yoshizawa, H.; Nagaosa, N.; Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 2001, 291, 2573–2576. [Google Scholar] [CrossRef]
- Tatara, G.; Kawamura, H. Chirality-driven anomalous Hall effect in weak coupling regime. J. Phys. Soc. Jpn. 2002, 71, 2613–2616. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef]
- Hamamoto, K.; Ezawa, M.; Nagaosa, N. Quantized topological Hall effect in skyrmion crystal. Phys. Rev. B 2015, 92, 115417. [Google Scholar] [CrossRef]
- Nakazawa, K.; Bibes, M.; Kohno, H. Topological Hall effect from strong to weak coupling. J. Phys. Soc. Jpn. 2018, 87, 033705. [Google Scholar] [CrossRef]
- Tai, L.; Dai, B.; Li, J.; Huang, H.; Chong, S.K.; Wong, K.L.; Zhang, H.; Zhang, P.; Deng, P.; Eckberg, C.; et al. Distinguishing the two-component anomalous Hall effect from the topological Hall effect. ACS Nano 2022, 16, 17336–17346. [Google Scholar] [CrossRef]
- Sampaio, J.; Cros, V.; Rohart, S.; Thiaville, A.; Fert, A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat. Nanotechnol. 2013, 8, 839–844. [Google Scholar] [CrossRef] [PubMed]
- Romming, N.; Hanneken, C.; Menzel, M.; Bickel, J.E.; Wolter, B.; von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Writing and deleting single magnetic skyrmions. Science 2013, 341, 636–639. [Google Scholar] [CrossRef]
- Osorio, S.A.; Sturla, M.B.; Rosales, H.D.; Cabra, D.C. Stability of skyrmions in perturbed ferromagnetic chiral magnets. Phys. Rev. B 2019, 99, 064439. [Google Scholar] [CrossRef]
- Wang, K.; Bheemarasetty, V.; Duan, J.; Zhou, S.; Xiao, G. Fundamental physics and applications of skyrmions: A review. J. Magn. Magn. Mater. 2022, 563, 169905. [Google Scholar] [CrossRef]
- Sarmiento, C.V.; Guimarães, A.P. Analysis of stability and transition dynamics of skyrmions and skyrmioniums in ferromagnetic nanodisks: A micromagnetic study at finite temperature. Phys. Rev. B 2024, 110, 064437. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A.; Aji, V. Theory of the Helical Spin Crystal: A Candidate for the Partially Ordered State of MnSi. Phys. Rev. Lett. 2006, 96, 207202. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A. Chirality induced anomalous-Hall effect in helical spin crystals. Phys. B Condens. Matter 2008, 403, 1336–1340. [Google Scholar] [CrossRef]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Adams, T.; Mühlbauer, S.; Pfleiderer, C.; Jonietz, F.; Bauer, A.; Neubauer, A.; Georgii, R.; Böni, P.; Keiderling, U.; Everschor, K.; et al. Long-Range Crystalline Nature of the Skyrmion Lattice in MnSi. Phys. Rev. Lett. 2011, 107, 217206. [Google Scholar] [CrossRef]
- Morikawa, D.; Shibata, K.; Kanazawa, N.; Yu, X.Z.; Tokura, Y. Crystal chirality and skyrmion helicity in MnSi and (Fe, Co)Si as determined by transmission electron microscopy. Phys. Rev. B 2013, 88, 024408. [Google Scholar] [CrossRef]
- Bauer, A.; Garst, M.; Pfleiderer, C. Specific Heat of the Skyrmion Lattice Phase and Field-Induced Tricritical Point in MnSi. Phys. Rev. Lett. 2013, 110, 177207. [Google Scholar] [CrossRef]
- Wilson, M.N.; Butenko, A.B.; Bogdanov, A.N.; Monchesky, T.L. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 2014, 89, 094411. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef]
- Adams, T.; Mühlbauer, S.; Neubauer, A.; Münzer, W.; Jonietz, F.; Georgii, R.; Pedersen, B.; Böni, P.; Rosch, A.; Pfleiderer, C. Skyrmion lattice domains in Fe1−xCoxSi. J. Phys. Conf. Ser. 2010, 200, 032001. [Google Scholar] [CrossRef]
- Münzer, W.; Neubauer, A.; Adams, T.; Mühlbauer, S.; Franz, C.; Jonietz, F.; Georgii, R.; Böni, P.; Pedersen, B.; Schmidt, M.; et al. Skyrmion lattice in the doped semiconductor Fe1−xCoxSi. Phys. Rev. B 2010, 81, 041203. [Google Scholar] [CrossRef]
- Bauer, A.; Garst, M.; Pfleiderer, C. History dependence of the magnetic properties of single-crystal Fe1−xCoxSi. Phys. Rev. B 2016, 93, 235144. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Lebech, B.; Bernhard, J.; Freltoft, T. Magnetic structures of cubic FeGe studied by small-angle neutron scattering. J. Phys. Condens. Matter 1989, 1, 6105. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef]
- Adams, T.; Chacon, A.; Wagner, M.; Bauer, A.; Brandl, G.; Pedersen, B.; Berger, H.; Lemmens, P.; Pfleiderer, C. Long-Wavelength Helimagnetic Order and Skyrmion Lattice Phase in Cu2OSeO3. Phys. Rev. Lett. 2012, 108, 237204. [Google Scholar] [CrossRef]
- Seki, S.; Kim, J.H.; Inosov, D.S.; Georgii, R.; Keimer, B.; Ishiwata, S.; Tokura, Y. Formation and rotation of skyrmion crystal in the chiral-lattice insulator Cu2OSeO3. Phys. Rev. B 2012, 85, 220406. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Ukleev, V.; Feoktystov, A.; Arima, T.h.; Kakurai, K.; Tokura, Y. Néel-Type Skyrmion Lattice in the Tetragonal Polar Magnet VOSe2O5. Phys. Rev. Lett. 2017, 119, 237201. [Google Scholar] [CrossRef]
- Kuo, T.W.; Chen, C.C.; Kakarla, D.C.; Tiwari, A.; Wang, C.W.; Gooch, M.; Deng, L.Z.; Chu, C.W.; Yang, H.D.; Wu, H.C. Enhanced Néel-type skyrmion stability in polar VOSe2O5 through tunable magnetic anisotropy under pressure. Phys. Rev. B 2025, 112, 024441. [Google Scholar] [CrossRef]
- Okubo, T.; Chung, S.; Kawamura, H. Multiple-q States and the Skyrmion Lattice of the Triangular-Lattice Heisenberg Antiferromagnet under Magnetic Fields. Phys. Rev. Lett. 2012, 108, 017206. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Kawamura, H. Frustration-induced skyrmion crystals in centrosymmetric magnets. J. Phys. Condens. Matter 2025, 37, 183004. [Google Scholar] [CrossRef]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Lin, S.Z.; Kamiya, Y.; Batista, C.D. Vortices, skyrmions, and chirality waves in frustrated Mott insulators with a quenched periodic array of impurities. Phys. Rev. B 2016, 94, 174420. [Google Scholar] [CrossRef]
- Utesov, O.I. Thermodynamically stable skyrmion lattice in a tetragonal frustrated antiferromagnet with dipolar interaction. Phys. Rev. B 2021, 103, 064414. [Google Scholar] [CrossRef]
- Utesov, O.I. Mean-field description of skyrmion lattice in hexagonal frustrated antiferromagnets. Phys. Rev. B 2022, 105, 054435. [Google Scholar] [CrossRef]
- Hayami, S. Skyrmion crystal and spiral phases in centrosymmetric bilayer magnets with staggered Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2022, 105, 014408. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Effective spin model in momentum space: Toward a systematic understanding of multiple-Q instability by momentum-resolved anisotropic exchange interactions. Phys. Rev. B 2022, 106, 174437. [Google Scholar] [CrossRef]
- Saha, S.R.; Sugawara, H.; Matsuda, T.D.; Sato, H.; Mallik, R.; Sampathkumaran, E.V. Magnetic anisotropy, first-order-like metamagnetic transitions, and large negative magnetoresistance in single-crystal Gd2PdSi3. Phys. Rev. B 1999, 60, 12162–12165. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.h.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef]
- Hirschberger, M.; Spitz, L.; Nomoto, T.; Kurumaji, T.; Gao, S.; Masell, J.; Nakajima, T.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; et al. Topological Nernst Effect of the Two-Dimensional Skyrmion Lattice. Phys. Rev. Lett. 2020, 125, 076602. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Iyer, K.K.; Paulose, P.L.; Sampathkumaran, E.V. Magnetic and transport anomalies in R2RhSi3(R=Gd, Tb, and Dy) resembling those of the exotic magnetic material Gd2PdSi3. Phys. Rev. B 2020, 101, 144440. [Google Scholar] [CrossRef]
- Spachmann, S.; Elghandour, A.; Frontzek, M.; Löser, W.; Klingeler, R. Magnetoelastic coupling and phases in the skyrmion lattice magnet Gd2PdSi3 discovered by high-resolution dilatometry. Phys. Rev. B 2021, 103, 184424. [Google Scholar] [CrossRef]
- Nakamura, S.; Kabeya, N.; Kobayashi, M.; Araki, K.; Katoh, K.; Ochiai, A. Spin trimer formation in the metallic compound Gd3Ru4Al12 with a distorted kagome lattice structure. Phys. Rev. B 2018, 98, 054410. [Google Scholar] [CrossRef]
- Hirschberger, M.; Nakajima, T.; Gao, S.; Peng, L.; Kikkawa, A.; Kurumaji, T.; Kriener, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; et al. Skyrmion phase and competing magnetic orders on a breathing kagome lattice. Nat. Commun. 2019, 10, 5831. [Google Scholar] [CrossRef]
- Hirschberger, M.; Hayami, S.; Tokura, Y. Nanometric skyrmion lattice from anisotropic exchange interactions in a centrosymmetric host. New J. Phys. 2021, 23, 023039. [Google Scholar] [CrossRef]
- Nakamura, S. Magnetic anisotropies and skyrmion lattice related to magnetic quadrupole interactions of the RKKY mechanism in the frustrated spin-trimer system Gd3Ru4Al12 with a breathing kagome structure. Phys. Rev. B 2025, 111, 184433. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444–449. [Google Scholar] [CrossRef]
- Matsuyama, N.; Nomura, T.; Imajo, S.; Nomoto, T.; Arita, R.; Sudo, K.; Kimata, M.; Khanh, N.D.; Takagi, R.; Tokura, Y.; et al. Quantum oscillations in the centrosymmetric skyrmion-hosting magnet GdRu2Si2. Phys. Rev. B 2023, 107, 104421. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Eremeev, S.; Glazkova, D.; Poelchen, G.; Kraiker, A.; Ali, K.; Tarasov, A.V.; Schulz, S.; Kliemt, K.; Chulkov, E.V.; Stolyarov, V.; et al. Insight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2. Nanoscale Adv. 2023, 5, 6678–6687. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, Y.; Ezawa, M. High-topological-number magnetic skyrmions and topologically protected dissipative structure. Phys. Rev. B 2016, 93, 024415. [Google Scholar] [CrossRef]
- Ozawa, R.; Hayami, S.; Motome, Y. Zero-Field Skyrmions with a High Topological Number in Itinerant Magnets. Phys. Rev. Lett. 2017, 118, 147205. [Google Scholar] [CrossRef] [PubMed]
- Amoroso, D.; Barone, P.; Picozzi, S. Spontaneous skyrmionic lattice from anisotropic symmetric exchange in a Ni-halide monolayer. Nat. Commun. 2020, 11, 5784. [Google Scholar] [CrossRef]
- Honda, S.; Tsuzuki, H.; Itoh, H.; Ohsawa, T. Magnetic structure of high-order skyrmion number produced in a nanodisk via micromagnetic simulation with long-range dipole-dipole interaction. Phys. Rev. B 2025, 112, 064417. [Google Scholar] [CrossRef]
- Hayami, S.; Okubo, T.; Motome, Y. Phase shift in skyrmion crystals. Nat. Commun. 2021, 12, 6927. [Google Scholar] [CrossRef]
- Eto, R.; Pohle, R.; Mochizuki, M. Low-Energy Excitations of Skyrmion Crystals in a Centrosymmetric Kondo-Lattice Magnet: Decoupled Spin-Charge Excitations and Nonreciprocity. Phys. Rev. Lett. 2022, 129, 017201. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M. Nonlinear nonreciprocal transport in antiferromagnets free from spin-orbit coupling. Phys. Rev. B 2022, 106, 014420. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Effect of magnetic anisotropy on skyrmions with a high topological number in itinerant magnets. Phys. Rev. B 2019, 99, 094420. [Google Scholar] [CrossRef]
- Hayami, S. Multiple-Q magnetism by anisotropic bilinear-biquadratic interactions in momentum space. J. Magn. Magn. Mater. 2020, 513, 167181. [Google Scholar] [CrossRef]
- Hayami, S. Multiple skyrmion crystal phases by itinerant frustration in centrosymmetric tetragonal magnets. J. Phys. Soc. Jpn. 2022, 91, 023705. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Noncoplanar multiple-Q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 2021, 103, 054422. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Meron, skyrmion, and vortex crystals in centrosymmetric tetragonal magnets. Phys. Rev. B 2021, 103, 104408. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Skyrmion crystals in centrosymmetric itinerant magnets without horizontal mirror plane. Sci. Rep. 2021, 11, 11184. [Google Scholar] [CrossRef]
- Butenko, A.B.; Leonov, A.A.; Rößler, U.K.; Bogdanov, A.N. Stabilization of skyrmion textures by uniaxial distortions in noncentrosymmetric cubic helimagnets. Phys. Rev. B 2010, 82, 052403. [Google Scholar] [CrossRef]
- Lin, S.Z.; Saxena, A.; Batista, C.D. Skyrmion fractionalization and merons in chiral magnets with easy-plane anisotropy. Phys. Rev. B 2015, 91, 224407. [Google Scholar] [CrossRef]
- Leonov, A.O.; Monchesky, T.L.; Romming, N.; Kubetzka, A.; Bogdanov, A.N.; Wiesendanger, R. The properties of isolated chiral skyrmions in thin magnetic films. New. J. Phys. 2016, 18, 065003. [Google Scholar] [CrossRef]
- Leonov, A.O.; Kézsmárki, I. Asymmetric isolated skyrmions in polar magnets with easy-plane anisotropy. Phys. Rev. B 2017, 96, 014423. [Google Scholar] [CrossRef]
- Hayami, S. In-plane magnetic field-induced skyrmion crystal in frustrated magnets with easy-plane anisotropy. Phys. Rev. B 2021, 103, 224418. [Google Scholar] [CrossRef]
- Day, P.; Moore, M.W.; Wilkinson, C.; Ziebeck, K.R.A. Neutron diffraction study of the incommensurate magnetic phase of Ni0.92Zn0.08Br2. J. Phys. C Solid State Phys. 1981, 14, 3423. [Google Scholar] [CrossRef]
- Regnault, L.; Rossat-Mignod, J.; Adam, A.; Billerey, D.; Terrier, C. Inelastic neutron scattering investigation of the magnetic excitations in the helimagnetic state of NiBr2. J. De Phys. 1982, 43, 1283–1290. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Nambu, Y.; Tonomura, H.; Sakai, O.; Jonas, S.; Broholm, C.; Tsunetsugu, H.; Qiu, Y.; Maeno, Y. Spin disorder on a triangular lattice. Science 2005, 309, 1697–1700. [Google Scholar] [CrossRef] [PubMed]
- Ghimire, N.; Ronning, F.; Williams, D.; Scott, B.; Luo, Y.; Thompson, J.; Bauer, E. Investigation of the physical properties of the tetragonal CeMAl4Si2 (M = Rh, Ir, Pt) compounds. J. Phys. Condens. Matter 2014, 27, 025601. [Google Scholar] [CrossRef] [PubMed]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Skyrmion Crystal from RKKY Interaction Mediated by 2D Electron Gas. Phys. Rev. Lett. 2020, 124, 207201. [Google Scholar] [CrossRef]
- Yoshimori, A. A new type of antiferromagnetic structure in the rutile type crystal. J. Phys. Soc. Jpn. 1959, 14, 807–821. [Google Scholar] [CrossRef]
- Kaplan, T.A. Some Effects of Anisotropy on Spiral Spin-Configurations with Application to Rare-Earth Metals. Phys. Rev. 1961, 124, 329–339. [Google Scholar] [CrossRef]
- Elliott, R.J. Phenomenological Discussion of Magnetic Ordering in the Heavy Rare-Earth Metals. Phys. Rev. 1961, 124, 346–353. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Nakamura, S.; Sakakibara, T.; Hedo, M.; Nakama, T.; et al. Giant Hall resistivity and magnetoresistance in cubic chiral antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2018, 87, 023701. [Google Scholar] [CrossRef]
- Kaneko, K.; Frontzek, M.D.; Matsuda, M.; Nakao, A.; Munakata, K.; Ohhara, T.; Kakihana, M.; Haga, Y.; Hedo, M.; Nakama, T.; et al. Unique Helical Magnetic Order and Field-Induced Phase in Trillium Lattice Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 013702. [Google Scholar] [CrossRef]
- Tabata, C.; Matsumura, T.; Nakao, H.; Michimura, S.; Kakihana, M.; Inami, T.; Kaneko, K.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic Field Induced Triple-q Magnetic Order in Trillium Lattice Antiferromagnet EuPtSi Studied by Resonant X-ray Scattering. J. Phys. Soc. Jpn. 2019, 88, 093704. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Takeuchi, T.; Harima, H.; Hedo, M.; Nakama, T.; et al. Unique Magnetic Phases in the Skyrmion Lattice and Fermi Surface Properties in Cubic Chiral Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 094705. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ganesan, V. A-phase, field-induced tricritical point, and universal magnetocaloric scaling in EuPtSi. Phys. Rev. B 2019, 100, 125113. [Google Scholar] [CrossRef]
- Takeuchi, T.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic field versus temperature phase diagram for H‖[001] in the trillium lattice antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 053703. [Google Scholar] [CrossRef]
- Matsumura, T.; Tabata, C.; Kaneko, K.; Nakao, H.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Single helicity of the triple-q triangular skyrmion lattice state in the cubic chiral helimagnet EuPtSi. Phys. Rev. B 2024, 109, 174437. [Google Scholar] [CrossRef]
- Matsumura, T.; Kurauchi, K.; Tsukagoshi, M.; Higa, N.; Nakao, H.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Helicity Unification by Triangular Skyrmion Lattice Formation in the Noncentrosymmetric Tetragonal Magnet EuNiGe3. J. Phys. Soc. Jpn. 2024, 93, 074705. [Google Scholar] [CrossRef]
- Takagi, R.; White, J.; Hayami, S.; Arita, R.; Honecker, D.; Rønnow, H.; Tokura, Y.; Seki, S. Multiple-q noncollinear magnetism in an itinerant hexagonal magnet. Sci. Adv. 2018, 4, eaau3402. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Field-Direction Sensitive Skyrmion Crystals in Cubic Chiral Systems: Implication to 4f-Electron Compound EuPtSi. J. Phys. Soc. Jpn. 2021, 90, 073705. [Google Scholar] [CrossRef]
- Singh, D.; Fujishiro, Y.; Hayami, S.; Moody, S.H.; Nomoto, T.; Baral, P.R.; Ukleev, V.; Cubitt, R.; Steinke, N.J.; Gawryluk, D.J.; et al. Transition between distinct hybrid skyrmion textures through their hexagonal-to-square crystal transformation in a polar magnet. Nat. Commun. 2023, 14, 8050. [Google Scholar] [CrossRef]
- Kaplan, T. Single-band Hubbard model with spin-orbit coupling. Z. Für Phys. B Condens. Matter 1983, 49, 313–317. [Google Scholar] [CrossRef]
- Shekhtman, L.; Aharony, A.; Entin-Wohlman, O. Bond-dependent symmetric and antisymmetric superexchange interactions in La2CuO4. Phys. Rev. B 1993, 47, 174–182. [Google Scholar] [CrossRef] [PubMed]
- Khomskii, D.; Mostovoy, M. Orbital ordering and frustrations. J. Phys. A 2003, 36, 9197. [Google Scholar] [CrossRef]
- Jackeli, G.; Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: From Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 2009, 102, 017205. [Google Scholar] [CrossRef]
- Li, Y.D.; Wang, X.; Chen, G. Anisotropic spin model of strong spin-orbit-coupled triangular antiferromagnets. Phys. Rev. B 2016, 94, 035107. [Google Scholar] [CrossRef]
- Maksimov, P.A.; Zhu, Z.; White, S.R.; Chernyshev, A.L. Anisotropic-Exchange Magnets on a Triangular Lattice: Spin Waves, Accidental Degeneracies, and Dual Spin Liquids. Phys. Rev. X 2019, 9, 021017. [Google Scholar] [CrossRef]
- Berg, B.; Lüscher, M. Definition and statistical distributions of a topological number in the lattice O(3) σ-model. Nucl. Phys. B 1981, 190, 412–424. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Locking of skyrmion cores on a centrosymmetric discrete lattice: Onsite versus offsite. Phys. Rev. Res. 2021, 3, 043158. [Google Scholar] [CrossRef]
- Kamiya, Y.; Batista, C.D. Magnetic Vortex Crystals in Frustrated Mott Insulator. Phys. Rev. X 2014, 4, 011023. [Google Scholar] [CrossRef]
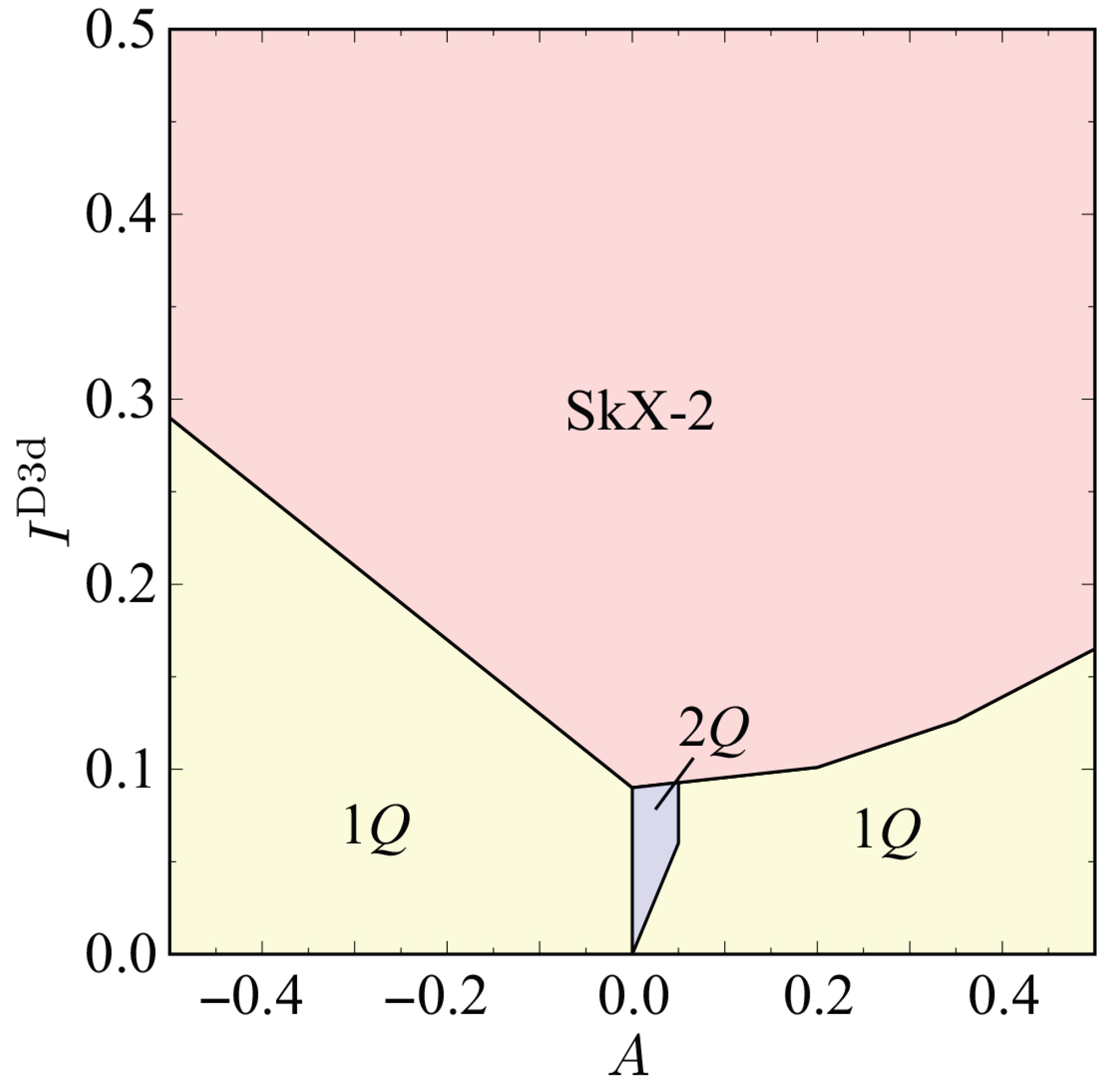

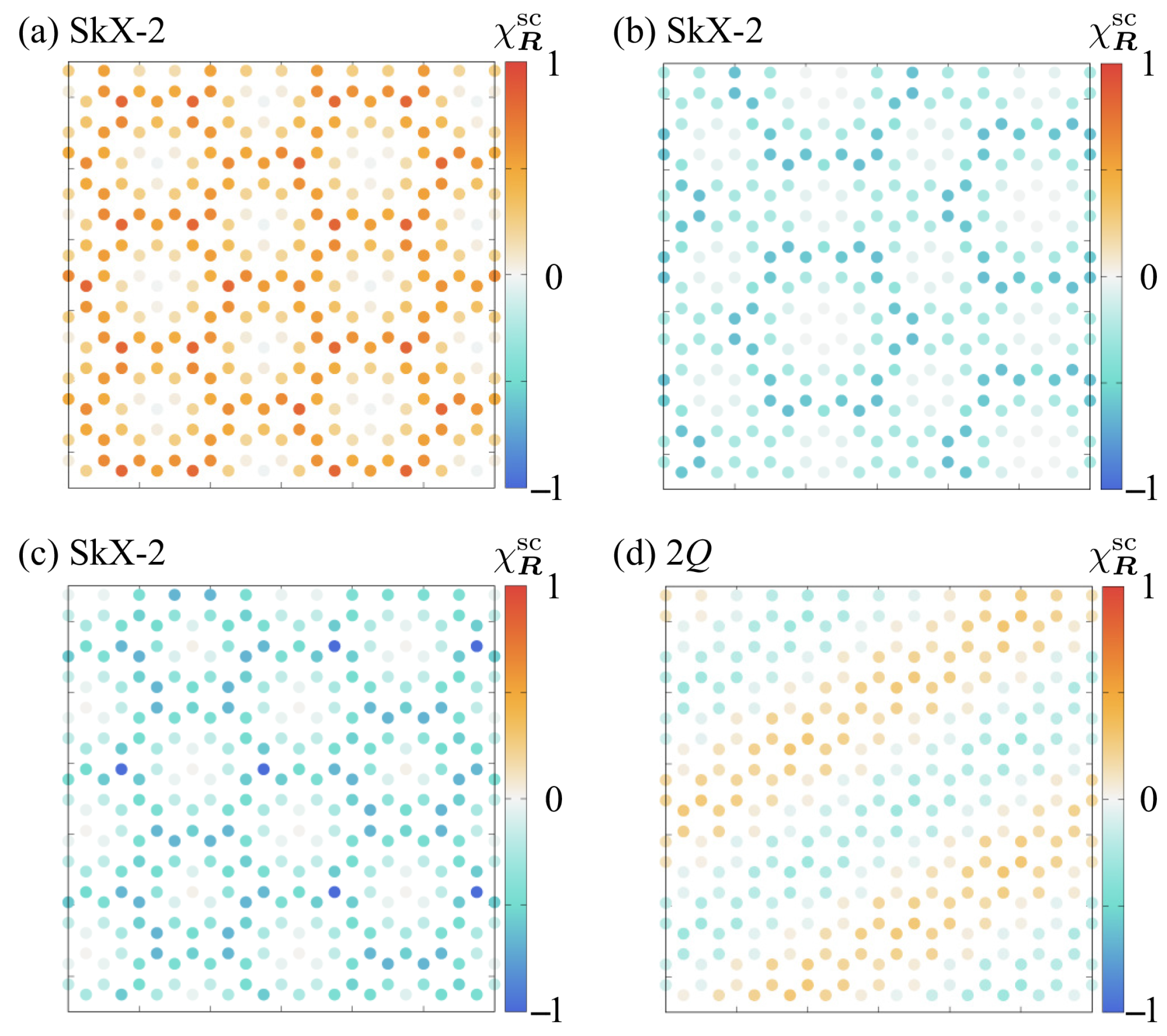
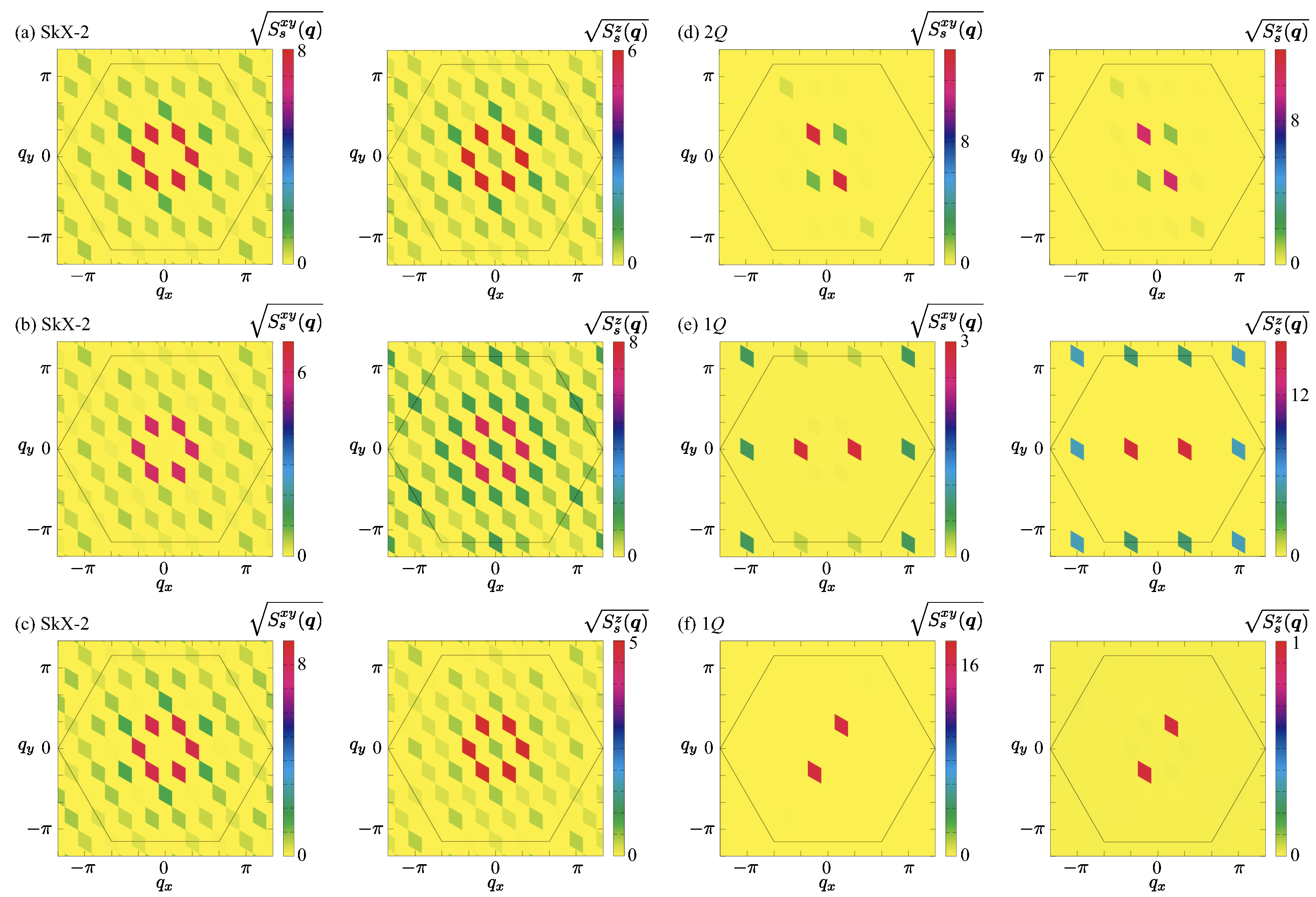
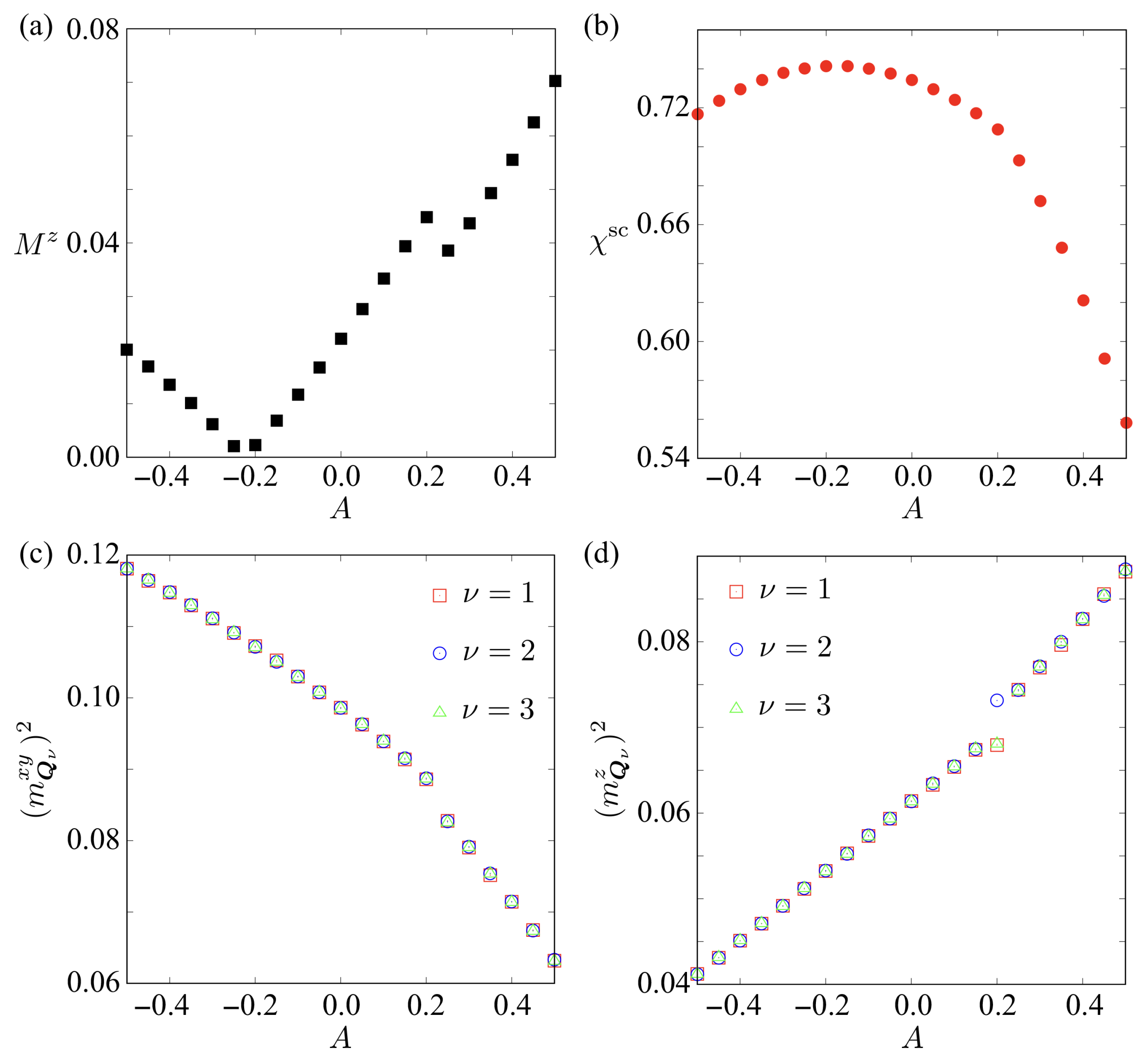



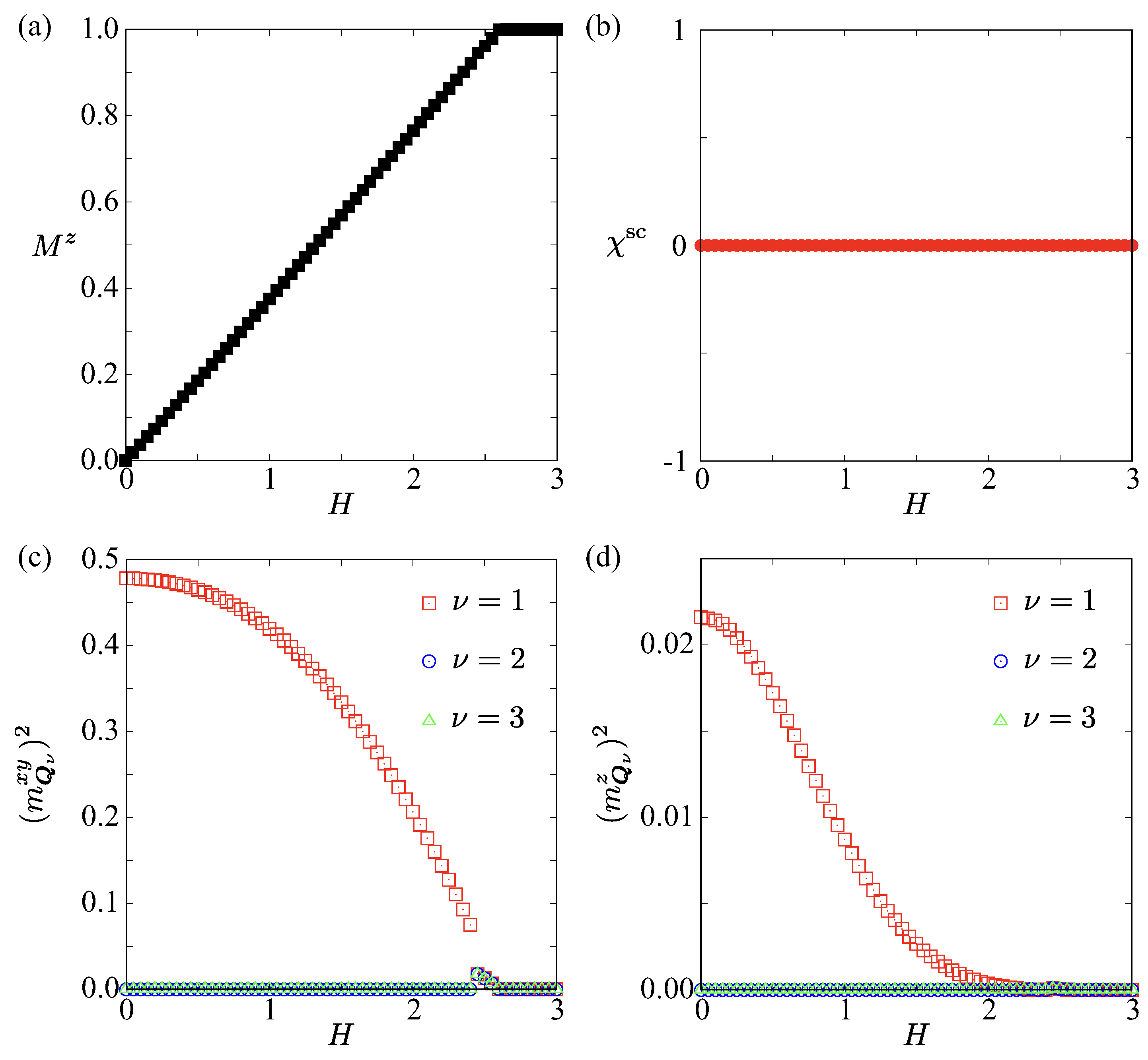



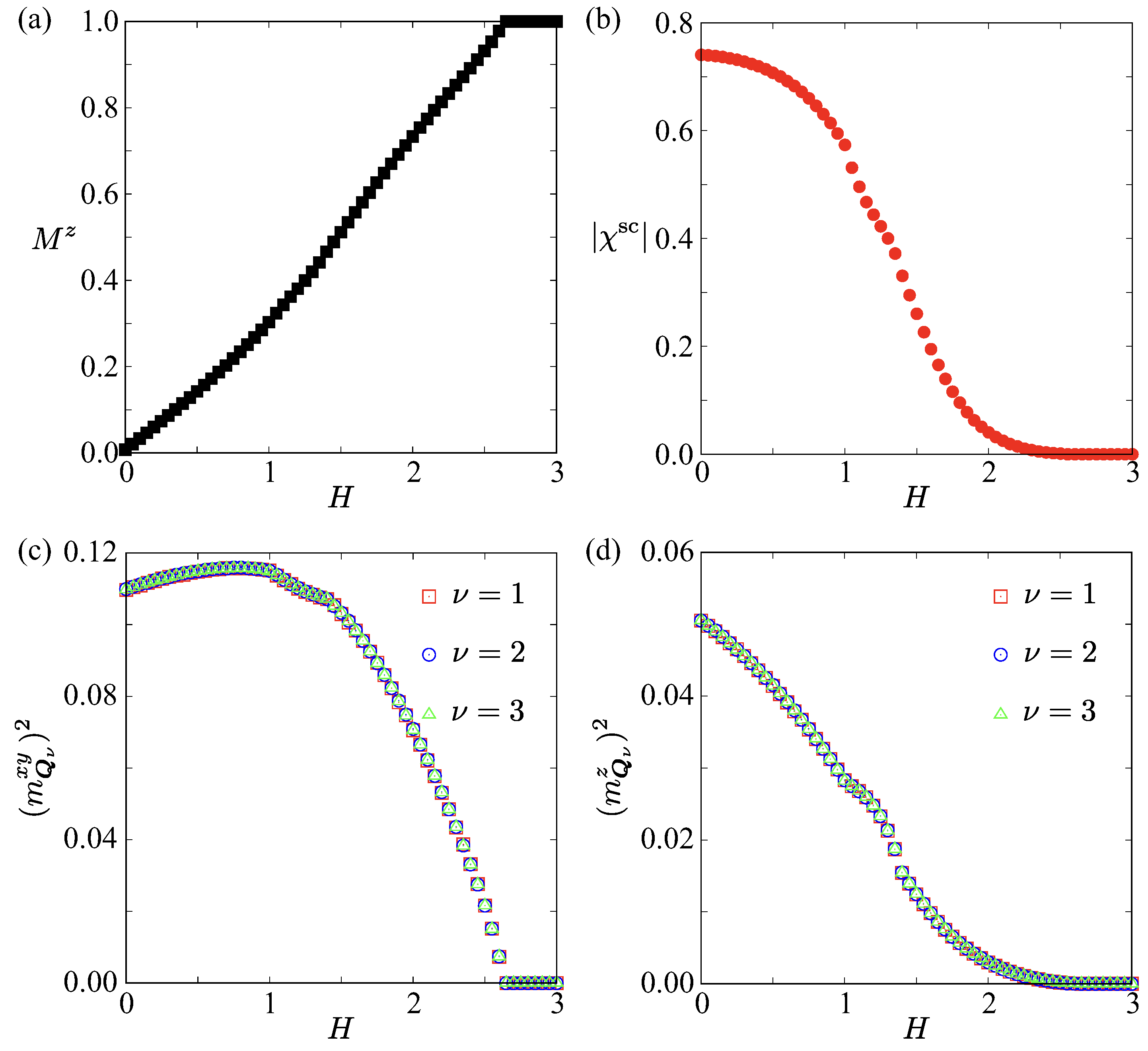
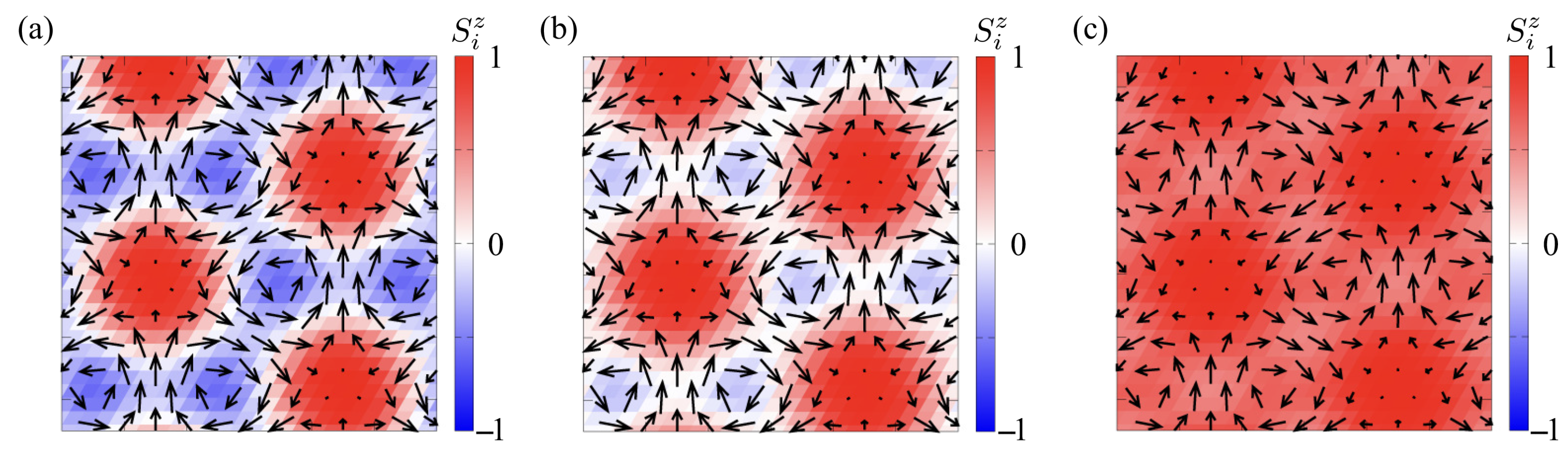
| Case | SkX | |||
|---|---|---|---|---|
| Zero-field phase diagram | −0.5 to 0.5 | 0 to 0.5 | ✓ | – |
| Weak D3d, easy-axis | 0.3 | 0.1 | ✓ | jump |
| Weak D3d, easy-plane | −0.3 | 0.1 | – | – |
| Strong D3d, easy-axis | 0.3 | 0.3 | ✓ | jump |
| Strong D3d, easy-plane | −0.3 | 0.3 | ✓ | continuous |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Hayami, S. Role of Single-Ion Anisotropy in Stabilizing Higher-Order Skyrmion Crystals in D3d-Symmetric Magnets. Magnetism 2026, 6, 7. https://doi.org/10.3390/magnetism6010007
Hayami S. Role of Single-Ion Anisotropy in Stabilizing Higher-Order Skyrmion Crystals in D3d-Symmetric Magnets. Magnetism. 2026; 6(1):7. https://doi.org/10.3390/magnetism6010007
Chicago/Turabian StyleHayami, Satoru. 2026. "Role of Single-Ion Anisotropy in Stabilizing Higher-Order Skyrmion Crystals in D3d-Symmetric Magnets" Magnetism 6, no. 1: 7. https://doi.org/10.3390/magnetism6010007
APA StyleHayami, S. (2026). Role of Single-Ion Anisotropy in Stabilizing Higher-Order Skyrmion Crystals in D3d-Symmetric Magnets. Magnetism, 6(1), 7. https://doi.org/10.3390/magnetism6010007






