Thickness Effect on Microwave Permeability of CoFeB Films on Flexible Substrate
Abstract
1. Introduction
2. Materials and Methods
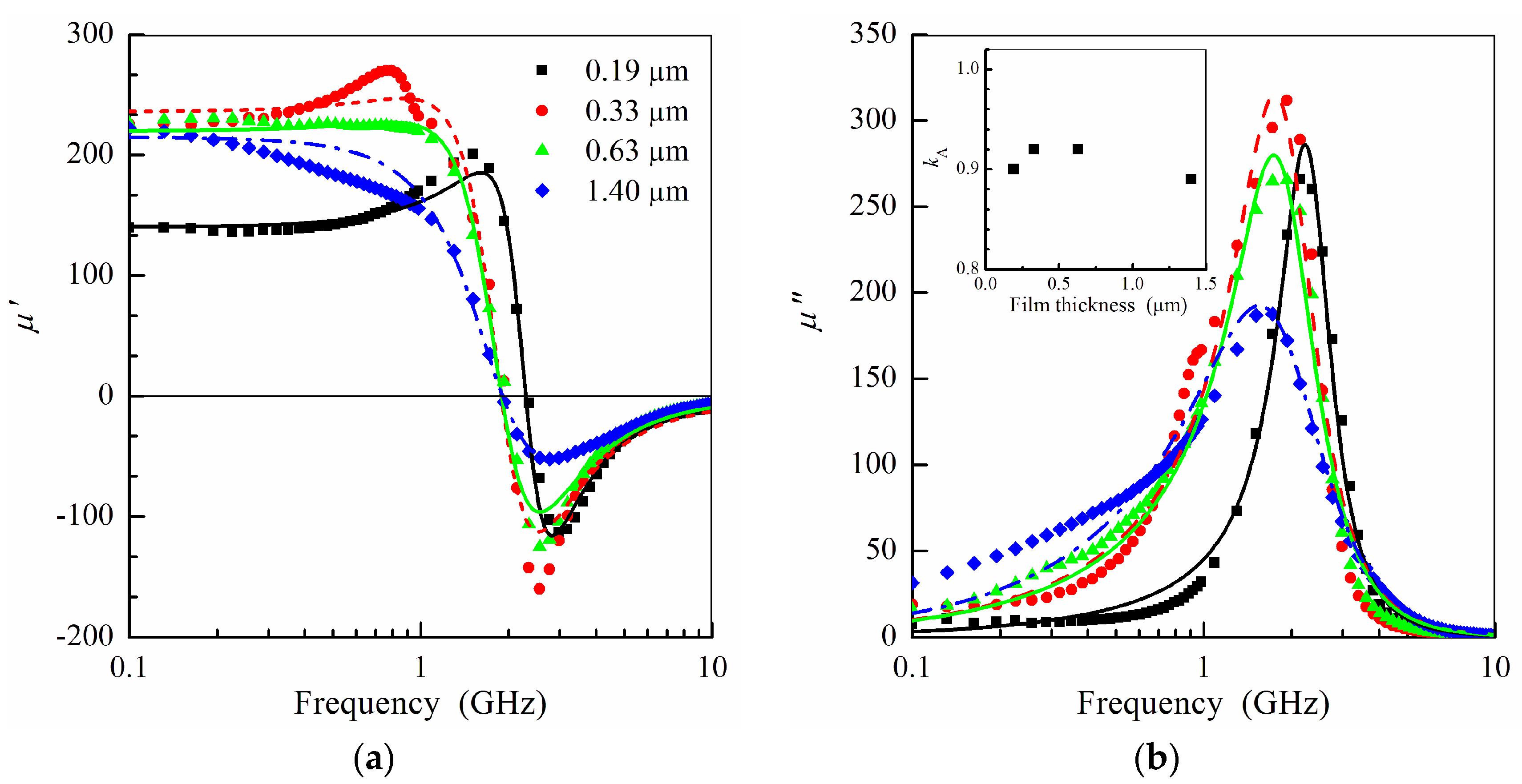
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, X.; Zhang, J.; Song, X.; Wang, H.; Zhang, K.; He, Z.; Wu, C.; Yu, Z.; Lan, Z.; Sun, K. Tunable resonance frequency of NiFe thin films by oblique deposition. J. Magn. Magn. Mater. 2022, 547, 168946. [Google Scholar] [CrossRef]
- Izotov, A.V.; Belyaev, B.A.; Boev, N.M.; Burmitskikh, A.V.; Leksikov, A.A.; Skomorokhov, G.V.; Solovev, P.N. Tailoring the microwave properties of thin Permalloy films using a periodically grooved substrate. Phys. B 2022, 629, 413654. [Google Scholar] [CrossRef]
- Goldman, S.; Celinski, Z. Magnetic properties of (Ni0.81Fe0.19/SiO2)n multilayers for high frequency on-wafer inductor applicati ons. J. Magn. Magn. Mater. 2023, 569, 170440. [Google Scholar] [CrossRef]
- Li, Q.; Jiang, Y.; Wu, C.; Jiang, X.; Li, Z.; Sun, K.; Lan, Z.; Yu, Z. Tailoring the in-plane magnetic anisotropy and permeability spectra of obliquely deposited Fe40Co40B20 films for 5G communications. J. Magn. Magn. Mater. 2023, 578, 170811. [Google Scholar] [CrossRef]
- Lei, T.; Zhang, W.; Bo, G.; Feng, C.; Li, N.; Zhao, R.; Ji, L.; Zhang, J.; Zhang, X. Tuning the ferromagnetic resonance frequency of microstructured permalloy film on flexible substrate. Phys. Status Solidi RRL 2024, 18, 2400081. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, R.; Sharma, V.; Khanna, M.K.; Kuanr, B.K. Influence of growth temperature on the magnetization dynamics of sputtered CoFeB thin films on various substrates and their microwave device functionality. J. Alloys Compd. 2024, 988, 174314. [Google Scholar] [CrossRef]
- Snoek, J.L. Dispersion and absorption of magnetic ferrites at frequencies above 1 MHz. Physica 1948, 14, 207–217. [Google Scholar] [CrossRef]
- Perrin, G.; Acher, O.; Peuzin, J.C.; Vucadinovic, N. Sum rules for gyromagnetic permeability of ferromagnetic thin films: The oretical and experimental results. J. Magn. Magn. Mater. 1996, 157/158, 289–290. [Google Scholar] [CrossRef]
- Acher, O.; Adenot, A.L. Bounds on the dynamic properties of magnetic materials. Phys. Rev. B 2000, 62, 11324–11327. [Google Scholar] [CrossRef]
- Rozanov, K.N.; Koledintseva, M.Y. Application of generalized Snoek’s law over a finite frequency range: A case study. J. Appl. Phys. 2016, 119, 073901. [Google Scholar] [CrossRef]
- Fergen, I.; Seemann, K.; Weth, A.v.d.; Shüppen, A. Soft ferromagnetic thin films for high frequency applications. J. Magn. Magn. Mater. 2002, 242–245, 146–151. [Google Scholar] [CrossRef]
- Klemmer, T.J.; Ellis, K.A.; Chen, L.H.; van Dover, B.; Jin, S. Ultrahigh frequency permeability of sputtered Fe–Co–B thin films. J. Appl. Phys. 2000, 87, 830–833. [Google Scholar] [CrossRef]
- Munakata, M.; Namikawa, M.; Motoyama, M.; Yagi, M.; Shimada, Y.; Yamaguchi, M.; Arai, K.I. Magnetic properties and fre quency characteristics of (CoFeB)x–(Si01.9)1–x and CoFeB films for RF applications. Trans. Magn. Soc. Jpn. 2002, 2, 388–393. [Google Scholar] [CrossRef]
- Kim, I.; Kim, J.; Kim, K.H.; Yamaguchi, M. Effects of boron contents on magnetic properties of Fe-Co-B thin films. IEEE Trans. Magn. 2004, 40, 2706–2708. [Google Scholar] [CrossRef]
- Bilzer, C.; Devolder, T.; Kim, J.-V.; Counil, G.; Chappert, C.; Cardoso, S.; Freitas, P.P. Study of the dynamic magnetic properties of soft CoFeB films. J. Appl. Phys. 2006, 100, 053903. [Google Scholar] [CrossRef]
- Liu, B.; Yang, Y.; Tang, D.; Zhang, B.; Lu, M.; Lu, H.; Shi, Y. Research on double resonance peaks and abnormal frequency shift in permeability spectra of annealed FeCoB films. J. Magn. Magn. Mater. 2011, 323, 375–378. [Google Scholar] [CrossRef]
- Xu, F.; Huang, Q.; Liao, Z.; Li, S.; Ong, C.K. Tuning of magnetization dynamics in sputtered CoFeB thin film by gas pressure. J. Appl. Phys. 2012, 111, 07A304. [Google Scholar] [CrossRef]
- Venkat Swamy, G.; Rakshit, R.K.; Pant, R.P.; Basheed, G.A. Origin of ‘in-plane’ and ‘out-of-plane’ magnetic anisotropies in as-deposited and annealed CoFeB ferromagnetic thin films. J. Appl. Phys. 2015, 117, 17A312. [Google Scholar] [CrossRef]
- Jhajhria, D.; Pandya, D.K.; Chaudhary, S. Interplay of composition and anisotropy on evolution of microstructural, static and dynamic magnetic properties of CoFeB thin films on annealing. J. Alloys Compd. 2018, 763, 728–735. [Google Scholar] [CrossRef]
- O’Dell, R.A.; Phillips, A.B.; Georgiev, D.G.; Jones, J.G.; Brown, G.J.; Heben, M.J. Post-deposition annealing effects on ferro magnetic CoFeB thin films. IEEE Trans. Magn. 2018, 54, 2800807. [Google Scholar]
- Arteaga-Duran, Á.; Sáenz-Hernandez, R.; Santillan-Rodriguez, C.; Botello-Zubiate, M.; Grijalva-Castillo, M.; Matutes-Aquino, J. Effects of thickness and thermal annealing of FeCoB thin films on ferromagnetic resonance and microwave propagation pro perties. IEEE Trans. Magn. 2019, 55, 2800303. [Google Scholar] [CrossRef]
- O’Dell, R.A.; Phillips, A.B.; Georgiev, D.G.; Jones, J.G.; Brown, G.J.; Heben, M.J. Substrate heating effects on composition, structure and ferromagnetic resonance properties of CoFeB thin films. J. Magn. Magn. Mater. 2019, 476, 516–523. [Google Scholar] [CrossRef]
- Gayen, A.; Modak, R.; Srinivasan, A.; Srinivasu, V.V.; Alagarsamy, P. Thickness dependent magneto-static and magneto-dynamic properties of CoFeB thin films. J. Vacuum Sci. Technol. A 2019, 37, 031513. [Google Scholar] [CrossRef]
- Arif, M.; Zhang, X.; Amir, M.; Liu, E.; Xu, F. Tailoring the magnetism and spin dynamics in CoFeB thin films by post annealing for spintronics applications. J. Mater. Sci. Mater. Electron. 2023, 34, 574. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Zhang, Y.; Dai, B.; Ren, Y.; Chen, M. Improvement of high-frequency magnetic properties of CoFeB thin film using oblique deposition for spin wave electronic devices. J. Mater. Sci. Mater. Electron. 2024, 35, 281. [Google Scholar] [CrossRef]
- Liu, Y.W.; Wang, B.M.; Zhan, Q.F.; Tang, Z.H.; Yang, H.L.; Liu, G.; Zuo, Z.H.; Zhang, X.S.; Xie, Y.L.; Zhu, X.J.; et al. Positive temperature coefficient of magnetic anisotropy in polyvinylidene fluoride (PVDF)-based magnetic com posites. Sci. Rep. 2014, 4, 6615. [Google Scholar]
- Tang, Z.; Ni, H.; Lu, B.; Zheng, M.; Huang, Y.A.; Lu, S.G.; Tang, M.; Gao, J. Thickness dependence of magnetic anisotropy and domains in amorphous Co40Fe40B20 thin films grown on PET flexible substrates. J. Magn. Magn. Mater. 2017, 426, 444–449. [Google Scholar] [CrossRef]
- Zhang, Q.; Peng, B.; Zhao, Y.; Li, C.; Zhu, S.; Shi, K.; Zhou, Z.; Zhang, X.; Liu, M.; Pan, J. Flexible CoFeB/silk films for biocompa tible RF/microwave applications. ACS Appl. Mater. Interfaces 2020, 12, 51654–51662. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Zhang, Y.; Fu, S.; Chai, G.; Cao, C.; Zhu, X.; Guo, Y.; Cheng, W.; Jiang, D.; et al. Stretching-tunable high-frequency magnetic properties of wrinkled CoFeB films grown on PDMS. ACS Appl. Mater. Interfaces 2021, 13, 29975–29983. [Google Scholar] [CrossRef]
- Yabukami, S.; Nozawa, K.; Tonthat, L.; Okita, K.; Sai, R. Impact of complex permeability measurements up to millimeter-wave frequency range. IEEE Trans. Magn. 2021, 57, 6100405. [Google Scholar] [CrossRef]
- Fu, S.; Xue, K.; Chai, G.; Xu, Y.; Shang, T.; Cheng, W.; Jiang, D.; Zhan, Q. Positive stretching dependence of resonance frequency in CoFeB films modulated by lateral growth pre-strain. J. Alloys Compd. 2022, 926, 166955. [Google Scholar] [CrossRef]
- Ben Youssef, J.; Vukadinovic, N.; Billet, D.; Labrune, M. Thickness-dependent magnetic excitations in permalloy films with nonuniform magnetization. Phys. Rev. B 2004, 69, 174402. [Google Scholar] [CrossRef]
- Svalov, A.V.; Aseguinolaza, I.R.; Garcia-Arribas, A.; Barandiaran, J.M.; Alonso, J.; Fernández-Gubieda, M.L.; Orue, I.; Kurlyandskaya, G.V. Structure and magnetic properties of thin Permalloy films near the “transcritical” state. IEEE Trans. Magn. 2010, 46, 333–336. [Google Scholar] [CrossRef]
- Silva, E.F.; Corrêa, M.A.; Della Pace, R.D.; Plá Cid, C.C.; Kern, P.R.; Carara, M.; Chesman, C.; Alves Santos, O.; Rodríguez-Suárez, R.L.; Azevedo, A.; et al. Thickness dependence of the magnetic anisotropy and dynamic magnetic response of ferromagnetic NiFe films. J. Phys. D Appl. Phys. 2017, 50, 185001. [Google Scholar] [CrossRef]
- Yua, J.; Chang, C.; Karns, D.; Ju, G.; Kubota, Y.; Eppler, W.; Brucker, C.; Weller, D. Thermal annealing effect on FeCoB soft underlayer for perpendicular magnetic recording. J. Appl. Phys. 2002, 91, 8357–8359. [Google Scholar] [CrossRef]
- Sharma, P.; Kimura, H.; Inoue, A.; Arenholz, E.; Guo, J.-H. Temperature and thickness driven spin-reorientation transition in amorphous Co-Fe-Ta-B thin films. Phys. Rev. B 2006, 73, 052401. [Google Scholar] [CrossRef]
- Coïsson, M.; Vinai, F.; Tiberto, P.; Celegato, F. Magnetic properties of FeSiB thin films displaying stripe domains. J. Magn. Magn. Mater. 2009, 321, 806–809. [Google Scholar] [CrossRef]
- Gayen, A.; Prasad, G.K.; Mallik, S.; Bedanta, S.; Perumal, A. Effects of composition, thickness and temperature on the magnetic properties of amorphous CoFeB thin films. J. Alloys Compd. 2017, 694, 823–832. [Google Scholar] [CrossRef]
- Lordan, D.; Wei, G.; McCloskey, P.; O’Mathuna, C.; Masood, A. Origin of perpendicular magnetic anisotropy in amorphous thin film. Sci. Rep. 2021, 11, 3734. [Google Scholar] [CrossRef]
- van de Riet, E.; Roozeboom, F. Ferromagnetic resonance and eddy currents in high-permeable thin films. J. Appl. Phys. 1997, 81, 350–354. [Google Scholar] [CrossRef]
- Rozanov, K.N.; Simonov, N.A.; Osipov, A.V. Microwave measurements of the magnetic film permeability. J. Commun. Technol. Electron. 2002, 47, 210–216. [Google Scholar]
- Iakubov, I.T.; Kashurkin, O.Y.; Lagarkov, A.N.; Maklakov, S.A.; Osipov, A.V.; Rozanov, K.N.; Ryzhikov, I.A.; Starostenko, S.N. A contribution from the magnetoelastic effect to measured microwave permeability of thin ferromagnetic films. J. Magn. Magn. Mater. 2012, 324, 3385–3388. [Google Scholar] [CrossRef]
- Buznikov, N.A.; Rozanov, K.N. The effect of stripe domain structure on dynamic permeability of thin ferromagnetic films with out-of-plane uniaxial anisotropy. J. Magn. Magn. Mater. 2005, 285, 314–326. [Google Scholar] [CrossRef]
- Buznikov, N.A.; Lagarkov, A.N.; Maklakov, S.A.; Maklakov, S.S.; Osipov, A.V.; Rozanov, K.N.; Zezyulina, P.A. Analysis of relationship between microwave magnetic properties and magnetic structure of permalloy films. Sensors 2024, 24, 6165. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.H.; Wang, B.M.; Yang, H.L.; Xu, X.Y.; Liu, Y.W.; Sun, D.D.; Xia, L.X.; Zhan, Q.F.; Chen, B.; Tang, M.H.; et al. Magneto-mechanical coupling effect in amorphous Co40Fe40B20 films grown on flexible substrates. Appl. Phys. Lett. 2014, 105, 103504. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.Y.; Yang, M.Y.; Zhang, B.; Yang, G.; Wang, S.G.; Wang, K.Y. Tuning the magnetic anisotropy of CoFeB grown on flexible substrates. Chin. Phys. B 2015, 24, 077501. [Google Scholar] [CrossRef]
- Bobrovskii, S.Y.; Iakubov, I.T.; Lagarkov, A.N.; Maklakov, S.A.; Maklakov, S.S.; Osipov, A.V.; Rozanov, K.N.; Ryzhikov, I.A.; Petrov, D.A.; Zezyulina, P.A. Variation of microwave magnetic properties for thin films of ferromagnetic metals with the film thickness. J. Magn. Magn. Mater. 2018, 459, 20–25. [Google Scholar] [CrossRef]
- Sugita, Y.; Fujiwara, H.; Sato, T. Critical thickness and perpendicular anisotropy of evaporated permalloy films with stripe domains. Appl. Phys. Lett. 1967, 10, 229–231. [Google Scholar] [CrossRef]
- Svalov, A.V.; Kurlyandskaya, G.V.; Hammer, H.; Savin, P.A.; Tutynina, O.I. Modification of the “transcritical” state in NiFeCuMo films produced by RF sputtering. Tech. Phys. 2004, 49, 868–871. [Google Scholar] [CrossRef]
- Amos, N.; Fernandez, R.; Ikkawi, R.; Lee, B.; Lavrenov, A.; Krichevsky, A.; Litvinov, D.; Khizroev, S. Magnetic force microscopy study of magnetic stripe domains in sputter deposited Permalloy thin films. J. Appl. Phys. 2008, 103, 07E732. [Google Scholar] [CrossRef]
- Zezyulina, P.A.; Iakubov, I.T.; Lagarkov, A.N.; Maklakov, S.A.; Maklakov, S.S.; Naboko, A.S.; Osipov, A.V.; Petrov, D.A.; Rozanov, K.N.; Ryzhikov, I.A. The effect of the perpendicular anisotropy and eddy currents on the microwave performance of single-layer and multi-layer permalloy films. IEEE Magn. Lett. 2016, 7, 3705804. [Google Scholar] [CrossRef]
- Acher, O.; Dubourg, S. Generalization of Snoek’s law to ferromagnetic films and composites. Phys. Rev. B 2008, 77, 104440. [Google Scholar] [CrossRef]
- Bozorth, R.M. Ferromagnetism; D. Van Nostrand: Princeton, NJ, USA, 1951. [Google Scholar]




| Film Thickness d, μm | Damping Factor β | Damping Factor β1 |
|---|---|---|
| 0.33 | 0.80 | 0.79 |
| 0.63 | 0.89 | 0.85 |
| 1.40 | 1.27 | 1.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buznikov, N.A.; Ivanov, P.A.; Komarov, I.V.; Lagarkov, A.N.; Maklakov, S.A.; Maklakov, S.S.; Osipov, A.V.; Rozanov, K.N.; Shiryaev, A.O.; Zezyulina, P.A. Thickness Effect on Microwave Permeability of CoFeB Films on Flexible Substrate. Magnetism 2025, 5, 30. https://doi.org/10.3390/magnetism5040030
Buznikov NA, Ivanov PA, Komarov IV, Lagarkov AN, Maklakov SA, Maklakov SS, Osipov AV, Rozanov KN, Shiryaev AO, Zezyulina PA. Thickness Effect on Microwave Permeability of CoFeB Films on Flexible Substrate. Magnetism. 2025; 5(4):30. https://doi.org/10.3390/magnetism5040030
Chicago/Turabian StyleBuznikov, Nikita A., Pavel A. Ivanov, Ilya V. Komarov, Andrey N. Lagarkov, Sergey A. Maklakov, Sergey S. Maklakov, Alexey V. Osipov, Konstantin N. Rozanov, Artem O. Shiryaev, and Polina A. Zezyulina. 2025. "Thickness Effect on Microwave Permeability of CoFeB Films on Flexible Substrate" Magnetism 5, no. 4: 30. https://doi.org/10.3390/magnetism5040030
APA StyleBuznikov, N. A., Ivanov, P. A., Komarov, I. V., Lagarkov, A. N., Maklakov, S. A., Maklakov, S. S., Osipov, A. V., Rozanov, K. N., Shiryaev, A. O., & Zezyulina, P. A. (2025). Thickness Effect on Microwave Permeability of CoFeB Films on Flexible Substrate. Magnetism, 5(4), 30. https://doi.org/10.3390/magnetism5040030





