Loss Mitigation in Self-Biased Microstrip Circulators
Abstract
1. Introduction
2. La-Co Hexaferrites for Circulator Junction Resonators
- Hard sublattice provides a magnetic bias, like an external permanent magnet.
- Soft sublattice acts similarly to the soft microwave ferrite.
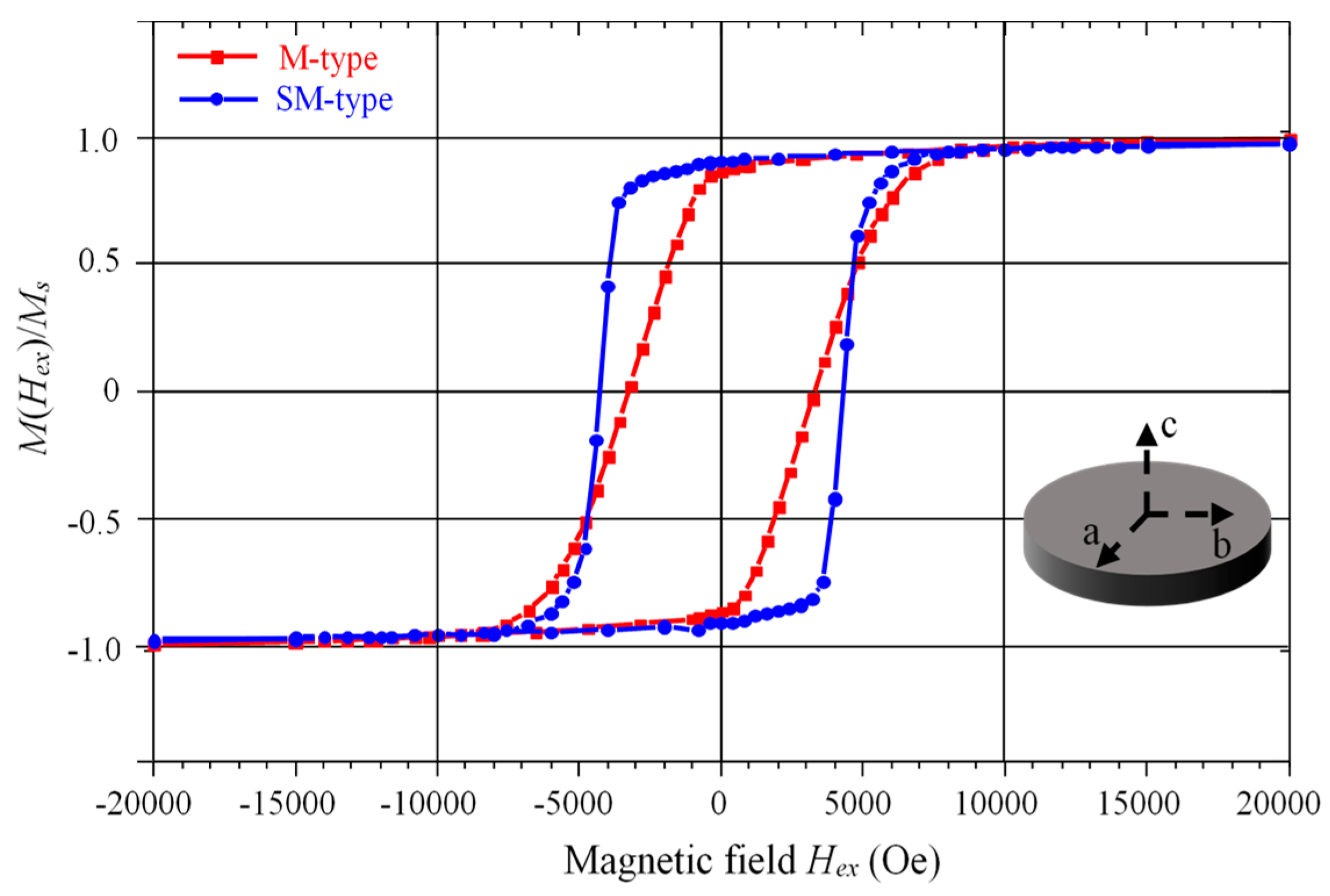
2.1. Properties of La-Co-Substituted Hexaferrites
2.2. DC Magnetic Field Profile in Hexaferrite Slab
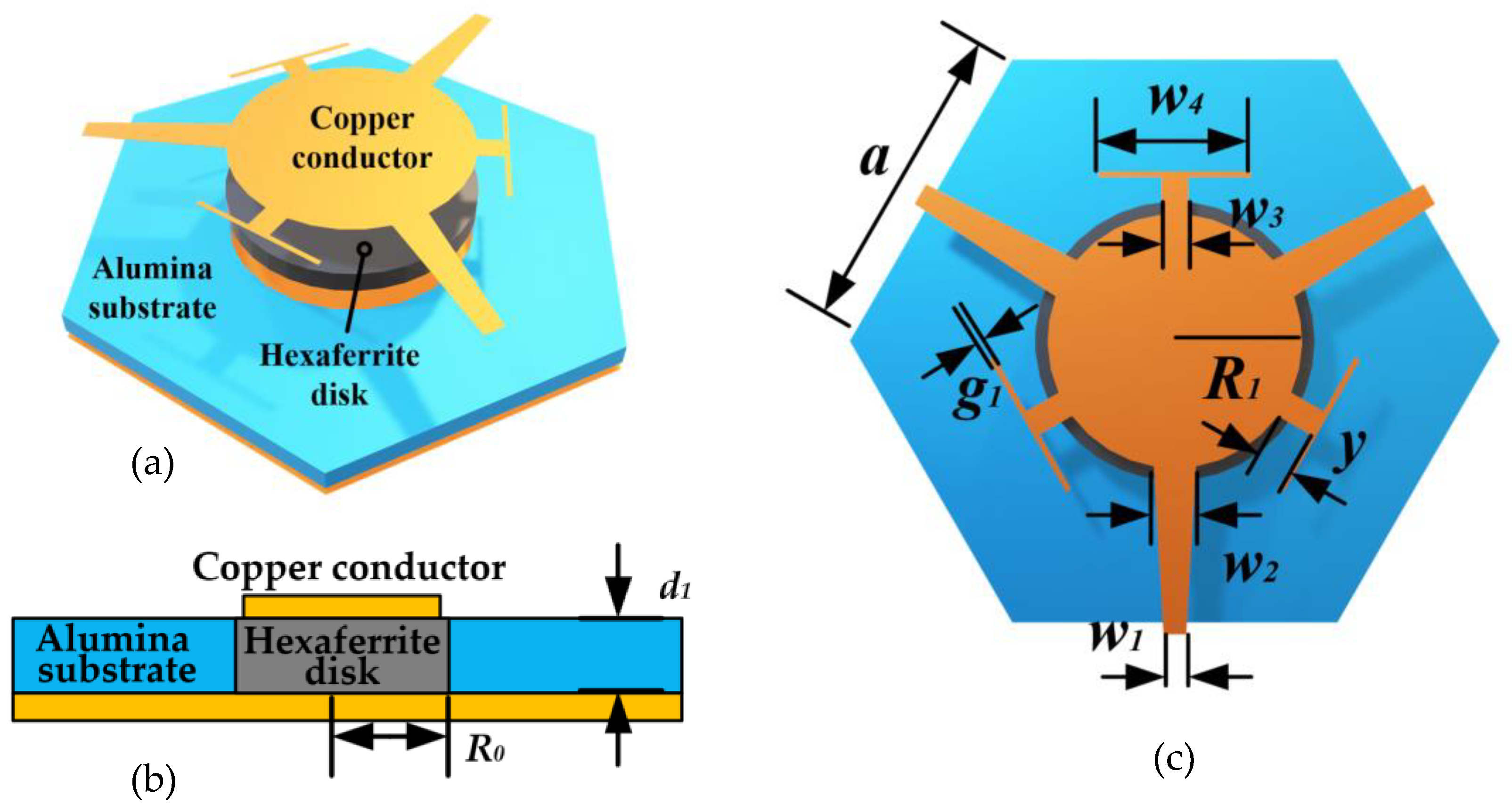
3. Self-Biased Microstrip Junction Circulators
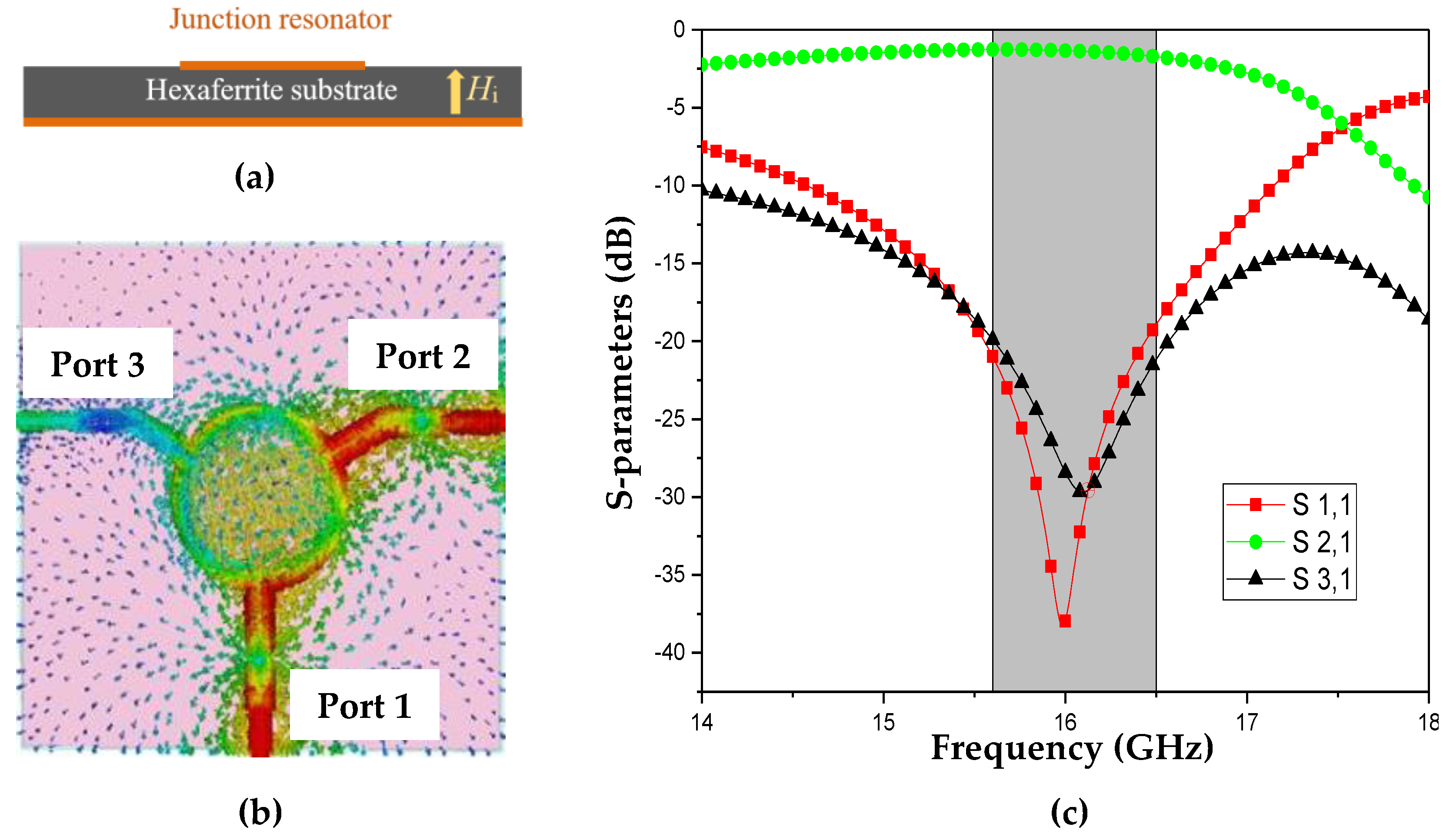
3.1. Analysis of Losses in Self-Biased Microstrip Circulators
- Hot spots exist in the small peripheral regions of the junction resonator near ports 1 and 2 only.
- Standing wave patterns appear in the matching transformers.
3.2. Self-Biased Microstrip Circulator on Composite Substrate
4. Self-Biased Microstrip Circulators at Low GHz Frequencies
4.1. Requirements to the Hexaferrite Materials for the Low GHz Self-Biased Circulators
- -
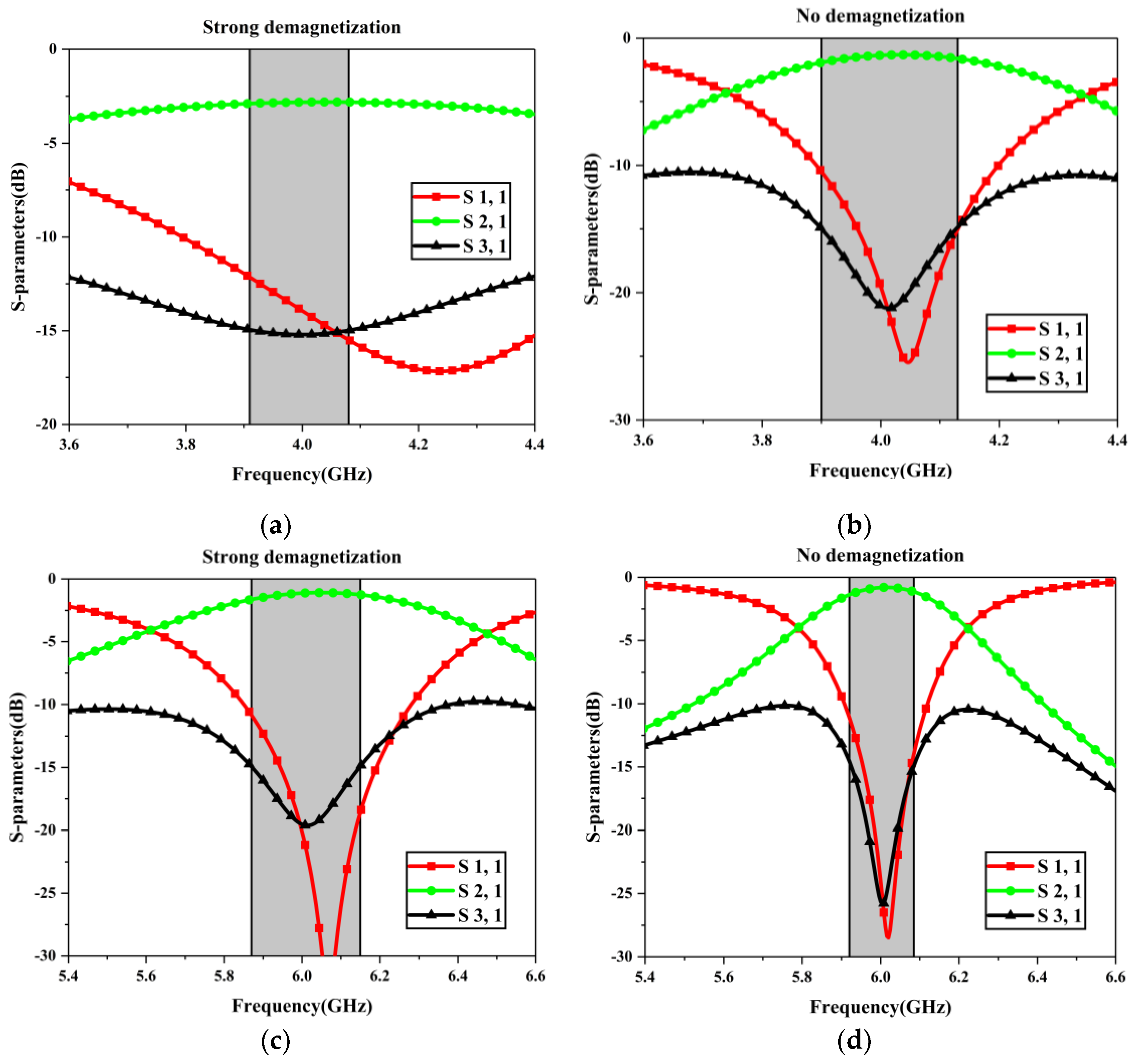
- The internal magnetic bias is Hi = Ha − weak demagnetisation (ND).
- -
- The internal magnetic bias is Hi = Ha – 4πMr − strong demagnetisation (SD).
4.2. Self-Biased Microstrip Circulators at Low GHz Frequencies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Helszajn, J. The Stripline Circulator; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 9780470264140. [Google Scholar]
- Linkhart, D.K. Microwave Circulator Design; Artech House: Boston, MA, USA, 2014; ISBN 9781608075836. [Google Scholar]
- Adams, R.S.; O’Neil, B.; Young, J.L. The Circulator and Antenna as a Single Integrated System. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 165–168. [Google Scholar] [CrossRef]
- Chen, Y.; Geiler, A.L.; Sakai, T.; Yoon, S.D.; Vittoria, C.; Harris, V.G. Microwave and Magnetic Properties of Self-Biased Barium Hexaferrite Screen Printed Thick Films. J. Appl. Phys. 2006, 99, 08M904. [Google Scholar] [CrossRef]
- Geiler, A.L.; Harris, V.G. Atom Magnetism: Ferrite Circulators—Past, Present, and Future. IEEE Microw. Mag. 2014, 15, 66–72. [Google Scholar] [CrossRef]
- Harris, V.G. Modern Microwave Ferrites. IEEE Trans. Magn. 2012, 48, 1075–1104. [Google Scholar] [CrossRef]
- O’Neil, B.K.; Young, J.L. Experimental Investigation of a Self-Biased Microstrip Circulator. IEEE Trans. Microw. Theory Tech. 2009, 57, 1669–1674. [Google Scholar] [CrossRef]
- Wang, J.; Yang, A.; Chen, Y.; Chen, Z.; Geiler, A.; Gillette, S.M.; Harris, V.G.; Vittoria, C. Self-Biased Y-Junction Circulator at Ku Band. IEEE Microw. Wirel. Compon. Lett. 2011, 21, 292–294. [Google Scholar] [CrossRef]
- Peng, B.; Xu, H.; Li, H.; Zhang, W.; Wang, Y.; Zhang, W. Self-Biased Microstrip Junction Circulator Based on Barium Ferrite Thin Films for Monolithic Microwave Integrated Circuits. IEEE Trans. Magn. 2011, 47, 1674–1677. [Google Scholar] [CrossRef]
- Fitchorov, T.; Geiler, A. Miniaturized, Low-Cost, Self-Biased Circulators for Space and Airborne Applications; Earth Science Technology Forum: Annapolis, MD, USA, 14–16 June 2016. [Google Scholar]
- Laur, V.; Vérissimo, G.; Quéffélec, P.; Farhat, L.A.; Alaaeddine, H.; Laroche, E.; Martin, G.; Lebourgeois, R.; Ganne, J.P. Self-Biased Y-Junction Circulators Using Lanthanum- and Cobalt-Substituted Strontium Hexaferrites. IEEE Trans. Microw. Theory Tech. 2015, 63, 4376–4381. [Google Scholar] [CrossRef]
- Self Biased Circulators and Isolators, Metamagnetics Inc. Available online: https://www.mtmgx.com/rf-microwave-smt-circulators-isolators/ (accessed on 13 November 2022).
- Kodera, T.; Sounas, D.L.; Caloz, C. Artificial Faraday Rotation Using a Ring Metamaterial Structure without Static Magnetic Field. Appl. Phys. Lett. 2011, 99, 031114. [Google Scholar] [CrossRef]
- Kodera, T.; Sounas, D.L.; Caloz, C. Magnetless Nonreciprocal Metamaterial (MNM) Technology: Application to Microwave Components. IEEE Trans. Microw. Theory Tech. 2013, 61, 1030–1042. [Google Scholar] [CrossRef]
- Reiskarimian, N.; Krishnaswamy, H. Magnetic-Free Non-Reciprocity Based on Staggered Commutation. Nat. Commun. 2016, 7, 11217. [Google Scholar] [CrossRef] [PubMed]
- Sounas, D.L.; Soric, J.; Alù, A. Broadband Passive Isolators Based on Coupled Nonlinear Resonances. Nat. Electron. 2018, 1, 113–119. [Google Scholar] [CrossRef]
- Hessien, M.M.; Radwan, M.; Rashad, M.M. Enhancement of Magnetic Properties for the Barium Hexaferrite Prepared through Ceramic Route. J. Anal. Appl. Pyrolysis 2007, 78, 282–287. [Google Scholar] [CrossRef]
- Drung, D.; Abmann, C.; Beyer, J.; Kirste, A.; Peters, M.; Ruede, F.; Schurig, T. Highly Sensitive and Easy-To-Use SQUID Sensors. IEEE Trans. Appl. Supercond. 2007, 17, 699–704. [Google Scholar] [CrossRef]
- Labeyrie, M.; Mage, J.; Robinson, T. Characterisation of Strontium Hexaferrite for Millimeter Waves Applications. IEEE Trans. Magn. 1986, 22, 976–980. [Google Scholar] [CrossRef]
- Baker-Jarvis, J.; Vanzura, E.J.; Kissick, W.A. Improved Technique for Determining Complex Permittivity with the Transmission/Reflection Method. IEEE Trans. Microw. Theory Tech. 1990, 38, 1096–1103. [Google Scholar] [CrossRef]
- Lax, B.; Button, K.J. Microwave Ferrites and Ferrimagnetics; McGrow-Hill: New York, NY, USA, 1962. [Google Scholar]
- Bosma, H. On Stripline Y-Circulation at UHF. IEEE Trans. Microw. Theory Tech. 1964, 12, 61–72. [Google Scholar] [CrossRef]
- Fay, C.E.; Comstock, R.L. Operation of the Ferrite Junction Circulator. IEEE Trans. Microw. Theory Tech. 1965, 13, 15–27. [Google Scholar] [CrossRef]
- Wu, Y.S.; Rosenbaum, F.J. Wide-Band Operation of Microstrip Circulators. IEEE Trans. Microw. Theory Tech. 1974, 22, 849–856. [Google Scholar] [CrossRef]
- Hexaferrite Materials. Available online: https://www.domen.ru/files/upload/2020-12-24_15:46:22_25d13f31ce5136b6.pdf (accessed on 12 November 2022). (In Russian).



| 4πMs, kGs | 4πMr , kGs | Hc, kOe | εf | tan δf | ΔH, Oe | ΔHeff, Oe |
|---|---|---|---|---|---|---|
| 4.5 | 4.0 | 19.1 | 25 | 0.002 | 1000 | 20 |
| Junction Resonators | ts, mm | Rd, mm | atri, mm | RL *, dB | Iso *, dB | IL *, dB |
|---|---|---|---|---|---|---|
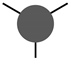 | 0.17 | 0.93 | - | 37.9 | 28.4 | 1.33 |
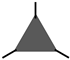 | 0.09 | - | 2.46 | 33.7 | 21.5 | 1.66 |
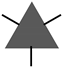 | 0.34 | - | 2.02 | 31.5 | 25.7 | 1.71 |
| ts, mm | IL, dB | RL, dB | Iso, dB | FBW, % |
|---|---|---|---|---|
| 0.253 | 1.58 | 24.27 | 24.0 | 3.5 |
| 0.17 | 1.33 | 39.7 | 28.4 | 5.6 |
| 0.14 | 1.31 | 27.8 | 35.4 | 6.7 |
| 0.12 | 1.29 | 26.0 | 38.6 | 6.9 |
| Material | 4πMs, kOe | 4πMr, kOe | Ha, kOe | εf | tan δf | ΔH, Oe |
|---|---|---|---|---|---|---|
| 08СЧА5В | 3.4 | 3.06 | 6 | 17 | 0.001 | 2500 |
| 08СЧА1В | 3.7 | 3.33 | 11 | 17 | 0.001 | 2500 |
| f0, GHz | Case | a | w1 | w2 | w3 | w4 | g1 | d1 | y | R0 * |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | SD | 12.0 | 0.35 | 1.17 | 1.1 | 4.0 | 0.2 | 0.4 | 1.65 | 2.9 |
| ND | 12.0 | 0.08 | 0.62 | 1.3 | 4.0 | 0.2 | 0.1 | 1.75 | 3.6 | |
| 6 | SD | 6.0 | 0.17 | 0.95 | 0.6 | 3.0 | 0.2 | 0.2 | 0.75 | 2.5 |
| ND | 6.0 | 0.08 | 0.93 | 0.6 | 2.8 | 0.2 | 0.1 | 1.30 | 2.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Schuchinsky, A.; Joseph, S.; Eker, T.; Huang, Y. Loss Mitigation in Self-Biased Microstrip Circulators. Magnetism 2023, 3, 121-134. https://doi.org/10.3390/magnetism3020010
Kong L, Schuchinsky A, Joseph S, Eker T, Huang Y. Loss Mitigation in Self-Biased Microstrip Circulators. Magnetism. 2023; 3(2):121-134. https://doi.org/10.3390/magnetism3020010
Chicago/Turabian StyleKong, Lingqi, Alexander Schuchinsky, Sumin Joseph, Taylan Eker, and Yi Huang. 2023. "Loss Mitigation in Self-Biased Microstrip Circulators" Magnetism 3, no. 2: 121-134. https://doi.org/10.3390/magnetism3020010
APA StyleKong, L., Schuchinsky, A., Joseph, S., Eker, T., & Huang, Y. (2023). Loss Mitigation in Self-Biased Microstrip Circulators. Magnetism, 3(2), 121-134. https://doi.org/10.3390/magnetism3020010









