New Framework to Study Electromagnetic Turbulence
Abstract
1. Introduction
1.1. Modification of Maxwell’s Equations
1.2. The Electromagnetic Viscosity Term
1.3. Time Rate of Magnetic Reconnection
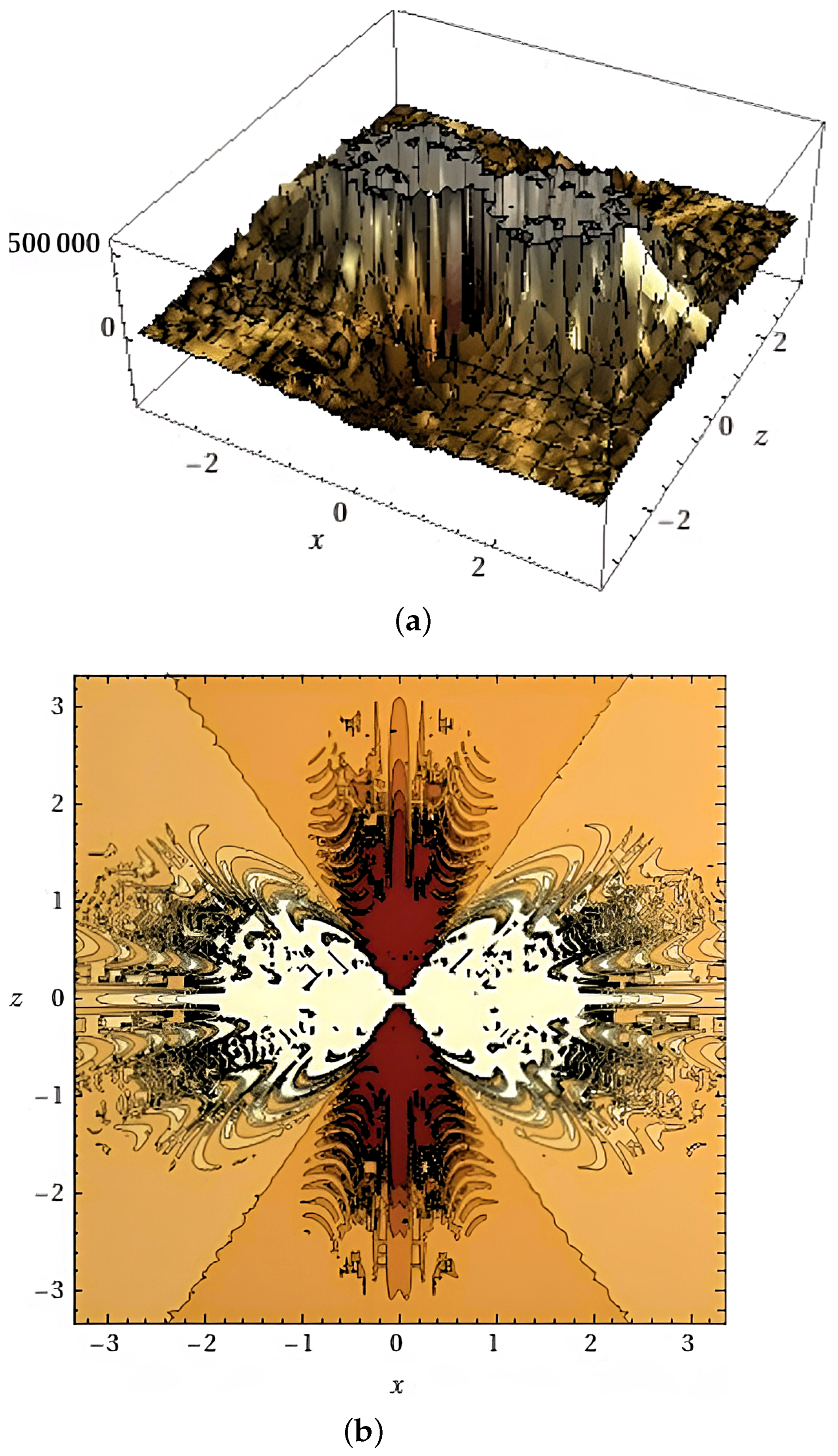
2. Spiral Structures and Turbulence
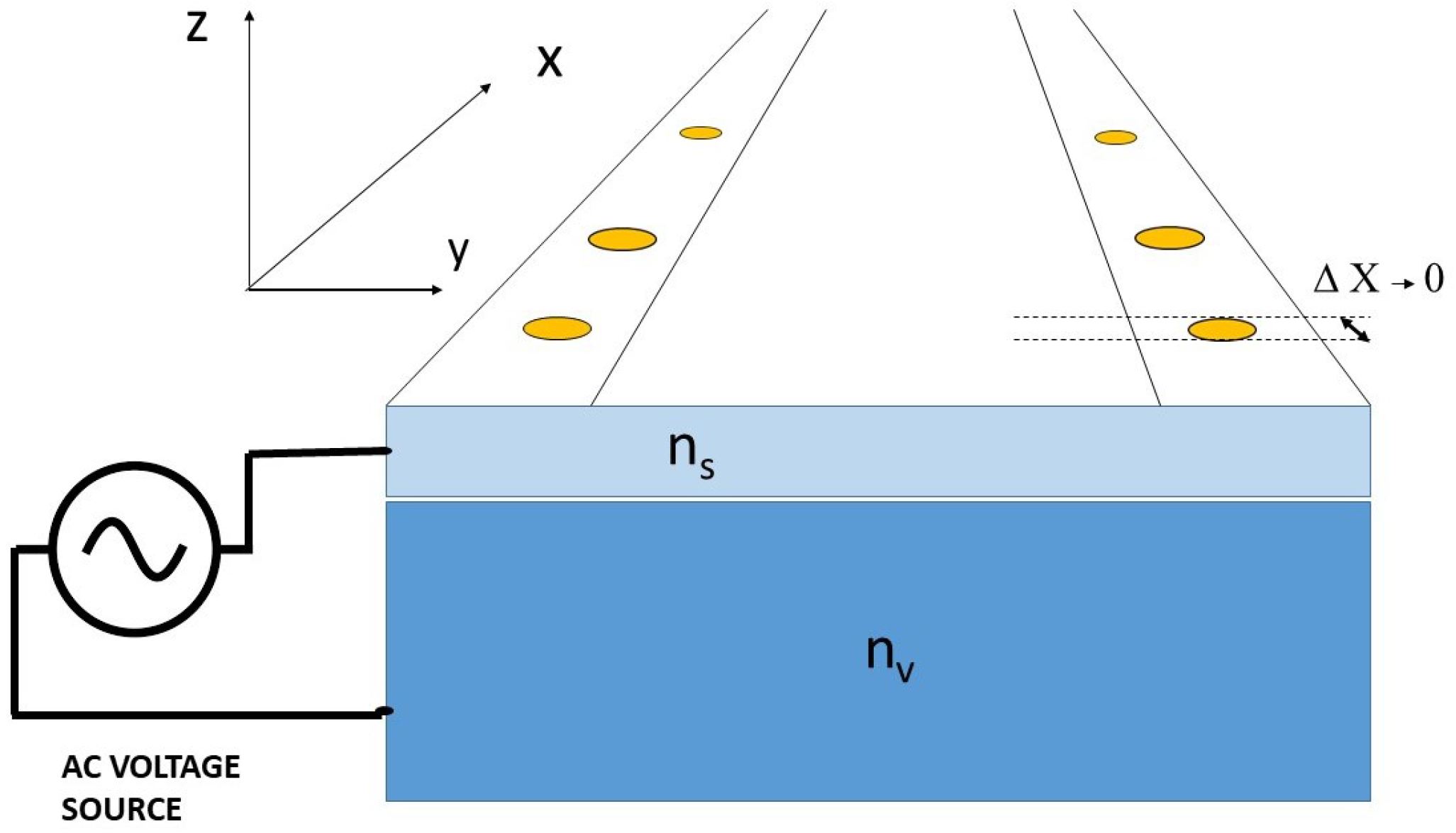
Controlled Electromagnetic Turbulence
3. Conclusions
Funding
Conflicts of Interest
References
- Tsytovich, V.N. Development of the Concepts of Plasma Turbulence. Sov. Phys. Usp. 1973, 15, 632. [Google Scholar] [CrossRef]
- Marsch, E. Kinetic Physics of the Solar Corona and Solar Wind. Living Rev. Sol. Phys. 2006, 3, 1–100. [Google Scholar] [CrossRef]
- Krommes, J.A. The Gyrokinetic Description of Microturbulence in Magnetized Plasmas. Annu. Rev. Fluid Mech. 2012, 44, 175–201. [Google Scholar] [CrossRef]
- Antoni, V.; Spada, E.; Vianello, N.; Spolaore, M.; Cavazzana, R.; Serianni, G.; Martines, E. Shear flows generated by plasma turbulence and their influence on transport. Plasma Phys. Control. Fusion 2005, 47, B13. [Google Scholar] [CrossRef]
- Biglari, H.; Diamond, P.H.; Terry, P.W. Influence of sheared poloidal rotation on edge turbulence. Phys. Fluids B 1990, 2, 1–4. [Google Scholar] [CrossRef]
- Burrell, K.H. Effects of EB velocity shear and magnetic shear on turbulence and transport in magnetic confinement devices. Phys. Plasmas 1997, 4, 1499–1518. [Google Scholar] [CrossRef]
- Keith, W.; Heikkila, W. Earth´s Magnetosphere Formed by the Low-Latitude Boundary Layer; Academic Press: London, UK, 2021. [Google Scholar]
- Hagelaar, G.J.M.; Oudini, N. Plasma transport across magnetic field lines in low-temperature plasma sources. Plasma Phys. Control. Fusion 2011, 53, 124032. [Google Scholar] [CrossRef]
- Saffman, P.G. Weak interactions and coherent structures in turbulence. In Transition and Turbulence; Meyer, R.E., Ed.; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Kiehn, R.M. Instability Patterns, Wakes and Topological Limit Sets. In Eddy Structure Identification in Free Turbulent Shear Flows. Fluid Mechanics and Its Applications; Bonnet, J.P., Glauser, M.N., Eds.; Springer: Dordrecht, The Netherlands, 1993; Volume 21. [Google Scholar]
- Wu, W.; Wang, J. Nonequilibrium thermodynamics of turbulence and stochastic fluid systems. New J. Phys. 2020, 22, 113017. [Google Scholar] [CrossRef]
- Martyushev, L.M. Maximum entropy production principle: History and current status. Phys.-Uspekhi 2021, 64, 558. [Google Scholar] [CrossRef]
- Rao, S. Modeling of Turbulent Flows and Boundary Layer. In Computational Fluid Dynamics; OH, H.W., Ed.; Books on Demand: Norderstedt, Germany, 2010; p. 285. [Google Scholar]
- Kadivara, M.; Tormey, D.; McGranaghan, G. A review on turbulent flow over rough surfaces: Fundamentals and theories. Int. J. Thermofluids 2021, 10, 100077. [Google Scholar] [CrossRef]
- Marmanis, H. Analogy between the Navier–Stokes equations and Maxwell’s equations: Application to turbulence. Phys. Fluids 1998, 10, 1428–1437. [Google Scholar] [CrossRef]
- Stawarz, J.E.; Matteini, L.; Parashar, T.N.; Franci, L.; Eastwood, J.P.; Gonzalez, C.A.; Gingell, I.L.; Burch, J.L.; Ergun, R.E.; Ahmadi, N.; et al. Comparative analysis of the various generalized Ohm’s law terms in magnetosheath turbulence as observed by Magnetospheric Multiscale. JGR Space Phys. 2021, 126, e2020JA028447. [Google Scholar] [CrossRef]
- Goedbloed, H.; Keppens, R.; Poedts, S. Magnetohydrodynamics of Laboratory and Astrophysical Plasmas; Cambridge University Press: Cambdridge, UK, 2019. [Google Scholar]
- Gao, X.-Z.; Pan, Y.; Zhao, M.-D.; Zhang, G.-L.; Zhang, Y.; Tu, C.; Li, Y.; Wang, H.-T. Focusing behavior of the fractal vector optical fields designed by fractal lattice growth model. Opt. Express 2018, 26, 1597–1614. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Gao, X.-Z.; Zhang, X.; Zhao, J.-H.; Zhao, P.-C.; Li, Y.; Tu, C.; Wang, H.-T. Diffraction properties and applications of spatially structured optical fields with fractal amplitude masks. Appl. Opt. 2019, 58, 8631–8637. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Sun, S.L.; Xiao, S.Y.; Li, X.; Song, Z.Y.; Sun, W.J.; Zhou, L. Manipulating electromagnetic waves with metamaterials: Concept and microwave realizations. Chin. Phys. B 2014, 23, 047808. [Google Scholar] [CrossRef]
- Lin, L.G.; Jian, T.; Hong, W.S. Research on Stealth Aircraft Control Circuit and Realization of Software Radio. IOP Conf. Ser. Mater. Sci. Eng. 2018, 439, 052021. [Google Scholar] [CrossRef]
- Mathur, S.; Mukhtar, A. Achieving near light speed to faster than light speed via wave propagation and electromagnetic field propulsion. Aeron Aero Open Access J. 2021, 5, 103–106. [Google Scholar]
- Lee, H.Y.; Kwak, M.S.; Lim, K.; Ahn, H.S.; Hwang, G.-T.; Ha, D.H.; Taylor, R.A.; Yi, S.N. Harvesting electrical energy using plasmon-enhanced light pressure in a platinum cut cone. Opt. Express 2021, 29, 35161–35171. [Google Scholar] [CrossRef]
- Lesieur, M. La Turbulence; Press Universitaires de Grenoble: Grenoble, France, 1994; p. 39. [Google Scholar]
- Martins, A.A.; Pinheiro, M.J. Fluidic electrodynamics: Approach to electromagnetic propulsion. Phys. Fluids 2009, 21, 097103. [Google Scholar] [CrossRef]
- Marmanis, H. Analogy between the Electromagnetic and Hydrodynamic Equations: Application to Turbulence. Ph.D. Thesis, Brown University, Providence, RI, USA, 1999. [Google Scholar]
- Batchelor, G.K. On the Spontaneous Magnetic Field in a Conducting Liquid in Turbulent Motion. Proc. R. Soc. A 1950, 201, 405. [Google Scholar]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Materials Processing; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- RBalescu; Senatorski, A. A new approach to the theory of fully developed turbulence. Ann. Phys. 1970, 58, 587–624. [Google Scholar] [CrossRef]
- Chen, H.; Kandasamy, S.; Orszag, S.; Shock, R.; Succi, S.; Yakhot, V. Extended Boltzmann kinetic equation for turbulent flows. Science 2003, 301, 633–636. [Google Scholar] [CrossRef] [PubMed]
- Biskamp, D. Magnetic Reconnection in Plasmas; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Lowes, F.J. Measuring magnetic field in the ‘diamagnetic’ ionosphere. Geophys. J. Int. 2007, 171, 115–118. [Google Scholar] [CrossRef]
- Schmidt, G. Physics of High-Temperature Plasmas—An Introduction; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Bhattacharjee, C. Classifying diamagnetic states of plasma near Schwarzschild event horizon: Local approximation. Phys. Lett. A 2020, 384, 126698. [Google Scholar] [CrossRef]
- Wang, W.; Liu, R.; Wang, Y.; Hu, Q.; Shen, C.; Jiang, C.; Zhu, C. Buildup of a highly twisted magnetic flux rope during a solar eruption. Nat. Commun. 2017, 8, 1330. [Google Scholar] [CrossRef]
- Chatwin, P. The vorticity equation as an angular momentum equation. Math. Proc. Camb. Philos. Soc. 1973, 74, 365–367. [Google Scholar] [CrossRef]
- Okamoto, N.; Davidson, P.A.; Kaneda, Y. On the decay of low-magnetic-Reynolds-number turbulence in an imposed magnetic field. J. Fluid Mech. 2010, 651, 295–318. [Google Scholar] [CrossRef]
- Zolotorev, M.S.; McDonald, K.T. Diffraction as a consequence of Faraday’s law. Am. J. Phys. 2000, 68, 674. [Google Scholar] [CrossRef]
- Kline, M. Electromagnetic Theory and Geometrical Optics; Research Report No. EM-171; New York University: New York, NY, USA, 1963. [Google Scholar]
- Marathay, A.S.; McCalmont, J.F. Vector diffraction theory for electromagnetic waves. J. Opt. Soc. Am. A 2001, 18, 2585–2593. [Google Scholar] [CrossRef]
- Fujii, M. A new mode of radio wave diffraction via the terrestrial surface plasmons on mountain range. Radio Sci. 2016, 51, 1396–1412. [Google Scholar] [CrossRef]
- Sreenivasan, K.; Meneveau, C. The fractal facets of turbulence. J. Fluid Mech. 1986, 173, 357–386. [Google Scholar] [CrossRef]
- Dubief, Y.; Delcayre, F. On coherent-vortex identification in turbulence. J. Turbul. 2000, 1, 011. [Google Scholar] [CrossRef]
- Zada, I.; Zhang, W.; Li, Y.; Sun, P.; Cai, N.; Gu, J.; Liu, Q.; Su, H.; Zhang, D. Angle dependent antireflection property of TiO2 inspired by cicada wings. Appl. Phys. Lett. 2016, 109, 153701. [Google Scholar] [CrossRef]
- Paratore, F.; Boyko, E.; Kaigala, G.V.; Bercovici, M. Electroosmotic Flow Dipole: Experimental Observation and Flow Field Patterning. Phys. Rev. Lett. 2019, 122, 224502. [Google Scholar] [CrossRef] [PubMed]
- Tu, N.H.; Yoshioka, K.; Sasaki, S.; Takamura, M.; Muraki, K.; Kumada, N. Active spatial control of terahertz plasmons in graphene. Commun. Mater. 2020, 1, 7. [Google Scholar] [CrossRef]
- Kim, J.; Han, K.; Hahn, J.W. Selective dual-band metamaterial perfect absorber for infrared stealth technology. Sci. Rep. 2017, 7, 6740. [Google Scholar] [CrossRef]
- Mouritz, A.P. (Ed.) Polymers for aerospace structures. In Introduction to Aerospace Materials; Woodhead Publishing: Sawston, UK, 2012; pp. 268–302. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinheiro, M.J. New Framework to Study Electromagnetic Turbulence. Magnetism 2022, 2, 356-367. https://doi.org/10.3390/magnetism2040025
Pinheiro MJ. New Framework to Study Electromagnetic Turbulence. Magnetism. 2022; 2(4):356-367. https://doi.org/10.3390/magnetism2040025
Chicago/Turabian StylePinheiro, Mario J. 2022. "New Framework to Study Electromagnetic Turbulence" Magnetism 2, no. 4: 356-367. https://doi.org/10.3390/magnetism2040025
APA StylePinheiro, M. J. (2022). New Framework to Study Electromagnetic Turbulence. Magnetism, 2(4), 356-367. https://doi.org/10.3390/magnetism2040025





