Wearable Inductive Sensing of the Arm Joint: Comparison of Three Sensing Configurations
Abstract
:1. Introduction
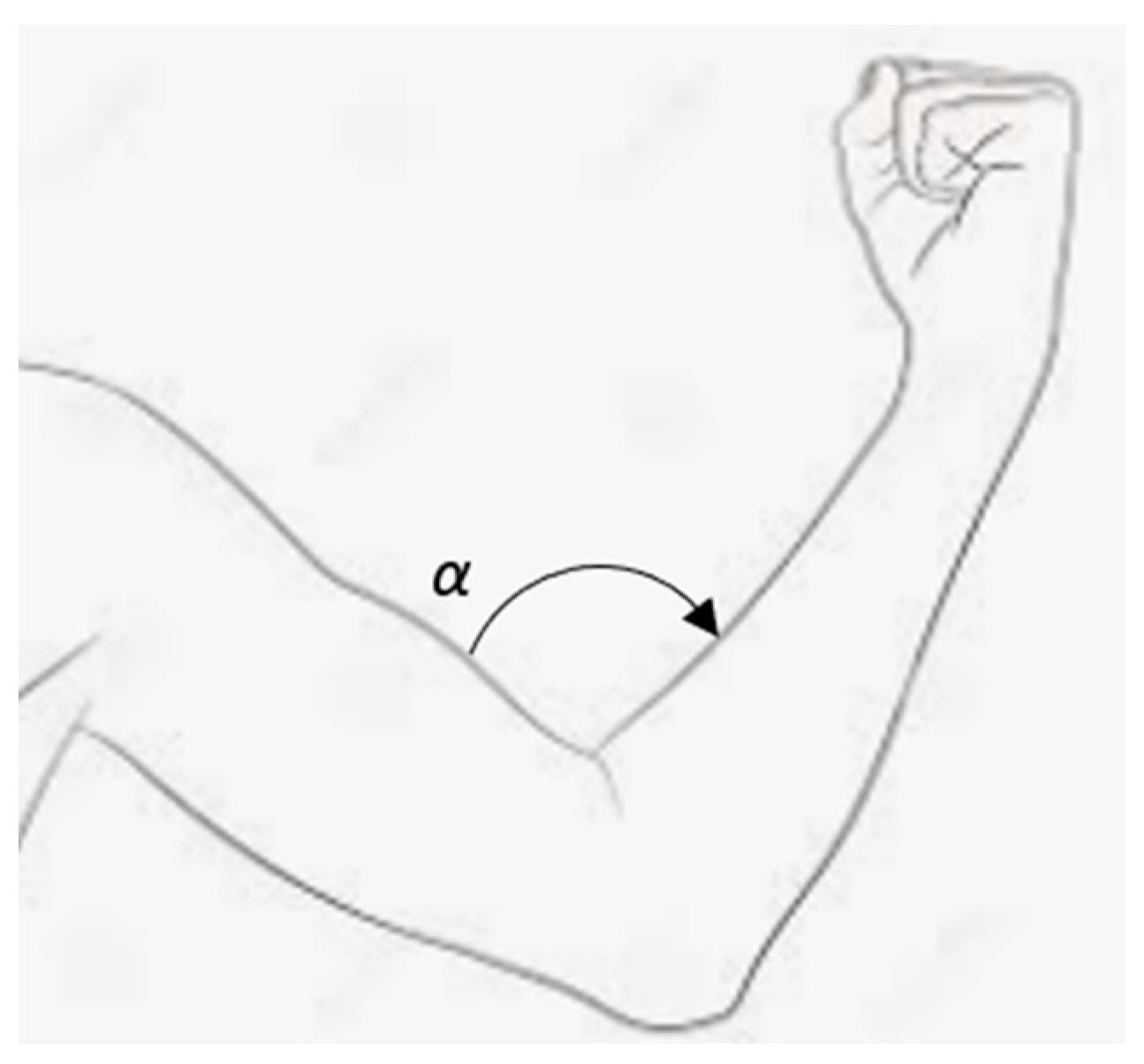
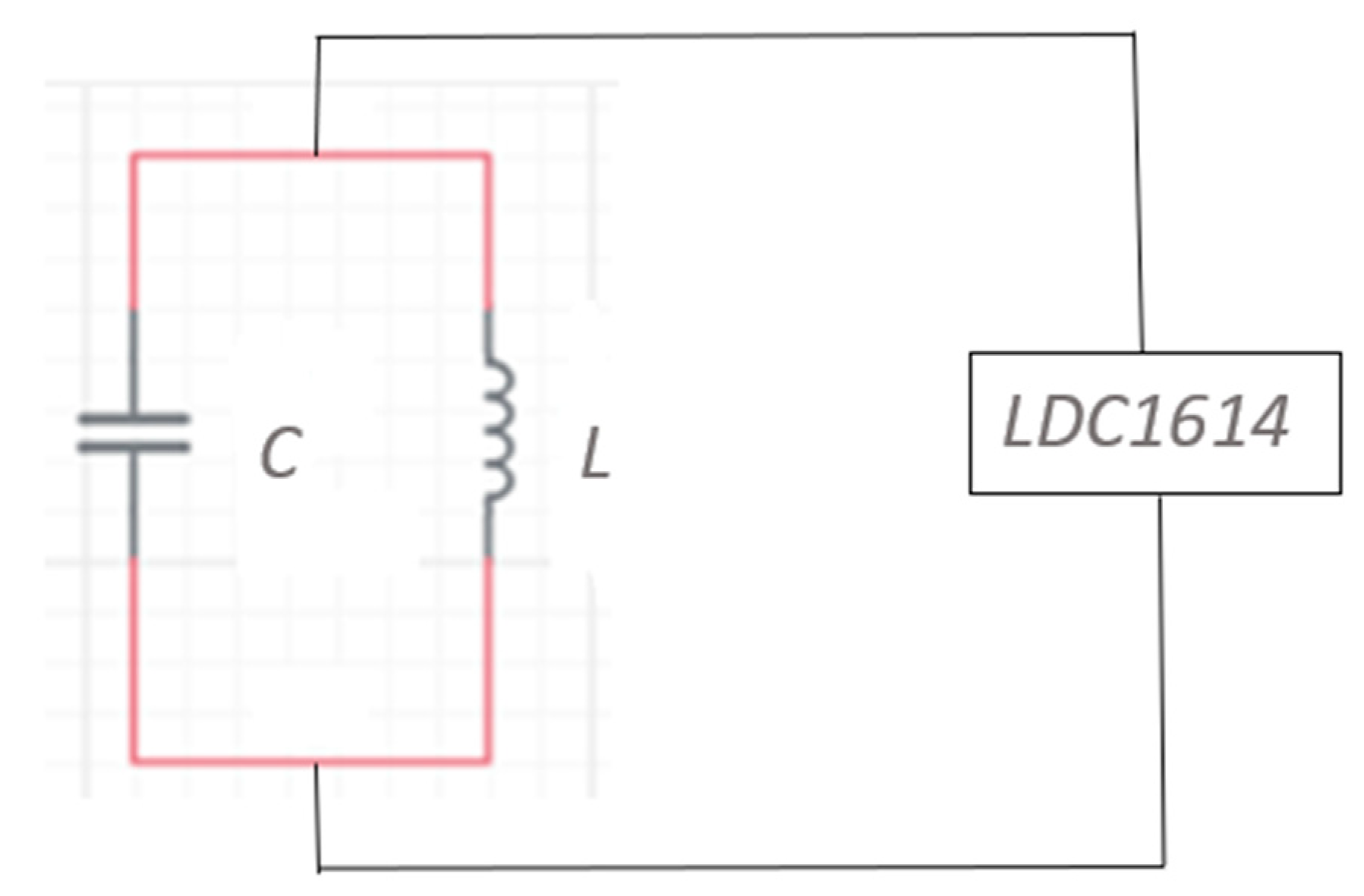
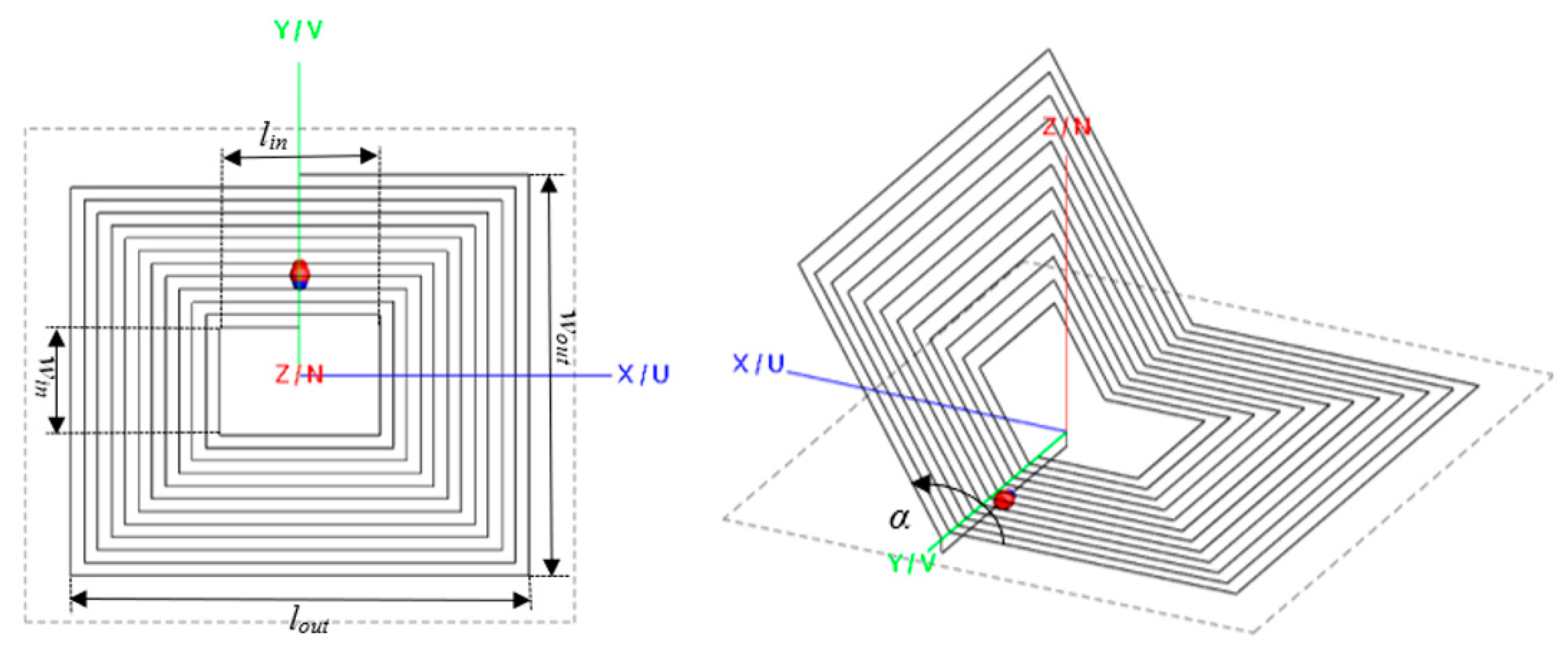
2. Methodology
3. Simulation Results
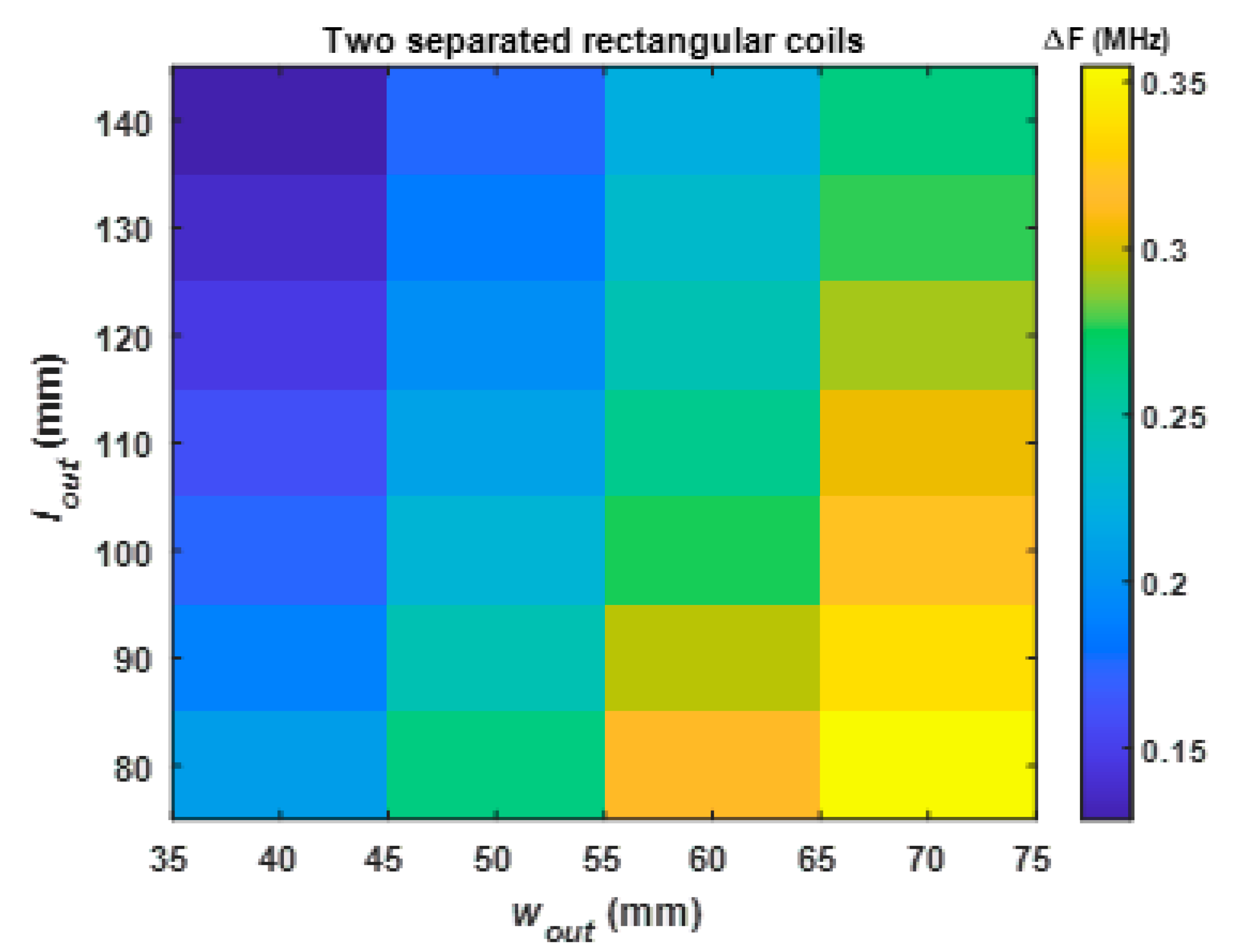
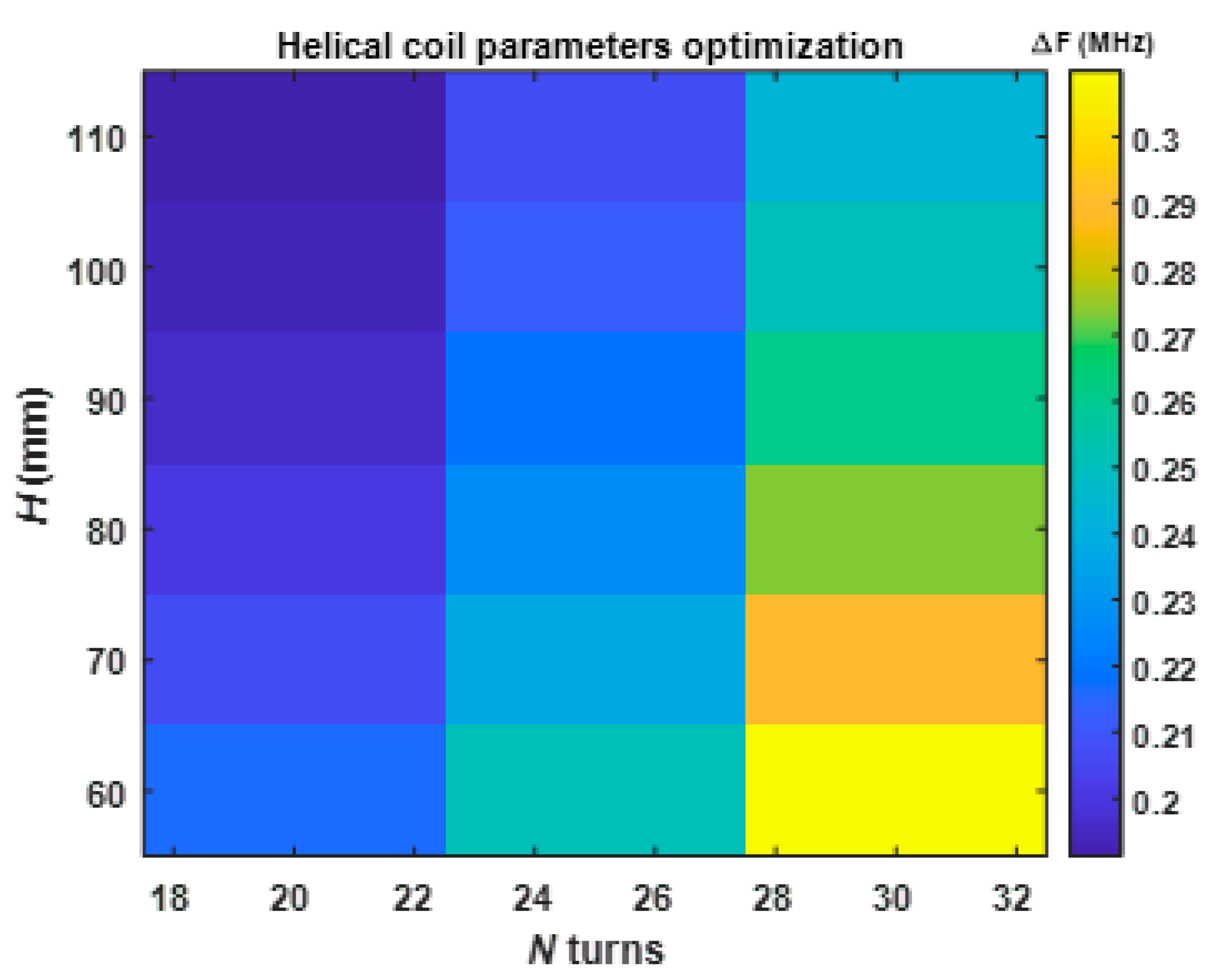
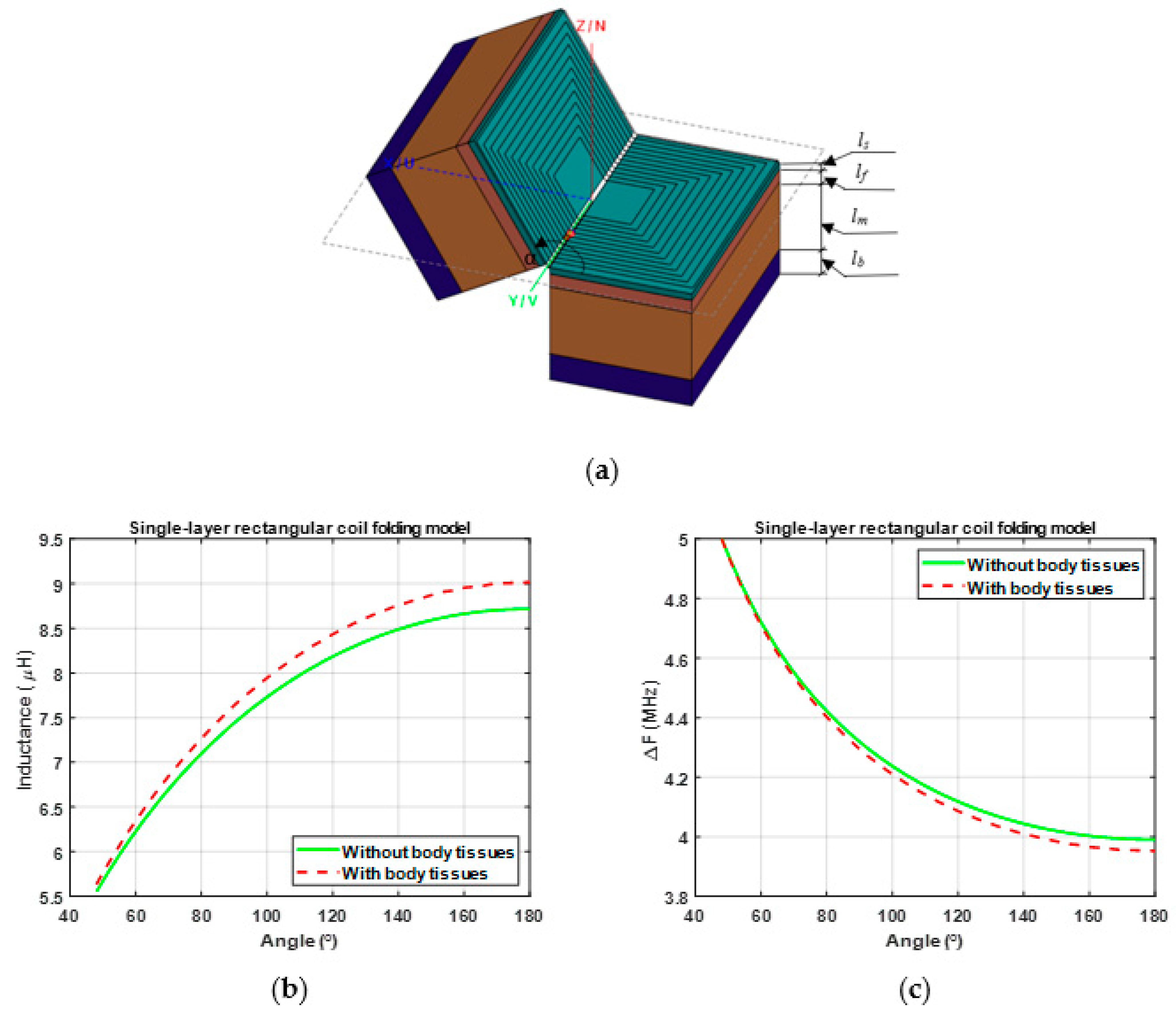
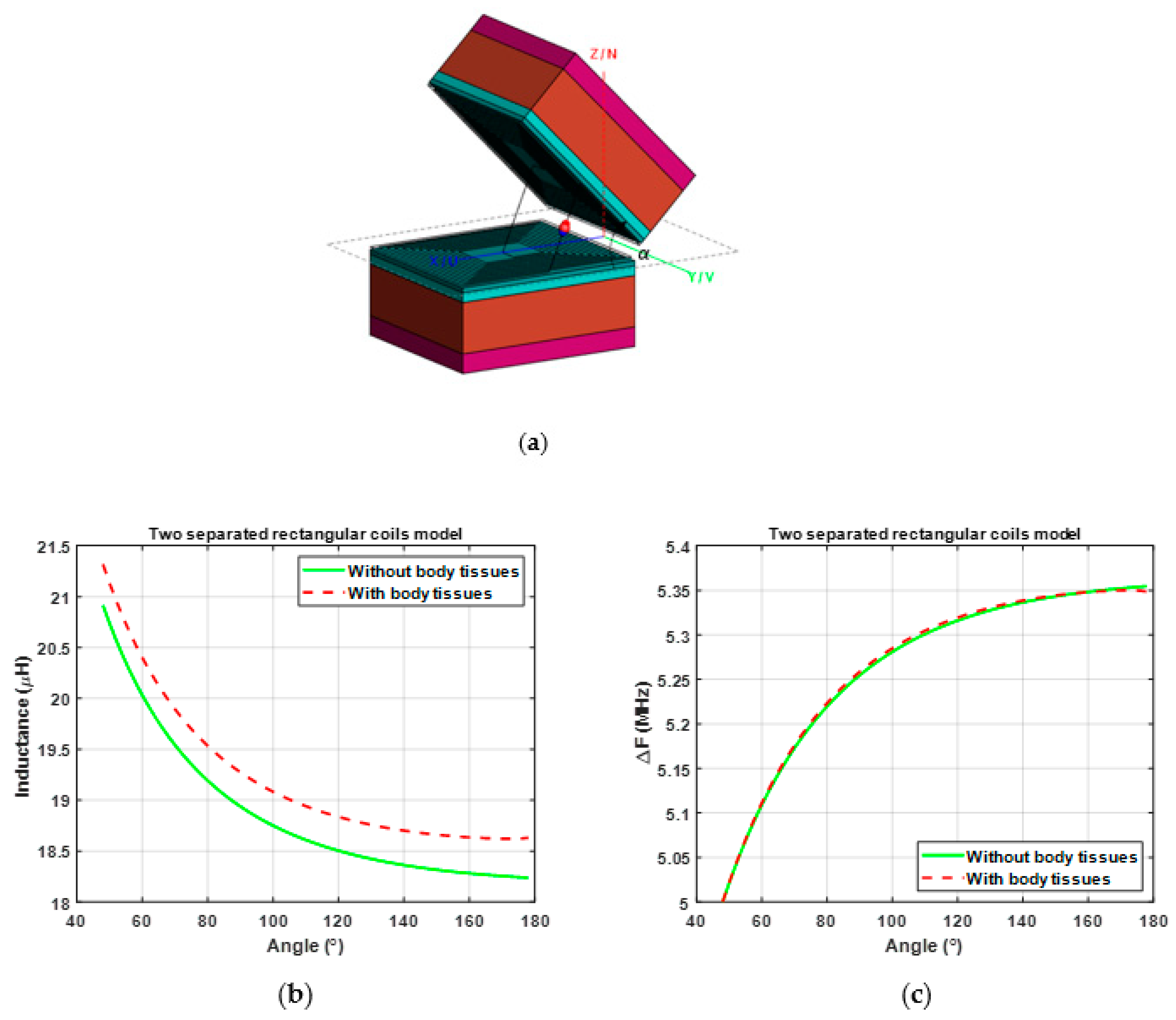
3.1. Parametric Study of the Sensing Configurations
3.2. Effect of Arm Tissues
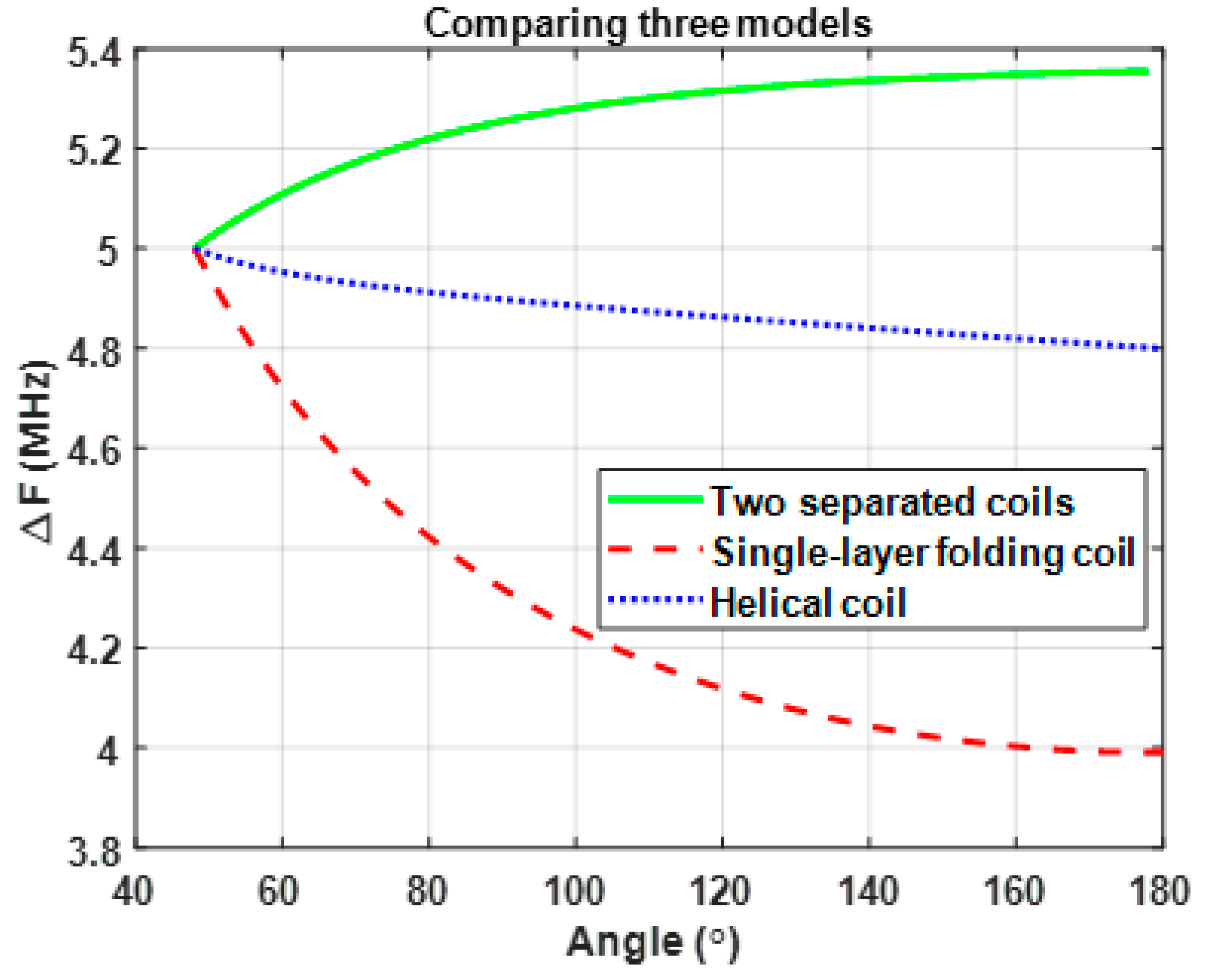
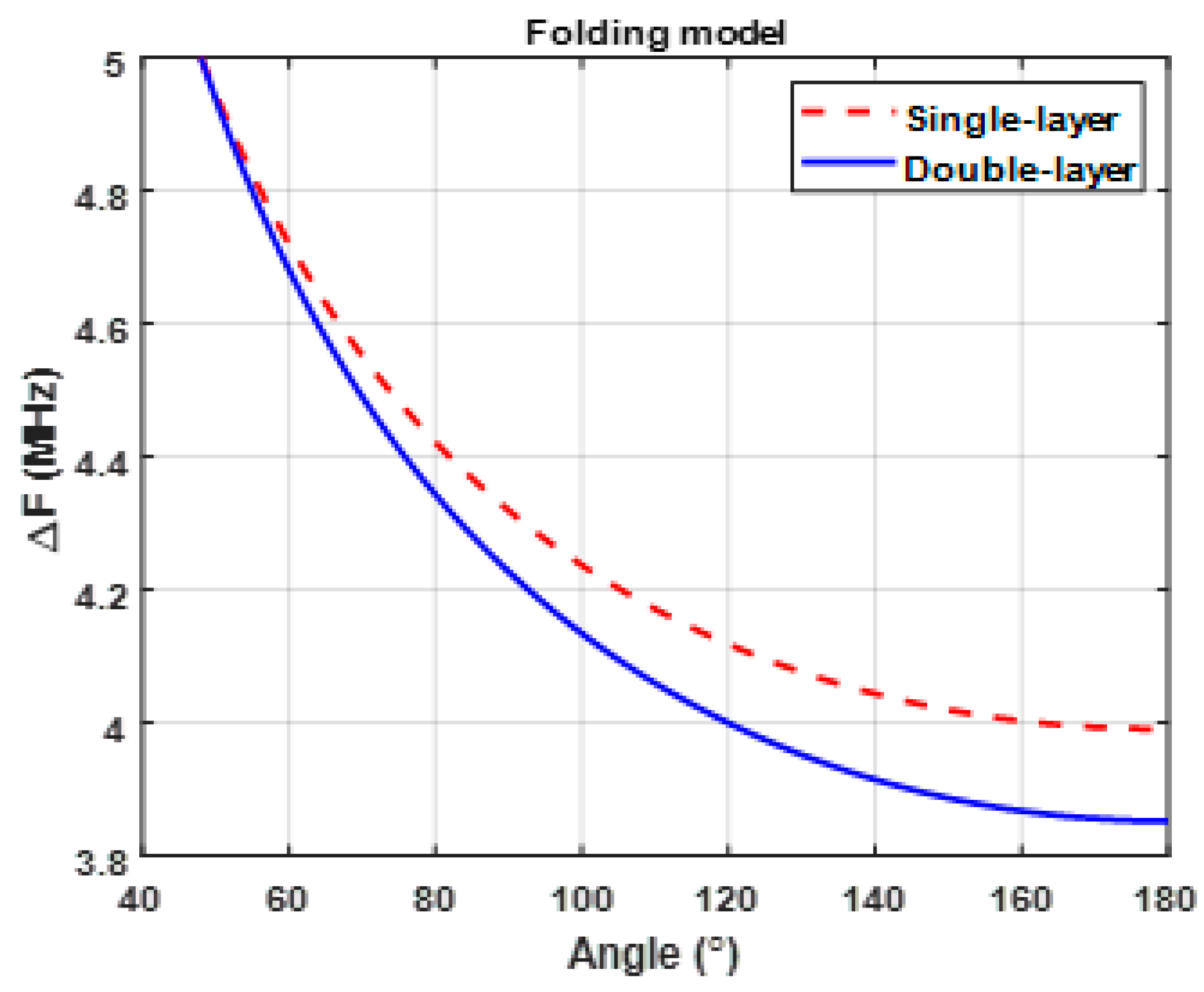
3.3. Comparing Single- and Double-Layer Folding Coils
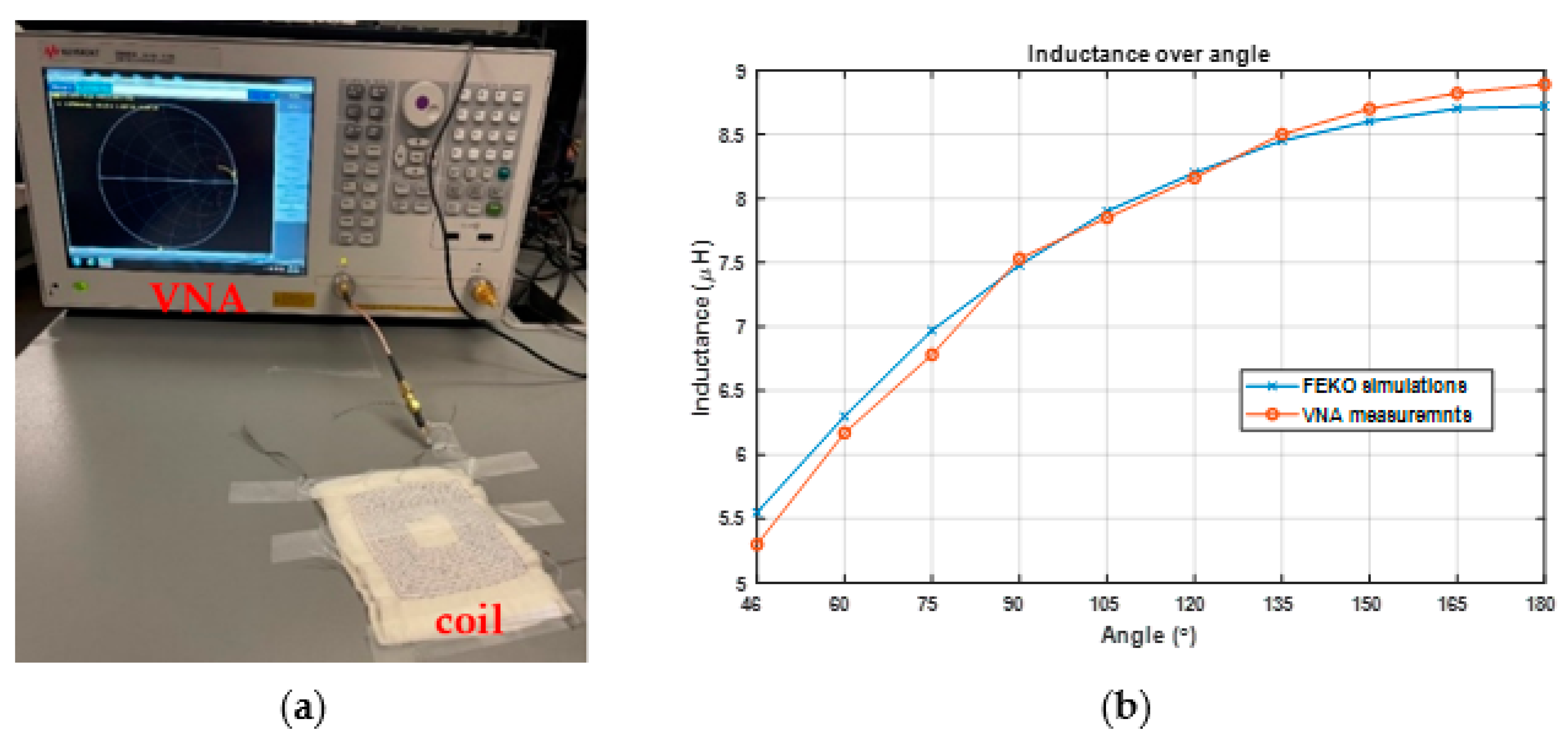
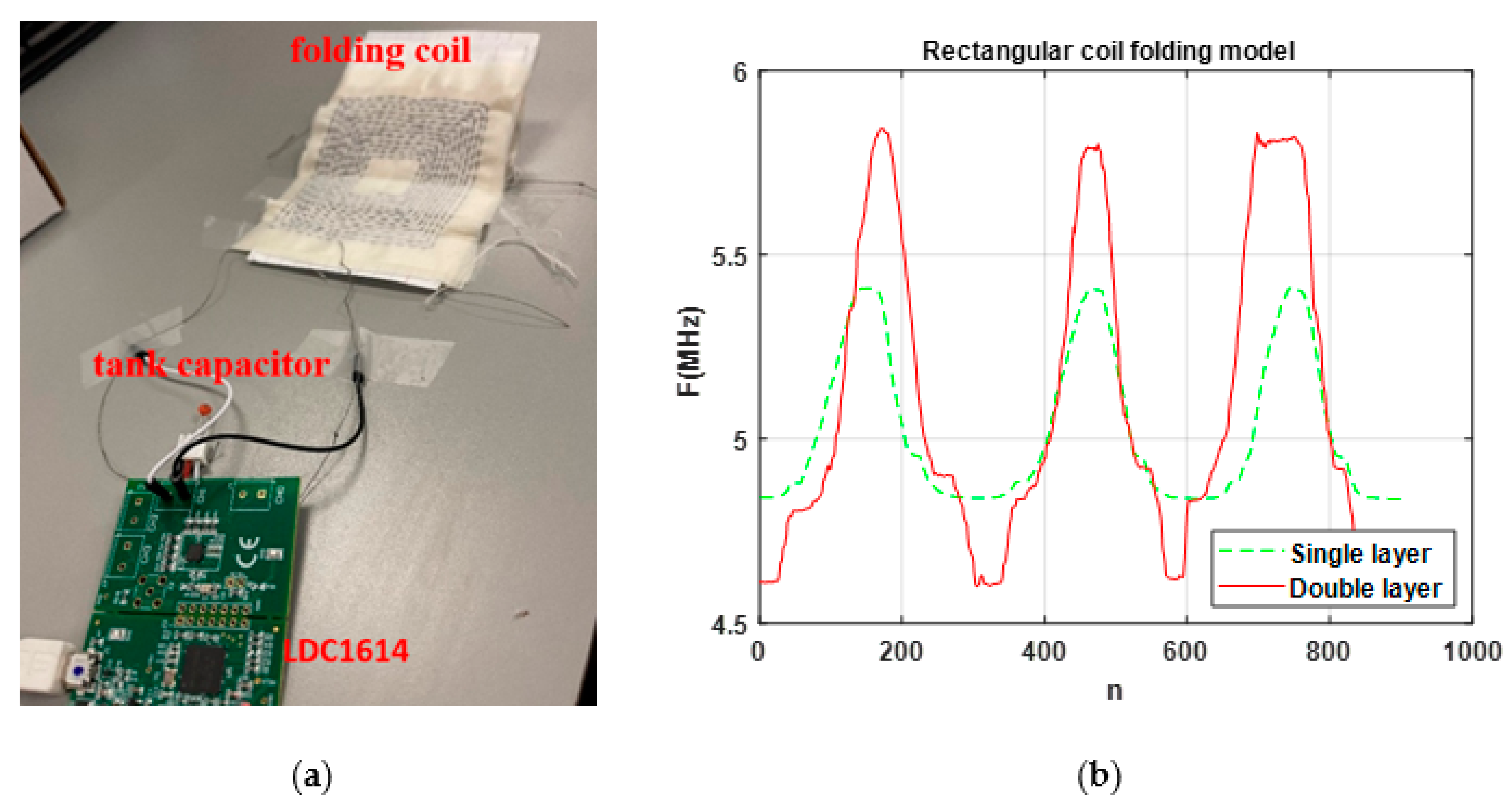
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wyatt, F. Sensing Methods for soft Robotics. Ph.D. Thesis, Mechanical Enginnering, University of Michigan, Ann Arbor, MI, USA, 2017. [Google Scholar]
- Blachowicz, T.; Ehrmann, G.; Ehrmann, A. Textile-based sensors for bio signal detection and monitoring. Sensors 2021, 21, 6042. [Google Scholar] [CrossRef] [PubMed]
- Herbert, R.; Kim, J.-H.; Kim, Y.S.; Lee, H.M.; Yeo, W.-H. Soft Material-Enabled, Flexible Hybrid Electronics for Medicine, Healthcare, and Human-Machine Interfaces. Materials 2018, 11, 187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patel, S.; Park, H.; Bonato, P.; Chan, L.; Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. Neuroeng. Rehabil. 2012, 9, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biscaldi, M.; Rauh, R.; Irion, L.; Jung, N.H.; Mall, V.; Fleischhaker, C.; Klein, C. Deficits in motor abilities and developmental frac-tionation of imitation performance in high-functioning autism spectrum disorders. Eur. Child Adolesc. Psychiatry 2013, 23, 599–610. [Google Scholar] [CrossRef] [PubMed]
- McLinden, J.; Deligani, R.J.; Abtahi, M.R.; Akbar, U.; Mankodiya, K.; Shahriari, Y. Disruptions of cortico-kinematic interactions in Parkinson’s disease. Behav. Brain. Res. 2021, 404, 113153. [Google Scholar] [CrossRef]
- Islam, G.M.N.; Ali, M.A.; Collie, S. Textile sensors for wearable applications: A comprehensive review. Cellulose 2020, 27, 6103–6131. [Google Scholar] [CrossRef]
- Zheng, Y.-L.; Ding, X.-R.; Yan Poon, C.-C.; Lai Lo, B.-P.; Zhang, H.; Zhou, X.-L.; Yang, G.-Z.; Zhao, N.; Zhang, Y.-T. Unobtrusive sensing and wearable devices for health informatics. IEEE Trans. Biomed. Eng. 2014, 61, 1538–1554. [Google Scholar] [CrossRef]
- Amjadi, M.; Kyung, K.U.; Park, I.; Sitti, M. Stretchable, skin-mountable, and wearable strain sensors and their potential applications: A review. Adv. Funct. Mater. 2016, 26, 11. [Google Scholar] [CrossRef]
- Chen, H.; Lv, L.; Zhang, J.; Zhang, S.; Xu, P.; Li, C.; Zhang, Z.; Li, Y.; Xu, Y.; Wang, J. Enhanced Stretchable and Sensitive Strain Sensor via Controlled Strain Distribution. Nanomaterials 2020, 10, 218. [Google Scholar] [CrossRef] [Green Version]
- Tan, C.; Dong, Z.; Li, Y.; Zhao, H.; Huang, X.; Zhou, Z.; Jiang, J.-W.; Long, Y.-Z.; Jiang, P.; Zhang, T.-Y.; et al. A high performance wearable strain sensor with advanced thermal management for motion monitoring. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef]
- Atalay, O. Textile-Based, Interdigital, Capacitive, Soft-Strain Sensor for Wearable Applications. Materials 2018, 11, 768. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, J.; Niu, M.; Yang, C. Highly flexible and stretchable optical strain sensing for human motion detection. Optical 2017, 4, 10. [Google Scholar] [CrossRef]
- Tavassolian, M.J.; Cuthbert, T.; Napier, C.; Peng, J.Y.; Menon, C. Textile-based inductive soft strain Sensors for fast frequency movement and their application in wearable devices measuring multiaxial hip joint angles during running. Adv. Intell. Syst. 2020, 2, 1900165. [Google Scholar] [CrossRef]
- Souri, H.; Banerjee, H.; Jusufi, A.; Radacsi, N.; Stokes, A.A.; Park, I.; Sitti, M.; Amjadi, M. Wearable and Stretchable Strain Sensors: Materials, Sensing Mechanisms, and Applications. Adv. Intell. Syst. 2020, 2, 39. [Google Scholar] [CrossRef]
- García Patiño, A.; Menon, C. Inductive textile sensor design and validation for a wearable monitoring device. Sensors 2021, 21, 225. [Google Scholar] [CrossRef]
- Mutashar, S.A.; Hannan, M.A.; Samad, S.; Hussain, A. Analysis and optimization of spiral circular inductive coupling Link for bio-implanted applications on air and within human tissue. Sensors 2014, 14, 11522–11541. [Google Scholar] [CrossRef] [Green Version]
- Gong, J.; Wu, Y.; Yan, L.; Seyed, T.; Yang, X.D. Tessutivo: Contextual interactions on interactive fabrics with inductive sensing. In Proceedings of the ACM Symposium on User Interface Software and Technology, New Orleans, LA, USA, 20–23 October 2019. [Google Scholar]
- Mehri, S.; Ammari, A.C.; Slama, J.B.H.; Rmili, H. Geometry Optimization Approaches of Inductively Coupled Printed Spiral Coils for Remote Powering of Implantable Biomedical Sensors. J. Sens. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Kiener, K.; Anand, A.; Fobelets, W. Low Power Respiration Monitoring Using Wearable 3D Knitted Helical Coils. IEEE Sens. J. 2021, 22, 1374–1381. [Google Scholar] [CrossRef]
- Fobelets, K.; Panteli, C. Proceeding paper ambulatory monitoring using knitted 3D helical coils. Eng. Proc. 2022, 15, 6. [Google Scholar]
- Wang, H.; Totaro, M.; Veerapandian, S.; Ilyas, M.; Kong, M.; Jeong, U.; Beccai, L. Folding and Bending Planar Coils for Highly Precise Soft Angle Sensing. Adv. Mater. Technol. 2020, 5, 11. [Google Scholar] [CrossRef]
- García Patiño, A. Design and development of a wearable inductive textile sensor to monitor back movements. Sensors 2020, 20, 905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poliakine, J.; Civet, Y.; Perriarda, Y. Design and manufacturing of high inductance planar coils for small scale sensing applications. Proced. Eng. 2016, 168, 1127–1130. [Google Scholar] [CrossRef]
- Wijesiriwardana, R. Inductive fiber-meshed strain and displacement transducers for respiratory measuring systems and mo-tion capturing systems. IEEE Sens. J. 2006, 6, 3. [Google Scholar] [CrossRef]
- Yu Sh, Y.; Chen, R.; Viswanathan, A. In Proceedings of the Survey of resonant converter topologies. Texas Instruments Power Supply Design Seminar SEM, Dallas, Texas. 2018, p. 2300. Available online: https://www.ti.com/seclit/ml/slup376/slup376.pdf (accessed on 4 May 2022).
- Aldoumani, M.; Yuce, B.; Zhu, D. Using the variable geometry in a planar inductor for an optimized performance. Electronics 2021, 10, 721. [Google Scholar] [CrossRef]
- Altair Feko. Available online: https://www.altair.com/feko/ (accessed on 4 May 2022).
- MATLAB. Available online: https://www.mathworks.com/products/matlab.html (accessed on 4 May 2022).
- Adafruit, Stainless Thin Conductive Yarn/Thick Conductive Thread-30 ft. Available online: https://www.adafruit.com/product/603#technical-details (accessed on 4 May 2022).
- Sensor Design for Inductive Sensing Applications Using LDC, Application Report, Texas Instruments, SNOA930C, May 2021. Available online: https://www.ti.com/lit/an/snoa930c/snoa930c.pdf?ts=1655864799663 (accessed on 22 June 2022).
- Forro, S.D.; Munjal, A.; Lowe, J.B. Anatomy, Shoulder and Upper Limb, Arm Structure And Function; Treasure Island (FL), StatPearls 2022. Available online: https://www.ncbi.nlm.nih.gov/books/NBK507841/ (accessed on 4 May 2022).
- LDC1612, LDC1614 Multi-Channel 28-Bit Inductance to Digital Converter (LDC) for Inductive Sensing. Available online: https://www.ti.com/product/LDC1614 (accessed on 4 May 2022).
- Sensing Solutions EVM GUI Tool v1.10.0. Available online: https://www.ti.com/product/LDC1614#product-details (accessed on 4 May 2022).



| Dielectric Medium | Relative Permittivity | Conductivity (S/m) |
|---|---|---|
| Dry human skin | 493.88 | 0.095366 |
| Fat bovine | 16.555 | 0.027382 |
| Ovine Parallel Muscle Fibers | 169.09 | 0.6646 |
| Human Bone Cancellous | 110.18 | 0.059701 |
| Angle | FEKO Simulations | VNA Measurements | ||
|---|---|---|---|---|
| Impedance (Ω) | Inductance (µH) | Impedance (Ω) | Inductance (µH) | |
| 46 | 96 + j174.5 | 5.55 | 210 + j173 | 5.3 |
| 90 | 96.5 + j235 | 7.48 | 135 + j235.5 | 7.53 |
| 135 | 96.5 + j264.5 | 8.45 | 135 + j267 | 8.5 |
| 180 | 97 + j274 | 8.7217 | 170 + j280 | 8.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Byberi, A.; K. Amineh, R.; Ravan, M. Wearable Inductive Sensing of the Arm Joint: Comparison of Three Sensing Configurations. Magnetism 2022, 2, 195-210. https://doi.org/10.3390/magnetism2030015
Byberi A, K. Amineh R, Ravan M. Wearable Inductive Sensing of the Arm Joint: Comparison of Three Sensing Configurations. Magnetism. 2022; 2(3):195-210. https://doi.org/10.3390/magnetism2030015
Chicago/Turabian StyleByberi, Armanda, Reza K. Amineh, and Maryam Ravan. 2022. "Wearable Inductive Sensing of the Arm Joint: Comparison of Three Sensing Configurations" Magnetism 2, no. 3: 195-210. https://doi.org/10.3390/magnetism2030015
APA StyleByberi, A., K. Amineh, R., & Ravan, M. (2022). Wearable Inductive Sensing of the Arm Joint: Comparison of Three Sensing Configurations. Magnetism, 2(3), 195-210. https://doi.org/10.3390/magnetism2030015








