The Fluctuation Theorem and Its Practical Limitations: A Numerical Example

Abstract

The Fluctuation Theorem establishes a relationship between microscopic reversibility and macroscopic irreversible phenomena, such as dissipation. In this short paper, we present an elementary derivation of this theorem within the framework of stochastic thermodynamics. Beginning with a brief examination of the time-reversible laws of motion that rule at the microscopic level, we discuss how through coarse-graining we arrive at the principle of detailed balance. This principle, which was originally proved for equilibrium processes, is extended to out-of-equilibrium situations in order to arrive at the Fluctuation Theorem. Though this extension is theoretically sound, one of the main purposes of this paper is to show that the origin of the practical limitations encountered, when applying this theorem to processes lasting longer than a certain duration, can be explained by the paucity of unlikely events that arise in out-of-equilibrium processes. The numerical results from the one-dimensional, one-particle stochastic model that is introduced here agree very well with the Fluctuation Theorem and, at the same time, bring to light the limits of its applicability in relation to the number of simulations or experiments and the duration of the process under study.

1. Introduction

Since the establishment of Boltzmann’s celebrated H-theorem, there has been what appears to be an unending debate about how the irreversible and dissipative nature of macroscopic phenomena emerges from time-reversible laws of motion at the microscopic level [1,2,3,4,5].

The Fluctuation Theorem is a modern development in statistical physics that links the microscopic with the macroscopic world. It enables us to quantify irreversibility from the probability of the trajectory of a given process and the probability of the occurrence of its time-reversed image [6,7,8,9]. It establishes a relation between reversible trajectories and dissipation.

There exist several versions of the Fluctuation Theorem, and all of them are based on the assumption of microscopic reversibility. To give some context in relation to the role played by reversibility in our subject, we discuss this topic at two different levels: (1) the microscopic level, where the laws of motion are deterministic and time-reversible; and (2) the coarse-grained level, where probabilistic arguments are used in describing the evolution of a system.

Within a stochastic thermodynamic framework, in which the external forces applied on a system are of the same order of magnitude as the forces originating from thermal noise, we present an elementary deduction of the Fluctuation Theorem. We show that a key step within this deduction is the generalization of the principle of detailed balance to out-of-equilibrium processes.

The Fluctuation Theorem has been verified experimentally by performing delicate experiments in which forces are manipulated at the molecular scale [10,11,12].

Several models have been developed to numerically verify the Fluctuation Theorem. We can cite the Lennard-Jones fluid model of Chelli and co-workers [13]. Other non-Hamiltonian dynamical systems have been proposed for the same purpose (see references 5, 6, 8, 9, 13, 14, and 16 of Reference [13]). To test the Fluctuation Theorem, in this paper, we develop a simpler one-dimensional, one-particle stochastic model, in which work is done by the gravitational force. The dynamics of this model obey the generalization of detailed balance. Our numerical results show a very good agreement with the Fluctuation Theorem and, at the same time, reveal two of its practical limitations: one is related to the minimum number of repetitions of simulations or experiments, and the other sets a limit to the duration of the process under study. The elementary level of our exposition allows us to easily grasp the origin of these limitations in light of the generalization of the principle of detailed balance.

2. Dynamical and Coarse-Grained Microscopic Reversibility

At the most fundamental level, microscopic processes are assumed to be governed by deterministic and time-reversible dynamical laws. Imagine an ideal gas composed of structureless particles inside a rigid container, completely isolated from the exterior world. Assume that the Newtonian laws of motion are obeyed. Any state of this system can be represented by a point in a 6N-dimensional space. If we knew with infinite precision the state of the system (position and velocity of each particle) at a given moment, then we could determine the state of the system at any past or future time. To accurately state what we mean by a dynamical law that is both deterministic and has a time-reversible symmetry, we consider the following example. Assume that, at a time t_a, an isolated system is found in a microscopic state a—a state which precisely describes the positions and velocities of all particles comprising the system. Let us further assume that the particles are structureless entities so that we do not have to take into account any additional degrees of freedom. Let us say that, at later times, the system visits, in the following order, the microscopic states b, c, d, e. (It is important to stress that, in each case, each label corresponds to a precise description of all particle positions and velocities.) Since the dynamics are deterministic, each time the system visits state a, the same state trajectory follows: a → b → c → d → e. Now, if at the end of this trajectory, when the system reaches state e, we inverted, with infinite precision, the velocity of every single particle, the system would then retrace exactly the original trajectory, now from point e to a, with the velocities inverted: e → d → c → b → a. This is what, in this paper, is termed dynamical microscopic reversibility, in order to distinguish it from what, below, we call coarse-grained microscopic reversibility, which, within the framework of the Fluctuation Theorem, is simply known as microscopic reversibility.

Rather than specifying the exact microscopic state of a system, it is usually the case that, in describing the state of a system, we do not keep track of the coordinates and velocities of all particles involved. Instead, we adopt a coarse-grained description, which can drastically reduce the number of degrees of freedom [5,9,14]. (Think of an object sitting on a table. We know that it is bombarded by a vast number of gas molecules in the atmosphere. In general, we do not care about the huge amount of information detailing their precise state and evolution. All we need is a number that relates to the average kinetic energy of the molecules: the air temperature. A single number.) Of course, a coarse-grained description can involve a very large number of degrees of freedom.

In a coarse-grained description, we can identify a state of a system by capital letters A, B, C, etc. (the state can be characterized by volume, total internal energy, etc.), with the understanding that each coarse-grained state might be compatible with a very large number of different microscopic configurations. This multiplicity of microscopic configurations corresponding to each state forces us to adopt a stochastic, probabilistic approach to describe the evolution of a system [9,14].

For convenience, we adopt a dimensionless time t, which can take the values t = 0, 1, 2, 3, …, etc.

Let P(M,t) be the probability that a system is in state M at time t, and let J(M→N) be the probability per unit time that the system jumps or transitions from state M to state N.

The following conditions have to be met [15]:

$$P\left(\mathrm{M},t\right)\ge 0;{\sum }_{M}P\left(\mathrm{M},t\right)=1;J\left(\mathrm{M}\to \mathrm{N}\right)\ge 0;{\sum }_{M}J\left(\mathrm{M}\to \mathrm{N}\right)=1,\text{ for any states }\mathrm{M},\mathrm{N}.$$

Let us assume that the evolution of a system (i.e., the evolution of its state probabilities) is given by [9,14]:

$$P\left(\mathrm{M},t+1\right)=P\left(\mathrm{M},t\right)+{\sum }_{\mathrm{N}\ne \mathrm{M}}\left[J\left(\mathrm{N}\to \mathrm{M}\right)P\left(\mathrm{N},t\right)-J\left(\mathrm{M}\to \mathrm{N}\right)P\left(\mathrm{M},t\right)\right].$$

(1)

Although a system is constantly changing its state, being kicked around by thermal noise, in equilibrium, the probabilities P remain constant. Therefore:

$${\sum }_{N\ne M}\left[J_{eq}\left(\mathrm{N}\to \mathrm{M}\right)P_{eq}\left(N,t\right)-J_{eq}\left(\mathrm{M}\to \mathrm{N}\right)P_{eq}\left(\mathrm{M},t\right)\right]=0,$$

(2)

where we have added the subscript eq to emphasize that this relation has been derived assuming a system in equilibrium.

In particular, Equation (2) is true if:

$$\left[J_{eq}\left(\mathrm{N}\to \mathrm{M}\right)P_{eq}\left(N\right)-J_{eq}\left(\mathrm{M}\to \mathrm{N}\right)P_{eq}\left(\mathrm{M}\right)\right]=0.$$

(3)

This expression is known as detailed balance, and it indicates that, in equilibrium, the probability of a system being in state M and then jumping to state N is equal to the probability of the system being in state N and then jumping to state M [2,14,15]. It is considered a condition for microscopic reversibility in the sense that if J_eq(N→M) exists, then J_eq(M→N) exists [8,9,14]. We call Equation (3) coarse-grained microscopic reversibility. In contrast to dynamical microscopic reversibility, it is of a probabilistic nature and can be associated with entropy-changing processes. Dynamical microscopic reversibility, on the other hand, relates to a situation in which we have a perfect knowledge of the past, present, and future, and thus, it can be associated with a constant entropy [5].

If a system is in equilibrium and in contact with a thermal bath at temperature T, the probability of finding the system in state M is given by:

$$P_{eq}\left(\mathrm{M}\right)={\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-\raisebox{1ex}{$E\left(\mathrm{M}\right)$}\!\left/ \!\raisebox{-1ex}{${\mathrm{k}}_{\mathrm{B}}\mathrm{T}$}\right.\right)}{Z}},$$

(4)

where E(M) is the energy of state M and k_B is Boltzmann’s constant. Z is the partition function:

$$Z={\sum }_{L,allstates}\exp \left(-{\displaystyle \raisebox{1ex}{$E\left(L\right)$}\!\left/ \!\raisebox{-1ex}{${\mathrm{k}}_{\mathrm{B}}\mathrm{T}$}\right.}\right).$$

(5)

Thus, from Equation (3), we obtain the following expression for the equilibrium jump probabilities in terms of the state energies:

$${\displaystyle \frac{J_{eq}\left(\mathrm{N}\to \mathrm{M}\right)}{J_{eq}\left(\mathrm{M}\to \mathrm{N}\right)}}=\exp \left({\displaystyle \frac{E\left(\mathrm{N}\right)-E\left(\mathrm{M}\right)}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}\right).$$

(6)

3. Work and Heat Dissipation

Here, we present a stochastic thermodynamic description of the evolution of a system that is driven out of equilibrium, as work is done on it by the variation of a work parameter, and heat is released to or absorbed from a thermal bath. We use the same arguments in the following section to derive a version of the Fluctuation Theorem.

Let A, B, C, …, be the coarse-grained states that are accessible to a system that is in contact with a thermal bath at temperature T. The system typically jumps from one state to another due to thermal noise. Thus, instead of characterizing the system by a single state, say M, we characterize it by giving the probabilities P(A), P(B), …, P(M), etc., of finding a system in state A, B, …, M, etc.

Assume that work is done on a system that is initially in equilibrium by varying a work parameter λ. Parameter λ can be a degree of freedom, the system volume, a magnetic field, etc. What is important to us is that as λ varies, the energy and other properties of a state may change with λ. Thus, we use M(λ) to indicate that the properties of state M depend on λ; for example, its energy E[M(λ)].

Assume the following work protocol: initially at t = 0, λ = λ₀; for t = 0, 1, 2, 3, …, λ takes the values λ₀, λ₁, λ₂, λ₃, …, respectively.

If the rate of change of λ is finite, it is likely that the system will achieve out-of-equilibrium states, and therefore, typically:

$$P\left[M\left({\lambda }_i\right)\right]\ne P_{eq}\left[M\left({\lambda }_i\right)\right]\mathrm{f}\mathrm{o}\mathrm{r}i>0.$$

(7)

The energy of any state M will, typically, also change with λ:

$$E\left[M\left({\lambda }_i\right)\right]\ne E\left[M\left({\lambda }_j\right)\right]\mathrm{f}\mathrm{o}\mathrm{r}i\ne j.$$

(8)

In this paper, the evolution of a system, as λ varies, is described by a series of two-step processes that we call system state updates, which take place every time unit. The first step is the work step, followed by the heat exchange step.

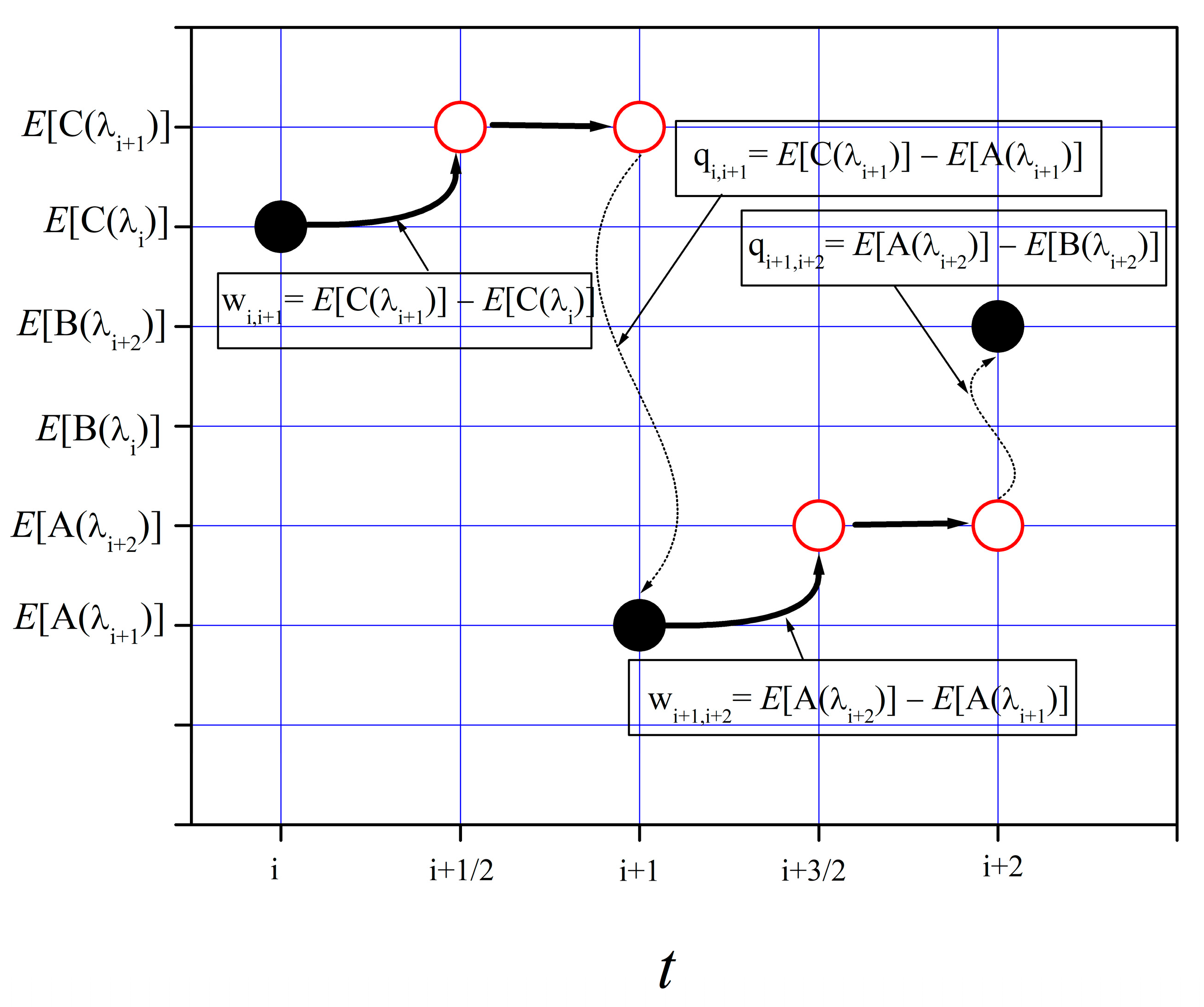
Consider the sketch of Figure 1. Work is represented by a curved solid arrow; heat exchange between the system and the heat reservoir is represented by a dashed, wavy thin arrow. Suppose that, at time t = i, the system is in state C(λ_i), as indicated by the left-most black circle. An amount of work w_i,i+1 is done on the system during the work step, from time i to an intermediate time i + 1/2, as the work parameter varies from λ_i to λ_i+1. Work w_i,i+1 is given by the corresponding change in the state energy: E[C(λ_i+1)] − E[C(λ_i)]. Following the work step, a heat exchange step occurs at t = i + 1, which, in this case, consists of the system transition from state C(λ_i+1) to state A(λ_i+1). This transition entails a transfer of energy, as heat, from the system to the heat bath, q_i,i+1 = E[C(λ_i+1)] − E[A(λ_i+1)]. This completes the system update from t = i to i + 1. Update completion is indicated by the second black circle. (The empty red circles represent intermediate states.) Figure 1 shows one more state update from t = i + 1 to i + 2. For this second system state update, we have w_i+1,i+2 = E[A(λ_i+2)] − E[A(λ_i+1)] and q_i+1,i+2 = E[A(λ_i+2)] − E[B(λ_i+2)]. We see that q_i+1,i+2, a negative value, is the heat absorbed by the system from the thermal bath.

4. The Fluctuation Theorem

We have discussed, from a stochastic thermodynamic viewpoint, how the state of a system in contact with a thermal bath evolves as work is performed on it by varying a work parameter λ. Using that formalism, in this section, we present a deduction of the Fluctuation Theorem that is partially based on Reference [8].

In Section 2, by assuming the validity of the principle of detailed balance, we have arrived at coarse-grained microscopic reversibility expressions for processes in which systems remain in equilibrium [Equations (3) and (6)]. This result is generalized to out-of-equilibrium processes in order to deduce the Fluctuation Theorem within a stochastic thermodynamic framework [8,9]. By adopting this generalization, we eliminate here the subscript eq that we have used in Equation (6):

$${\displaystyle \frac{J\left(\mathrm{N}\to \mathrm{M}\right)}{J\left(\mathrm{M}\to \mathrm{N}\right)}}=\exp \left({\displaystyle \frac{E\left(\mathrm{N}\right)-E\left(\mathrm{M}\right)}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}\right)=\exp \left({\displaystyle \frac{q_{\mathrm{N}\to \mathrm{M}}}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}\right),$$

(9)

where q_N→M is the energy released to the thermal bath as heat from the system, as the system transitions from state N to M. It might seem pointless to use the subscript eq in Equation (6) and then simply eliminate it in Equation (9). However, we have done just that in order to highlight the following: from a theoretical viewpoint, this generalization is a valid result [9], as long as the transition probabilities Js are well defined; however, as we discuss below, the determination of those Js, resulting from what would be characterized as unlikely events or large fluctuations, presents us with experimental and computational limitations to the applicability of Equation (9) in practical situations.

Assume that, at time t = 0, a system is in equilibrium and the work parameter λ = λ₀. The values for the work parameter are dictated by the following work protocol: λ takes the values λ₁, λ₂, λ₃, …, λ_f at times t = 1, 2, 3, …, f, respectively, with t = f being the final time. Let P₀ = P_eq[σ₀(λ₀)] be the equilibrium probability of the system being initially in state σ₀(λ₀), and let

$${\mathit{J}}_{\to }=J\left[{\sigma }_0\left({\lambda }_0\right)\to {\sigma }_1\left({\lambda }_1\right)\right]J\left[{\sigma }_1\left({\lambda }_1\right)\to {\sigma }_2\left({\lambda }_2\right)\right]\dots J\left[{\sigma }_{f-1}\left({\lambda }_{f-1}\right)\to {\sigma }_f\left({\lambda }_f\right)\right]$$

(10)

be the conditional probability of the system following the forward trajectory σ₀(λ₀), σ₁(λ₁), σ₂(λ₂), …, σ_f(λ_f), given an initial state σ₀(λ₀).

We also consider the inverse trajectory: let P_f = P_eq[σ_f(λ_f)] be the equilibrium probability of the system being initially in state σ_f(λ_f), and let

$${\mathit{J}}_{⇠}=J\left[{\sigma }_f\left({\lambda }_f\right)\to {\sigma }_{f-1}\left({\lambda }_{f-1}\right)\right]J\left[{\sigma }_{f-1}\left({\lambda }_{f-1}\right)\to {\sigma }_{f-2}\left({\lambda }_{f-2}\right)\right]\dots J\left[{\sigma }_1\left({\lambda }_1\right)\to {\sigma }_0\left({\lambda }_0\right)\right]$$

(11)

be the conditional probability of the system following the backward trajectory σ_f(λ_f), σ_f−1(λ_f−1), σ_f−2(λ_f−2), …, σ₀(λ₀), given an initial state σ_f(λ_f).

The initial entropies of the system for the forward and backward trajectories are:

$$S_{syst}\left[{\sigma }_0\left({\lambda }_0\right)\right]={\mathrm{k}}_{\mathrm{B}}\mathrm{l}\mathrm{n}{\mathsf{\Omega }}_0$$

(12)

and

$$S_{syst}\left[{\sigma }_f\left({\lambda }_f\right)\right]={\mathrm{k}}_{\mathrm{B}}\mathrm{l}\mathrm{n}{\mathsf{\Omega }}_{\mathrm{f}},$$

(13)

where Ω₀ and Ω_f are the numbers of microscopic configurations compatible with the equilibrium states for λ₀ and λ_f, respectively. Thus, we obtain the following equilibrium probabilities ratio:

$${\displaystyle \frac{{\mathit{P}}_{\mathbf{0}}}{{\mathit{P}}_{\mathit{f}}}}={\displaystyle \frac{{\mathsf{\Omega }}_0}{{\mathsf{\Omega }}_{\mathrm{f}}}}=\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{S_{syst}\left[{\sigma }_f\left({\lambda }_f\right)\right]-S_{syst}\left[{\sigma }_0\left({\lambda }_0\right)\right]}{k_B}}\right]=\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{{\mathsf{\Delta }S}_{syst}}{k_B}}\right],$$

(14)

where ΔS_syst = S_syst(λ_f) − S_syst(λ_o).

According to Equation (9), the ratio of the probabilities Js is given by:

$${\displaystyle \frac{{\mathit{J}}_{\to }}{{\mathit{J}}_{⇠}}}={\displaystyle \frac{J\left[{\sigma }_0\left({\lambda }_0\right)\to {\sigma }_1\left({\lambda }_1\right)\right]J\left[{\sigma }_1\left({\lambda }_1\right)\to {\sigma }_2\left({\lambda }_2\right)\right]\dots J\left[{\sigma }_{f-1}\left({\lambda }_{f-1}\right)\to {\sigma }_f\left({\lambda }_f\right)\right]}{J\left[{\sigma }_1\left({\lambda }_1\right)\to {\sigma }_0\left({\lambda }_0\right)\right]J\left[{\sigma }_2\left({\lambda }_2\right)\to {\sigma }_1\left({\lambda }_1\right)\right]\dots J\left[{\sigma }_f\left({\lambda }_f\right)\to {\sigma }_{f-1}\left({\lambda }_{f-1}\right)\right]}}=\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{Q}{k_{B}T}}\right),$$

(15)

where Q = q_1,2 + q_{2,3 +} q_3,4 + … + q_f−1,f.

The ratio of the forward and backward trajectory probabilities is:

$${\displaystyle \frac{{\mathit{P}}_{\mathbf{0}}}{{\mathit{P}}_{\mathit{f}}}}{\displaystyle \frac{{\mathit{J}}_{\to }}{{\mathit{J}}_{⇠}}}=\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{{\mathsf{\Delta }S}_{syst}}{k_B}}+{\displaystyle \frac{Q}{k_{B}T}}\right).$$

(16)

This is the Fluctuation Theorem. It is a very interesting result: the exponential of two random values, ΔS_syst and Q, gives us precise information about the probabilities of system trajectories.

Equation (16) refers to a single trajectory from t = 0 to f. If we now consider all possible trajectories from t = 0 to f, we obtain the ensemble average:

$$\langle exp\left({\displaystyle \frac{{\mathsf{\Delta }S}_{syst}}{k_B}}-{\displaystyle \frac{Q}{k_{B}T}}\right)\rangle \equiv {\sum }_{\begin{array}{c}Allpossible\\ forward\\ trajectories\end{array}}\left[{\mathit{P}}_{\mathbf{0}}{\mathit{J}}_{\to }exp\left({\displaystyle \frac{{\Delta S}_{syst}}{k_B}}-{\displaystyle \frac{Q}{k_{B}T}}\right)\right]={\sum }_{\begin{array}{c}Allpossible\\ backward\\ trajectories\end{array}}{\mathit{P}}_{\mathit{f}}{\mathit{J}}_{⇠}.$$

(17)

The second sum encompasses the probabilities of all possible backward trajectories and has to be equal to 1:

$${\sum }_{\begin{array}{c}Allpossible\\ backward\\ trajectories\end{array}}{\mathit{P}}_{\mathit{f}}{\mathit{J}}_{⇠}=1$$

(18)

Thus, we obtain the Integral Fluctuation Theorem:

$$\langle exp\left({\displaystyle \frac{{\mathsf{\Delta }S}_{syst}}{k_B}}-{\displaystyle \frac{Q}{k_{B}T}}\right)\rangle =1.$$

(19)

In principle, this expression, which is a direct consequence of Equation (16), is valid for both equilibrium and out-of-equilibrium processes. For processes where a system remains close to equilibrium, as in the linear response regime, the distribution of the generated entropy, $∆S_{syst}+{\displaystyle \frac{Q}{T}}$, displays a Gaussian distribution, and the Fluctuation–Dissipation Theorem is obeyed (see Sections 3.11, 4.2, and 6.2 of Reference [9]).

In Section 6, we test Equation (19) numerically for a case in which ΔS_syst = 0.

5. Stochastic Model

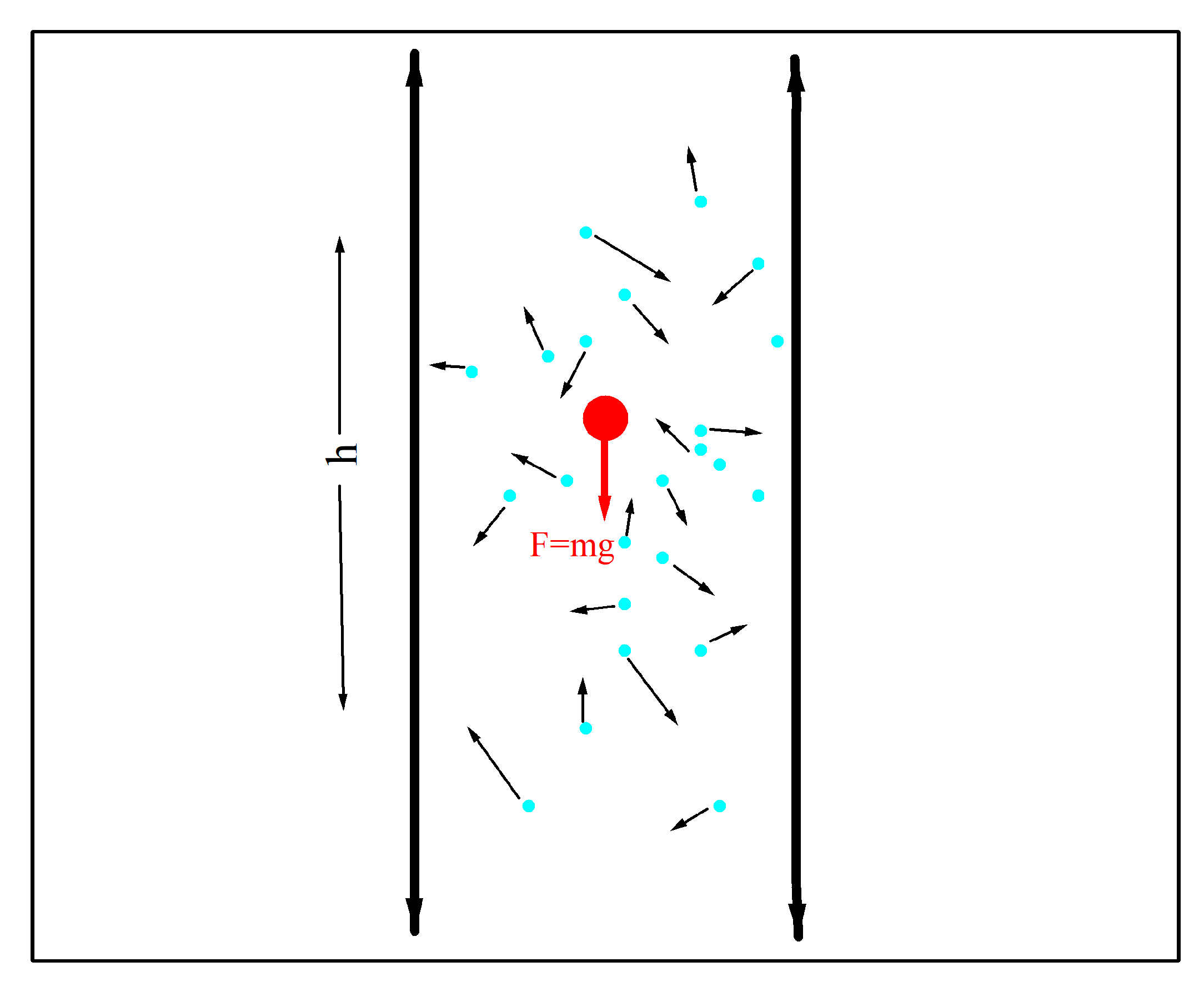
In this section, we present a one-dimensional stochastic model that consists of a very small spherical particle of mass m that moves along the center of a vertical tube that is filled with a fluid. The particle only moves vertically. (Figure 2 shows the particle, red circle, and a segment of the tube). The fluid is composed of atoms or molecules (represented by blue dots), which are much smaller and lighter than the spherical particle. During the period of time considered here, the particle does not reach the top or bottom end of the tube. The particle can only occupy sites with a height h = …, −2Δh, −Δh, 0, Δh, 2Δh, …, where Δh is the height unit.

The particle is subjected to two forces: the gravitational force, F = mg, where g is the gravitational acceleration, and the thermal noise, which is due to the random, irregular collisions between the particle and the molecules or atoms comprising the fluid. Whereas the constant gravitational force pulls the particle downwards, the collisions with the molecules or atoms give rise to macroscopic phenomena such as viscosity and buoyancy.

The energy difference between two contiguous sites is q = mgΔh, where q is the energy released to the thermal bath as heat when the particle decreases its height by Δh. The particle absorbs the same amount of energy q from the heat bath when pushed by the thermal noise increases its height by Δh.

If we assume that the force due to the collisions between the spherical particle and the atoms or molecules (thermal noise) are comparable to the gravitational force, we can set:

$$\mathrm{q}=\mathrm{m}\mathrm{g}∆\mathrm{h}={\mathrm{k}}_{\mathrm{B}}\mathrm{T}.$$

(20)

On average, the particle moves downward; however, occasionally, it does take upward steps. (In the absence of the gravitational force, the particle would display a typical Brownian motion, like a pollen grain immersed in water.)

The rules of motion are simple. At t = 0, the sphere is located at h = 0. The sphere cannot move more than one site per time unit. Let J_↑, J_↓, and J₀ be the probabilities, per time unit, of the sphere moving upward one site, moving downward one site, and remaining at the same height, respectively. Equation (9) imposes the following condition on J_↑ and J_↓:

$${\displaystyle \frac{J_{\downarrow }}{J_{\uparrow }}}=\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{q}{k_{B}T}}\right).$$

(21)

Thus, we propose the following jump probabilities:

$$J_0={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$Z$}\right.},$$

(22)

$$J_{\uparrow }={\displaystyle \raisebox{1ex}{$\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{q}/2\right)$}\!\left/ \!\raisebox{-1ex}{$Z$}\right.},$$

(23)

$$J_{\downarrow }={\displaystyle \raisebox{1ex}{$\mathrm{e}\mathrm{x}\mathrm{p}\left(+\mathrm{q}/2\right)$}\!\left/ \!\raisebox{-1ex}{$Z,$}\right.}$$

(24)

where Z = 1 + exp(−q/2) + exp(+q/2), in order for J₀ + J_↑ + J_↓ = 1.

Since q > 0, $J_{\downarrow }>J_{\uparrow }$ and the model display, on average, a downward motion. On average, the kinetic energy of the particle does not increase, and the loss of potential energy as the particle moves down is dissipated as heat. Upward displacements can be considered as fluctuations, with energy flowing in the opposite direction.

The total heat dissipated to the thermal bath from t = 0 to t, as the particle has reached a height h(t), is given by:

$$Q\left(t\right)=-{\displaystyle \frac{h\left(t\right)q}{∆h}}.$$

(25)

Figure 3 shows Q from 30 repetitions of the process in which the sphere moves for 100 time units. We can observe sporadic Q-decreasing events that correspond to instances in which energy is transferred from the heat bath to the sphere, which then moves up. However, on average, Q increases as the sphere moves down.

By studying Figure 3, we can conclude that for t = 100, Q < 0 would represent a very large fluctuation (unlikely event). However, for shorter times, negative Qs are observed.

6. Numerical Corroboration and Limitations of the Fluctuation Theorem

In this section, we present the results from a series of numerical simulations, generated by the stochastic model of the previous section, in order to test the Fluctuation Theorem (Equation (19)).

For our one-particle system, Equation (19) reduces to:

$$\langle \mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{Q}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}\right)\rangle =1,$$

(26)

since ∆S_syst = 0. The entropy production is solely originated from the dissipation of energy as heat: S_diss = Q/T.

Typically, the trajectories of the sphere produce positive Qs (reflecting a net downward displacement). However, Equation (26) requires that a fraction of the repetitions results in Q < 0 (net upward net displacement). For none of the 30 repetitions shown in Figure 3 did this occur. In fact, such events are quite unlikely. For this reason, we now consider processes in which the sphere moves for 10, 20, and 50 time units.

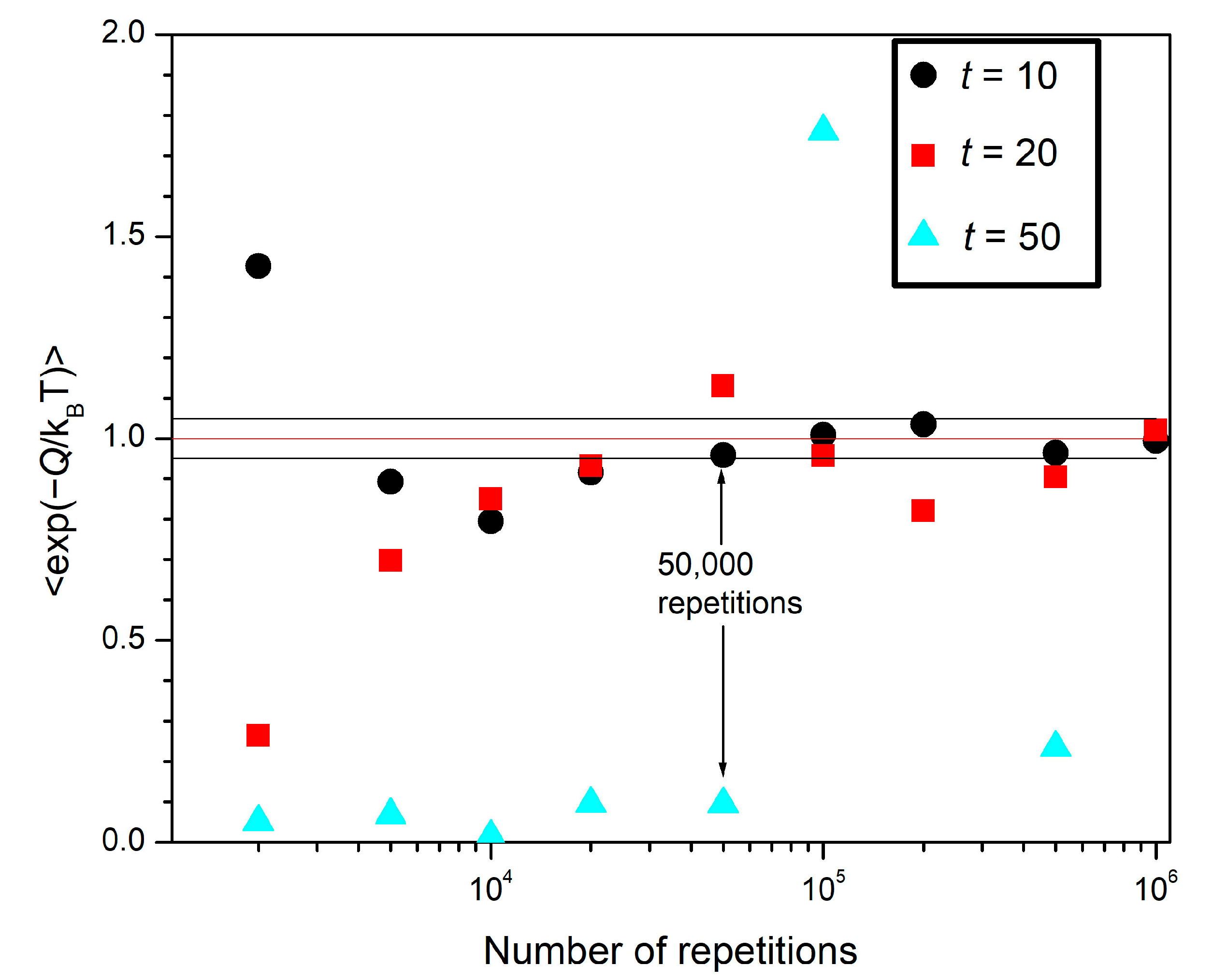
Recall that the brackets of Equations (19) and (26) represent an average over all possible trajectories. In this section, they represent averages over a finite number of trajectories: those generated by our simulations. In Figure 4, we plot the exponential average $\langle \mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{Q}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}\right)\rangle$ versus the number of repetitions for different sets of simulations for t = 10, 20, and 50.

The black circles in Figure 4 correspond to Q for a process lasting 10 time units. When the number of repetitions is small, perhaps less than 10,000, the value of the exponential average $\langle \mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{Q}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}\right)\rangle$ varies from case to case, without showing any clear sign of approaching any value (a consequence of the implicit randomness of the rules of motion). However, for 50,000 or more repetitions, we see that the exponential average approaches 1 (indicated by the red horizontal line), in accordance with Equation (26). The two black horizontal lines indicate a ± 0.05 error. A less pronounced approximation to 1 is displayed in the case of t = 20 (red squares). This is expected from the trends displayed in Figure 3: the greater the time t is, the smaller the probability is that a negative value of Q is attained (which would correspond to a net upward displacement). For t = 50 (light blue triangles), there is not a tendency of Q toward any value, even for 10⁶ repetitions (in fact, we omitted two values of Q that were around the 6.0 mark in order to keep the scale of the plot).

The following conclusion can be drawn from Figure 4: the longer the duration of the process, the larger the number of repetitions necessary to observe a meaningful approximation to the Fluctuation Theorem. This can be better understood by recalling that, in Section 4, we pointed out that one key assumption in a stochastic thermodynamic deduction of the Fluctuation Theorem is the generalization of the coarse-grained microscopic reversibility principle (which is derived from detailed balance) to out-of-equilibrium processes. This implies that very unlikely events have to be considered in the evaluation of the average in Equation (26). In our case, the unlikely events are the processes resulting in Q < 0, which are more unlikely for longer durations (see Figure 3).

Thus, our numerical results indicate that, within the scope of the stochastic model presented in the previous section, there are two practical limitations regarding the applicability of the Fluctuation Theorem. First, the minimum-number-of-repetitions limitation indicates that there exists a minimum for the number of repetitions of an experiment or simulation; below this minimum number, the numerical approximation to Equations (19) and (26) might not be accurate. Second, the long-time limitation tells us that there is a maximum duration of a process beyond which we cannot apply the Fluctuation Theorem. It is important to note that this long-time limitation was observed experimentally by Wang and co-workers [12].

7. Conclusions

An elementary derivation of the Fluctuation Theorem within the framework of stochastic thermodynamics has been presented. We have highlighted the fact that this deduction rests on the generalization of detailed balance, a principle valid for both equilibrium and out-of-equilibrium processes. We have presented a one-particle, one-dimensional stochastic model, whose results agree very well with the Fluctuation Theorem. Although our model is simpler than other models used in the past, it allows us to illustrate two limitations of this theorem regarding its applicability to practical situations: one is related to the minimum number of experiments or simulations; the other sets a limit to the duration of the process under study. The discussion we have presented about the generalization of detailed balance helps us understand the origin of such limitations.