The Use of Gas Dynamics to Estimate the Influence of Flanges on Gear Windage Power Loss
Abstract
1. Introduction
2. Test Bench and Experimental Results
2.1. Test Bench and Test Sample
2.2. Experimental Approach
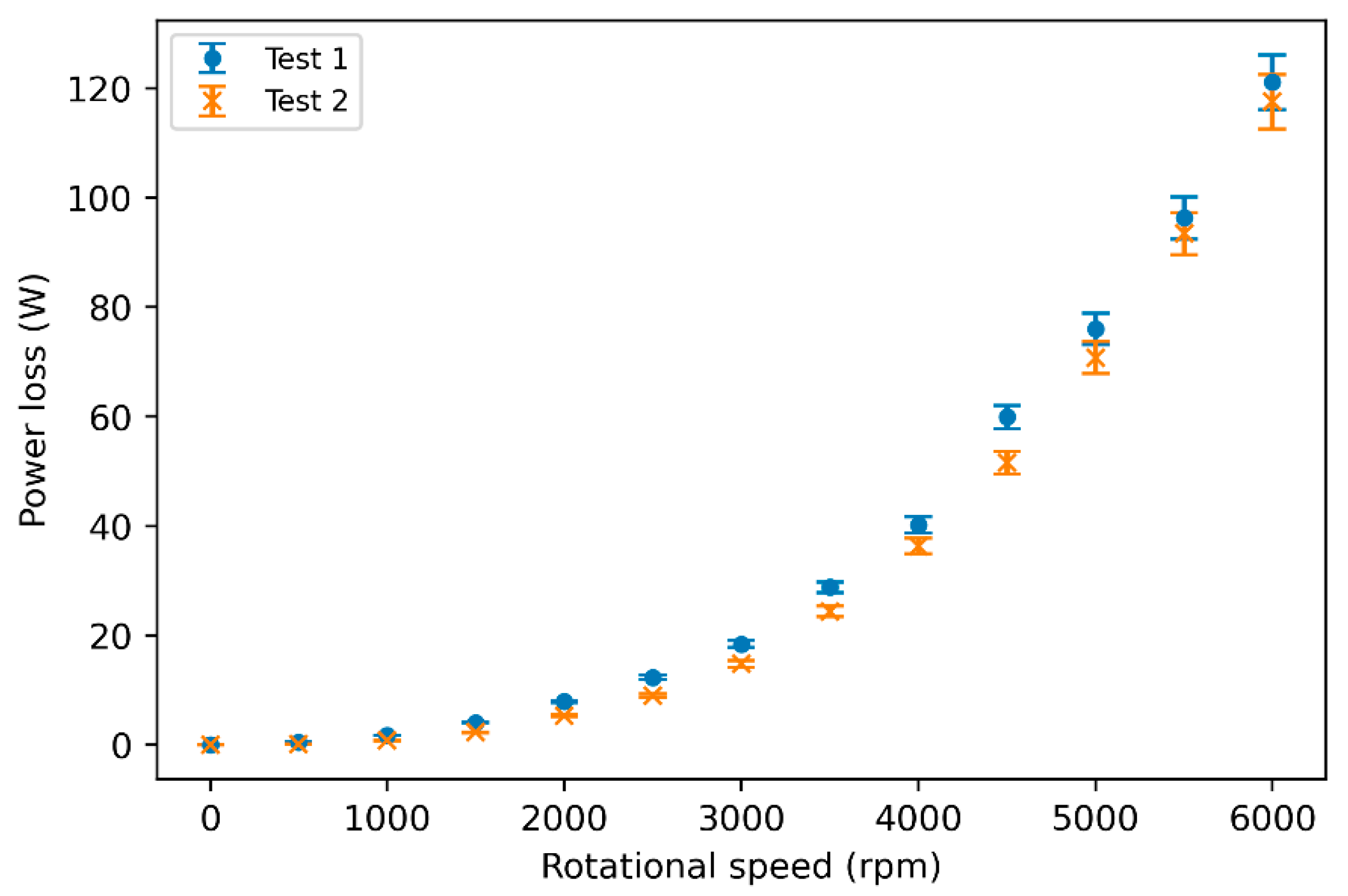
2.2.1. Torque Measurement
2.2.2. Windage Losses Determination
- : Power loss of the shaft and gear assembly [W].
- : Torque of the shaft line and gear assembly [Nm].
- : Rotational speed [rad/s].
- : Windage loss of the gear [W].
- : Power loss of the shaft line [W].
2.2.3. Repeatability
2.3. Experimental Results and Analysis of the Relevance of Diab’s Model
2.3.1. Gears Without Obstacles
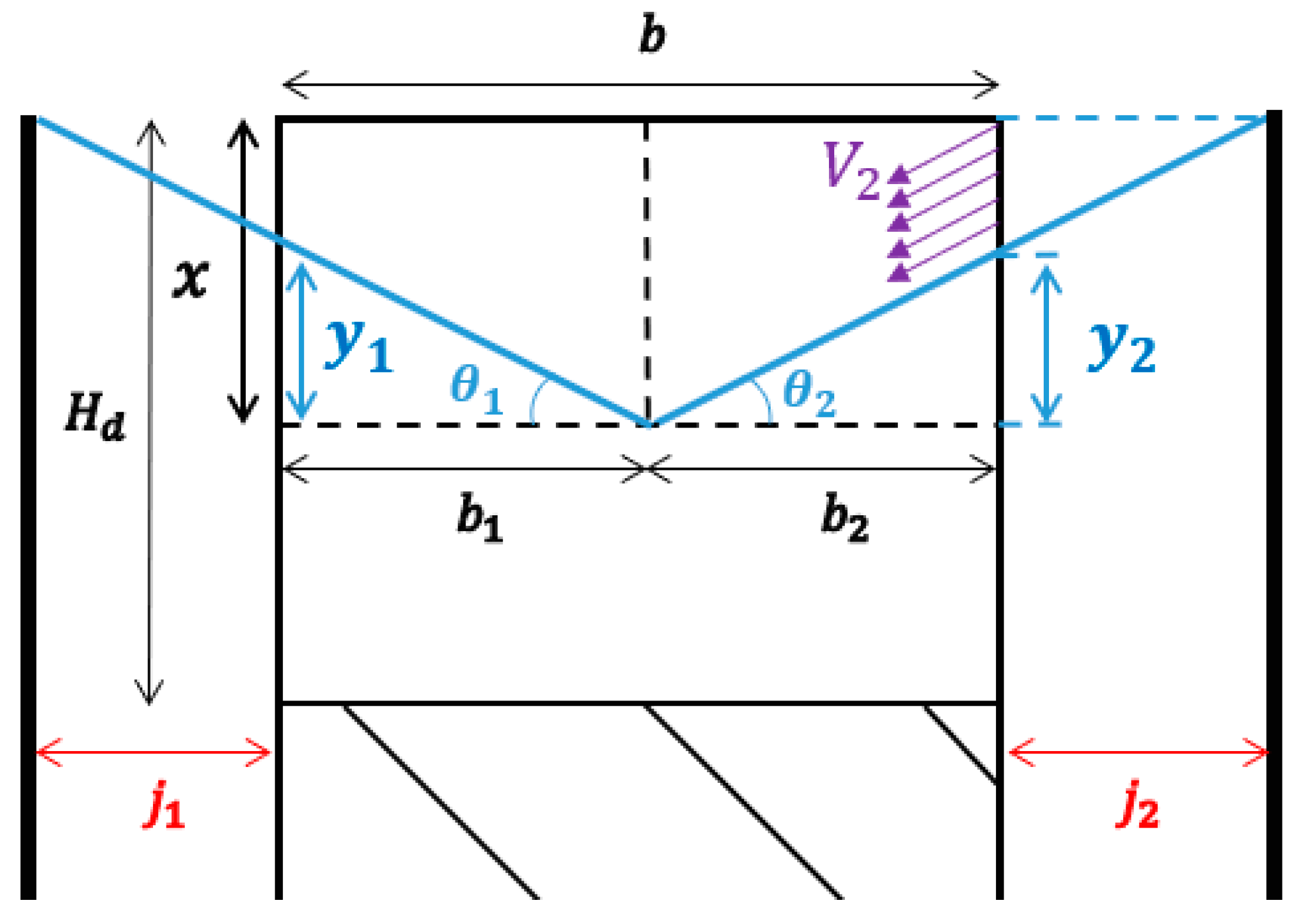
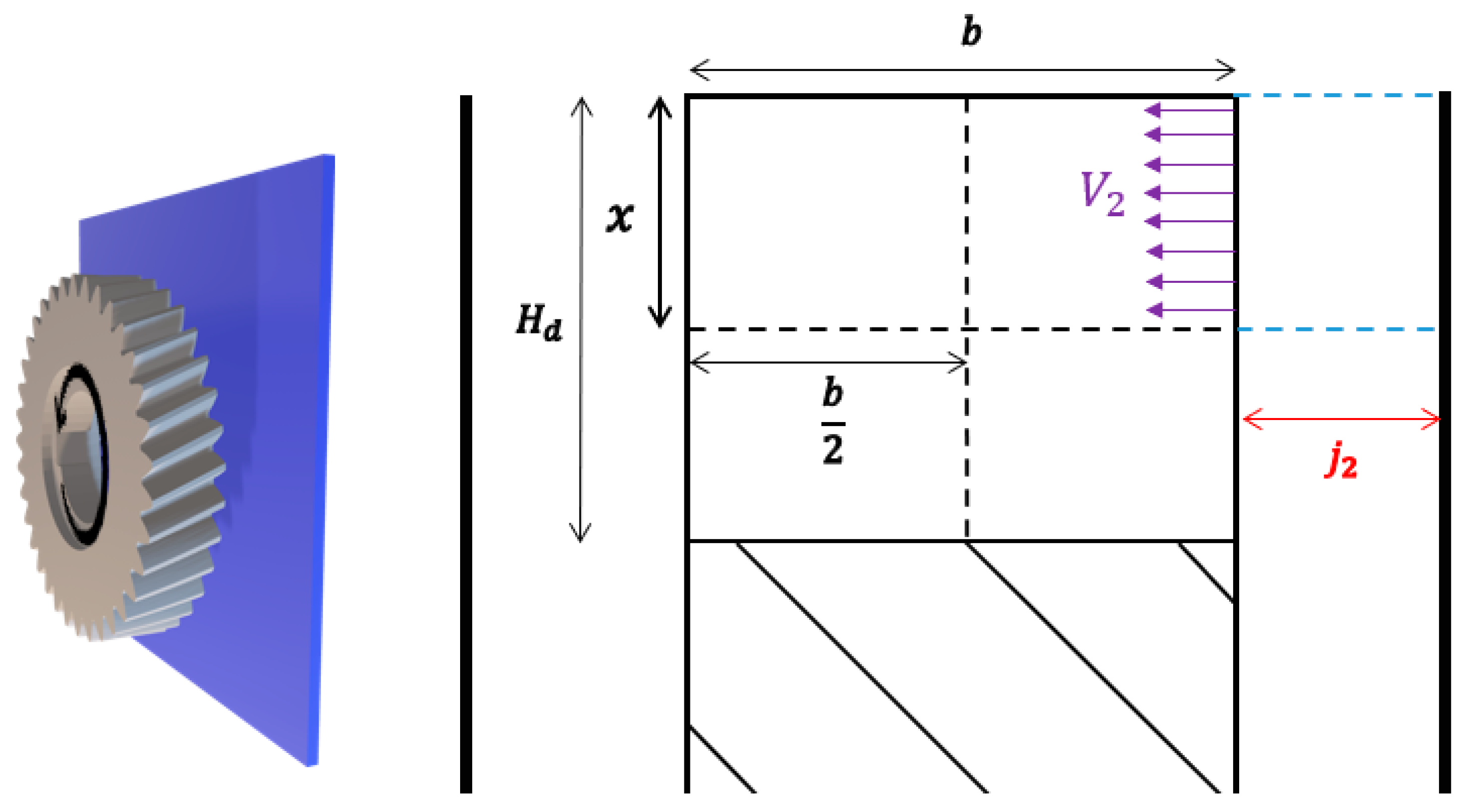
2.3.2. Walls and Flanges
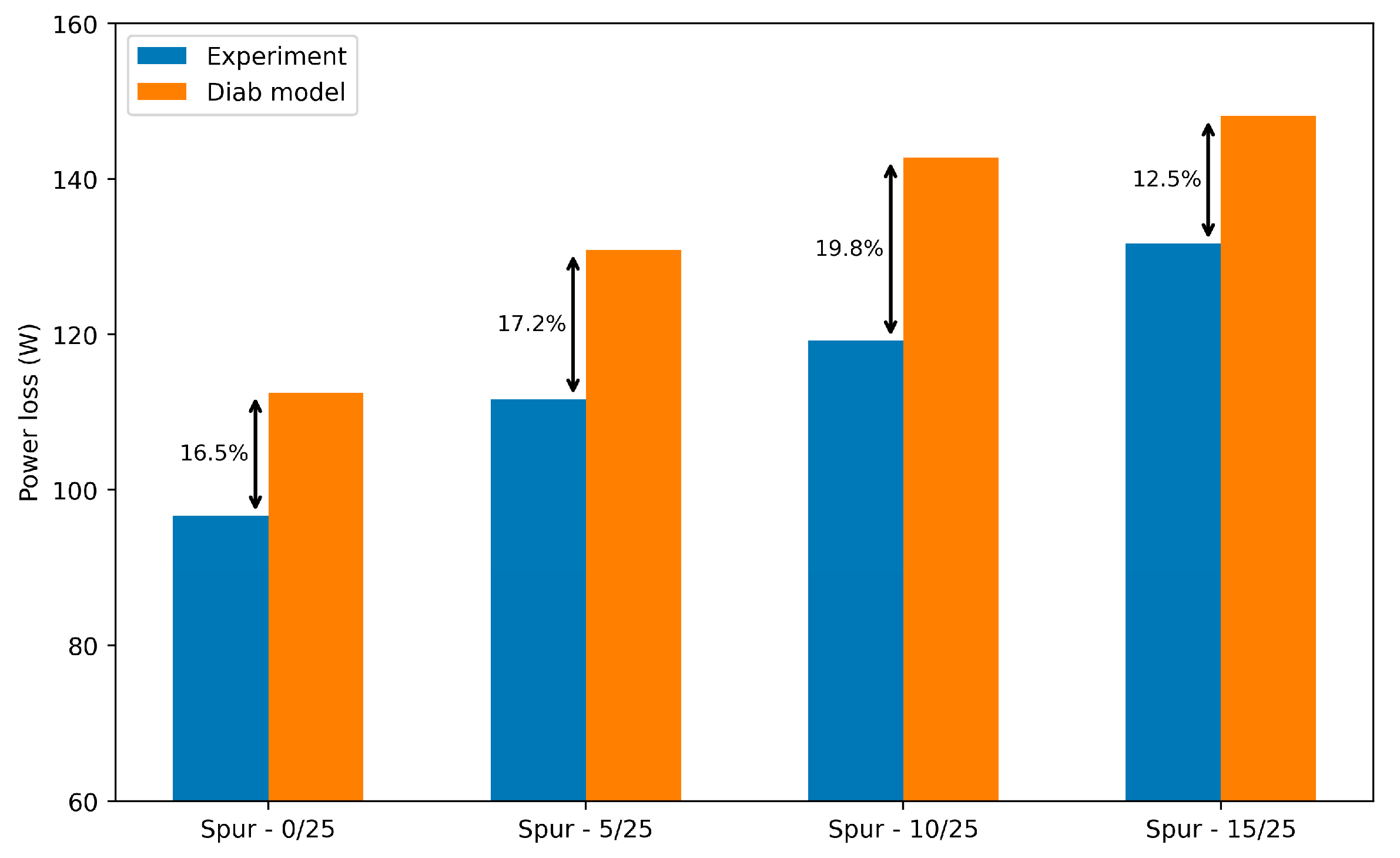
Spur Gear
- with,
- : Distance between gear faces and obstacles [m].
- : Gear head radius [m].
- : Obstacle radius [m].
- if .
- otherwise.
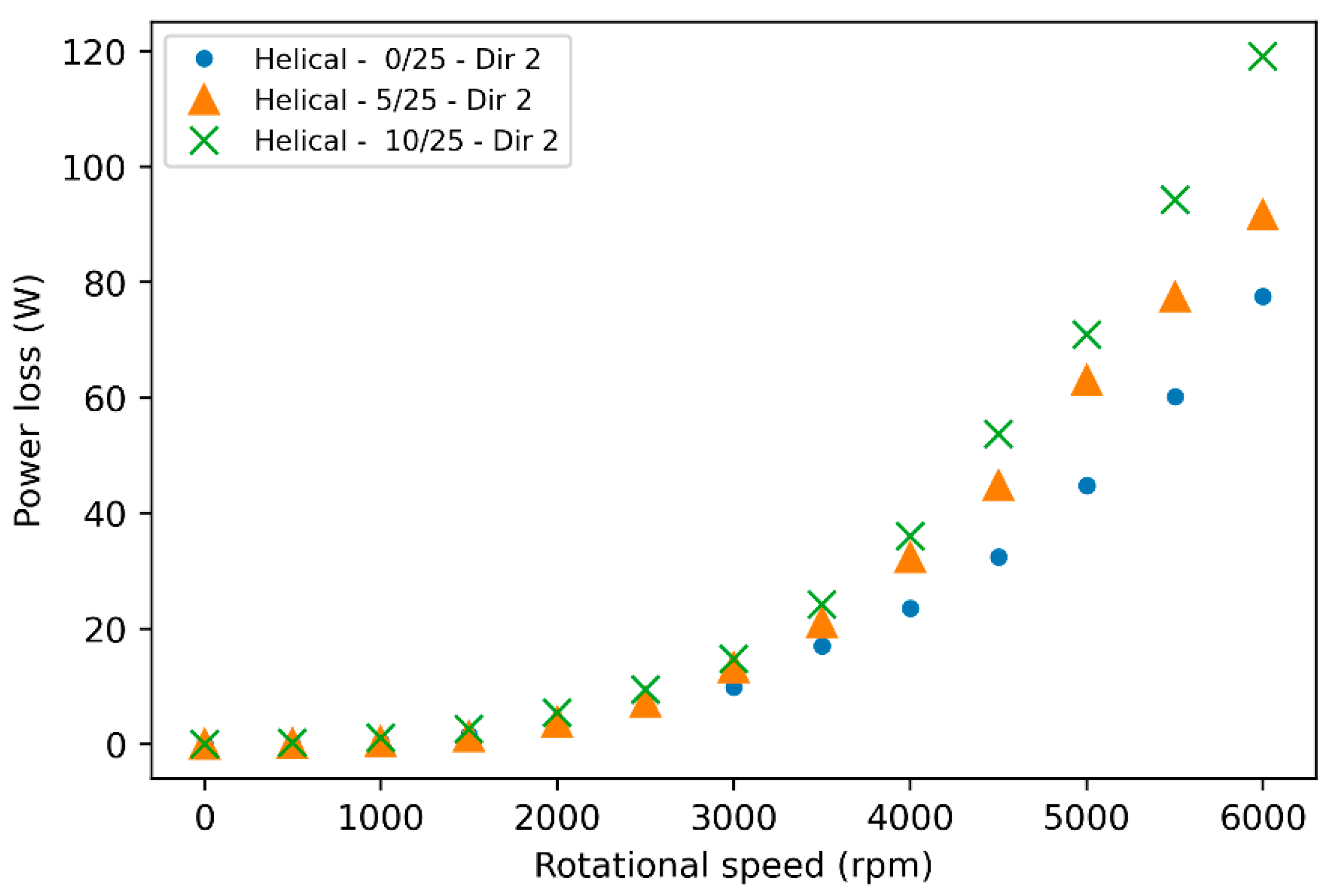
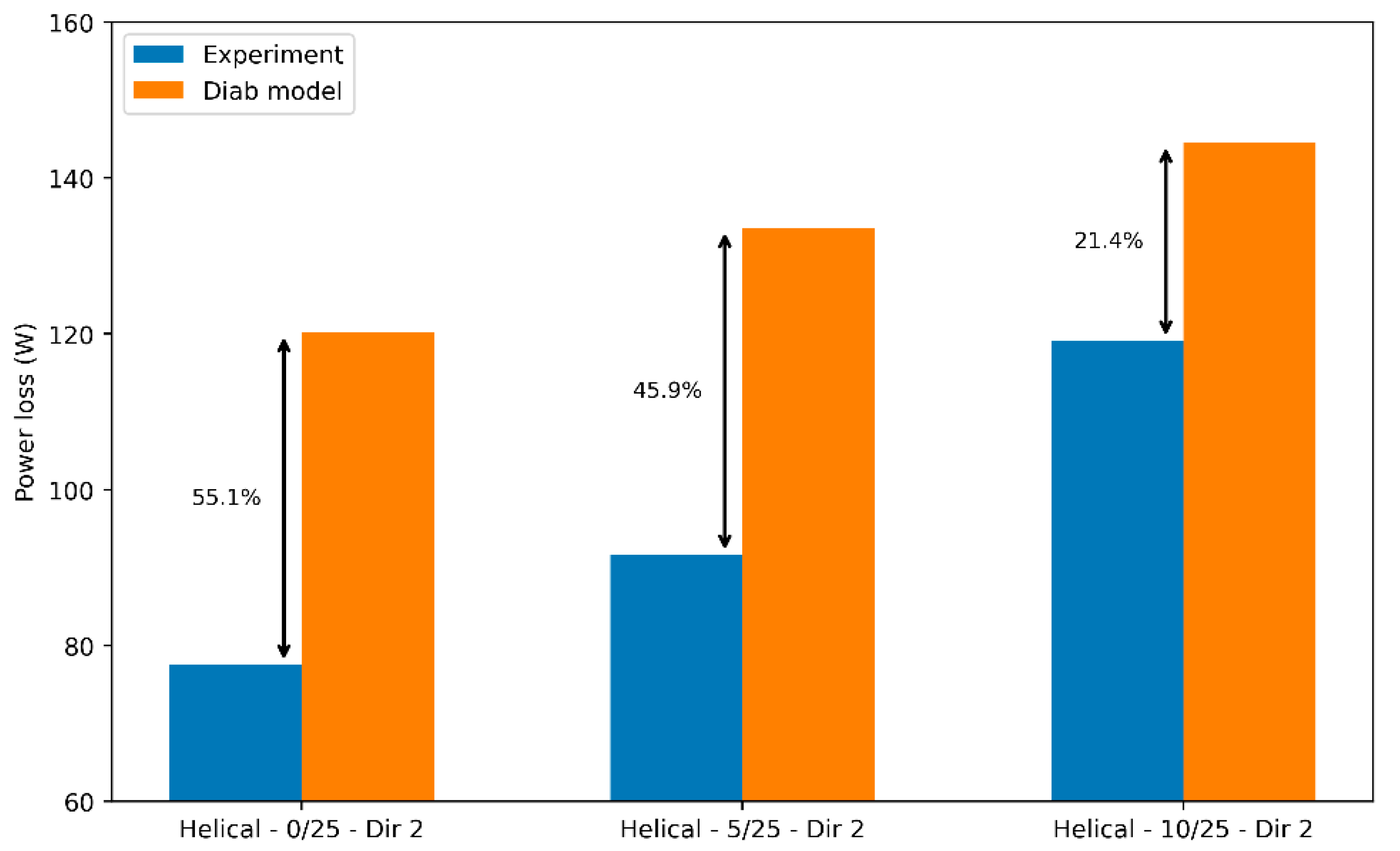
Helical Gear
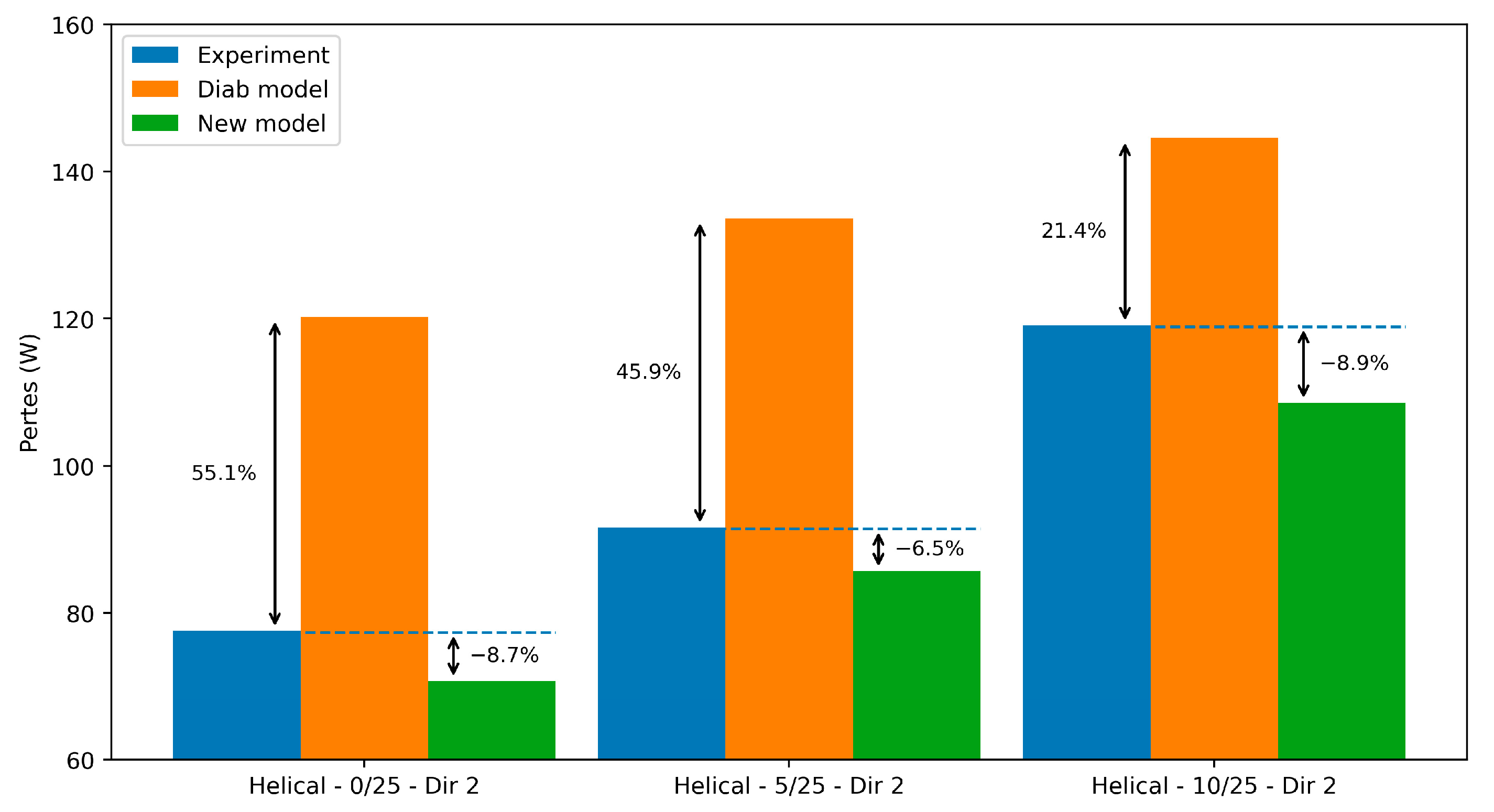
- Helical–0/25–Dir 2: With the flange in direct contact with the gear flank ( mm), air aspiration into the inter tooth space is minimized, reducing aerodynamic losses. The flange acts as a barrier, limiting transverse flow and the characteristic helical gear pumping effect.
- Helical–5/25–Dir 2: Increasing to 5 mm allows more air to be drawn into the gear, slightly increasing losses—especially above 4000 rpm, where depression-induced pumping intensifies.
- Helical–10/25–Dir 2: With mm, airflow into the gear increases further, and so do the losses. At 6000 rpm, this configuration shows the highest loss levels, confirming the strong influence of j1 on airflow and turbulence.
2.3.3. Conclusion on the Diab Model
3. New Windage Power Loss Model
3.1. Density Correction Factor
3.1.1. Spur Gear
- If :
- If :
- If :
- If :
- : Tip radius [m].
- : Pitch radius [m].
- : Tooth thickness at the pitch circle [m].
- : Involute function of the pitch circle [-].
- : Pressure angle at the pitch circle and at the tooth tip, respectively [rad].
- : Circumference of the pitch diameter [m].
- : Contribution of the teeth on the circumference [m].
- : Available length for the flow after subtracting the dead lengths .
- : Windage losses of the gear in air [W].
- : Angular rotational speed of the gear [rad/s].
3.1.2. Helical Gear
- : Windage losses of the gear in air [W].
- : Angular rotational speed of the gear [rad/s].
- If 2, meaning the air ejection direction from the gear towards side 2, then,
- If 1, meaning the air ejection direction from the gear towards side 1, then,
3.2. Comparison with Experiments
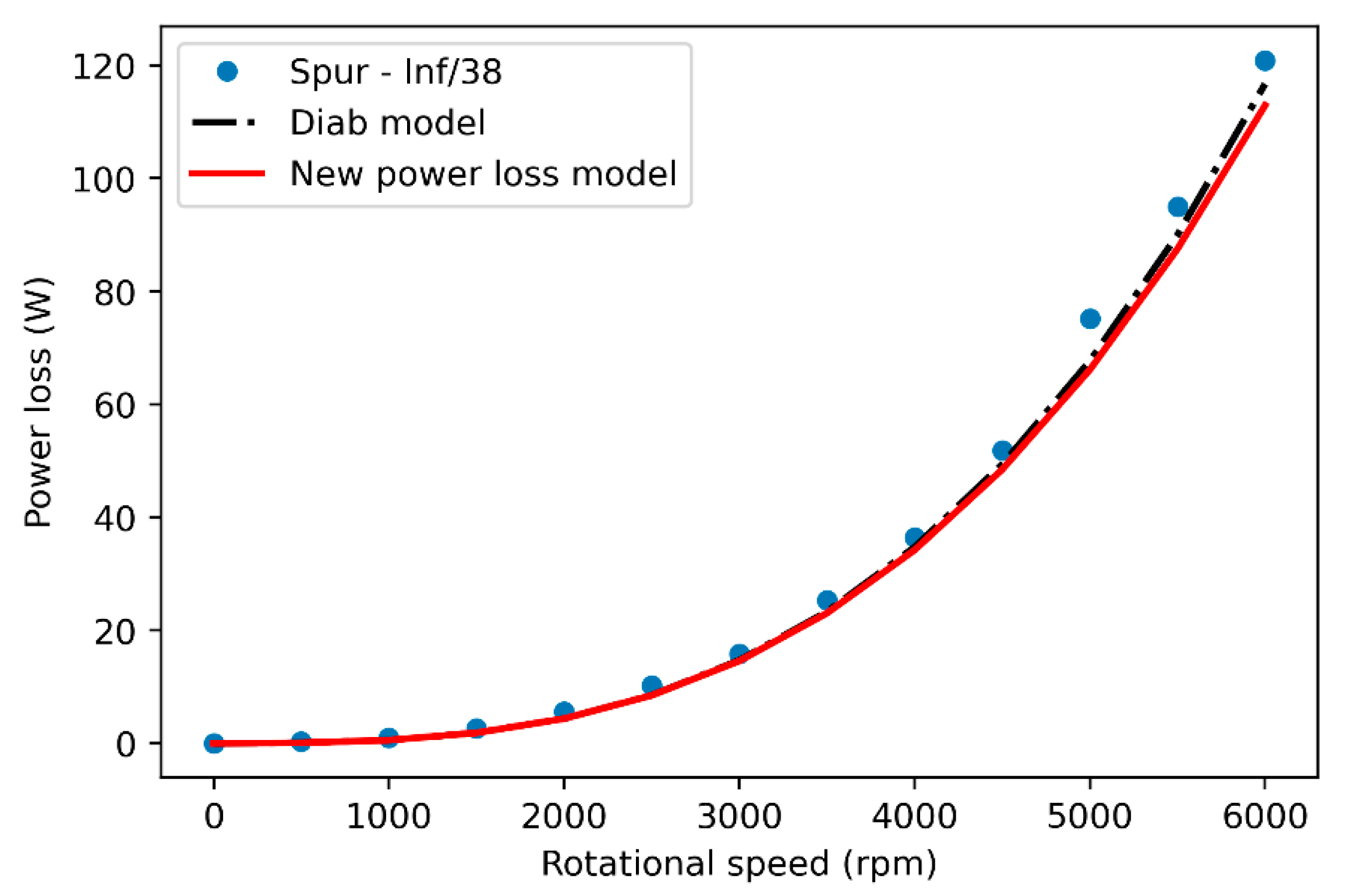
3.2.1. Spur Gear
3.2.2. Helical Gear
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Tooth width | [m] | |
| Apparent tooth width for helical gear | [m] | |
| Tooth width on side 1 and side 2 | [m] | |
| Shaft line and gearwheel assembly torque | [Nm] | |
| Dimensioned drag moment for gearing | [-] | |
| Dimensioned drag moment for gearing on side 1 and side 2 | [-] | |
| Dimensioned drag moment on gear faces | [-] | |
| Windage loss torque related to the gear face surfaces | [Nm] | |
| Total scaled drag moment | [-] | |
| Windage loss torque related to the gear teeth | [Nm] | |
| Addendum coefficient | [-] | |
| Specific heat capacity | [J/kgK] | |
| Tooth tip diameter of the gear | [m] | |
| Direction of ejected air | [-] | |
| Tooth height | [m] | |
| Heaviside function | [-] | |
| Distance between gear faces and obstacles | [m] | |
| Distance ratio between the obstacles and the gear faces | [m] | |
| Coefficient for laminar and turbulent regime | [-] | |
| Coefficient for laminar and turbulent regime | [-] | |
| Ventilation loss of the gear | [W] | |
| Power loss of the shaft line | [W] | |
| Power loss of the shaft and gear assembly | [W] | |
| Total air ejection flow over the gear teeth | [m3/s] | |
| Tooth air ejection rate | [m3/s] | |
| Critical radius delimiting the zone in laminar regime from that in turbulent regime | [m] | |
| Obstacle radius | [m] | |
| Gear pitch radius | [m] | |
| Gear tip radius | [m] | |
| Reynolds number | [-] | |
| Critical Reynolds number | [-] | |
| Air suction surfaces on side 1 and side 2 | [m2] | |
| Active air ejection surface | [m2] | |
| Tooth thickness at the pitch circle | [m] | |
| Tooth tip thickness | [m] | |
| Air temperature inside the housing | [K] | |
| Air injection velocity on side 1 and side 2 | [m/s] | |
| Active tooth length | [m] | |
| Profile shift coefficient | [-] | |
| Dead tooth length | [m] | |
| Number of teeth | [m] | |
| Pressure angle at the pitch circle of the gear | [rad] | |
| Pressure angle at the tooth tip | [rad] | |
| Helix angle | [-] | |
| Heat capacity ratio; for air | [-] | |
| Air suction angle | [rad] | |
| Air density reduction factor on side 1 and side 2 | [-] | |
| Reduction factor associated with an obstacle in Diab’s model | [-] | |
| Fluid density | [kg/m3] | |
| Corrected fluid density on side 1 and side 2 | [kg/m3] | |
| Tooth tip profile angle | [°] | |
| Gear angular speed | [rad/s] |
Appendix A. Diab Model
- : Windage losses of the gear in air [W].
- : Gear angular speed [rad/s].
- : Total scaled drag moment [-].
- : Dimensionless drag moment on gear faces [-].
- : Dimensionless drag moment for gearing [-].
- Face losses
- : Critical Reynolds number [-].
- : Critical radius delimiting the zone in laminar regime from that in turbulent regime [m].
- ; : Laminar flow coefficients [-].
- = 0.074; : Coefficients for the turbulent regime [-].
- 2.
- Tooth losses
- : Reduction factor for deflectors ( = 1 if no obstacle) [-].
- : Number of teeth [-].
- : Tooth width [m].
- : Addendum coefficient [-].
- : Offset coefficient [-].
- : Helix angle [°].
References
- Wu, J.; Wei, P.; Liu, G.; Chen, D.; Zhang, X.; Chen, T.; Liu, H. A comprehensive evaluation of DLC coating on gear bending fatigue, contact fatigue, and scuffing performance. Wear 2024, 536–537, 205177. [Google Scholar] [CrossRef]
- Wu, J.; Wei, P.; Zhu, C.; Zhang, P.; Liu, H. Development and application of high strength gears. Int. J. Adv. Manuf. Technol. 2024, 132, 3123–3148. [Google Scholar] [CrossRef]
- Michaelis, K.; Höhn, B.; Hinterstoißer, M. Influence factors on gearbox power loss. Ind. Lubr. Tribol. 2011, 63, 46–55. [Google Scholar] [CrossRef]
- Hildebrand, L.; Dangl, F.; Sedlmair, M.; Lohner, T.; Stahl, K. CFD analysis on the oil flow of a gear stage with guide plate. Forsch. Ingenieurwes 2022, 86, 395–408. [Google Scholar] [CrossRef]
- Mauz, W. Hydraulische Verluste von Stirnradgetriebe bei Umfangsgeschwindigkeit bis 60 m/s. Ph.D. Thesis, IMK University of Stuttgart, Stuttgart, Germany, 1987. [Google Scholar]
- Kármán, V.T. Über laminare und turbulente Reibung. ZAMM—J. Appl. Math. Mech./Z. Für Angew. Math. Mech. 1921, 1, 233–252. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory, 7th ed.; McGraw-Hill: New York, NY, USA, 1979; p. 817. [Google Scholar]
- Daily, J.W.; Nece, R.E. Chamber Dimension Effects on Induced Flow and Frictional Resistance of En-closed Rotating Disks. J. Basic. Eng. 1960, 82, 217–230. [Google Scholar] [CrossRef]
- Mann, R.W.; Marston, C.H. Friction Drag on Bladed Disks in Housings as a Function of Reynolds Number, Axial and Radial Clearance, and Blade Aspect Ratio and Solidity. J. Basic. Eng. 1961, 83, 719–723. [Google Scholar] [CrossRef]
- Handschuh, R.F.; Kilmain, C.J. Preliminary Comparison of Experimental and Analytical Efficiency Results of High-Speed Helical Gear Trains. In 9th International Power Transmission and Gearing Conference, Parts A and B; American Society of Mechanical Engineers: New York, NY, USA, 2003; Volume 4, pp. 949–955. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–596. [Google Scholar]
- Diab, Y.; Ville, F.; Velex, P.; Changenet, C. Windage losses in high speed gears-preliminary experimental and theoretical results. J. Mech. Des. 2004, 126, 903–908. [Google Scholar] [CrossRef]
- Hill, M.J.; Kunz, R.F.; Noack, R.W.; Long, L.N.; Morris, P.J.; Handschuh, R.F. Application and Validation of Unstructured Overset CFD Technology for Rotorcraft Gearbox Windage Aerodynamics Simulation. In 64th Annual Forum of the American Helicopter Society; The Vertical Flight Society (VFS): Fairfax, VA, USA, 2008. [Google Scholar]
- Pallas, S.; Marchesse, Y.; Changenet, C.; Ville, F.; Velex, P. A windage power loss model based on CFD study about the volumetric flow rate expelled by spur gears. Mech. Ind. 2012, 13, 317–323. [Google Scholar] [CrossRef]
- Dai, Y.; Yang, C.; Zhu, X. Investigations of the Windage Losses of a High-Speed Shrouded Gear via the Lattice Boltzmann Method. Appl. Sci. 2024, 14, 9174. [Google Scholar] [CrossRef]
- Huang, B.; Zhang, H.; Ding, Y. CFD Modelling and Numerical Simulation of the Windage Characteristics of a High-Speed Gearbox Based on Negative Pressure Regulation. Processes 2023, 11, 804. [Google Scholar] [CrossRef]
- Winfree, D.D. Reducing Gear Windage Losses From High Speed Gears. In 8th International Power Transmission and Gearing Conference; American Society of Mechanical Engineers: New York, NY, USA, 2000; Volume 6, pp. 747–756. [Google Scholar] [CrossRef]
- Voeltzel, N.; Marchesse, Y.; Changenet, C.; Ville, F.; Velex, P. On the influence of helix angle and face width on gear windage losses. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2016, 230, 1101–1112. [Google Scholar] [CrossRef]
- Goldstein, S. On the resistance to the rotation of a disc immersed in a fluid. Math. Proc. Camb. Philos. Soc. 1935, 31, 232–241. [Google Scholar] [CrossRef]
- Dawson, P.H. Windage Loss in Larger High-Speed Gears. Proc. Inst. Mech. Eng. Part A Power Process Eng. 1984, 198, 51–59. [Google Scholar] [CrossRef]
- Townsend, D. Dudley’s Gear Handbook—The Design, Manufacture, and Application of Gears, 2nd ed.; McGarw Hill Education: Columbus, OH, USA, 1992; pp. 1–847. [Google Scholar]
- Anderson, N.E.; Loewenthal, S.H. Effect of geometry and operating conditions on spur gear system power loss. J. Mech. Des. 1981, 103, 151–159. [Google Scholar] [CrossRef]
- Niel, D.; Changenet, C.; Ville, F.; Octrue, M. Thermomecanical study of high speed rolling element bearing: A simplified approach. Proc. Inst. Mech. Eng. Part. J J. Eng. Tribol. 2019, 233, 541–552. [Google Scholar] [CrossRef]
- Cann, P.M.E.; Lubrecht, A.A. Bearing performance limits with grease lubrication: The interaction of bearing design, operating conditions and grease properties. J. Phys. D Appl. Phys. 2007, 40, 5446–5451. [Google Scholar] [CrossRef]
- Shigley, J.E.; Mitchell, L.D.; Saunders, H. Mechanical Engineering Design (4th Ed.). J. Mech. Transm. Autom. Des. 1985, 107, 145. [Google Scholar] [CrossRef]















| Gear Type | Spur | Helical |
|---|---|---|
| Module (mm) | 5 | 4 |
| Width (mm) | 24 | 30 |
| Tooth height (mm) | 11.25 | 9 |
| Pressure angle (°) | 20 | 25 |
| Helix angle (°) | 0 | 20.5 |
| Number of teeth | 30 | 35 |
| Test Series: | Spur–0/25 | Spur–5/25 | Spur–10/25 | Spur–15/25 |
|---|---|---|---|---|
| 0 | 5 | 10 | 15 | |
| 25 | 25 | 25 | 25 | |
| Rotational speed | 0–6000 | |||
| Test Series: | Helical–0/25–Dir 2 | Helical–5/25–Dir 2 | Helical–10/25–Dir 2 |
|---|---|---|---|
| 0 | 5 | 10 | |
| 25 | 25 | 25 | |
| 2 | 2 | 2 | |
| Rotational speed | 0–6000 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, T.; Diab, Y.; Changenet, C.; Touret, T.; Guilbert, B. The Use of Gas Dynamics to Estimate the Influence of Flanges on Gear Windage Power Loss. Dynamics 2025, 5, 33. https://doi.org/10.3390/dynamics5030033
Torres T, Diab Y, Changenet C, Touret T, Guilbert B. The Use of Gas Dynamics to Estimate the Influence of Flanges on Gear Windage Power Loss. Dynamics. 2025; 5(3):33. https://doi.org/10.3390/dynamics5030033
Chicago/Turabian StyleTorres, Thibaut, Yasser Diab, Christophe Changenet, Thomas Touret, and Bérengère Guilbert. 2025. "The Use of Gas Dynamics to Estimate the Influence of Flanges on Gear Windage Power Loss" Dynamics 5, no. 3: 33. https://doi.org/10.3390/dynamics5030033
APA StyleTorres, T., Diab, Y., Changenet, C., Touret, T., & Guilbert, B. (2025). The Use of Gas Dynamics to Estimate the Influence of Flanges on Gear Windage Power Loss. Dynamics, 5(3), 33. https://doi.org/10.3390/dynamics5030033






