Temporal Ramsey Graphs: The Ramsey Kinematic Approach to the Motion of Systems of Material Points
Abstract
1. Introduction
2. Results
2.1. A Coloring Procedure Applicable to the Motion of Point Masses: Bi-Coloring for a Pair of Particles
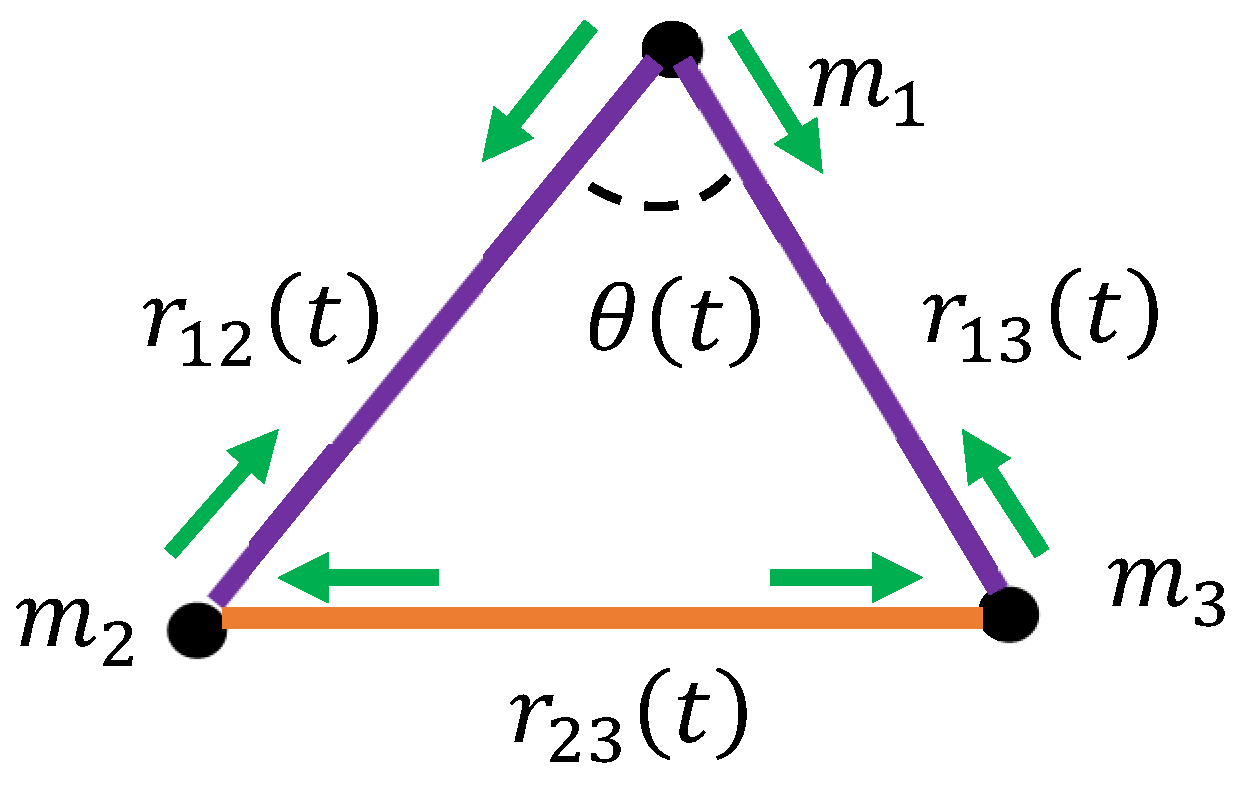
2.2. The Coloring for a Triad of Particles: Checking the Transitivity of the Coloring Procedure
2.3. Kinematic Graphs Emerging from the Motion of Multi-Particle Systems
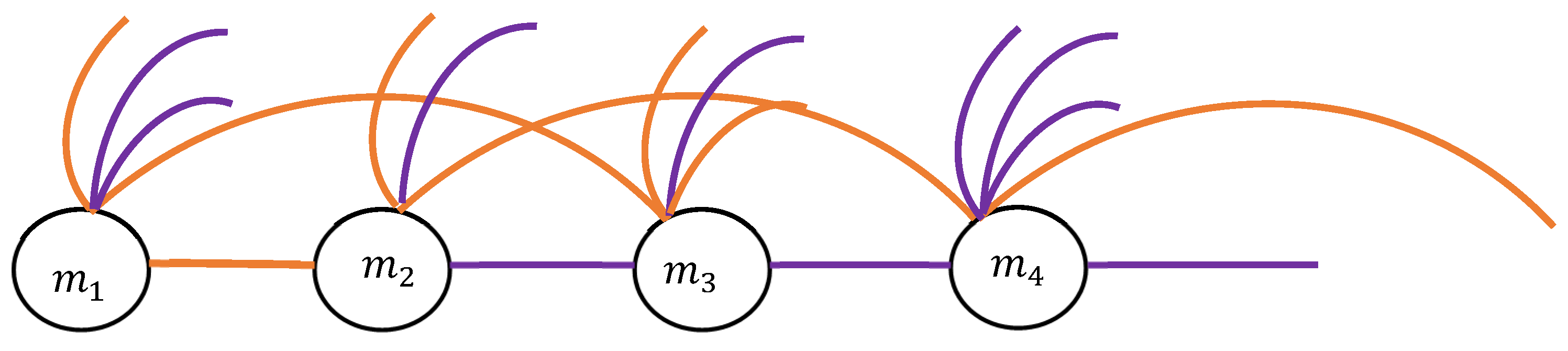
2.4. Generalization for Infinite Systems of Material Points
3. Discussion
- (i)
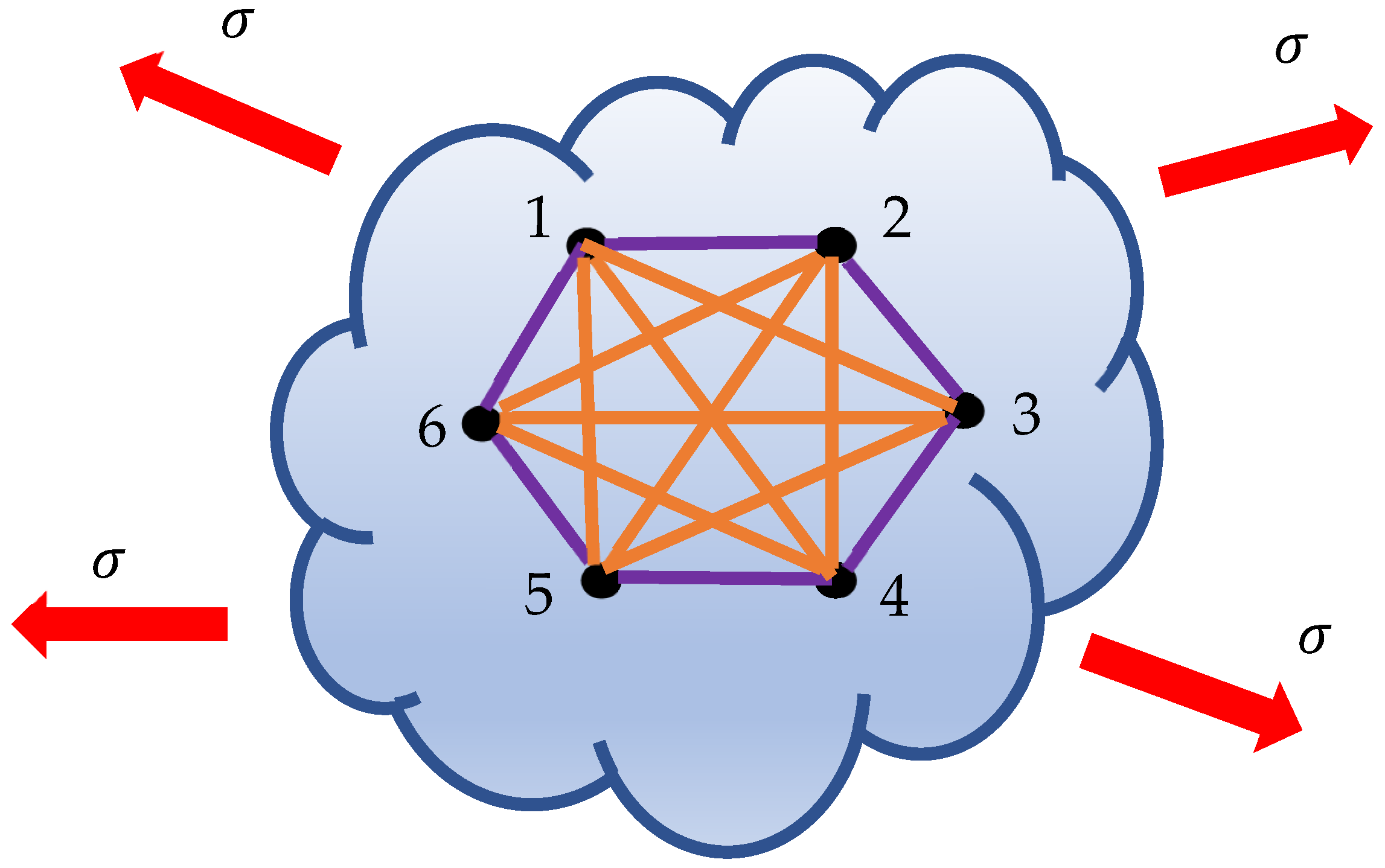
- The introduced Ramsey kinematics may be useful for the analysis of turbulence. Turbulence has been investigated for a long time within the Eulerian approach [30]. However, the fundamental mechanisms of turbulent flows, as well as their mixing and transport properties, can be more naturally understood within the Lagrangian paradigm [31,32,33]. In particular, the relative separation of a pair of tracers is closely related to the growth of a blob of a passive scalar in a turbulent flow [31,32,33]. Our results demonstrate that in any set of six tracers, we will always find three which converge or move away from each other. And, consequently, in any set of 18 tracers, there will be always present the tetrad of tracers which converge or move away from each other [31,32,33].
- (ii)
- The developed approach may be useful for analyses of the strain of a deformable body (not necessarily elastic). Consider the deformable body depicted in Figure 8. Points are fixed within the body, and then the stress is applied (see Figure 8). The points are displaced relative to other. We connect the points with links; the coloring of the links is described using Equations (2) and (3).
- (iii)
- The analysis introduced may be applied to the study of the motion of elementary particles. For example, the decay of an excited 24Mg nucleus into six α particles from a selection of central 12C+ 12C reactions at a 95 MeV beam energy was studied [34]. The kinematic graph emerging from the motion of six motile particles, depicted in Figure 6, is applicable to an analysis of the motion of six α particles.
- (iv)
- (v)
- Celestial mechanics. It is interesting that ancient astronomers distinguished six planets, namely Mercury, Earth, Venus, Mars, Jupiter, and Saturn [38].
- (vi)
- The study of the motion of swarms of bacteria, when the formation of triads and tetrads of bacteria is important [39].
- (i)
- An extension to the suggested approach to relativistic particles.
- (ii)
- An extension of the approach to the motion of deformable bodies.
- (iii)
- An extension of the approach to the motion of large numbers of particles (which may be separated into subsets of six particles).
- (iv)
- The development of the a-colored kinematic Ramsey approach: the first kind of link connects particles which converge; the second kind of link connects particles which move away from each other; and the third kind of link connects particles which are at rest relative to one another.
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wigner, E.P. The Unreasonable Effectiveness of Mathematics in the Natural Sciences. In Mathematics and Science; World Scientific: Singapore, 1990; pp. 291–306. [Google Scholar]
- Grinbaum, A. The effectiveness of mathematics in physics of the unknown. Synthese 2019, 196, 973–989. [Google Scholar] [CrossRef]
- Plotnitsky, A. On the Reasonable and Unreasonable Effectiveness of Mathematics in Classical and Quantum Physics. Found. Phys. 2011, 41, 466–491. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: New York, NY, USA, 2008. [Google Scholar]
- Bollobás, B. Modern Graph Theory; Springer: Berlin, Germany, 2013; Volume 184. [Google Scholar]
- Kosowski, A.; Manuszewski, K. Classical coloring of graphs. Contemp. Math. 2008, 352, 1–20. [Google Scholar]
- Kano, M.; Li, X. Monochromatic and Heterochromatic Subgraphs in Edge-Colored Graphs—A Survey. Graphs Comb. 2008, 24, 237–263. [Google Scholar] [CrossRef]
- Chartrand, G.; Chatterjee, P.; Zhang, P. Ramsey chains in graphs. Electron. J. Math. 2023, 6, 1–14. [Google Scholar] [CrossRef]
- Chartrand, G.; Zhang, P. New directions in Ramsey theory. Discret. Math. Lett. 2021, 6, 84–96. [Google Scholar]
- Graham, R.L.; Rothschild, B.L.; Spencer, J.H. Ramsey Theory, 2nd ed.; Wiley-Interscience Series in Discrete Mathematics and Optimization; John Wiley & Sons, Inc.: New York, NY, USA, 1990; pp. 10–110. [Google Scholar]
- Graham, R.; Butler, S. Rudiments of Ramsey Theory, 2nd ed.; American Mathematical Society: Providence, RI, USA, 2015; pp. 7–46. [Google Scholar]
- Di Nasso, M.; Goldbring, I.; Lupini, M. Nonstandard Methods in Combinatorial Number Theory, Lecture Notes in Mathematics; Springer: Berlin, Germany, 2019; Volume 2239. [Google Scholar]
- Katz, M.; Reimann, J. Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics; Student Mathematical Library; American Mathematical Society: Providence, RI, USA, 2018; Volume 87, pp. 1–34. [Google Scholar]
- Erdős, P. Solved and unsolved problems in combinatorics and combinatorial number theory. Congr. Numer. 1981, 32, 49–62. [Google Scholar]
- Conlon, D.; Fox, J.; Sudakov, B. Recent developments in graph Ramsey theory. Surv. Comb. 2015, 424, 49–118. [Google Scholar]
- de Gois, C.; Hansenne, K.; Gühne, O. Uncertainty relations from graph theory. Phys. Rev. A 2023, 107, 062211. [Google Scholar] [CrossRef]
- Xu, Z.-P.; Schwonnek, R.; Winter, A. Bounding the Joint Numerical Range of Pauli Strings by Graph Parameters. PRX Quantum 2024, 5, 020318. [Google Scholar] [CrossRef]
- Hansenne, K.; Qu, R.; Weinbrenner, L.T.; de Gois, C.; Wang, H.; Ming, Y.; Yang, Z.; Horodecki, P.; Gao, W.; Gühne, O. Optimal overlapping tomography. arXiv 2024, arXiv:2408.05730. [Google Scholar]
- Wouters, J.; Giotis, A.; Kang, R.; Schuricht, D.; Fritz, L. Lower bounds for Ramsey numbers as a statistical physics problem. J. Stat. Mech. 2022, 2022, 0332. [Google Scholar]
- Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds. Dynamics 2023, 3, 272–281. [Google Scholar] [CrossRef]
- Frenkel, M.; Shoval, S.; Bormashenko, E. Fermat Principle, Ramsey Theory and Metamaterials. Materials 2023, 16, 7571. [Google Scholar] [CrossRef]
- Bormashenko, E.; Shvalb, N. A Ramsey-Theory-Based Approach to the Dynamics of Systems of Material Points. Dynamics 2024, 4, 845–854. [Google Scholar] [CrossRef]
- Michail, O. An introduction to temporal graphs: An algorithmic perspective. Internet Math. 2016, 12, 239–280. [Google Scholar] [CrossRef]
- Michail, O.; Spirakis, P.G. Traveling salesman problems in temporal graphs. Theor. Comput. Sci. 2016, 634, 1–23. [Google Scholar]
- Erlebach, T.; Hoffmann, M.; Kammer, F. On temporal graph exploration. J. Comput. Syst. Sci. 2021, 119, 1–18. [Google Scholar]
- Choudum, S.A.; Ponnusamy, B. Ramsey numbers for transitive tournaments. Discret. Math. 1999, 206, 119–129. [Google Scholar] [CrossRef]
- Gilevich, A.; Shoval, S.; Nosonovsky, M.; Bormashenko, E. Converting Tessellations into Graphs: From Voronoi Tessellations to Complete Graphs. Mathematics 2024, 12, 2426. [Google Scholar] [CrossRef]
- Choudum, S.A.; Ponnusamy, B. Ordered Ramsey numbers. Discret. Math. 2002, 247, 79–92. [Google Scholar]
- Li, Y.; Lin, Q. Elementary Methods of the Graph Theory; Applied Mathematical Sciences; Springer: Cham, Switzerland, 2020; pp. 3–44. [Google Scholar]
- Ramsey, F.P. On a Problem of Formal Logic. In Classic Papers in Combinatorics; Gessel, I., Rota, G.C., Eds.; Modern Birkhäuser Classics; Birkhäuser: Boston, MA, USA, 2009; pp. 264–286. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Polanco, J.I.; Arun, S.; Naso, A. Multiparticle Lagrangian statistics in homogeneous rotating turbulence. Phys. Rev. Fluids 2023, 8, 034602. [Google Scholar]
- Salazar, J.P.L.C.; Collins, L.R. Two-Particle Dispersion in Isotropic Turbulent Flows. Ann. Rev. Fluid Mech. 2009, 41, 405–432. [Google Scholar]
- Morell, L.; Bruno, M.; D’Agostino, M. Full disassembly of excited 24Mg into six α particles. Phys. Rev. C 2019, 99, 054610. [Google Scholar]
- Shaffer, F.; Hay, R.; Karri, S.B.R.; Knowlton, T. Particle clusters in and above fluidized beds. Powder Technol. 2010, 203, 3–11. [Google Scholar]
- Fedorets, A.A.; Bormashenko, E.; Dombrovsky, L.A.; Nosonovsky, M. Droplet clusters: Nature-inspired biological reactors and aerosols. Philos. Trans. R. Soc. A 2019, 377, 20190121. [Google Scholar]
- Nourhani, A. Biomimetic swarm of active particles with coupled passive-active interactions. Soft Matter 2025. online ahead of print. [Google Scholar]
- Motz, L.; Weaver, J.H. The Planets and Their Motions. In The Unfolding Universe; Springer: Boston, MA, USA, 1989. [Google Scholar]
- Samantaray, K.; Mishra, S.R.; Purohit, G.; Mohanty, P.S. AC Electric Field Mediated Assembly of Bacterial Tetrads. ACS Omega 2020, 5, 5881–5887. [Google Scholar]
- Wang, Y.; Yuan, Y.; Ma, Y.; Wang, G. Time-Dependent Graphs: Definitions, Applications, and Algorithms. Data Sci. Eng. 2019, 4, 352–366. [Google Scholar]


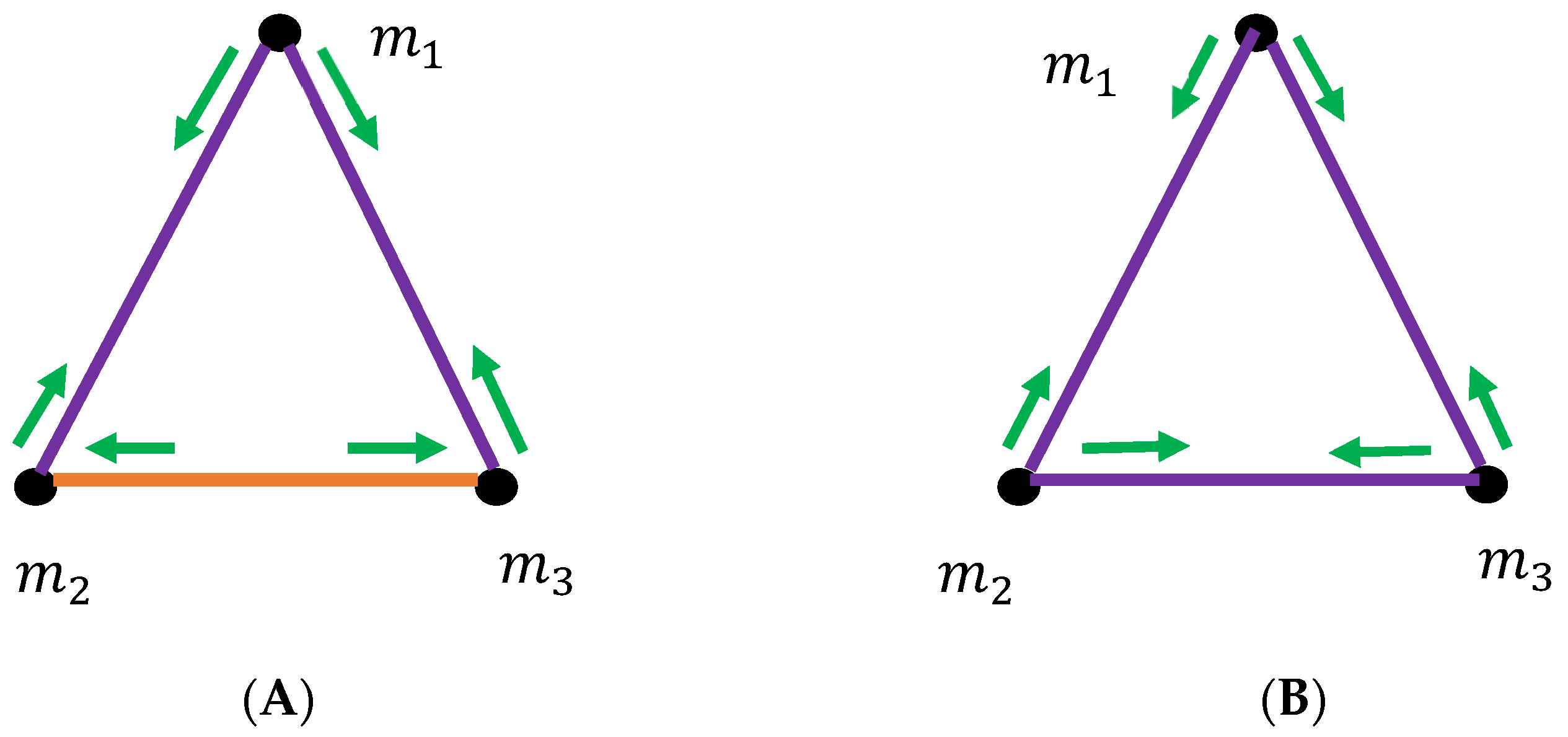


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E. Temporal Ramsey Graphs: The Ramsey Kinematic Approach to the Motion of Systems of Material Points. Dynamics 2025, 5, 11. https://doi.org/10.3390/dynamics5020011
Bormashenko E. Temporal Ramsey Graphs: The Ramsey Kinematic Approach to the Motion of Systems of Material Points. Dynamics. 2025; 5(2):11. https://doi.org/10.3390/dynamics5020011
Chicago/Turabian StyleBormashenko, Edward. 2025. "Temporal Ramsey Graphs: The Ramsey Kinematic Approach to the Motion of Systems of Material Points" Dynamics 5, no. 2: 11. https://doi.org/10.3390/dynamics5020011
APA StyleBormashenko, E. (2025). Temporal Ramsey Graphs: The Ramsey Kinematic Approach to the Motion of Systems of Material Points. Dynamics, 5(2), 11. https://doi.org/10.3390/dynamics5020011





