An Optimum Design for a Fast-Response Solenoid Valve: Application to a Limaçon Gas Expander
Abstract
1. Introduction
2. Limaçon Expander with Inlet Valve
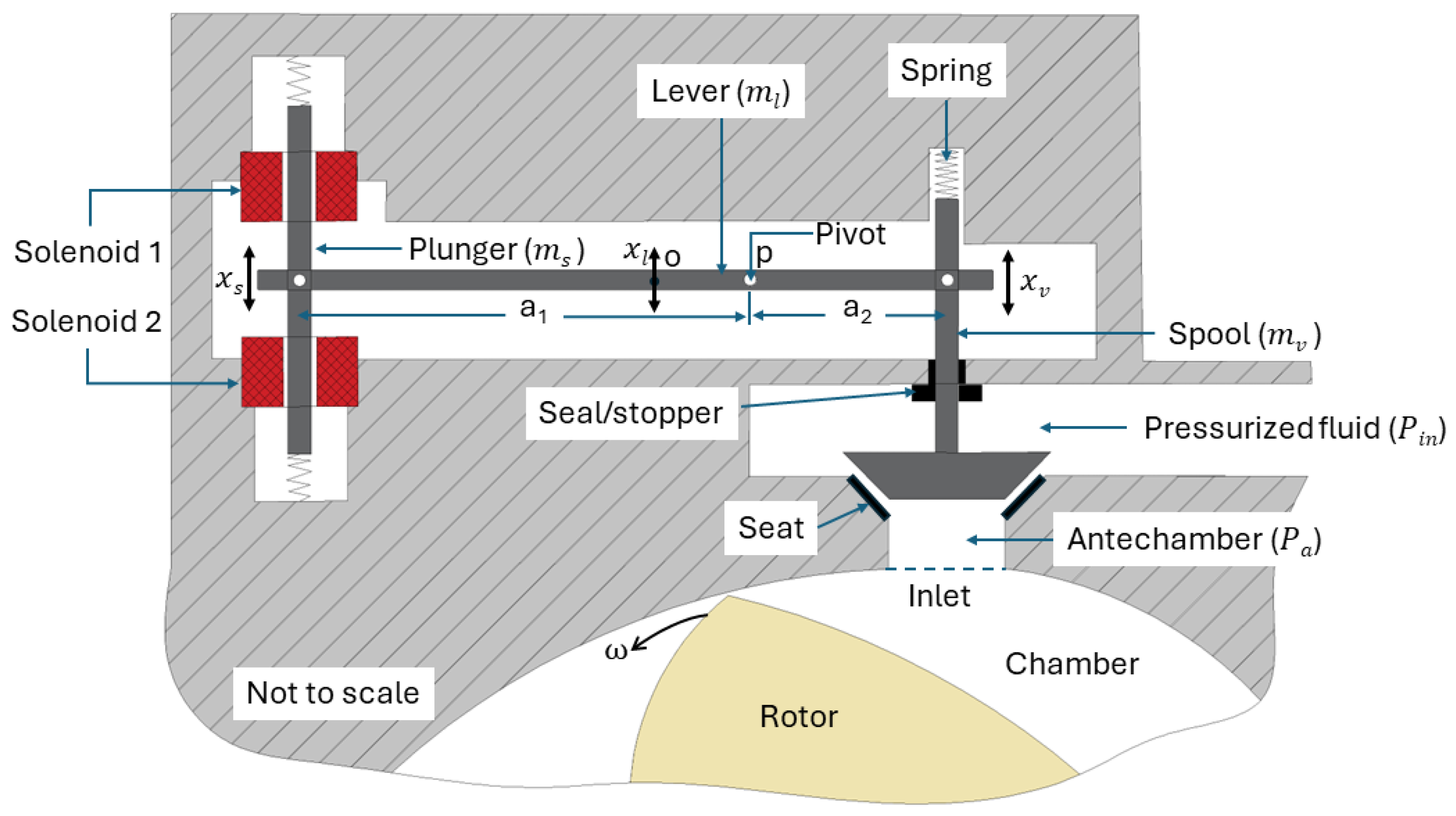
2.1. Push–Pull Solenoid Valve
- is the vertical displacement of the plunger,
- , , and are the displacement, inertia, and rotation of the lever at its center of gravity,
- is the spring stiffness,
- is the initial spring deflection,
- is the force generated by solenoids;
- is the pressure force acting on the valve disk; and
- is the force exerted on the valve disk or spool when in contact with the seat or stopper.
- is the plunger displacement for solenoid ;
- and are constants given by Yuan et al. [40]. The displacements and velocity due to solenoids 1 and 2 are given by:
- Solenoid 1: and ;
- Solenoid 2: and ; where S is the stroke of the valve spool.
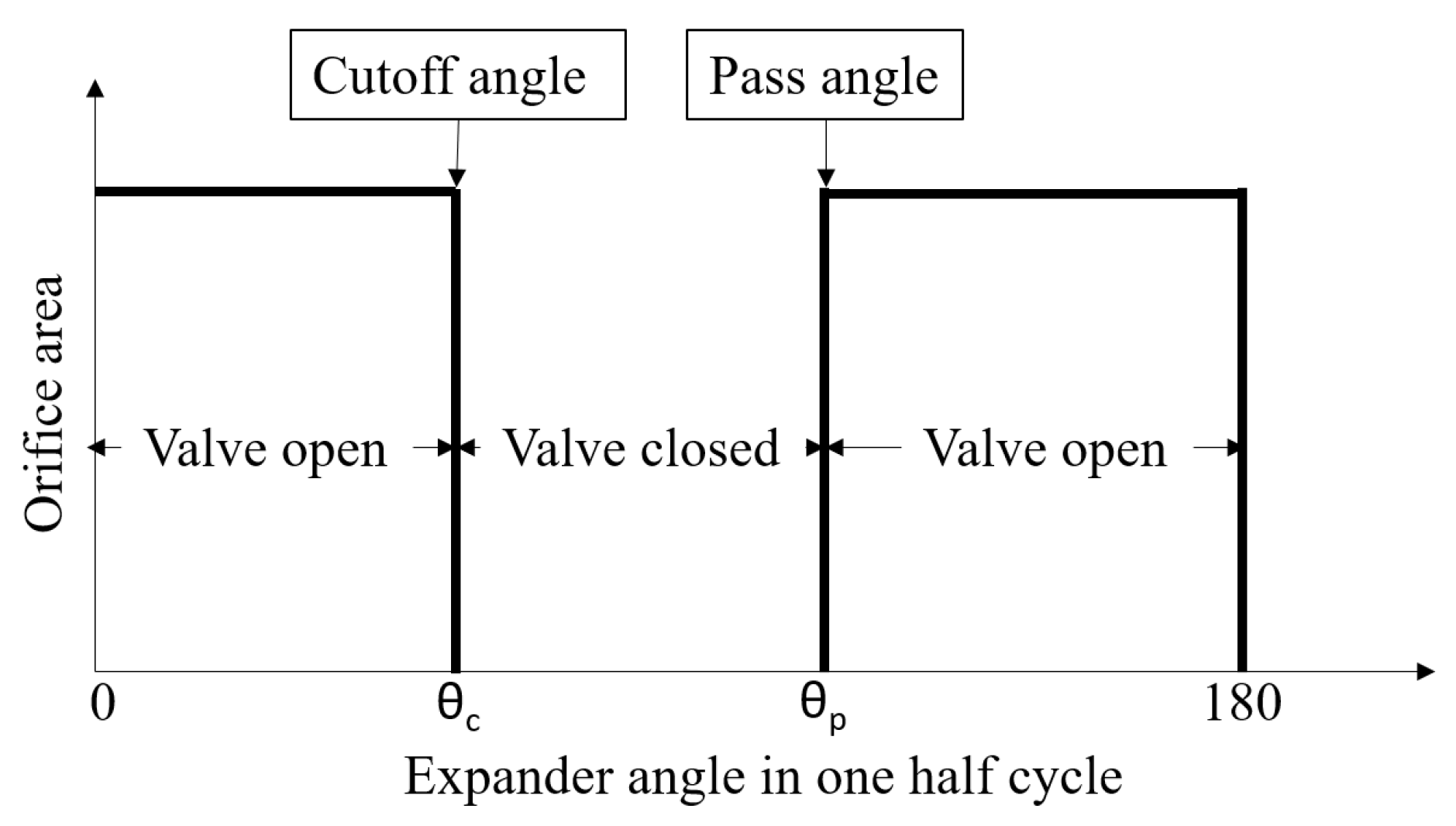
2.2. Limaçon Gas Expander
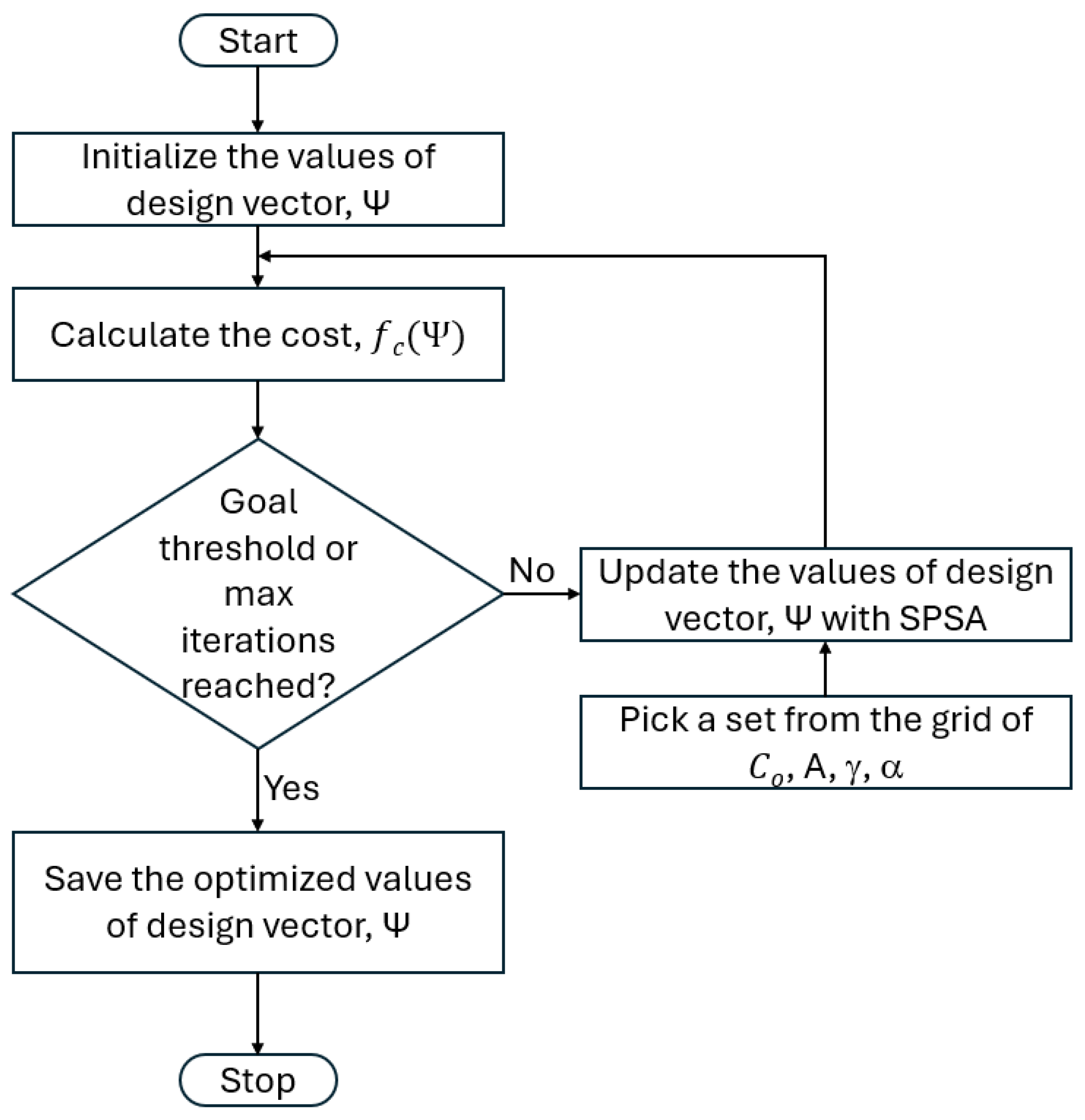
3. Optimization Process
- j is the iteration step number where , N is the number of iterations;
- and are the cost function evaluation at two adjacent perturbed points;
- is the random perturbation vector of the same size as assigned either +1 or −1 values in a binary Bernoulli distribution;
- is the perturbation size at each iteration;
- and is the adaptive step size at each iteration;
4. Results
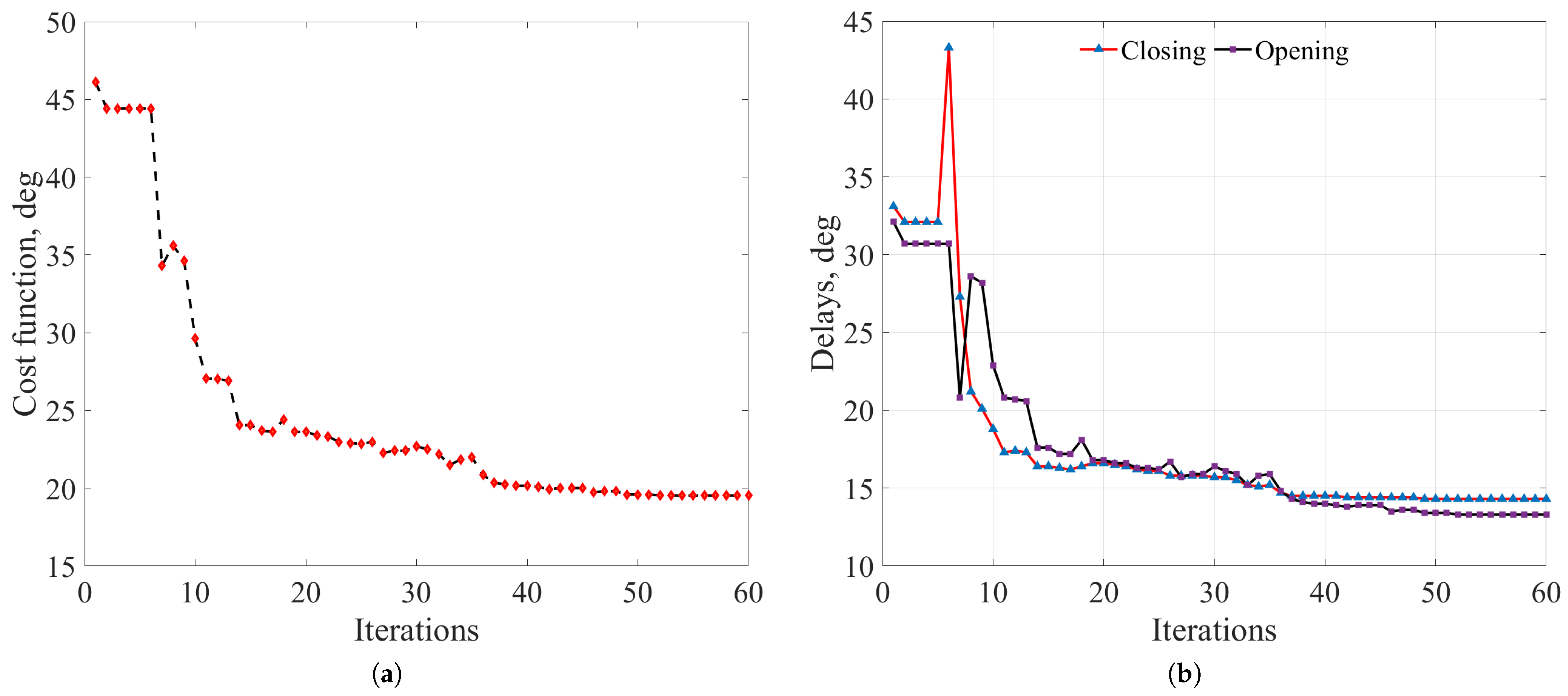
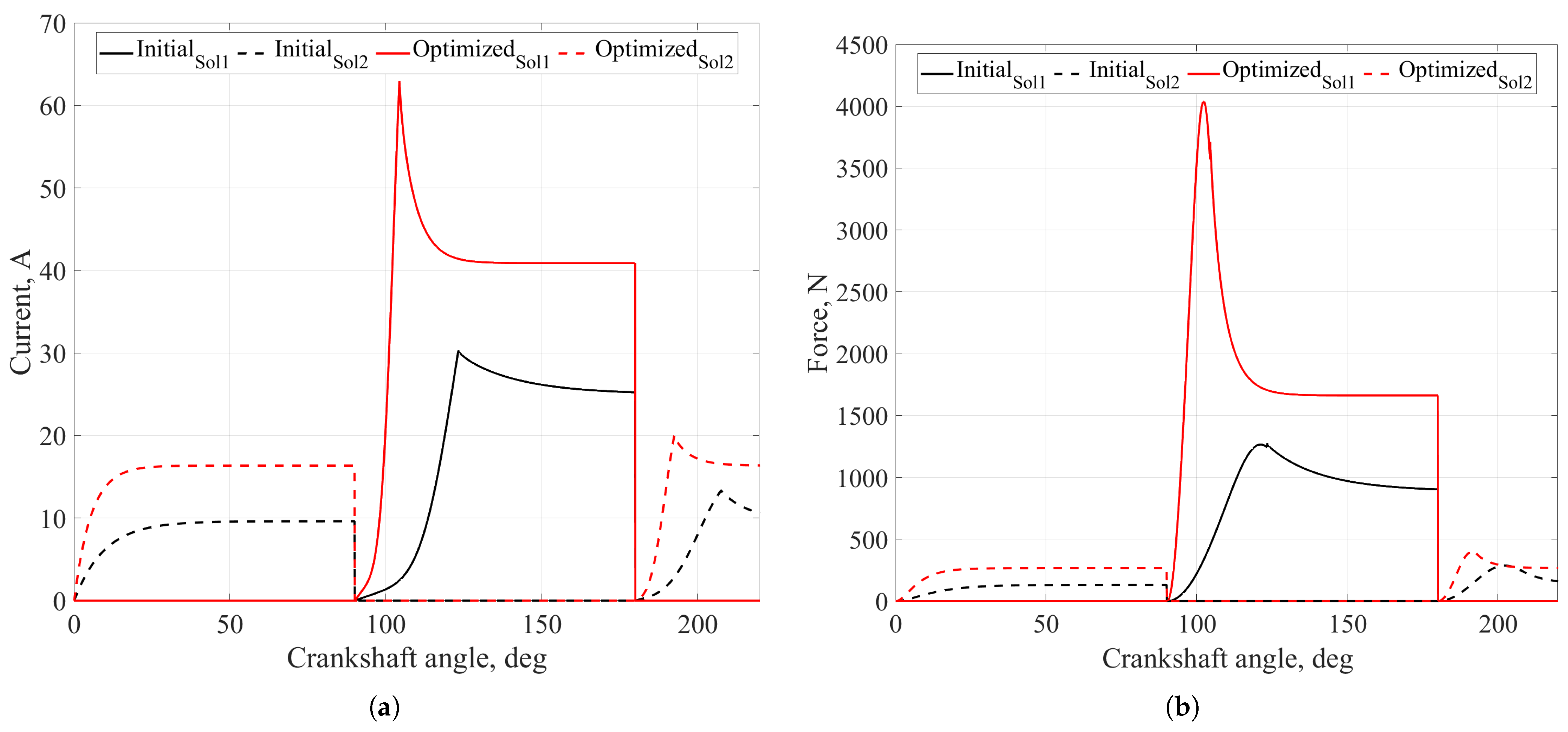
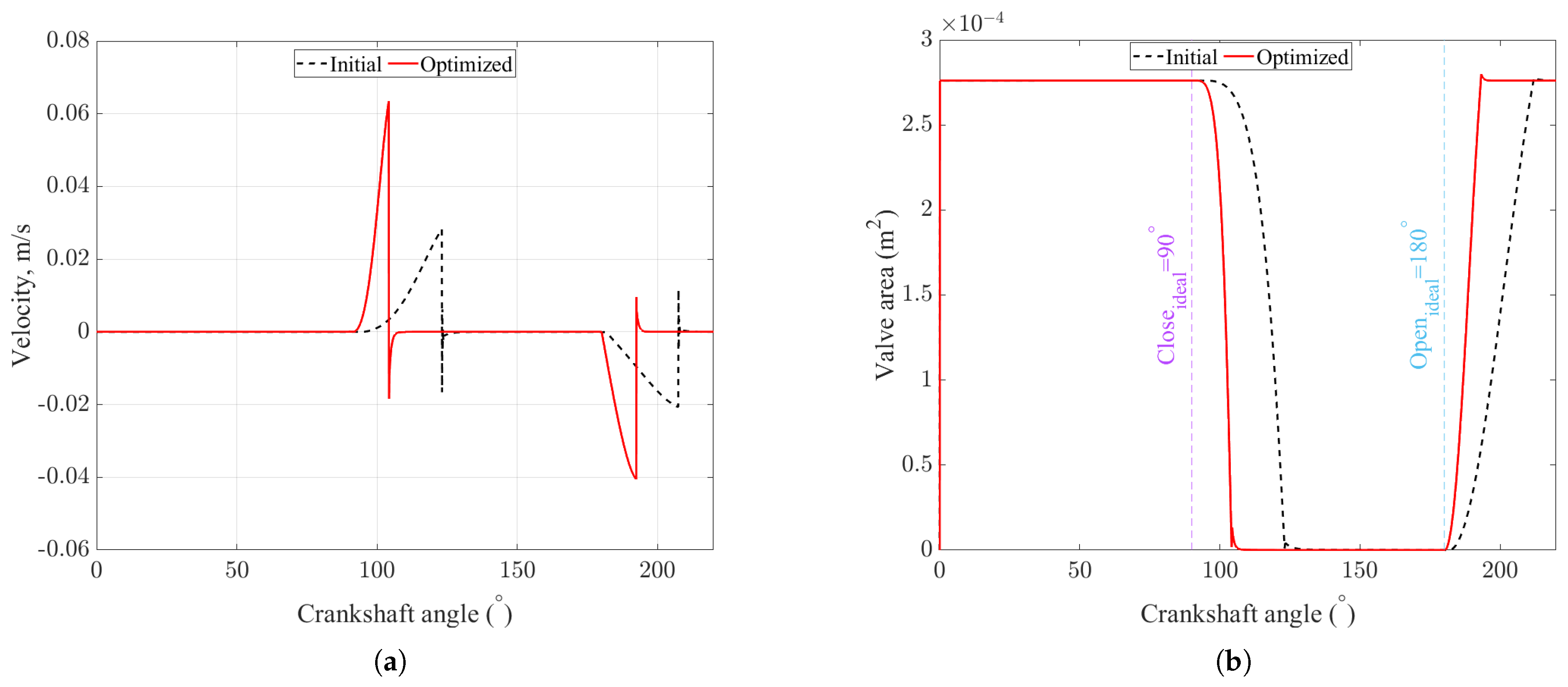
4.1. Optimized Valve Dynamics
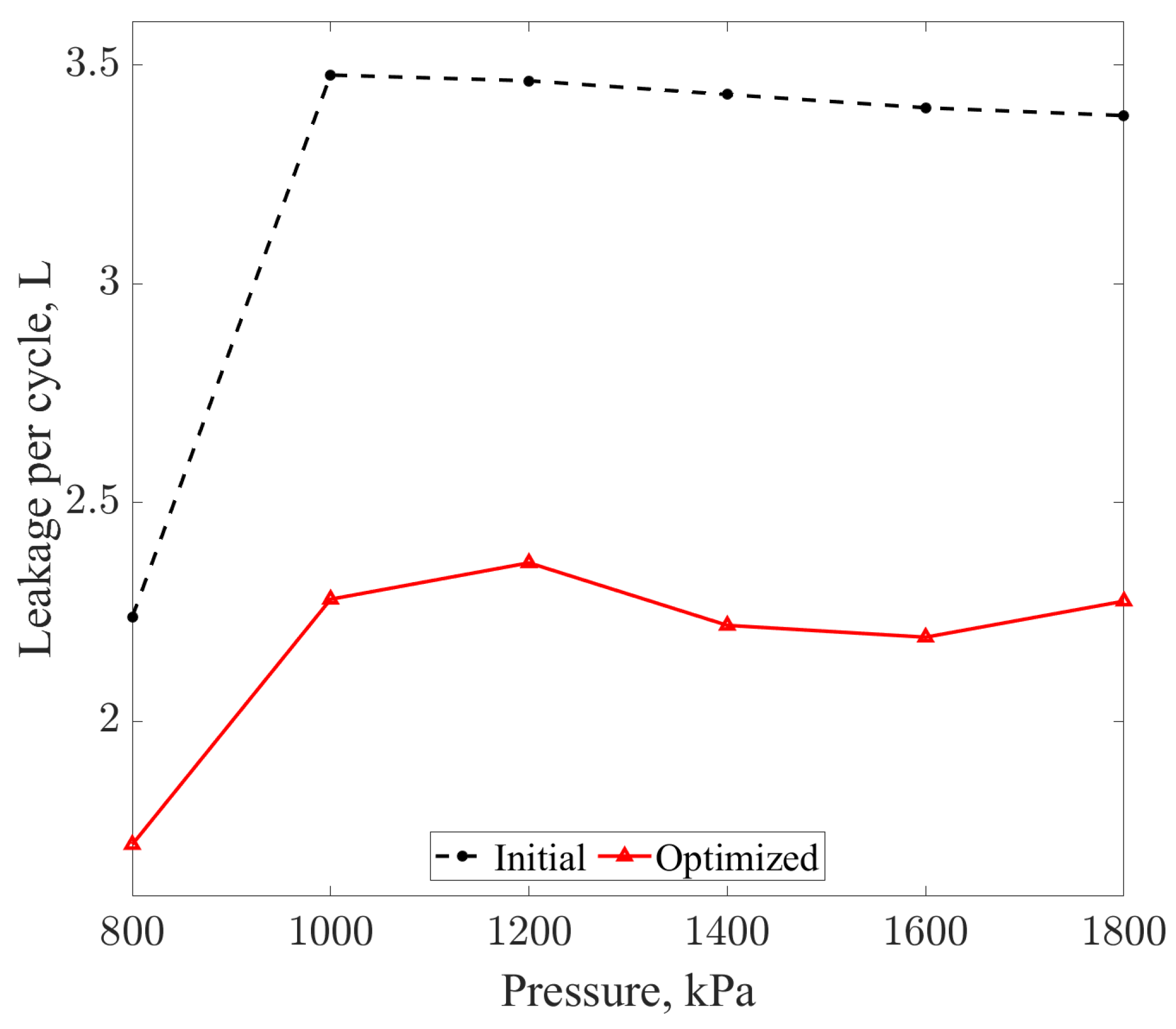
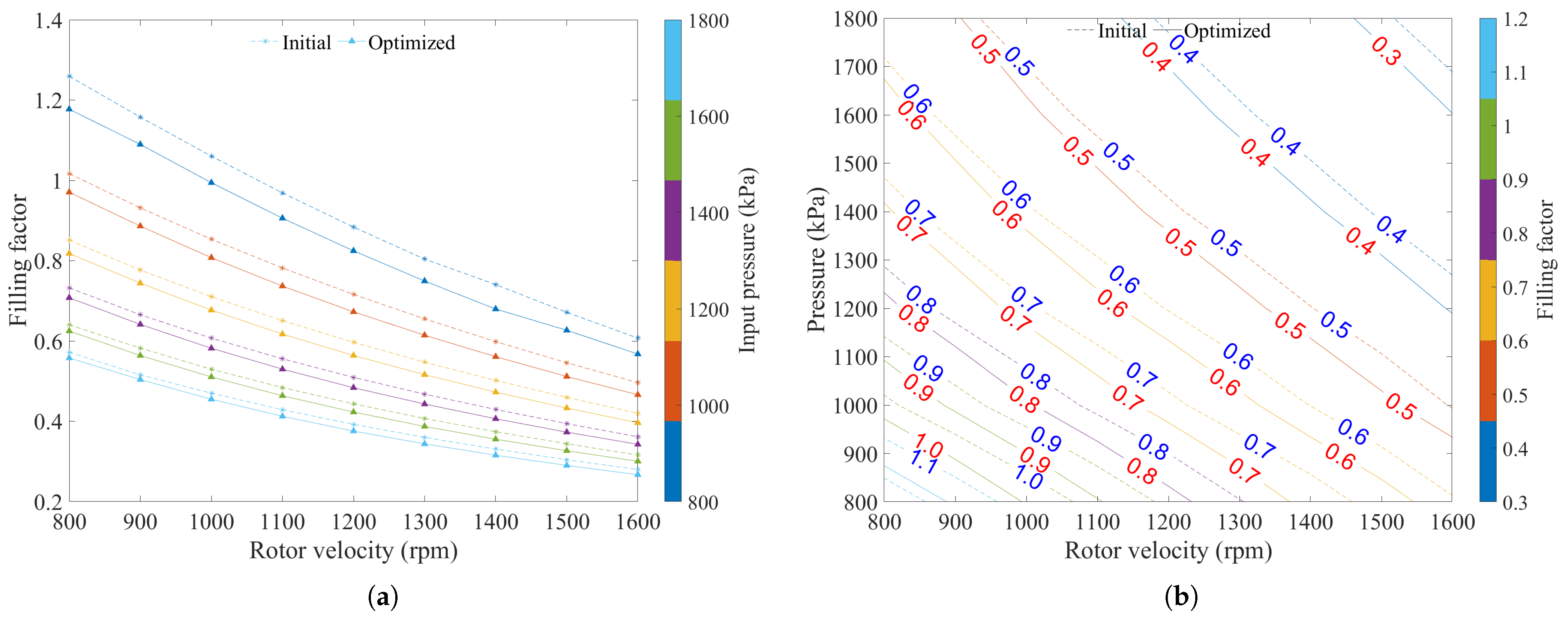
4.2. Application to a Limaçon Gas Expander
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ORC | Organic Rankine cycle |
| NSGA | Non-dominated sorting genetic algorithm |
| HSV | High-speed on/off valve |
| BPNN | Back propagation neural network |
| SPSA | Simultaneous perturbation stochastic approximation |
References
- IEA. World Energy Outlook 2022; Licence: CC BY 4.0 (report); CC BY NC SA 4.0 (Annex A); IEA: Paris, France, 2022; Available online: https://www.iea.org/reports/world-energy-outlook-2022 (accessed on 10 April 2024).
- Crew, B. Solving the energy crisis. Nature 2022, 609, 7926. [Google Scholar] [CrossRef] [PubMed]
- Quoilin, S.; Broek, M.V.D.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of Organic Rankine Cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Wieland, C.; Schifflechner, C.; Dawo, F.; Astolfi, M. The organic Rankine cycle power systems market: Recent developments and future perspectives. Appl. Therm. Eng. 2023, 224, 119980. [Google Scholar] [CrossRef]
- Putrus, G.; Bentley, E. 20—Integration of distributed renewable energy systems into the smart grid. In Electric Renewable Energy Systems; Rashid, M.H., Ed.; Academic Press: Boston, FL, USA, 2016; pp. 487–518. [Google Scholar] [CrossRef]
- Haddad, C.; Périlhon, C.; Danlos, A.; François, M.X.; Descombes, G. Some Efficient Solutions to Recover Low and Medium Waste Heat: Competitiveness of the Thermoacoustic Technology. Energy Procedia 2014, 50, 1056–1069. [Google Scholar] [CrossRef]
- Liu, Q.; Lasala, S. Waste heat recovery from fossil-fired power plants by organic rankine cycles. In Organic Rankine Cycles for Waste Heat Recovery-Analysis and Applications; IntechOpen: London, UK, 2019. [Google Scholar]
- Auld, A.; Berson, A.; Hogg, S. Organic Rankine cycles in waste heat recovery: A comparative study. Int. J. Low-Carbon Technol. 2013, 8, i9–i18. [Google Scholar] [CrossRef]
- Holdmann, G. The Chena Hot Springs 400kW Geothermal Power Plant: Experience Gained During the First Year of Operation. Trans. Geotherm. Resour. Counc. 2008, 31, 515–519. [Google Scholar]
- Tian, H.; Shu, G. 17—Organic Rankine Cycle systems for large-scale waste heat recovery to produce electricity. In Organic Rankine Cycle (ORC) Power Systems; Macchi, E., Astolfi, M., Eds.; Woodhead Publishing: Sawston, UK, 2017; pp. 613–636. [Google Scholar] [CrossRef]
- Macchi, E. 1—Theoretical basis of the Organic Rankine Cycle. In Organic Rankine Cycle (ORC) Power Systems; Macchi, E., Astolfi, M., Eds.; Woodhead Publishing: Sawston, UK, 2017; pp. 3–24. [Google Scholar] [CrossRef]
- Lemort, V.; Quoilin, S.; Cuevas, C.; Lebrun, J. Testing and modeling a scroll expander integrated into an Organic Rankine Cycle. Appl. Therm. Eng. 2009, 29, 3094–3102. [Google Scholar] [CrossRef]
- Francesconi, M.; Briola, S.; Antonelli, M. A Review on Two-Phase Volumetric Expanders and Their Applications. Appl. Sci. 2022, 12, 10328. [Google Scholar] [CrossRef]
- Sultan, I.A.; Schaller, C.G. Optimum Positioning of Ports in the Limaçon Gas Expanders. J. Eng. Gas Turbines Power 2011, 133, 103002. [Google Scholar] [CrossRef]
- Collings, P.; Mckeown, A.; Wang, E.; Yu, Z. Experimental Investigation of a Small-Scale ORC Power Plant Using a Positive Displacement Expander with and without a Regenerator. Energies 2019, 12, 1452. [Google Scholar] [CrossRef]
- Hijriawan, M.; Pambudi, N.A.; Wijayanto, D.S.; Biddinika, M.K.; Saw, L.H. Experimental analysis of R134a working fluid on Organic Rankine Cycle (ORC) systems with scroll-expander. Eng. Sci. Technol. Int. J. 2022, 29, 101036. [Google Scholar] [CrossRef]
- Hsieh, J.C.; Chen, Y.H.; Hsieh, Y.C. Experimental study of an organic Rankine cycle with a variable-rotational-speed scroll expander at various heat source temperatures. Energy 2023, 270, 126956. [Google Scholar] [CrossRef]
- Kaczmarczyk, T.Z.; Żywica, G. Experimental research of a micropower volumetric expander for domestic applications at constant electrical load. Sustain. Energy Technol. Assess. 2022, 49, 101755. [Google Scholar] [CrossRef]
- Marchionni, M.; Fatigati, F.; Di Bartolomeo, M.; Di Battista, D.; Petrollese, M. Experimental and Numerical Dynamic Investigation of an ORC System for Waste Heat Recovery Applications in Transportation Sector. Energies 2022, 15, 9339. [Google Scholar] [CrossRef]
- Kolasiński, P.; Błasiak, P.; Rak, J. Experimental and Numerical Analyses on the Rotary Vane Expander Operating Conditions in a Micro Organic Rankine Cycle System. Energies 2016, 9, 606. [Google Scholar] [CrossRef]
- Fatigati, F.; Di Bartolomeo, M.; Di Battista, D.; Cipollone, R. Experimental Validation of a New Modeling for the Design Optimization of a Sliding Vane Rotary Expander Operating in an ORC-Based Power Unit. Energies 2020, 13, 4204. [Google Scholar] [CrossRef]
- Galindo, J.; Ruiz, S.; Dolz, V.; Royo-Pascual, L.; Haller, R.; Nicolas, B.; Glavatskaya, Y. Experimental and thermodynamic analysis of a bottoming Organic Rankine Cycle (ORC) of gasoline engine using swash-plate expander. Energy Convers. Manag. 2015, 103, 519–532. [Google Scholar] [CrossRef]
- Dawo, F.; Eyerer, S.; Pili, R.; Wieland, C.; Spliethoff, H. Experimental investigation, model validation and application of twin-screw expanders with different built-in volume ratios. Appl. Energy 2021, 282, 116139. [Google Scholar] [CrossRef]
- Vimalakanthan, K.; Read, M.; Kovacevic, A. Numerical Modelling and Experimental Validation of Twin-Screw Expanders. Energies 2020, 13, 4700. [Google Scholar] [CrossRef]
- Ping, X.; Yang, F.; Zhang, H.; Zhang, W.; Zhang, J.; Song, G.; Wang, C.; Yao, B.; Wu, Y. Prediction and optimization of power output of single screw expander in organic Rankine cycle (ORC) for diesel engine waste heat recovery. Appl. Therm. Eng. 2021, 182, 116048. [Google Scholar] [CrossRef]
- Fatigati, F.; Vittorini, D.; Coletta, A.; Cipollone, R. Assessment of the differential impact of scroll and sliding vane rotary expander permeability on the energy performance of a small-scale solar-ORC unit. Energy Convers. Manag. 2022, 269, 116169. [Google Scholar] [CrossRef]
- Alshammari, F.; Usman, M.; Pesyridis, A. Expanders for Organic Rankine Cycle Technology. In Organic Rankine Cycle Technology for Heat Recovery; Wang, E., Ed.; IntechOpen: Rijeka, Croatia, 2018; Chapter 3. [Google Scholar] [CrossRef]
- Wang, C.; Liu, M.; Li, Z.; Xing, Z.; Shu, Y. Performance improvement of twin-screw air expander used in PEMFC systems by two-phase expansion. Energy 2023, 273, 127249. [Google Scholar] [CrossRef]
- Li, L.; Tao, L.; Gou, Y.; Zhang, S. Improvement and Experimental Study of Scroll Expander for Organic Rankine Cycle. Energy Eng. 2020, 117, 225–235. [Google Scholar] [CrossRef]
- Fatigati, F.; Di Giovine, G.; Cipollone, R. Feasibility Assessment of a Dual Intake-Port Scroll Expander Operating in an ORC-Based Power Unit. Energies 2022, 15, 770. [Google Scholar] [CrossRef]
- Sultan, I.A. The Limaçon of Pascal: Mechanical Generation and Utilization for Fluid Processing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 813–822. [Google Scholar] [CrossRef]
- Sultan, I.A. Profiling Rotors for Limaçon-to-Limaçon Compression-Expansion Machines. J. Mech. Des. 2005, 128, 787–793. [Google Scholar] [CrossRef]
- Sultan, I.A. Optimum design of limaçon gas expanders based on thermodynamic performance. Appl. Therm. Eng. 2012, 39, 188–197. [Google Scholar] [CrossRef]
- Sultan, I.A.; Phung, T.H.; Alhelal, A. Improving Process Efficiency by Waste Heat Recuperation: An Application of the Limaçon Technology. Sustain. Miner. Energy Sect. 2016, 475–498. [Google Scholar] [CrossRef]
- Phung, T.H.; Sultan, I.A. Characterization of Limacon Gas Expanders with Consideration to the Dynamics of Apex Seals and Inlet Control Valve. J. Eng. Gas Turbines Power 2018, 140, 122501. [Google Scholar] [CrossRef]
- Zhong, Q.; Wang, J.; Xu, E.; Yu, C.; Li, Y. Multi-objective optimization of a high speed on/off valve for dynamic performance improvement and volume minimization. Chin. J. Aeronaut. 2024; in press. [Google Scholar] [CrossRef]
- Qingtong, L.; Fanglong, Y.; Songlin, N.; Ruidong, H.; Hui, J. Multi-objective optimization of high-speed on-off valve based on surrogate model for water hydraulic manipulators. Fusion Eng. Des. 2021, 173, 112949. [Google Scholar] [CrossRef]
- Wu, S.; Zhao, X.; Li, C.; Jiao, Z.; Qu, F. Multiobjective Optimization of a Hollow Plunger Type Solenoid for High Speed On/Off Valve. IEEE Trans. Ind. Electron. 2018, 65, 3115–3124. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, L.; Zhao, J.; Grekhov, L. Research on Multi-Objective Optimization of High-Speed Solenoid Valve Drive Strategies under the Synergistic Effect of Dynamic Response and Energy Loss. Energies 2024, 17, 300. [Google Scholar] [CrossRef]
- Self-Calibration of Push-Pull Solenoid Actuators in Electrohydraulic Valves, Vol. Fluid Power Systems and Technology. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 13–19 November 2004. [CrossRef]
- Tuymer, W.J.; Machu, E.H. Compressor valves. In Compressor Handbook; Hanlon, P.C., Ed.; McGraw-Hill: New York, NY, USA, 2001; pp. 20.1–20.29. [Google Scholar]




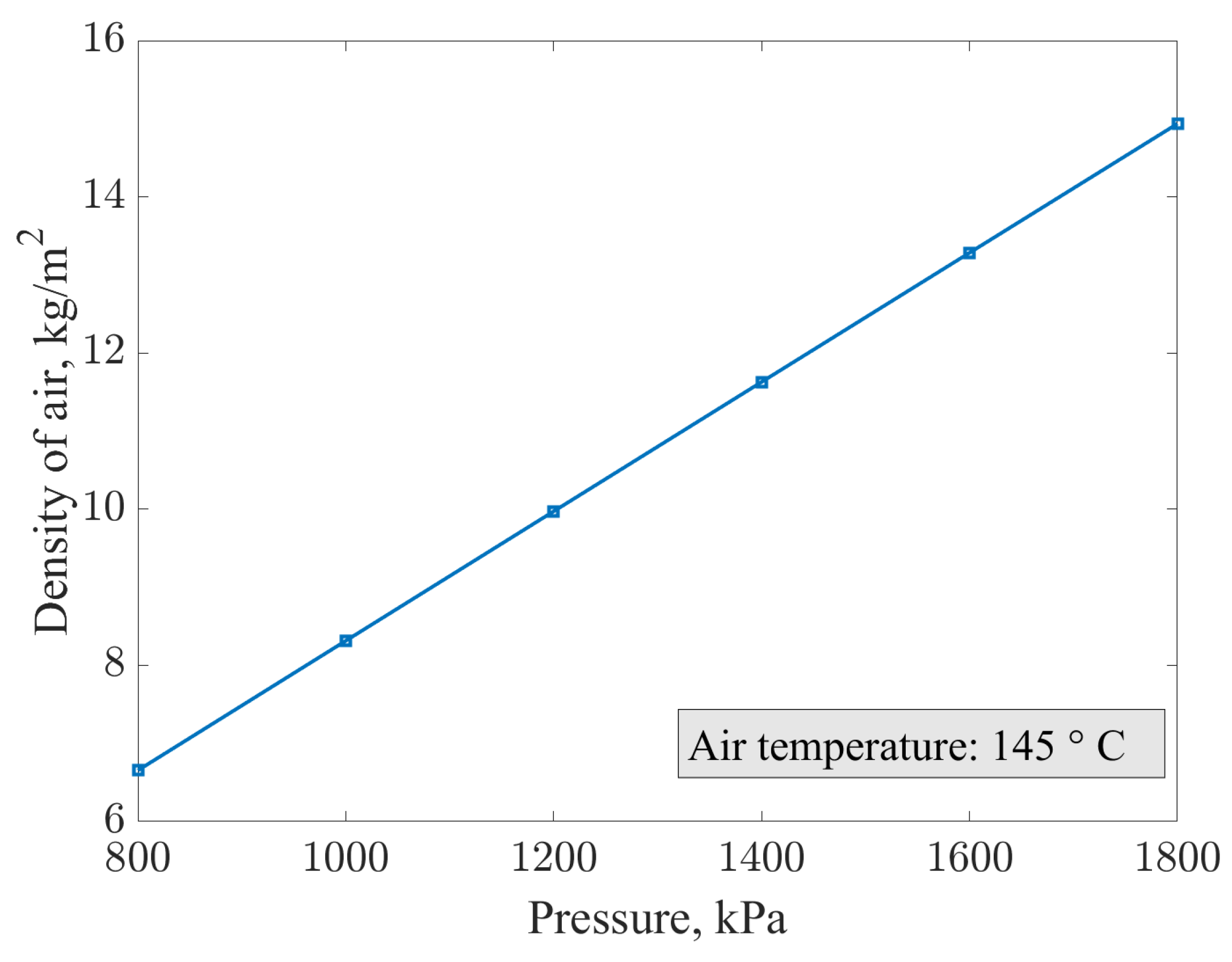
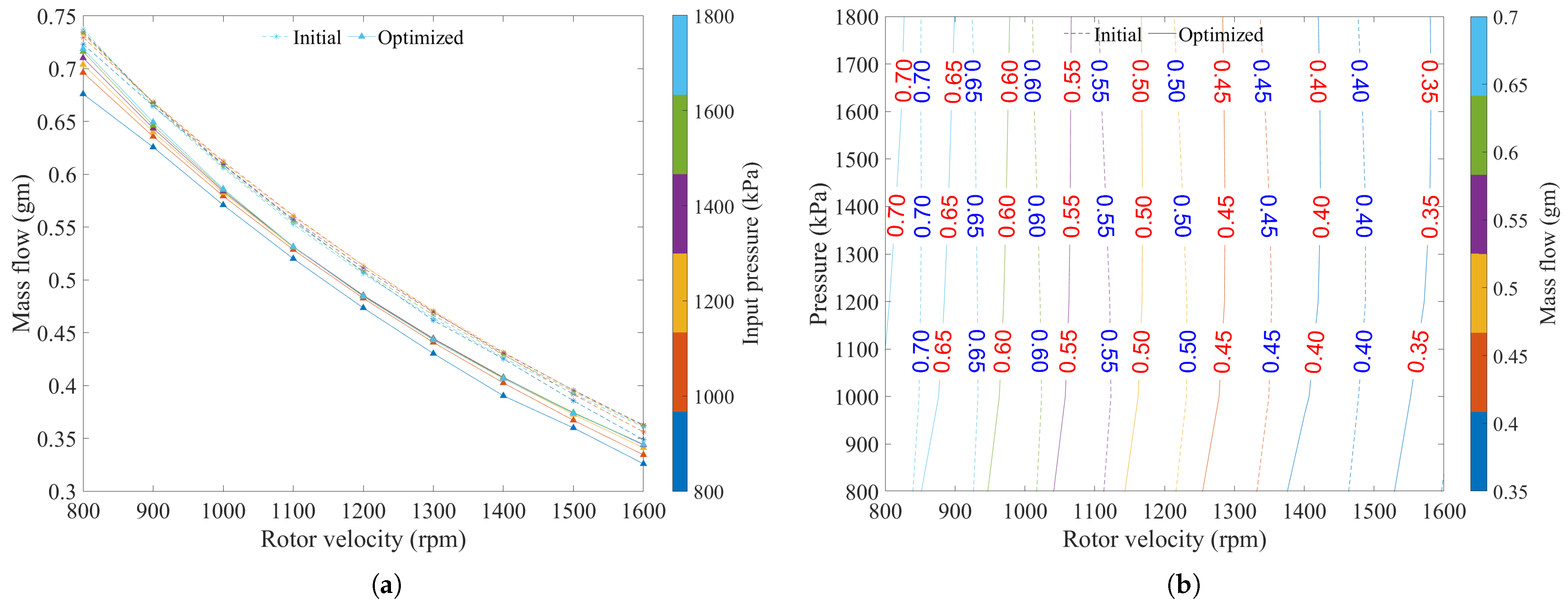

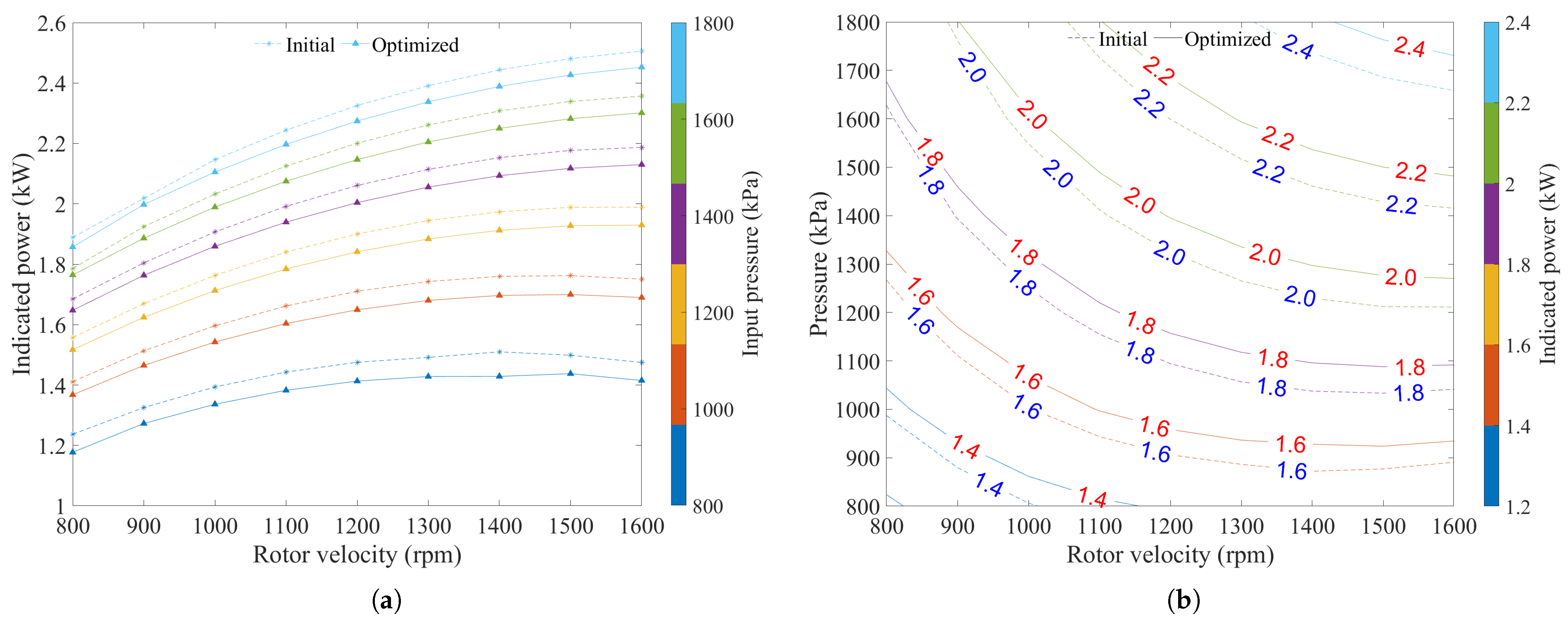
| Parameters | Initial Value | Minimum Value | Maximum Value | Optimized Value |
|---|---|---|---|---|
| Mass of valve, () | 34 × 10−3 | 20 × 10−3 | 50 × 10−3 | 48.22 × 10−3 |
| Mass of plunger, () | 45 × 10−3 | 30 × 10−3 | 70 × 10−3 | 30 × 10−3 |
| Mass of lever, () | 30 × 10−3 | 10 × 10−3 | 50 × 10−3 | 15.6 × 10−3 |
| Inertia of lever, () | 2 × 10−4 | 1 × 10−4 | 3 × 10−4 | 1.75 × 10−4 |
| Arm ratio, b | 3 | 2 | 5 | 4.6 |
| Length of the shorter lever arm, (m) | 0.015 | 0.005 | 0.003 | 0.029 |
| Solenoid 1 input voltage, () | 100 | 100 | 500 | 388.3 |
| Solenoid 2 input voltage, () | 75 | 20 | 300 | 150.38 |
| Solenoid 1 resistance, () | 40 | 50 | 100 | 94.98 |
| Solenoid 2 resistance, () | 78 | 50 | 100 | 91.92 |
| Spring stiffness, () | 10 | 5 | 15 | 15 |
| Damping coefficient, C | 50.45 | 20 | 75 | 26.82 |
| Parameters | Value |
|---|---|
| Rotor chord length () | mm |
| Base circle radius (r) | mm |
| Limaçon aspect ratio () | 0.171 |
| Housing-rotor clearance () | mm |
| Clearance ratio () | 0.0153 |
| Design coefficient (c) | 1.73 |
| Depth of rotor housing (H) | mm |
| Fluid type | Air |
| Outlet pressure () | 100 |
| Inlet port start angle | ° |
| Outlet port start angle | 140° |
| Inlet port end angle | ° |
| Outlet port end angle | 175° |
| Inlet port length | mm |
| Outlet port length | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.S.; Sultan, I.; Phung, T.; Kumar, A. An Optimum Design for a Fast-Response Solenoid Valve: Application to a Limaçon Gas Expander. Dynamics 2024, 4, 457-474. https://doi.org/10.3390/dynamics4020024
Hossain MS, Sultan I, Phung T, Kumar A. An Optimum Design for a Fast-Response Solenoid Valve: Application to a Limaçon Gas Expander. Dynamics. 2024; 4(2):457-474. https://doi.org/10.3390/dynamics4020024
Chicago/Turabian StyleHossain, Md Shazzad, Ibrahim Sultan, Truong Phung, and Apurv Kumar. 2024. "An Optimum Design for a Fast-Response Solenoid Valve: Application to a Limaçon Gas Expander" Dynamics 4, no. 2: 457-474. https://doi.org/10.3390/dynamics4020024
APA StyleHossain, M. S., Sultan, I., Phung, T., & Kumar, A. (2024). An Optimum Design for a Fast-Response Solenoid Valve: Application to a Limaçon Gas Expander. Dynamics, 4(2), 457-474. https://doi.org/10.3390/dynamics4020024








