Multiplicative Renormalization of Stochastic Differential Equations for the Abelian Sandpile Model
Abstract
1. Introduction
2. Stochastic Differential Equation for the ASM with the Time-Scale Separation between Energy Injection and Avalanche Relaxation
2.1. Stochastic Differential Equation for the Coarse-Grained ASM
2.2. Co-Variance of Random Forces with Time-Scale Separation
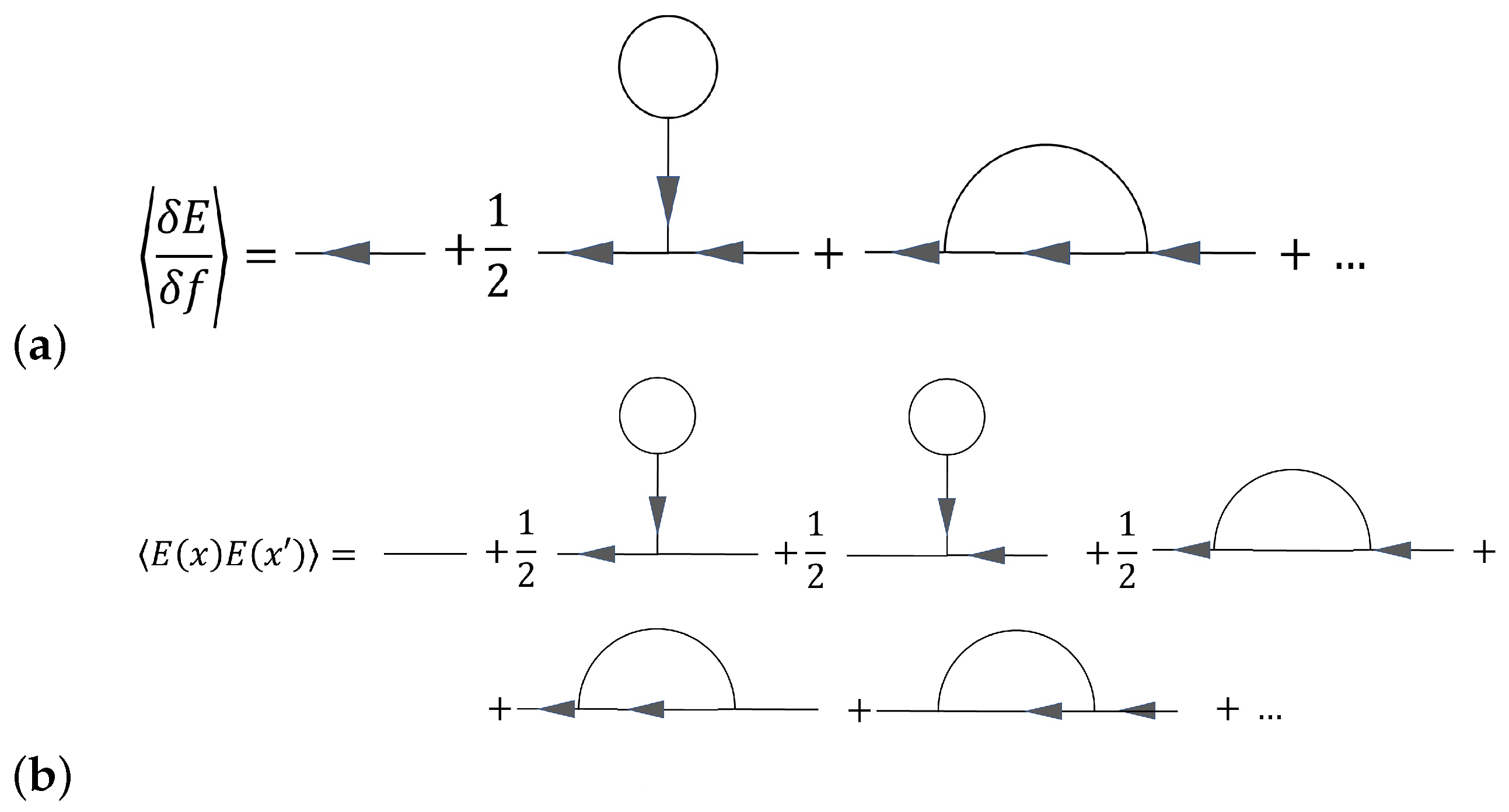
3. Functional Integral Formulation and Feynman Diagram Technique for the ASM
4. Multiplicative UV-Renormalization of the ASM
5. Calculation of an Infinite Number of Renormalization Constants in the ASM
6. RG-Equations for the ASM
7. Plane of Fixed Points in the ASM
- If there were no time-scale separation in the ASM (zero correlation time for all wave numbers k), i.e., for the “white noise” model of energy injection uncorrelated in space and time, viz.,we have , and , so that all where is the Kronecker symbol. Therefore, there are no IR-stable fixed points in the ASM. The time scale separation is important for the existence of critical scaling regimes in the ASM.
- In the opposite case of the “frozen” configuration of stochastic force, the first, trivial solution comes into play, and therefore . Therefore, there are no IR-stable fixed points in the ASM in this case.
8. On the Critical Scaling in the ASM
9. Discussion and Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACM | Abelian sandpile model |
| IR | Infra-red (momentum scale) |
| RG | Renormalization group |
| SOC | Self-organized criticality |
| UV | Ultra-violet (momentum scale) |
References
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of 1/ƒ noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef] [PubMed]
- Dhar, D. Self-organized Critical State of Sandpile Automaton Models. Phys. Rev. Lett. 1990, 64, 1613–1616. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-C. Scaling theory of self-organized criticality. Phys. Rev. Lett. 1989, 63, 470. [Google Scholar] [CrossRef] [PubMed]
- Bak, P. How Nature Works; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Newman, M.E.J.; Sneppen, K. Avalanches, scaling, and coherent noise. Phys. Rev. E 1996, 54, 6226. [Google Scholar] [CrossRef] [PubMed]
- Sneppen, K.; Newman, M.E.J. Coherent noise, scale invariance and intermittency in large systems. Phys. D 1997, 110, 209. [Google Scholar] [CrossRef][Green Version]
- Eyink, G.L.; Hussein, A. The breakdown of Alfven’s theorem in ideal plasma flows: Necessary conditions and physical conjectures. Phys. D 2006, 223, 82. [Google Scholar] [CrossRef]
- Jensen, H.J. Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems; Cambridge Lecture Notes in Physics 10; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Watkins, N.; Pruessner, G.; Chapman, S.; Crosby, N.B.; Jensen, H. 25 Years of Self-organized Criticality: Concepts and Controversies. Space Sci. Rev. 2016, 198, 3–44. [Google Scholar] [CrossRef]
- Bak, P.; Paczuski, M. Complexity, contingency, and criticality. Proc. Natl. Acad. Sci. USA 1995, 92, 6689–6696. [Google Scholar] [CrossRef]
- Ma, S.K. Modern Theory of Critical Phenomena; Reading, B., Ed.; Routledge: Londin, UK, 1976. [Google Scholar]
- Zinn-Justin, J. Quantum Field Theory and Critical Phenomena; Clarendon: Oxford, UK, 1990. [Google Scholar]
- Vasiliev, A.N. The Field Theoretic Renormalization Group in Critical Behaviour Theory and Stochastic Dynamics; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Volchenkov, D. Renormalization group and instantons in stochastic nonlinear dynamics: From self-organized criticality to thermonuclear reactors. Eur. Phys. J.-Spec. Top. 2009, 170, 1–142. [Google Scholar] [CrossRef]
- Turcotte, D.L. Self-organized criticality. Rep. Prog. Phys. 1999, 62, 1377. [Google Scholar] [CrossRef]
- Chialvo, D.R. Emergent complex neural dynamics. Nat. Phys. 2010, 6, 744–750. [Google Scholar] [CrossRef]
- Bak, P.; Christensen, K.; Danon, L.; Scanlon, T. Unified Scaling Law for Earthquakes. Phys. Rev. Lett. 2002, 88, 178501. [Google Scholar] [CrossRef] [PubMed]
- Turcotte, D.L. Seismicity and self-organized criticality. Phys. Earth Planet. Inter. 1999, 111, 275–293. [Google Scholar] [CrossRef]
- Sheinman, M.; Sharma, A.; Alvarado, J.; Koenderink, G.H.; MacKintosh, F.C. Anomalous Discontinuity at the Percolation Critical Point of Active Gels. Nat. Phys. 2013, 9, 591. [Google Scholar] [CrossRef]
- Beggs, J.M.; Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 2003, 23, 11167–11177. [Google Scholar] [CrossRef]
- Hesse, J.; Gross, T. Self-organized criticality as a fundamental property of neural systems. Front. Syst. Neurosci. 2014, 8, 166. [Google Scholar] [CrossRef]
- Meisel, C.; Storch, A.; Hallmeyer-Elgner, S.; Bullmore, E.; Gross, T. Failure of adaptive self-organized criticality during epileptic seizure attacks. PLoS Comput. Biol. 2012, 8, e1002312. [Google Scholar] [CrossRef]
- Plenz, D.; Ribeiro, T.L.; Miller, S.R.; Kells, P.A.; Vakili, A.; Capek, E.L. Self-Organized Criticality in the Brain. Front. Phys. 2021, 9, 639389. [Google Scholar] [CrossRef]
- Audard, M.; Güdel, M.; Drake, J.J.; Kashyap, V.L. Extreme-Ultraviolet Flare Activity in Late-Type Stars. Astrophys. J. 2000, 541, 396. [Google Scholar] [CrossRef]
- Wang, F.; Dai, Z. Self-organized criticality in X-ray flares of gamma-ray-burst afterglows. Nat. Phys. 2013, 9, 465–467. [Google Scholar] [CrossRef]
- McKenzie, D.; Kennedy, M. Power laws reveal phase transitions in landscape controls of fire regimes. Nat. Commun. 2012, 3, 726. [Google Scholar] [CrossRef] [PubMed]
- Hantson, S.; Scheffer, M.; Pueyo, S.; Xu, C.; van Nes, E.H.; Holmgren, M.; Mendelsohn, J. Rare, Intense, Big fires dominate the global tropics under drier conditions. Sci. Rep. 2017, 7, 14374. [Google Scholar] [CrossRef] [PubMed]
- Li, Z. Self-organized criticality dynamic of forest fire model. Indian J. Phys. 2023, 97, 1959–1964. [Google Scholar] [CrossRef]
- Kron, T.; Grund, T.U. Society as a Self-Organized Critical System. Cybern. Hum. Knowing 2009, 16, 65–82. [Google Scholar]
- A cikalin, Ş.N.; Artun, E.C. The concept of self-organized criticality: The case study of the Arab uprising. In Chaos, Complexity and Leadership 2017: Explorations of Chaos and Complexity Theory; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; Volume 5, pp. 73–85. [Google Scholar]
- Zhukov, D. How the theory of self-organized criticality explains punctuated equilibrium in social systems. Methodol. Innov. 2022, 15, 163–177. [Google Scholar] [CrossRef]
- Hoffmann, H.; Payton, D.W. Optimization by Self-Organized Criticality. Sci. Rep. 2018, 8, 2358. [Google Scholar] [CrossRef]
- Ramos, R.T.; Sassi, R.B.; Piqueira, J.R.C. Self-organized criticality and the predictability of human behavior. New Ideas Psychol. 2011, 29, 38–48. [Google Scholar] [CrossRef]
- Walter, N.; Hinterberger, T. Self-organized criticality as a framework for consciousness: A review study. Front. Psychol. 2022, 13, 911620. [Google Scholar] [CrossRef]
- Díaz-Guilera, A. Noise and dynamics of self-organized critical phenomena. Phys. Rev. A 1992, 45, 8551. [Google Scholar] [CrossRef]
- Collins, J. Renormalization: An Introduction to Renormalization, the Renormalization Group, and the Operator -Product Expansion; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Pietronero, L.; Vespignani, A.; Zapperi, S. Renormalization scheme for self-organized criticality in sandpile models. Phys. Rev. Lett. 1994, 72, 1690. [Google Scholar] [CrossRef]
- Zapperi, S.; Vespignani, A.; Pietronero, L. Real Space Renormalization Group for Self Organized Criticality in Sandpile Models. MRS Online Proc. Libr. 1994, 367, 67–71. [Google Scholar] [CrossRef]
- Díaz-Guilera, A. Dynamic renormalization group approach to self-organized critical phenomena. Europhys. Lett. 1994, 26, 177. [Google Scholar] [CrossRef]
- Hasty, J.M. A Renormalization Group Study of Self-Organized Criticality; Georgia Institute of Technology: Atlanta, GA, USA, 1997. [Google Scholar]
- Corral, A.; Díaz-Guilera, A. Symmetries and fixed point stability of stochastic differential equations modeling self-organized criticality. Phys. Rev. E 1997, 55, 2434. [Google Scholar] [CrossRef]
- Giacometti, A.; Díaz-Guilera, A. Dynamical properties of the Zhang model of self-organized criticality. Phys. Rev. E 1998, 58, 247. [Google Scholar] [CrossRef]
- Chang, T. Self-organized criticality, multi-fractal spectra, sporadic localized reconnections and intermittent turbulence in the magnetotail. Phys. Plasmas 1999, 6, 4137–4145. [Google Scholar] [CrossRef]
- Antonov, N.V.; Kakin, P.I. Effects of random environment on a self-organized critical system: Renormalization group analysis of a continuous model. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2016; Volume 108, p. 02009. [Google Scholar]
- Antonov, N.V.; Gulitskiy, N.M.; Kakin, P.I.; Serov, V.D. Effects of turbulent environment and random noise on self-organized critical behavior: Universality versus nonuniversality. Phys. Rev. E 2021, 103, 042106. [Google Scholar] [CrossRef]
- Antonov, N.V.; Gulitskiy, N.M.; Kakin, P.I.; Semeikin, M.N. Dimensional transmutation and nonconventional scaling behavior in a model of self-organized criticality. Int. J. Mod. Phys. A 2022, 37, 2240022. [Google Scholar] [CrossRef]
- Antonov, N.V.; Kakin, P.I.; Lebedev, N.M.; Luchin, A.Y. Renormalization group analysis of a self-organized critical system: Intrinsic anisotropy vs. random environment. J. Phys. Math. Theor. 2023, 56, 375002. [Google Scholar] [CrossRef]
- Antonov, N.V.; Vasil’ev, A.N. The quantum-field renormalization group in the problem of a growing phase boundary. J. Exp. Theor. Phys. 1995, 81, 485–489. [Google Scholar]
- Antonov, N.V. The renormalization group in the problem of turbulent convection of a passive scalar impurity with nonlinear diffusion. J. Exp. Theor. Phys. 1997, 85, 898–906. [Google Scholar] [CrossRef]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics; MIT Press: Cambridge, MA, USA, 1971; Volumes 1 and 2. [Google Scholar]
- Nakao, H.; Imamura, T. Mechanism in Leading to Richardson’s Four-Thirds Law. J. Phys. Soc. Jpn. 1992, 61, 2772–2778. [Google Scholar] [CrossRef]
- Dubkov, A.A.; Spagnolo, B.; Uchaikin, V.V. Lévy Flight Superdiffusion: An Introduction. Int. J. Bifurc. Chaos 2008, 18, 2649–2672. [Google Scholar] [CrossRef]
- Pietronero, L.; Tartaglia, P.; Zhang, Y.-C. Theoretical studies of self-organized criticality. Phys. Stat. Mech. Its Appl. 1991, 173, 22–44. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Antonov, N.V.; Vasil’ev, A.N. The Field Theoretic Renormalization Group in Fully Developed Turbulence; Gordon and Breach: London, UK, 1999. [Google Scholar]
- Martin, P.C.; Siggia, E.D.; Rose, H.A. Statistical Dynamics of Classical Systems. Phys. Rev. A 1973, 8, 423. [Google Scholar] [CrossRef]
- de Dominicis, C.; Peliti, L. Field-theory renormalization and critical dynamics above Tc: Helium, antiferromagnets, and liquid-gas systems. Phys. Rev. B 1978, 18, 353. [Google Scholar] [CrossRef]
- Wyld, H.W. Formulation of the theory of turbulence in an incompressible fluid. Ann. Phys. 1961, 14, 143. [Google Scholar] [CrossRef]
- di Santo, S.; Villegas, P.; Burioni, R.; Muñoz, M. Simple unified view of branching process statistics: Random walks in balanced logarithmic potentials. Phys. Rev. E 2017, 95, 032115. [Google Scholar] [CrossRef]
- Villegas, P.; di Santo, S.; Burioni, R.; Muñoz, M.A. Time-series thresholding and the definition of avalanche size. Phys. Rev. E 2019, 100, 012133. [Google Scholar] [CrossRef]
- Laurson, L.; Illa, X.; Santucci, S.; Tallakstad, K.T.; Maloy, K.J.; Alava, M.J. Evolution of the average avalanche shape with the universality class. Nat. Commun. 2013, 4, 2927. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Bohn, F.; Sommer, R.L.; Durin, G.; Zapperi, S.; Sethna, J.P. Universality beyond power laws and the average avalanche shape. Nat. Phys. 2011, 7, 316. [Google Scholar] [CrossRef]
- Altshuler, E.; Johansen, T. Colloquium: Experiments in vortex avalanches. Rev. Mod. Phys. 2004, 76, 471. [Google Scholar] [CrossRef]
- Alessandro, B.; Beatrice, C.; Bertotti, G.; Montorsi, A. Domain-wall dynamics and Barkhausen effect in metallic ferromagnetic materials. I, Theory. J. Appl. Phys. 1990, 68, 2901. [Google Scholar]
- Peters, O.; Hertlein, C.; Christensen, K. A Complexity View of Rainfall. Phys. Rev. Lett. 2001, 88, 018701. [Google Scholar] [CrossRef] [PubMed]
- Kinney, R.; Crucitti, P.; Albert, R.; Latora, V. Modeling cascading failures in the North American power grid. Eur. Phys. J. B-Condens. Matter Complex Syst. 2005, 46, 101. [Google Scholar] [CrossRef]
- Watson, H.W.; Galton, F. On the Probability of the Extinction of Families. J. Anthropol. Inst. Great Br. Irel. 1875, 4, 138–144. [Google Scholar] [CrossRef]
- Liggett, T. Interacting Particle Systems; Springer Series: Classics in Mathematics; Springer: New York, NY, USA, 2004. [Google Scholar]
- Binney, J.; Dowrick, N.; Fisher, A.; Newman, M. The Theory of Critical Phenomena; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Karrer, B.; Newman, M.E.; Zdeborová, L. Percolation on Sparse Networks. Phys. Rev. Lett. 2014, 113, 208702. [Google Scholar] [CrossRef]
- Hwa, T.; Kardar, M. Dissipative transport in open systems: An investigation of self-organized criticality. Phys. Rev. Lett. 1989, 62, 1813. [Google Scholar] [CrossRef]
- Hwa, T.; Kardar, M. Avalanches, hydrodynamics and discharge events in models of sandpiles. Phys. Rev. A 1992, 45, 7002. [Google Scholar] [CrossRef]
| Q | E | |||||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 0 | 0 | 0 | 0 | 1 | 0 | |
| d | 0 | 0 |
| Assumption on Random Force | IR-Stability | |||
|---|---|---|---|---|
| Uncorrelated in space | Domain-wise | |||
| “White noise” | No | |||
| “Frozen” configuration | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volchenkov, D. Multiplicative Renormalization of Stochastic Differential Equations for the Abelian Sandpile Model. Dynamics 2024, 4, 40-56. https://doi.org/10.3390/dynamics4010003
Volchenkov D. Multiplicative Renormalization of Stochastic Differential Equations for the Abelian Sandpile Model. Dynamics. 2024; 4(1):40-56. https://doi.org/10.3390/dynamics4010003
Chicago/Turabian StyleVolchenkov, Dimitri. 2024. "Multiplicative Renormalization of Stochastic Differential Equations for the Abelian Sandpile Model" Dynamics 4, no. 1: 40-56. https://doi.org/10.3390/dynamics4010003
APA StyleVolchenkov, D. (2024). Multiplicative Renormalization of Stochastic Differential Equations for the Abelian Sandpile Model. Dynamics, 4(1), 40-56. https://doi.org/10.3390/dynamics4010003






