Search for Damped Oscillating Structures from Charged Pion Electromagnetic Form Factor Data
Abstract
1. Introduction
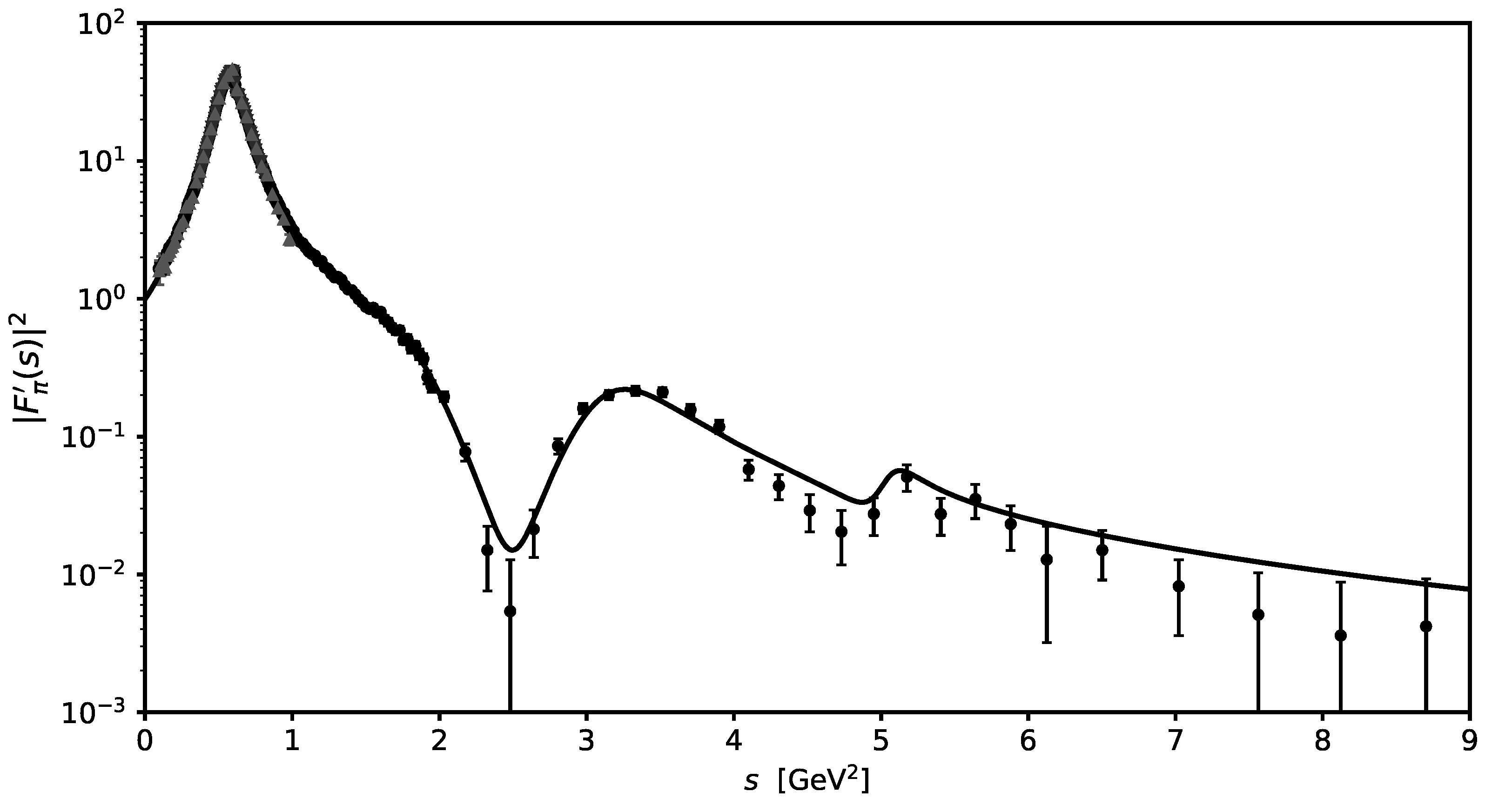
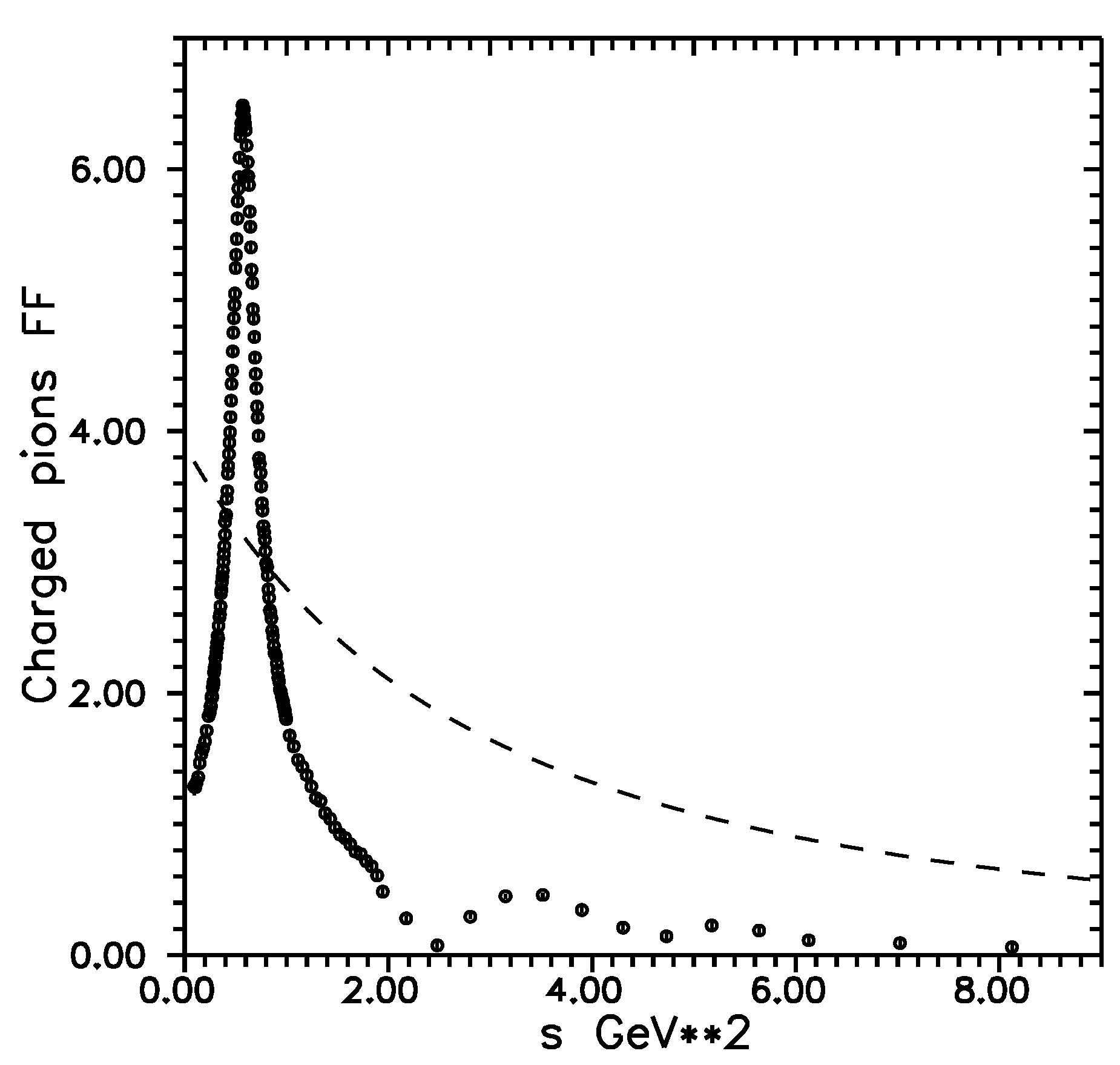
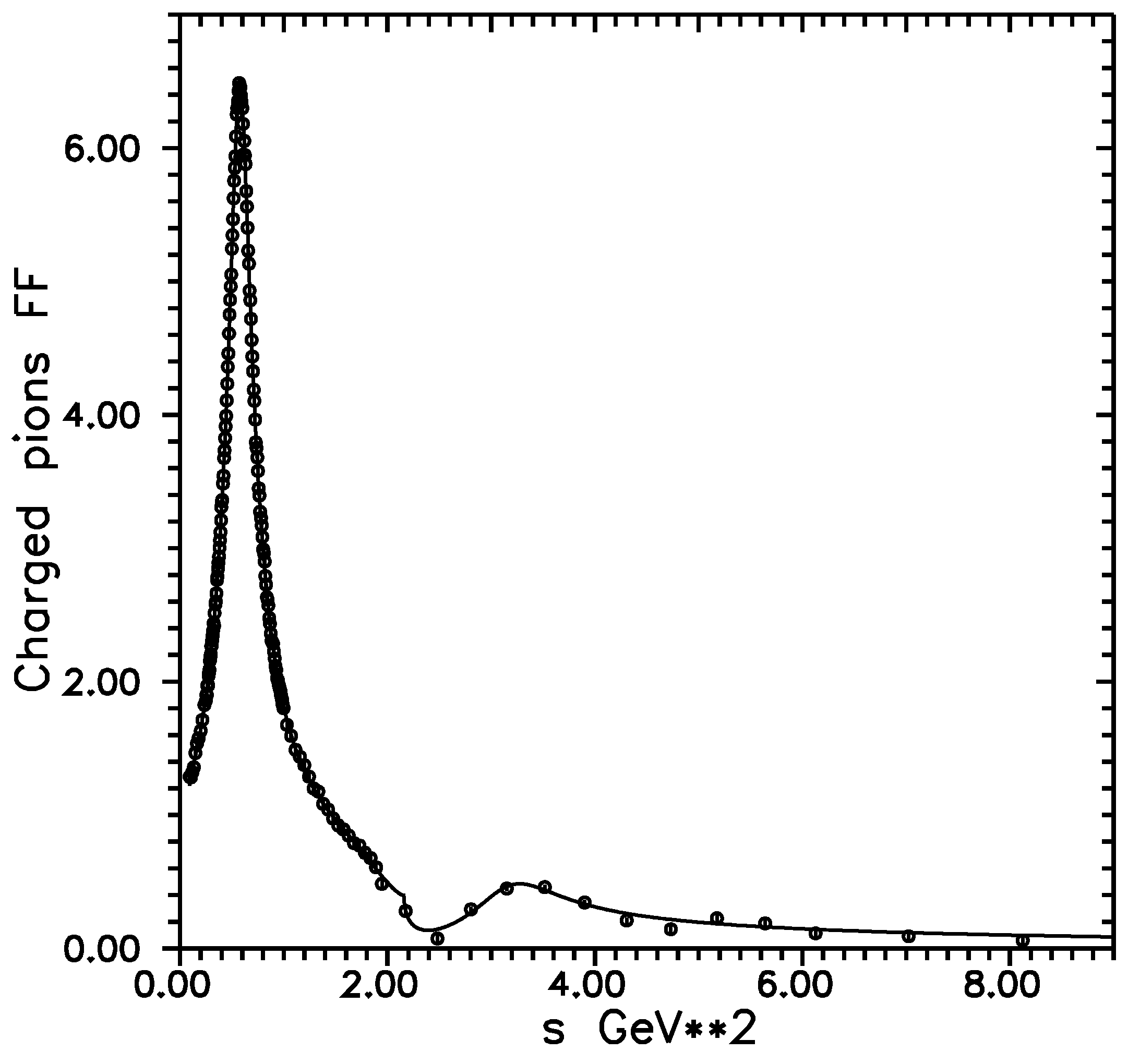
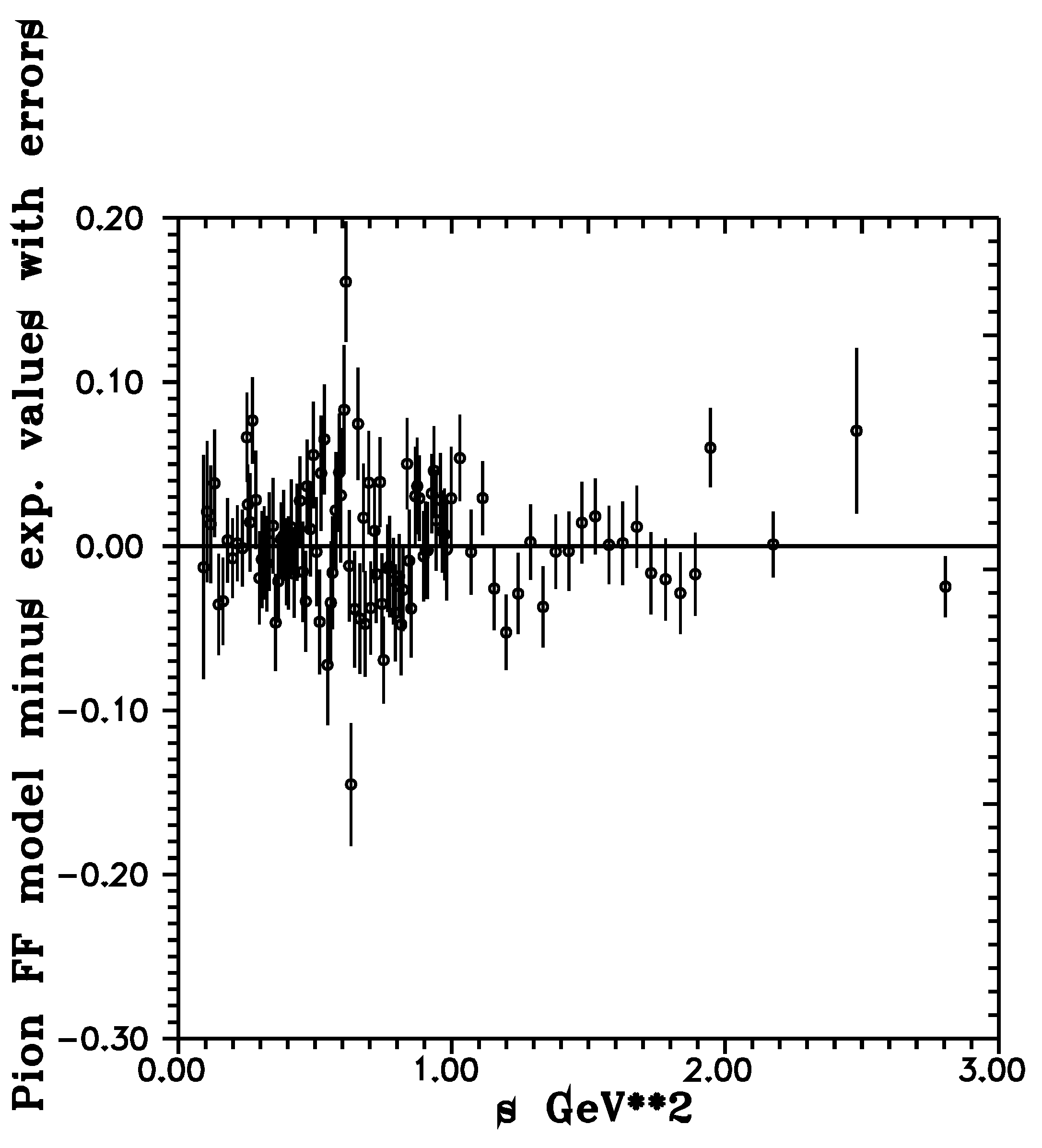
2. Search for Damped Oscillation Structures in the Charged Pion EM FF Timelike Data
3. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pedlar, T.K.; Cronin-Hennessy, D.; Gao, K.Y.; Gong, D.T.; Hietala, J.; Kubota, Y.; Klein, T.; Lang, B.W.; Li, S.Z.; Poling, R.; et al. Precision measurements of the timelike electromagnetic form factors of pion, kaon, and proton. Phys. Rev. Lett. 2005, 95, 261803. [Google Scholar] [CrossRef]
- BES Collaboration; Ablikim, M.; Bai, J.Z.; Ban, Y.; Bian, J.G.; Cai, X.; Chen, H.F.; Chen, H.S.; Chen, H.X.; Chen, J.C.; et al. Measurement of the cross section for e+e−→ at center-of-mass energies from 2.0 to 3.07 GeV. Phys. Lett. B 2005, 630, 14–20. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Ai, X.C.; Albayrak, O.; Albrecht, M.; Ambrose, D.J.; Amoroso, A.; An, F.F.; An, Q.; Bai, J.Z.; et al. Measurement of the e+e−→π+π− cross section between 600 and 900 MeV using initial state radiation. Phys. Lett. 2016, B753, 629–638. [Google Scholar] [CrossRef]
- Akhmetshin, R.R.; Amirkhanov, A.N.; Anisenkov, A.V.; Aulchenko, V.M.; Banzarov, V.S.; Bashtovoy, N.S.; Berkaev, D.E.; Bondar, A.E.; Bragin, A.V.; Eidelman, S.I.; et al. Study of the process e+e−→ in the c.m. energy range from threshold to 2 GeV with the CMD-3 detector. Phys. Lett. B 2016, 759, 634–640. [Google Scholar] [CrossRef]
- Akhmetshin, R.R.; Amirkhanov, A.N.; Anisenkov, A.V.; Aulchenko, V.M.; Banzarov, V.S.; Bashtovoy, N.S.; Berkaev, D.E.; Bondar, A.E.; Bragin, A.V.; Eidelman, S.I.; et al. Observation of a fine structure in e+e−→hadrons production at the nucleon-antinucleon threshold. Phys. Lett. B 2019, 794, 64–68. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Alekseev, M.; Amoroso, A.; An, F.; An, Q.; Anita; et al. Measurement of Proton Electromagnetic Form Factors in e+e−→ in the Energy Region 2.00–3.08 GeV. Phys. Rev. Lett. 2020, 124, 042001. [Google Scholar] [CrossRef]
- Aubert, B.; Barate, R.; Boutigny, D.; Couderc, F.; Karyotakis, Y.; Lees, J.P.; Poireau, V.; Tisserand, V.; Zghiche, A.; Grauges, E.; et al. Study of e+e−→ using initial state radiation with BABAR. Phys. Rev. D 2006, 73, 012005. [Google Scholar] [CrossRef]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Yu, G.; et al. Study of e+e−→ via initial-state radiation at BABAR. Phys. Rev. D 2013, 87, 092005. [Google Scholar] [CrossRef]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Yu, G.; et al. Production of charged pions, kaons, and protons in e+e− annihilations into hadrons at = 10.54 GeV. Phys. Rev. D 2013, 88, 032011. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Alekseev, M.; Amoroso, A.; An, F.; An, Q.; Bai, Y.; et al. Study of the process e+e−→ via initial state radiation at BESIII. Phys. Rev. D 2019, 99, 092002. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Aliberti, R.; Amoroso, A.; An, M.R.; An, Q.; Bai, X.H.; et al. Measurement of proton electromagnetic form factors in the time-like region using initial state radiation at BESIII. Phys. Lett. B 2021, 817, 136328. [Google Scholar] [CrossRef]
- Baldini Ferroli, R.; Pacetti, S.; Zallo, A. No Sommerfeld resummation factor in e+e−→? Eur. Phys. J. A 2012, 48, 33. [Google Scholar] [CrossRef]
- Tomasi-Gustafsson, E.; Rekalo, M.P. Search for evidence of asymptotic regime of nucleon electromagnetic form-factors from a compared analysis in space- and time-like regions. Phys. Lett. B 2001, 504, 291–295. [Google Scholar] [CrossRef]
- Dunning, J.R.; Chen, K.W.; Cone, A.A.; Hartwig, G.; Ramsey, N.F.; Walker, J.K.; Wilson, R. Quasi-Elastic Electron-Deuteron Scattering and Neutron Form Factors. Phys. Rev. 1966, 141, 1286–1297. [Google Scholar] [CrossRef]
- Akhiezer, A.I.; Rekalo, M.P. Polarization phenomena in electron scattering by protons in the high energy region. Sov. Phys. Dokl. 1968, 13, 572. [Google Scholar]
- Akhiezer, A.I.; Rekalo, M.P. Polarization effects in the scattering of leptons by hadrons. Sov. J. Part. Nucl. 1974, 4, 277. [Google Scholar]
- Jones, M.K.; Aniol, K.A.; Baker, F.T.; Berthot, J.; Bertin, P.Y.; Bertozzi, W.; Besson, A.; Bimbot, L.; Boeglin, W.U.; Brash, E.J.; et al. GEp/GMp Ratio by Polarization Transfer in . Phys. Rev. Lett. 2000, 84, 1398–1402. [Google Scholar] [CrossRef] [PubMed]
- Gayou, O.; Aniol, K.A.; Averett, T.; Benmokhtar, F.; Bertozzi, W.; Bimbot, L.; Brash, E.J.; Calarco, J.R.; Cavata, C.; Chai, Z.; et al. Measurement of GEp/GMp in to Q2 = 5.6 GeV2. Phys. Rev. Lett. 2002, 88, 092301. [Google Scholar] [CrossRef]
- Punjabi, V.; Perdrisat, C.F.; Aniol, K.A.; Baker, F.T.; Berthot, J.; Bertin, P.Y.; Bertozzi, W.; Besson, A.; Bimbot, L.; Boeglin, W.U.; et al. Proton elastic form factor ratios to Q2 = 3.5 GeV2 by polarization transfer. Phys. Rev. C 2005, 71, 055202. [Google Scholar] [CrossRef]
- Zhan, X.; Allada, K.; Armstrong, D.S.; Arrington, J.; Bertozzi, W.; Boeglin, W.; Chen, J.-P.; Chirapatpimol, K.; Choi, S.; Chudakov, E.; et al. High-precision measurement of the proton elastic form factor ratio μpGE/GM at low Q2. Phys. Lett. B 2011, 705, 59–64. [Google Scholar] [CrossRef]
- Puckett, A.J.R.; Brash, E.J.; Jones, M.K.; Luo, W.; Meziane, M.; Pentchev, L.; Perdrisat, C.F.; Punjabi, V.; Wesselmann, F.R.; Afanasev, A.; et al. Polarization transfer observables in elastic electron-proton scattering at Q2 = 2.5, 5.2, 6.8, and 8.5 GeV2. Phys. Rev. C 2017, 96, 055203. [Google Scholar] [CrossRef]
- Bianconi, A.; Tomasi-Gustafsson, E. Periodic interference structures in the timelike proton form factor. Phys. Rev. Lett. 2015, 114, 232301. [Google Scholar] [CrossRef] [PubMed]
- Ablikim, M. Oscillating features in the electromagnetic structure of the neutron. Nat. Phys. 2021, 17, 1200–1204. [Google Scholar] [CrossRef]
- Bianconi, A.; Tomasi-Gustafsson, E. Phenomenological analysis of near-threshold periodic modulations of the proton timelike form factor. Phys. Rev. C 2016, 93, 035201. [Google Scholar] [CrossRef]
- Tomasi-Gustafsson, E.; Pacetti, S. Interpretation of recent form factor data in terms of an advanced representation of baryons in space and time. Phys. Rev. C 2022, 106, 035203. [Google Scholar] [CrossRef]
- Lorenz, I.T.; Hammer, H.W.; Meißner, U.G. New structures in the proton-antiproton system. Phys. Rev. D 2015, 92, 034018. [Google Scholar] [CrossRef]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Tico, J.G.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; et al. Precise Measurement of the e+e−→π+π−(γ) Cross Section with the Initial-State Radiation Method at BABAR. Phys. Rev. 2012, D86, 032013. [Google Scholar] [CrossRef]
- Xiao, T.; Dobbs, S.; Tomaradze, A.; Seth, K.K.; Bonvicini, G. Precision measurement of the hadronic contribution to the muon anomalous magnetic moment. Phys. Rev. D 2018, 97, 032012. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Aliberti, R.; Amoroso, A.; An, Q.; Bai, X.H.; Bai, Y.; et al. Corrigendum to “Measurement of the e+e−→π+π− cross section between 600 and 900 MeV using initial state radiation” [Phys. Lett. B 753 (2016) 629–638]. Phys. Lett. B 2021, 812, 135982. [Google Scholar] [CrossRef]
- Dubnicka, S.; Dubnickova, A. Analyticity in a phenomenology of electro-weak structure of hadrons. Acta Phys. Slov. 2010, 60, 1–153. [Google Scholar] [CrossRef]
- Particle Data Group; Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; et al. Review of Particle Physics. PTEP 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Biagini, M.E.; Dubnicka, S.; Etim, E.; Kolar, P. Phenomenological evidence for a third radial excitation of rho (770). Il Nuovo Cimento D 1991, 104, 363–370. [Google Scholar] [CrossRef]
- Garcia-Martin, R.; Kaminski, R.; Pelaez, J.R.; Ruiz de Elvira, J.; Yndurain, F.J. The Pion-pion scattering amplitude. IV: Improved analysis with once subtracted Roy-like equations up to 1100 MeV. Phys. Rev. 2011, D83, 074004. [Google Scholar] [CrossRef]
- Bartoš, E.; Dubnička, S.; Liptaj, A.; Dubničková, A.Z.; Kamiński, R. What are the correct ρ0(770) meson mass and width values? Phys. Rev. 2017, D96, 113004. [Google Scholar] [CrossRef]





| (GeV) | (GeV) | (GeV) |
| (GeV) | (GeV) | |
| (GeV) | (GeV) | |
| (GeV) | (GeV) | |
| s[GeV] | s[GeV] | s[GeV] | s[GeV] | ||||
|---|---|---|---|---|---|---|---|
| — | — | — | — | — | — |
| s [GeV] | s [GeV] | s [GeV] | s [GeV] | ||||
|---|---|---|---|---|---|---|---|
| — | — |
| s [GeV] | s [GeV] | s [GeV] | s [GeV] | ||||
|---|---|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartoš, E.; Dubnička, S.; Dubničková, A.Z. Search for Damped Oscillating Structures from Charged Pion Electromagnetic Form Factor Data. Dynamics 2023, 3, 137-151. https://doi.org/10.3390/dynamics3010009
Bartoš E, Dubnička S, Dubničková AZ. Search for Damped Oscillating Structures from Charged Pion Electromagnetic Form Factor Data. Dynamics. 2023; 3(1):137-151. https://doi.org/10.3390/dynamics3010009
Chicago/Turabian StyleBartoš, Erik, Stanislav Dubnička, and Anna Zuzana Dubničková. 2023. "Search for Damped Oscillating Structures from Charged Pion Electromagnetic Form Factor Data" Dynamics 3, no. 1: 137-151. https://doi.org/10.3390/dynamics3010009
APA StyleBartoš, E., Dubnička, S., & Dubničková, A. Z. (2023). Search for Damped Oscillating Structures from Charged Pion Electromagnetic Form Factor Data. Dynamics, 3(1), 137-151. https://doi.org/10.3390/dynamics3010009









