Multiobjective Optimization of a Fed-Batch Bienzymatic Reactor for Mannitol Production

Abstract

Enzymatic reactions can successfully replace complex chemical syntheses using milder reaction conditions and generating less waste. The developed model-based numerical analysis turned out to be a beneficial tool to determine the optimal operating policies of complex multienzymatic reactors. As proved, for such cases, the determination of a Fed-Batch Reactor (FBR) optimal operating policy results in a difficult multiobjective optimization problem. Exemplification is made for the bienzymatic reduction of D-fructose to mannitol by using MDH (mannitol dehydrogenase) and nicotinamide adenine dinucleotide (NADH) cofactor with the in situ continuous regeneration of NADH at the expense of formate degradation in the presence of FDH (formate dehydrogenase). For such a coupled system, the model-based engineering evaluations must account for multiple competing (opposable) optimization objectives. Among the multiple novelty elements: i) an optimally operated FBR with a tightly controlled variable feeding (of the time stepwise type) during the batch can lead to higher performance; ii) the optimally operated FBR reported better performance compared to an optimally single or cyclic BR, or to optimally serial batch-to-batch reactors (SeqBR), when considering a multiobjective optimization; iii) the concomitant variable feeding with substrate, enzymes, and cofactor during the FBR “time-arcs” is an option seldom approached in the literature but which is proved here, leading to consistent economic benefits.

1. Introduction

“Remarkable progresses made in the development of new enzymes and in realizing complex coupled enzymatic systems, able to in-situ recover the reaction cofactor(s), reported important applications in the industrial biocatalysis, presenting important advantages. Examples include the large number of biosynthesis processes used to produce fine -chemicals, or organic compounds in food, pharma, or detergent industry, such as: the production of monosaccharides derivatives, organic acids, alcohols, amino -acids, etc., by using single- or multi-enzymatic reactors” [1,2].

“Mannitol is a natural hexitol with important applications in medicine and the food industry [3,4]. The present global market of mannitol is around $100 million in 2013, of an average price of $42–80 per kg, and with a production growth rate of 5% annually. Around 50,000 tons/year of mannitol are produced currently by the costly chemical hydrogenation alone [5], and the rest by the less expensive enzymatic routes” [6]. In short, the main routes to produce mannitol at a large scale are the following [4,7]:

(i) The chemical catalytic hydrogenation of fructose, sucrose (inverted sugar), or of the 50% glucose–50% fructose syrup (HFCS) coming from the enzymatic hydrolysis of starch [1,8]. The chemical route is very costly because it requires the use of high pressures (50–80 atm), high temperatures (120–160 °C), and a costly Raney nickel or another catalyst [4,5,7,8].

(ii) Biological routes. HFCS conversion (83% yield) uses a cell culture of Candida magnoliae [9,10] with high conversions of glucose or sucrose by using a culture of Streptococcus Mutans [11]. Reviews are given by [4,12].

As reviewed by Slatner et al. [13], these routes suffer a large number of disadvantages, which include: (a) the yields are much lower than those of the enzymatic alternatives; (b) a significant fraction (15%) of the substrate is converted into allergenic byproducts such as lactate, acetate, ethanol, and carbon dioxide, leading to costly purifying steps of the product; (c) the used cell cultures are too sensitive to the operating conditions; (d) a too-high yield sensitivity vs. temperature is reported in the range of 25–40 °C.

(iii) The bienzymatic process with the NADH cofactor in in situ continuous regeneration. This very effective technology proposed by Slatner et al. [13] uses two coupled enzymatic reactions: (1) “the enzymatic reduction of fructose to mannitol in the presence of mannitol dehydrogenase (MDH) and the cofactor NADH as a proton donor. (2) The resulted NAD⁺ is continuously regenerated in-situ by the expense of the enzymatic decomposition of ammonium formate in the presence of format dehydrogenase (FDH)”, according to Figure 1. The use of another cofactor, such as NADPH, is not recommended, being much more expensive [14], and very unstable [15]. This route presents multiple advantages: (i) It is less expensive while requiring mild operating conditions (normal pressure, pH = 7, 25 °C); (ii) the selectivity is practically 100%, with the separation of the mannitol at the batch being easy and less costly; (iii) as proved in this paper, the optimal FBR operation can lead to the much-reduced consumption of costly enzymes (FDH, MDH, and NADH) compared to optimally single or cyclic BR, or to an optimally serial SeqBR; (iv) the continuous in situ enzymatic regeneration of the NADH cofactor largely reduces the production costs [4,16,17].

A rough evaluation of the enzymatic process performances compared to those of the biological processes (classical fermentation), and those of the chemical catalytic processes, was performed by Moulijn et al. [18] by pointing out their large number of advantages compared to the classical syntheses.

Over the last decades, remarkable progress in the development of new enzymes has been made by integrating genetic and engineering methods [19,20], and by realizing coupled multienzymatic systems in the industrial biocatalysis.

Multienzymatic systems with parallel or sequential reactions are modern and effective alternatives to the complex chemical syntheses by covering several choices [21]: (i). For two enzymes on the same support, the substrate for the second enzyme is generated in situ by the first reaction [22]; (ii). The second enzymatic reaction regenerates the cofactor of the first enzymatic one (e.g., the regeneration of NADH in the present study); (iii). The second enzymatic reaction shifts the equilibrium of the main reaction by removing the intermediate or byproduct from the system [23]; (iv). The second enzyme prolongs the life of the first enzyme by a particular mechanism (e.g., catalase prolongs the life of an oxidase [24]).

“Even if the multi-enzymatic systems are advantageous, the engineering part for optimizing such a process is not an easy task because it must account for the interacting enzymatic reactions, enzymes deactivation kinetics (if significant), multiple and often opposed optimization objectives, technological constraints, and uncertainties coming from multiple sources (model/constraints inaccuracies, disturbances in the control variables), and a highly nonlinear process dynamics [25,26,27,28,29,30]. All these parametric/model/data uncertainties require to update (with a certain frequency) the enzymatic process model, the optimal operating policies of the reactor being determined by using rather deterministic (model-based) optimization rules [31]. Multi-objective criteria, including economic benefits, operating and materials costs, product quality, etc., are used to off-line, or to on-line derive feasible optimal operating/control policies for various bioreactor types” [30] by using specific numerical algorithms [26,32,33,34,35].

This is why enzymatic reactors have been developed in simple constructive/operating alternatives (see some examples in Figure 2, and [27,28]). “In spite of their larger volumes, continuously mixing tank reactors (CSTR), operated in a BR (simple, cyclic, parallel) mode, or in a FBR mode, are preferred for processes requiring a high mass transfer” (a homogeneous medium for quickly interacting multienzymatic reactions), and a rigorous temperature/pH control. As revealed by Maria and Peptănaru [27], the SeqBR also proved to be an effective alternative compared to simple, cyclic (repeated), or parallel optimal BR-s. Regardless if free or immobilized enzymes are used enzymes, other effective complex operating alternatives proved their effectiveness, in particular, “those in which substrate(s)/cofactor and/or enzyme(s) are intermittently (BRP, [28,36]), or continuously ([FXBR (fixed-bed solid–-liquid continuous reactor), MA(S)CR (mechanically agitated solid–-liquid (semi-)continuous reactor))] added during the batch by following a suitable optimally variable policy (usually off-line, model-based determined). A similar discussion was provided by Koller [37].

In spite of inherent difficulties, trials to improve the BR productivity have been reported in the literature, by using SeqBR, cyclic BR, or parallel BR. Examples includes a sequence of 2–5 FBR-s [38,39,40], or a 14-times cyclic BR [41], or 48 parallel BR-s [42], or 24 parallel BR-s [43]. As expected, the optimized FBR reported better performances compared to the simple BR, due to its higher operating flexibility [28,44,45,46]. Concerning the optimal SeqBR, by varying the initial condition of its every BR of the series” [27], it reproduces somewhat the FBR operation principle, namely the time stepwise variation of the control variables [28]. “However, FBR policy differs in principle from those of a SeqBR, as long as the set of control variables are kept constant over a ’time-arc’, which is not the case for the SeqBR when the variation of control variables concerns only the initial load of each BR of the series. On the other hand, the chemical reactor theory demonstrated that a series of a large number of CSTR-s tends to have the best performances of a plug-flow reactor [47]. Consequently, it is expected that an optimal FBR, or an optimal SeqBR will present better performances than a repeated operation of an optimal single BR with the same initial conditions, even if optimal.”

By using the kinetic model of Maria [36], built-up and validated based on the large amount of experimental kinetic data of Slatner et al. [13] for the approached bienzymatic process, the present study aims at deriving the optimal operating policy of a bienzymatic FBR to concomitantly fulfill multiple opposite objectives, including: the minimization of the costly enzymes (MDH, FDH) and cofactor (NADH) consumption, concomitantly with mannitol production maximization under some technological constraints, as formulated in Section 3.3. The study is accompanied by a model-based analysis of the optimized FBR performances compared to those of an optimally single or cyclic BR, or to an optimally serial SeqBR, from a multiobjective perspective. As proved, the FBR with both a variable feed flow rate and species inlet concentrations reported superior performances vs. the other operating alternatives. The main gain in the optimized FBR performance compared to a single simple BR repeatedly (cyclic) operated, or to an optimized series of BRs (SeqBR), comes from the simultaneous variation of a larger number (4) of control variables, not only of the reactor feed flow rate (FL), but also of the inlet fructose concentration [F]inlet,j, as well as the inlet concentrations of the two enzymes [MDH]inlet,j, and [FDH]inlet,j (see the results presented in Section 4).

The price paid for achieving the best performance of the FBR by using a time stepwise variable operating policy is the need to previously prepare different substrates/enzymes/cofactor stocks to be continuously fed during every time-arc (that is, a batch time division in which the feeding is constant as flow rate and composition). The feeding characteristics differ between time-arcs, being determined by the FBR optimization vs. several criteria. This FBR optimal operation disadvantage is offset by its net higher productivity compared to those of a single BR, cyclic BR, or SeqBR by consuming less costly enzymes and cofactors. Similar conclusions are also reported in the literature for both enzymatic and biological processes [25,26,32,44,45,48].

This paper presents a significant number of novel aspects, as follows: (i) “The in silico (model-based) demonstrative engineering analysis of a complex bi-enzymatic process, leading to obtain an optimal operating policy of the approached FBR.” (ii) This study is one of the first systematic comparative analyses in the literature concerning the efficiency of various batch operating modes (BR, FBR, and SeqBR) from a multiobjective perspective and for a concrete multienzymatic case study. (iii) To our knowledge, there are very few studies optimizing an FBR by concomitantly considering a larger (4) number of control variables simultaneously varied during the batch. (iv) This bienzymatic process is already known, but the associated engineering analyses related to its optimal development/control are missing in the literature. (v) “The scientific value of this paper is not virtual, as long as the numerical analysis is based on a kinetic model of Maria [36] constructed and validated by using the extensive experimental data sets of Slatner et al. [13]. (vi) The in-silico analysis suggests that an optimally operated FBR with a relatively small number of time-arcs (10 here) can lead to high performances.” (vii) The concomitant variable feeding with the substrate/enzymes/cofactor during the FBR process is an option seldom approached in the literature. (viii) As proved in this paper, the model-based offline optimal operation of the FBRs can lead to consistent economic benefits.

Figure 2. Simplified schemes of various operating modes of the BR to conduct enzymatic or biological processes. See [28] for the complete modeling hypotheses of each BR type. BR = “isothermal, iso-pH, and iso-DO; perfectly mixed liquid phase. Reactants/biocatalyst(s)/additives added at the beginning of the batch only. BRP = a BR with reactants and/or biocatalyst(s)/supplements added during the batch in a Pulse-like addition of equal/uneven solution volumes, with a certain frequency (to be determined) [28,49]. FBR = A BR with substrates/biocatalyst(s)/supplements added during the batch following a certain (optimal) policy (to be determined) [28]. SBR = in continuous mode, there is a CSTR with a continuous feeding and evacuation with equal flow -rates. Substrates/biomass/enzymes /supplements are added during the batch following a certain (optimal) policy (to be determined). SeqBR = a series of (usually identical) BR-s. The batch-to-batch operation implies that the every BR content is transferred to the next BR, with adjusting the reactant(s) and/or biocatalyst(s) amounts (concentrations) to reach optimal levels” (determined offline, see [27]).

Figure 2. Simplified schemes of various operating modes of the BR to conduct enzymatic or biological processes. See [28] for the complete modeling hypotheses of each BR type. BR = “isothermal, iso-pH, and iso-DO; perfectly mixed liquid phase. Reactants/biocatalyst(s)/additives added at the beginning of the batch only. BRP = a BR with reactants and/or biocatalyst(s)/supplements added during the batch in a Pulse-like addition of equal/uneven solution volumes, with a certain frequency (to be determined) [28,49]. FBR = A BR with substrates/biocatalyst(s)/supplements added during the batch following a certain (optimal) policy (to be determined) [28]. SBR = in continuous mode, there is a CSTR with a continuous feeding and evacuation with equal flow -rates. Substrates/biomass/enzymes /supplements are added during the batch following a certain (optimal) policy (to be determined). SeqBR = a series of (usually identical) BR-s. The batch-to-batch operation implies that the every BR content is transferred to the next BR, with adjusting the reactant(s) and/or biocatalyst(s) amounts (concentrations) to reach optimal levels” (determined offline, see [27]).

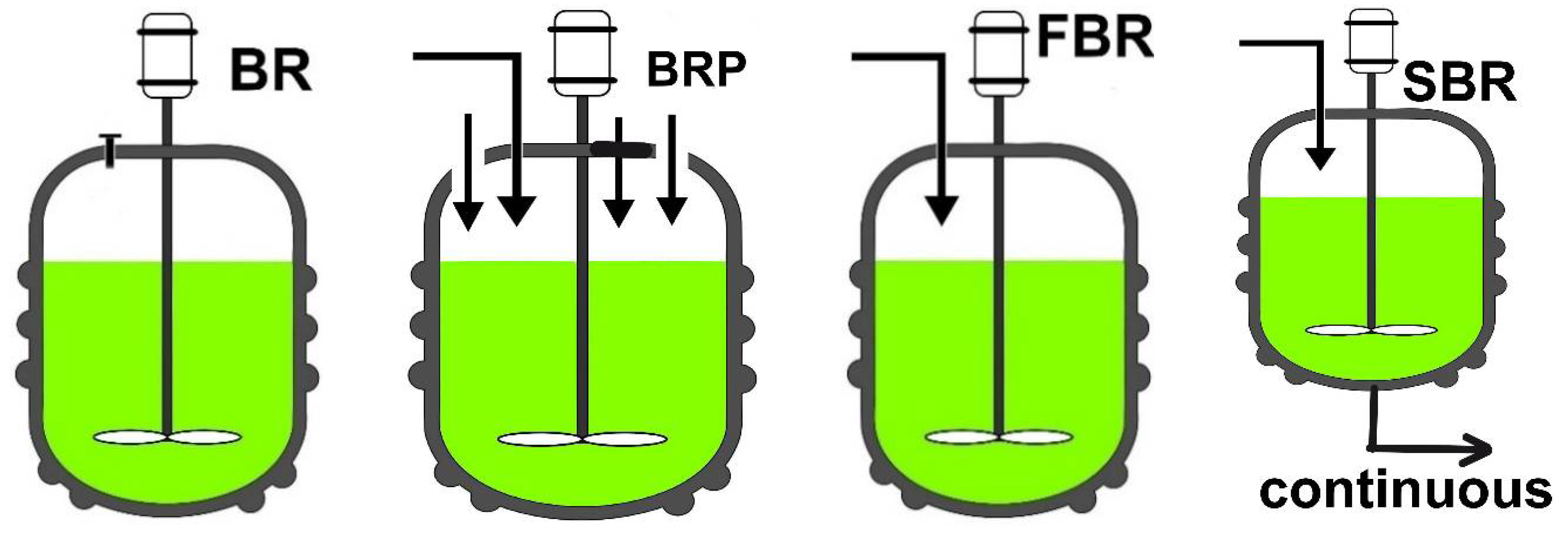
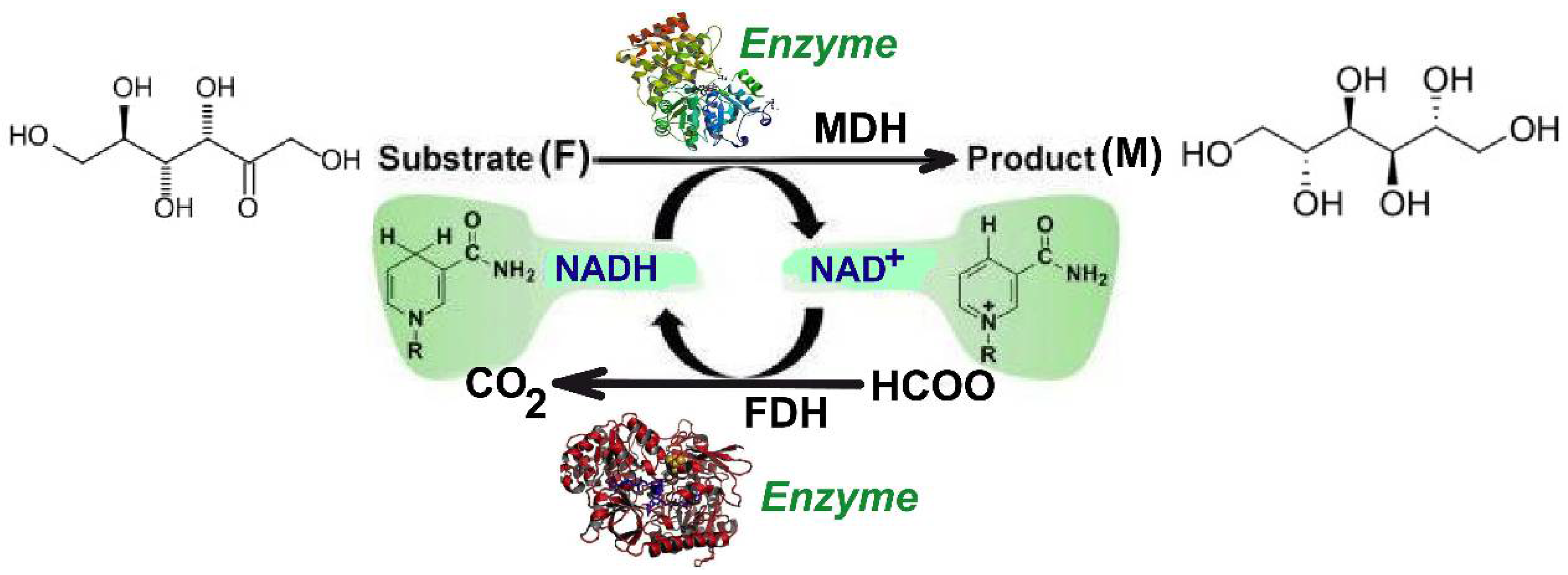
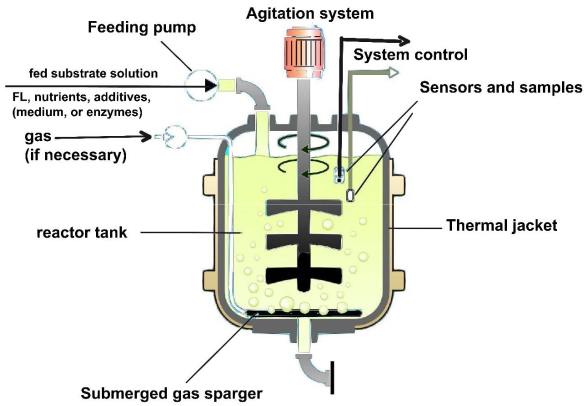
2. Dynamic Models for the Bienzymatic Process and FBR

The approached BR in this analysis is that of Slatner et al. [13]. Its main characteristics, presented in (Table 1), reveal a quite flexible operating domain, including large ranges for the initial concentrations of substrates (fructose [F]o and formate [HCOO]o), cofactor [NADH]o, and enzymes ([MDH]o, [FDH]o). Such an observation opens large number of options when optimizing the FBR operating mode. The BR or FBR constructive scheme is presented in (Figure 3).

For the same reason, Slatner et al. [13] used this BR to study the kinetics of the here approached bienzymatic process. The extended experiments were conducted at 25 °C, pH 7.0, under large ranges of initial conditions, that is: [F]o ∈ [0.1–3] M; [NADH]o ∈ [0.008–0.5] M; [HCOO]o = [F]o; [NAD]o = 0.0005 M; {[MDH]o, [FDH]o} ∈ 0.1–2 kU/L. The collected kinetic data allowed Maria [36] to build up a kinetic model of the bienzymatic process. Based on these experimental datasets and other qualitative observations, a simple “Michaelis-Menten kinetic model of Ping-Pong-Bi-Bi type was proposed for both reaction rates R1 and R2 (Table 2) by analogy with a similar process of pseudo 2-nd order kinetics [24]. For simplicity, this model includes a non-competitive inhibition with respect to reactants even if the mannitol inhibition might be significant [13]. Enzymes MDH and FDH inactivation during the reaction have been neglected due to lack of available data. The rate constants have been estimated by using an effective nonlinear least squares procedure [51,52], with adopting a simple dynamic model for the BR [36]. The adequacy of the resulted kinetic model of (Table 2) was proved to be very good vs. the experimental data (not presented here), for the all tested large number of initial conditions” [36].

As revealed by Slatner et al. [13], for this approached process (Table 2), the pH is maintained constant at 7 ± 0.1 (optimum for MDH) by an “automatic addition of HCl, due to the shift in pH towards the alkaline region observed when FDH-catalyzes oxidation of ammonium formate. Besides, the reactor initial load contains a medium of Tris-HCI buffer of pH 7.0. Some other compounds (Dithiothreitol) are added to stabilize the MDH.”

To simulate the FBR dynamics in the present engineering analysis, the simple mathematical model of (Table 3) was adopted. The model includes the differential mass balances of the process key species, that is: F, HCOO, M, MDH, FDH, NADH, NAD, CO2, besides the liquid volume dynamics (V_L) in the reactor. The FBR dynamic model is presented in the below Equation (2i) and Table 3.

This classic ideal model of the FBR assumes the following hypotheses [53]: (a) “isothermal, iso-pH; (b) additives (for the pH-control) are added initially and during the batch operation in recommended quantities; (c) perfectly mixed liquid phase (with no concentration gradients)” [28] and Table 3.

Table 1. Nominal reaction conditions of Slatner et al. [13] “for the enzymatic reduction of D-fructose to mannitol using MDH, and NADH cofactor in an experimental BR, with the in-situ continuous regeneration of the cofactor at the expense of formate degradation in the presence of FDH. The used FDH (EC 1.2.1.2) from Candida boidinii has a specific NAD⁺-dependent activity of 2.4 U/mg, measured at 25 °C and pH 7.0. The MDH (EC 1.1.1.67) from Pseudomonas fluorescens DSM 50106 was over-expressed in E. coli JM 109.” The values in parentheses are used in the present engineering calculations.

Parameter	Values and Remarks [13]
Temperature/Pressure/pH (buffer solution)	25 °C/Normal (1 atm.)/7
Molar initial concentrations
Fructose, [F]o	0.1–1 M ([13]) (0.1–4 M) (this paper, in the range of kinetic model validity); (a)
[NADH]o	0.008–0.5 M ([13]) (0.1–0.5 M) (this paper); 0.1 M (initial guess for optimal FBR)
[NAD+]o	0.0005 M [13]
Formate initial [HCOO]o	Identical to initial [F]o
Others: [M]o = [CO2]o = 0	None
$[C{O}_2]*$= CO2 saturation level at 25 °C and pH = 7 ± 0.1	0.0313 M [54,55] pH control by an “automatic addition of HCl” [13]
$\mathrm{Batch} \mathrm{time} (t_f$)	48 h (this paper), and for an optimal single BR [27] 40 h for each BR in the SeqBR series of NBR = 10 BR [27]
$\mathrm{Bioreactor} \mathrm{liquid} \mathrm{initial} \mathrm{volume} (V_{L,0}$)	0.5 L (adopted); variable due to the continuous feeding of the FBR. Max. 3 L
$\mathrm{The} \mathrm{feed} \mathrm{flow} \mathrm{rate} (F_L$)	0.02 L h−1 (initial). Its time stepwise dynamics are to be optimized in the adopted range of 0.01–0.04 L h−1 (limited by the reactor volume)
FDH enzyme (referred to the reactor liquid)	Initial value = 0. Its time stepwise additions are to be optimized in the range of 0.1–2 kU/L.
MDH enzyme (referred to the reactor liquid)	Initial value = 0. Its time stepwise additions are to be optimized in the range of 0.1–2 kU/L. Some other compounds (dithiothreitol) are added by [13] to stabilize the MDH.

Footnotes: (a) The work at higher fructose concentrations is not recommended due to several reasons: lack of kinetic model validity; a higher reaction medium viscosity; limited solubility at 25 °C of fructose (4000 g/L) and of mannitol (ca. 200 g/L); a higher substrate inhibition effect.

Table 1. Nominal reaction conditions of Slatner et al. [13] “for the enzymatic reduction of D-fructose to mannitol using MDH, and NADH cofactor in an experimental BR, with the in-situ continuous regeneration of the cofactor at the expense of formate degradation in the presence of FDH. The used FDH (EC 1.2.1.2) from Candida boidinii has a specific NAD⁺-dependent activity of 2.4 U/mg, measured at 25 °C and pH 7.0. The MDH (EC 1.1.1.67) from Pseudomonas fluorescens DSM 50106 was over-expressed in E. coli JM 109.” The values in parentheses are used in the present engineering calculations.

Parameter	Values and Remarks [13]
Temperature/Pressure/pH (buffer solution)	25 °C/Normal (1 atm.)/7
Molar initial concentrations
Fructose, [F]o	0.1–1 M ([13]) (0.1–4 M) (this paper, in the range of kinetic model validity); (a)
[NADH]o	0.008–0.5 M ([13]) (0.1–0.5 M) (this paper); 0.1 M (initial guess for optimal FBR)
[NAD+]o	0.0005 M [13]
Formate initial [HCOO]o	Identical to initial [F]o
Others: [M]o = [CO2]o = 0	None
$[C{O}_2]*$= CO2 saturation level at 25 °C and pH = 7 ± 0.1	0.0313 M [54,55] pH control by an “automatic addition of HCl” [13]
$\mathrm{Batch} \mathrm{time} (t_f$)	48 h (this paper), and for an optimal single BR [27] 40 h for each BR in the SeqBR series of NBR = 10 BR [27]
$\mathrm{Bioreactor} \mathrm{liquid} \mathrm{initial} \mathrm{volume} (V_{L,0}$)	0.5 L (adopted); variable due to the continuous feeding of the FBR. Max. 3 L
$\mathrm{The} \mathrm{feed} \mathrm{flow} \mathrm{rate} (F_L$)	0.02 L h−1 (initial). Its time stepwise dynamics are to be optimized in the adopted range of 0.01–0.04 L h−1 (limited by the reactor volume)
FDH enzyme (referred to the reactor liquid)	Initial value = 0. Its time stepwise additions are to be optimized in the range of 0.1–2 kU/L.
MDH enzyme (referred to the reactor liquid)	Initial value = 0. Its time stepwise additions are to be optimized in the range of 0.1–2 kU/L. Some other compounds (dithiothreitol) are added by [13] to stabilize the MDH.

Footnotes: (a) The work at higher fructose concentrations is not recommended due to several reasons: lack of kinetic model validity; a higher reaction medium viscosity; limited solubility at 25 °C of fructose (4000 g/L) and of mannitol (ca. 200 g/L); a higher substrate inhibition effect.

Table 2. The kinetic model proposed by Maria [36] for the approached bienzymatic process. “The two coupled enzymatic reactions are: (R1) reduction of D-fructose to mannitol using MDH and NADH cofactor and, (R2) in-situ continuous regeneration of the cofactor NADH by the expense of formate degradation in the presence of FDH (Figure 1).” Rate constants have been estimated to match the experimental kinetic data of [13].

Reactions:	Rate Expressions:
$F+NADH{ (+\mathrm{H}}^{+})\underset{}{\stackrel{MDH}{\to }}M+NA{D}^{+}$	$R1=\frac{kc1\cdot C_{MDH}\cdot C_F\cdot C_{NADH}}{KM1+K_F{C}_F+K_{NH}{C}_{NADH}}$
$HCO{O}^{-}+NA{D}^{+}\underset{}{\stackrel{FDH}{\to }}C{O}_2\uparrow +NADH$	$R2=\frac{kc2\cdot C_{FDH}\cdot C_{HCOO}\cdot C_{NAD}}{KM2+K_{HC}{C}_{HCOO}+K_{NAD}{C}_{NAD}}$
Rate constants$kc1$ = 2 × 10−3; $kc2$ = 8.3259 × 10−3; 1/h//(U/L); $KM1$ = 7.2367 × 10−2 M; $KM2$ = 8.8047 × 10−2 M; $K_F$ = 1; $K_{NH}$ = 1; $K_{HC}$ = 5.0061 × 10−2; $K_{NAD}$ = 90.181 [27]
Process stoichiometry:$\frac{d{c}_F}{dt}= -\mathrm{R}1 ; \frac{d{c}_{NADH}}{dt}= -\mathrm{R}1+\mathrm{R}2$; $\frac{d{c}_{NAD}}{dt}= - \frac{d{c}_{NADH}}{dt}$; $\frac{d{c}_{HCOO}}{dt}= -\mathrm{R}2$; $\frac{d{c}_M}{dt}=+\mathrm{R}1 ; \frac{d{c}_{CO2}}{dt}=+\mathrm{R}2$

Table 2. The kinetic model proposed by Maria [36] for the approached bienzymatic process. “The two coupled enzymatic reactions are: (R1) reduction of D-fructose to mannitol using MDH and NADH cofactor and, (R2) in-situ continuous regeneration of the cofactor NADH by the expense of formate degradation in the presence of FDH (Figure 1).” Rate constants have been estimated to match the experimental kinetic data of [13].

Reactions:	Rate Expressions:
$F+NADH{ (+\mathrm{H}}^{+})\underset{}{\stackrel{MDH}{\to }}M+NA{D}^{+}$	$R1=\frac{kc1\cdot C_{MDH}\cdot C_F\cdot C_{NADH}}{KM1+K_F{C}_F+K_{NH}{C}_{NADH}}$
$HCO{O}^{-}+NA{D}^{+}\underset{}{\stackrel{FDH}{\to }}C{O}_2\uparrow +NADH$	$R2=\frac{kc2\cdot C_{FDH}\cdot C_{HCOO}\cdot C_{NAD}}{KM2+K_{HC}{C}_{HCOO}+K_{NAD}{C}_{NAD}}$
Rate constants$kc1$ = 2 × 10−3; $kc2$ = 8.3259 × 10−3; 1/h//(U/L); $KM1$ = 7.2367 × 10−2 M; $KM2$ = 8.8047 × 10−2 M; $K_F$ = 1; $K_{NH}$ = 1; $K_{HC}$ = 5.0061 × 10−2; $K_{NAD}$ = 90.181 [27]
Process stoichiometry:$\frac{d{c}_F}{dt}= -\mathrm{R}1 ; \frac{d{c}_{NADH}}{dt}= -\mathrm{R}1+\mathrm{R}2$; $\frac{d{c}_{NAD}}{dt}= - \frac{d{c}_{NADH}}{dt}$; $\frac{d{c}_{HCOO}}{dt}= -\mathrm{R}2$; $\frac{d{c}_M}{dt}=+\mathrm{R}1 ; \frac{d{c}_{CO2}}{dt}=+\mathrm{R}2$

Table 3. “Key-species mass balances in the FBR model, by including the enzymatic process kinetic model together with the associated rate constants of (Table 2).” The ideal model hypotheses of Maria [28] assumes a homogeneous liquid composition with negligible mass transport resistance in the bulk phase.

Species	Remarks
Substrate (fructose, F) and cofactor (NADH) mass balances: $\frac{d{c}_F}{dt}=\frac{F_{L,j}}{V_L}\left(c_{F,inlet,j}-c_F\right) - \mathrm{R}1$ $c_{F,inlet,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization; $c_{F,0}$$=c_{F,inlet,1}$ $\begin{array}{l}\frac{d{c}_{NADH}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{NADH,inlet,j}-c_{NADH}\right)\\ -\mathrm{R}1+\mathrm{R}2\end{array}$ $c_{NADH,inlet,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization; $c_{NADH,0}$$=c_{NADH,inlet,1}$	For the optimal FBR with adopted Ndiv = 10, the feeding policy is (a): $$\left[\begin{array}{cc}{c}_{F,inlet}& c_{NADH,inlet}\end{array}\right]=\left\{\begin{array}{c}\left[\begin{array}{cc}{c}_{F,inlet,1}& c_{NADH,inlet,1}\end{array}\right]\mathrm{if}0\le t\mathrm{T}1\\ \left[\begin{array}{cc}{c}_{F,inlet,2}& c_{NADH,inlet,2}\end{array}\right]\mathrm{if}\mathrm{T}1\le t\mathrm{T}2\\ \left[\begin{array}{cc}{c}_{F,inlet,3}& c_{NADH,inlet,3}\end{array}\right]\mathrm{if}\mathrm{T}2\le t\mathrm{T}3\\ \left[\begin{array}{cc}{c}_{F,inlet,4}& c_{NADH,inlet,4}\end{array}\right]\mathrm{if}\mathrm{T}3\le t\mathrm{T}4\\ \left[\begin{array}{cc}{c}_{F,inlet,5}& c_{NADH,inlet,5}\end{array}\right]\mathrm{if}\mathrm{T}4\le t\mathrm{T}5\\ \left[\begin{array}{cc}{c}_{F,inlet,6}& c_{NADH,inlet,6}\end{array}\right]\mathrm{if}\mathrm{T}5\le t\mathrm{T}6\\ \left[\begin{array}{cc}{c}_{F,inlet,7}& c_{NADH,inlet,7}\end{array}\right]\mathrm{if}\mathrm{T}6\le t\mathrm{T}7\\ \left[\begin{array}{cc}{c}_{F,inlet,8}& c_{NADH,inlet,8}\end{array}\right]\mathrm{if}\mathrm{T}7\le t\mathrm{T}8\\ \left[\begin{array}{cc}{c}_{F,inlet,9}& c_{NADH,inlet,9}\end{array}\right]\mathrm{if}\mathrm{T}8\le t\mathrm{T}9\\ \left[\begin{array}{cc}{c}_{F,inlet,10}& c_{NADH,inlet,10}\end{array}\right]\mathrm{if}\mathrm{T}9\le t\mathrm{T}10=t_f\end{array}\right.$$
Formate (HCOO) and exhausted cofactor (NAD+) mass balances: $\frac{d{c}_{HCOO}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{HCOO,inlet,j}-c_{HCOO}\right) - \mathrm{R}2$ $\frac{d{c}_{NAD}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{NAD,inlet,j}-c_{NAD}\right)+\mathrm{R}1 - \mathrm{R}2$ j = 1,..,$N_{div}$ time stepwise values	$c_{HCOO,inlet,j}=0 , \forall j$ $c_{HCOO,0}$$=c_{HCOO}$$(\mathrm{t}=0)=c_{F,0}$ $c_{NAD,inlet,j}=0 , \forall j$ $c_{NAD,0}$$=c_{NAD}$$(\mathrm{t}=0)=5 ·{ 10}^{-4}$ M [13]
Mannitol (M) and CO2 mass balances: $\frac{d{c}_M}{dt}=\frac{F_{L,j}}{V_L}\left(c_{M,inlet,j}-c_M\right)+\mathrm{R}1$ $\frac{d{c}_{CO2}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{CO2,inlet,j}-c_{CO2}\right)+\mathrm{R}2$ j = 1,..,$N_{div}$ time stepwise values	$c_{M,inlet,j}=0 , \forall j$ $c_{M,0}$$=c_M$ (t = 0) = 0. $c_{CO2,inlet,j}=0 , \forall j$ $c_{CO2,0}$$=c_{CO2}$ (t = 0) = 0. $\mathrm{If} c_{CO2} \ge c_{CO2}^{*}$$, \mathrm{then} c_{CO2}=c_{CO2}^{*}$; (b)
Enzymes MDH and FDH mass balances (c): $\frac{d{c}_{MDH}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{MDH,inlet,j}-c_{MDH}\right)$ $c_{MDH,inlet,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization; $c_{MDH,0}$ = 0. $\frac{d{c}_{FDH}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{FDH,inlet,j}-c_{FDH}\right)$ $c_{FDH,inlet,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization; $c_{FDH,0}$ = 0.	For the optimal FBR with adopted Ndiv = 10, the feeding policy is (a): $$\left[\begin{array}{cc}{c}_{MDH,inlet}& c_{FDH,inlet}\end{array}\right]=\left\{\begin{array}{c}\left[\begin{array}{cc}{c}_{MDH,inlet,1}& c_{FDH,inlet,1}\end{array}\right]\mathrm{if}0\le t\mathrm{T}1\\ \left[\begin{array}{cc}{c}_{MDH,inlet,2}& c_{FDH,inlet,2}\end{array}\right]\mathrm{if}\mathrm{T}1\le t\mathrm{T}2\\ \left[\begin{array}{cc}{c}_{MDH,inlet,3}& c_{FDH,inlet,3}\end{array}\right]\mathrm{if}\mathrm{T}2\le t\mathrm{T}3\\ \left[\begin{array}{cc}{c}_{MDH,inlet,4}& c_{FDH,inlet,4}\end{array}\right]\mathrm{if}\mathrm{T}3\le t\mathrm{T}4\\ \left[\begin{array}{cc}{c}_{MDH,inlet,5}& c_{FDH,inlet,5}\end{array}\right]\mathrm{if}\mathrm{T}4\le t\mathrm{T}5\\ \left[\begin{array}{cc}{c}_{MDH,inlet,6}& c_{FDH,inlet,6}\end{array}\right]\mathrm{if}\mathrm{T}5\le t\mathrm{T}6\\ \left[\begin{array}{cc}{c}_{MDH,inlet,7}& c_{FDH,inlet,7}\end{array}\right]\mathrm{if}\mathrm{T}6\le t\mathrm{T}7\\ \left[\begin{array}{cc}{c}_{MDH,inlet,8}& c_{FDH,inlet,8}\end{array}\right]\mathrm{if}\mathrm{T}7\le t\mathrm{T}8\\ \left[\begin{array}{cc}{c}_{MDH,inlet,9}& c_{FDH,inlet,9}\end{array}\right]\mathrm{if}\mathrm{T}8\le t\mathrm{T}9\\ \left[\begin{array}{cc}{c}_{MDH,inlet,10}& c_{FDH,inlet,10}\end{array}\right]\mathrm{if}\mathrm{T}9\le t\mathrm{T}10=t_f\end{array}\right.$$
Liquid volume in the reactor (d): $\frac{d{V}_L}{dt}=F_{L,j}$ $F_{L,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization. The unknown $F_{L,0}$$=F_L$$(\mathrm{t}=0)=F_{L,1}$ $\mathrm{is} \mathrm{determined} \mathrm{together} \mathrm{with} \mathrm{the} \mathrm{all} F_{L,j}$ values from the FBR optimization.	For the optimal FBR with adopted Ndiv =10, the feeding policy is (a):$F_L=\left\{\begin{array}{c}{F}_{L,1} \mathrm{if} 0 \le t < \mathrm{T}1 \\ F_{L,2} \mathrm{if} \mathrm{T}1 \le t < \mathrm{T}2\\ F_{L,3} \mathrm{if} \mathrm{T}2 \le t < \mathrm{T}3\\ F_{L,4} \mathrm{if} \mathrm{T}3 \le t < \mathrm{T}4\\ F_{L,5} \mathrm{if} \mathrm{T}4 \le t < \mathrm{T}5\\ F_{L,6} \mathrm{if} \mathrm{T}5 \le t < \mathrm{T}6\\ F_{L,7} \mathrm{if} \mathrm{T}6 \le t < \mathrm{T}7\\ F_{L,8} \mathrm{if} \mathrm{T}7 \le t < \mathrm{T}8\\ F_{L,9} \mathrm{if} \mathrm{T}8 \le t < \mathrm{T}9\\ F_{L,10} \mathrm{if} \mathrm{T}9 \le t < \mathrm{T}10=t_f\end{array}\right.$

Footnotes: (a) For the adopted N_div = 10, the j = 1,…, $N_{div}$ time-arcs approx. switching points are: T1 = 4.8 h.; T2 = 9.6 h.; T3 = 14.4 h.; T4 = 19.2 h.; T5 = 24 h.; T6 = 28.8 h.; T7 = 33.6 h.; T8 = 38.4 h.; T9 = 43.2 h.; T10 = $t_f$ = 48 h. (b) The saturation level of CO₂ is given in Table 1. (c) Enzymes deactivation is neglected. (d) The $F_{L,j}$ time stepwise feed flow rates are determined simultaneously with the other control variables (Section 3.1) to ensure the FBR optimal operation (see Section 3.2).

Table 3. “Key-species mass balances in the FBR model, by including the enzymatic process kinetic model together with the associated rate constants of (Table 2).” The ideal model hypotheses of Maria [28] assumes a homogeneous liquid composition with negligible mass transport resistance in the bulk phase.

Species	Remarks
Substrate (fructose, F) and cofactor (NADH) mass balances: $\frac{d{c}_F}{dt}=\frac{F_{L,j}}{V_L}\left(c_{F,inlet,j}-c_F\right) - \mathrm{R}1$ $c_{F,inlet,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization; $c_{F,0}$$=c_{F,inlet,1}$ $\begin{array}{l}\frac{d{c}_{NADH}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{NADH,inlet,j}-c_{NADH}\right)\\ -\mathrm{R}1+\mathrm{R}2\end{array}$ $c_{NADH,inlet,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization; $c_{NADH,0}$$=c_{NADH,inlet,1}$	For the optimal FBR with adopted Ndiv = 10, the feeding policy is (a): $$\left[\begin{array}{cc}{c}_{F,inlet}& c_{NADH,inlet}\end{array}\right]=\left\{\begin{array}{c}\left[\begin{array}{cc}{c}_{F,inlet,1}& c_{NADH,inlet,1}\end{array}\right]\mathrm{if}0\le t\mathrm{T}1\\ \left[\begin{array}{cc}{c}_{F,inlet,2}& c_{NADH,inlet,2}\end{array}\right]\mathrm{if}\mathrm{T}1\le t\mathrm{T}2\\ \left[\begin{array}{cc}{c}_{F,inlet,3}& c_{NADH,inlet,3}\end{array}\right]\mathrm{if}\mathrm{T}2\le t\mathrm{T}3\\ \left[\begin{array}{cc}{c}_{F,inlet,4}& c_{NADH,inlet,4}\end{array}\right]\mathrm{if}\mathrm{T}3\le t\mathrm{T}4\\ \left[\begin{array}{cc}{c}_{F,inlet,5}& c_{NADH,inlet,5}\end{array}\right]\mathrm{if}\mathrm{T}4\le t\mathrm{T}5\\ \left[\begin{array}{cc}{c}_{F,inlet,6}& c_{NADH,inlet,6}\end{array}\right]\mathrm{if}\mathrm{T}5\le t\mathrm{T}6\\ \left[\begin{array}{cc}{c}_{F,inlet,7}& c_{NADH,inlet,7}\end{array}\right]\mathrm{if}\mathrm{T}6\le t\mathrm{T}7\\ \left[\begin{array}{cc}{c}_{F,inlet,8}& c_{NADH,inlet,8}\end{array}\right]\mathrm{if}\mathrm{T}7\le t\mathrm{T}8\\ \left[\begin{array}{cc}{c}_{F,inlet,9}& c_{NADH,inlet,9}\end{array}\right]\mathrm{if}\mathrm{T}8\le t\mathrm{T}9\\ \left[\begin{array}{cc}{c}_{F,inlet,10}& c_{NADH,inlet,10}\end{array}\right]\mathrm{if}\mathrm{T}9\le t\mathrm{T}10=t_f\end{array}\right.$$
Formate (HCOO) and exhausted cofactor (NAD+) mass balances: $\frac{d{c}_{HCOO}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{HCOO,inlet,j}-c_{HCOO}\right) - \mathrm{R}2$ $\frac{d{c}_{NAD}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{NAD,inlet,j}-c_{NAD}\right)+\mathrm{R}1 - \mathrm{R}2$ j = 1,..,$N_{div}$ time stepwise values	$c_{HCOO,inlet,j}=0 , \forall j$ $c_{HCOO,0}$$=c_{HCOO}$$(\mathrm{t}=0)=c_{F,0}$ $c_{NAD,inlet,j}=0 , \forall j$ $c_{NAD,0}$$=c_{NAD}$$(\mathrm{t}=0)=5 ·{ 10}^{-4}$ M [13]
Mannitol (M) and CO2 mass balances: $\frac{d{c}_M}{dt}=\frac{F_{L,j}}{V_L}\left(c_{M,inlet,j}-c_M\right)+\mathrm{R}1$ $\frac{d{c}_{CO2}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{CO2,inlet,j}-c_{CO2}\right)+\mathrm{R}2$ j = 1,..,$N_{div}$ time stepwise values	$c_{M,inlet,j}=0 , \forall j$ $c_{M,0}$$=c_M$ (t = 0) = 0. $c_{CO2,inlet,j}=0 , \forall j$ $c_{CO2,0}$$=c_{CO2}$ (t = 0) = 0. $\mathrm{If} c_{CO2} \ge c_{CO2}^{*}$$, \mathrm{then} c_{CO2}=c_{CO2}^{*}$; (b)
Enzymes MDH and FDH mass balances (c): $\frac{d{c}_{MDH}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{MDH,inlet,j}-c_{MDH}\right)$ $c_{MDH,inlet,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization; $c_{MDH,0}$ = 0. $\frac{d{c}_{FDH}}{dt}=\frac{F_{L,j}}{V_L}\left(c_{FDH,inlet,j}-c_{FDH}\right)$ $c_{FDH,inlet,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization; $c_{FDH,0}$ = 0.	For the optimal FBR with adopted Ndiv = 10, the feeding policy is (a): $$\left[\begin{array}{cc}{c}_{MDH,inlet}& c_{FDH,inlet}\end{array}\right]=\left\{\begin{array}{c}\left[\begin{array}{cc}{c}_{MDH,inlet,1}& c_{FDH,inlet,1}\end{array}\right]\mathrm{if}0\le t\mathrm{T}1\\ \left[\begin{array}{cc}{c}_{MDH,inlet,2}& c_{FDH,inlet,2}\end{array}\right]\mathrm{if}\mathrm{T}1\le t\mathrm{T}2\\ \left[\begin{array}{cc}{c}_{MDH,inlet,3}& c_{FDH,inlet,3}\end{array}\right]\mathrm{if}\mathrm{T}2\le t\mathrm{T}3\\ \left[\begin{array}{cc}{c}_{MDH,inlet,4}& c_{FDH,inlet,4}\end{array}\right]\mathrm{if}\mathrm{T}3\le t\mathrm{T}4\\ \left[\begin{array}{cc}{c}_{MDH,inlet,5}& c_{FDH,inlet,5}\end{array}\right]\mathrm{if}\mathrm{T}4\le t\mathrm{T}5\\ \left[\begin{array}{cc}{c}_{MDH,inlet,6}& c_{FDH,inlet,6}\end{array}\right]\mathrm{if}\mathrm{T}5\le t\mathrm{T}6\\ \left[\begin{array}{cc}{c}_{MDH,inlet,7}& c_{FDH,inlet,7}\end{array}\right]\mathrm{if}\mathrm{T}6\le t\mathrm{T}7\\ \left[\begin{array}{cc}{c}_{MDH,inlet,8}& c_{FDH,inlet,8}\end{array}\right]\mathrm{if}\mathrm{T}7\le t\mathrm{T}8\\ \left[\begin{array}{cc}{c}_{MDH,inlet,9}& c_{FDH,inlet,9}\end{array}\right]\mathrm{if}\mathrm{T}8\le t\mathrm{T}9\\ \left[\begin{array}{cc}{c}_{MDH,inlet,10}& c_{FDH,inlet,10}\end{array}\right]\mathrm{if}\mathrm{T}9\le t\mathrm{T}10=t_f\end{array}\right.$$
Liquid volume in the reactor (d): $\frac{d{V}_L}{dt}=F_{L,j}$ $F_{L,j}$$=\mathrm{control} \mathrm{variable}; \mathrm{j}=1,..,N_{div}$ time stepwise unknown values to be determined from the FBR optimization. The unknown $F_{L,0}$$=F_L$$(\mathrm{t}=0)=F_{L,1}$ $\mathrm{is} \mathrm{determined} \mathrm{together} \mathrm{with} \mathrm{the} \mathrm{all} F_{L,j}$ values from the FBR optimization.	For the optimal FBR with adopted Ndiv =10, the feeding policy is (a):$F_L=\left\{\begin{array}{c}{F}_{L,1} \mathrm{if} 0 \le t < \mathrm{T}1 \\ F_{L,2} \mathrm{if} \mathrm{T}1 \le t < \mathrm{T}2\\ F_{L,3} \mathrm{if} \mathrm{T}2 \le t < \mathrm{T}3\\ F_{L,4} \mathrm{if} \mathrm{T}3 \le t < \mathrm{T}4\\ F_{L,5} \mathrm{if} \mathrm{T}4 \le t < \mathrm{T}5\\ F_{L,6} \mathrm{if} \mathrm{T}5 \le t < \mathrm{T}6\\ F_{L,7} \mathrm{if} \mathrm{T}6 \le t < \mathrm{T}7\\ F_{L,8} \mathrm{if} \mathrm{T}7 \le t < \mathrm{T}8\\ F_{L,9} \mathrm{if} \mathrm{T}8 \le t < \mathrm{T}9\\ F_{L,10} \mathrm{if} \mathrm{T}9 \le t < \mathrm{T}10=t_f\end{array}\right.$

Footnotes: (a) For the adopted N_div = 10, the j = 1,…, $N_{div}$ time-arcs approx. switching points are: T1 = 4.8 h.; T2 = 9.6 h.; T3 = 14.4 h.; T4 = 19.2 h.; T5 = 24 h.; T6 = 28.8 h.; T7 = 33.6 h.; T8 = 38.4 h.; T9 = 43.2 h.; T10 = $t_f$ = 48 h. (b) The saturation level of CO₂ is given in Table 1. (c) Enzymes deactivation is neglected. (d) The $F_{L,j}$ time stepwise feed flow rates are determined simultaneously with the other control variables (Section 3.1) to ensure the FBR optimal operation (see Section 3.2).

3. Optimization Problem Formulation

By using a step-by-step approach, this section presents the numerical methodology used to solve the FBR optimization problem, that is: the math translation of the formulated objectives, the problem constraints, and the used numerical rules. All these aspects are discussed in detail by intentionally using Section 3.1 to Section 3.6, and a regular, but simple, (bio)chemical engineering language, while keeping the necessary math rigor.

3.1. The Control Variable Choice

Due to its improvements, the approached bienzymatic alternative proposed by Slatner et al. [13] is the most promising and cheaper technology to produce mannitol at an industrial scale [6,7,13]. However, due to the costly enzymes, reflected in the product cost, one of the sensitive issues to be solved is an engineering one, related to the chosen reactor operating strategy able to minimize the enzymes (MDH, FDH) consumption but keeping the mannitol high yields ([M]_final) for the imposed technological limits for the F/HCOO substrates and NADH cofactor.

Recent advances try to bypass this problem by using the biological route, which couples the two reactions of (Figure 1) “in the same genetic modified micro-organism (Bacillus megaterium) used as host for both enzymes synthesis, and cofactor regeneration” [12]. However, this last route is not yet available at an industrial scale due to the numerous disadvantages related to the control of the biological reactor.

In the present case, such problems related to cell cultures are inexistent. Additionally, to greatly increase the FBR flexibility and efficiency, a larger number of control variables can be used. By analyzing the species relative importance, the following five control variables have been chosen:

-

The fed enzymes ($c_{MDH,inlet,j}$;$c_{FDH,inlet,j}$),

-

The fed substrate ($c_{F,inlet,j}$), and the fed cofactor ($c_{NADH,inlet,j}$);

-

The feed flow rate ($F_{L,j}$) of the solution containing the substrates, enzymes, and the cofactor.

In the above notations, the index “j = 1, N_div” denotes the time stepwise value to be determined by optimization for every of N_div “time-arc” in which the FBR batch-time is divided.

As an important observation, the optimal FBR operating strategy to be determined in this study is more complex than the simple operation of a BR or of other reactors from Figure 2. Mainly, the substrate (F), enzymes (MDH, FDH), and the cofactor (NADH) concentrations in the feeding solution of the variable feed flow rate (F_L) are no longer kept constant as well. Thus, in the FBR case, the most convenient optimal operation is the following: (i) “the batch-time is divided in N_div (equal time-arcs) of equal lengths, and (ii) the control variables are kept constant only over every time-arc at optimal values determined from solving an optimization problem (e.g., maximization of the mannitol (M) production in this case). The time-intervals of equal lengths Δt = t_f /N_div are obtained by dividing the batch time t_f into N_div parts t_j−1 ≤ t ≤ t_j, where t_j = j·Δt are switching points (where the reactor input is continuous and differentiable)”. Time-intervals for the present case study with an adopted N_div = 10 are shown in footnote (a) of Table 3. Consequently, there are 5 × N_div = 50 unknown in total to be determined by applying an optimization procedure.

For this case, initial concentrations of the other compounds are null (that is, [M]o, and [CO₂]o), or at values recommended by Slatner et al. [13] (that is [NAD]o, and [HCOO]o = [F]o, see Table 3).

Here, it is to observe that there are several other operating variables that could be considered when optimizing the FBR (e.g., [HCOO]o ≠ [F]o, or even the batch time ($t_f$) imposed by Slatner et al. [13]). However, as the number of control variables increases, the associated nonlinear optimization problem, subjected to nonlinear constraints (NLP), becomes more multimodal, and even more difficult to solve, by greatly increasing the computation time to find the global feasible optimum of the NLP problem.

The practical implementation of such a variable feeding strategy (as the feed flow rate and composition) over the batch assumes the previous preparation of the stock solutions with different concentrations for the substrate (F), enzymes (MDH, FDH), and cofactor (NADH), at levels which resulted from the optimization calculations to be fed for every time-arc (that is a batch-time division in which the feeding is constant as flow-rate and composition). Of course, every stock solution presents species (F, NDH, MDH, FDH) concentrations that are different from each other.

In the present case of the FBR operation adopting N_div = 10 (equal time-arcs), it results in the requirement to prepare in advance 10 stock solutions, each with the concentrations of F, NADH, MDH, and FDH to be determined from the optimization calculations (Section 4). Then, each of these stock solutions are fed into the FBR according to the optimal feed flow rate determined (by optimization, Section 4) for each time-arc. Of course, the feedings of the 10 stock solutions during the 10 time-arcs are different, not only in species concentrations (F, NADH, MDH, FDH), but also in flow rates.

3.2. Optimization Objectives and the Composite Objective Function (W) Choice

To explore the efficiency limits of the studied FBR of Table 1 by testing a larger number of economical objectives, the following goals are selected:

(i)

maximum FBR productivity in mannitol;

(ii)

minimum consumption of the costly enzymes MDH and FDH;

(iii)

minimum consumption of the cofactor NADH—even if NADH is not very expensive [14], its separation over the product purification is relatively costly [56];

(iv)

an adjustable substrate $c_{F,inlet,j}$ consumption (within defined limits) to ensure its maximum conversion to mannitol.

As revealed by Slatner et al. [13], the enzymatic reduction of D-fructose to mannitol by using MDH and NADH as a cofactor takes place very selectively and without byproducts. So, the fructose reduction occurs quantitatively. Thus, here the fructose conversion is the most influencing indicator for FBR productivity (Fobj1 in Equation (1B)).

In mathematical terms, the above multiobjectives (i–iv) problem translates in the following NLP problem:

$$\begin{array}{l}\mathrm{Given} \left[\mathrm{NAD}\right]\mathsf{o}, \mathrm{Find} \mathrm{the} \mathrm{control} \mathrm{variables}:\\ F_{L,j}; c_{MDH,inlet,j}; c_{FDH,inlet,j}; c_{F,inlet,j}; c_{NADH,inlet,j}, \\ \mathrm{For} \mathrm{j} = 1,\dots , {\mathbf{N}}_{\mathbf{div}}, \mathrm{with} \mathrm{the} \mathrm{adopted} {\mathbf{N}}_{\mathbf{div}} = 10 \mathrm{time}-\mathrm{arcs} \mathrm{and} \mathrm{the}\underline{\mathrm{FBR}} \mathrm{initial} \mathrm{condition} \mathrm{of} \mathrm{Table} 3, \mathrm{so} \mathrm{as} \mathrm{to} \mathrm{obtain}: \mathrm{Min} \mathrm{W}(\mathit{c}, {\mathit{c}}_{\mathit{o}}, \mathit{k}),\\ \mathrm{with} \mathrm{the} \mathrm{following} \mathrm{composite} \mathrm{objective} \mathrm{function}:\hfill \\ \mathrm{W}(c, c_o, k)=\mathrm{Min}(1/\mathrm{Fobj}1) \wedge \mathrm{Min}\left(\mathrm{Fobj}2\right) \wedge \mathrm{Min}\left(\mathrm{Fobj}3\right) \wedge \mathrm{Min}\left(\mathrm{Fobj}4\right)\hfill \end{array}$$

(1A)

“The time-arcs are of equal length Δt = t_f /N_div, being obtained by dividing the batch time t_f into N_div parts t_j−1 ≤ t ≤ t_j, where t_j = j·Δt are the switching points between arcs. Notations: Λ = ‘and’ (simultaneously), in the math sense; c = species concentration vector; c_o = initial value of c; k = vector of the kinetic model rate constants”; W = the overall (composite) objective function. The components Fobj1–Fobj4 of the composite objective function are the following:

$$\begin{array}{l}\mathrm{Fobj}1=\left[\mathrm{M}\left({\mathrm{t}}_{\mathrm{f}}\right)\right], \mathrm{with} \left[\mathrm{M}\right] \mathrm{in} \mathrm{M} \mathrm{units}.\\ \mathrm{Fobj}2={\displaystyle \sum _{j=1}^{N_{div}}{c}_{MDH,inlet,j}} F_{L,j} \Delta t_j, \mathrm{with} \mathrm{MDH} \mathrm{conc}. \mathrm{in} \mathrm{kU}/\mathrm{L} \mathrm{units}.\\ \mathrm{Fobj}3={\displaystyle \sum _{j=1}^{N_{div}}{c}_{FDH,inlet,j}} F_{L,j} \Delta t_j, \mathrm{with} \mathrm{FDH} \mathrm{conc}. \mathrm{in} \mathrm{kU}/\mathrm{L} \mathrm{units}.\\ \mathrm{Fobj}4={\displaystyle \sum _{j=1}^{N_{div}}{c}_{NADH,inlet,j}} F_{L,j} \Delta t_j, \mathrm{with} \mathrm{NADH} \mathrm{conc}. \mathrm{in} \mathrm{M} \mathrm{units}.\\ \Delta t_j=t_f / N_{div}, \mathrm{for} \mathrm{all} “\mathrm{j}”(\mathrm{that} \mathrm{is}, \mathrm{equal} \mathrm{time}-\mathrm{arcs} \mathrm{in} \mathrm{the} \mathrm{present} \mathrm{case} \mathrm{study})\end{array}$$

(1B)

Equation (1A,B) can be re-written in a form much more accessible to the numerical calculus, as follows:

$$\begin{array}{l}\mathrm{Given} \left[\mathrm{NAD}\right]\mathsf{o}, \mathrm{Find} \mathrm{the} \mathrm{control} \mathrm{variables}:\\ F_{L,j}; c_{MDH,inlet,j}; c_{FDH,inlet,j}; c_{F,inlet,j}; c_{NADH,inlet,j},\\ \mathrm{For} \mathrm{j} = 1,\dots , {\mathbf{N}}_{\mathbf{div}}, \mathrm{with} \mathrm{the} \mathrm{adopted} {\mathbf{N}}_{\mathbf{div}} = 10 \mathrm{time}-\mathrm{arcs} \mathrm{and} \mathrm{the}\underline{\mathrm{FBR}} \mathrm{initial} \mathrm{condition} \mathrm{of} \mathrm{Table} 3, \mathrm{so} \mathrm{as} \mathrm{to} \mathrm{obtain}:\\ \mathrm{Min} \mathsf{W}(\mathit{c}, {\mathit{c}}_{\mathit{o}}, \mathit{k}),\\ \mathrm{with} \mathrm{the} \mathrm{composite} \mathrm{objective} \mathrm{function}:\\ \mathsf{W}(\mathit{c}, {\mathit{c}}_{\mathit{o}}, \mathit{k}) = (\mathrm{Fobj}2 + \mathrm{Fobj}3 + \mathrm{Fobj}4)/\mathrm{Fobj}1\\ \mathrm{Where} \mathrm{the} \mathrm{components} \mathrm{Fobj}1-\mathrm{Fobj}4 \mathrm{are} \mathrm{defined} \mathrm{in} \mathrm{the} \mathrm{Equation} \left(1\mathsf{B}\right)\end{array}$$

(1C)

As an observation, the use of the overall objective function ’W’ in Equation (1C) corresponds to the so-called ‘inverted utility function method’ [57]. Because the four components Fobj1–Fobj4 of W are opposed (that is, the realization of one objective is done to the detriment of another objective), other optimization procedures can be applied as well, for instance the Pareto front method [26]. However, the adopted multiobjective optimization rule with this composite objective function presents the advantage of simplicity, with an easy application and interpretation.

Concerning the adopted overall objective function ‘W’ in (1C) some observations are necessary: (i) “The chosen units for M, MDH, FDH, and NADH allow the direct comparison of Fobj1–Fobj4, and their concomitant use in ‘W’, because they present the same order of magnitude; (ii) The way by which “W” was elaborated, implicitly ensures the simultaneous realization of the all objectives formulated in Equation (1A), that is consumption minimization of the two enzymes (MDH, FDH) and of the cofactor (NADH), together with the mannitol M production maximization. (iii) Of course, other formulations of the ‘W’ function are also possible, depending on the weight (relative importance) given to each component objective (Fobj1–Fobj4) (see the example [58])”.

3.3. Optimization Problem Constraints

The NLP optimization problem Equation (1C) is highly nonconvex and nonlinear, being subjected to the following technological/physical meaning/model constraints:

Nonlinear process and reactor model:

$$\begin{array}{l}\frac{\mathsf{d}{c}_j}{\mathsf{d}t}=\frac{F_{L,u}}{V_L} \left(c_{j,inlet,u}-c_j\right)+{\displaystyle \sum _{\mathsf{i}=1}^{{\mathsf{n}}_{\mathsf{r}}}{\nu }_{ij}{r}_i} (\underline{\mathbf{FBR}} \mathrm{nonlinear} \mathrm{dynamic} \mathrm{model} \mathrm{of} \mathrm{Table} 3); \mathrm{J}=\mathrm{species} \mathrm{index} (\mathrm{F}, \mathrm{M},\\ {\mathrm{HCOO}}^{-}, \mathrm{NADH}, {\mathrm{NAD}}^{+}, {\mathrm{CO}}_2, \mathrm{MDH}, \mathrm{FDH}); {\nu }_{ij}=\mathrm{the} \mathrm{stoichiometric} \mathrm{coefficient} \mathrm{of} \mathrm{the} \mathrm{species} “\mathrm{j}” \mathrm{in} \mathrm{the} “\mathrm{i}-\mathrm{th}”\\ \mathrm{reaction};r_i=\mathrm{the} “\mathrm{i}-\mathrm{th}” \mathrm{reaction} \mathrm{rate}; \mathrm{u}=1,\dots , {\mathsf{N}}_{\mathsf{div}} \mathrm{denotes} \mathrm{the} \mathrm{time}-\mathrm{arc} \mathrm{number} \mathrm{of} \mathrm{the} \underline{\mathrm{FBR}} \mathrm{optimal} \mathrm{feeding}\\ \mathrm{policy}; {\mathsf{n}}_{\mathsf{r}}=\mathrm{no}. \mathrm{of} \mathrm{reactions}.\\ \frac{d{V}_L}{dt}=F_{L,u}, \mathrm{the} \mathrm{liquid} \mathrm{volume} \mathrm{dynamics} \mathrm{of} (\mathrm{Table} 3),\\ \mathrm{With} \mathrm{the} \mathrm{initial} \mathrm{conditions} \mathrm{of} \left(\mathrm{Table}3\right), \mathrm{that} \mathrm{is}:\\ c_{j,o}=c_j\left(t=0\right); \mathrm{where} \mathrm{j}=(\mathrm{F}, \mathrm{NADH}, \mathrm{MDH}, \mathrm{FDH}) \mathrm{are} \mathrm{to} \mathrm{be} \mathrm{optimized};\\ c_{j,o}=0, \mathrm{for} \mathrm{j}=(\mathrm{M}, {\mathrm{CO}}_2), \mathrm{and} \mathrm{for} \mathrm{j}=\left({\mathrm{NAD}}^{+}\right) \mathrm{are} \mathrm{given} \mathrm{in} (\mathrm{Table} 3),\\ c_{j,o} \mathrm{for} \mathrm{j}=\left(\mathrm{HCOO}\right) \mathrm{is} \left[\mathrm{HCOO}\right]\mathrm{o}=\left[\mathrm{F}\right]\mathrm{o},\end{array}$$

(2i)

Physical significance constraints:

$$c_j(t)\ge \mathit{0}, \mathrm{for} \mathrm{all} \mathrm{the} \mathrm{species} “\mathrm{j}”, \mathrm{and} \mathrm{for} \mathrm{all} t \in [0-t_f],$$

(2ii)

Searching ranges for the control variables are those suggested and experimentally validated by Slatner et al. [13], as below indicated. It no to note that [HCOO]o = [F]o, as recommended by [13].

$$\begin{array}{l}[c_{MDH,inlet,u}; c_{FDH,inlet,u}] \in [0.1-2] \mathrm{kU}/\mathrm{L}; \\ c_{F,inlet,u} \in [0.1-4] \mathrm{M}; c_{NADH,inlet,u} \in [0.1-0.5] \mathrm{M};\\ F_{L,u} \in [0.01-0.04] \mathrm{L}/\mathrm{h}. (\mathrm{due} \mathrm{to} \mathrm{the} \mathbf{FBR} \mathrm{capacity}). \end{array}$$

(2iii)

u= 1,…, N_div denotes the time-arc number of the FBR optimal feeding policy.

$$V_L=\mathrm{variable} (\mathrm{see} \underline{2\mathrm{i}}); (\mathbf{FBR} \mathrm{liquid} \mathrm{volume});$$

(2iv)

One excludes the unfeasible trivial solution:

W = Fobj1 = Fobj2 = Fobj3 = Fobj4 = 0

(2v)

3.4. Time Stepwise Divisions Choice

The simplest FBR operating mode is to keep constant during the batch the control variables selected in the Section 3.1. It is understood that such a policy will not necessarily ensure the optimal FBR performances. That is because it lacks of adapting the feeding dynamics to the needs of the reactions progress.

Actually, the optimal variable control policy “implies a time step-wise variable feeding of the bioreactor for all the selected control variables, over an adopted (N_div = 10 here) equal time-arcs that covers the whole batch time. In the present study, the time-arcs are of equal length Δt = t_f /N_div, being obtained by dividing the batch time t_f into N_div parts t_j−1 ≤ t ≤ t_j, where t_j = j·Δt are the switching points between arcs. Each time-arc “j”, of length Δt_j (j = 1, N_div) is characterized by optimal levels (to be determined) of the control variables,” that is: the feed flow rate $F_{L,j}$, the substrate, and the main cofactor ($c_{F,inlet,j}$; $c_{NADH,inlet,j}$), and the two enzymes ($c_{MDH,inlet,j}$; $c_{FDH,inlet,j}$), (see Equation (1C)).

Besides seeking the optimal operation of Equation (1C), this type of FBR variable feeding operation “includes enough degrees of freedom to offer a wide range of FBR operating facilities that, in principle, might be investigated (see also the discussion given by” [28,59], as, for instance:

(a)

“by choosing unequal time-arcs, of lengths to be determined by the optimization rule;

(b)

by considering the whole batch time as an optimization variable;

(c)

by increasing the number of equal time-arcs (N_div) to obtain a more refined and adaptable FBR operating policy, but keeping the same non-uniform feeding policy for the chosen control variables.

(d)

by extend the search min/max limits of the control variables, or even by considering them as unknown (to be determined).

(e)

by feeding the bioreactor with a variable feed flow-rate, but with a solution of an uniform concentration for the all other control variables, over a small or large number (N_div) of time-arcs.

All the alternatives (a–e) are not approached here from the following reasons:

• Alternatives (a–c) are not good options, because as (N_div) increases, the necessary computational effort to solve the NLP problem {Equation (1C) + Equation (2i–v)} grows significantly due to considerable increase in the number of searching variables. Thus, the quick (real-time) implementation of the derived FBR operating policy becomes questionable. Additionally, multiple optimal operating policies can exist for the resulted over-parameterized constrained NLP optimization problem, thus increasing the difficulty to quickly locate a feasible globally optimal solution of the FBR optimization problem.”

The alternative (c) is also not advisable because, “as the (N_div) increases, the operating policy is more difficult and more costly to be implemented, since the optimal feeding policy requires a larger number of stocks with feeding substrate/NADH/enzymes solutions of different concentrations, separately prepared in advance to be fed for every time-arc Δt_j (j = 1,…, N_div) of the FBR operation. Also, the NLP optimization problem is more difficult to solve because of the increased number of operating parameters to be determined from locating the feasible minimum of the multi-modal composite objective function—a challenging problem due to the multiple solutions difficult to discriminate and evaluate. Besides, FBR operation with using a too large number (N_div) of small time-arcs (Δt_j) can raise special operating problems when including PAT (Process Analytical Technology) tools [60].

A brief survey of the FBR optimization literature [27,28,46,61] reveals that a small number (N_div) ≤ 10 is commonly used for such FBR due to the above-mentioned reasons. In fact, the present numerical analysis does not intend to exhaust all the possibilities of the approached FBR optimization. Thus, an extended analysis of the operating Alternatives (a)–(d) of the FBR operation, or the influence of the parametric uncertainty deserves a separate investigation, being beyond the scope of this paper. To not complicate the computational analysis, a value of (N_div) = 10 equal time-arcs have been adopted here”, leading to equal time-arcs of length $t_f$/(N_div) = 4.8 h.

• The alternative (d) is unlikely because it cannot limit the excessive consumption of substrates and cannot prevent the hydrodynamic stress or the excessive product dilution. Moreover, such an alternative might indicate unrealistic results outside the validity of the used kinetic model [36], whose plausibility is strictly restricted to the investigated experimental domain (Table 1). “In our numerical analysis, carefully documented upper bounds of control variables Equation (2iii) were tested to ensure realistic results for the FBR optimal operating policy.”
• “The alternative (e) is also not feasible, even if a larger (N_div) will be used (see (c)). That is because, it is well-known that the variability of the FBR feeding over the batch time-arcs is the main degree-of-freedom used to obtain FBR optimal operating policies of superior quality” [25,28,45,59]. By giving up to the variable feed flow rate, the enzymes, substrate, and cofactor concentrations, suboptimal FBR operating policies will be obtained and of low performance.

3.5. The Used Solver and the Problem Solution Particularities

During the FBR optimization, when simulating the FBR dynamics, the time evolution of the species concentrations in the bulk phase and of the liquid–volume are obtained by solving the FBR dynamic model of Table 3 “with the initial condition $c_{j,o}$ (t = 0) stipulated in Equation (2i). The imposed batch time $t_f$, and the optimal medium conditions are those of (Table 1). The dynamic model solution was obtained with a high precision, by using the variable-order stiff integrator (ode15s) of the MATLAB™.” All calculations were performed in the framework of the MATLAB™ computational platform with an original code developed by the authors.

Because the FBR differential model of Table 3, the optimization objective Equation (1C), and the problem constraints Equation (2i–v) are all highly nonlinear, the formulated problem of Equation (1C) with the explicit/implicit nonlinear constraints Equation (2i–v) “translates into a nonlinear optimization problem (NLP) with a multi-modal composite objective function, and a non-convex searching domain. To obtain the global feasible solution with enough precision, by avoiding local sub-optimal solutions, the multi-modal optimization solver MMA of Maria [51,52,62] has been used, as being proved in previous works to be more effective compared to the common (commercial) algorithms. The computational time was reasonably short (minutes) by using a common PC, thus offering a quick implementation of the obtained FBR optimal operating policy.”

3.6. Optimized BR and SEQBR Policies

To further compare the FBR optimal operating policy with equivalent batch operations, two alternatives have been chosen from the literature, those who analyzed the same bienzymatic process of mannitol production, respectively, namely:

(a)

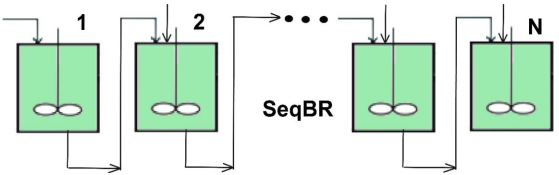
The optimization of the initial load of a simple single BR of Maria [27,36]. The optimal BR policies have been derived by using an equivalent composite multiobjective function seeking the minimum enzyme (MDH,FDH) consumption simultaneously with realizing a maximum mannitol production under the multiple constraints similar to Equation (2i–v). To realize the equivalence in the direct comparison terms of the present FBR with (N_div) = 10 equal time-arcs, a N = 10× times repeated (cyclic) BR (of the same size) and an optimized series SeqBR of N_BR = 10 equal BR-s (of the same size) are considered below in the discussion (Section 4).

(b)

The optimization of a SeqBR with a series of N_BR = 10 BR-s (Figure 2) [27]. At the end of each batch, the content of the BR from the series is passed to the next BR but adjusting its initial load (that is [F]o, [NADH]o, [MDH]o, [FDH]o) according to the optimal operating strategy derived by using an equivalent composite multiobjective function realizing the minimum enzyme (MDH,FDH) consumption simultaneously with the maximum mannitol production under multiple constraints similar to Equation (2i–v). For a direct comparison to the analyzed FBR with (N_div) = 10 equal time-arcs, N_BR = 10 equal BR-s (of the same size) are considered below in the discussion (Section 4).

“To determine the optimal BR policy (a), and the optimal SeqBR policy (b), the same numerical rules of (Section 3.5) have been used, that is the variable-order stiff integrator (“ode15s”) of the MATLAB™, and the multi-modal optimization solver MMA of Maria [51,52,62], together with the authors’ orginal code, all being implemented on the MATLAB™ computational platform. To confront the BR optimization result, a simple exhaustive numerical algorithm has also been used by Maria [36]. As revealed by Maria and Peptănaru [27], optimal SeqBR is superior to the optimal (cyclic) BR, and to the experimental BR trials of Slatner et al. [13] in terms of enzymes consumption (3×–12× less for FDH, and MDH),” to obtain the same high fructose conversions.

4. FBR Optimization Results and Discussion

4.1. The Resulted FBR Optimal Operating Policy

The optimal operating policy of the FBR, obtained by solving the optimization problem Equation (1C) with the control variables of Section 3.1, and the constraints Equation (2i–v), for an adopted N_div =10 (Section 3.4), is presented as follows:

(a)

In Figure 4A, the simulated key species concentrations dynamics, that is $c_j(t)$ in Equation (2a).

(b)

In Figure 4B, the variable policy of the feed flow rate ($F_{L,j}$, j = 1,…, N_div) and the liquid volume dynamics.

(c)

In Figure 4C, the variable feeding policy with the substrate ($c_{F,inlet,j}$, j = 1,…,N_div), and with NADH ($c_{NADH,inlet,j}$, j = 1,…, N_div),

(d)

In Figure 4D, the variable feeding policy with MDH enzyme ($c_{MDH,inlet,j}$, j=1,…,N_div).

(e)

In Figure 4E, the variable feeding policy with FDH enzyme ($c_{FDH,inlet,j}$, j=1,…,N_div).

Figure 4. (A) Simulated dynamic trajectories of species concentrations in the optimally operated FBR with the time stepwise feeding of figures (B–E). (B) The optimal feed flow rate (FL) policy and the liquid volume (VL) increase during the batch. (C) The optimal feeding policy with the substrate (F) and cofactor NADH. (D) The optimal feeding policy with the MDH enzyme and its accumulation in the reactor. (E) The optimal feeding policy with the FDH enzyme and its accumulation in the reactor. Initial conditions and the control variables ranges are given in Table 1 and Table 3.

Figure 4. (A) Simulated dynamic trajectories of species concentrations in the optimally operated FBR with the time stepwise feeding of figures (B–E). (B) The optimal feed flow rate (FL) policy and the liquid volume (VL) increase during the batch. (C) The optimal feeding policy with the substrate (F) and cofactor NADH. (D) The optimal feeding policy with the MDH enzyme and its accumulation in the reactor. (E) The optimal feeding policy with the FDH enzyme and its accumulation in the reactor. Initial conditions and the control variables ranges are given in Table 1 and Table 3.

“It is to observe that, due to the above formulated optimization problem, the FBR optimal operating policy is given for each of the time-intervals (of equal length) uniformly distributed over the batch-time. It is also to underline that, as revealed by (Figure 4A) the simulated key-species concentrations time-trajectories are monotonous functions, despite their time step-wise variable addition in the FBR, thus revealing the reaction efficiency.

Such an optimal time step-wise variable feeding of the bioreactor presents advantages and inherent disadvantages. The advantages are related to the higher flexibility of the FBR operation, leading to a higher productivity in mannitol as proved in the below Section 4.2. Beside, the imposed limits of the control variables prevent excessive substrate consumption, or an excessive reactor content dilution, or violation of validity limits of the process kinetic model.

As a disadvantage, the FBR-s with such a time-variable control is more difficult to be operated compared to the simple BR, as long as the time step-wise optimal feeding policy requires different stocks of feeding substrates/cofactor/enzymes solutions of different concentrations prepared to be used over the batch. This is the price paid for achieving FBR best performances. This need to previously prepare different solutions stocks to be fed for every time-arc (that is a batch-time division in which the feeding is constant) is offset by the net higher productivity of FBR compared to those of BR as below discussed, and pointed-out in the literature [26,27,45,46,58,59]. In fact, the best operating alternative (FBR vs. BR) is related to many others economic factors (operating policy implementation costs, product cost compared to its production costs, product price fluctuation, etc.)”, not discussed here.

The present biochemical engineering numerical analysis is of an in silico type, being based on the dynamic model of the bienzymatic process and of the enzymatic reactor. Even if we have no experimental data with which to compare our optimization results, their credentials (i.e., a valid optimal operating policy for the studied FBR) are high enough, as long as the kinetic model is enough adequate, because:

(i)

The used kinetic model was built-up by Maria [36] by using the large number of experimental kinetic data sets of Slatner et al [13] (Section 2).

(ii)

The experimental program conducted by Slatner et al. [13] covers a large domain for the control variables (mentioned in Section 2).

However, if after implementing such an optimal operating policy, “significant inconsistencies are observed between the model-predicted reactor dynamics and the experimental evidence, the numerical optimization stage is applied again, after an intermediate step (between batches) necessary to off-line improve the model adequacy (by updating the model parameters)” [28].

4.2. Comparative Discussion of the Optimization Results

By analyzing the resulted optimal FBR feeding policy, and the species dynamics in the reactor bulk presented in (Figure 4A–E), several observations are to be made:

(i)

“There is a close connection between the coupling reactions, enzyme concentrations, and the supra-unitary NADH/NAD⁺ ratio over the batch (Figure 4A). This means that the two reactions are well coupled, [NADH] being higher than [NAD⁺] for most of the time, that is a NADH/NAD⁺ ratio higher than 1 most of the time, thus maintaining a process efficiency [36].

(ii)

The cofactor NADH regeneration is very efficient, the formate decomposition being quasi-complete and leading to saturation [CO₂]* = 0.0313 M (Table 1) in short time (earlier than 10 h in Figure 4A), with removal of the CO₂ excess from the system over the rest of the batch-time.”

(iii)

“As revealed by repeated simulations of Maria [36] (not presented here), the BR performances are more sensitive to [MDH] and [NADH] than to [FDH].”

(iv)

Bulk [MDH] grows continuously due to its continuous feeding (Figure 4D). By contrast, [FDH] evolution in the bulk phase is more special (Figure 4E). It grows continuously due to the continuous feeding with FDH until a certain time (10 h). After this time, [FDH] in bulk declines because its reduced feeding rate cannot compensate the reactor content dilution rate.

On the other hand, optimal FBR performances can be compared with those of the 10× repeated optimal BR, and with those of an optimized SeqBR with N_BR = 10 BR in series, as reported by Maria and Peptănaru [27] for the same process (see Section 3.6). Such a direct comparison is presented in

Table 4. Comparison of the operating alternatives [27,36] of the studied “bi-enzymatic reduction of D-fructose to mannitol with the continuous in-situ regeneration of the NADH cofactor”.

Reactor Type	F consumption (Moles/h)	M Production (M/h)	MDH Consumption (kU/L)	FDH Consumption (kU/L)	NADH Consumption (moles/h)	Remarks
Optimal BR (a,c)	0.021–0.062 (c)	0.017–0.054 (c)	1–13.88 (c)	3–10 (c)	0.002–0.010 (c)	10 BR cycles of 48 h each
Optimal SeqBR (b)	0.025–0.075 (b)	0.012–0.044 (b)	1.112	1.755	0.0025–0.0125 (b)	Series of 10 BR, 40 h run for each BR
Optimal FBR (this paper)	0.0362	0.0262	0.0882 kU/(0.5–1.2 L FBR)	0.1686 kU/(0.5–1.2 L FBR)	0.0014	Single batch of 48 h

^(a) BR with a batch time of $t_f$ = 48 h [27,36]; ^(b) optimal SeqBR with search intervals corresponding to initial load of [F]o = 1–4 M and [NADH]o = 0.1–0.5 M for every BR of the series [27]. Search intervals are [$c_{MDH,0}$; $c_{FDH,0}$] ∈ [0.1–2] kU/L. The interval corresponds to an initial load of [F]o = 1–3 M and [NADH]o = 0.1–0.5 M. All other initial loads (that is [NAD⁺]o, [HCOO]o = [F]o) are the same as those of Table 1. ^(c) The interval corresponds to an initial load of [F]o = 0.1–3 M, [NADH]o = 0.008–0.5 M; [NAD⁺]o = 0.0005 M; [HCOO]o = [F]o. Search intervals are [$c_{MDH,0}$; $c_{FDH,0}$] ∈ [0.1–2] kU/L [27,36].

. Species consumption was evaluated by using the following relationship:

$$\mathrm{species} \mathrm{consumption}={\displaystyle \sum _{j=1}^{N_{div}}{F}_{L,j}}\times {[species]}_{inlet,j}\times \Delta t$$

(3)

In the Equation (3), the resulted consumption units are the following: “moles” for j = F, NADH, and “kU” for j = MDH, FDH. The hourly consumptions in Table 4 refer to the overall batch time stipulated in the column “remarks”.

By comparatively analyzing the optimal operating policies resulted from the optimal operation of the repeated BR, FBR, and SeqBR over a significant range of initial/fed [F]o, and [NADH]o, presented in Table 4 and by Maria and Peptănaru [27], several conclusions can be derived, as follows:

(v)

As a general conclusion, the optimally operated FBR reported better performance compared to the optimal SeqBR, which, in turn, reported better performance than the repeated optimally operated BR. Thus, for a comparable mannitol (M) production: (a) the MDH enzyme consumption of FBR is much smaller, that is 10x (vs. SeqBR) and 130x (vs. BR); (b) the FDH enzyme consumption in FBR is also smaller at 9x (vs. SeqBR) and 15–50x (vs. BR); (c) the NADH consumption in FBR is smaller by 2–9x (vs. SeqBR) and 1.5–7x (vs. BR); (d) compared to the experimental (nonoptimal) BR trials of Slatner et al. [13] (within the range of [F]o = 0.1–1 M, [NADH]o = 0.25–1 mM; [NAD⁺]o = 0.0005 M; [HCOO]o = [F]o; [$c_{MDH,0}$;$c_{FDH,0}$] ∈ [0.1–2] kU/L), the optimal FBR reported much smaller enzyme consumptions, that is, 10x for MDH and 4.5x for FDH.

(vi)

As revealed by Figure 4D,E, it is not necessary to keep the enzymes feeding at a high level over the whole batch. On the contrary, an initial high addition over the first 1–2 time-arcs, followed by a continuous addition of a low level, are enough to ensure the necessary enzyme concentrations so to result in the required high reaction rates. The same observation is also valid for the NADH feeding policy.

(vii)

One of the better FBR performance costs is the final 2× dilution of the reactor content (Figure 4B). However, balancing the product dilution with the considerable savings in terms of the expensive enzymes and the regenerated cofactor, the use of FBR is worth the investment in its (model-based) offline optimal control.

(viii)

The relatively large time-arcs (of ca. 5 h) of the FBR allow an easy operation control over each time-arc, but also when switching between them.

(ix)

As proved by the present numerical analysis, “solving this engineering problem by using an experimental procedure, as tried by Slatner et al. [13], may not be the best choice because it involves high costs due to the required large number of batch tests”, even if at a small lab-scale.

(x)

In the FBR variable operating case, conversion is more difficult to interpret because the substrate is continuously added to the initial one. Due to this FBR operation particularity, the substrate consumption cannot be referred solely to its initial concentration but rather to the added substrate during the batch, following the variable concentration of Figure 4C. This is why the substrate F consumption is computed with the Equation (3) formula. In the present case, the formal conversion is high, that is: (transformed F in M)/(totally fed F) = 72.5%. The lack of substrate near total conversion is not a critical issue as long as there are lot of solutions to solve the product separations problems, that is, the use: (i) of immobilized enzymes and (ii) of efficient technologies to separate saccharides, as is well-presented in the literature [63,64,65].

5. Conclusions

“A relevant case study analyzed in this paper proves that, for the coupled multi-enzymatic systems, derivation of the multi-objective optimal operating policies (minimum enzyme/cofactor consumption, with maximum reactor productivity) for an enzymatic reactor is not a trivial engineering problem” [36,66,67,68].

Even if it is case dependent, the present model-based numerical analysis indicates that, for multienzymatic systems, the performance of an optimally operated FBR is much better in terms of enzyme and cofactor consumption (10x–130x less MDH, 5x–50x less FDH, and 7–9x less NADH) compared to the optimized repeated (cyclic) BR, or to optimal serial batch-to-batch reactors (SeqBR) from the same multiobjective perspective. The optimized FBR also presents much better performance compared to the experimental BR’s large number of costly and exhaustive trials, as performed by Slatner et al. [13], to obtain a high fructose conversion.

The use of an adequate process model can offer an approximate, if not exact, solution to the reactor multiobjective optimization problem with a moderate computational effort. Such an in silico engineering approach allows saving considerable experimental effort at the expense of a computationally intensive step.

The numerical methodology presented here can be repeated with any supplementary problems if the kinetic models for enzymatic inactivation are available. The same rule can also be applied to derive multiobjective operating policies to other enzymatic reactor types (BRP, FXBR, MA(S)CR, [28]) with free or immobilized enzymes by using suitable reactor dynamic models.

This numerical analysis can also be extended to the cases where the control variables are not deterministic (as here) but which present a random (known) distribution centered on the set point (see [26] for an example).