Description of a Dynamical Framework to Analyse the Helicopter Tail Rotor
Abstract
:1. Introduction
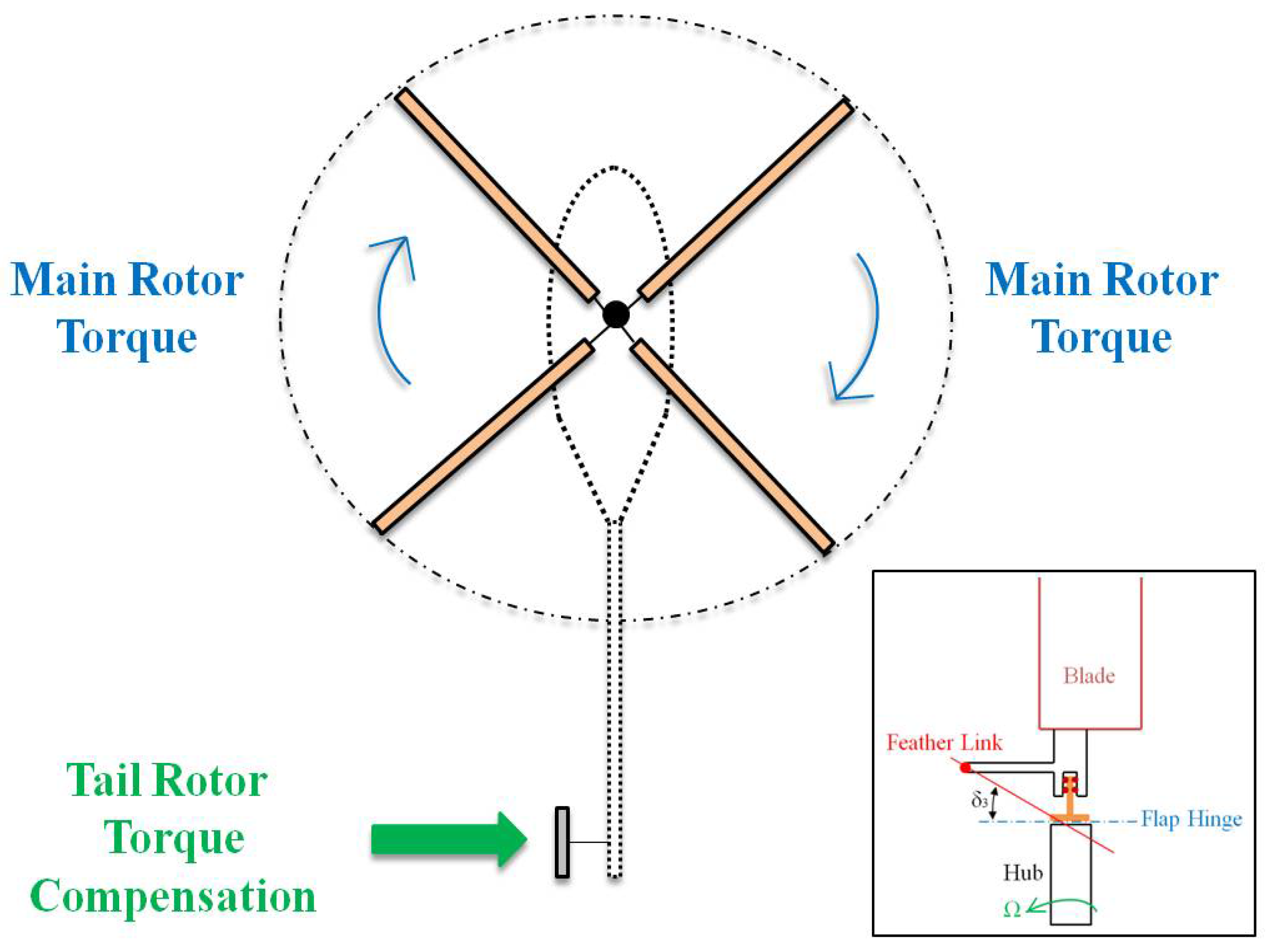
2. Tail Rotor Dynamics
3. Modelling
3.1. General Structure of the Helicopter
3.2. Features of the Modelling Tool
4. Results: Helicopter Model Response
4.1. Response of the Tail Rotor Feather Angle
4.2. Response of the Tail Rotor Flap Motion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zaw, M.T.; Tun, H.M.; Naing, Z.M. Development of mathematical model and stability analysis for UAH. Int. J. Sci. Res. Publ. 2014, 4, 686–695. [Google Scholar]
- Beaulieu, M.N.; Botez, R.M. Simulation and prediction of main rotor, tail rotor, and engine parameters from flight tests. Proc. IMechE Part G J. Aerosp. Eng. 2008, 222, 817–834. [Google Scholar] [CrossRef]
- Available online: https://www.3ds.com/products-services/simulia/products/simpack/ (accessed on 30 June 2021).
- Rezaeian, A. Helicopter ground resonance analysis using multibody dynamics. In Proceedings of the ERF 2010-36th European Rotorcraft Forum, Paris, France, 7–9 September 2010. [Google Scholar]
- Yavrucuk, I.; Tarimci, O.; Katircioglu, M.; Kubali, E.; Yilmaz, D.C. A new helicopter simulation and analysis tool: Helidyn+. In Proceedings of the Thirty-Sixth European Rotorcraft Forum, Paris, France, 7–9 September 2010. [Google Scholar]
- Thanapalan, K.K.T. Modelling of a helicopter system. In Proceedings of the 1st Virtual Control Conference, Aalborg University, Aalborg, Denmark, 1 September 2010. [Google Scholar]
- Chierichetti, M.; McColl, C.; Ruzzene, M. Prediction of UH-60A blade loads: Insight on load confluence algorithm. AIAA J. 2014, 52, 2007–2018. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Bottasso, C.L.; Nikishkov, Y.G. Modeling rotorcraft dynamics with finite element multibody procedures. Math. Comput. Model. 2001, 33, 1113–1137. [Google Scholar] [CrossRef]
- Peters, D.A.; Karunamoorthy, S.; Cao, W.M. Finite state induced flow models. Part I: Two-dimensional thin airfoil. J. Aircr. 1995, 32, 313–322. [Google Scholar] [CrossRef]
- Peters, D.A.; He, C.J. Finite state induced flow models. Part II: Three-dimensional rotor dis. J. Aircr. 1995, 32, 323–333. [Google Scholar] [CrossRef]
- Masarati, P. Computed torque control of redundant manipulators using general-purpose software in real-time. Multibody Syst. Dyn. 2014, 32, 403–428. [Google Scholar] [CrossRef]
- Castillo-Rivera, S.; Tomas-Rodriguez, M. Helicopter nonlinear aerodynamics modelling using vehiclesim. Adv. Eng. Softw. 2016, 100, 252–265. [Google Scholar] [CrossRef]
- Zupancic, B.; Sodja, A. Advanced multi-domain modelling: Advantages and dangers. In Proceedings of the UKSim 13th International Conference on Modelling and Simulation, Cambridge, UK, 30 March–1 April 2011; Available online: https://ieeexplore.ieee.org/document/5754245 (accessed on 13 September 2021).
- Bertogalli, V.; Bittanti, S.; Lovera, M. Simulation and identification of helicopter rotor dynamics using a general-purpose multibody code. J. Frankl. Inst. 1999, 336, 783–797. [Google Scholar] [CrossRef]
- Stanislawski, J. Simulation investigation of tail rotor behavior in directional maneuver of helicopter. Trans. Inst. Aviat. 2008, 193, 32–80. [Google Scholar]
- O’Rourke, M.J. Simulation model for tail rotor failure. J. Aircr. 1994, 31, 197–205. [Google Scholar] [CrossRef]
- Rajendran, S.; Gu, D. Fault tolerant control of a small helicopter with tail rotor failures in forward flight. In Proceedings of the 19th World Congress of the International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Guivarch, D.; Mermoz, E.; Marino, Y.; Sartor, M. A new modeling framework to predict helicopter dynamic systems loads. In Proceedings of the 74th Annual Vertical Flight Society Forum and Technology Display 2018 (FORUM 74), Phoenix, AZ, USA, 14–17 May 2018; ISBN 978-1-5108-6329-3. [Google Scholar]
- Available online: https://www.carsim.com/ (accessed on 30 June 2021).
- Chen, R.T.N. Flap-Lag Equations of Motion of Rigid, Articulated Rotor Blades with Three Hinge Sequences. NASA Technical Memorandum 100023, 1987. Available online: https://catalogue.nla.gov.au/Record/4019811 (accessed on 13 September 2021).
- Castillo-Rivera, S.; Tomas-Rodriguez, M. Helicopter flap/lag energy exchange study. Nonlinear Dyn. 2017, 88, 2933–2946. [Google Scholar] [CrossRef] [Green Version]
- Kada, B. Helicopter nonlinear dynamics modeling for motion simulation and real-time control. In Proceedings of the 10th International Conference on Advances in Engineering and Technology (AET-18), Kuala Lumpur, Malaysia, 8–9 January 2018. [Google Scholar]
- Aviation School Online. The Power of the Power Curve. Available online: https://www.aviationschoolsonline.com/ (accessed on 30 June 2021).
- Lawrence, B.; Berger, T.; Tischler, M.B. Integrating flight dynamics & control analysis and simulation in rotorcraft conceptual design. In Proceedings of the American Helicopter Society 72nd Annual Forum, West Palm Beach, FL, USA, 17–19 May 2016. [Google Scholar]
- Johnson, W. Helicopter Theory; Princeton University Press: Princeton, NJ, USA, 1980. [Google Scholar]
- Watkinson, J. The Art of the Helicopter; Elsevier Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Padfield, G.D. Helicopter Flight Dynamics: The Theory and Application of Flying Qualities and Simulation Modelling; Blackwell Publishing: Hoboken, NJ, USA, 2007. [Google Scholar]
- Newman, S. The Foundations of Helicopter Flight; Edward Arnold: London, UK, 1994. [Google Scholar]
- Castillo-Rivera, S.; Tomas-Rodriguez, M. Rotorcraft fuselage/main rotor coupling dynamics modelling and analysis. Int. J. Nonlinear Sci. Numer. Simul. 2021, 22, 317–340. [Google Scholar] [CrossRef]
- Tomas-Rodriguez, M.; Sharp, R. Automated modelling of rotorcraft dynamics with special reference to autosim. In Proceedings of the 3rd Annual IEEE Conference on Automation Science and Engineering, Scottsdale, AZ, USA, 22–25 September 2007. [Google Scholar]
- Fletcher, T.M.; Brown, R.E. Helicopter tail rotor thrust and main rotor wake coupling in crosswind flight. J. Aircr. 2010, 47, 2136–2148. [Google Scholar] [CrossRef] [Green Version]
- Castillo-Rivera, S. Advanced Modelling of Helicopter Nonlinear Dynamics and Aerodynamics. Ph.D. Thesis, City University London, London, UK, 2014. [Google Scholar]


| Parameters | Magnitude | Units |
|---|---|---|
| Helicopter mass | 2200 | kg |
| Tail rotor blade mass | 6.21 | kg |
| Fuselage-tail rotor longitudinal distance | 6.00 | m |
| Fuselage-tail rotor vertical distance | 1.72 | m |
| Delta-three angle | −0.785 | rad |
| Main rotor angular speed | 44.40 | rad/s |
| Tail rotor gearing | 5.25 | - |
| Case | Collective Feather (Rad) | Collective Feather Change (Rad) |
|---|---|---|
| 1 | 0.24 | 0.18 |
| 2 | 0.21 | 0.17 |
| 3 | 0.26 | 0.23 |
| Case | Theoretical Maximum Disc Tilt (Degrees) | VS Maximum Disc Tilt (Degrees) |
|---|---|---|
| 1 | 1.00 | 1.07 |
| 2 | 3.00 | 2.64 |
| 3 | 5.00 | 5.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo-Rivera, S.; Tomas-Rodriguez, M. Description of a Dynamical Framework to Analyse the Helicopter Tail Rotor. Dynamics 2021, 1, 171-180. https://doi.org/10.3390/dynamics1020010
Castillo-Rivera S, Tomas-Rodriguez M. Description of a Dynamical Framework to Analyse the Helicopter Tail Rotor. Dynamics. 2021; 1(2):171-180. https://doi.org/10.3390/dynamics1020010
Chicago/Turabian StyleCastillo-Rivera, Salvador, and Maria Tomas-Rodriguez. 2021. "Description of a Dynamical Framework to Analyse the Helicopter Tail Rotor" Dynamics 1, no. 2: 171-180. https://doi.org/10.3390/dynamics1020010
APA StyleCastillo-Rivera, S., & Tomas-Rodriguez, M. (2021). Description of a Dynamical Framework to Analyse the Helicopter Tail Rotor. Dynamics, 1(2), 171-180. https://doi.org/10.3390/dynamics1020010






