1. Introduction
An AAA is an enlargement of the abdominal aorta, such that the diameter is more than 3 cm or 50% larger than its healthy, baseline value. Accurate monitoring, diagnostics, and timely intervention are crucial for preventing the high morbidity and mortality rates associated with such pathology. EVAR treatment represents the gold standard when the aortic anatomy is feasible, and its planning is, in fact, fundamental for technical success and endograft durability.
The cardiovascular community has proposed guidelines to streamline the surgery decision-making process and planning of abdominal aortic aneurysms. One such approach, proposed by Ouriel et al. [
1], is based on a threshold-based method using maximum diameter measurements. The suggested threshold values are 55 mm for men and 50 mm for women. However, this approach has proven to be unreliable in predicting abdominal aortic aneurysm ruptures, as indicated by subsequent studies. In fact, Finol et al. [
2] showed how the rupture risk does not linearly depend on the maximum diameter. To improve decision-making criteria, El Chaikoff et al. [
3] introduced more complex methods for rupture risk assessment, moving beyond purely geometrical, threshold-based approaches. Additionally, Parkinson et al. [
4] demonstrated that the rupture rate for abdominal aortic aneurysms ranging from 40 mm to 49 mm, though low, was still significant. Similarly, Darling et al. [
5] reported that 23% of abdominal aortic aneurysms ruptured at sizes under 50 mm. Over the past decade, DL techniques have been vastly employed in the semantic segmentation of the aortic lumen in EVAR planning. Lately, Fantazzini et al. [
6] have contributed to the segmentation task by training single- and multi-view U-Net models for aortic lumen semantic segmentation on 70 CTAs. However, the need for more widely distributed datasets is crucial, as the network is trained on a limited spectrum of abdominal aortic aneurysm anatomical features. An extension of previous work by the same research group proposed a novel model for the automatic segmentation and geometrical analysis of abdominal aortic aneurysms, along with the identification of intraluminal thrombus presence, as presented in Brutti et al. [
7]. The model’s clinical validation involved a comparison between network measurements and those made by expert users. In another study by Adam et al. [
8], fully automated routine presurgical measurements of the axial aortic lumen and outer-to-outer aortic wall diameter for endovascular aortic repair were proposed. The authors trained a V-Net [
9] in large datasets consisting of 489 and 62 CTA sets for training and testing, respectively. The results showed mean Dice–Sørensen coefficients of 0.95 for diseased abdominal aortas and 0.84 for healthy aortas, indicating reliable performance. However, both studies acknowledged the necessity of including vastly different abdominal aortic aneurysm topologies in the training and validation sets to improve the model’s consistency and stability. Lastly, Lopez-Linares et al. [
10] similarly proposed a work in which a fully automatic segmentation pipeline is adopted for a thrombus and an aortic lumen for postoperative CTAs. A convolutional neural network was trained on postoperative CTA images to automatically segment the aortic lumen and thrombus after EVAR. The absence of any required input makes the model very suitable for the interoperability and replicability of the results. A mean Dice–Sørensen coefficient of 0.83 is obtained. Although the results fit with the ones provided by the state of the art, such an approach does not clinically validate the model. Aortic measurements are, in fact, crucial to assessing how well the network does approximate 3D surface reconstruction.
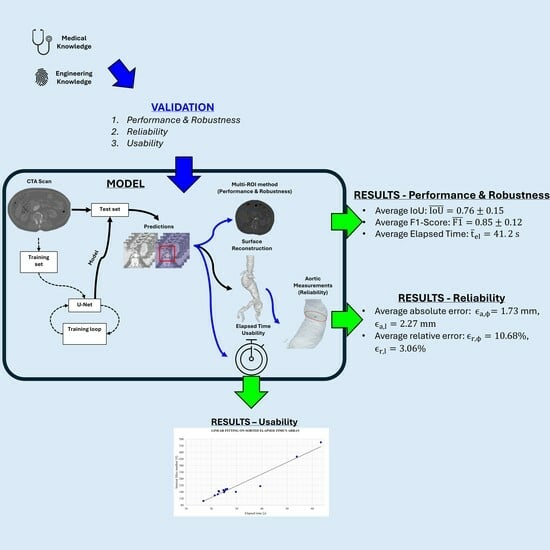
The purpose of this study is to validate a 3D reconstruction methodology for the abdominal aortic vessel. Its application will not be solely limited to EVAR planning; it also serves as an initial step in the development of an automatic patient-specific CFD workflow with the goal of future works aiming to assess the aortic wall’s rupture risk. This first step is to obtain an anatomically accurate 3D model of the reconstructed aorta. By addressing the segmentation performance, robustness, and clinical reliability of the pipeline on several anatomies, the model’s usability and clinical consistency are assessed. The employment of such a mono-input 3D surface generation algorithm in complex hemodynamic solvers will enhance the quantitative CFD analysis of the aneurysmatic blood flow. To accomplish this, obtaining quality meshes is key in terms of the numerical stability and accuracy of the solution. The DL approach will help users in obtaining anatomically correct 3D models, which will be used for EVAR planning and patient-specific hemodynamic digital analysis.
2. Materials and Methods
2.1. Study Design
This study evaluates the performance, replicability and usability of a DL-based aortic lumen reconstruction and measurement pipeline, which is crucial when planning safety-critical tasks like abdominal aortic aneurysm EVAR. The goal is to develop and validate a robust single-class model that is capable of accurately detecting specific aorto-iliac anatomies. Four key characteristics—segmentation performance, robustness, reliability, and usability—are assessed based on [
11,
12].
Segmentation performances are evaluated by means of intersection over union and F1-score metrics; the former evaluates more accurately bad classification instances, and they, respectively, reflect the worst and average performance of the network among each test set anatomy.
Robustness is tested on input ROI translation along absolute and partial cardinal directions. By predicting multiple input instances, the network’s behavior is observed so as to assess segmentation metrics sensitivity with respect to input perturbations.
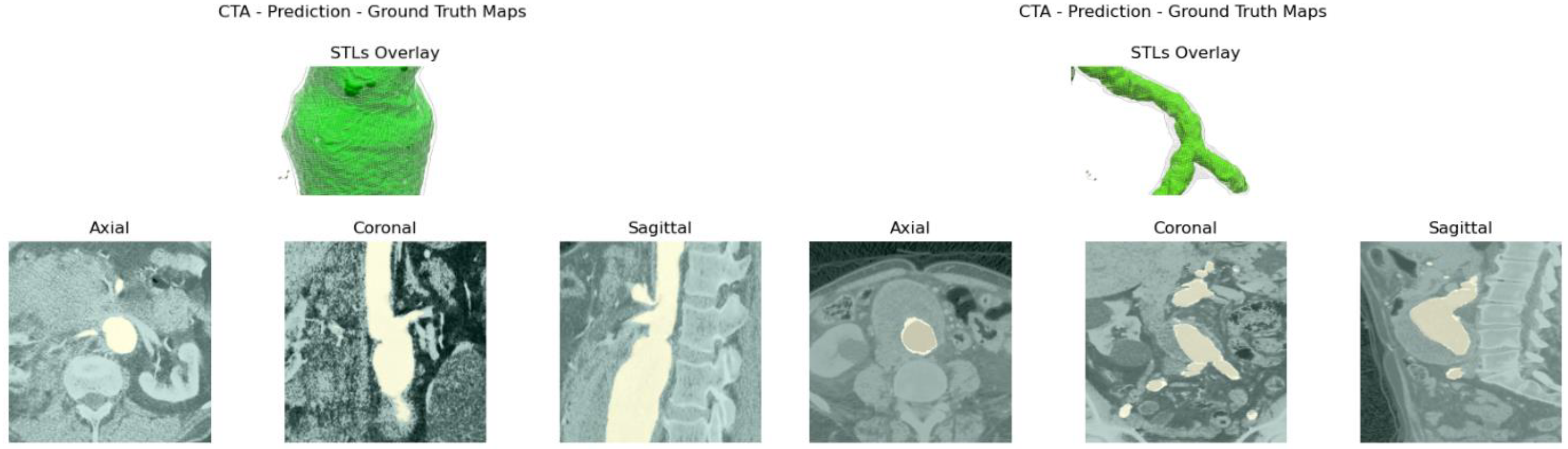
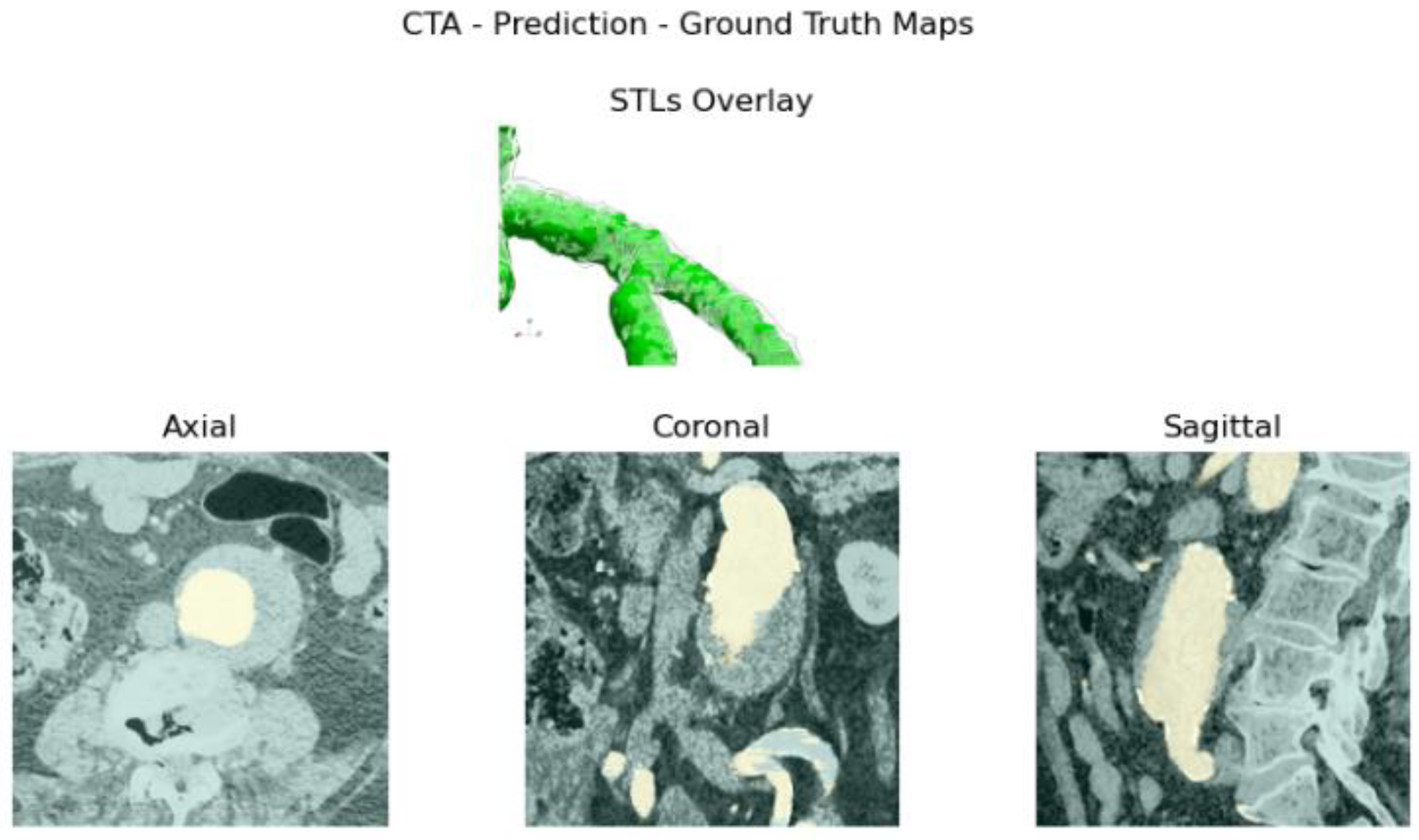
Reliability is validated by comparing manual measurements, performed by a vascular surgeon, on 3D reconstructions computed by the model, together with the ones obtained with reference software. Usability is evaluated based on input requirements and elapsed time.
The methodology workflow is schematized in
Figure 1. From the original CTA image and its relative mask, the original–GT image couples are extracted by a Python (v. 3.11.6) script. Masks and GT are obtained from widely known reference software ITK-Snap, (v. 4.0.2) [
13] (ITK-SNAP Home,
itksnap.org). Once the dataset is built, the network is trained. At testing time, the raw prediction’s output stack is processed to obtain the reconstructed aortic lumen’s surface and test metrics, following the performance, robustness, reliability, and usability assessments cited above.
Several tools are exploited by the model and the evaluation algorithm. Images are semi-automatically processed with ITK-Snap and Python [
14]. The network is implemented using the Pytorch framework. Centerlines are obtained with the VMTK [
15] toolkit. Measurements are performed manually on the widely known post-processing toolkit Paraview [
16]. It must be underlined that all segmentations are performed exclusively using a CPU device to assess the algorithm performance in the most general usage context. The user is provided with a graphics user interface to perform CTA slicing, prediction, centerline extraction and 3D reconstructions.
2.2. Data Acquisition and GT Extraction
In this study, training, evaluation, and test data were provided by a single sanitary structure of the Lombardia region in anonymous form. The following diagnostic devices are used to collect imaging data: General Electric’s LightSpeed16 Rad (Cincinnati, OH, USA), Philip’s (Amsterdam, Netherlands) iCT SP, Ingenuity CT, and Brilliance 16. The spatial resolution ranges from 0.779 mm to 0.977 in the x and y directions. Axial slices are extracted by slicing the DICOM volume of interest. The data pool is composed of axial CTA and includes aneurysmatic patients with a mean age of 75.6 ± 7.67. The data pool consists of 114,141 images split into training, validation and testing with an 80%–15%–5% distribution.
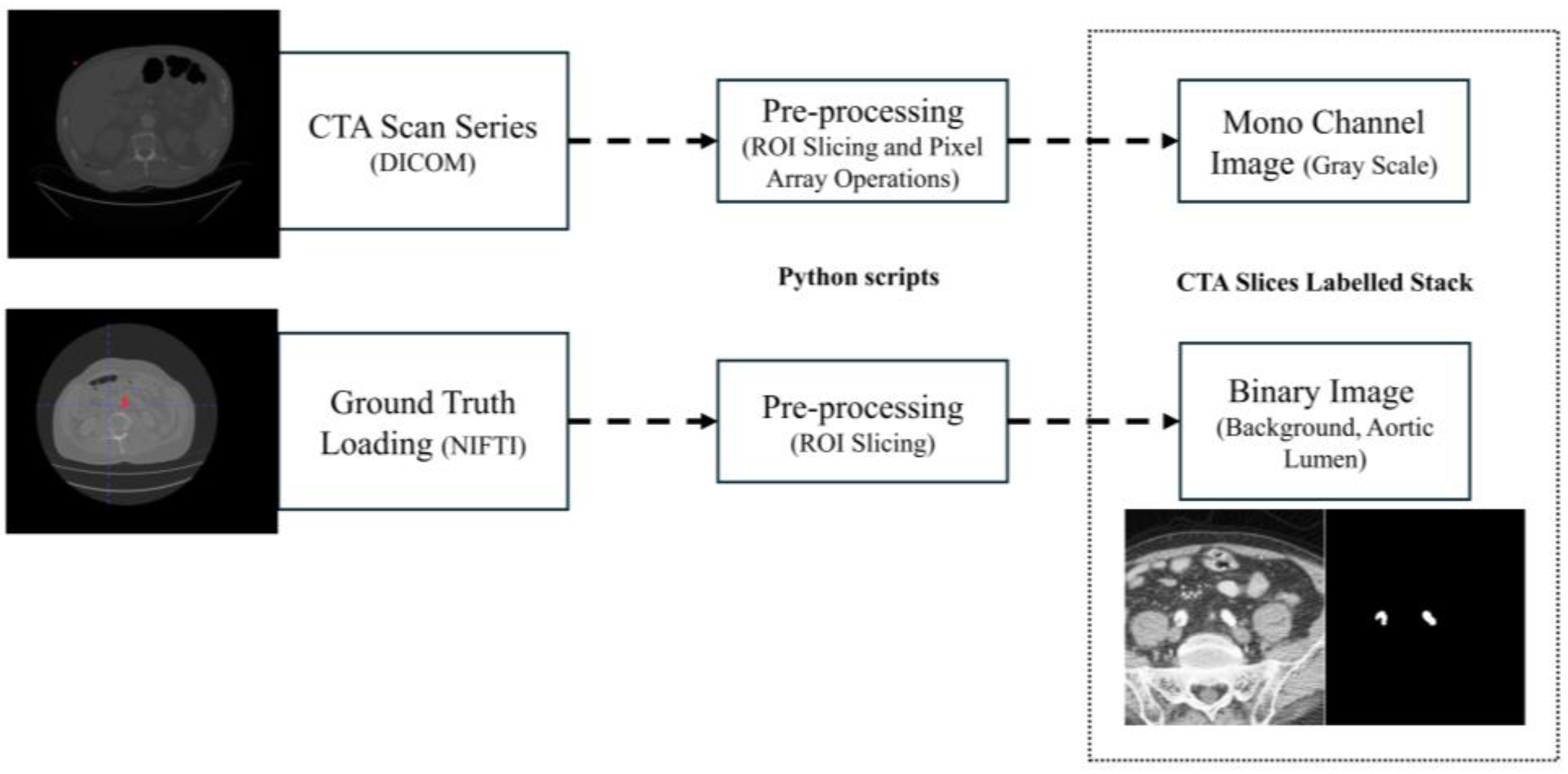
GT extraction is performed using ITK-Snap’s thresholding semi-automatic active contouring and a custom Python script to generate input and target images. ITK-snap (v. 4.0.2) is the chosen reference labeling software for its wide consensus across the biomedical engineering community. The interest area includes the abdominal section, ranging from common iliac arteries to the celiac trunk. Upper and lower threshold values are selected to isolate CTA’s contrast medium in the abdominal aortic region. Usually, this process takes some parameter tuning, repeating the labeling multiple times. Despite this, its low characteristic operative time and simple active contouring based semi-automatic segmentation guarantee a reasonable amount of time effort by the trained personnel. The engineering team has been trained in the aortic lumen labeling task under the supervision of a vascular surgeon.
The Python script extracts the input CTA and GT, respectively, starting from the DICOM series pixel array and NIFTI (Neuroimaging Informatics Technology Initiative) GT array proxy files, the latter obtained from ITK-Snap labeling method. Then, images and GT volumes are cropped along the ROI. Finally, histogram equalization is applied to the original images. The output of the script is a stack of mono-channel gray CTA images and a stack of mono-channel binary GT images. The extraction algorithm is schematized in
Figure 2. The target patient’s CTA and GT NIFTI file is loaded into the Python script following DICOM Series attributes [
17], such as Image Position Patient, Pixel Spacing, Slice Thickness and Spacing Between Slices, to sort and extract angiography series. The algorithm now pre-processes GT and CTA slice images input volumes, proceeding as shown below:
- 1.
ROI extraction: Once loaded, ROI slicing is performed, extracting the inner volume from the DICOM pixel array and NIFTI array proxies with dimension.
- 2.
Pre-processing: The sorted and cropped three-dimensional image volume is equalized. Original images and GT stacks are then stored into an anonymized folder in image format.
2.3. Model Architecture
The architecture of choice is a 2D U-Net [
18] for axial CTA images segmentation, as one of the most popular architectures used for the semantic segmentation of CTA images, which is suitable for a proof of concept. The input is a gray image with shape
,
with
and
. The output is a raw logits tensor with shape
,
with
. During training, which takes place from scratch, a binary stochastic gradient descent optimizer with an initial learning rate of 0.001 is used. Binary cross-entropy on logits loss is the model’s criterion of choice. Moreover, a learning rate scheduler is adopted to reduce the learning rate value when loss plateauing occurs with a decay factor 0.5. A manually tuned static binarization threshold is used. Image augmentation is performed by applying horizontal and vertical random flips, color jittering, and center cropping. Such a choice is given to provide the network with more flexibility when predicting on different image orientations and intensity spectra. Zoom factors are considered as performing center cropping.
The algorithm converged after 87 epochs, imposing 0.0001 as convergence criteria and four epochs as patience. To achieve the best-performing model, several trainings are launched on different hyperparameter sets and dataset distributions. The best-performing model is selected based on IoU and F1 metrics and AOC value at the testing time.
2.4. Test Dataset Description
The developed test and training sets’ inclusion criteria aim to the prioritization of (i) pathologic vessels affected by abdominal aortic aneurysm, (ii) complex anatomies such as tortuous and asymmetric vessels, (iii) large abdominal aortic aneurysms with a diameter greater than 5 cm, (iv) other major aorto-iliac pathologies, and (v) data coming from different diagnostic equipment: General Electrics’ BrightSpeed, Philips’ Optima CT660, and Siemens’ Definition Edge. Patients with aortic dissection and thoracic aneurysms were not included in either of the sets. Two women and twelve men were in the test set; the mean age was . All participants included had an aneurysmatic aorta.
Each training, the evaluation and test CTA scan in the dataset were anonymized. Due to the retrospective nature of such a study and the anonymization of source data, the ethical committee did not retain necessary an ethical approval; sensible data and information were neither included nor published.
In this study, only pathologic vessels are segmented, subdividing them first into A and AC. The descriptor A indicates an aneurysmatic aorta in one or more sections/branches, e.g., iliac aneurysm, whilst AC accounts for anatomically complex pathologic vessels related to other significant complications such as stenosis, occlusion, and penetrating arteriosclerotic ulcers. To further characterize test set anatomies, two properties are set for each patients’ vessel by means of the following qualitative vessel’s properties: (i) aneurysm location and (ii) other significant pathologies. Lastly, to accurately investigate the network’s performance on feature recognition of high-interest sections, aneurysm and other pathologies’ locations are introduced as characterizing anatomical properties. In
Table 1, the aforementioned classification and description of the test set’s anatomies is reported.
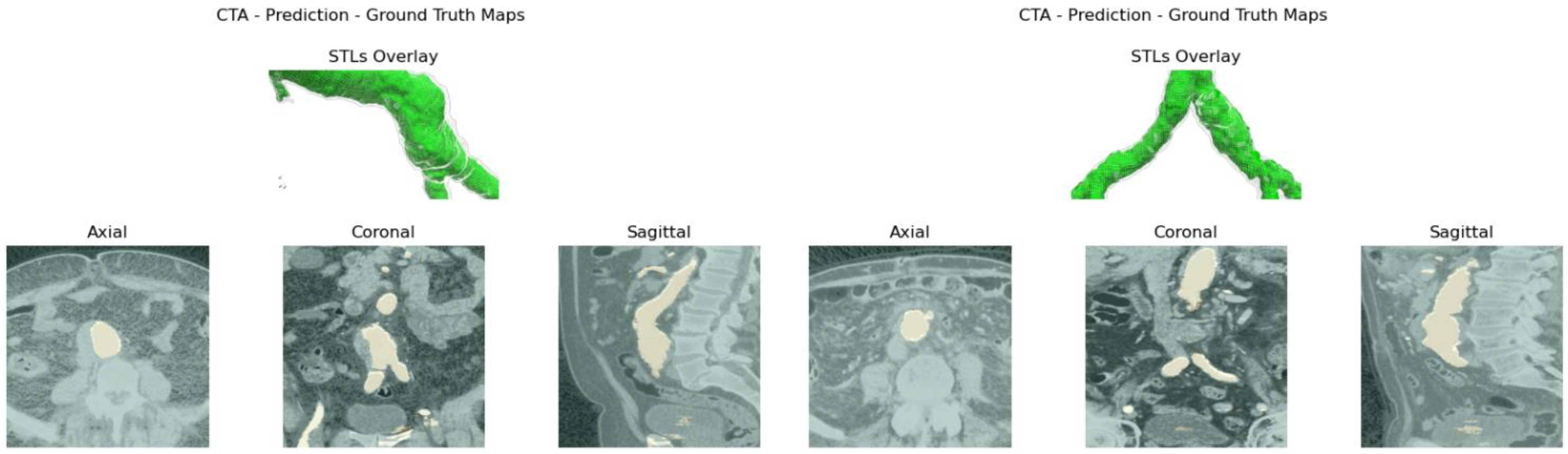
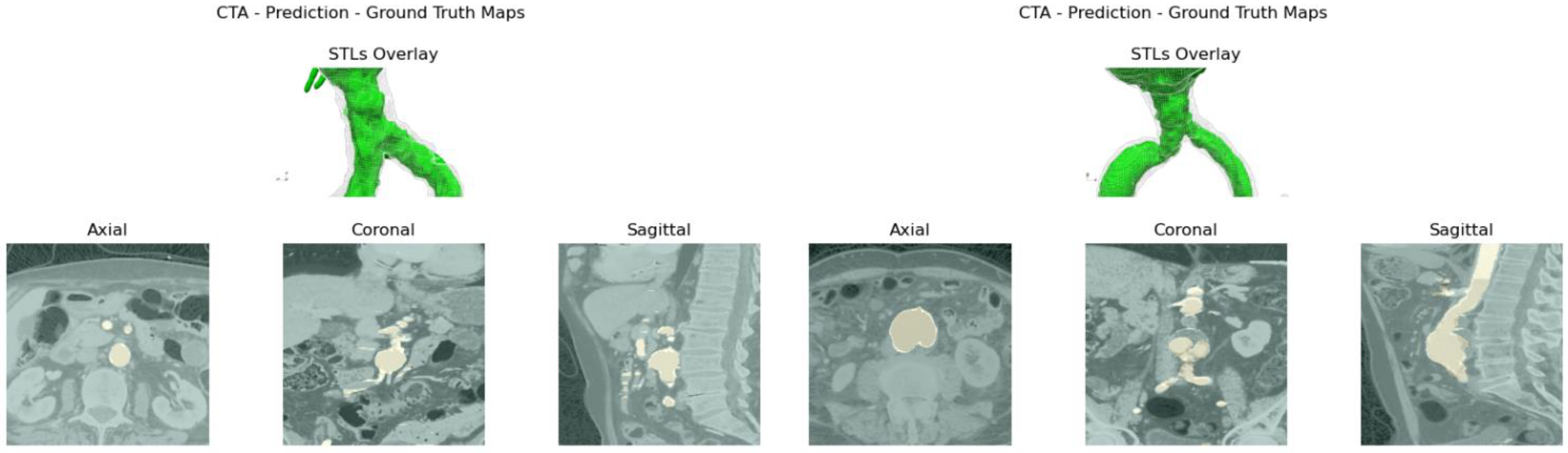
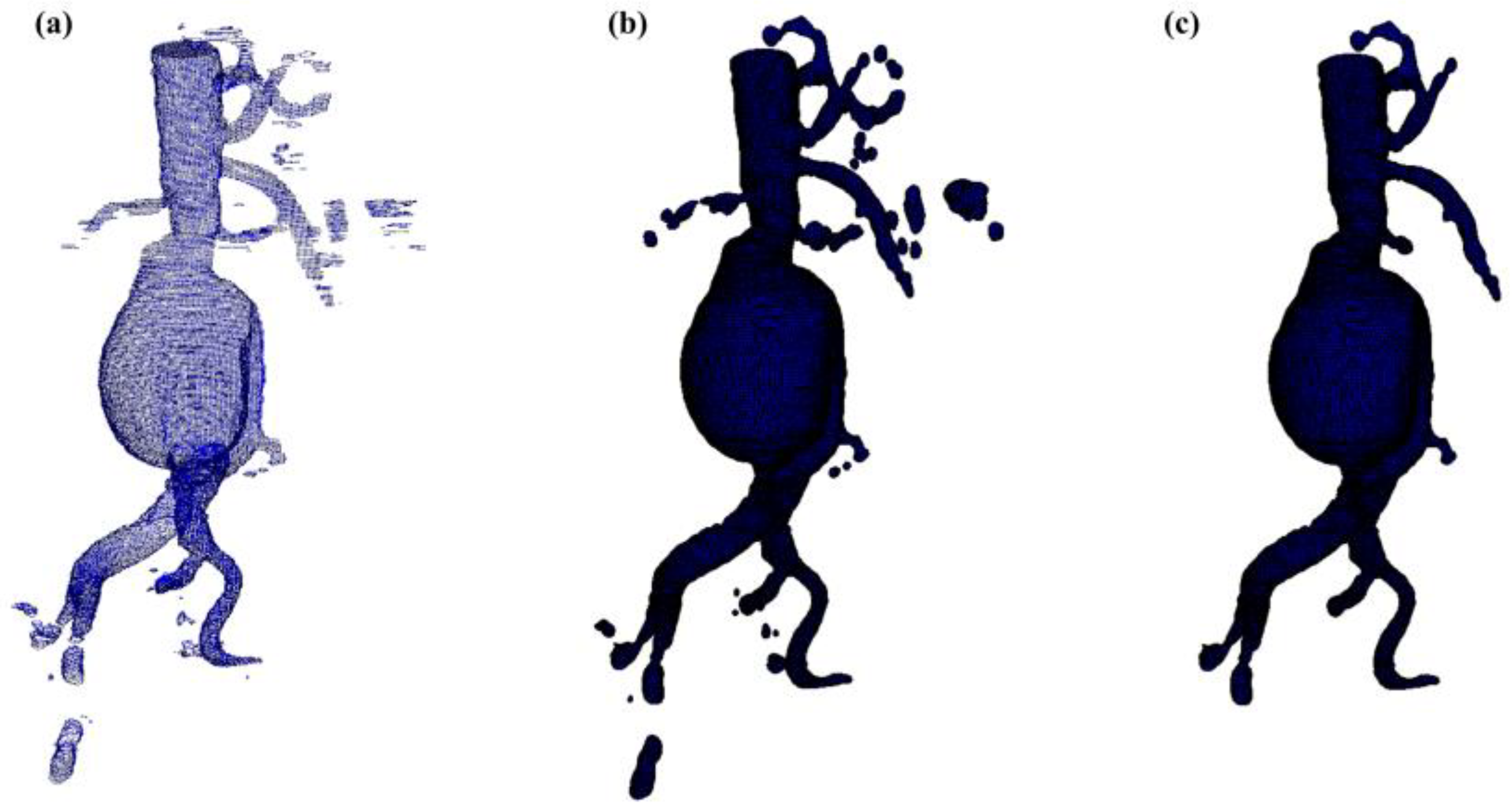
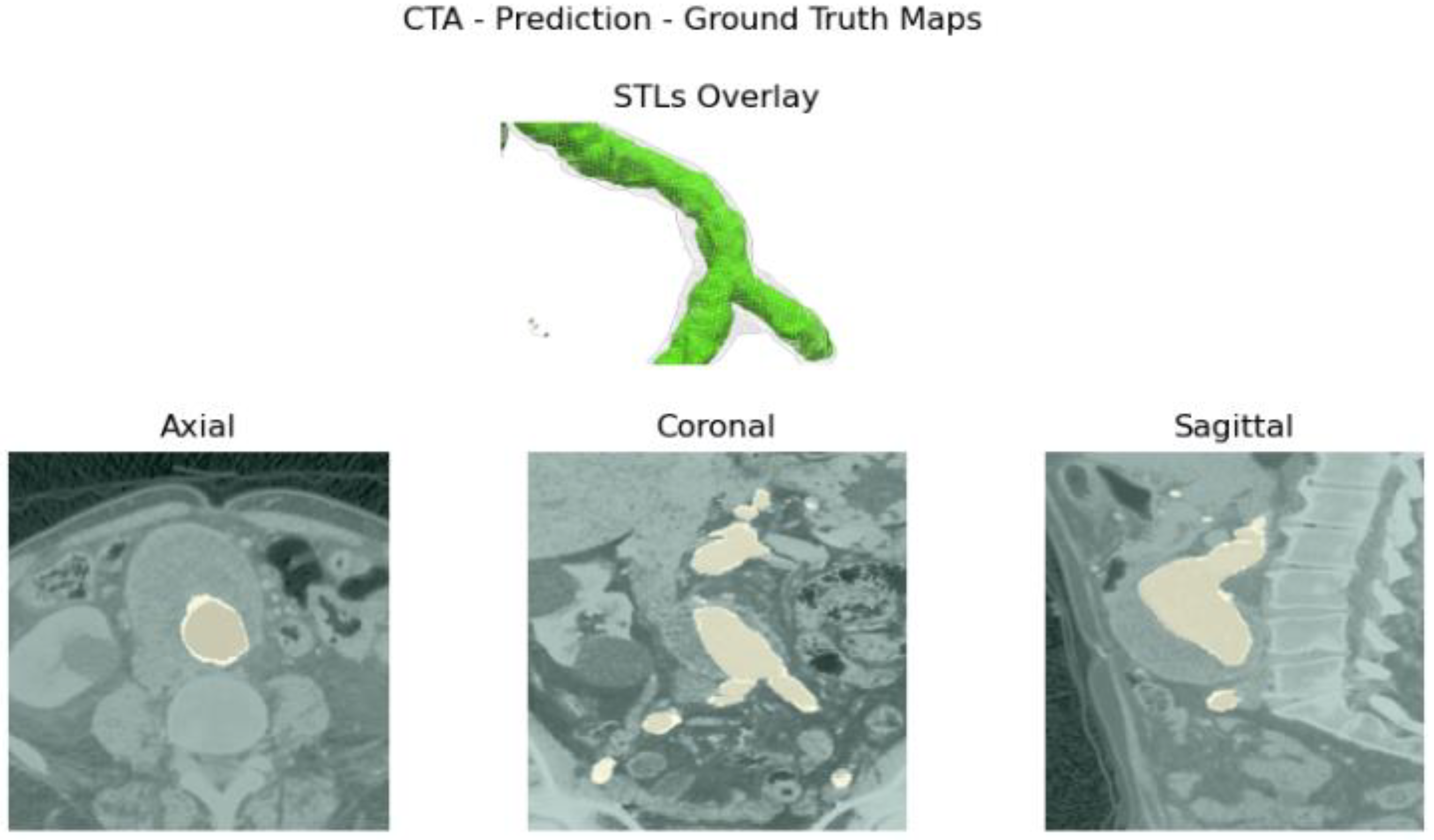
2.5. Surface Generation Algorithm
Aortic lumen 3D surface reconstruction is obtained from raw predictions using the following method: firstly, the point cloud is extracted from the predicted volume. Secondly, each axial closed contour is computed alongside its centroid. Vertex normal vectors are computed, guaranteeing correct orientation of the surface curvature, inwardly to the aortic lumen’s centerline inner point. This is mandatory to prevent holes and non-manifold, unclosed surfaces. Proceeding from bottom to top, point cloud normal are computed for each axial section of the cloud following the Python pseudo-code below:
- 1.
Axial single contour
coordinates matrix
extraction with marching squares algorithm [
19] from U-Net predictions. With
the column vector contains, respectively, the x, y and z coordinates of each single contour’s point. Each contour belonging to an axial section is characterized by the same z coordinate.
- 2.
Axial contour centroid extraction .
- 3.
Normal computation for each point of the contour on each section of the point cloud.
:
#Bottom patches
#Top patches
#Wall patches
,
with
A 3D triangulated aortic lumen surface is obtained using a screened Poisson surface reconstruction algorithm [
20]. The obtained mesh is then automatically cleaned from any spurious and/or disconnected components. The algorithm is visually represented in
Figure 3.
2.6. Model Evaluation
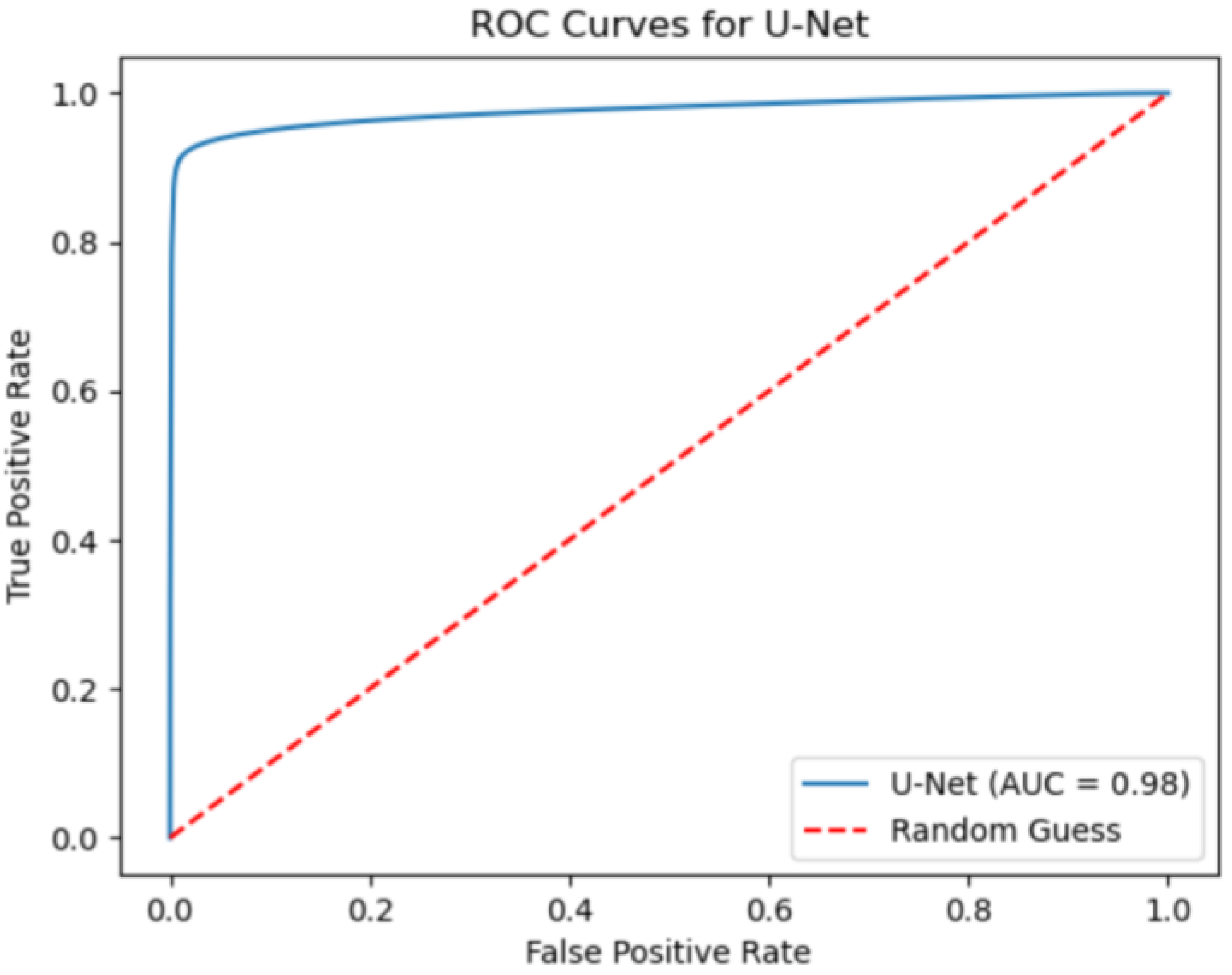
Segmentation performance is evaluated by means of IoU and F1-score metrics. Each metric is computed with its mean value and standard deviation along the total slice number. Moreover, the AOC, ROC, confusion matrix, precision and recall are also evaluated over the test set.
Robustness is assessed by perturbating the region of interest as input only. For each test CTA, the aortic lumen on nine different ROIs is predicted—one for each absolute or partial cardinal direction: C, N, S, W, E, NW, NE, SW, and SE. Each ROI volume is extracted following a fixed rule which imposes a positive or negative variation in the ROI’s origin’s coordinates. The magnitude of such a perturbation corresponds to the α = 12.5% of the ROI axial shape. To evaluate such an incremental value in pixels, one can simply perform the following:
, where
is the ROI’s edge dimensions in pixels. For example, the coordinates of the ROI’s center for the north (N) direction can be expressed by the following:
, where
and
are the axial section of the volume of interest’s center. It has to be underlined that the absolute origin of a single axial section is the upper left corner of the image with a positive x direction from left to right and positive y direction from top to bottom. To correctly analyze how perturbing the input ROI influences predictions’ anatomical coherence from one orientation to another proceeding slice-wise, the IoU, F1-score average and standard deviation values between predictions for the perturbed ROI along a generic direction and its relative GT are computed. The IoU and F1-score are defined as follows in Equations (1) and (2):
where
are, respectively, the true positives, false positives, and false negatives.
and
are, respectively, the output of the network and GT tensors. Moreover, for each patient and each ROI orientation, the global metrics’ average and standard deviation value are computed. The global average over each patient and each predicted volume obtained with ROI perturbations is also computed, following Equation (3).
where
is the average generic metric (F1 or IoU),
is the total number of test patients,
is the total number of slices for test patient
,
is the value of the generic metric at slice number
and orientation
for patient
, and
is the total number of direction for the input ROI perturbations.
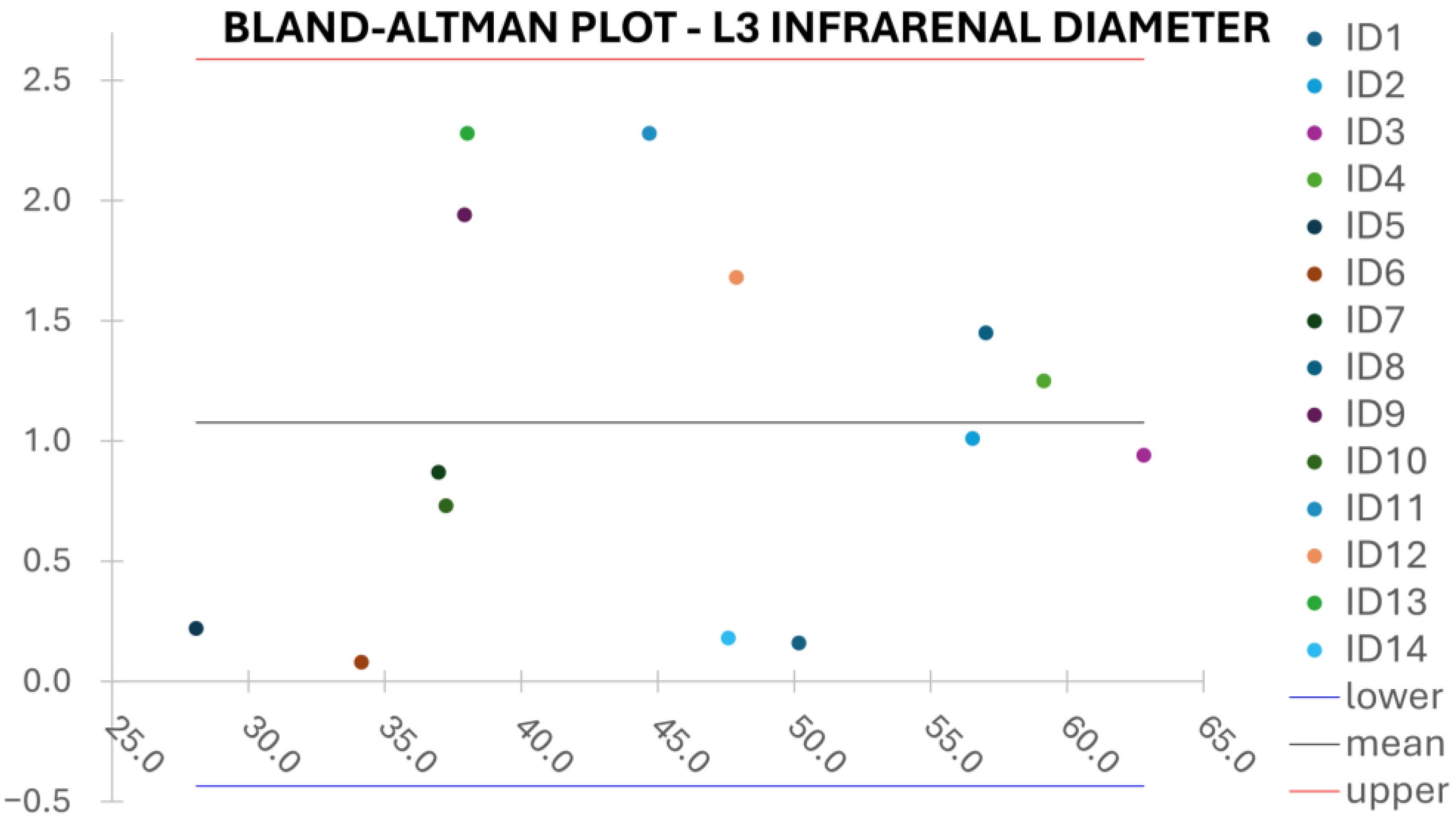
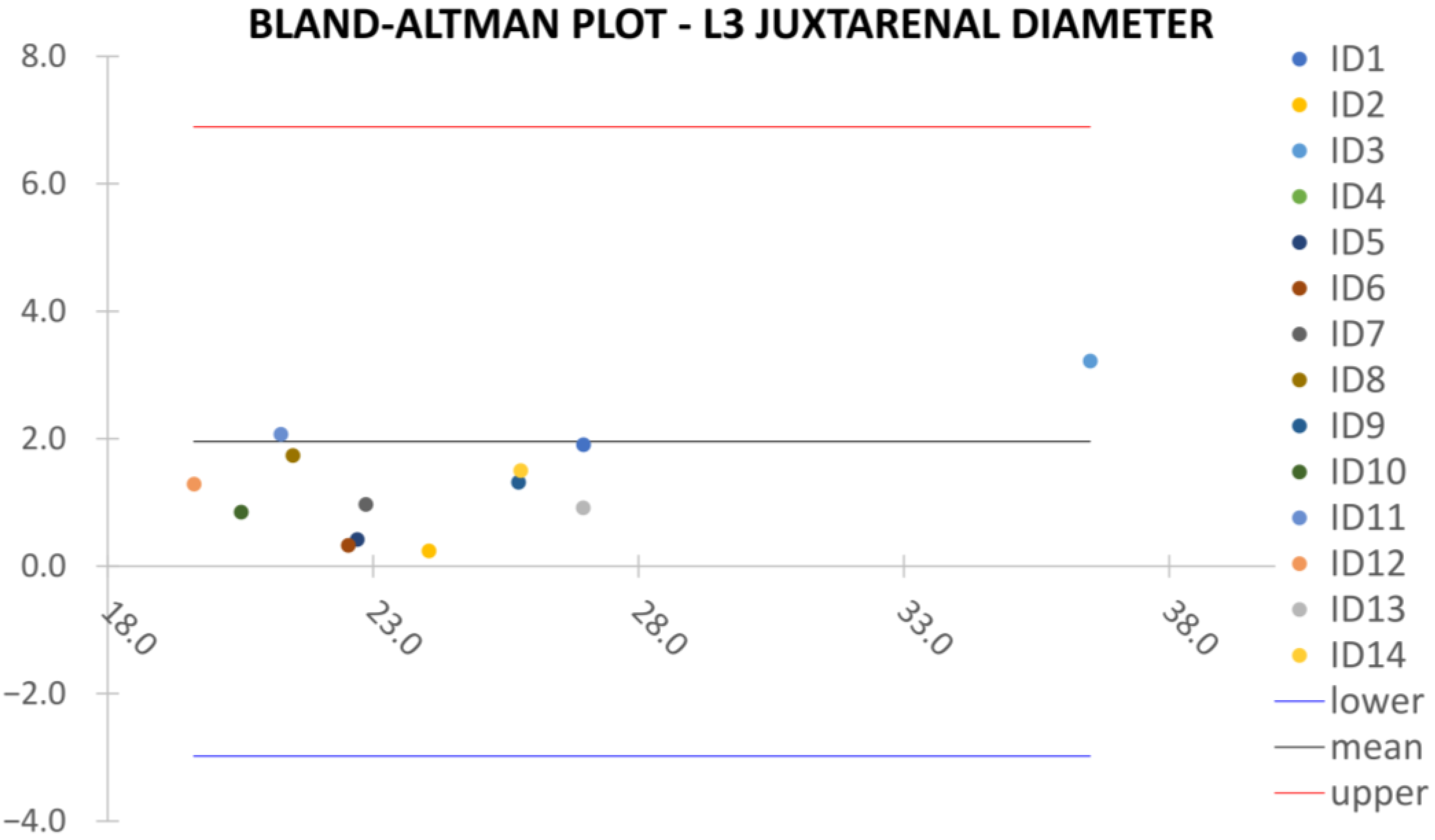
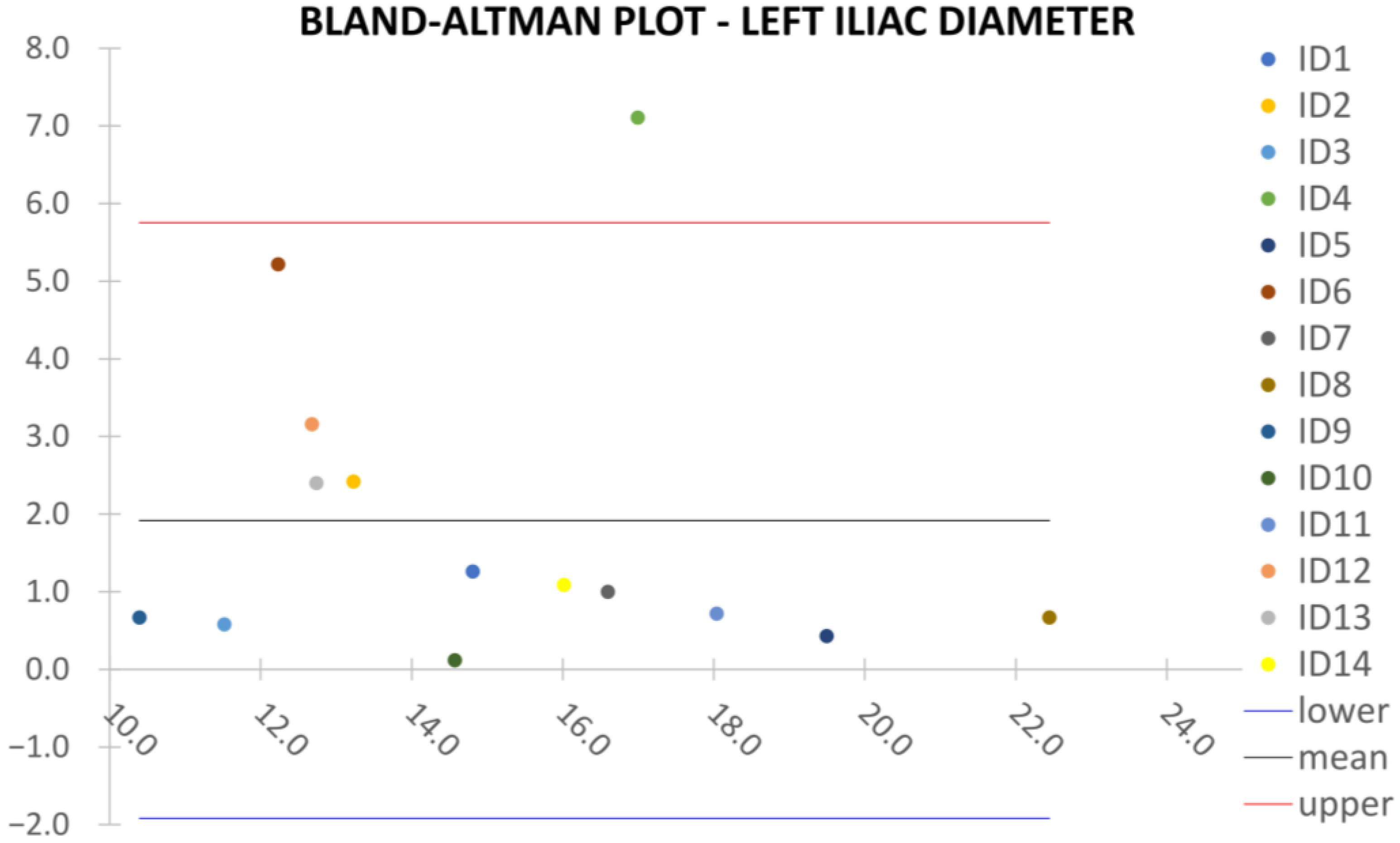
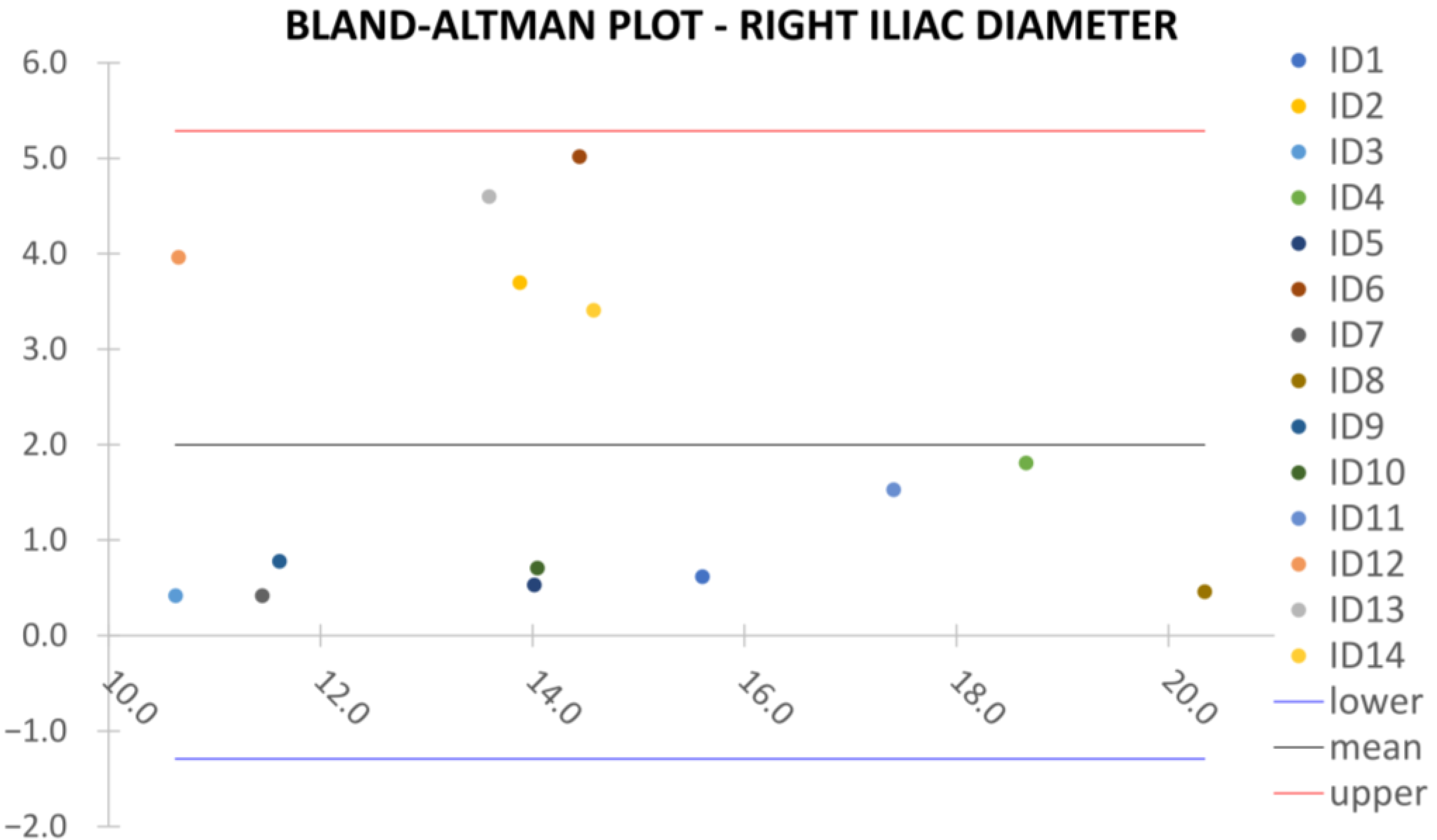
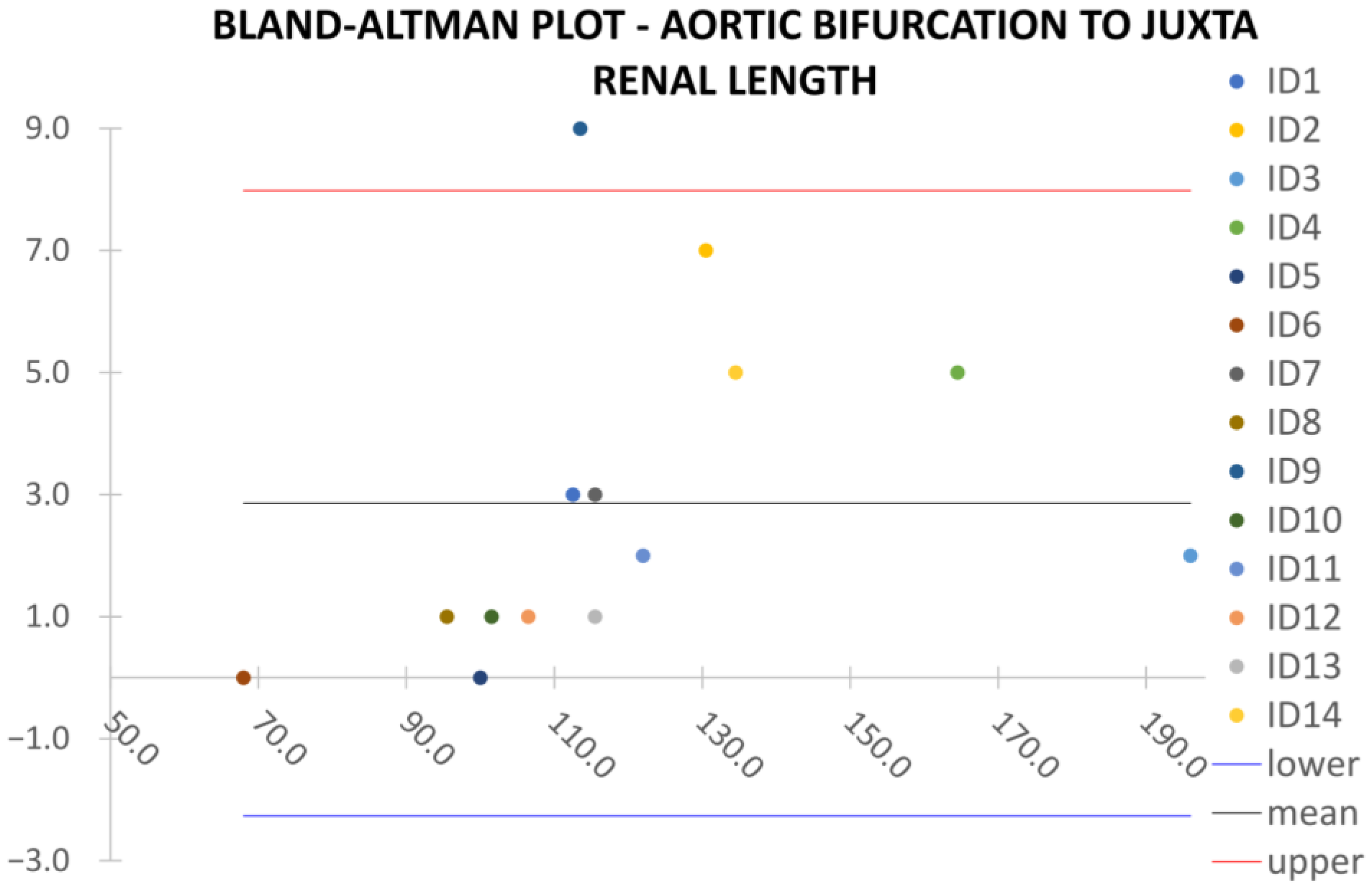
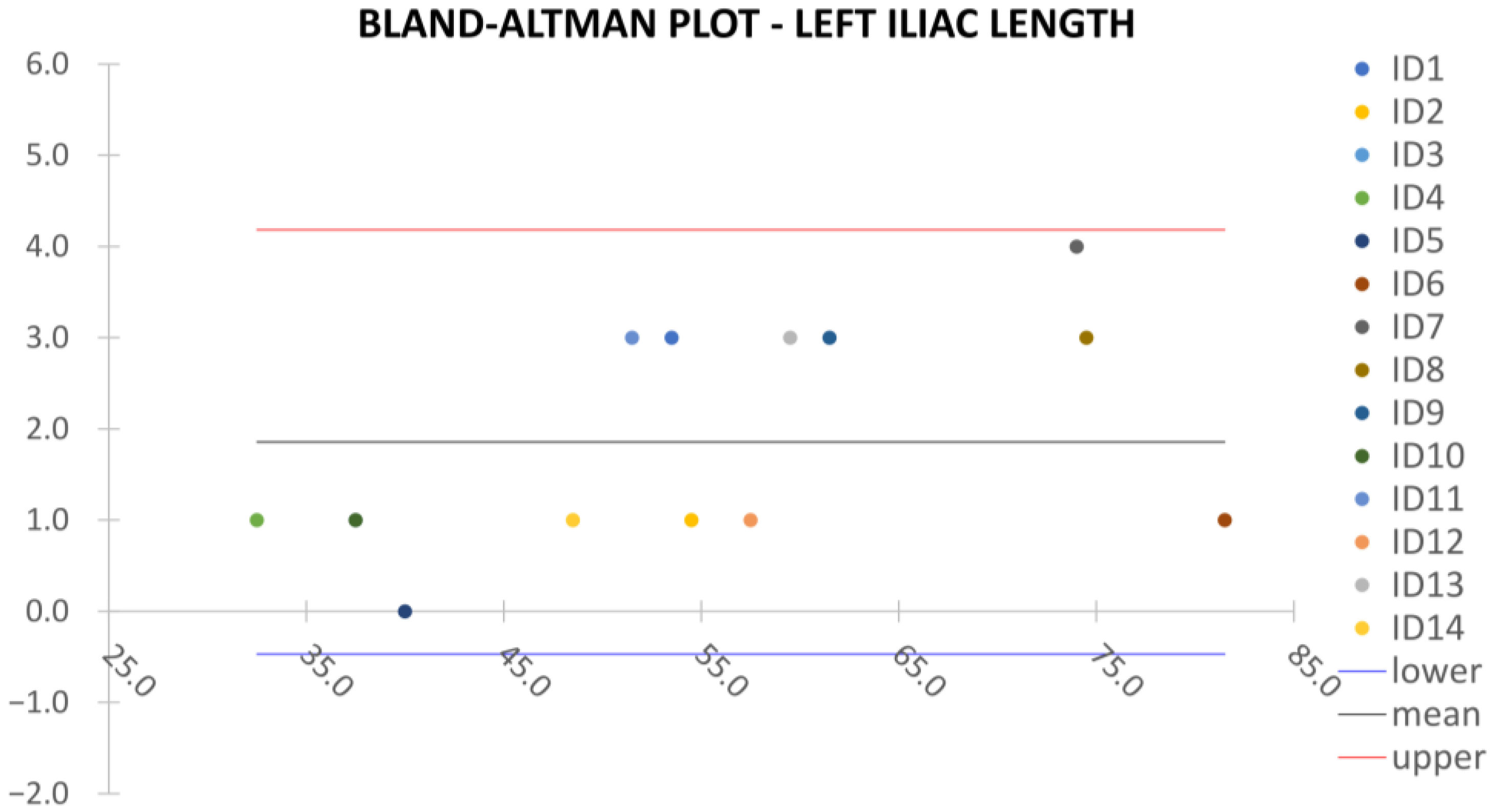
Clinical reliability is assessed by comparing centerline-based measurements performed on both the ITK-Snap and U-Net reconstructed geometries by means of absolute and relative percentage errors, as defined in Equations (4) and (5).
where
and
are the diameter or centerline length values, respectively, measured on ITK-Snap and U-Net 3D reconstruction geometries. Bland–Altman plots are also provided in the Appendix section from
Figure A1,
Figure A2,
Figure A3 and
Figure A4 for diameters and from
Figure A5,
Figure A6 and
Figure A7 for the centerline’s length. Once a region of interest is reconstructed, the vessel’s centerline is computed. The user can then perform the required reference measurements, taken on a plane orthogonal to the centerline, as shown in
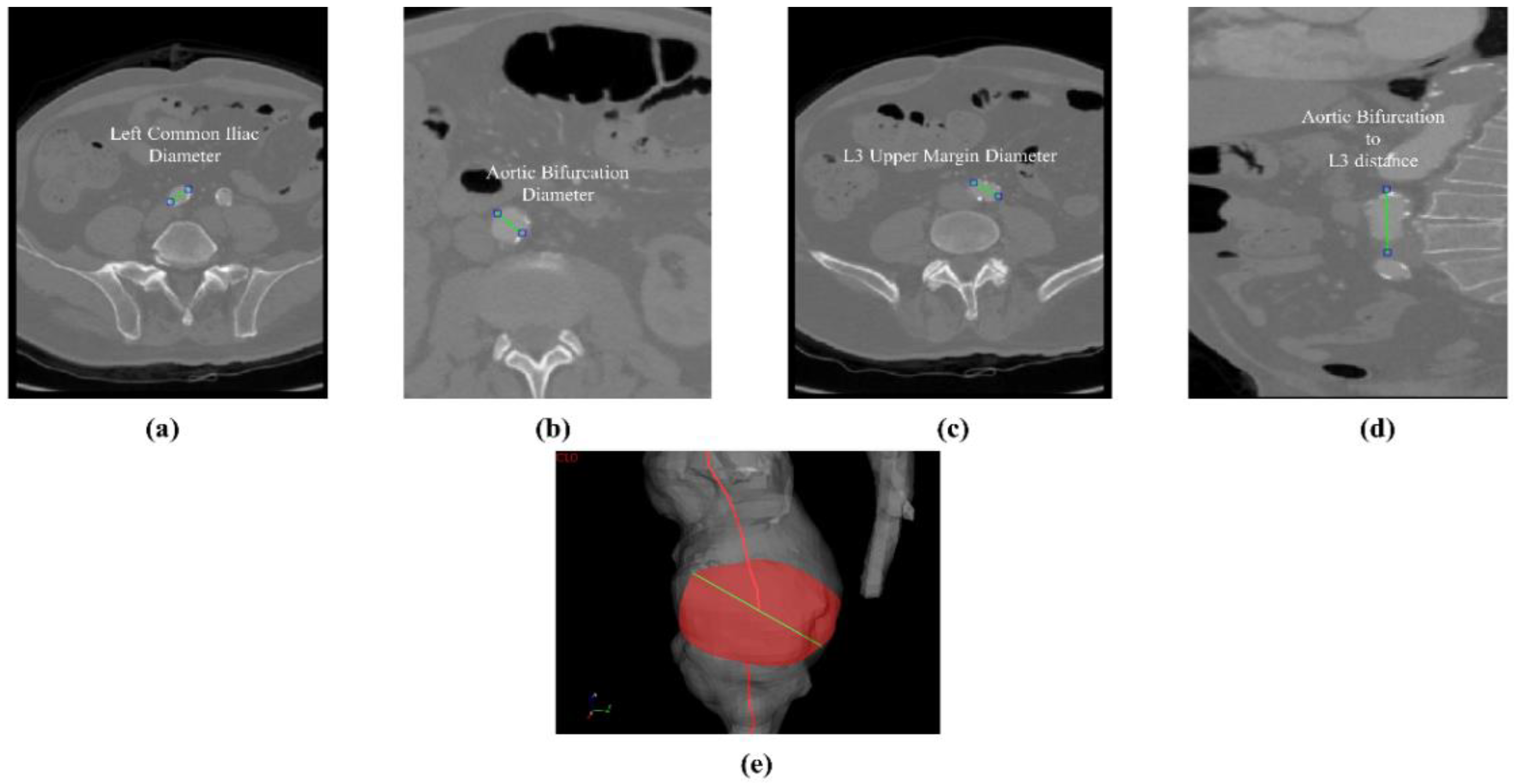
Figure 4e. The abdominal aneurysm and iliac arteries’ lumen diameter are measured at three distinct locations:
Right/Left Iliac Luminal Diameter,
,
: right and left common iliac artery proximally to their bifurcation, as shown in
Figure 4a.
L3 Infra Renal Aortic Diameter,
: located on the third lumbar vertebral body’s upper margin (L3), as shown in
Figure 4b, and at a distance
from AB, as shown in
Figure 4d.
Juxta Renal Aortic Diameter,
: the aortic lumen immediately below the lowest renal artery, as shown in
Figure 4c.
The coronal plane was used to measure the vertical distance between the aortic bifurcation and L3 body
, as shown in
Figure 4d. The centerline-based aortic lumen’s length measure between reference sections is taken considering the following bound segments:
Lowest RA to Aortic Bifurcation length, ;
Aortic Bifurcation to Right/Left Iliac Bifurcation, , .
The centerline’s length is computed as a sum of the Euclidean distances between the centerline points location as
, where
is the total number of points of the interest centerline’s branch, and
is the position vector, which is referenced at the starting point of the centerline itself. Such a validation strategy is different from the recognized preoperative AAA measurement standards, according to the latest ESVS European Society of Vascular Surgery guidelines outlined in Wanhainen et al. [
21]. To minimize measurement errors, the approach is modified and standardized by both vascular surgeon and engineers as previously described. The diameter was measured on the longest axis of the lumen from the inner-to-inner wall. Arterial thrombus and calcification were not included as the studied U-Net is of the mono-class type.
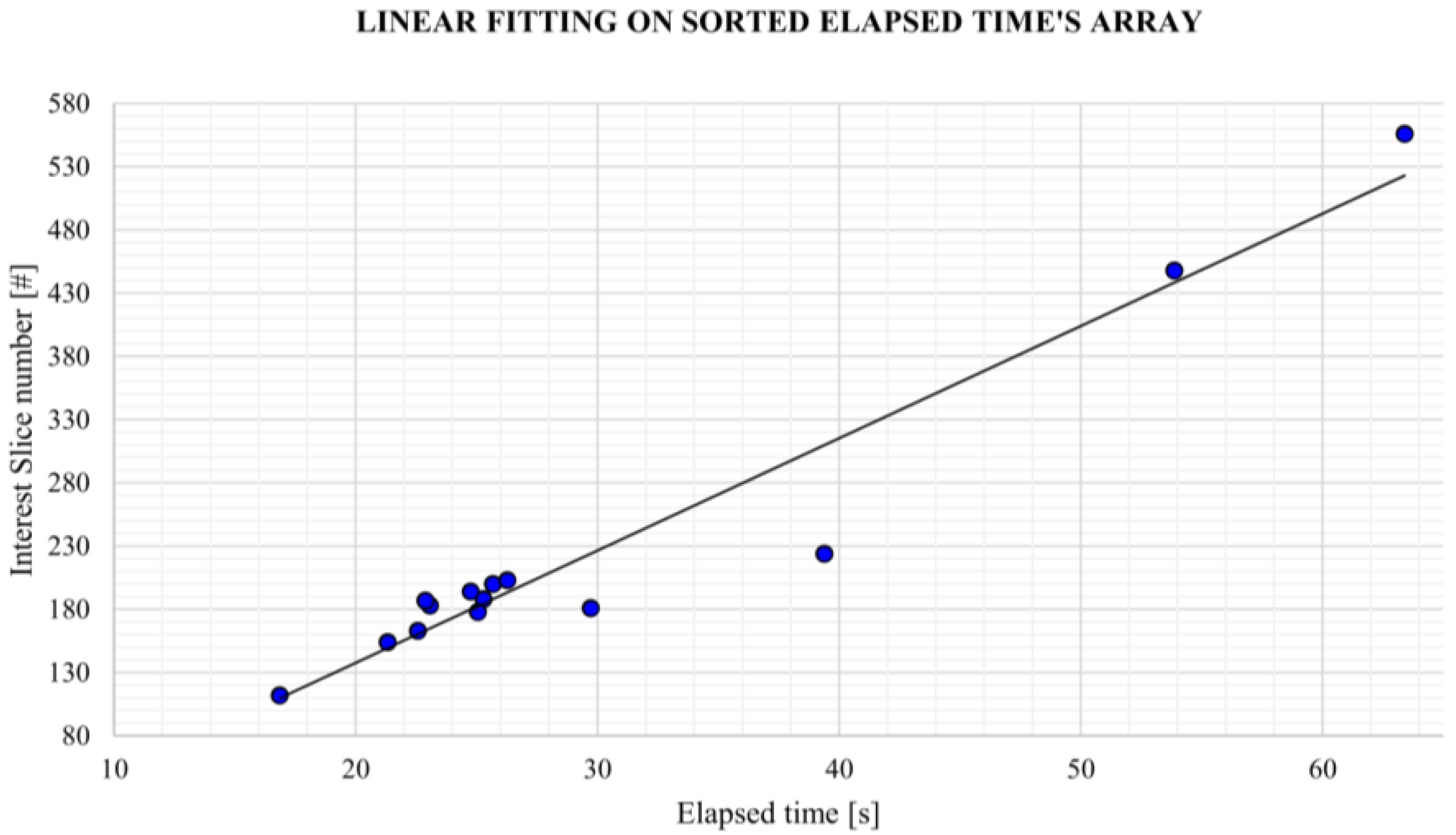
Usability and performance are also assessed by computing the average elapsed time to obtain the aortic lumen reconstruction and the average elapsed time per slice. It should be emphasized that all the reconstructions obtained by the algorithm presented in this study were retrieved from central ROI orientation predictions and CPU devices.
4. Discussion
In this study, a DL-based algorithm to segment and reconstruct the abdominal aorta has been proposed. Validation has been focused on the model’s performance, robustness, reliability, and usability based on the network’s metrics and reference measurements for EVAR planning taken by a vascular surgeon. The goal was to lay the groundwork for the development of more complex enhanced diagnostic techniques and preoperative planning, which was used by medical personnel without requiring prior training. The result’s reproducibility highly reduces the risk of accidental errors, thus enhancing the overall reliability of the algorithm. Providing a complex validation pipeline for aneurysmatic aortic lumen 3D reconstruction, the proposed replicable model is considered a starting point toward an enhanced 3D aortic diagnostic framework.
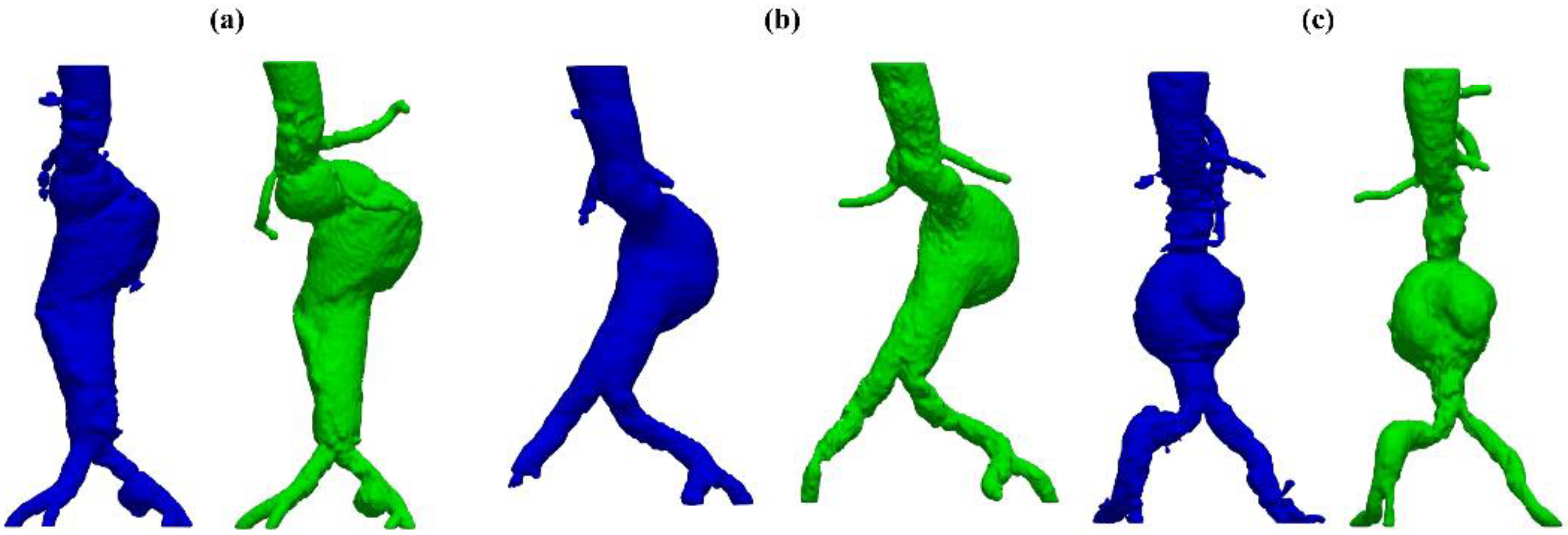
Despite some fluctuations in metrics, the network showed a good approximation of the aortic lumen, with sufficient results reproducibility and reliable 3D-based aortic measurements, even considering the uncertainty due to user input replicability. Segmentation performance analysis reports an average intersection over union and F1-score of 0.760 ± 0.150 and 0.850 ± 0.120, respectively, as well as an absolute error on aortic measurements provided and average value of , and , respectively. Some cases are characterized by high across-slice standard deviation. However, it is crucial to bear in mind that GT extraction from CTA is performed using the ITK-Snap semi-automatic threshold segmentation mode. By proceeding this way, in certain cases, such an extraction method might exclude border pixels, which belong to the aortic lumen. This leads to an increase in false negatives, affecting the network’s performance and measurement process. The mentioned behavior can be observed in many cases: for example, cases ID_2, ID_6, ID_12, and ID_13. Moreover, a large spectrum of anatomies can determine a general decrease in test set metrics. Despite these limitations, 3D reconstructions still demonstrated good agreement with the ones obtained using the reference software.
Although this study has been conducted on a small test set, the results are overall in accordance with previous studies reporting AI-driven infra-renal abdominal aortic segmentation and automatic measurements of lumen diameter [
22,
23] whilst also including various anatomies and aorto-iliac pathologies. Although one may consider the average relative error high, as it exceeds the standard 5% value for the majority of cases, it has to be underlined that in the definition of relative error, the magnitude of such quantity is strongly influenced by the GT measure’s value order of magnitude. In fact, considering Equation (5), it can be seen how by keeping constant absolute errors, the value of the relative error will increase if referring to small distances, such as diameters, which lay in the
order of magnitude. Thus, to perform a fair evaluation of the dispersion between U-Net and ITK-Snap 3D measurements, this important property of the relative error’s definition must be considered, which allows the relative error uncertainty interval to be larger, as a small order of magnitude of the measure is considered. On the other hand, such behavior is negligible for the aortic section’s length, as the order of magnitude lays around
mm, as most relative errors on the aortic section’s length lay inside the 5% value.
To improve the model’s performance and reconstruction quality, the dataset’s anatomical spectrum needs to be enriched to include both wider areas and secondary vessels and particularly complex anatomies, which return unstable 3D reconstructions.
The network’s performance on secondary vessels segmentation also needs to be improved in the model’s next versions by expanding aortic lumen labeling ROI so as to include wider semantic areas. High standard deviations shown by metrics across slices can be drastically reduced by performing fine tuning on a specific subset of the training dataset which contains challenging anatomies.
The urge to obtain a model able to segment challenging data inevitably leads to taking into consideration a multi-center study. Comprising CTA scans from several institutes might boost network performance with larger and semantically richer datasets.
Future developments will involve the implementation of multi-class CNN for aortic lumen and intraluminal thrombus semantic segmentation to extend clinical usability to post-EVAR CTA scans. Intraluminal thrombus is, in fact, clinically crucial when estimating the outer maximum aortic diameter. Further steps also involve coupling a custom CFD solver to the AI model for the numerical simulation of patient-specific aortic flows which can further represent the true hemodynamic state of the diseased vessel. Quantitative hemodynamic data correlation with geometric vessel properties will enhance simulation accuracy, especially if laid on a knowledge-based semantic structure such as taxonomy or ontology, favoring digital translatability to patient-specific diagnostics addressing complex problems such as rupture risk assessment.