Young vs. Old Population: Does Urban Environment of Skyscrapers Create Different Obesity Prevalence?
Abstract
:1. Introduction
1.1. Background
1.2. The Current Study: Descriptions and Contributions
2. Methodology
3. Results
| Variable | Obs. | Mean | Std. Dev. | Min | Max | |
|---|---|---|---|---|---|---|
| Obesity prevalence | Prevalence of population in the US state that suffers from obesity (BMI ≥ 30 where ) measured in percentage points | 928 | 22.54 | 6.55 | 7.6 | 37.6 |
| (Year − 2011) | The year in which the prevalence of obesity was measured in the state (0 = 2011; 9 = 2020) | 928 | 4.53 | 2.86 | 0 | 9 |
| Skyscrapers | Number of skyscrapers in the state | 928 | 15.86 | 42.87 | 0 | 267 |
| Old | 1 = Old age cohort (65+) 0 = Young age cohort (18–25) | 928 | 0.5 | 0.50 | 0 | 1 |
| Column (1) | |
|---|---|
| Variables | Obesity Prevalence |
| (Year − 2011) | 0.514 *** |
| (<0.01) | |
| Skyscrapers×Skyscrapers | 0.000218 *** |
| (1.43 × 10−6) | |
| Old ×Skyscrapers×Skyscrapers | 0.000138 ** |
| (0.0458) | |
| Skyscrapers | −0.0645 *** |
| (5.62 × 10−9) | |
| Old ×Skyscrapers | −0.0377 ** |
| (0.0348) | |
| Old | 10.61 *** |
| (<0.01) | |
| Constant | 15.63 *** |
| (<0.01) | |
| Observations | 928 |
| R squared | 0.708 |
| p value RESET Test | 0.3220 |
| Minimum Young (18–25) | |
| Skyscrapers | 147 [126, 170] |
| Projected Prevalence of Obesity | 13.2 [11.87, 14.52] |
| Minimum Old (66+) | |
| Skyscrapers | 144 [137, 150] |
| Projected Prevalence of Obesity | 21.23 [19.48, 22.99] |
| Minimum Old–Young Differences | 8.21 [5.83, 10.25] |
| Maximum Old–Young Differences | 10.61 [10.06, 11.13] |
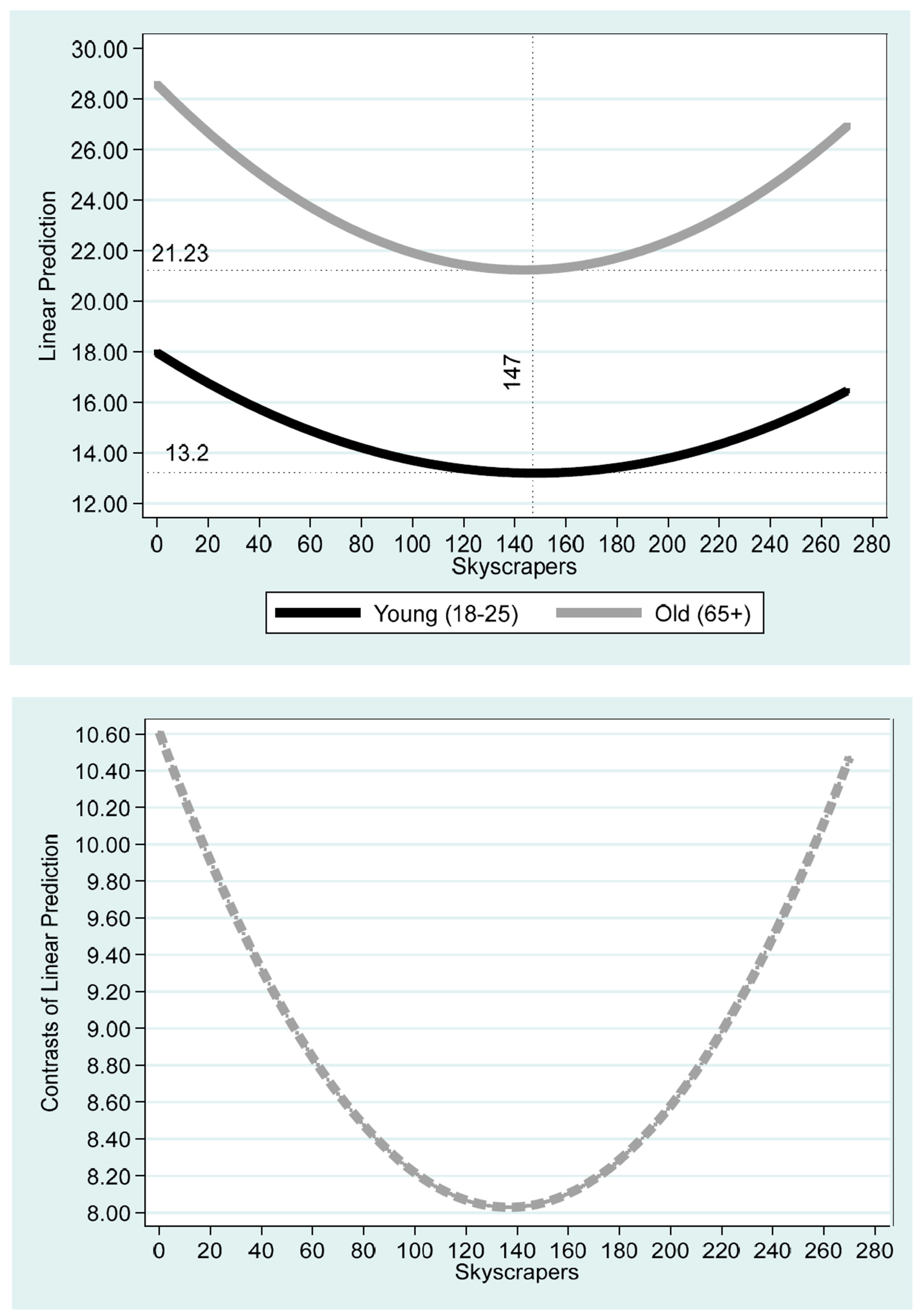
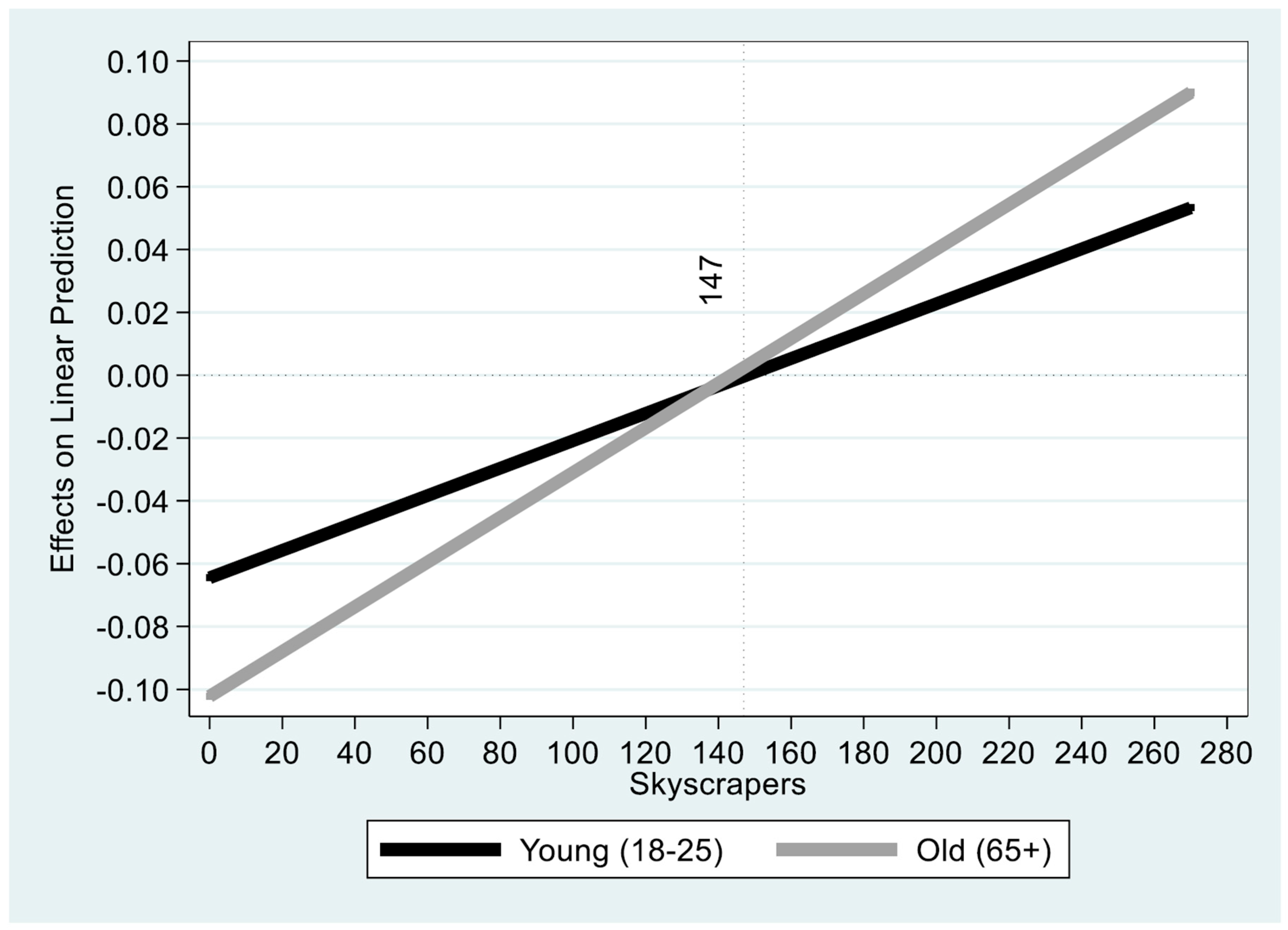
| Column (1) | Column (2) | |
|---|---|---|
| Variables | Obesity_Prevalence | Obesity_Prevalence |
| (Year − 2011) | 0.553 *** | 0.583 *** |
| (<0.01) | (<0.01) | |
| Skyscrapers×Skyscrapers | 0.000218 *** | 0.000218 *** |
| (1.28 × 10−6) | (1.38 × 10−6) | |
| age_25_34× Skyscrapers×Skyscrapers | 0.000180 ** | - |
| (0.0150) | - | |
| age_35_44× Skyscrapers×Skyscrapers | 0.000170 ** | - |
| (0.0187) | - | |
| age_45_54× Skyscrapers×Skyscrapers | 0.000103 * | 0.000103 * |
| (0.0859) | (0.0862) | |
| age_55_64× Skyscrapers×Skyscrapers | 0.000108 | - |
| (0.102) | - | |
| age_65_or_older× Skyscrapers×Skyscrapers | 0.000138 ** | 0.000138 ** |
| (0.0459) | (0.0466) | |
| Skyscrapers | −0.0644 *** | −0.0644 *** |
| (4.32 × 10−9) | (4.88 × 10−9) | |
| age_25_34× Skyscrapers | −0.0485 *** | - |
| (0.00862) | - | |
| age_35_44× Skyscrapers | −0.0464 ** | - |
| (0.0103) | - | |
| age_45_54× Skyscrapers | −0.0379 ** | −0.0379 ** |
| (0.0120) | (0.0121) | |
| age_55_64× Skyscrapers | −0.0420 ** | - |
| (0.0124) | - | |
| age_65_or_older× Skyscrapers | −0.0377 ** | −0.0377 ** |
| (0.0348) | (0.0352) | |
| Constant | 15.46 *** | 15.32 *** |
| (<0.01) | (<0.01) | |
| age_25_34 | 11.55 *** | - |
| (<0.01) | - | |
| age_35_44 | 16.56 *** | - |
| (<0.01) | - | |
| age_45_54 | 18.44 *** | 18.44 *** |
| (<0.01) | (<0.01) | |
| age_55_64 | 17.56 *** | - |
| (<0.01) | - | |
| age_65_or_older | 10.61 *** | 10.61 *** |
| (<0.01) | (<0.01) | |
| Observations | 2784 | 1392 |
| R squared | 0.723 | 0.806 |
| F values | 419.5 *** | 575.9 *** |
| D.F. Numerator | 18 | 9 |
| D.F. Denominator | 2765 | 1382 |
| Critical F value | 1.94 | 2.42 |


4. Robustness Test
| Round | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| First | 0.6557 *** | 0.4887 *** | 0.3830 *** | 0.4911 *** | 0.4414 *** | 0.4927 *** | 0.6363 *** | 0.3559 *** | 0.4096 *** | 0.5428 *** | |
| Second | 0.6582 *** | 0.4875 *** | 0.3858 *** | 0.4872 *** | 0.4380 *** | 0.4641 *** | 0.6901 *** | 0.3564 *** | 0.4158 *** | 0.5518 *** | |
| Third | 0.6812 *** | 0.4880 *** | 0.3830 *** | 0.4886 *** | 0.4297 *** | 0.4755 *** | 0.6313 *** | 0.3433 *** | 0.4170 *** | 0.5976 *** | |
| Fourth | 0.6625 *** | 0.5342 *** | 0.3835 *** | 0.4916 *** | 0.4632 *** | 0.5000 *** | 0.6405 *** | 0.3718 *** | 0.3980 *** | 0.5657 *** | |
| Fifth | 0.6646 *** | 0.4797 *** | 0.3357 *** | 0.4866 *** | 0.4400 *** | 0.4950 *** | 0.6900 *** | 0.3446 *** | 0.4021 *** | 0.5726 *** | |
| Obs. | 90 | 90 | 92 | 94 | 94 | 94 | 94 | 94 | 92 | 94 | 928 |
5. Discussion
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BMI | Body Mass Index |
| MVPA | Medium-to-Vigorous Physical Activity |
| PA | Physical Activity |
| RESET | Regression Specification Error Test |
| SDT | Self-Determination Theory |
| WHO | World Health Organization |
| WHR | Waist–Hip Ratio |
Appendix A. Core Elements and Related Topics and Activities in the CRI LEP
| Core Elements | Selected Examples of Topics and Activities |
|---|---|
| Nutrition |
|
| Physical Activity |
|
| Behavior Change |
|
| Sense of Purpose |
|
| Integrative Health |
|
| Social Support and Follow-up Services |
|
References
- Glaeser, E. Cities, Productivity, and Quality of Life. Science 2011, 333, 592–594. [Google Scholar] [CrossRef] [PubMed]
- Glaeser, E. Triumph of the City: How Our Greatest Invention Makes Us Richer, Smarter, Greener, Healthier, and Happier; Penguin Books: New York, NY, USA, 2011. [Google Scholar]
- Glaeser, E. Viewpoint: Triumph of the city. J. Transp. Land Use 2012, 5, 1–4. [Google Scholar] [CrossRef]
- Mills, E.S. An Aggregative Model of Resources Allocation in a Metropolitan Area. Am. Econ. Rev. 1967, 57, 197. [Google Scholar]
- O’Sullivan, A. Urban Economics, 8th ed.; McGraw Hills International Edition: Singapore, 2012. [Google Scholar]
- Alonso, W. A Model of the Urban Land Market: Location and Densities of Dwellings and Businesses. Ph.D. Dissertation, University of Pennsylvania, Philadelphia, PA, USA, 1960. [Google Scholar]
- Alonso, W. Location and Land Use; Harvard University Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Muth, R. Cities and Housing; University of Chicago Press: Chicago, IL, USA, 1969. [Google Scholar]
- McDonald, J.F.; McMillen, D.P. Urban Economics and Real Estate: Theory and Policy, 2nd ed.; John Wiley & Sons Incorporated: Hoboken, NJ, USA, 2011. [Google Scholar]
- McDonald, J.F. William Alonso, Richard Muth, Resources for the Future, and the Founding of Urban Economics. J. Hist. Econ. Thought 2007, 29, 67–84. [Google Scholar] [CrossRef]
- Mills, E.S.; Hamilton, B.W. Urban Economics, 4th ed.; Harper Collins College Publishers: New York, NY, USA, 1989. [Google Scholar]
- Arbel, Y.; Fialkoff, C.; Kerner, A. Climate Change and Housing Choice: The Impact of Climate Differences on Capital-Land Elasticity of Substitution. J. Real Estate Lit. 2018, 26, 191–209. [Google Scholar] [CrossRef]
- Arbel, Y.; Fialkoff, C.; Kerner, A. The Association of Pension Income with the Incidence of Type I Obesity among Retired Israelis. J. Obes. 2019, 2019, 5101867. [Google Scholar] [CrossRef] [PubMed]
- Arbel, Y.; Fialkoff, C.; Kerner, A. The Chicken and Egg Problem: Obesity and the Urban Monocentric Model. J. Real Estate Financ. Econ. 2020, 61, 576–606. [Google Scholar] [CrossRef]
- Arbel, Y.; Arbel, Y.; Kerner, A.; Kerner, M. Do high-rise buildings influence melanoma? Tall buildings as positive externalities. Cities 2022, 131, 104002. [Google Scholar] [CrossRef]
- World Health Organization (WHO). June 2021: Obesity and Overweight. Available online: https://www.who.int/news-room/fact-sheets/detail/obesity-and-overweight (accessed on 10 October 2022).
- Zaccardi, F.; Franks, P.W.; Dudbridge, F.; Davies, M.J.; Khunti, K.; Yates, T. Mortality risk comparing walking pace to handgrip strength and a healthy lifestyle: A UK Biobank study. Eur. J. Prev. Cardiol. 2021, 28, 704–712. [Google Scholar] [CrossRef] [PubMed]
- Frank, L.D.; Iroz-Elardo, N.; MacLeod, K.E.; Hong, A. Pathways from built environment to health: A conceptual framework linking behavior and exposure-based impacts. J. Transp. Health 2019, 12, 319–335. [Google Scholar] [CrossRef]
- National Research Council (US); Committee on Physical Activity, Transportation, Land Use, Transportation Research Board; Institute of Medicine. Does the Built Environment Influence Physical Activity? Examining the Evidence—Special Report 282; Transportation Research Board: Washington, DC, USA, 2015; Volume 282.
- Ewing, R.; Meakins, G.; Hamidi, S.; Nelson, A.C. Relationship between urban sprawl and physical activity, obesity, and morbidity—Update and refinement. Health Place 2014, 26, 118–126. [Google Scholar] [CrossRef] [PubMed]
- Mulalic, I.; Rouwendal, J. Does improving public transport decrease car ownership? Evidence from a residential sorting model for the Copenhagen metropolitan area Reg. Sci. Urban Econ. 2020, 83, 103543. [Google Scholar] [CrossRef]
- World Health Organization (WHO): Physical Activity. 2022. Available online: https://www.who.int/news-room/fact-sheets/detail/physical-activity (accessed on 10 October 2023).
- Winston, T.N. Handbook on Burnout and Sleep Deprivation: Risk Factors, Management Strategies and Impact on Performance and Behavior; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2015. [Google Scholar]
- Fatima, Y.; Doi, S.A.R.; Mamun, A.A. Longitudinal impact of sleep on overweight and obesity in children and adolescents: A systematic review and bias-adjusted meta-analysis. Obes. Rev. 2015, 16, 137–149. [Google Scholar] [CrossRef]
- Mayne, S.L.; Morales, K.H.; Williamson, A.A.; Grant, S.F.A.; Fiks, A.G.; Basner, M.; Dinges, D.F.; Zemel, B.S.; Mitchell, J.A. Associations of the residential built environment with adolescent sleep outcomes. Sleep 2021, 44, zsaa276. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Zhou, J. Effects of the built environment on automobile-involved pedestrian crash frequency and risk. J. Transp. Health 2016, 3, 448–456. [Google Scholar] [CrossRef]
- Feuillet, T.; Salze, P.; Charreire, H.; Menai, M.; Enaux, C.; Perchoux, C.; Hess, F.; Kesse-Guyot, E.; Hercberg, S.; Simon, C.; et al. Built environment in local relation with walking: Why here and not there? J. Transp. Health 2016, 3, 500–512. [Google Scholar] [CrossRef]
- Nigg, C.; Oriwol, D.; Wunsch, K.; Burchartz, A.; Kolb, S.; Worth, A.; Woll, A.; Niessner, C. Population density predicts youth’s physical activity changes during COVID-19—Results from the MoMo study. Health Place 2021, 70, 102619. [Google Scholar] [CrossRef]
- Hino, K.; Asami, Y. Change in walking steps and association with built environments during the COVID-19 state of emergency: A longitudinal comparison with the first half of 2019 in Yokohama, Japan. Health Place 2021, 69, 102544. [Google Scholar] [CrossRef]
- Handy, S.; Cao, X.; Mokhtarian, P.L. Self-Selection in the Relationship between the Built Environment and Walking: Empirical Evidence from Northern California. J. Am. Plan. Assoc. 2006, 72, 55–74. [Google Scholar] [CrossRef]
- Sun, G.; Oreskovic, N.M.; Lin, H. How do changes to the built environment influence walking behaviors? A longitudinal study within a university campus in Hong Kong. Int. J. Health Geogr. 2014, 13, 28–37. [Google Scholar] [CrossRef]
- Chaix, B.; Simon, C.; Charreire, H.; Thomas, F.; Kestens, Y.; Karusisi, N.; Vallée, J.; Oppert, J.-M.; Weber, C.; Pannier, B. The environmental correlates of overall and neighborhood based recreational walking (a cross-sectional analysis of the RECORD Study). Int. J. Behav. Nutr. Phys. Act. 2014, 11, 20. [Google Scholar] [CrossRef] [PubMed]
- Wasfi, R.A.; Dasgupta, K.; Eluru, N.; Ross, N.A. Exposure to walkable neighbourhoods in urban areas increases utilitarian walking: Longitudinal study of Canadians. J. Transp. Health 2016, 3, 440–447. [Google Scholar] [CrossRef]
- Beales, P.R.; Farooqi, I.S.; O’Rahilly, S. Genetics of Obesity Syndromes; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Sallis, J.F.; Cerin, E.; Conway, T.L.; Adams, M.A.; Frank, L.D.; Pratt, M.; Salvo, D.; Schipperijn, J.; Smith, G.; Cain, K.L.; et al. Physical activity in relation to urban environments in 14 cities worldwide: A cross-sectional study. Lancet 2016, 387, 2207–2217. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.Y.; Choi, D.H.; Jung, C.H.; Kang, S.K.; Mok, J.O.; Kim, C.H. Obesity and Physical Activity. J. Obes. Metab. Syndr. 2017, 26, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Lee, A.; Cardel, M.; Donahoo, W.T. Social and Environmental Factors Influencing Obesity. In Endotext [Internet]; Feingold, K.R., Anawalt, B., Boyce, A., Chrousos, G., de Herder, W.W., Dhatariya, K., Dungan, K., Grossman, A., Hershman, J.M., Hofland, J., Eds.; MDText.com, Inc.: South Dartmouth, MA, USA, 2019. Available online: https://www.ncbi.nlm.nih.gov/books/NBK278977/ (accessed on 10 October 2023).
- Allender, S.; Cowburn, G.; Foster, C. Understanding participation in sport and physical activity among children and adults: A review of qualitative studies. Health Educ. Res. 2006, 21, 826–835. [Google Scholar] [CrossRef] [PubMed]
- Roberts, G.C.; Nerstad, C.G.L.; Lemyre, P.N. Motivation in Sport and Performance. Oxf. Res. Encycl. Psychol. 2018. [Google Scholar] [CrossRef]
- Ahmed, D.; Ho, W.K.Y.; Al-Haramlah, A.; Mataruna-Dos-Santos, L.J. Motivation to participate in physical activity and sports: Age transition and gender differences among India’s adolescents. Cogent Psychol. 2020, 7, 1798633. [Google Scholar] [CrossRef]
- Kalajas-Tilga, H.; Koka, A.; Hein, V.; Tilga, H.; Raudsepp, L. Motivational processes in physical education and objectively measured physical activity among adolescents. J. Sport Health Sci. 2020, 9, 462–471. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, A.; Noetel, M.; Parker, P.; Ryan, R.M.; Ntoumanis, N.; Reeve, J.; Beauchamp, M.; Dicke, T.; Yeung, A.; Ahmadi, M.; et al. A classification system for teachers’ motivational behaviors recommended in self-determination theory interventions. J. Educ. Psychology. 2023. [Google Scholar] [CrossRef]
- Molanorouzi, K.; Khoo, S.; Morris, T. Motives for adult participation in physical activity: Type of activity, age, and gender. BMC Public Health 2015, 15, 66. [Google Scholar] [CrossRef]
- Young, B.W.; Callary, B.; Rathwell, S. Psychological Considerations for the Older Athlete. Oxf. Res. Encycl. Psychol. 2018. [Google Scholar] [CrossRef]
- Tsai, T.-H.; Wong, A.M.; Lee, H.-F.; Tseng, K.C. A Study on the Motivation of Older Adults to Participate in Exercise or Physical Fitness Activities. Sustainability 2022, 14, 6355. [Google Scholar] [CrossRef]
- Firestone, M.J.; Yi, S.S.; Bartley, K.F.; Eisenhower, D.L. Perceptions and the role of group exercise among New York City adults, 2010–2011: An examination of interpersonal factors and leisure-time physical activity. Prev. Med. 2015, 72, 50–55. [Google Scholar] [CrossRef] [PubMed]
- Center for Disease Control and Prevention (CDC). Nutrition, Physical Activity, and Obesity: Data, Trends and Maps. Available online: https://nccd.cdc.gov/dnpao_dtm/rdPage.aspx?rdReport=DNPAO_DTM.ExploreByTopic&islClass=OWS&islTopic=&go=GO (accessed on 10 October 2023).
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach, 4th ed.; International Student Edition; South Western CENGAGE Learning: Boston, MA, USA, 2009. [Google Scholar]
- Yin, C.; Sun, B. Does Compact Built Environment Help to Reduce Obesity? Influence of Population Density on Waist–Hip Ratio in Chinese Cities. Int. J. Environmental. Res. Public Health 2020, 17, 7746. [Google Scholar] [CrossRef] [PubMed]
- Chiang, A.; Wainwright, K. Fundamental Methods of Mathematical Economics, 4th ed.; McGraw Hills International Edition: Singapore, 2015. [Google Scholar]
- Lam, T.M.; Vaartjes, I.; Grobbee, D.E.; Karssenberg, D.; Lakerveld, J. Associations between the built environment and obesity: An umbrella review. Int. J. Health Geogr. 2021, 20, 1–24. [Google Scholar] [CrossRef]
- Ihle, A.; Gouveia, É.R.; Gouveia, B.R.; Zuber, S.; Mella, N.; Desrichard, O.; Cullati, S.; Oris, M.; Maurer, J.; Kliegel, M. The relationship of obesity predicting decline in executive functioning is attenuated with greater leisure activities in old age. Aging Ment. Health 2021, 25, 613–620. [Google Scholar] [CrossRef]
- Mathus-Vliegen, E.M.H. Prevalence, pathophysiology, health consequences and treatment options of obesity in the elderly: A guideline. Obes. Facts 2012, 5, 460–483. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, R. Introductory Econometrics with Applications, 5th ed.; South Western Thomson Learning: Mason, OH, USA, 2002. [Google Scholar]
- Greene, W.H. Econometric Analysis, 7th ed.; Pearson Education Limited: Sumas, WA, USA, 2012. [Google Scholar]
- OECD Obesity Update. 2017. Available online: https://www.oecd.org/health/obesity-update.htm (accessed on 10 October 2023).
- Pleasant, A. Assisting Vulnerable Communities: Canyon Ranch Institute’s and Health Literacy Media’s Health Literacy and Community-Based Interventions. In Health Literacy: New Directions in Research, Theory and Practice; Logan, R.A., Siegel, E.R., Eds.; IOS Press: Amsterdam, The Netherlands, 2017; pp. 127–164. [Google Scholar]
- Hamidi, S.; Ewing, R.; Sabouri, S. Longitudinal analyses of the relationship between development density and the COVID-19 morbidity and mortality rates: Early evidence from 1,165 metropolitan counties in the United States. Health Place 2020, 64, 102378. [Google Scholar] [CrossRef]
- Arbel, Y.; Arbel, Y.; Kerner, A.; Kerner, M. What is the optimal country for minimum COVID-19 morbidity and mortality rates? Environ. Sci. Pollut. Res. 2023, 30, 59212–59232. [Google Scholar] [CrossRef]
- Arbel, Y.; Arbel, Y.; Arbel, Y.; Kerner, A.; Kerner, M. Can reduction in infection and mortality rates from coronavirus be explained by an obesity survival paradox? An analysis at the US statewide level. Int. J. Obes. 2020, 44, 2339–2342. [Google Scholar] [CrossRef] [PubMed]
- Arbel, Y.; Arbel, Y.; Arbel, Y.; Kerner, A.; Kerner, M. Is obesity a risk factor for melanoma? BMC Cancer 2023, 23, 178. [Google Scholar] [CrossRef] [PubMed]
- Arbel, Y.; Arbel, Y.; Arbel, Y.; Kerner, A.; Kerner, M. Can Obesity Prevalence Explain COVID-19 Indicators (Cases, Mortality, and Recovery)? A Comparative Study in OECD Countries. J. Obes. 2022, 10, 4320120. [Google Scholar] [CrossRef] [PubMed]
- Arbel, Y.; Fialkoff, C.; Kerner, A.; Kerner, M. Can increased recovery rates from coronavirus be explained by prevalence of ADHD? An analysis at the US statewide level. J. Atten. Disord. 2021, 25, 1951–1954. [Google Scholar] [CrossRef] [PubMed]
- Anas, A.; Arnott, R.; Small, K.A. Urban Spatial Structure. J. Econ. Lit. 1998, 36, 1426–1464. [Google Scholar]
- Black, J.L.; Macinko, J. Neighborhood sand obesity. Nutr. Rev. 2008, 66, 2–20. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Glass, T.; Curriero, F.; Stewart, W.; Schwartz, B. The built environment and obesity: A systematic review of the epidemiologic evidence. Health Place 2010, 16, 175–190. [Google Scholar] [CrossRef] [PubMed]
- Booth, K.M.; Pinkston, M.M.; Poston, W.S. Obesity and the built environment. J. Am. Diet Assoc. 2005, 105 (Suppl. S1), S110–S117. [Google Scholar] [CrossRef] [PubMed]
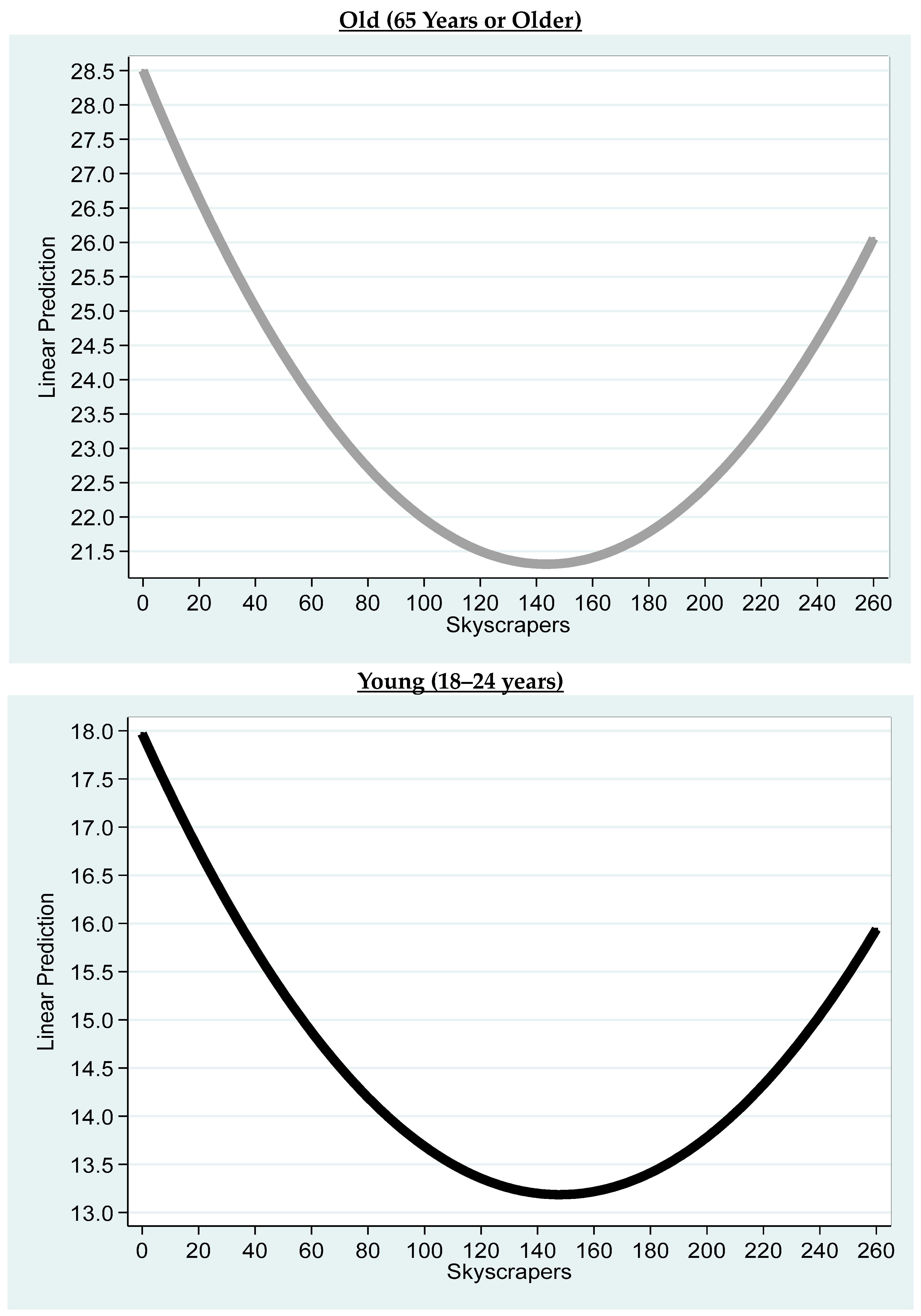
| Column (1) | Column (2) | |
|---|---|---|
| Old | Young | |
| Variables | Obesity_prevalence | Obesity_prevalence |
| (Year − 2011) | 0.520 *** | 0.519 *** |
| (<0.01) | (<0.01) | |
| 0.000349 *** | 0.000219 * | |
| (0.00232) | (0.0912) | |
| Skyscrapers | −0.100 *** | −0.0647 ** |
| (0.000344) | (0.0409) | |
| Constant | 26.15 *** | 15.62 *** |
| (<0.01) | (<0.01) | |
| Observations | 464 | 464 |
| Number of State 1 | 47 | 47 |
| Wald Chi squared (3) | 402.69 *** | 147.57 *** |
| 2.6687 | 2.9673 | |
| 1.6121 | 2.6649 | |
| 0.7327 | 0.5535 |
| Round | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| First | 0.3254 | 0.6100 | 0.6411 | 0.5963 | 0.2833 | 0.1110 | 0.6158 | 0.6659 | 0.5780 | 0.5977 | |
| Second | 0.6284 | 0.6287 | 0.5897 | 0.0598 | 0.6427 | 0.6537 | 0.6605 | 0.1739 | 0.6205 | 0.1539 | |
| Third | 0.6849 | 0.3242 | 0.0799 | 0.6390 | 0.5038 | 0.4619 | 0.1327 | 0.3052 | 0.2493 | 0.6190 | |
| Fourth | 0.6525 | 0.2400 | 0.6571 | 0.6791 | 0.6834 | 0.6397 | 0.2350 | 0.6833 | 0.0235 | 0.6792 | |
| Fifth | 0.5958 | 0.6295 | 0.3456 | 0.6583 | 0.6332 | 0.6201 | 0.7326 | 0.6202 | 0.6611 | 0.6297 | |
| Obs. | 90 | 90 | 92 | 94 | 94 | 94 | 94 | 94 | 92 | 94 | 928 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arbel, Y.; Arbel, Y.; Kerner, A.; Kerner, M. Young vs. Old Population: Does Urban Environment of Skyscrapers Create Different Obesity Prevalence? BioMed 2023, 3, 440-459. https://doi.org/10.3390/biomed3040036
Arbel Y, Arbel Y, Kerner A, Kerner M. Young vs. Old Population: Does Urban Environment of Skyscrapers Create Different Obesity Prevalence? BioMed. 2023; 3(4):440-459. https://doi.org/10.3390/biomed3040036
Chicago/Turabian StyleArbel, Yuval, Yifat Arbel, Amichai Kerner, and Miryam Kerner. 2023. "Young vs. Old Population: Does Urban Environment of Skyscrapers Create Different Obesity Prevalence?" BioMed 3, no. 4: 440-459. https://doi.org/10.3390/biomed3040036
APA StyleArbel, Y., Arbel, Y., Kerner, A., & Kerner, M. (2023). Young vs. Old Population: Does Urban Environment of Skyscrapers Create Different Obesity Prevalence? BioMed, 3(4), 440-459. https://doi.org/10.3390/biomed3040036






