Abstract
We conducted a systematic survey of COVID-19 endpoint prediction literature to: (a) identify publications that include data that adhere to FAIR (findability, accessibility, interoperability, and reusability) principles and (b) develop and reuse mortality prediction models that best generalize to these datasets. The largest such cohort data we knew of was used for model development. The associated published prediction model was subjected to recursive feature elimination to find a minimal logistic regression model which had statistically and clinically indistinguishable predictive performance. This model could still not be applied to the four external validation sets that were identified, due to complete absence of needed model features in some external sets. Thus, a generalizable model (GM) was built which could be applied to all four external validation sets. An age-only model was used as a benchmark, as it is the simplest, effective, and robust predictor of mortality currently known in COVID-19 literature. While the GM surpassed the age-only model in three external cohorts, for the fourth external cohort, there was no statistically significant difference. This study underscores: (1) the paucity of FAIR data being shared by researchers despite the glut of COVID-19 prediction models and (2) the difficulty of creating any model that consistently outperforms an age-only model due to the cohort diversity of available datasets.
1. Introduction
Coronavirus disease 2019 (COVID-19) is among the worst pandemics in history, having caused almost 4.69 million deaths worldwide in about 228 million confirmed cases as of 21 September 2021 [1]. Additionally, the pandemic has crippled healthcare systems, economies, and societies across the world, creating risks of extreme poverty and famine in millions of people [2]. COVID-19 also has a psychological impact, with various groups of people in society being at risk of developing anxiety or stress as a result of quarantine and, in the case of healthcare workers, a changed work dynamic [3].
The virus responsible for COVID-19, called Severe Acute Respiratory Syndrome Coronavirus 2-(SARS-CoV-2), is a novel, highly contagious strain of beta-coronaviruses belonging to the same subgenus as the epidemic viruses Severe Acute Respiratory Syndrome Coronavirus and Middle East Respiratory Syndrome Coronavirus [4]. The symptoms of COVID-19 range from mild to severe, potentially causing acute respiratory distress syndrome and in the worst cases, death [5]. Considering that the available COVID-19 treatments have limited applicability in terms of the target demographic, SARS-CoV-2′s highly contagious nature and potential to cause severe symptoms can strain healthcare systems, leading to a shortage of critical healthcare resources. It is therefore important to stratify hospitalized patients based on their risk of mortality, so that the allocation of healthcare resources can be optimized.
Many attempts at developing mortality prediction models have already been performed. In a systematic review performed by Wynants et al., which included preprint publications until 5 May 2020, 39 validated prognostic models for mortality were identified from a total of 37,421 screened records [6]. The commonly used features used in these models were radiologic findings, demographics, comorbidities, and routine blood measurements. Out of these 39, only one model consisting of age, sex, number of comorbidities, respiratory rate, peripheral oxygen saturation, Glasgow coma scale, urea, and C-reactive protein-(CRP) by S.R. Knight et al. was deemed worthy for further validation studies [7]. However, the model made use of features that are not commonly found in publicly available datasets, thereby limiting its applicability.
Age is a crucial prognosticator for COVID-19 patient outcomes, as has been demonstrated through a meta-analysis of over 600,000 case subjects [8]. However, age does not fully explain mortality in COVID-19 inpatients. To achieve more accurate risk stratification, combinations of features need to be analyzed for their predictive performances as compared to age-only models (AOMs). In our previous study [9], we aimed to develop a prognostic model that outperforms an AOM using only demographic features and comorbidities. Although that study found some features to be significantly associated with COVID-19 patient mortality, we were unsuccessful in developing a model that outperformed age alone in the external validation set.
In this study, we aimed to create a prognostic model that included demographics, comorbidities, and routine blood measurements by only using publicly available data that could be repurposed by independent researchers. Such repurposing of data is an underutilized approach to developing and/or researching the effectiveness of prediction models in the battle against COVID-19. Such an approach could greatly accelerate machine learning studies, as recycling publicly available data could remove the necessity of acquiring inpatient data from hospitals manually. We excluded imaging data from the scope of this work as models that do not require imaging are more likely to be used for triage during admission in a wide variety of hospital settings. The starting point for this work was a publication by Magro et al., published 14 January 2021 [10]. There were two reasons this paper was significant: (a) they made public two datasets, one with 1810 patients (to be used for model development in this study), and the other with 381 patients (an external validation set in this study); and (b) they provided a web model (WM), which we planned to compare against an AOM.
The stepwise objectives of this work can be summarized as: (1) perform a systematic search to identify relevant public datasets that can be used in this study, (2) identify if any of them have associated mortality prediction models that can be validated on the public datasets, (3) assess whether the WM developed by Magro et al. can be reduced to a minimal model-(MM) containing fewer features that can achieve statistically and clinically indistinguishable performance, (4) in case the MM contains features that some of the external validation sets identified during our systematic search do not, create a generalizable model (GM) that can be applied to all identified external validation sets, and (5) compare all models identified and created during our study to the AOM in the external validation sets to identify the highest-performing model among them. The AOM is used as a benchmark not because it is the best possible model, but because it is the simplest possible useful model, and any model that performs worse than it on one or more of the external validation sets is unlikely to be suitable for widespread clinical use.
2. Materials and Methods
2.1. Systematic Search for Publicly Available Data
To obtain datasets for external validation, a summary table was made of the 168 studies included in Wynants et al.’s third update (final search date 1 July 2020) of their systematic review [6]. The summary table contains the paper title, first author, DOI, whether the model is diagnostic or prognostic, and data availability (viz., no data statement, public and findable, public but not findable, available upon request, and reused dataset). For the papers that did have a data statement, an additional table was created to include the following information: whether imaging was used, final model type (e.g., logistic regression, random forest, and deep learning), deep learning network architecture (if applicable), features included in final model, the outcome that was modeled, and types of data in the published dataset (e.g., demographic, comorbidities, symptoms, and imaging). The summary table and associated figures can be found in the Supplementary Material. In addition to the systematic summary of Wynants et al.’s review, a Kaggle (www.kaggle.com) search (final search date of 2 June 2021) was performed to identify publicly available relevant datasets. The search terms used were combinations of: “COVID-19”, “SARS-CoV-2”, “coronavirus”, “mortality”, “prognostic”, “prediction”, “data”, “dataset”, and “clinical”. A search result was considered to be valid if the associated dataset was developed for and used in a peer-reviewed journal article on COVID-19.
The previously mentioned Magro et al. paper [10] includes data from 3 hospitals: the data from the first two (located in Bergamo and Pavia, which they called the derivation cohort) was used for model development. The data from the third hospital (located in Rome) was our first external validation set. All datasets found from the search described in the previous paragraph served as additional external validation datasets. In all cases, SARS-CoV-2 infection was defined as a laboratory confirmed positive real-time reverse transcriptase polymerase chain reaction (RT-PCR) test from nasal and pharyngeal swabs.
2.2. Statistical Analysis
The model development set was partitioned in two for training (75%) and internal validation (25%) using random stratified subsampling. For creating cohort summary tables, each dataset (whether training or validation) was separated into mortality and non-mortality groups. For all groups, continuous features were reported as median with interquartile range and binary features as count with percentage. Differences between mortality and non-mortality groups were tested through the Wilcoxon rank sum test for continuous features and Fisher’s exact test for binary features. A standard p-value threshold of 0.05 was used for statistical significance. No multiple hypothesis correction was done because the p-value was not the basis of feature selection. R for Windows (version 4.0.4) was used for this analysis as well as all further analyses. The mortality group was considered to be the positive class for all machine learning analyses.
2.3. Missing Data
The size of the training set is important for the quality of the trained model(s). The size of a validation set (internal and external), by contrast, is less important. Thus, missing data was imputed only in the training set using the missForest method, which uses the Random Forest (RF) algorithm for imputation. A RF model is constructed for each feature based on all remaining features to predict the feature’s missing values [11,12]. For the validation sets, no imputation was performed: a patient entry was removed if it had missing values for one or more of the relevant features, under the missing completely at random assumption. We found this assumption to be acceptable as there was no information in any of the published papers associated with the datasets used in our work to suggest that the missing data had some systematic reason for being missing. For the training set, to ensure that imputation did not introduce any bias, the analysis mentioned in the above subsection was done with and without imputation to observe if there was any qualitative difference.
2.4. Univariate Analysis
The area under the receiver operating characteristic curve (AUC), unlike Pearson or Spearman correlation, is independent of the class imbalance of a dataset i.e., its value is approximately the same whether a set is balanced between the two outcome classes (mortality and non-mortality, in this case) or not [13,14]. Thus, it was the metric chosen for univariate analysis. AUC was computed for each feature in the training set to check predictive ability; this AUC computation used the feature values directly, rather than converting each feature to a machine learning model first (e.g., using logistic regression). Thus, it was possible for AUC values to be lower than 0.5. These lower values mean that the correlation between the feature and the outcome is negative, i.e., higher values of the feature are associated with lower probabilities of the event (i.e., mortality). AUCs lower than 0.5 in the training set were converted to (1–AUC). This univariate analysis was also performed on the internal validation set to confirm that the AUCs were similar between the training and internal validation sets. If the training set AUC for a feature had to be converted to (1–AUC), this transformation was also applied to that feature in the internal validation set. We note that when actual classifiers were built using the methods stated in Section 2.5, no such transformation to the AUC values was needed. The results of the univariate analysis were used to drive the feature selection mentioned in Section 2.5.1. In addition to the univariate analysis, pairwise feature correlation maps were created (Pearson’s R and Spearman’s ρ) to check for feature redundancies. An absolute value of R or ρ ≥ 0.70 was defined as a strong correlation. If such strong correlations between features were discovered, they would be accounted for in the feature selection mentioned in Section 2.5.2.
2.5. Mortality Prediction Model Building
For all models, we used logistic regression, as it is easily explainable to a clinician and layperson, and is convertible to a nomogram, and thus easy to deploy clinically. No imbalance adjustment was performed in the training set. Instead, the optimal classification threshold for each dataset was chosen to maximize Youden’s J statistic.
2.5.1. Minimal Model (MM)
To determine whether using fewer features than the ones included in Magro et al.’s web model (WM) could achieve similar predictive performances, features were dropped one at a time from the WM, starting with the weakest feature (i.e., lowest AUC). After removing a feature, a new logistic regression model was trained. A reduction in AUC > 0.01 and the DeLong test p-value (threshold of 0.05) on the internal validation set were used to determine whether a model performed significantly differently from the WM [15]. If no difference was detected, the next iteration was carried out. The model with the fewest features before a significant difference was observed was considered the MM.
The MM is meant to be a parsimonious version of the WM of Magro et al. The reason having fewer features in a model may be beneficial, besides the usual machine learning arguments such as a reduced chance of overtraining, is that for clinical deployment, fewer features would need to be collected (i.e., reduced overhead) and it would be quicker to apply the model in real-time (e.g., when the physician is inputting the values on a smart interface). This would be a huge benefit in the hectic conditions that are typical during a case surge when such a triage tool is more likely to be used.
2.5.2. Generalizable Model (GM)
This model would only be created if all external validation sets did not contain the features included in the MM. The GM would consist of features that were common to all the validation datasets. Further feature selection would only be done if the GM contained more than five features, and the feature selection strategy would be the same as for the MM.
2.5.3. Model Comparison
In the external validation sets, the AOM would be compared to either the MM or the GM. In addition, any model found while performing the search described in Section 2.1 would be included in the comparison if possible.
3. Results
3.1. Systematic Search for Publicly Available Data
Of the 168 articles summarized from the review paper of Wynants et al. [6], 111 did not have any data availability statement. Of the remaining articles, 37 did not have public or findable data. Fourteen articles from the remaining subset concerned diagnostic models and were therefore excluded. Of the six articles that remained, three contained imaging data and hence were outside the scope, and the remaining three did not have any blood measurements. Thus, none of the 168 articles could be included in this work. Three publicly available datasets with their respective publications were identified from the Kaggle search [16,17,18]. These studies were not in the review [6], as they were all published after the inclusion date. The dataset from Yan et al. [16] is a time series describing 375 patients’ data obtained from electronic health records from Tongji hospital, Wuhan, China. Minimal, median, and maximal follow-up times for the time series data were 0, 11, and 35 days, respectively. The dataset contains information on demographics, routine blood measurements, and outcome data. Only records of features at time of admission have been included in this work. The dataset from Quanjel et al. [17] contains 305 records describing data from St Antonius Hospital, Nieuwegein, The Netherlands. It contains information regarding demographics, routine blood measurements, and hospital admission dates, discharge dates, and outcome data. Lastly, the dataset from Dupuis et al. [18] contains data from a French multicenter cohort of intensive care units (ICUs) involved in the management of patients critically ill with COVID-19 named Outcomerea. It contains 178 observations including demographics, routine blood measurements, symptoms, comorbidities, and outcome data. The datasets from [16,17,18] are subsequently referred to as Chinese, Dutch, and French external validation datasets, respectively.
The work of Yan et al. [16] included a mortality prediction rule that did not include age, but rather used the percentage of lymphocytes (% Lymph), and levels of C-reactive protein (CRP) and lactate dehydrogenase (LDH). The prediction rule is shown in Figure 1.
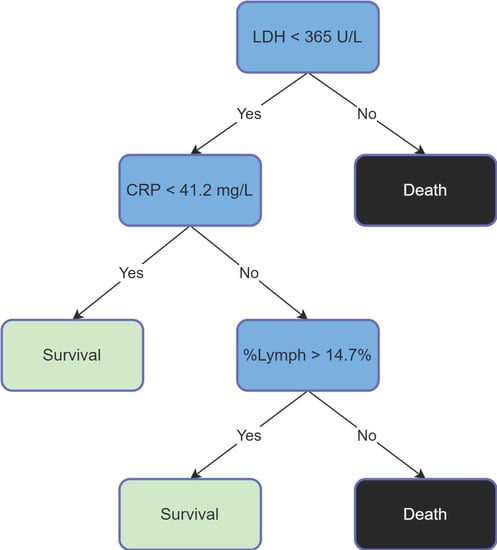
Figure 1.
Yan’s Prediction Rule [16].
3.2. Patient Characteristics
Table 1 shows patient characteristics for the training set, with and without imputation. It is observed that the imputation does not affect whether a feature is significant with respect to mortality. As mentioned, for the external validation datasets, a patient entry was removed if it had missing values for one or more of the relevant features. The Italian external validation dataset had 25 patients removed, the Dutch dataset had no patients removed, 62 were removed from the French dataset, and 31 patients were removed from the Chinese dataset. Thereafter, these datasets had 356, 305, 116, and 344 patients respectively. Table 2 summarizes the patient characteristics of all external validation sets.

Table 1.
Patient characteristics for the training set, without (top) and with (bottom) imputation.

Table 2.
Patient characteristics for all external validation sets.
3.3. Univariate Analysis
The AUCs of individual features in the training set were similar with and without imputation. Figure 2 shows the AUCs of all the features after imputation. The top three features were age, CRP, and LDH. To aid model-building, pairwise feature correlation maps were also calculated, as shown in Figure 3. No strong correlation (>0.7) was observed.
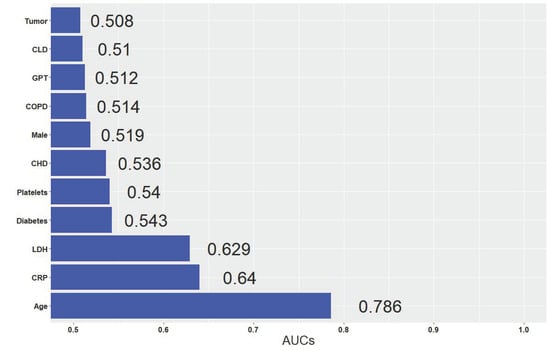
Figure 2.
AUCs of individual features in the imputed training set.
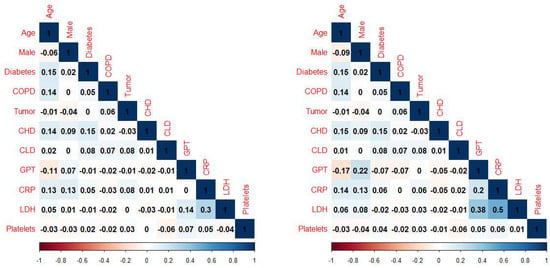
Figure 3.
Pairwise feature correlation (Pearson on left, Spearman on right) maps in the imputed training set.
3.4. Model Building and Comparison
The WM of Magro et al. included age, sex, LDH, chronic heart disease (CHD), chronic liver disease (CLD), diabetes, and days elapsed from first symptoms until hospitalization. Surprisingly, it did not include CRP, despite the fact that our univariate analysis identified it as a top-three feature for the training set. Furthermore, in the public dataset the authors published, days elapsed from first symptoms until hospitalization was not included. Thus, our implementation of the WM was not the same as the one published by Magro et al. However, they found the AUC of their WM, which used Fine and Gray competing risks multivariate model (with discharge as a competing event) was 0.822 (95% CI 0.722–0.922) in the derivation cohort and 0.820 (95% CI 0.724–0.920) in the validation cohort. In comparison, our implementation of the WM (which could not include one feature because of it not being published and used logistic regression instead of the competing risk model) had an AUC of 0.821 (95% CI 0.797–0.844) in the imputed training set.
When creating the MM, the order in which we tried removing features from our WM (viz., CLD, diabetes, sex, CHD, LDH, and age) was based on the AUC in the internal validation set. The MM based on performance in the internal validation set included age, LDH, CHD, and sex. Unfortunately, the MM could not be used on all the external validation sets, due to CHD not being included in some of them. Thus, a GM had to be built. As mentioned, the GM features were based on availability, and included, age, sex, LDH, and CRP. Table 3 reports the performance of the various models on the validation sets. For the internal and Italian external validation sets, we report metrics for the WM, the MM, the GM, and the AOM. Yan’s prediction rule is not included, because the Italian data did not contain % Lymph as a feature. For the Dutch, French, and Chinese external validation sets, we report the GM, the AOM, and Yan’s prediction rule.

Table 3.
Model performances in all validation sets. AU-PRC = area under precision-recall curve.
In the internal and Italian external validation sets, the GM was statistically significantly better than the AOM (p < 0.001 and p = 0.02, respectively), and statistically indistinguishable from the WM. In the Chinese dataset, the GM performed much better than the AOM (AUCs of 0.934 and 0.833, respectively; p < 0.001). In the Dutch dataset, GM was statistically significantly better than AOM (p = 0.04). In the French dataset, AOM and GM were statistically indistinguishable. When comparing Yan’s prediction rule to the GM, the GM was superior (for both balanced accuracy and AUC) for the Dutch and French datasets; in the Chinese dataset, they were quite similar, despite Yan’s rule being trained on that dataset.
4. Discussion
This work focused on repurposing publicly available data to identify important features for mortality prediction for hospitalized COVID-19 patients and to develop and validate a predictive model using those features. The aim was for this model to outperform an AOM, as well as achieving similar or better performances than the models that had previously been derived using the datasets included in this study. An associated aim was to develop the MM to check whether a model with fewer features (i.e., the MM) can perform as well as the original model (i.e., the WM). This indeed turned out to be the case, as the WM contained seven features, and the MM only four. We hope that other model developers will be motivated by this to check whether their model of choice can work just as effectively with fewer features. The reader may be unsure why we developed an MM and a GM, instead of a single model. This is because the two models have different aims. The GM cannot be considered an MM. The main reason is that the MM must start from the features included in the WM before features are removed one at a time. Thus, it does not include CRP (as it was not included in the WM), even though CRP was included in the dataset that Magro et al. made public. The second reason is that a fundamental requirement for the MM is that its performance must be statistically indistinguishable from the original model (WM). By contrast, the GM does not need to satisfy this requirement, it only needs to be applicable to all included datasets.
The biggest benefit of repurposing data is that it reduces the overhead of time and labor needed to obtain a curated dataset suited to answering a research question. It also enables researchers who are typically not part of the medical data science domain or not collaborating with a clinical center to contribute their expertise. To accelerate such research, there is an urgent need of journals mandating such anonymized or pseudonymized datasets be made public together with a publication of the paper, when patient confidentiality is not at risk. In particular, if the data is anonymized, it no longer falls under the General Data Protection Regulation (GDPR) of the European Union. At the very least, a paper should not be published without an explicit data availability statement. Ideally, such data should adhere to the FAIR criteria. For findability, the data needs to have a globally unique identifier, as well as being rich in metadata that are registered in a searchable source. To meet the accessibility criteria, the (meta)data needs to be retrievable using an open, free, standardized, and universal communications protocol. For interoperability, the (meta)data is required to be written in formal, widely applicable language and use vocabularies adhering to FAIR principles. Finally, to be reusable, the data needs to contain a large variety of domain-relevant attributes and it needs to be made available with a clear data license statement. These principles are described in more detail within the original article describing the FAIR guidelines [19]. There is a great need for a publicly available interface that allows researchers to search and download COVID-19 patient data based on tailored inclusion characteristics. For cancer imaging data, such a platform already exists, i.e., The Cancer Imaging Archive [20].
Several studies have already shown that age is an important predictor for COVID-19 mortality [21,22]. This was confirmed in this study, where the median age was significantly higher for the mortality group across all datasets. Other studies have shown that elevated CRP levels are associated with a risk of dying of COVID-19 [23,24]. This held true for most cohorts, with the median CRP level being significantly higher for the mortality group in all except the French dataset, which has a bias due to only containing ICU patients. Being male is also believed to be a risk factor for mortality in COVID-19 patients [25,26]. This was not observed, except in the Chinese dataset. However, in the Italian and Dutch cohorts, over 60% of the total cohort was male, and in the French cohort (ICU), over 80% was male. Researchers have shown that elevated levels of LDH are associated with an increased risk of mortality for COVID-19 patients [27,28]. This was confirmed through this study, with LDH being significantly elevated at admission in deceased COVID-19 patients across all cohorts. Lymphopenia, the occurrence of abnormally low lymphocyte levels in the blood, has also been demonstrated to be associated with COVID-19 outcome severity [29]. In this study, this was true for the Dutch and Chinese cohorts, but not for the French one, again possibly because of the ICU bias. Lymphopenia as a risk factor could not be evaluated from the Italian cohorts, as the data lacked entries on the percentage of lymphocytes in blood. Lastly, comorbidities have been shown to be associated with an increased risk of death in COVID-19 patients, as has been confirmed by numerous studies [30,31,32]. This could be confirmed using the Italian cohorts, though not using the cohorts from the three other countries due to them not including data on comorbidities. Within the Italian derivation cohort, the frequencies of diabetes, COPD, cancer, CHD, and CLD were found to be significantly increased in the mortality group.
For the purpose of COVID-19 mortality prediction model development, we recommend researchers to choose model features not only based on their predictive capabilities, but also on their availability within the routine clinical workflow. This should ultimately lead to quicker discoveries of more widely applicable, generalizable prediction models based on patient data that is readily available at admission. The pandemic has put enormous strain on healthcare systems, and thus a model that uses features that require additional procedures such as imaging to be performed are less likely to be used widely. It is also vital to create a platform that would serve as an open source repository for a curated subset of predictive models for COVID-19 outcomes. We have created such a prototype platform (covid19risk.ai) and documented its creation [33]. This platform needs to grow, and we encourage model developers to contact us for showcasing their model on the website. With such a platform in place, future developments would allow researchers to search for all predictive models that match certain criteria and then use these models as benchmarks when assessing the performance of any new models.
According to the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) statement [34], for the WM, MM, GM, and AOM developed in this paper, this study is classified as type 3 (development and validation using separate data). For Yan’s prediction rule, this study is classified as type 4 (validation of a published prediction model using separate data). We do not include a TRIPOD checklist with this work because based on the results found in this study, we are not promoting any of these models for widespread use.
This study suffered from several limitations: (1) Each of the datasets comprised different features, thereby greatly limiting the options of developing a generalizable model. (2) Publicly available FAIR data is very limited. In the absence of more such datasets, it is not possible to make a clear recommendation whether using the GM is preferable to an AOM or Yan’s prediction rule. (3) There are discrepancies between the datasets regarding the definition of the mortality time window. In this study it has been assumed that all discharged patients have not died of COVID-19 after being discharged, which may not be accurate. (4) Records of certain patients had to be removed in the validation cohorts due to missing values. This decision is based on the “missing completely at random” assumption [35], which may not be valid. (5) As all of the datasets used in this study come from a time period that is pre-vaccination, we cannot deduce how the findings of this paper would be affected if datasets based on cohorts of vaccinated patients (who contracted a breakthrough infection and were hospitalized) were used. (6) The living review used for finding datasets for this study had a final search date of 1 July 2020. While this was complemented with a Kaggle search (final search date of 2 June 2021), given that most researchers do not post their public datasets on Kaggle, it is likely that datasets which could have been used for this study were missed. (7) Had such additional datasets been found, they would possibly have associated mortality prediction models, which could then be added to the list of models that the GM could be compared against, leading to a more rigorous evaluation than was possible in this study.
The reader may be surprised that we do not group the external validation cohorts together, as this would provide us with a larger sample size for statistical comparisons, as well as allow for a sort of meta-evaluation of model performance. The reason we choose to not do this is because for external datasets collected without any overarching protocol, coming from clinical sites all over the world with different patterns of admission and different standards of care, such a combination may not be meaningful, and the performance on such a combined dataset hard to interpret.
For some external datasets in this study, some predictive features are simply absent. For example, CHD (a key feature of the MM) was not present in the Chinese, Dutch, and French datasets. It is possible to create a CHD feature for each of these datasets, although this would be considered synthetic feature creation rather than data imputation. Fundamentally, such synthetic data could only be generated by making certain assumptions based on the training set. Thus, the performance of any model on such synthetic data would be overly optimistic, as the behavior of this synthetic feature would be mimicking the behavior of the corresponding real feature in the training set.
How to impute missing values when a model is used in a clinical setting is a matter of debate. We believe it is the responsibility of model developers to provide a clear explanation of what to do if a patient has one or more of the necessary features missing. If the model developers do recommend imputation, they need to specify which method should be used. Since even a basic method such as mean or median imputation requires knowledge of the mean or median values of all model features for the cohort on which the model is being deployed, this is likely to be an impractical approach in the emergency rooms of hospitals. More pragmatically, the model developers could rank the features in order of importance, and then mention how removing a feature affects the predictive performance (e.g., how much reduction in sensitivity and specificity is to be expected). Then it would be up to the clinician to decide whether the model is still worth using if an important feature is missing, or if the feature can be easily obtained. In particular, for multi-factorial models which contain data from multiple independent sources (say genomics, imaging, etc.), the model developers should provide information about what is the added benefit of such data, so the clinician can decide if such data is worth collecting. We think that if a feature is missing for a patient and the feature cannot be obtained quickly, the model should not be used for the patient unless the performance of the model without that feature has been quantified, documented, and judged to be adequate for clinical use.
5. Conclusions
We performed a systematic search to identify all relevant public datasets that can be used to create a mortality prediction model using demographics, comorbidities, and routine blood measurements. A search based on a systematic review [6] yielded no results that passed our inclusion criteria, and a Kaggle search provided only three datasets. From the web model of Magro et al., we were successfully able to create a minimal model that had statistically indistinguishable performance. This model included age, LDH, CHD, and sex. However, since the external validation datasets did not include CHD, we had to create a generalizable model, which included age, sex, LDH, and CRP. We also found Yan’s prediction rule during our search, which could be used as an additional comparison. While the GM outperformed the age-only model in three of the external datasets, it was statistically indistinguishable in the fourth external dataset. Thus, we are unable to make a strong recommendation for using the GM in all cases. This study underscores the need for a platform that facilitates a search for COVID-19 datasets, and a platform for finding relevant prediction models that need to be outperformed by any new model. The latter platform has a functioning prototype (covid19risk.ai) and needs to be expanded through future collaboration.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/biomed2010002/s1.
Author Contributions
Conceptualization, A.C.; methodology, A.C.; software, A.C. and G.W.; validation, A.C.; formal analysis, G.W.; investigation, G.W.; resources, P.L.; data curation, G.W. and A.C.; writing—original draft preparation, G.W. and A.C.; writing—review and editing, H.W. and P.L.; visualization, G.W. and A.C.; supervision, A.C. and H.W.; project administration, P.L.; funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
European Commission’s Horizon 2020 Research and Innovation programme under grant agreement 101016131 (ICOVID) and the Innovative Medicines Initiative 2 Joint Undertaking under grant agreement No. 101005122 (DRAGON).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This work only used publicly available data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- WHO Coronavirus (COVID-19) Dashboard. Available online: https://covid19.who.int/ (accessed on 21 September 2021).
- Impact of COVID-19 on People’s Livelihoods, Their Health and Our Food Systems. Available online: https://www.who.int/news/item/13-10-2020-impact-of-covid-19-on-people’s-livelihoods-their-health-and-our-food-systems (accessed on 21 September 2021).
- Saladino, V.; Algeri, D.; Auriemma, V. The psychological and social impact of Covid-19: New perspectives of well-being. Front. Psychol. 2020, 11, 2550. [Google Scholar] [CrossRef] [PubMed]
- Cascella, M.; Rajnik, M.; Aleem, A.; Dulebohn, S.; Di Napoli, R. Features, evaluation, and treatment of coronavirus (COVID-19). StatPearls 2021. Available online: https://www.statpearls.com/ArticleLibrary/viewarticle/52171 (accessed on 21 September 2021).
- Heustess, A.M.; Allard, M.A.; Thompson, D.K.; Fasinu, P.S. Clinical Management of COVID-19: A Review of Pharmacological Treatment Options. Pharmaceuticals 2021, 14, 520. [Google Scholar] [CrossRef] [PubMed]
- Wynants, L.; Van Calster, B.; Collins, G.S.; Riley, R.D.; Heinze, G.; Schuit, E.; Bonten, M.M.; Dahly, D.L.; Damen, J.A.; Debray, T.P.; et al. Prediction models for diagnosis and prognosis of COVID-19: Systematic review and critical appraisal. BMJ 2020, 369, m1328. [Google Scholar] [CrossRef] [Green Version]
- Knight, S.R.; Ho, A.; Pius, R.; Buchan, I.; Carson, G.; Drake, T.M.; Dunning, J.; Fairfield, C.J.; Gamble, C.; Green, C.A.; et al. Risk stratification of patients admitted to hospital with covid-19 using the ISARIC WHO Clinical Characterisation Protocol: Development and validation of the 4C Mortality Score. BMJ 2020, 370, m3339. [Google Scholar] [CrossRef] [PubMed]
- Bonanad, C.; García-Blas, S.; Tarazona-Santabalbina, F.; Sanchis, J.; Bertomeu-González, V.; Fácila, L.; Ariza, A.; Núñez, J.; Cordero, A. The effect of age on mortality in patients with COVID-19: A meta-analysis with 611,583 subjects. J. Am. Med. Dir. Assoc. 2020, 21, 915–918. [Google Scholar] [CrossRef]
- Chatterjee, A.; Wu, G.; Primakov, S.; Oberije, C.; Woodruff, H.; Kubben, P.; Henry, R.; Aries, M.J.; Beudel, M.; Noordzij, P.G.; et al. Can predicting COVID-19 mortality in a European cohort using only demographic and comorbidity data surpass age-based prediction: An externally validated study. PLoS ONE 2021, 16, e0249920. [Google Scholar] [CrossRef]
- Magro, B.; Zuccaro, V.; Novelli, L.; Zileri, L.; Celsa, C.; Raimondi, F.; Gori, M.; Cammà, G.; Battaglia, S.; Genova, V.G.; et al. Predicting in-hospital mortality from Coronavirus Disease 2019: A simple validated app for clinical use. PLoS ONE 2021, 16, e0245281. [Google Scholar] [CrossRef]
- Stekhoven, D.J.; Bühlmann, P. MissForest—non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef] [Green Version]
- Waljee, A.K.; Mukherjee, A.; Singal, A.G.; Zhang, Y.; Warren, J.; Balis, U.; Marrero, J.; Zhu, J.; Higgins, P.D. Comparison of imputation methods for missing laboratory data in medicine. BMJ Open 2013, 3, e002847. [Google Scholar] [CrossRef]
- Chatterjee, A.; Woodruff, H.; Wu, G.; Lambin, P. Limitations of Only Reporting the Odds Ratio in the Age of Precision Medicine: A Deterministic Simulation Study. Front. Med. 2021, 8, 640854. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, T. ROC graphs: Notes and practical considerations for researchers. Mach. Learn. 2004, 31, 1–38. [Google Scholar]
- De Long, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, H.T.; Goncalves, J.; Xiao, Y.; Wang, M.; Guo, Y.; Sun, C.; Tang, X.; Jing, L.; Zhang, M.; et al. An interpretable mortality prediction model for COVID-19 patients. Nat. Mach. Intell. 2020, 2, 283–288. [Google Scholar] [CrossRef]
- Quanjel, M.J.; Van Holten, T.C.; Gunst-van der Vliet, P.C.; Wielaard, J.; Karakaya, B.; Söhne, M.; Moeniralam, H.S.; Grutters, J.C. Replication of a mortality prediction model in Dutch patients with COVID-19. Nat. Mach. Intell. 2021, 3, 23–24. [Google Scholar] [CrossRef]
- Dupuis, C.; De Montmollin, E.; Neuville, M.; Mourvillier, B.; Ruckly, S.; Timsit, J.F. Limited applicability of a COVID-19 specific mortality prediction rule to the intensive care setting. Nat. Mach. Intell. 2021, 3, 20–22. [Google Scholar] [CrossRef]
- Wilkinson, M.D.; Dumontier, M.; Aalbersberg, I.J.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.W.; Da Silva Santos, L.B.; Bourne, P.E.; et al. The FAIR Guiding Principles for scientific data management and stewardship. Sci. Data 2016, 3, 1–9. [Google Scholar] [CrossRef] [Green Version]
- The Cancer Imaging Archive. Available online: https://www.cancerimagingarchive.net/ (accessed on 21 September 2021).
- Levin, A.T.; Hanage, W.P.; Owusu-Boaitey, N.; Cochran, K.B.; Walsh, S.P.; Meyerowitz-Katz, G. Assessing the age specificity of infection fatality rates for COVID-19: Systematic review, meta-analysis, and public policy implications. Eur. J. Epidemiol. 2020, 35, 1123–1138. [Google Scholar] [CrossRef]
- Liu, Y.; Mao, B.; Liang, S.; Yang, J.W.; Lu, H.W.; Chai, Y.H.; Wang, L.; Zhang, L.; Li, Q.H.; Zhao, L.; et al. Association between age and clinical characteristics and outcomes of COVID-19. Eur. Respir. J. 2020, 55, 2001112. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Hou, J.; Ma, F.Z.; Li, J.; Xue, S.; Xu, Z.G. The common risk factors for progression and mortality in COVID-19 patients: A meta-analysis. Arch. Virol. 2021, 166, 2071–2087. [Google Scholar] [CrossRef]
- Dai, Z.; Zeng, D.; Cui, D.; Wang, D.; Feng, Y.; Shi, Y.; Zhao, L.; Xu, J.; Guo, W.; Yang, Y.; et al. Prediction of COVID-19 patients at high risk of progression to severe disease. Front. Public Health 2020, 8, 574915. [Google Scholar] [CrossRef]
- Peckham, H.; De Gruijter, N.M.; Raine, C.; Radziszewska, A.; Ciurtin, C.; Wedderburn, L.R.; Rosser, E.C.; Webb, K.; Deakin, C.T. Male sex identified by global COVID-19 meta-analysis as a risk factor for death and ITU admission. Nat. Commun. 2020, 11, 6317. [Google Scholar] [CrossRef]
- Kelada, M.; Anto, A.; Dave, K.; Saleh, S.N. The role of sex in the risk of mortality from COVID-19 amongst adult patients: A systematic review. Cureus 2020, 12, e10114. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Ye, J.; Chen, Q.; Hu, W.; Wang, L.; Fan, Y.; Lu, Z.; Chen, J.; Chen, Z.; Chen, S.; et al. Elevated lactate dehydrogenase (LDH) level as an independent risk factor for the severity and mortality of COVID-19. Aging (Albany NY) 2020, 12, 15670. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, H.; Mu, S.; Wei, W.; Jin, C.; Tong, C.; Song, Z.; Zha, Y.; Xue, Y.; Gu, G. Lactate dehydrogenase, an independent risk factor of severe COVID-19 patients: A retrospective and observational study. Aging (Albany NY) 2020, 12, 11245. [Google Scholar] [CrossRef]
- Zhao, Q.; Meng, M.; Kumar, R.; Wu, Y.; Huang, J.; Deng, Y.; Weng, Z.; Yang, L. Lymphopenia is associated with severe coronavirus disease 2019 (COVID-19) infections: A systemic review and meta-analysis. Int. J. Infect. Dis. 2020, 96, 131–135. [Google Scholar] [CrossRef] [PubMed]
- Somasekar, J.; Kumar, P.P.; Sharma, A.; Ramesh, G. Machine learning and image analysis applications in the fight against COVID-19 pandemic: Datasets, research directions, challenges and opportunities. Mater. Today Proc. 2020. Available online: https://www.sciencedirect.com/science/article/pii/S2214785320370620 (accessed on 21 October 2021).
- Noor, F.M.; Islam, M.M. Prevalence and associated risk factors of mortality among COVID-19 patients: A meta-analysis. J. Community Health 2020, 45, 1270–1282. [Google Scholar] [CrossRef]
- Najera, H.; Ortega-Avila, A.G. Health and Institutional Risk Factors of COVID-19 Mortality in Mexico, 2020. Am. J. Prev. Med. 2021, 60, 471–477. [Google Scholar] [CrossRef]
- Halilaj, I.; Chatterjee, A.; Van Wijk, Y.; Wu, G.; Van Eeckhout, B.; Oberije, C.; Lambin, P. Covid19Risk.ai: An Open Source Repository and Online Calculator of Prediction Models for Early Diagnosis and Prognosis of COVID-19. BioMed 2021, 1, 41–49. [Google Scholar] [CrossRef]
- Collins, G.S.; Reitsma, J.B.; Altman, D.G.; Moons, K.G. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD) the TRIPOD statement. Circulation 2015, 131, 211–219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhaskaran, K.; Smeeth, L. What is the difference between missing completely at random and missing at random? Int. J. Epidemiol. 2014, 43, 1336–1339. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).