Perspectives on Mathematical Modeling Education: Conceptions and Research

Definition

Mathematical modeling is a cyclical process in which mathematics is used to represent, explore, and better understand real-world situations by mathematizing a problem and validating the results. Unlike traditional word problems, modeling tasks require learners to make assumptions, define quantities, apply mathematics, interpret results, and revise solutions within authentic contexts. Mathematical modeling is increasingly recognized as essential in mathematics education, highlighted in standards such as the Common Core State Standards for Mathematics through mathematical practice 4 (MP4): model with mathematics. This entry explores the evolving landscape of mathematical modeling education. First, it reviews the diverse conceptions of modeling and the various frameworks used to describe the modeling process, including distinctions between holistic and atomistic approaches. Second, it examines the current state of research, including the documented benefits of modeling for student engagement and access, as well as the challenges teachers face in enacting modeling tasks. Finally, the entry discusses implications for future research and practice, emphasizing the need for targeted teacher preparation and continued theoretical refinement to better support the integration of modeling into mathematics instruction.

1. Introduction

Mathematical modeling, often shortened to modeling, has become a prominent focus in contemporary mathematics education. At its core, modeling involves using mathematics as a tool to interpret and analyze real-world phenomena, moving well beyond the scope of conventional textbook word problems. Modeling tasks invite learners to grapple with authentic situations by identifying assumptions, specifying relevant quantities, applying mathematical tools, and refining their solutions through interpretation and revision. The importance of this practice is underscored in documents such as the Common Core State Standards for Mathematics that position “model with mathematics” (MP4) as a central mathematical practice [1].

This entry examines the growing body of work on mathematical modeling education, with particular attention to developments in Western contexts. It begins by tracing different ways modeling has been conceptualized and the range of frameworks that describe how the process unfolds, from holistic cycles to more fine-grained step-oriented perspectives. The discussion then turns to empirical research, highlighting evidence of how modeling can support student engagement and equitable access to mathematics, as well as the persistent challenges teachers encounter when implementing modeling tasks. The entry concludes with implications for future directions, calling for more robust teacher preparation and theoretical development to strengthen the role of modeling in mathematics instruction.

While this entry primarily attends to perspectives from the West, it is important to acknowledge that research and practice in mathematical modeling education also has rich traditions in Eastern contexts such as China and Japan. Across both regions, modeling is valued for its potential to connect mathematics with real-world problems, develop problem-solving competencies, and prepare students for future science, technology, engineering, and mathematics (STEM) endeavors. Yet differences emerge in emphasis and implementation. In the West, modeling is often framed as an open-ended process of inquiry that supports creativity, collaboration, and sense-making, while in the East it is more commonly positioned as structured application, closely tied to canonical mathematics, competitive contexts, or national curricular goals. These contrasts reflect broader cultural and educational traditions, but they also share a commitment to advancing students’ mathematical thinking. A fuller exploration of Eastern perspectives, however, lies beyond the scope of this entry.

2. Defining Mathematical Modeling

Mathematical modeling has gained substantial attention in recent decades as a central component of mathematics education. Despite this growing emphasis, there is no universally accepted definition of what mathematical modeling entails. Instead, a wide array of interpretations, perspectives, and frameworks populate the literature, each reflecting different goals, educational traditions, and perspectives on how mathematics interacts with the real world [2]. This conceptual diversity presents both opportunities and challenges for mathematics educators seeking to implement modeling practices in the classroom.

At its core, mathematical modeling involves an authentic real-world situation that can be addressed by multiple pathways and solutions. A widely referenced definition from the Guidelines for Assessment and Instruction in Mathematical Modeling Education (GAIMME) describes modeling as “a process that uses mathematics to represent, analyze, make predictions or otherwise provide insight into real-world phenomena” [3] (p. 8). This process is distinctive for its cyclic nature, where, starting from a real-world situation, students or modelers formulate a mathematical representation, work through it, and then return to the context to assess the validity and applicability of their solution.

One key feature distinguishing mathematical modeling from other forms of mathematical problem solving is the authenticity and complexity of the problems involved. Modeling tasks often emerge from real-world contexts that are open-ended and lack a single correct solution. These problems may be messy, data-rich, or ill-defined, requiring students to simplify situations, clarify assumptions, and make decisions about which variables or relationships are relevant. This need for sense making and interpretation demands a range of skills and offers a rich site for the development of mathematical thinking. Strong reasoning, both mathematical and real-world, is required for students to produce rich solutions.

The process of translating between real-world scenarios and mathematical abstractions, often referred to as mathematization, is central to modeling. This includes algebra skills like constructing relationships among variables, creating equations or diagrams, and determining which tools or representations are most appropriate. Once a mathematical model is developed and solved, students must interpret their results in terms of the original context and assess whether their model offers meaningful or useful insights. The process is iterative, often requiring multiple cycles of refinement to produce a model that is both accurate and insightful.

2.1. Frameworks for the Modeling Process

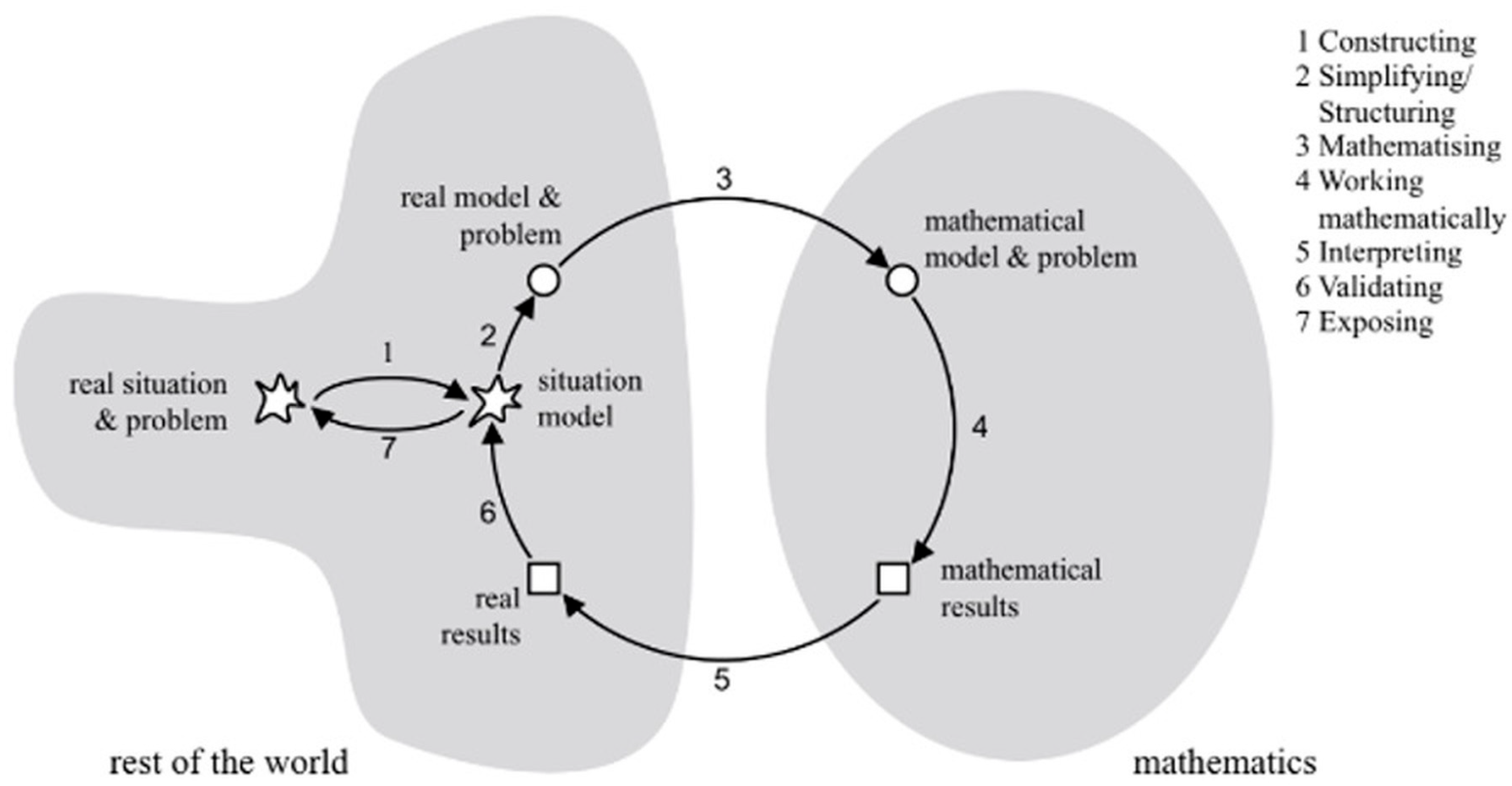
Various researchers have articulated different albeit similar frameworks for the modeling process, offering guidance for both instruction and assessment. Furthermore, different modeling frameworks can be designed for research and practice. Consider Blum [4]’s mathematical modeling cycle in Figure 1, which was designed primarily for research usage. This modeling cycle emphasizes the distinction between the real world and the mathematical world. The process begins when a modeler encounters a real-world situation and identifies a problem to solve. To proceed, the modeler must first develop an understanding of the context, forming what is known as a situation model [5]. This understanding is then refined by making simplifying assumptions and decisions, which lead to the creation of a real model—a structured version of the problem that is ready to be translated into mathematical terms. The next step involves mathematizing the real model to generate a mathematical model, which can be worked with to produce mathematical results. These results are then interpreted back into the real-world context to generate real results. The modeler must then check whether these real results appropriately address the original situation. If they do not, revisions are made and the process is repeated. This iterative nature of the modeling process is represented in the cycle’s structure. The final stage, called exposing, involves presenting or communicating the model and its conclusions [4].

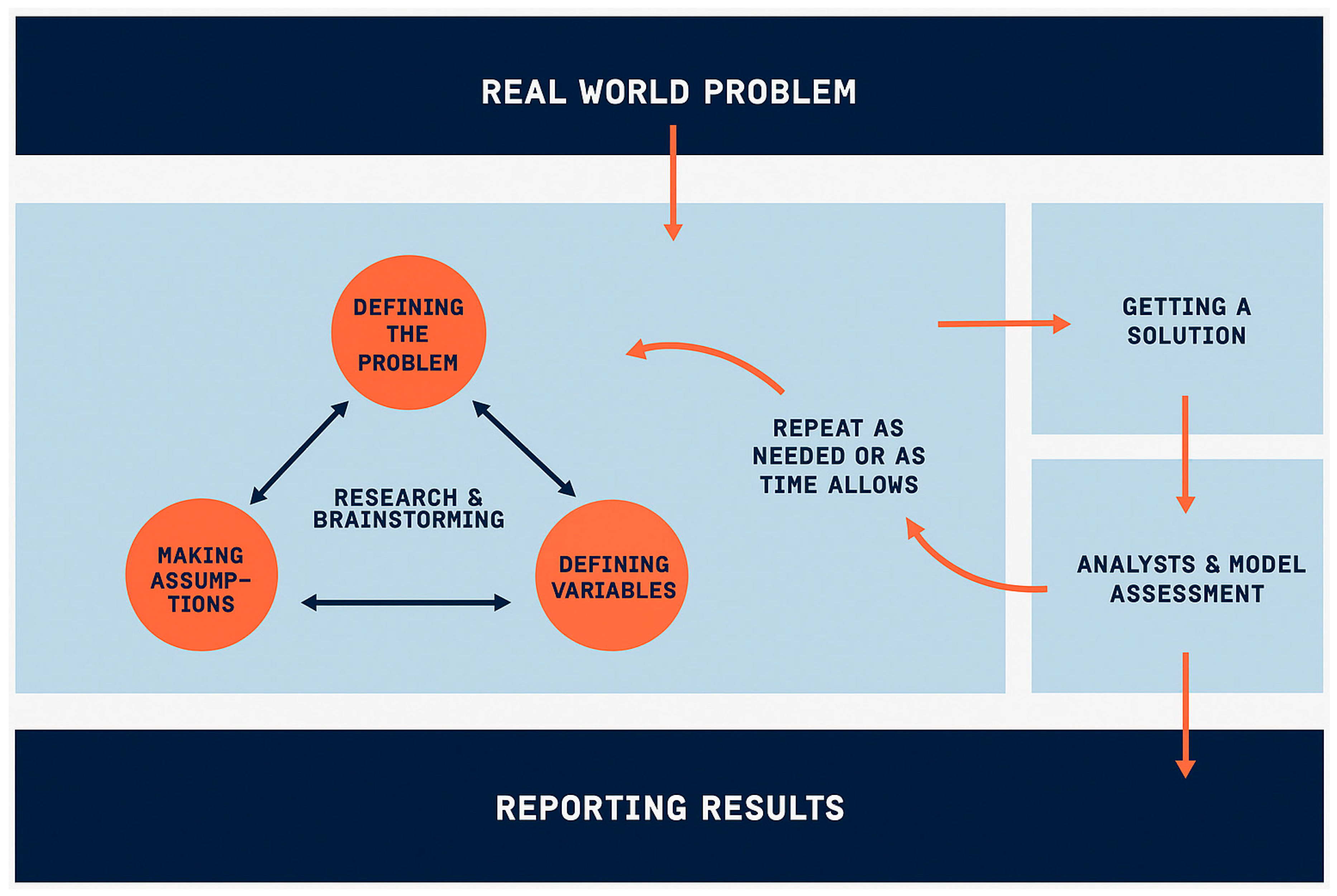
Next, consider Bliss et al. [6]’s mathematical modeling cycle in Figure 2, which was primarily designed for practitioner usage. This modeling cycle was featured in a practitioner handbook from the Society for Industrial and Applied Mathematics (SIAM) and shares several similarities with Blum [4]’s framework. Both highlight the iterative nature of modeling, using arrows to represent how modelers may revisit earlier steps as needed. However, Bliss and colleagues place particular emphasis on the early stages of modeling, which involve researching the context, brainstorming possible approaches, and moving flexibly between defining the problem, identifying variables, and making assumptions. Once a potential solution is developed, it is carefully analyzed and evaluated. If the solution falls short, the modeler may return to the initial stages to adjust their thinking. As with other modeling cycles, this one concludes with the communication or reporting of results. While these two modeling cycles separate the real world and the mathematical world, not all modeling cycles show a strict separation. For example, the semiotic-cognitive mathematical modeling cycle acknowledges the presence of the real world and mathematical world, but without showing them as completely separate [7].

In general, many mathematical modeling frameworks outline the following stages [8]:

• Understanding the Problem: Identify and analyze the context to formulate a clear problem statement.
• Making Assumptions and Defining Variables: Simplify the real-world situation by deciding what aspects to include and what can be ignored.
• Formulating a Mathematical Model: Translate the simplified real-world scenario into a mathematical structure, which may involve algebraic expressions, graphs, equations, or other representations.
• Solving the Mathematical Model: Apply mathematical procedures and techniques to generate results.
• Interpreting and Validating Results: Relate the mathematical outcomes back to the real-world context and assess whether the model makes sense or needs refinement.
• Reporting Findings: Communicate the solution and its implications, often including limitations of the model and suggestions for improvement.

Importantly, research has shown that these steps are not strictly linear. Modelers often move back and forth among stages, revisiting assumptions or redefining variables as new information or understanding emerges [9]. Moreover, validation, a crucial but often underemphasized aspect, can occur at multiple points in the modeling process rather than only at the end.

2.2. Modeling Competencies and Holistic and Atomistic Approaches to Modeling

Maaß [10] identified a set of core modeling competencies: understanding the problem, setting up a mathematical model, solving the model, interpreting results, and validating the solution, each of which can be broken down into sub-competencies. For instance, “understanding the problem” may involve identifying relevant quantities and making assumptions, while “formulating a model” requires selecting appropriate mathematical tools and representations. Maaß’s set of competencies and sub-competencies are just one commonly cited example, and different conceptualizations and distinctions exist among mathematical modeling researchers [11]. Building on this, Niss and Højgaard [12] distinguished between general and specific definitions of mathematical competence. General definitions take a broad holistic view, understood as an integrated capacity to use mathematics meaningfully. Specific definitions, by contrast, break competence into more narrowly defined sub-competencies that can be taught and assessed individually. This distinction parallels the holistic–atomistic approaches in modeling: holistic tasks align with the general view of competence, while atomistic tasks resonate with the specific view. Given the complexity of the modeling process, educators have developed different instructional approaches to support student engagement with modeling. These can be broadly classified as holistic or atomistic approaches [13].

A holistic approach involves engaging students in the full modeling cycle from start to finish [13]. Students confront real-world problems, make assumptions, construct and solve models, interpret their results, and refine their work through multiple iterations. Holistic tasks are often open-ended, allowing for multiple solution paths and varied representations. This approach emphasizes the integration of all modeling competencies and provides opportunities for students to see how mathematical thinking is used in context. In this sense, holistic tasks embody the general view of competence as an overarching, integrated ability.

An example of a holistic mathematical modeling task is the Chernobyl disaster task [14]. In this task, students are shown an informational video about the Chernobyl disaster and are then asked to consider being recruited by the National Regulatory Commission to determine which radioactive substance(s) released at the Chernobyl disaster had the greatest impact. The term “greatest impact” is open to interpretation by the student, allowing this task to be open-ended and produce multiple realistic solutions. Students are provided a spreadsheet with data on the radioactive substances, their half-life, initial amount released, and safe exposure limit. After making an assumption about what is meant by “greatest impact”, students engage in mathematics to determine how much of a radioactive substance is left today and when the safe exposure limit would be reached. Students investigate multiple radioactive substances to determine which had the greatest impact. Students may also consider other factors like influence on people and the environment to help base their decision. Their mathematics and exploration of other factors allow students to engage cyclically in the modeling process to come up with a solution that they can defend as the most realistic.

Another example of a holistic mathematical modeling task is the shoebox filled with cash [15]. In this task, students must determine whether a witness who saw a man drop a shoebox stuffed with USD 70,000 in small bills is telling the truth. This task is holistic because it begins with an open-ended real-world problem that requires students to engage in all parts of the modeling cycle.

In contrast, an atomistic approach focuses on specific components or sub-competencies within the modeling process [13]. For example, students might only work on formulating assumptions, interpreting results, or validating a given model. Atomistic tasks are often used to build foundational skills in modeling or to isolate key ideas for instructional focus. While they may lack the richness of a full modeling cycle, atomistic tasks are valuable for scaffolding learning and helping students gradually build confidence with different aspects of modeling. This reflects the specific view of competence, where particular sub-skills are developed in isolation before students can coordinate them holistically.

An example of an atomistic mathematical modeling task is the long jump task [16], adapted from College and Career Readiness Sample Mathematics Tasks [17] and shown in Figure 3 below. Students are provided with long jump times for three jumpers and asked to determine why each one should go to the championship. Coming up with a justification for each jumper helps students develop experience with making assumptions. For example, if Elsa were selected to go to the championship, what assumption was made about who should go? One explanation would be that someone assumed the jumper with the highest jump overall should go to the championship. By engaging in justifications about assumptions made, students practice making reasonable assumptions but do not engage fully in the cyclic process of modeling. While there is some open-endedness as to what each justification might be, the student is not necessarily engaged in mathematical calculations or models to answer the question. By not engaging in all parts of the modeling cycle, this task is considered an atomistic one.

Another example of an atomistic mathematical modeling task could involve different ways to set prices at four distinct candy stores. Students could be provided with four models of different representations (e.g., table, graph, written description, algebraic relationship) and ask the students to compare the models for the best deal [13]. This task is considered atomistic because students are focusing specifically on interpreting, evaluating, and contrasting models. Students are not creating the model themselves or engaging in the full process of mathematical modeling.

Both holistic and atomistic approaches have merit, and effective modeling instruction often balances the two depending on the learners’ needs and instructional goals. Likewise, Niss and Højgaard [12] argue that both general and specific definitions of competence are necessary and complementary; the general view provides a vision of what it means to be competent, while the specific view makes competence operational for teaching and assessment.

2.3. Mathematical Modeling vs. Modeling Mathematics

Adding to the complexity of conceptions in the field is the distinction between mathematical modeling and modeling mathematics. While these two constructs are sometimes used interchangeably, they refer to fundamentally different processes with different educational purposes (see

Table 1. Modeling mathematics vs. mathematical modeling.

	Modeling Mathematics	Mathematical Modeling
Context	Mathematical	Real world
Goal	Explore abstract concepts	Model a situation and make predictions
Example	Using base-ten blocks to model place value	Using prior marathon running times to predict runner speed 10 years from now

). In short, mathematical modeling is not modeling mathematics, and visa versa.

Mathematical modeling begins in the real world. It involves identifying a situation or problem from everyday life, society, or the workplace, and using mathematical tools to analyze or solve it. This process is typically open-ended, context-dependent, and highly interpretive. As articulated by the Common Core Standards writing team [18], it involves using mathematics or statistics to model a real-world situation and to derive insights or predictions based on that model.

Modeling mathematics, by contrast, begins in the world of mathematics. It involves using representations, such as physical manipulatives, diagrams, or virtual tools, to illustrate and explore abstract mathematical concepts. For example, using base-ten blocks to model place value or using a graph to represent a linear function would be considered modeling mathematics. As van de Walle [19] put it, this practice involves “any object, picture, or drawing that represents the concept or onto which the relationship for that concept can be imposed” (p. 31).

The key distinction lies in the direction of abstraction. Blum [20] distinguishes mathematical modeling as working form the extra-mathematical perspective, moving from the real world into mathematics and then back to the real world, while modeling mathematics remains within the intra-mathematical perspective, only moving within the mathematical domain. Both are important for student learning, and both support different kinds of reasoning and understanding.

Yet, despite these clear distinctions in theory, many educators struggle to differentiate the two in practice. Research has shown that confusion persists among teachers regarding how these constructs operate differently in the classroom and what each contributes to student learning [21]. This underscores the need for targeted professional development that prepares teachers to recognize, design, and facilitate tasks aligned with both constructs.

2.4. Mathematical Modeling in Educational Policy and Standards

Policy documents have also shaped the landscape of modeling in education. The Common Core State Standards for Mathematics (CCSSM), introduced in 2010, positioned modeling as both a mathematical content area and a standard for mathematical practice. Practice standard MP4, “model with mathematics”, encourages students to apply mathematics to solve problems arising in everyday life, society, and the workplace [1]. Additionally, research shows that nearly 40% of high school mathematics content standards involve modeling in some meaningful way [22].

This formal recognition of modeling as essential to mathematical literacy has led to increased efforts to integrate modeling tasks into K-12 classrooms. It has also spurred the development of curricular materials and teacher professional development programs focused on authentic modeling experiences. However, as Cirillo and colleagues [23] have argued, the standards often lack clear guidance on what modeling should look like in practice. This has resulted in inconsistent implementation and varying interpretations of what counts as a modeling activity.

To address these gaps, several frameworks have emerged to help teachers conceptualize modeling in actionable terms. These frameworks emphasize the importance of student engagement with real-world contexts, the iterative nature of model development, and the need for reflection and revision. They also encourage teachers to select or design tasks that align with students’ lived experiences and encourage them to see mathematics as a tool for sense making in the world around them.

2.5. Concluding Thoughts on Defining Mathematial Modeling

The landscape of mathematical modeling education is complex and evolving. While mathematical modeling and modeling mathematics represent distinct yet complementary practices, both are essential to helping students develop deep transferable understandings of mathematics. Whether approached holistically or atomistically, modeling supports a range of competencies, cognitive, procedural, and interpretive, that are central to mathematical literacy.

To better understand how these conceptions play out in practice, it is helpful to examine the current body of research documenting both the promises and the challenges of modeling in classroom settings. This includes investigations into how students experience modeling tasks, how teachers enact them, and how professional development can support more effective implementation.

As the field continues to grow, educators, researchers, and policymakers must work together to clarify definitions, develop supportive frameworks, and provide meaningful opportunities for teacher learning. Doing so will ensure that students are not only equipped to engage in modeling tasks but also empowered to use mathematics as a lens through which to understand and navigate the world

3. Research on Mathematical Modeling Education

In recent years, there has been growing interest and attention to mathematical modeling as an integral component of mathematics education. This attention has been spurred in part by policy documents, such as the Common Core State Standards for Mathematics (CCSSM), which position mathematical modeling as a key mathematical practice (MP4: model with mathematics) [1]. In turn, a body of research has emerged that examines the benefits of modeling for students, the pedagogical and epistemological challenges teachers encounter in implementing modeling tasks, and the kinds of support structures, particularly professional development, that can improve teaching practice around modeling. Furthermore, this research has taken on several different perspectives on modeling, including realistic modeling, educational modeling, models and modeling perspective, socio-critical modeling, and epistemological modeling [2]. This entry focuses on the realistic and educational perspectives, with this section synthesizing that research to articulate both the promise and complexity of mathematical modeling in contemporary educational settings. See

Table 2. Benefits of and challenges with mathematical modeling.

Benefits	Challenges
Accessible and engaging	Teachers’ conceptions of mathematical modeling
Can build on students’ interests	Implementing the modeling process
Opportunity for both mathematical and real-world connections	Anticipating multiple student approaches and perspectives
Well-integrated mathematical practices	Finding time to implement tasks
Opportunity for productive struggle	Supporting students through the iterative process

for an overview of these benefits and challenges.

3.1. Documented Benefits of Mathematical Modeling

One of the most commonly cited advantages of mathematical modeling is its potential to make mathematics more engaging and accessible for a broader range of students. Modeling tasks are typically characterized by their open-endedness, which creates a low barrier to entry while simultaneously offering complex and rigorous mathematical opportunities for those ready to take on more advanced challenges. This “low-floor high-ceiling” nature of modeling enables students with varied levels of prior mathematical knowledge to participate meaningfully in mathematical activity. Well-constructed open-ended modeling tasks allow students to engage deeply and demonstrate problem-solving abilities they may not have displayed before in the mathematics classroom [24].

This accessibility stems in part from how modeling tasks leverage students’ real-world knowledge. Students can draw not only from prior mathematical knowledge but also from their experiences and understandings outside of school [25]. Modeling situates mathematics in familiar or personally meaningful contexts, enabling students to use what they know about the world to frame and solve problems (e.g., [26,27]). Some modeling tasks even engage students in issues of social justice, giving students opportunities to incorporate cultural-, civic-, or community-based knowledge into their mathematical reasoning (e.g., [28]). This real-world grounding is not only pedagogically powerful but also culturally responsive.

Another documented benefit of modeling is its impact on student engagement and motivation. Students often describe modeling tasks as fun, relevant, and enjoyable, especially when compared with more traditional procedure-oriented lessons [23]. When students see mathematics as meaningful and connected to their lives, they are more likely to participate and persist.

In addition, mathematical modeling provides opportunities for students to engage in multiple standards for mathematical practice. Anhalt and colleagues [29], for example, studied pre-service secondary mathematics teachers in the United States with no prior experience in mathematical modeling. Researchers collected participants’ artifacts of work on modeling tasks, reflective responses, and took field notes as the study unfolded. The study employed qualitative analytical methods, structured around modeling sub-competencies and mathematical practices. The researchers found that these pre-service teachers frequently engaged in practices such as making sense of problems (MP1), using tools strategically (MP5), and modeling with mathematics (MP4). This shows that modeling can support a holistic vision of mathematical thinking, one that invites students to reason, reflect, iterate, and engage in authentic problem solving.

These tasks also promote rich mathematical discourse and collaborative engagement. Modeling often occurs in small teams and culminates in group presentations of models and solutions. These moments serve as powerful opportunities for students to explain their thinking, receive feedback, and revise their ideas. Additionally, mathematical modeling creates opportunities to blend key mathematical ideas with student-driven exploration, supports the assessment of both content knowledge and essential 21st century skills, and fosters enthusiasm and engagement among both students and teachers during instruction [30]. When supported by effective facilitation, such discussions help students build a deeper understanding of mathematics while fostering important habits of communication, collaboration, and adaptability, skills increasingly valued in 21st century careers and civic life.

Finally, modeling encourages productive struggle, a hallmark of meaningful learning [31,32]. Students frequently encounter ambiguity and multiple solution paths, prompting them to grapple with uncertainty and persevere through challenges. These cognitive and emotional experiences mirror the complexity of real-world problem solving and build students’ confidence, persistence, and critical thinking skills. As such, the benefits of modeling go beyond academic outcomes in the classroom and contribute to broader goals of preparing students for the complexities of life, work, and problem solving in an increasingly data-driven interdisciplinary world.

3.2. Challenges in Implementing Mathematical Modeling Tasks

Despite its many benefits, mathematical modeling is often difficult for teachers to effectively implement. A core challenge lies in teachers’ conceptual understanding of what modeling entails. Many in-service and pre-service teachers confuse modeling with the use of manipulatives or view it as a fixed linear procedure. Asempapa and Sturgill [33], for instance, found that teachers frequently mischaracterized modeling tasks, revealing gaps in foundational knowledge that make implementation difficult.

In addition to conceptual confusion, teachers face challenges across three key domains: mathematical, pedagogical, and epistemological [34]. Mathematically, modeling requires practices like simplifying complex scenarios, making assumptions, and revising solutions, which differ from those typically emphasized in procedural instruction. These features of modeling can feel foreign or intimidating to educators used to well-defined problems with single correct answers.

Additionally, Deniz and Kurt [35] conducted a qualitative case study to investigate the mathematical modeling processes and challenges faced by eighth-grade students during model-eliciting activities (MEAs) in a STEM-focused classroom in Turkey. The researchers employed multiple qualitative data collection tools to capture the modeling process, including observations, interviews, artifacts of classwork, audio–visual recordings, and student presentations. Using the modeling cycle from Blum and Ferri [36], they analyzed the modeling efforts of five student groups. The study identified seven key categories of difficulty: understanding the problem, building a model, applying mathematics, explaining results, group work, model validation, and time management. These findings are important because they highlight specific cognitive and collaborative challenges that middle school students encounter, offering insight into how modeling instruction can be better structured and supported.

Pedagogically, the open-ended nature of modeling can make it difficult for teachers to anticipate student responses or manage the diversity of approaches students may take. Facilitating modeling tasks, especially in collaborative settings, demands that teachers orchestrate discussions that are exploratory, nonlinear, and sometimes unresolved. Leading effective discourse around modeling presentations involves skills like connecting multiple strategies, supporting student reasoning, and navigating ambiguity. Frameworks like Smith and Stein [37]’s five practices for orchestrating discussions (anticipating, monitoring, selecting, sequencing, and connecting) can help, but they require significant preparation and practice.

Related studies in problem-based learning, a field with pedagogical overlap, highlight facilitation strategies that may support modeling classrooms, such as promoting group cohesion, encouraging discourse, and managing group dynamics [38]. However, implementing these strategies requires that teachers shift their instructional stance and be comfortable relinquishing control over the direction and content of classroom conversations. This shift can be uncomfortable for teachers, especially when students’ ideas challenge traditional notions of correctness or completeness.

Another persistent challenge is time. Teachers often report difficulty fitting modeling tasks into a packed curriculum focused on content coverage. Some perceive a tension between modeling and the mastery of foundational skills, even though research suggests these goals can be complementary. Teachers also report uncertainty about how to assess student work on modeling tasks, given their complexity, variability, and the lack of clear rubrics or standardized expectations [39].

Epistemologically, teachers may be uneasy with the iterative nonlinear nature of modeling itself. Traditional math instruction tends to value definitive answers and clear procedures, while modeling embraces revision, uncertainty, and multiple valid approaches. This discomfort can hinder teachers’ willingness to adopt modeling or limit how authentically they implement it.

Importantly, these challenges are not insurmountable. Studies show that with sustained support, such as long-term professional development and opportunities for reflection, teachers can grow in their confidence and capacity to effectively facilitate modeling tasks. Manouchehri and others [34] emphasize the importance of collaborative learning environments where teachers can experiment, reflect, and learn from one another as they deepen their understanding of modeling.

3.3. Supporting Teachers Through Professional Development

Given the complexity of mathematical modeling and the challenges teachers face in implementing it effectively, professional development (PD) is critical to building teacher capacity. Research shows that high-quality PD can enhance teachers’ knowledge, pedagogy, and beliefs about modeling, ultimately improving their classroom practice.

Several studies have emphasized the importance of structured multi-phase PD programs. For instance, Maaß and Gurlitt [40]’s LEMA project included five comprehensive modules: background knowledge, task selection, lesson design, assessment, and reflection. While participants gained confidence and technical skill in facilitating modeling, their beliefs about modeling’s role in the classroom remained largely unchanged, highlighting the need for PD that also targets teacher beliefs. Similarly, Tan and Ang [41] developed a four-phase PD model incorporating theory, practice, classroom implementation, and reflection. Their participants reported improved confidence in selecting and enacting modeling tasks, crediting the iterative nature of the program for helping them refine their practice over time.

More embedded approaches, such as in situ and responsive PD, have also shown promise. Jung and Brady [42] demonstrated the power of co-teaching, where teachers engaged directly in planning and implementing modeling lessons alongside researchers. While observing expert modeling was helpful, active participation proved more impactful for teacher learning. Likewise, Taite et al. [43] and Taite [16] used an action research approach to study year-long collaborative PD that was flexible and teacher-responsive. These investigations purposefully involved teacher participants in the research process and design by allowing these teachers to choose a specific pedagogical goal related to mathematical modeling to improve upon across PD sessions. Teachers initially struggled with student engagement and managing modeling discussions but eventually grew more confident. Notably, they shifted from simply eliciting student ideas to facilitating deeper discourse that challenged and refined student thinking, showing growth in both pedagogical skill and professional judgment.

Teachers’ evolving perspectives on modeling are also a key area of focus. Alhammouri and DiNapoli [31] found that teachers moved through phases of discovery, appreciation, and conflict as they participated in PD. Teachers came to value the openness and authenticity of modeling but also struggled with its messiness and ambiguity, which conflicted with traditional views of mathematics. This tension revealed that meaningful changes in practice require PD that not only develops skills but also creates space for teachers to reflect on and reorient their beliefs about mathematics and teaching.

Ramos-Rodríguez et al. [44] also highlighted belief shifts in their case study of four secondary mathematics in-service teachers during a PD program. The researchers first administered a pre-test to help capture the teachers’ initial conceptions of mathematical modeling. Throughout the PD program, the teachers’ instruction, reflections, and modeling tasks they designed were monitored to observe evolution over time. The researchers were especially interested in examining the characteristics of the modeling tasks proposed by the teachers before, during, and after the PD program. Via qualitative case study focused on tracking perspective shifts, the researchers found that teachers moved from pragmatic and conceptual views of modeling toward more educational and socio-critical perspectives. Importantly, they became increasingly intentional about the perspectives they embraced or rejected. This progression suggests that thoughtfully designed PD can encourage teachers to adopt more socially responsive and pedagogically grounded approaches to modeling.

Tailoring PD to teachers’ needs is another critical factor. Gaston and Lawrence [45] argue that effective PD must account for teachers’ varying levels of mathematical and pedagogical readiness. They recommend providing opportunities for teachers to experience modeling firsthand, assess student work, and reflect on student-centered teaching strategies. Given the interdisciplinary nature of modeling, PD should also draw on STEM contexts beyond mathematics alone.

Finally, preparing pre-service teachers is essential for long-term change. Wickstrom and Jung [46] emphasize the importance of giving future teachers access to realistic modeling tasks and guided reflection. Such experiences can help pre-service teachers develop a clear understanding of both the nature of modeling and effective ways to support student engagement in modeling classrooms.

Taken together, these studies underscore that professional development for mathematical modeling must be multi-dimensional, addressing not only content and pedagogy but also teachers’ beliefs, identities, and contexts.

Table 3. Effective mathematical modeling professional development.

Characteristics of Effective Mathematical Modeling PD
Opportunity for classroom implementation with feedback
Time for design and discussion of tasks
Supportive and collaborative environment
Teachers experiencing modeling tasks as students themselves
Personal and contextualized to teachers’ backgrounds and classroom experiences

offers a summary of the common characteristics of effective modeling-focused PD across these studies.

3.4. Concluding Thoughts on Mathematical Modeling Education Research

The current landscape of research on mathematical modeling education presents a picture of both great promise and substantial complexity. Modeling offers unique opportunities for student engagement, access, and deep mathematical thinking. Yet, it also presents a host of pedagogical and epistemological challenges that require thoughtful sustained professional learning for teachers.

As these challenges come into sharper focus, so too does the need for research and practice that not only documents barriers but also actively builds capacity for meaningful change. Moving from documentation to transformation requires theoretical refinement, deeper understanding of teacher learning, and the development of tools and frameworks that can guide practice across diverse contexts.

To support the integration of modeling in mathematics classrooms, future work must continue to investigate how teachers learn to design, implement, and reflect on modeling tasks. In particular, research should explore how teacher beliefs evolve through practice and what structures best support that evolution. As mathematical modeling becomes more central to mathematics curricula, the field must ensure that teachers are not only equipped with technical tools but also with pedagogical mindsets that embrace complexity, uncertainty, and student-centered inquiry.

4. Implications for Future Research and Practice

While research on mathematical modeling in education has grown significantly over the past two decades, important questions remain regarding how best to prepare teachers, structure learning environments, and refine theoretical frameworks that guide instruction and research. In fact, mathematics education organizations like the Association of Mathematics Teacher Educators (AMTE), the National Council of Teachers of Mathematics (NCTM), and Psychology of Mathematics Education (PME) continue to push for more attention on mathematical modeling, as evidenced by recent research (e.g., [47]), working groups (e.g., [48]), position statements (e.g., [49]), workshops for teachers (e.g., [50]), and teacher resources (e.g., [51]) being offered and supported by the organization. The benefits of mathematical modeling for students, such as increased engagement, access to meaningful mathematics, and opportunities for creative and critical reasoning, are well-documented. However, these benefits are not automatic. They depend heavily on the decisions that teachers make and the kinds of learning environments they create. As a result, the field must continue to deepen its understanding of the professional knowledge, beliefs, and instructional moves that enable robust modeling experiences in classrooms. This section identifies key directions for future work, emphasizing the need for targeted teacher development and ongoing theoretical refinement to support the integration of modeling in mathematics education.

4.1. Preparing Teachers for the Complexities of Mathematical Modeling

One of the clearest implications of the current literature is that teachers need sustained targeted preparation to effectively integrate modeling into their instructional practice (e.g., [30,41]). Unlike more conventional forms of problem solving, mathematical modeling involves open-ended context-rich tasks that require students to define the problem, make assumptions, construct representations, and revise solutions based on real-world constraints. Facilitating such activity demands a fundamentally different orientation to mathematics teaching, one that embraces ambiguity, values student thinking, and supports discourse across diverse mathematical pathways.

Yet, many teachers, particularly those who have not previously encountered modeling in their own schooling, struggle to enact this vision. Research consistently shows that teachers often hold limited or incorrect understandings of what modeling entails (e.g., [33]). Some conflate modeling with using physical representations (e.g., base-ten blocks or algebra tiles), while others see it as a linear procedure with fixed steps. These misconceptions can lead to the implementation of modeling tasks in ways that diminish their exploratory and authentic character.

Professional development efforts must therefore be designed to go beyond simply introducing tasks. They should aim to support teachers in developing deeper conceptual understandings of modeling as a mathematical process and in building the pedagogical repertoire needed to facilitate student-centered inquiry. For example, programs like the LEMA project [40] and the four-phase model proposed by Tan and Ang [41] demonstrate how structured iterative professional development experiences can help teachers become more confident and effective in implementing modeling. Still, as research from Alhammouri & DiNapoli [31] and Taite et al. [43] illustrate, even well-designed professional development cannot resolve all tensions. Teachers may still experience discomfort or internal conflict as they reconcile modeling with their beliefs about mathematics and pedagogy.

Future teacher preparation and professional learning efforts must therefore attend to these affective and epistemological dimensions [49,52]. Alhammouri & DiNapoli [31] found that teachers’ engagement with modeling tasks prompted both appreciation and dissonance. Many expressed surprise at how different modeling felt from their prior mathematics experiences. Some struggled with letting go of control, grappling with the idea that problems could be interpreted in multiple ways or that there might not be a single “correct” solution. These findings suggest that for modeling to be fully embraced, teachers need opportunities to interrogate their assumptions about what counts as mathematical reasoning and whose knowledge is valued.

Moreover, professional development should incorporate structured opportunities for reflection, not only on instructional strategies but also on teachers’ beliefs, positionalities, and classroom norms [53]. Reflection should be situated in rich pedagogical experiences, such as analyzing student work, co-teaching modeling lessons, or engaging in collaborative design cycles. As research has shown, the act of teaching modeling can itself be transformative. When teachers participate in modeling as learners, they experience firsthand the uncertainty, creativity, and cognitive demand that modeling entails. These experiences can shift how they perceive both mathematics and student agency.

Going forward, future research should investigate how various models of professional development, whether through coaching, lesson study, co-teaching, or action research, support shifts in teacher practice and perspective over time. Longitudinal studies will be especially valuable for understanding how teachers’ conceptual and pedagogical growth evolves with repeated engagement and classroom implementation.

4.2. Advancing Theoretical Frameworks for Mathematical Modeling Education

In addition to practical support for teachers, the field of mathematical modeling education requires continued refinement of the theoretical tools that guide both research and practice. One challenge in the literature is the wide variability in how modeling is conceptualized. Across studies, definitions of modeling range from task-oriented approaches, focused on features like real-world context and open-endedness, to process-oriented views that highlight cycles of problem formulation, mathematization, analysis, and revision. This lack of consistency can make it difficult to compare studies or develop generalizable insights across contexts.

Theoretical frameworks can help bring coherence to this landscape. For example, Blomhøj and Jensen [54]’s modeling cycle and its many adaptations offer a useful structure for understanding how students and teachers engage in modeling activity. However, these frameworks often assume a certain level of mathematical and pedagogical fluency. They may not fully account for the range of teacher moves or student experiences that occur in diverse classrooms, particularly those with varying linguistic, cultural, and socioeconomic resources.

Research by Cirillo et al. [23,25] points to the importance of attending to how modeling tasks intersect with issues of equity and access. They argue that modeling can serve as a culturally responsive practice when students are encouraged to draw on knowledge from their homes and communities. In this sense, modeling is not just a pedagogical tool but also a site for identity development and sociopolitical learning. Future theoretical work should explore how modeling can support justice-oriented goals in mathematics education, including student empowerment, critical reasoning, and real-world problem solving that is grounded in community concerns.

Additionally, frameworks for classroom discourse and facilitation, such as Smith and Stein [37]’s five practices for orchestrating mathematical discussions, can be adapted and extended to modeling contexts. Zhang et al. [38] offer further insight into how facilitation strategies can support collaborative problem solving in small groups, emphasizing moves that foster community, sustain dialogue, and promote metacognitive awareness. These frameworks provide language and structure for describing the complex interpersonal and intellectual work that teachers provide when facilitating modeling. Teacher questioning strategies during modeling can also be explored further to support student thinking and learning. Taite [16] contributed to a preliminary questioning framework for modeling that builds on the general math classroom questioning types from Boaler and Brodie [55]. When it came to the math modeling classroom, it was observed that teacher questioning during students’ modeling presentations fell into four main categories: sense making, operational, higher-order thinking, and increasing validity (see

Table 4. Preliminary questioning framework for mathematical modeling [16].

Category	Question Types
Sense Making	Gathering Information	Probing	Restating
Operational	Generating Discussion	Presentation and Communication Skills	Logistical	Praise
Higher-Order Thinking	Extending Thinking	Linking and Applying	Exploring Mathematical Meanings
Increasing Validity	Orienting and Refocusing	Establishing Context	Nature of Modeling

). Some of the questioning types like gathering information and generating discussion are described by Boaler and Brodie, while others like restating and nature of modeling are more specific to modeling from Taite [16]’s study. The types of questions within these categories should be explored further as a way to help teachers expand their repertoire of questioning to strengthen students’ modeling solutions.

To support theory building, future research should document and analyze the nuanced ways in which teachers facilitate modeling discussions, including how they position students, manage uncertainty, and navigate competing instructional goals. Fine-grained analyses of teacher talk, student interactions, and classroom artifacts can shed light on the micro-level decisions that shape modeling experiences. Moreover, attention to affective dynamics, such as frustration, curiosity, and satisfaction, can enrich our understanding of how students and teachers experience modeling as both cognitively and emotionally engaging work.

4.3. Embracing Complexity and Supporting Meaningful Integration

Ultimately, efforts to expand modeling in mathematics education must embrace the complexity of the endeavor. Modeling is not easily reducible to a checklist of best practices or a one-size-fits-all curriculum supplement. Rather, it is a dynamic multifaceted practice that challenges conventional norms of teaching and learning. Its successful integration depends on the alignment of multiple factors: teacher beliefs and knowledge, curriculum design, assessment practices, classroom culture, and institutional supports.

Research shows that modeling has the potential to broaden participation in mathematics by making space for different ways of knowing and doing. When students engage in modeling, they have opportunities to formulate questions, make choices, and explain their reasoning, activities that are often marginalized in more procedural approaches to math instruction. This potential, however, is only realized when teachers are prepared to support student agency and to navigate the ambiguity and openness that modeling entails.

For this reason, the field must continue to prioritize teacher learning as central to modeling reform. This includes not only pre-service teacher education, but also ongoing embedded professional development that allows teachers to experiment, reflect, and grow. Teacher education programs should expose candidates to modeling early and often, giving them multiple opportunities to engage in modeling as learners, observe it in practice, and develop the facilitation skills needed to support diverse learners.

In parallel, future research should continue to refine how modeling is defined, enacted, and studied. This includes expanding our theoretical vocabulary, examining the social and cultural dimensions of modeling, and developing tools that help researchers and practitioners make sense of complex teaching and learning interactions. Comparative and cross-national studies could also offer valuable insight into how different educational systems approach modeling, what challenges they face, and what innovations they develop.

4.4. Concluding Thoughts on Future Implications

Mathematical modeling stands at the intersection of mathematics, pedagogy, and the real world. As a practice, it invites students to engage deeply with mathematical ideas while addressing meaningful problems that matter to them and their communities. As an instructional approach, it challenges teachers to reimagine their roles, to trust in students’ reasoning, and to embrace complexity and uncertainty. The current state of research highlights both the promise and the challenges of modeling in mathematics education. Going forward, the field must invest in sustained, reflective, and theoretically grounded approaches to teacher preparation and professional development. Only then can modeling move from the margins of mathematics instruction to become a central, equitable, and transformative component of classroom practice.