Limaçon Technology in Power Generation
Definition
1. Introduction
2. Thermodynamic Cycles—Power Cycle
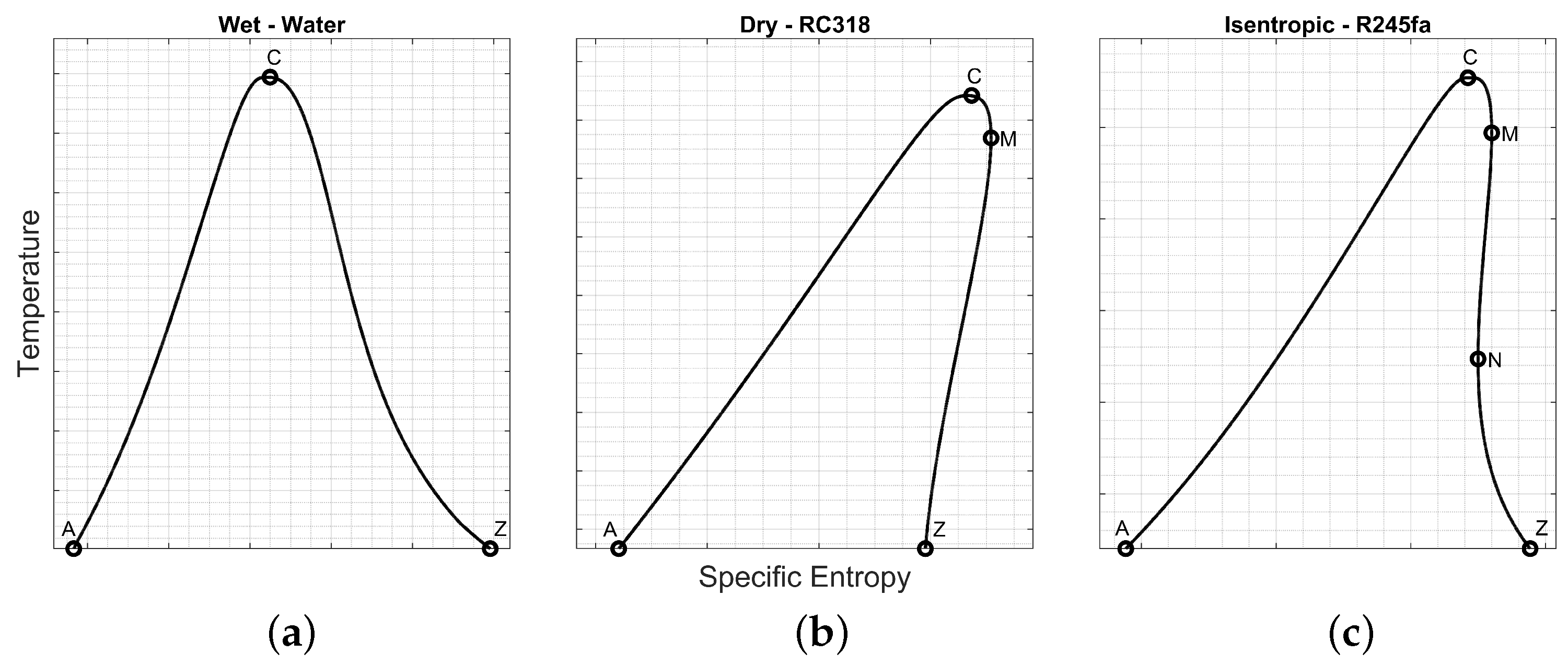
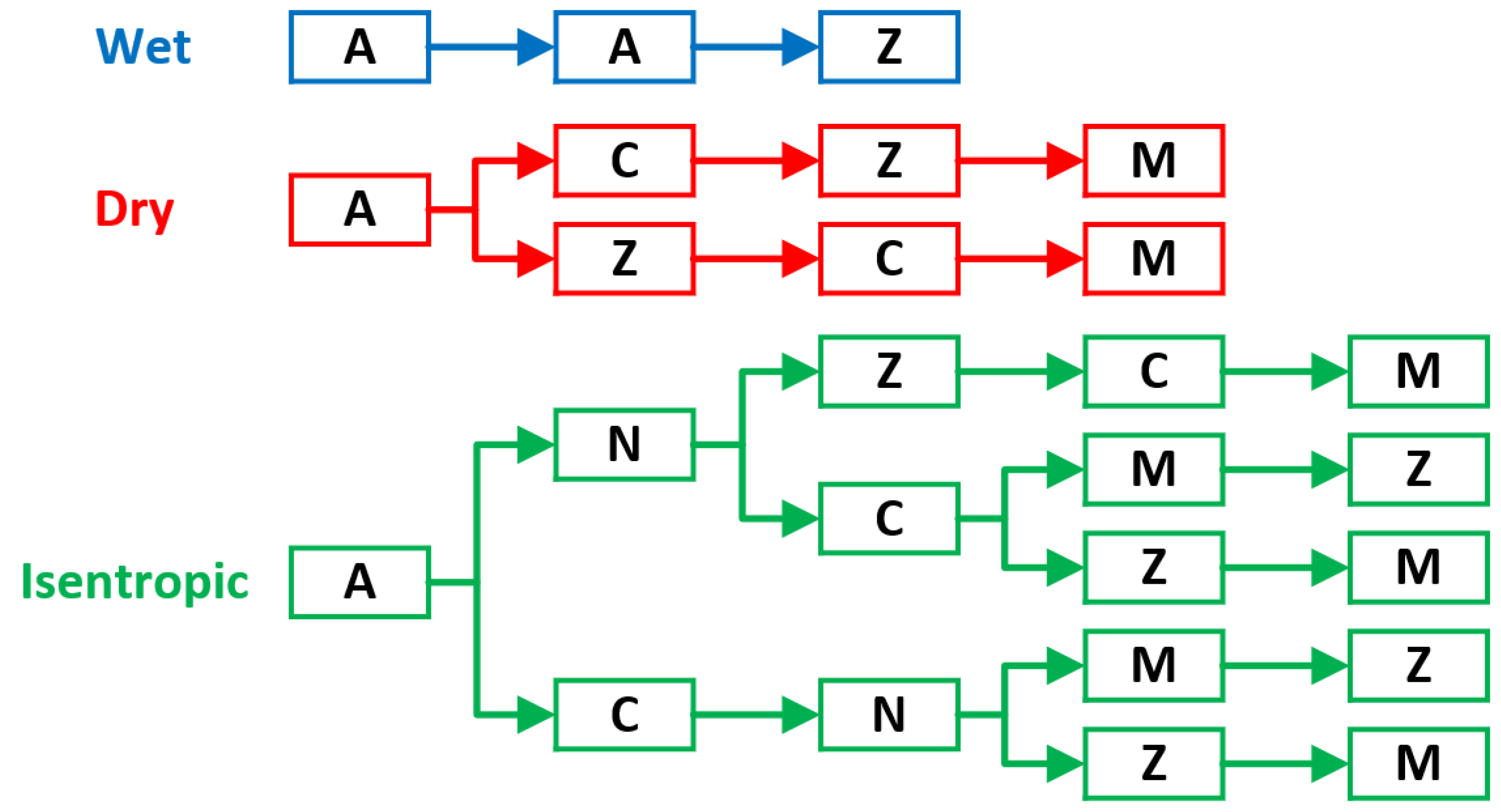
- Wet: a working fluid that has a negatively sloped saturated vapour curve. Examples are water, methane, and refrigerant R32.
- Dry: a working fluid that has a positively sloped saturated vapour curve. Examples are butane, RC318, and Novec649.
- Isentropic: a working fluid which has a near infinite slope; essentially, the saturated vapour line is vertical (or near to). Fluids that are typically categorised as isentropic include pentane and R245fa.
- A: The first point on the saturation dome.
- C: The critical point.
- Z: The last point on the saturation dome.
- M: The point of maximum entropy between C and Z; only present for dry and isentropic fluids.
- N: The point of minimum entropy between C and Z; only present for isentropic fluids.
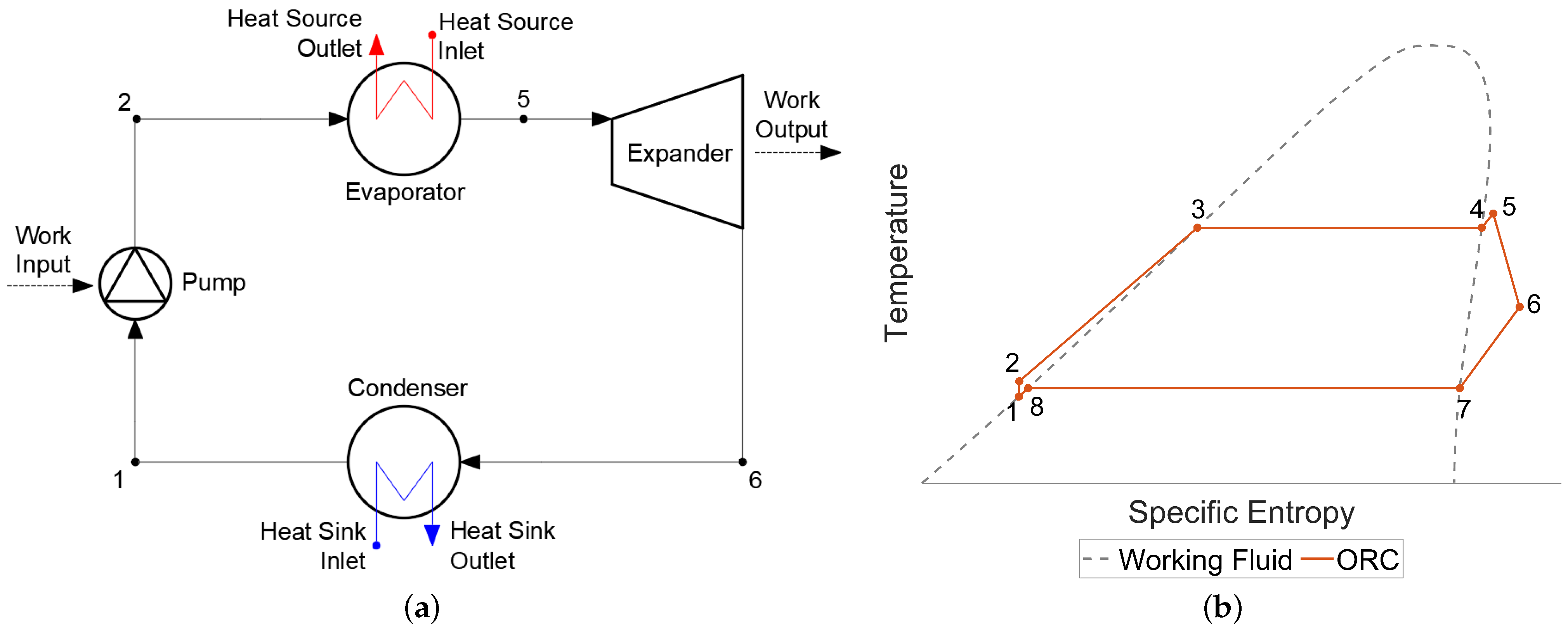
2.1. Organic Rankine Cycle (ORC)
- 1–2. Compression of the working fluid by the pump, resulting in a compressed liquid at the evaporator pressure. This process consumes work.
- 2–3. Preheating of the working fluid to a saturated vapour.
- 3–4. Evaporation of the working fluid to a saturated vapour.
- 4–5. Superheating of the working fluid to a superheated vapour.
- 5–6. Expansion of the working fluid in the expander, resulting in a superheated vapour at the condenser pressure and the production of mechanical work.
- 6–7. Desuperheating of the working fluid, resulting in a saturated vapour.
- 7–8. Condensation of the working fluid, resulting in a saturated liquid.
- 8–1. Subcooling of the working fluid, resulting in a compressed liquid.
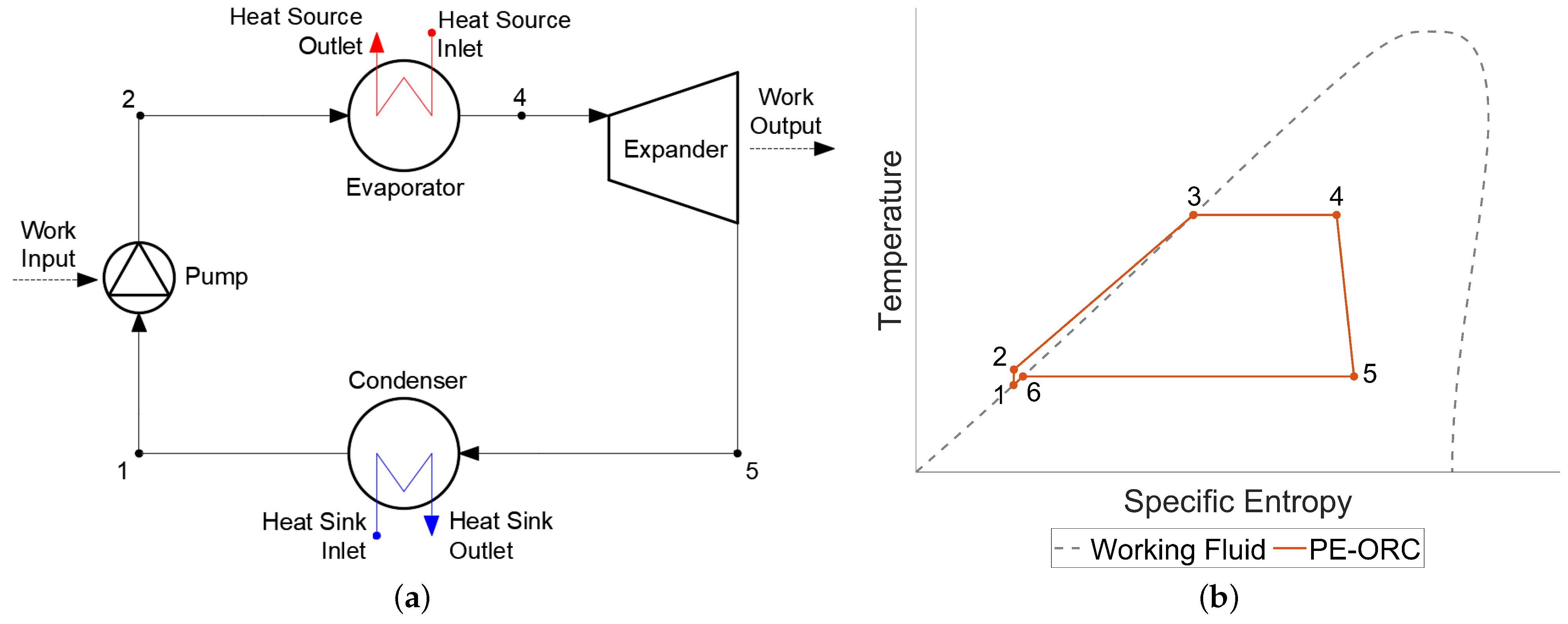
2.2. Partial Evaporation Organic Rankine Cycle (PE-ORC)
- 1–2. Compression of the working fluid by the pump, resulting in a compressed liquid at the evaporator pressure.
- 2–3. Preheating of the working fluid to a saturated vapour.
- 3–4. Partial evaporation of the working fluid to a two-phase mixture.
- 4–5. Expansion of the working fluid in the expander, resulting in a two-phase mixture
- 6–7. Condensation of the working fluid, resulting in a saturated liquid.
- 7–1. Subcooling of the working fluid, resulting in a compressed liquid.
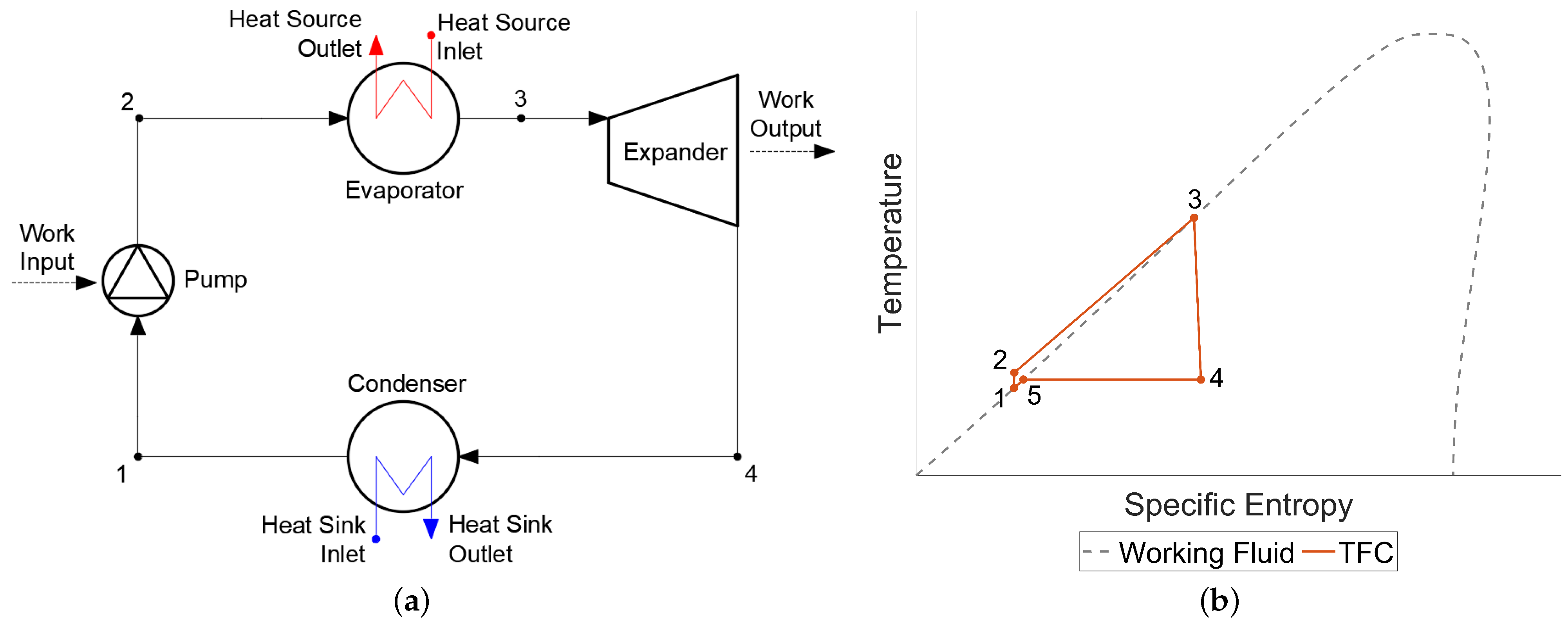
2.3. Trilateral Flash Cycle (TFC)
- 1–2. Compression of the working fluid by the pump, resulting in a compressed liquid at the evaporator pressure.
- 2–3. Preheating of the working fluid to a saturated vapour.
- 3–4. Expansion of the working fluid in the expander, resulting in a two-phase mixture
- 4–5. Condensation of the working fluid, resulting in a saturated liquid.
- 5–1. Subcooling of the working fluid, resulting in a compressed liquid.
3. Power Generation System Components
3.1. Heat Exchangers
3.1.1. Shell-and-Tube Heat Exchangers
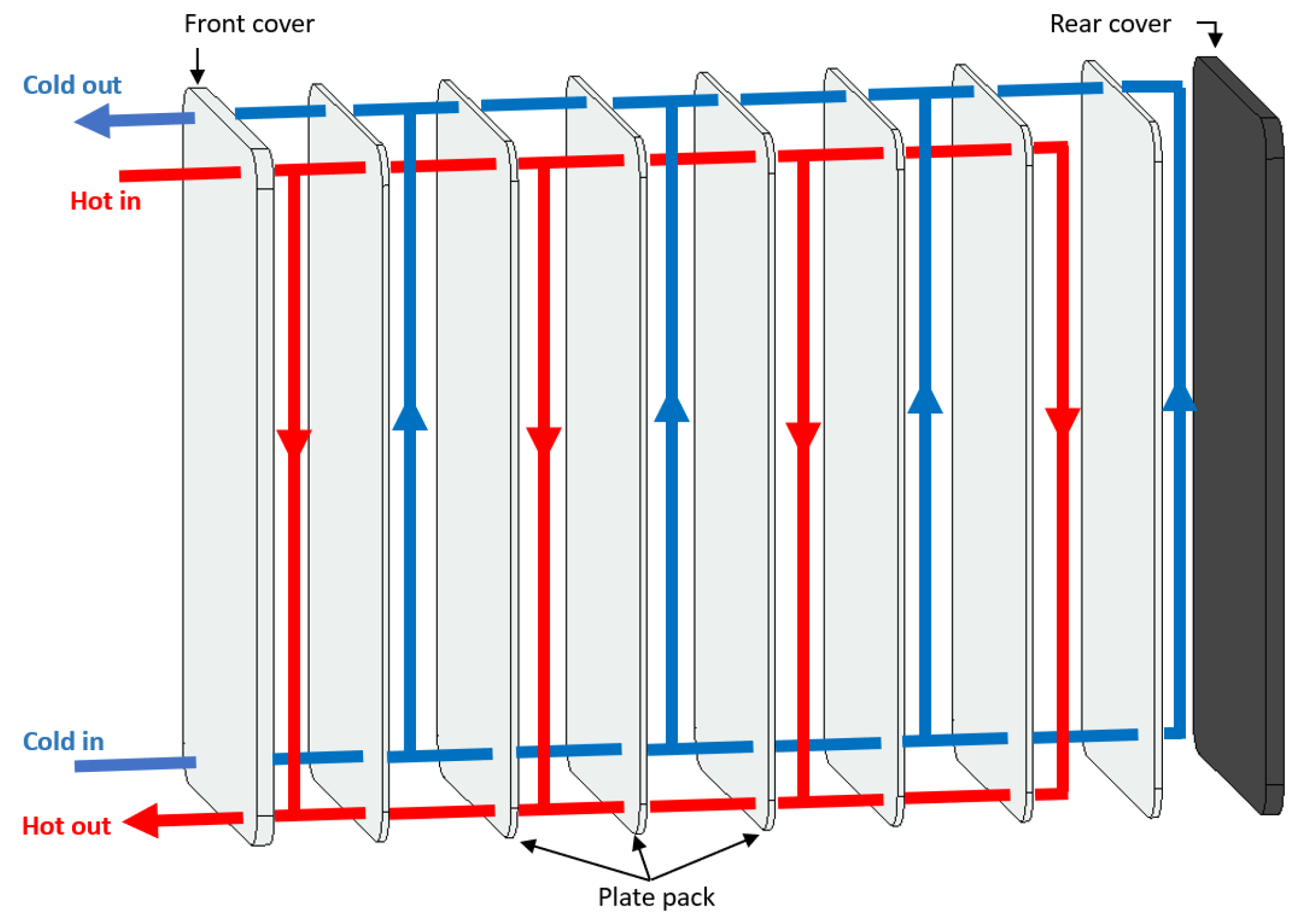
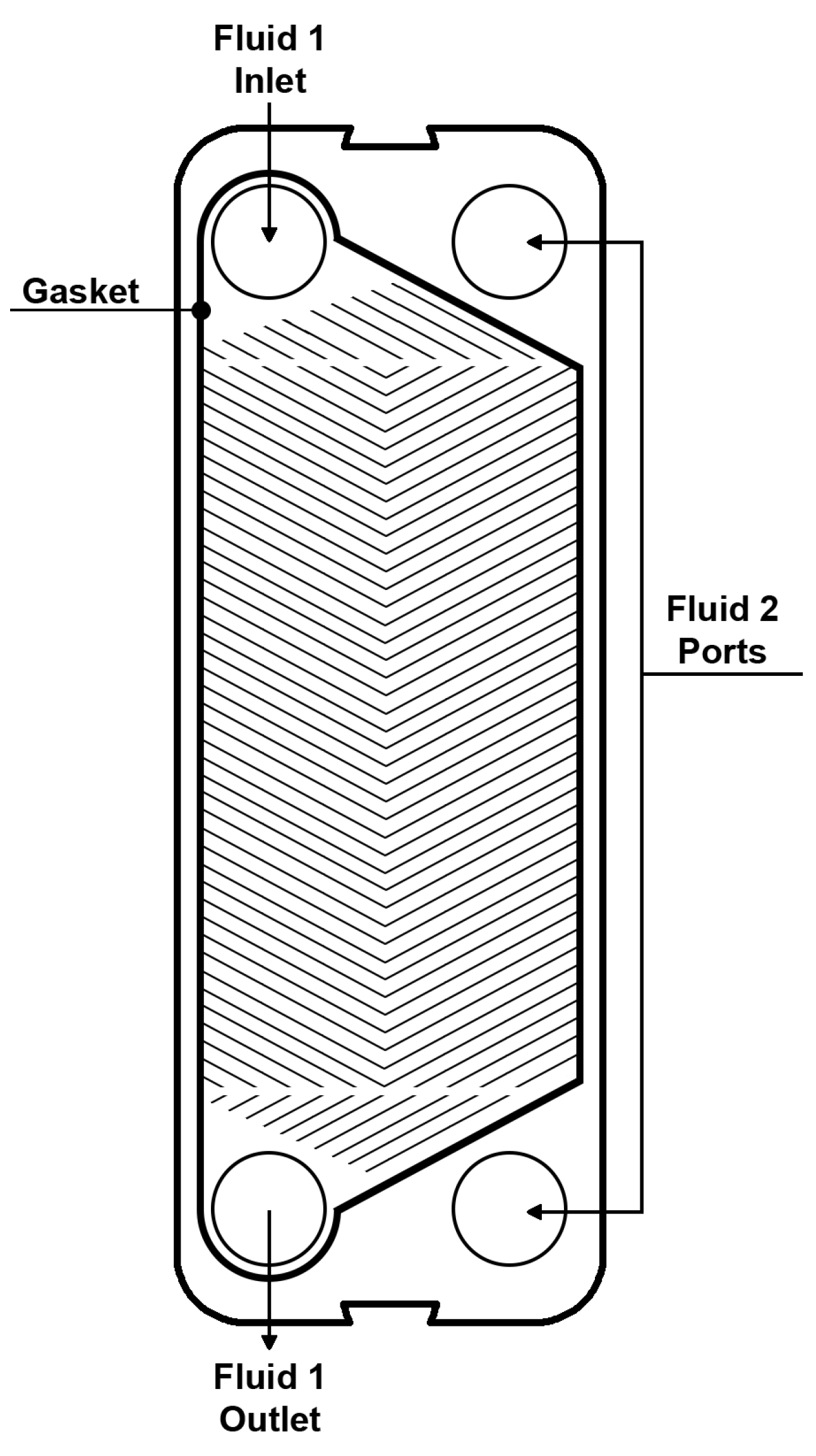
3.1.2. Plate Heat Exchangers
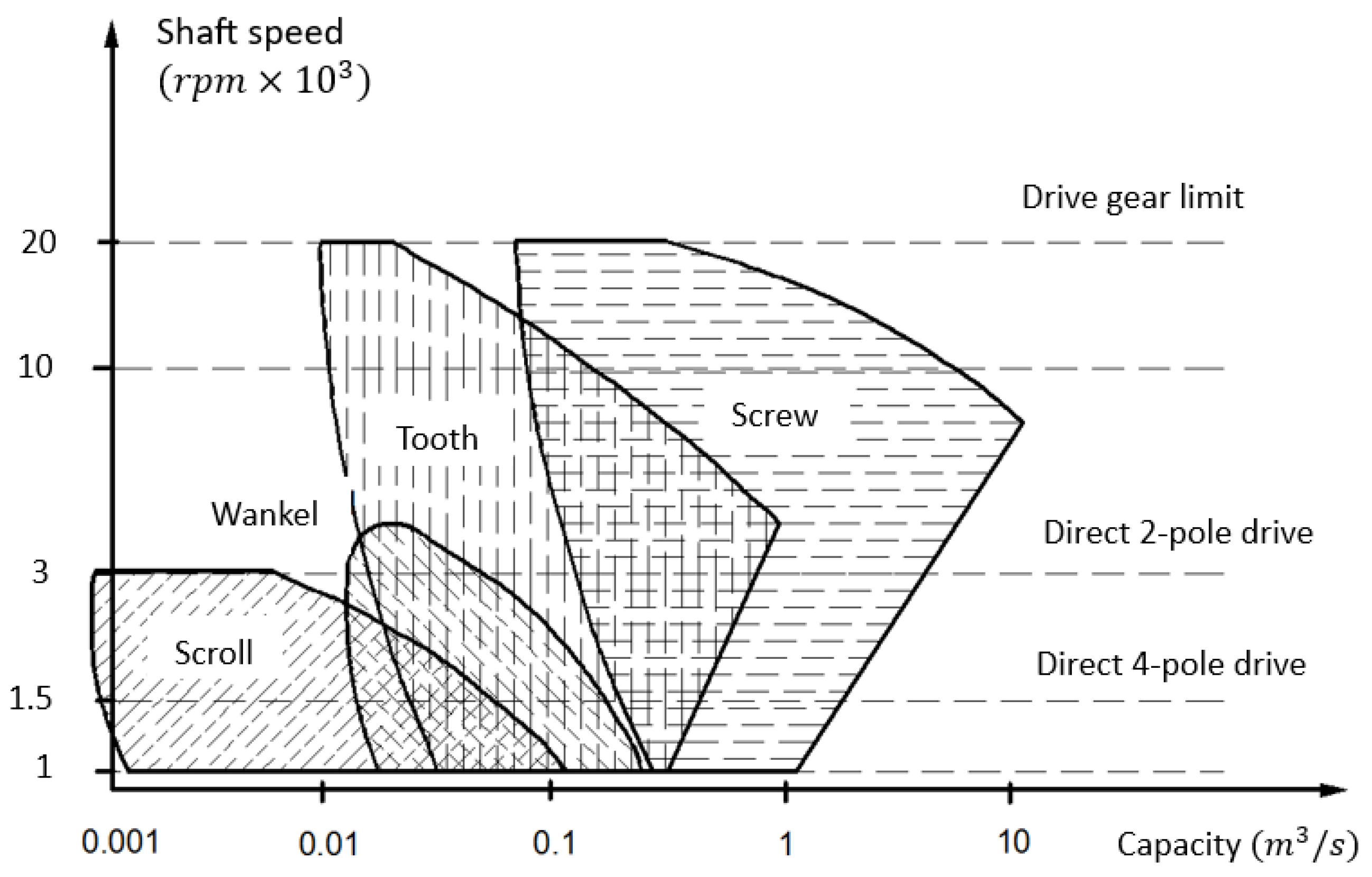
3.2. Prime Movers
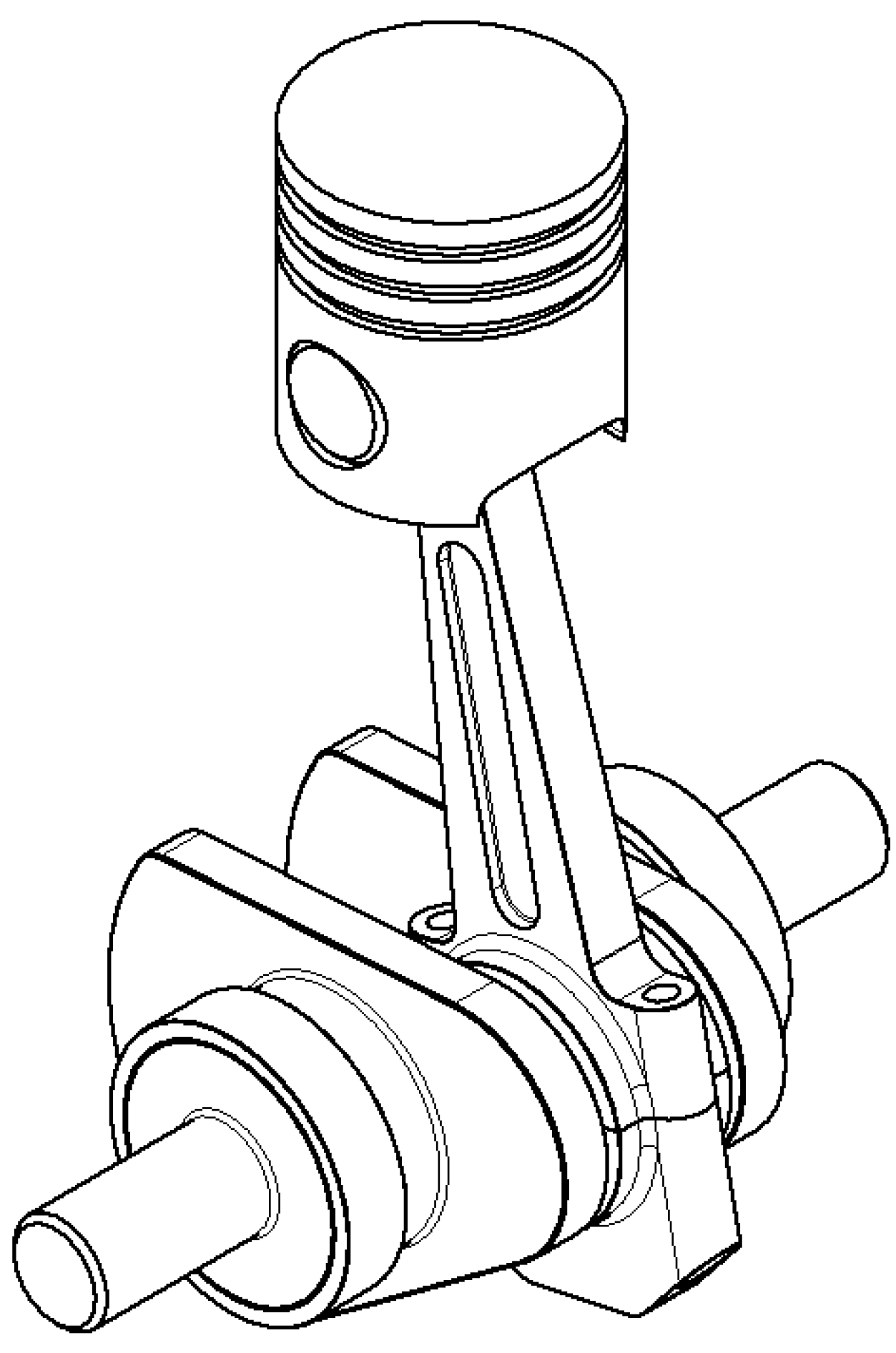
3.3. Reciprocating Piston Expander
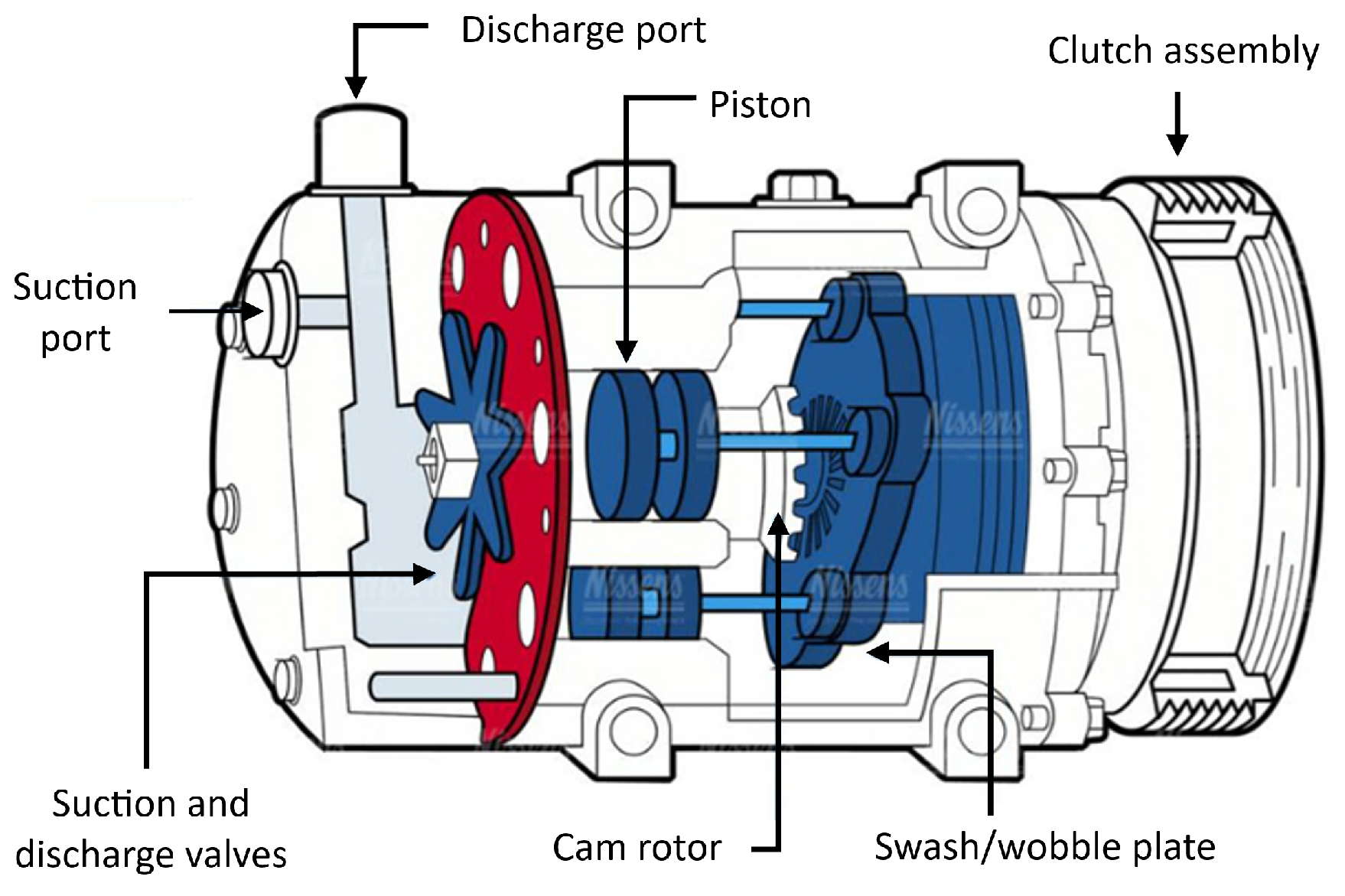
3.4. Axial Piston Expander
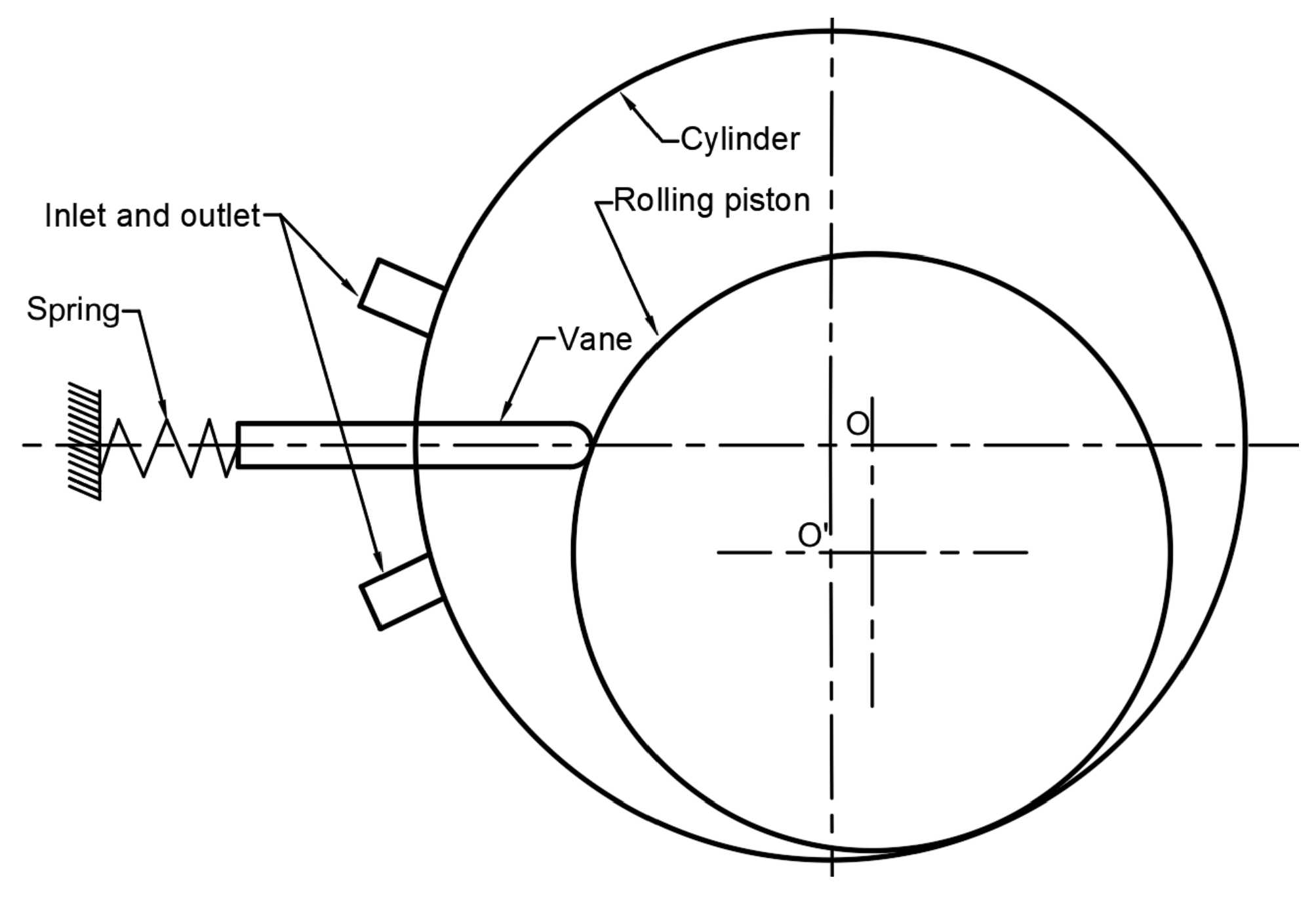
3.5. Rolling Piston Expander
3.6. Rotary Vane Machine
3.7. Scroll Expander
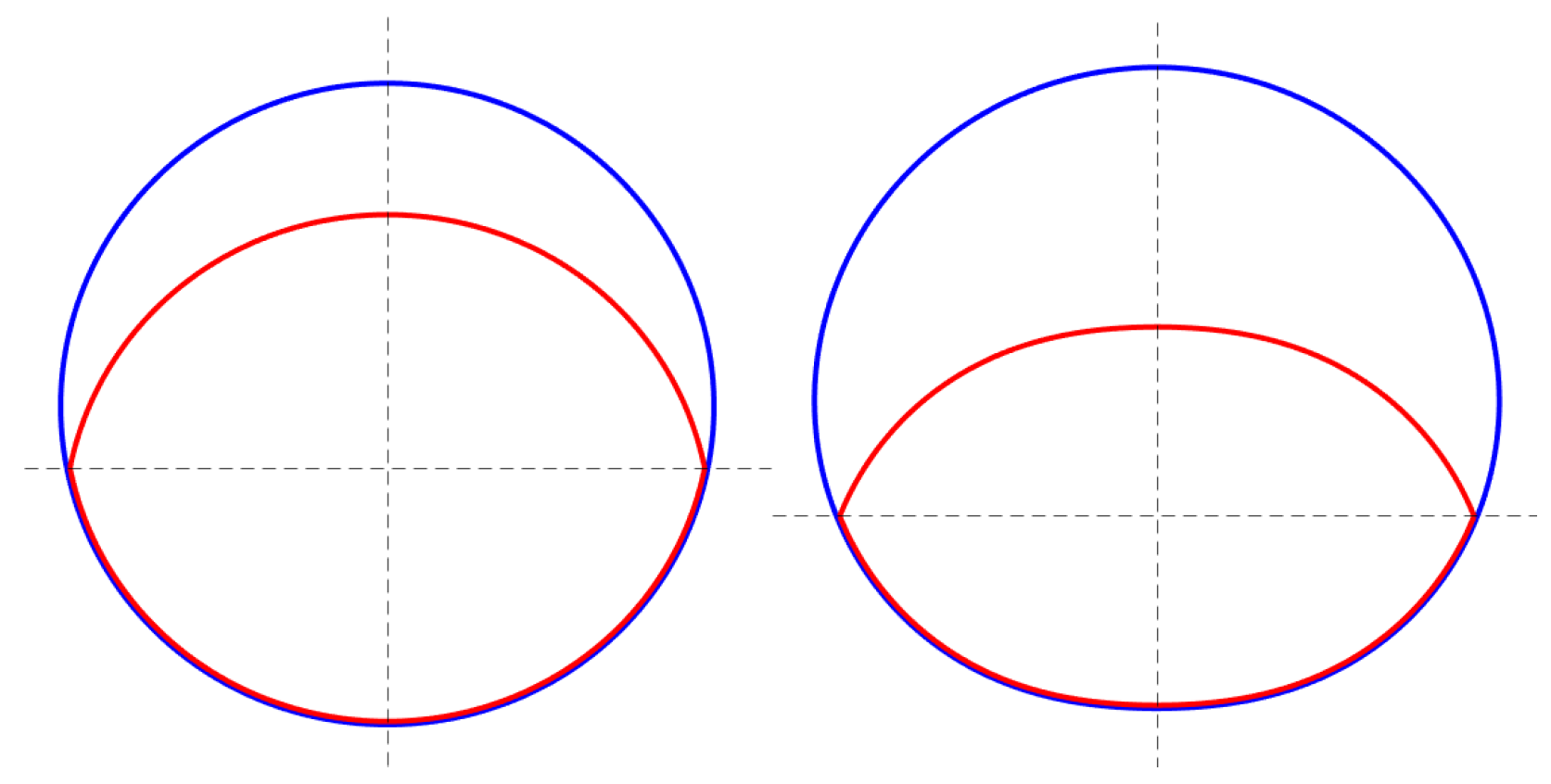
3.8. Limaçon Machine
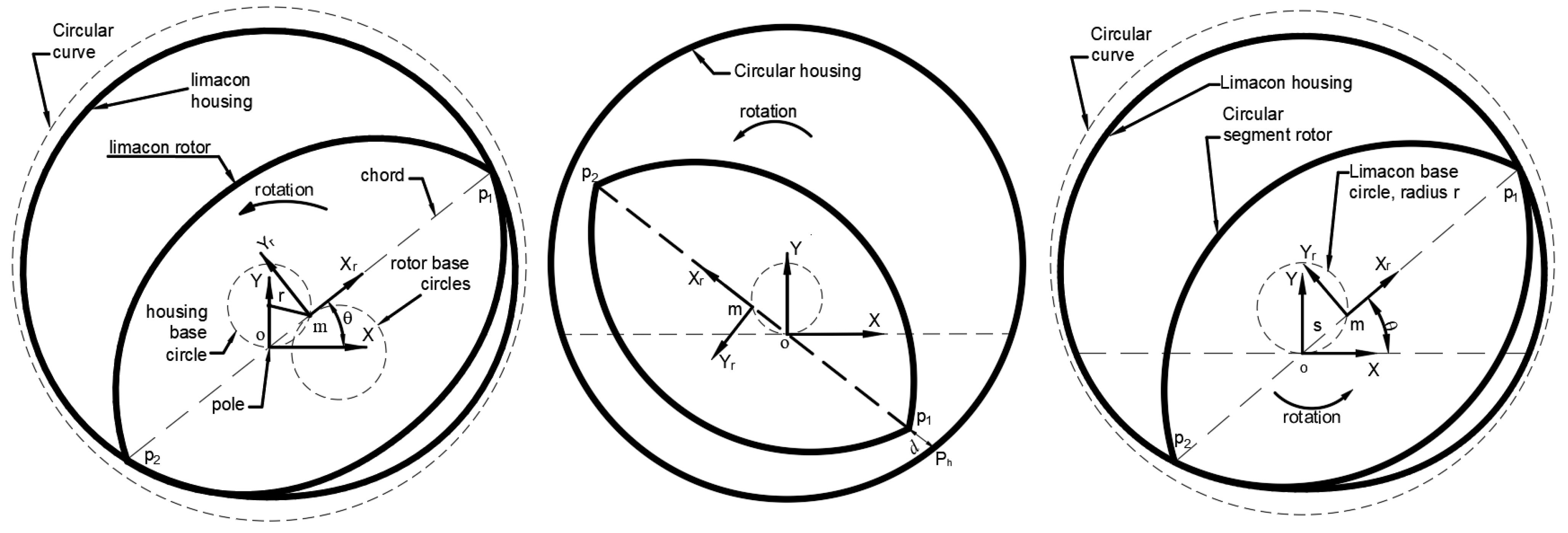
3.8.1. Embodiments
- Limaçon-to-limaçon (L2L) machine: the housing and rotor are both manufactured to the limaçon curves,
- Circolimaçon (CL) machine: the housing and rotor are manufactured to the circular curves,
- Limaçon-to-circular (L2C) machine: the housing is of the limaçon curve while the rotor is manufactured to the circular curve.
- Limaçon-to-limaçon (L2L) machine
- Circolimaçon (CL) machine
- Limaçon-to-circular (L2C) machine
3.8.2. Inlet and Outlet Port Positions and Areas
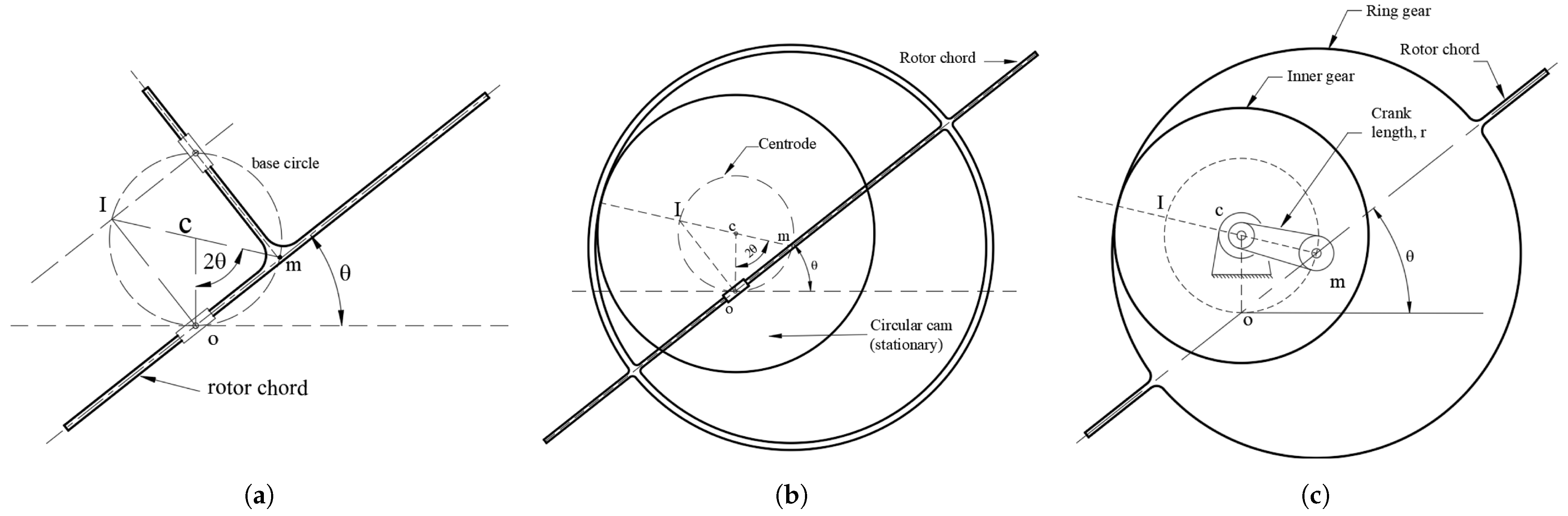
3.8.3. Limaçon Drive
- the midpoint, m, if the rotor chord, , remains attached to the circumference of the base circle and rotates about the centre of that circle at twice the angular speed of the chord itself about m.
- the chord is permanently attached to the pole, o, of the machine, the origin of the fixed frame, about which the chord can rotate and slide.
- the instantaneous centre of velocity of the rotor falls on the base circle and diametrically opposite the rotor midpoint, m. The base circle can be considered as the centrode of the linkage.
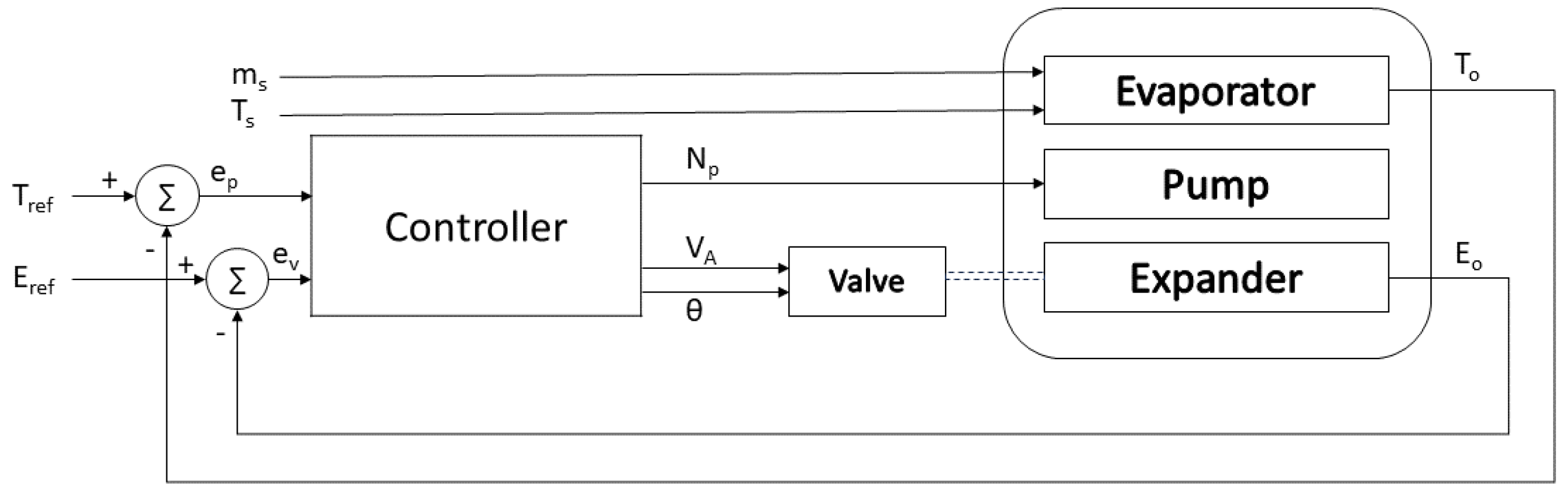
4. Control System
4.1. Cycle Control
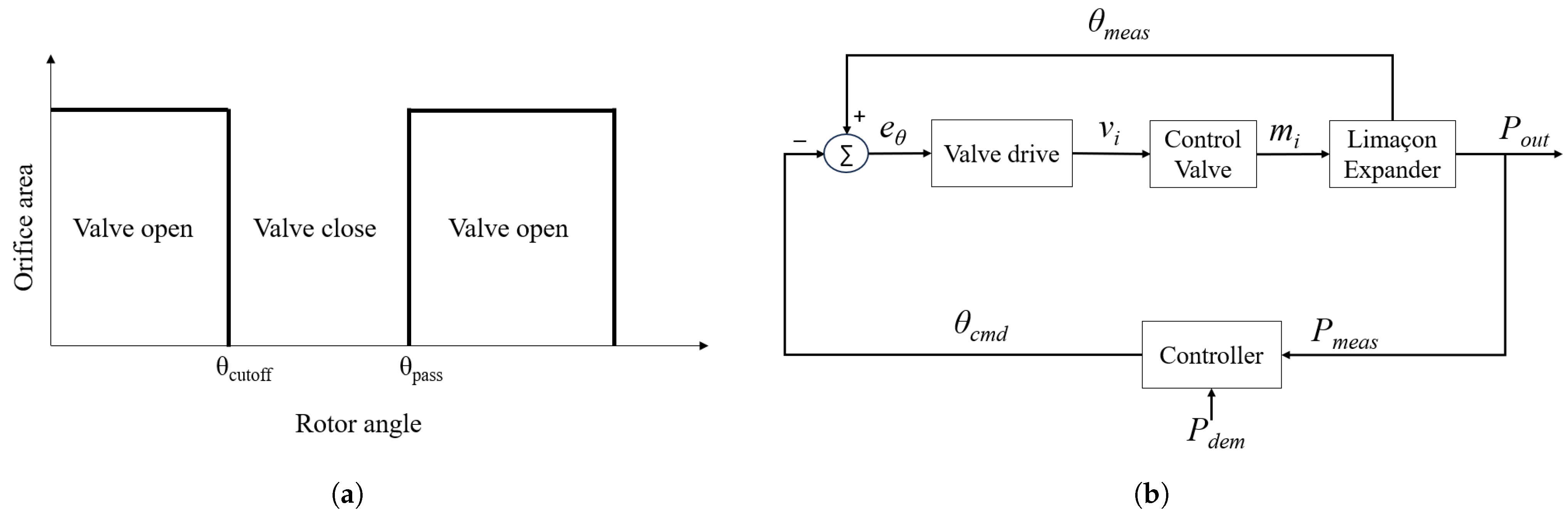
4.2. Expander Control
Controller Designs
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moran, M.; Shapiro, H.; Boettner, D.; Bailey, M. Fundamentals of Engineering Thermodynamics; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Montazerinejad, H.; Eicker, U. Recent development of heat and power generation using renewable fuels: A comprehensive review. Renew. Sustain. Energy Rev. 2022, 165, 112578. [Google Scholar] [CrossRef]
- De Souza, R.; Casisi, M.; Micheli, D.; Reini, M. A Review of Small–Medium Combined Heat and Power (CHP) Technologies and Their Role within the 100% Renewable Energy Systems Scenario. Energies 2021, 14, 5338. [Google Scholar] [CrossRef]
- Qiu, G.; Liu, H.; Riffat, S. Expanders for micro-CHP systems with organic Rankine cycle. Appl. Therm. Eng. 2011, 31, 3301–3307. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Györke, G.; Deiters, U.K.; Groniewsky, A.; Lassu, I.; Imre, A.R. Novel classification of pure working fluids for Organic Rankine Cycle. Energy 2018, 145, 288–300. [Google Scholar] [CrossRef]
- Tian, H.; Shu, G. 17—Organic Rankine Cycle systems for large-scale waste heat recovery to produce electricity. In Organic Rankine Cycle (ORC) Power Systems; Macchi, E., Astolfi, M., Eds.; Woodhead Publishing: Cambridge, UK, 2017; pp. 613–636. [Google Scholar] [CrossRef]
- Quoilin, S.; Broek, M.V.D.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of Organic Rankine Cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Hung, T.; Wang, S.; Kuo, C.; Pei, B.; Tsai, K. A study of organic working fluids on system efficiency of an ORC using low-grade energy sources. Energy 2010, 35, 1403–1411. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Usman, M.; Imran, M.; Lee, D.H.; Park, B.S. Experimental investigation of off-grid organic Rankine cycle control system adapting sliding pressure strategy under proportional integral with feed-forward and compensator. Appl. Therm. Eng. 2017, 110, 1153–1163. [Google Scholar] [CrossRef]
- Dumont, O.; Parthoens, A.; Dickes, R.; Lemort, V. Experimental investigation and optimal performance assessment of four volumetric expanders (scroll, screw, piston and roots) tested in a small-scale organic Rankine cycle system. Energy 2018, 165, 1119–1127. [Google Scholar] [CrossRef]
- Lemort, V.; Quoilin, S.; Cuevas, C.; Lebrun, J. Testing and modeling a scroll expander integrated into an Organic Rankine Cycle. Appl. Therm. Eng. 2009, 29, 3094–3102. [Google Scholar] [CrossRef]
- Campana, C.; Cioccolanti, L.; Renzi, M.; Caresana, F. Experimental analysis of a small-scale scroll expander for low-temperature waste heat recovery in Organic Rankine Cycle. Energy 2019, 187, 115929. [Google Scholar] [CrossRef]
- Talluri, L.; Dumont, O.; Manfrida, G.; Lemort, V.; Fiaschi, D. Experimental investigation of an Organic Rankine Cycle Tesla turbine working with R1233zd(E). Appl. Therm. Eng. 2020, 174, 115293. [Google Scholar] [CrossRef]
- Dawo, F.; Buhr, J.; Schifflechner, C.; Wieland, C.; Spliethoff, H. Experimental assessment of an Organic Rankine Cycle with a partially evaporated working fluid. Appl. Therm. Eng. 2023, 221, 119858. [Google Scholar] [CrossRef]
- Daniarta, S.; Kolasiński, P.; Imre, A.R. Thermodynamic efficiency of trilateral flash cycle, organic Rankine cycle and partially evaporated organic Rankine cycle. Energy Convers. Manag. 2021, 249, 114731. [Google Scholar] [CrossRef]
- Tammone, C.; Pili, R.; Haglind, F.; Indrehus, S. Techno-Economic Analysis of the Partial Evaporation Organic Rankine Cycle Systems for Geothermal Applications; Technical University of Munich: München, Germany, 2021. [Google Scholar] [CrossRef]
- Öhman, H.; Lundqvist, P. Experimental investigation of a Lysholm Turbine operating with superheated, saturated and 2-phase inlet conditions. Appl. Therm. Eng. 2013, 50, 1211–1218. [Google Scholar] [CrossRef]
- White, M.T. Investigating the wet-to-dry expansion of organic fluids for power generation. Int. J. Heat Mass Transf. 2022, 192, 122921. [Google Scholar] [CrossRef]
- Öhman, H.; Lundqvist, P. Screw expanders in ORC applications, review and a new perspective. In Proceedings of the 3rd International Seminar on ORC Power Systems, Brussels, Belgium, 12–14 October 2015. [Google Scholar] [CrossRef]
- Dawo, F.; Buhr, J.; Wieland, C.; Hartmut, S. Experimental Investigation of the Partially Evaporated Organic Rankine Cycle for Various Heat Source Conditions; Technical University of Munich: München, Germany, 2021. [Google Scholar] [CrossRef]
- Arbab, I.; Sohel, R.; Mahdi, A.; Thomas, C.; Abhijit, D.; Aliakbar, A. Prospects of Trilateral Flash Cycle (TFC) for Power Generation from Low Grade Heat Sources. E3S Web Conf. 2018, 64, 06004. [Google Scholar] [CrossRef]
- Smith, I.K. Development of the Trilateral Flash Cycle System: Part 1: Fundamental Considerations. Proc. Inst. Mech. Eng. Part A J. Power Energy 1993, 207, 179–194. [Google Scholar] [CrossRef]
- Lecompte, S.; Huisseune, H.; van den Broek, M.; Vanslambrouck, B.; De Paepe, M. Review of organic Rankine cycle (ORC) architectures for waste heat recovery. Renew. Sustain. Energy Rev. 2015, 47, 448–461. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Rana, S.; Ahmadi, M.; Date, A.; Akbarzadeh, A. Trilateral Flash Cycle (TFC): A promising thermodynamic cycle for low grade heat to power generation. Energy Procedia 2019, 160, 208–214. [Google Scholar] [CrossRef]
- Fischer, J. Comparison of trilateral cycles and organic Rankine cycles. Energy 2011, 36, 6208–6219. [Google Scholar] [CrossRef]
- Bianchi, G.; Kennedy, S.; Zaher, O.; Tassou, S.A.; Miller, J.; Jouhara, H. Two-phase chamber modeling of a twin-screw expander for Trilateral Flash Cycle applications. Energy Procedia 2017, 129, 347–354. [Google Scholar] [CrossRef]
- Bianchi, G.; Kennedy, S.; Zaher, O.; Tassou, S.A.; Miller, J.; Jouhara, H. Numerical modeling of a two-phase twin-screw expander for Trilateral Flash Cycle applications. Int. J. Refrig. 2018, 88, 248–259. [Google Scholar] [CrossRef]
- Smith, I.K.; Stošič, N.; Aldis, C.A. Development of the Trilateral Flash Cycle System: Part 3: The Design of High-Efficiency Two-Phase Screw Expanders. Proc. Inst. Mech. Eng. Part A J. Power Energy 1996, 210, 75–93. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.; Hu, S.; Yang, F.; Duan, Y. Effects of shell-and-tube heat exchanger arranged forms on the thermo-economic performance of organic Rankine cycle systems using hydrocarbons. Energy Convers. Manag. 2020, 203, 112248. [Google Scholar] [CrossRef]
- Bell, K.; Engineering Experiment Station. Final Report of the Cooperative Research Program on Shell and Tube Heat Exchangers; Engineering Experimental Station Bulletin, University of Delaware, Engineering Experimental Station: Newark, DE, USA, 1963. [Google Scholar]
- Kern, D. Process Heat Transfer; Echo Point Books and Media: Brattleboro, VT, USA, 2017. [Google Scholar]
- Serth, R.W.; Lestina, T.G. 7—The Stream Analysis Method. In Process Heat Transfer, 2nd ed.; Serth, R.W., Lestina, T.G., Eds.; Academic Press: Boston, MA, USA, 2014; pp. 223–265. [Google Scholar] [CrossRef]
- Yamamoto, T.; Furuhata, T.; Arai, N.; Mori, K. Design and testing of the Organic Rankine Cycle. Energy 2001, 26, 239–251. [Google Scholar] [CrossRef]
- Wang, R.; Kuang, G.; Zhu, L.; Wang, S.; Zhao, J. Experimental Investigation of a 300 kW Organic Rankine Cycle Unit with Radial Turbine for Low-Grade Waste Heat Recovery. Entropy 2019, 21, 619. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Sundén, B.; Manglik, R. Plate Heat Exchangers: Design, Applications and Performance; Developments in heat transfer; WIT Press: Southampton, UK, 2007. [Google Scholar]
- Georges, E.; Declaye, S.; Dumont, O.; Quoilin, S.; Lemort, V. Design of a small-scale organic Rankine cycle engine used in a solar power plant. Int. J. Low-Carbon Technol. 2013, 8, i34–i41. [Google Scholar] [CrossRef]
- Kuboth, S.; Neubert, M.; Preißinger, M.; Brüggemann, D. Iterative Approach for the Design of an Organic Rankine Cycle based on Thermodynamic Process Simulations and a Small-Scale Test Rig. Energy Procedia 2017, 129, 18–25. [Google Scholar] [CrossRef]
- Saitoh, T.; Yamada, N.; Ichiro Wakashima, S. Solar Rankine Cycle System Using Scroll Expander. J. Environ. Eng. 2007, 2, 708–719. [Google Scholar] [CrossRef]
- Quoilin, S.; Lemort, V.; Lebrun, J. Experimental study and modeling of an Organic Rankine Cycle using scroll expander. Appl. Energy 2010, 87, 1260–1268. [Google Scholar] [CrossRef]
- Declaye, S.; Quoilin, S.; Lemort, V. Design and Experimental Investigation of a Small Scale Organic Rankine Cycle Using a Scroll Expander. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 10–15 July 2010; p. 1153. [Google Scholar]
- Santos, M.; André, J.; Costa, E.; Mendes, R.; Ribeiro, J. Design strategy for component and working fluid selection in a domestic micro-CHP ORC boiler. Appl. Therm. Eng. 2020, 169, 114945. [Google Scholar] [CrossRef]
- Shah, R.; Subbarao, E.; Mashelkar, R. Heat Transfer Equipment Design; Advanced study institute book; Taylor & Francis: Abingdon, UK, 1988. [Google Scholar]
- Persson, J.; Sohlenius, G. Performance Evaluation of Fluid Machinery During Conceptual Design. CIRP Ann. 1990, 39, 137–140. [Google Scholar] [CrossRef]
- Toyota Industries Corporation. Types of Compressor and Structure. Available online: https://www.toyota-industries.com/products/relation/compressor_kind_1/index.html (accessed on 29 April 2024).
- Nissens Experts. Fixed Displacement Piston AC Compressor. Available online: https://support.nissens.com/en/material/component-explained-fixed-displacement-piston-compressor (accessed on 29 April 2024).
- Duke Engine. Duke Engine Pure Power. Available online: https://www.dukeengines.com (accessed on 29 April 2024).
- Imran, M.; Usman, M. Mathematical modelling for positive displacement expanders. In Positive Displacement Machines—Modern Design Innovations and Tools; Academic Press: Cambridge, MA, USA, 2019; pp. 293–343. [Google Scholar] [CrossRef]
- Sultan, I.A. The limaçon of Pascal: Mechanical generation and utilization for fluid processing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 813–822. [Google Scholar] [CrossRef]
- Phung, T.H.; Sultan, I.A. Geometric design of the limaçon-to-circular fluid processing machine. J. Mech. Des. 2021, 143, 103501. [Google Scholar] [CrossRef]
- Li, K.; Sultan, I.; Phung, T. Mathematical modeling and parametric study of the limaçon rotary compressor. Int. J. Refrig. 2022, 134, 219–231. [Google Scholar] [CrossRef]
- Wolfram Mathworld. Available online: https://mathworld.wolfram.com/Limacon.html (accessed on 9 September 2024).
- Wheildon, W.M. Rotary Engine. Patent No. 553,086, 1 January 1896. [Google Scholar]
- Planche, B.R. Rotary Machine. Patent No. 1,340,625, 18 May 1920. [Google Scholar]
- Planche, B.R. Rotary Engine or Pump. Patent No. 1,636,486, 19 July 1927. [Google Scholar]
- Sultan, I.A. Profiling rotors for limaçon-to-limaçon compression-expansion machines. J. Mech. Des. 2006, 128, 787–793. [Google Scholar] [CrossRef]
- Costa, S.I.R.; Grou, M.A.; Figueiredo, V.L.X. Mechanical Curves—A Kinematic Greek Look Through Computer. Int. J. Math. Educ. Sci. Technol. 1996, 30, 459–469. [Google Scholar]
- Sultan, I.A. A Geometric Design Model for the Circolimaçon Positive Displacement Machine. J. Mech. Des. 2008, 130, 062307. [Google Scholar] [CrossRef]
- Sultan, I.A.; Schaller, C.G. Optimum Positioning of Ports in the Limaçon Gas Expanders. J. Eng. Gas Turbine Power 2011, 133, 103002. [Google Scholar] [CrossRef]
- Phung, T.H.; Sultan, I.A. Characterization of Limaçon Gas Expanders With Consideration to the Dynamics of Apex Seals and Inlet Control Valve. J. Eng. Gas Turbine Power 2018, 140, 122501. [Google Scholar] [CrossRef]
- Trapalis, Y. Rotary Mechanism. WO 2005/021933 A1, March 2005. [Google Scholar]
- Moore, B.A. Apparatus for Controlling Epicycloidal Motion of a Rotor in a Rotary Engine. U.S. Patent 3,913,408, February 1975. [Google Scholar]
- Feynes, F. Rotary Compressor. U.S. Patent 1,802,887, July 1927. [Google Scholar]
- Frager, M.; Menard, H. Rotary Volumetric Apparatus. U.S. Patent 3,029,741, April 1962. [Google Scholar]
- Imran, M.; Pili, R.; Usman, M.; Haglind, F. Dynamic modeling and control strategies of organic Rankine cycle systems: Methods and challenges. Appl. Energy 2020, 276, 115537. [Google Scholar] [CrossRef]
- Ren, H.P.; Wang, X.; Fan, J.T.; Kaynak, O. Adaptive Backstepping Control of a Pneumatic System With Unknown Model Parameters and Control Direction. IEEE Access 2019, 7, 64471–64482. [Google Scholar] [CrossRef]
- Loukianov, A.G.; Sanchez, E.; Lizalde, C. Force tracking neural block control for an electro-hydraulic actuator via second-order sliding mode. Int. J. Robust Nonlinear Control 2008, 18, 319–332. [Google Scholar] [CrossRef]
- Yoon, Y.; Yang, M.; Sun, Z. Robust position tracking control of a camless engine valve actuator with time-varying reference frequency. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 3292–3297. [Google Scholar] [CrossRef]
- Meng, F.; Zhang, H.; Cao, D.; Chen, H. System Modeling, Coupling Analysis, and Experimental Validation of a Proportional Pressure Valve With Pulsewidth Modulation Control. IEEE/ASME Trans. Mechatronics 2016, 21, 1742–1753. [Google Scholar] [CrossRef]
- Gu, W.; Yao, J.; Yao, Z.; Zheng, J. Robust Adaptive Control of Hydraulic System With Input Saturation and Valve Dead-Zone. IEEE Access 2018, 6, 53521–53532. [Google Scholar] [CrossRef]
- Rahmat, M.F.; Husain, A.R.; Ishaque, K.; Irhouma, M. Self-Tuning Position Tracking Control of an Electro-Hydraulic Servo System in the Presence of Internal Leakage and Friction. Int. Rev. Autom. Control 2010, 3, 673–683. [Google Scholar]
- Mercorelli, P.; Werner, N. A cascade controller structure using an internal PID controller for a hybrid piezo-hydraulic actuator in camless internal combustion engines. In Proceedings of the 2013 9th Asian Control Conference (ASCC), Istanbul, Turkey, 23–26 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Persson, L.J.; Plummer, A.R.; Bowen, C.R.; Brooks, I. Design and modelling of a novel servovalve actuated by a piezoelectric ring bender. In Fluid Power Systems Technology, ASME/BATH 2015 Symposium on Fluid Power and Motion Control, October 12–14, 2015, Chicago, IL, USA; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Chung, S.K.; Koch, C.R.; Lynch, A.F. Flatness-Based Feedback Control of an Automotive Solenoid Valve. IEEE Trans. Control. Syst. Technol. 2007, 15, 394–401. [Google Scholar] [CrossRef]
- Seoa, J.; Venugopal, R.; Kennéa, J.P. Feedback linearization based control of a rotational hydraulic drive. IFAC Proc. Vol. (IFAC-Pap.) 2007, 7, 940–945. [Google Scholar] [CrossRef]
- Angue Mintsa, H.; Venugopal, R.; Kenne, J.P.; Belleau, C. Feedback Linearization-Based Position Control of an Electrohydraulic Servo System With Supply Pressure Uncertainty. IEEE Trans. Control Syst. Technol. 2012, 20, 1092–1099. [Google Scholar] [CrossRef]
- He, H.; Quan, S.; Wang, Y.X. Hydrogen circulation system model predictive control for polymer electrolyte membrane fuel cell-based electric vehicle application. Int. J. Hydrogen Energy 2020, 45, 20382–20390. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, Z.; Li, K.; Liu, J.; Zhang, Y.; Dan, D.; Wu, C.; Wang, P.; Wang, X. An improved intelligent model predictive controller for cooling system of electric vehicle. Appl. Therm. Eng. 2021, 182, 116084. [Google Scholar] [CrossRef]
- Soufi, Y.; Kahla, S.; Bechouat, M. Particle swarm optimization based sliding mode control of variable speed wind energy conversion system. Int. J. Hydrogen Energy 2016, 41, 20956–20963. [Google Scholar] [CrossRef]
- Samani, R.; Khodadadi, H. A particle swarm optimization approach for sliding mode control of electromechanical valve actuator in camless internal combustion engines. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Haus, B.; Aschemann, H.; Mercorelli, P.; Werner, N. Nonlinear modelling and sliding mode control of a piezo-hydraulic valve system. In Proceedings of the 2016 21st International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 29 August–1 September 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Lin, Y.; Shi, Y.; Burton, R. Modeling and robust discrete-time sliding-mode control design for a fluid power electrohydraulic actuator (EHA) system. IEEE/ASME Trans. Mechatronics 2013, 18, 1–10. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; 503p. [Google Scholar] [CrossRef]
- Fang, J.; Wang, X.; Wu, J.; Yang, S.; Li, L.; Gao, X.; Tian, Y. Modeling and Control of A High Speed On/Off Valve Actuator. Int. J. Automot. Technol. 2019, 20, 1221–1236. [Google Scholar] [CrossRef]
- Han, C.; Choi, S.B.; Han, Y.M. A Piezoelectric Actuator-Based Direct-Drive Valve for Fast Motion Control at High Operating Temperatures. Appl. Sci. 2018, 8, 1806. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, T.; Xie, Q.I.; Wei, Q. Intelligent Electro-Pneumatic Position Tracking System Using Improved Mode-Switching Sliding Control With Fuzzy Nonlinear Gain. IEEE Access 2008, 6, 34462–34476. [Google Scholar] [CrossRef]
- Feng, G.; Lei, S.; Gu, X.; Guo, Y.; Wang, J. Predictive control model for variable air volume terminal valve opening based on backpropagation neural network. Build. Environ. 2021, 188, 107485. [Google Scholar] [CrossRef]
- Ghoniem, M.; Awad, T.; Mokhiamar, O. Control of a new low-cost semi-active vehicle suspension system using artificial neural networks. Alex. Eng. J. 2020, 59, 4013–4025. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belfiore, C.; Hossain, S.; Phung, T.; Sultan, I. Limaçon Technology in Power Generation. Encyclopedia 2024, 4, 1865-1890. https://doi.org/10.3390/encyclopedia4040122
Belfiore C, Hossain S, Phung T, Sultan I. Limaçon Technology in Power Generation. Encyclopedia. 2024; 4(4):1865-1890. https://doi.org/10.3390/encyclopedia4040122
Chicago/Turabian StyleBelfiore, Christopher, Shazzad Hossain, Truong Phung, and Ibrahim Sultan. 2024. "Limaçon Technology in Power Generation" Encyclopedia 4, no. 4: 1865-1890. https://doi.org/10.3390/encyclopedia4040122
APA StyleBelfiore, C., Hossain, S., Phung, T., & Sultan, I. (2024). Limaçon Technology in Power Generation. Encyclopedia, 4(4), 1865-1890. https://doi.org/10.3390/encyclopedia4040122







