Definition
The Pandemic Equation describes multiple pandemic waves and has been applied to describe the COVID-19 pandemic. Using the generalized approaches of solid-state physics, we derive the Pandemic Equation, which accounts for the effects of pandemic mitigation measures and multiple pandemic waves. The Pandemic Equation uses slow and fast time scales for “curve flattening” and describing vaccination and mitigation measures and the Scaled Fermi–Dirac distribution functions for describing transitions between pandemic waves. The Pandemic Equation parameters extracted from the pandemic curves can be used for comparing different scenarios of the pandemic evolution and for extrapolating the pandemic evolution curves for the periods of time on the order of the instantaneous Pandemic Equation characteristic time constant. The parameter extraction for multiple locations could also allow for uncertainty quantification for such pandemic evolution predictions.
Keywords:
outbreak; endemic; pandemic; COVID-19; Ebola; SARS; plaque; pandemic equation; HIV; Spanish Flu 1. Introduction
A pandemic is defined as an epidemic that occurs on more than one continent [1]. An epidemic is a more severe event than an outbreak of a disease, which is a sudden increase in disease occurrence. An epidemic is a large number of outbreaks spreading to a large geographical area.
Epidemics and pandemics such as the Athenian Plague (430 BC [2], Antonine Plague (165–180 AD) [3], Justian Plague (541 AD) [4]. Black Death (1346–1353), the Seven Cholera Pandemics (1827–1961), Spanish Flu (1918) [5], HIV, Ebola, Severe Acute Respiratory Syndrome (SARS) (2002–2003), and COVID-19 have caused deaths and economic hardship. The predicted dramatic increase in world population of slums (from 1.1 billion people today to over 3 billion expected in 30 years from now [6]) with no access to pure drinking water and related population migration are some of the reasons that mean that future pandemics are unavoidable and might be harder to control. Other factors making pandemics more difficult to control include the overuse of antibiotics and pesticides, widespread problems with healthcare systems worldwide, corruption, wars, and racial problems. In addition, the World Health Organization is relying more and more on private donations from donors who might have their own agenda to promote, making preventing and controlling pandemics more difficult [7]. Unavoidably, pandemics cause stereotypes and psychological problems, exacerbating the pandemic problems.
This is why an expected future mysterious and disastrous pandemic Disease X (20 times more infectious than the COVID-19 pandemic) was discussed in DAVOS 24 (one of the sessions was called “Preparing for Disease X”) [8].
A part of such preparation is the development of simple but effective mathematical approaches to monitor and analyze pandemics, such as the Pandemic Equation [9,10].
When a pandemic comes it develops more rapidly in hot spots and infection rates are dramatically different in different locations. The optimum measures to control a pandemic also vary a lot from nation to nation, from one community to another, or from a university campus to an elementary school. To achieve that control, we need to analyze complex and vastly varying data accurately interpolating overall time and space dependencies of infection rates, related hospital admissions, and deaths, as well as such dependencies for certain groups, for example, immune-suppressed people.
To this end, the Pandemic Equation borrowed such an approach from the quantum theory of solids comprised of practically infinite numbers of nuclei and electrons.
Solids are comprised of nuclei and electrons whose masses are as different as the mass of a behemoth and a sparrow, and the electronic motion, compared to the nucleus motion as fast as a flight of a sparrow, to a behemoth motion. Similarly, the Pandemic Equation uses a fast time scale of an exponential pandemic growth or decay but varies the characteristic time of its evolution on a much slower time scale.
Another concept borrowed from the solid-state theory is the Fermi–Dirac Distribution function. This function describes a gradual transition between two states and the abruptness of such a transition is controlled by a temperature parameter varying from a very abrupt at low temperatures to very gradual at high temperatures. This function is generalized in this paper to introduce a Scaled Fermi–Dirac function. This function is perfectly suited for the interpolation of complicated transitions in pandemic events related to mitigation measures or the introduction of new drugs.
Pandemics often come in waves having many peaks and valleys. As an example, see Figure 1 showing the weekly deaths caused by the COVID-19 pandemic. The Pandemic Equation describes a pandemic as a summary of such waves. A more accurate approach introduced in this paper is using another concept similar to so-called Vegard’s law in materials science. This law interpolates the properties of a mixture by a linear combination of the properties of the mixture components. In this paper, we introduce a Scaled Vegard’s Law that accurately interpolates the transition between the pandemic waves.
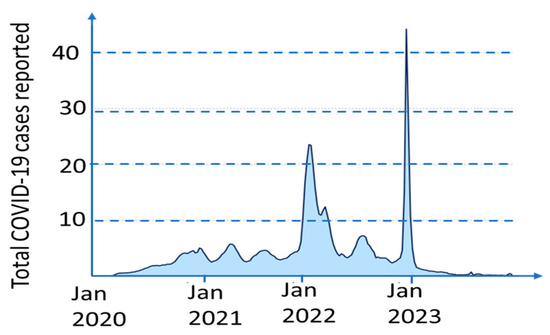
Figure 1.
Weekly COVID-19 cases reported worldwide (in millions). Data from [11].
The COVID-19 pandemic was unique in terms of enormous data collection, and we applied the Pandemic Equation method to the COVID-19 epidemic. However, the results of the COVID-19 analysis could teach us valuable lessons and help combat future possible pandemics.
The Pandemic Equation parameters extracted from the pandemic curves can be used for comparing different scenarios of the pandemic evolution and for extrapolating the pandemic evolution curves for the periods of time on the order of the instantaneous Pandemic Equation characteristic time constant. The parameter extraction for multiple locations could also allow for uncertainty quantification for such pandemic evolution predictions.
2. COVID-19 Pandemic
The reported COVID cases and COVID deaths are probably underestimated, as seen in Figure 2, which compares excess mortality during the pandemic with the reported COVID-19 deaths in the United States.

Figure 2.
Excess deaths and COVID-19 deaths in the United States. (Data from [11]).
The infection rate and COVID-19-related hospitalizations all come in waves. These waves rise, crest, and dip, and then rise, crest, and dip again. This applies to all other pandemics as well. It is better seen from Figure 2 since averaging the data in Figure 1 over the entire world smoothed the wave transitions. As seen in Figure 3 and Figure 4, death rates differ between different countries and even various locations in one country.
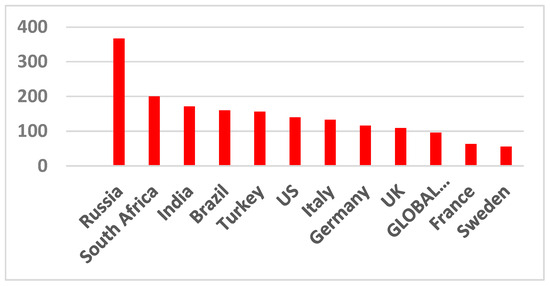
Figure 3.
Excess mortality during the pandemic and the reported COVID-19 deaths. Data from [12].

Figure 4.
Cumulative coronavirus deaths by share of the population in each county for 7 days in March 2023. (Data from [13,14]. Map from [15]).
New pandemic waves occur due to new emerging variants caused by mutation and recombination. The virus is asexual and replicates making copies of itself. Mistakes (mutations) during reproduction cause new strains. Some strains are not competitive and die out, but some are more easily spread or more deadly. Recombination occurs when a host cell is infected with two different variants at the same time, exchanging one part of a virus for another. For example, the overtaking of the Delta variant by Omicron [16].
The severity of the COVID-19 peaks is clear from comparing its impact with the USA annual death rates for varied reasons (see Figure 5).
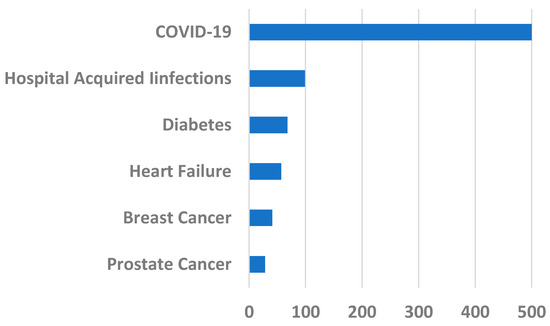
Figure 5.
USA annual death rates in 2020 in thousands for different causes. Data from [17].
Simulations could drive the response to a pandemic (see [18,19,20,21,22,23,24,25,26,27], review papers [28,29,30,31,32,33,34,35,36] and references therein). The complexity of a pandemic indicates a need for a transparent and easily understood pandemic monitoring tool, which is especially acute. The Pandemic Equation is such a tool using generalized approaches, approximations, and mathematics and concepts previously applied for the description of solid-state physics phenomena, such as the Born–Oppenheimer Approximation [37] and Fermi–Dirac distribution function [38,39]. Our approach to pandemic modeling is based on (1) using different time scales: short time scales over which one could use the Logistic Equation [40,41] solution and much longer times scales over which the characteristic times of pandemic variation in the Logistic Equation slowly vary, (2) introducing the Scaled Fermi–Dirac (SFD) function that approximates transitions between the pandemic waves, and (3) generalization of the Vegard’s Law [42]. The advantage of the Pandemic Equation is its ability to describe separate pandemic waves and accurately interpolate the transitions in between. Another advantage is that its predictive ability has a well-defined time scale (on the order of the slow characteristic time. This makes it suitable for use with AI models, as reviewed in references [31,34,35], and for using uncertainty quantification models for evaluating the quality of such predictions.
3. Logistic Equation
As explained above, a pandemic is a complex event involving outbreaks of disease on several continents and at multiple and widespread geographic locations. A pandemic could be traced and characterized at different levels: globally and locally at the continent, country, state, or even county or campus level. At each level, there is a number of people, Nt, that could be infected, which is the relevant infection pool. As mentioned in the introduction, a pandemic is an epidemic that occurs on more than one continent, and an epidemic is a large number of outbreaks spreading to a large geographical area. A pandemic has to be monitored locally and globally. For local monitoring, Nt is the local pandemic pool, such as the total number of people in a certain locality, such as a county, city, town, or even a university campus. For more global monitoring, Nt is the population of a state or even of a continent. The mathematics of global and local pandemic monitoring are similar. Only the scale is different. As explained below, the Pandemic Equation could even monitor the spatial dependence of the pandemic assuming the anisotropic Gaussian distribution of infections. This definition of Nt allows us to compare the solutions of the Pandemic Equation with the actual reported data at all levels.
The relevant characteristics of the infection include the total number of infections, N1; the number of hospital admissions to treat the disease, N2; the number of disease-related deaths N3; or the access mortality number, N4. Each such characteristic has its characteristic time constant τk corresponding to the infection characteristics Nk. The Logistic Equation describes an outbreak, endemic, or pandemic event in a simple but not exactly accurate way:
Here k = 1,2,3, or 4, and τk are the characteristic time constant of the initial pandemic growth. This equation could be rewritten in a dimensionless form using :
The solution of Equation (1) is
Here, .
The daily number of new infection events, , is more important for following the pandemic evolution than the total number of infections to date, . From Equation (7), the daily number of new infection events, , is
The maximum of this symmetric curve is reached at .
The change in the initial condition (initial fraction of infection events ) only shifts the pandemic curve in time by a few periods (see Figure 6).
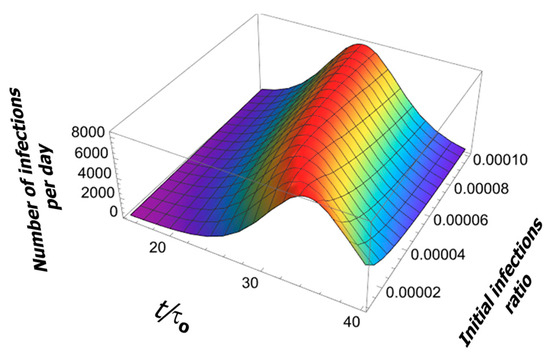
Figure 6.
Effect of initial conditions on the solution of Logistic Equation.
As seen in Figure 7, the solution of the Logistic Equation describes the pandemic evolution only at the initial pandemic stage (till approximately week 14). After that, the actual time dependence is quite different. The solution of the Logistic Equation with the same initial increase in the infection rate predicts a much larger peak. The actual dependence is flattened. This effect is referred to as “curve flattening”. As schematically shown in Figure 7, the curve flattening effect brings the peak infection rate below the capability of the health system to treat the infection.
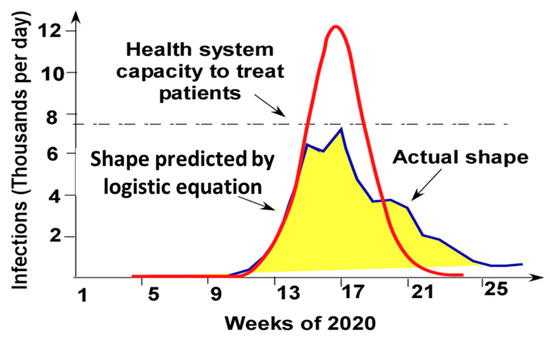
Figure 7.
Weekly COVID-19 case in Connecticut interpolated by the solution of the Logistic Equation. (Connecticut data from [43]) (The health system capacity is shown for illustration only and might be different from the capacity of the Connecticut health system.).
The actual dependence is asymmetrical: the decay stage is longer than the growth stage. There are significant deviations from a smooth curve shape. These deviations might be related to the introduction of a new protocol in treating the disease, to the changes in people’s behavior, to mitigation measures, such as demanding to wear masks or closing or opening the economy.
As shown in Figure 7, the Logistic Equation only describes a single pandemic wave, whereas the pandemic develops in many overlapping waves (for example, see Figure 1 and Figure 2).
The Pandemic Equation addresses all these issues for a much more realistic description of a pandemic.
4. Pandemic Equation
The Pandemic Equation uses the solution of the Logistic Equation but introduces the time dependence of the pandemic characteristic time constant, which is, in most cases, just a slow linear dependence on time . This approach is similar to the Born–Oppenheimer approximation used in solid-state physics, to separate rapid electronic motion and much slower nuclei motion. Nuclei are thousands of times heavier than electrons and rapid electron motion could be considered using “frozen” nuclei positions. Likewise, the Pandemic Equation uses the solution of the Logistic Equation for short periods of time, but the characteristic time constant slowly varies with time, as described by Equation (8). Parameter ak is the curve flattening parameter (see Table 1 listing the parameters used in the Pandemic Equation).

Table 1.
Pandemic Equation parameters.
Table 1 defines Pandemic Equation parameters.
Parameter αk determines the asymmetry of the pandemic evolution curve, as shown in Figure 8.
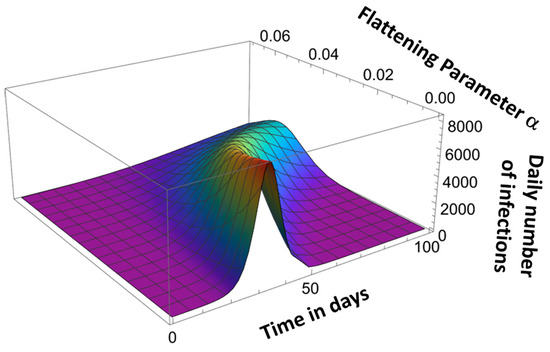
Figure 8.
Effect of flattening parameter α.
In the solid-state theory, the Fermi–Dirac (FD) function, FFD, is used to describe the transition between a non-degenerate and degenerate energy state, i.e., the transition from the occupied electronic states to empty electron states with the temperature, T, determining the transition interval. We now introduce the Scaled Fermi–Dirac unction (SFD) where the temperature itself is a function of energy
In the simplest case, this dependence is linear: . Here, q is the electronic charge, EF is the Fermi level energy, and kB is the Boltzmann constant (see Figure 9a). As can be seen, this function describes the transition from zero to unity centered at the Fermi level with the transition width on the order of 3 kBT. To apply the FFD function to describe the transitions in the pandemic evolution curves, we have replaced the variables. Figure 9b shows the same function using the variables relevant to the Pandemic Equation (time, t, instead of energy E, the time of transition instead of the Fermi level, EF, and the characteristic transition time constant instead of kBT/q):
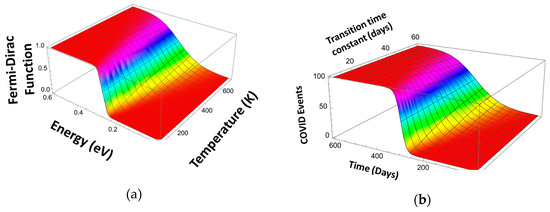
Figure 9.
Fermi–Dirac distribution function for electrons (Fermi level 0.3) (a) and applied to describe a pandemic event (b).
(Index w designates different mitigation events.)
The Pandemic Equation could use the function, such as that shown in Figure 9, to describe the mitigation measures that determine the transition from a high to a lower infection rate. This more accurate pandemic evolution model must account for a slow variation in the mitigation event characteristic time constant with time. Here , is the time-independent initial characteristic transition time constant, and is the mitigation event flattening parameter.
We call the function defined by Equation (4) the Scaled Fermi–Dirac (SFD) distribution function. The SFD distribution function could find applications in solid-state physics to describe the electron temperature increase in the electric field more accurately since electrons with a higher energy could also have a higher energy of random motion (i.e., a higher temperature [44]). Figure 10 shows the effect of parameter on the FDS distribution function.

Figure 10.
FDS distribution function for (a) and (b). (Compare with Figure 9b for ).
Based on the above discussion, we can now introduce the generalized Pandemic Equation that describes multiple mitigation events (see [9,10] and references therein):
Here,
Figure 11a illustrates the effect of the mitigation events. Figure 11a simulates the effect of vaccination of the different degrees of effectiveness. Figure 11b represents the effects of opening and closing the economy.
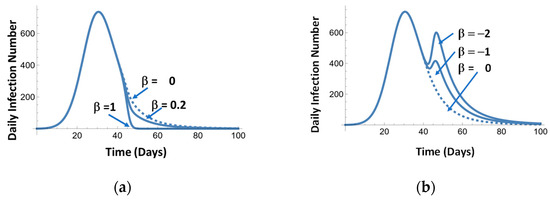
Figure 11.
Examples of mitigation effects: positive β (a) and positive and negative β (b).
A generalized Pandemic Equation accounts for the infection space dependence:
Here is the total number of the infection events in a given location, and is given by Equation (8). , are the coordinates of the maximum infection event location using the x-y coordinate system related by the angle with respect to the north–south direction, and and are the standard deviations (see Figure 12 and Figure 13). The standard deviation values are extracted from the published pandemic data. Index j corresponds to the different peaks of the pandemic events in space.

Figure 12.
Space-dependent infection rates with two hot spots (a) and three hot spots (b).
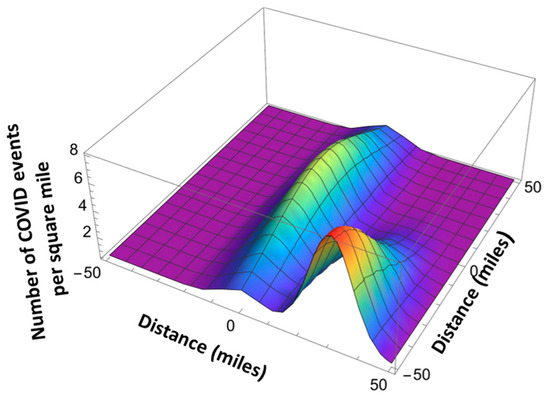
Figure 13.
Anisotropic space dependence of Pandemic Equation solution.
This formalism could be applied to the description of the multiple pandemic waves using the SDF function to describe the transition between the pandemic waves l and l + 1:
Here, ; ; .
We call Equation (9) the Scaled Vegard’s Law (SVL). The SVL is the generalization of Vegard’s Law that is used in solid-state theory, material science, and chemistry for a description of properties of mixtures and ternary materials:
Here, a is the unit constant of a ternary compound comprising binary components with unit constants a1 and a2 and molar fraction x of compound 1. In contrast to Vegard’s Law, the SVL interpolates a large variety of transitions. Figure 14 shows that SVL could interpolate transitions from those corresponding to the conventional Vegard’s Law to highly nonlinear transitions.
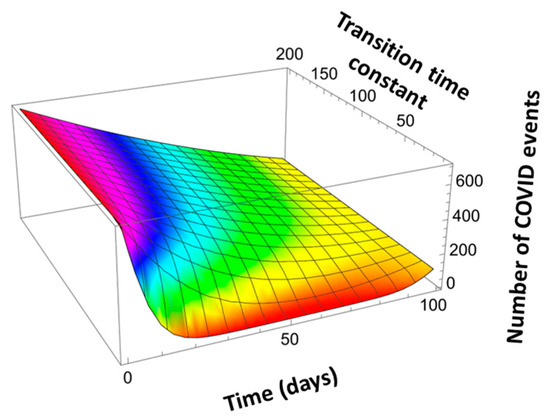
Figure 14.
Scaled Vegard’s Law applied to describe COVID event transitions from 700 per day at t = 0 to 100 per day at t = 100 days for varying time constant τ = τ1 = τ2.
As seen in Figure 15, this approach allows us to describe all five waves of the COVID-19 pandemic by fitting each pandemic wave independently and interpolating the transition between the waves using SVL.
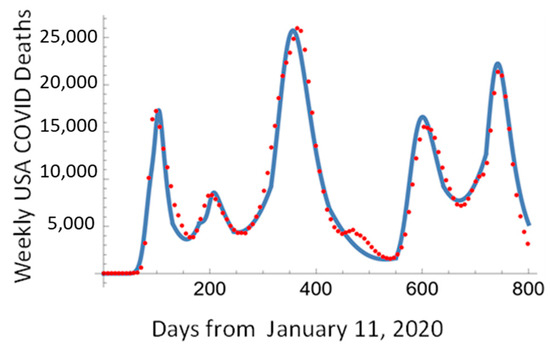
Figure 15.
The daily death rate in the USA fitted using the Pandemic Equation solution and SVL.
As seen from Figure 15, the Pandemic Equation and SLG interpolation described the five waves of the COVID-19 pandemic.
5. Conclusions
Epidemics and pandemics have affected humankind throughout history. The last pandemic, COVID-19, is unique because of the many steps implemented to mitigate the pandemic that differed between different countries and even different localities. There is also an unprecedented amount of data characterizing COVID-19 development. The Pandemic Equation applies the generalized approaches of the quantum theory of solids to describe pandemic events using different time scales: a fast time scale, at which the solutions of the Logistic Equation apply and a slow time scale, at which the parameters of the Logistic Equation change. To describe the transitions between the pandemic events, the Pandemic Equation is using Scaled Fermi–Dirac distribution functions and the Scaled Vegard’s Law. These generalizations might also find applications in solid-state theory. One example is the behavior of hot electrons having the Fermi–Dirac distribution function with a non-Maxwellian tail [36].
The Pandemic Equation is a valuable tool for researching and quantifying the effects of health care and mitigation measures on pandemic evolution and will allow humankind to better prepare for possible future pandemics and epidemics. Further research will focus on the development of artificial intelligence models to automatically extract optimum Pandemic Equation parameters.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author is also Vice-President and Chief Technology Officer of Electronics of the Future, Inc. The company had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Morens, D.M.; Folkers, G.K.; Fauci, A.S. What is a pandemic? J. Infect. Dis. 2009, 200, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Sampath, S.; Khedr, A.; Qamar, S.; Tekin, A.; Singh, R.; Green, R.; Kashyap, R. Pandemics Throughout the History. Cureus 2021, 13, e18136. [Google Scholar] [CrossRef] [PubMed]
- Sáez, A. The Antonine plague: A global pestilence in the II century DC. Rev. Chil. Infectol. 2016, 33, 218–221. [Google Scholar] [CrossRef] [PubMed]
- Smith, C.A. Plague in the ancient world: A study from Thucydides to Justinian. Stud. Hist. J. 1996, 28, 19. [Google Scholar]
- Available online: https://www.cdc.gov/flu/pandemic-resources/1918-pandemic-h1n1.html (accessed on 22 October 2023).
- Available online: https://unstats.un.org/sdgs/report/2023/goal-11/ (accessed on 3 February 2024).
- Shah, S. Pandemic: Tracking Contagions, from Cholera to Coronaviruses and Beyond; Picador: New York, NY, USA, 2017. [Google Scholar]
- Prater, E. Disease X’ Could Cause the Next Pandemic, according to the WHO—Or Ebola, SARS, or Nipah. 9 Pathogens Researchers Are Keeping a Watchful Eye on. Fortune Well. 12 January 2024. Available online: https://fortune.com/well/2024/01/12/what-is-disease-x-world-economic-forum-pandemic-planning/ (accessed on 12 April 2024).
- Shur, M. Pandemic Equation for Describing and Predicting COVID19 Evolution. J. Healthc. Inform. Res. 2021, 5, 168–180. [Google Scholar] [CrossRef] [PubMed]
- Shur, M. Interdisciplinary Fundamental Concepts in STEM: Solid State Physics and COVID-19 Pandemic Evolution. Int. J. Eng. Sci. Technol. 2023, 5, 119–127. [Google Scholar] [CrossRef]
- Available online: https://covid19.who.int/ (accessed on 27 December 2023).
- Available online: https://www.whitehouse.gov/cea/written-materials/2022/07/12/excess-mortality-during-the-pandemic-the-role-of-health-insurance/ (accessed on 14 October 2022).
- Available online: https://www.bbc.com/news/61333847 (accessed on 14 April 2023).
- Available online: https://www.nytimes.com/interactive/2021/us/covid-cases.html (accessed on 27 December 2023).
- Available online: https://covid.cdc.gov/covid-data-tracker/#county-view?list_select_state=Virginia&data-type=CommunityLevels&list_select_county=51059 (accessed on 10 May 2022).
- Mallapaty, S. COVID-19: How Omicron overtook Delta in three charts. Nature 2022. [Google Scholar] [CrossRef]
- Available online: https://www.ontherighttrack.com/news/the-healthcare-paradox (accessed on 28 July 2022).
- Adam, D. Special report: The simulations driving the world’s response to COVID-19. Nature 2020, 580, 316–318. [Google Scholar] [CrossRef]
- Singh, R.K.; Rani, M.; Bhagavathula, A.S.; Sah, R.; Rodriguez-Morales, A.J.; Kalita, H.; Nanda, C.; Sharma, S.; Sharma, Y.D.; Rabaan, A.A.; et al. Prediction of the COVID-19 Pandemic for the Top 15 Affected Countries: Advanced Autoregressive Integrated Moving Average (ARIMA) Model. JMIR Public Health Surveil. 2020, 6, e19115. [Google Scholar] [CrossRef]
- Metcalf, J.E.; Morris, D.H.; Park, S.W. Mathematical models to guide pandemic response. Science 2020, 369, 6502. [Google Scholar] [CrossRef]
- Berryman, A.A. The Origins and Evolution of Predator-Prey Theory. Ecology 1992, 73, 1530–1535. [Google Scholar] [CrossRef]
- Bourdelais, P. Mapping the Course of an Epidemic: The Example of Two Cholera Epidemics in France (1832 and 1854). Available online: https://cams.ehess.fr/modeling-propagation-covid-19-abstracts-and-slides (accessed on 12 April 2024).
- Di Domenico, L.; Pullano, G.; Sabbatini, C.E.; Boëlle, P.Y.; Colizza, V. Impact of lockdown on COVID-19 epidemic in Île-de-France and possible exit strategies. BMC Med. 2020, 18, 240. [Google Scholar] [CrossRef] [PubMed]
- Reiner, R.; Collins, J.K.; Murray, C.J.L. Forecasting the Trajectory of the COVID-19 Pandemic into 2023 under Plausible Variant and Intervention Scenarios: A Global Modelling Study. Available online: https://www.medrxiv.org/content/10.1101/2023.03.07.23286952v1.full (accessed on 12 April 2024).
- Calvetti, D.; Somersalo, E. Post-pandemic modeling of COVID-19: Waning immunity determines recurrence frequency. Math Biosci. 2023, 365, 109067. [Google Scholar] [CrossRef]
- Tashiro, A.; Shaw, R. COVID-19 Pandemic Response in Japan: What Is behind the Initial Flattening of the Curve? Sustainability 2020, 12, 5250. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Cao, L.; Liu, Q. COVID-19 Modeling: A Review. medRxiv 2022. preprint. [Google Scholar] [CrossRef]
- Rahimi, I.; Chen, F.; Gandomi, A.H. A review on COVID-19 forecasting models. Neural Comput. Applic. 2023, 35, 23671–23681. [Google Scholar] [CrossRef] [PubMed]
- Y’uce, M.; Filiztekin, E.; ‘Ozkaya, K.G. COVID-19 diagnosis -a review of current methods. Biosens. Bioelectron. 2021, 172, 112752. [Google Scholar]
- Mohamadou, Y.; Halidou, A.; Kapen, P.T. A review of mathematical modeling, artificial intelligence and datasets used in the study, prediction and management of COVID-19. Appl. Intell. 2020, 50, 3913. [Google Scholar] [CrossRef]
- Shankar, S.; Mohakuda, S.S.; Kumar, A.; Nazneen, P.S.; Yadav, A.K.; Chatterjee, K.; Chatterjee, K. Systematic review of predictive mathematical models of COVID-19 epidemic. Med. J. Armed Forces India 2021, 77, S385–S392. [Google Scholar] [CrossRef]
- Park, M.; Cook, A.R.; Lim, J.T.; Sun, Y.; Dickens, B.L. A systematic review of COVID-19 epidemiology based on current evidence. J. Clin. Med. 2020, 9, 967. [Google Scholar] [CrossRef]
- Rasheed, J.; Jamil, A.; Hameed, A.A.; Al-Turjman, F.; Rasheed, A. COVID-19 in the age of artificial intelligence: A comprehensive review. Interdiscip. Sci. Comput. Life Sci. 2021, 13, 153–175. [Google Scholar] [CrossRef] [PubMed]
- Shi, F.; Wang, J.; Shi, J.; Wu, Z.; Wang, Q.; Tang, Z.; He, K.; Shi, Y.; Shen, D. Review of artificial intelligence techniques in imaging data acquisition, segmentation, and diagnosis for COVID-19. IEEE Rev. Biomed. Eng. 2021, 14, 4–15. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Y.; Jia, Y.; Chen, L.; Guo, L.; Shu, B.; Long, E. COVID-19 epidemic prediction and the impact of public health interventions: A review of COVID-19 epidemic models. Infect. Dis. Model. 2021, 6, 324–342. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Oppenheimer, J.R. Zur Quantentheorie der Molekeln. Ann. Der Phys. 1927, 389, 457–484. [Google Scholar] [CrossRef]
- Dirac, P.A.M. On the Theory of Quantum Mechanics. Proc. R. Soc. A 1926, 112, 661–677. [Google Scholar] [CrossRef]
- Fermi, E. Sulla quantizzazione del gas perfetto monoatomico. Rend. Lincei 1926, 3, 145–149. [Google Scholar]
- Verhulst, P.-F. Recherches mathématiques sur la loi d’accroissement de la population. Nouv. Mém. L’academie R. Sci. Belles-Lett. Brux. 1845, 18, 1–40. [Google Scholar] [CrossRef]
- Bacaër, N. A Short History of Mathematical Population Dynamics; eBook; Springer: London, UK, 2011. [Google Scholar] [CrossRef]
- Vegard, L. Die Konstitution der Mischkristalle und die Raumfüllung der Atome. Z. Für Phys. 1921, 5, 17–26. [Google Scholar] [CrossRef]
- Available online: https://hartfordhealthcaremedicalgroup.org/about-us/news-center/news-detail?articleId=36336&publicid=395 (accessed on 25 October 2023).
- Hu, C. Lucky-electron model of channel hot electron emission. In Proceedings of the 1979 International Electron Devices Meeting, Washington, DC, USA, 3–5 December 1979; pp. 22–25. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).