Heat Conduction Control Using Deep Q-Learning Approach with Physics-Informed Neural Networks

Abstract

As modern systems become more complex, their control strategy no longer relies only on measurement data from probes; it also requires information from mathematical models for non-measurable places. On the other hand, those mathematical models can lead to unbearable computation times due to their own complexity, making the control process non-viable. To overcome this problem, it is possible to implement any kind of surrogate model that enables the computation of such estimates within an acceptable time frame, which allows for making decisions. Using a Physics-Informed Neural Network as a surrogate model, it is possible to compute the temperature distribution at each time step, replacing the need for running direct numerical simulations. This approach enables the use of a Deep Reinforcement Learning algorithm to train a control strategy. On this work, we considered a one-dimensional heat conduction problem, in which temperature distribution feeds a control system. Such control system has the objective of reacing and maintaining constant temperature value at a specific location of the 1D problem by activating a heat source; the desired location somehow cannot be directly measured so, the PINN approach allows to estimate its temperature with a minimum computational workload. With this approach, the control training becomes much faster without the need of performing numerical simulations or laboratory measurements.

1. Introduction

Differential equations serve as the primary representation of complex interactions that are primarily non-linear in the study of real-world phenomena [1]. Although it is possible to model those systems, the analytical solutions of the resulting equations are typically only available for simple cases that are primarily of interest in academic settings. Complex cases that do not have an analytical solution often remain unresolved for a significant period, making it challenging to use them in a real application to make timely decisions to apply certain control measures. Often, surrogate models and numerical solutions are utilized to address this issue, leading to alternative methods for finding the actual solution.

Some research studies employ data-driven models to facilitate the capture of knowledge from spatial and temporal discretizations. For instance, the research conducted by Iakovlev et al. [2] highlights the capacity of a trained model to effectively handle unstructured grids, arbitrary time intervals, and noisy observations.

One way of modeling data is through the employment of neural networks [3,4], which are computational models that approximate the behavior of a system and are composed of multiple layers to represent data with multiple levels of abstraction [5]. This approach has achieved superior results across a wide range of applications [6], such as visual object recognition, video classification [7], and voice recognition [8].

The typical process for training a neural network involves having a set of data that contain true inputs and their corresponding true outputs. Then, the neural network parameters, weights, and biases are initialized with random values. After such initialization, the goal resides in minimizing the error between true known data and the prediction generated by a neural network model. The error is minimized by modifying the neural network parameters using an optimization strategy.

The objective of standard neural network training is to reduce the error between the model’s predicted values and real values. However, there are cases where gathering the true resulting values is not possible, thereby preventing the application of this training process. To address such an issue, an alternative approach for training neural network models, as proposed by Lagaris et al. [9], states that the training can be performed using a set of differential equations.

The objective is for the error generated by these equations to approach zero when evaluating a given set of data, collocation points, that are contained in the differential equations domain. This set of data also involves initial and boundary conditions for such differential equations. This methodology does not rely on training using the expected results; instead, it employs evaluation data exclusively. This leads to quicker training procedures compared to methods that involve running simulations or conducting experiments before or during the training phase.

This training approach has been defined as Physics-Informed Neural Networks (PINNs). Some work has been successfully conducted in the fields of robotics [10], power transformers [11], and control strategies [12].

Despite the conceptual simplicity of PINNs, their training process can be challenging [3]. In addition to configuring neural network hyperparameters, such as number of layers, nodes per layer, activation functions, and loss functions, PINNs demand balancing multiple terms of the loss function, partitioning of the results, and time marching to prevent convergence to undesirable solutions [13,14,15,16,17,18].

On the other hand, a system model defined using a PINN strategy can be used as a digital twin to provide information to a decision-making system that could also take information delivered by sensors [19], or coupled with a control system to define actuation actions in real-time situations [20]. In the same sense of digital twin, Liu et al. [21] proposed a multi-scale model utilizing PINNs to predict the thermal conductivity of polyurethane phase-change material foam composites.

In terms of the control of non-linear dynamical systems, the implementation of digital twins in the form of neural networks has been increasingly employed. Those digital twins are employed to estimate the state of the system at any given location and time, acting as virtual sensors. An example of such an implementation to estimate flow around obstacles, stabilize vortex shedding, and reduce drag force has been presented in the work of Fan et al. [22] and Déda et al. [23]. One way to define control strategies is through the implementation of reinforcement learning algorithms, which is a machine learning area able to iteratively improve a policy within a model-free framework [24].

One of the reinforcement learning algorithms is the Deep Q-Learning algorithm. Let us suppose a discrete time controller that uses a Markov decision process to define an action according to a structure of events. Once an action is defined and executed, this action changes the state of the system. The system states are compared against a reference. The result of such a comparison generates a reward related to such an action. The system then defines another possible action, executes it, and generates another related reward. This process is repeated until an objective is achieved. Those rewards are successively appended and used to train the process model. The Deep Q-Learning algorithm is a reinforcement learning algorithm that uses the Bellman equation to evaluate future incomes (Q-value) [25], starting from the current state, and a neural network (Deep) [26] to simultaneously evaluate the Q-values for all possible actions at some stage.

This work presents a strategy for controlling the central point temperature of a rod in which a heat source is applied at one end, and at the other end, it has free convection to ambient air as a heat transfer phenomenon. The control strategy is trained with the Deep Q-Learning approach using a Physics-Informed Neural Network to evaluate the state of the system and forecast near-future states. This approach is also compared with a standard control strategy. The problem is presented as a uni-dimensional and continuous medium problem, which implies the control strategy has to deal with the delay effects caused by the control action and the heat loss to the ambient.

2. Materials and Methods

In this section, the Deep-Q Learning framework is presented by introducing the Physics-Informed Neural Network model and control model employed further in this work.

2.1. Control System

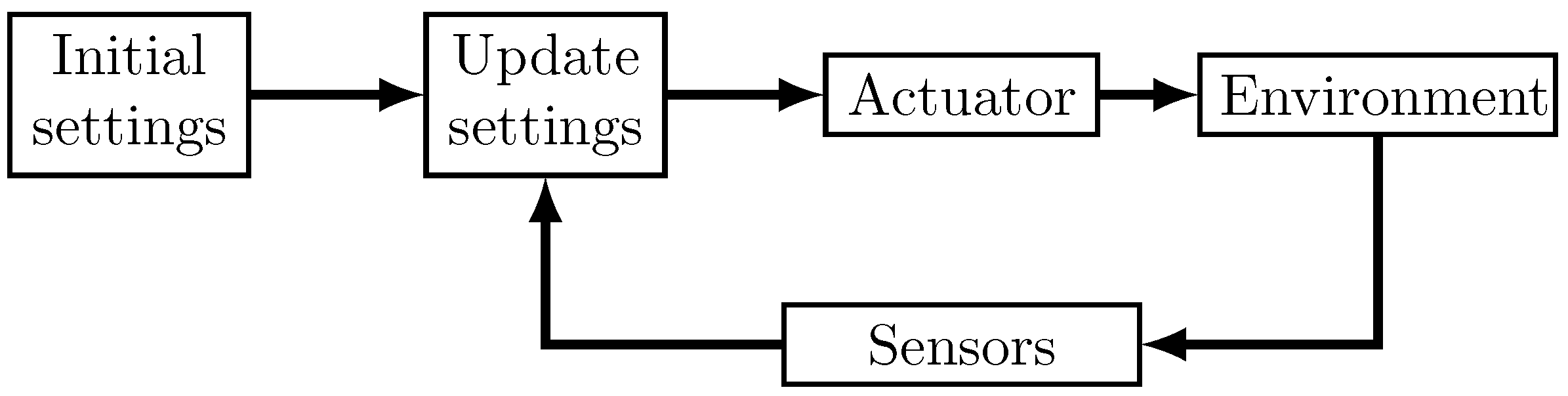
A simple control system can be represented by a few components with information traveling between them (see Figure 1). One of the components represents a set of actuators which are initially configured with some possible values. The action coming out from those actuators results in an impact on the environment that is composed out of the system and its bounds interactions, the states of which are measured by sensors. Another component is the control unit, which uses the information obtained by the sensors to update the system settings to obtain an objective.

In this system, the two components that are more relevant to this work are the environment and the control system. Regarding the environment, it can be replaced by a simulator, enabling one to predict its behavior for some system settings and therefore allow one to train the control beforehand. The control system needs to be defined, i.e., one needs to define a policy that decides the best system setting for an environmental state, represented by the sensor’s measurements.

In this work, the environment behavior will be modeled with a PINN strategy, and the definition of the control unit will be made with a reinforcement learning strategy (Deep Q-Learning).

2.2. PINN

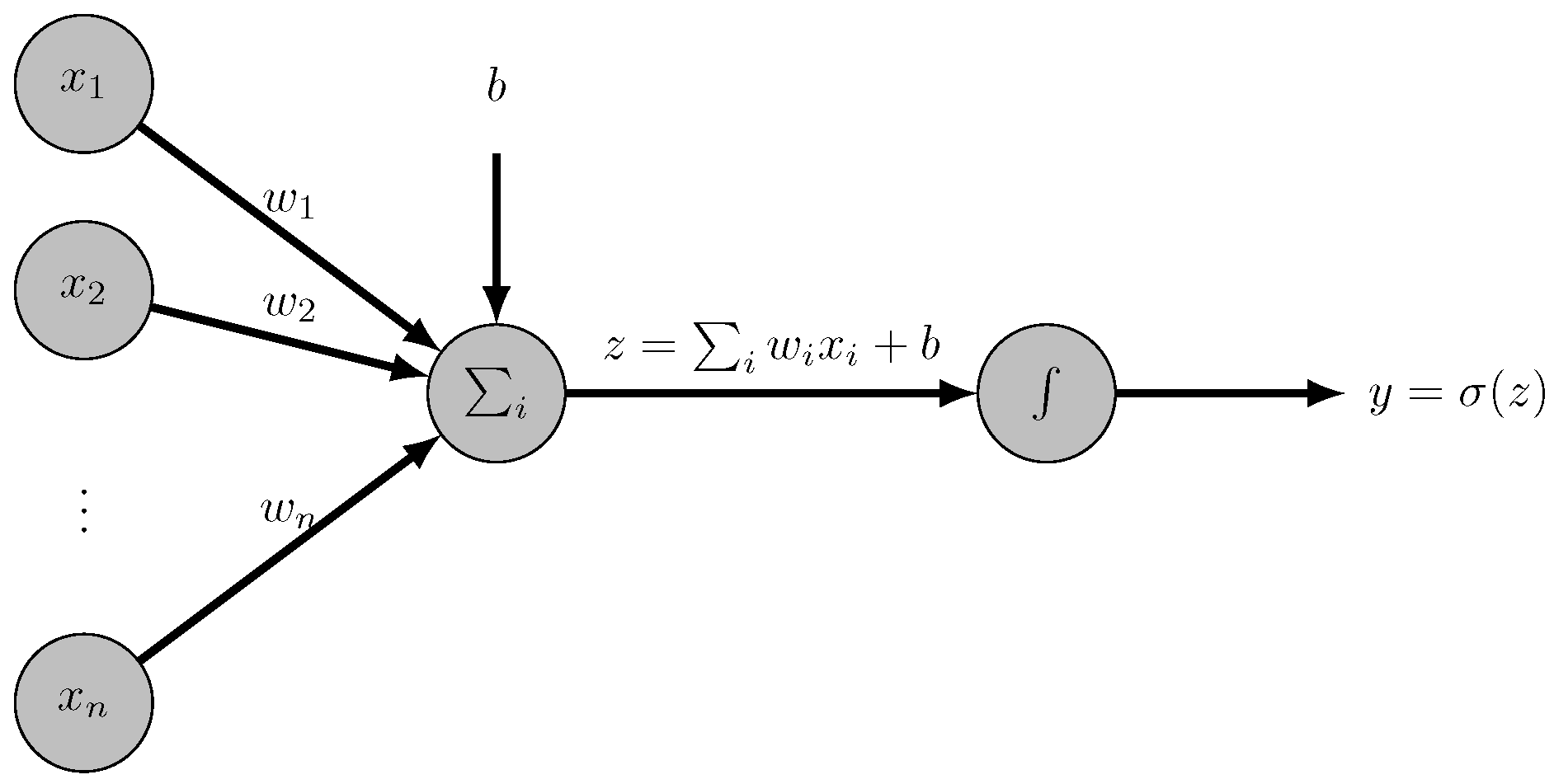
Artificial neural networks have been developed since the 1950s, inspired by rats’ cortex functioning [27,28]. A neural network is a set of simple computational units, perceptrons (see Figure 2), where a set of inputs are multiplied by weights, and its sum with a bias is sent to an activation function. This activation function can be used to polarize the result, i.e., the image is close to a minimum (corresponding to without a property) or close to a maximum (corresponding to having a property).

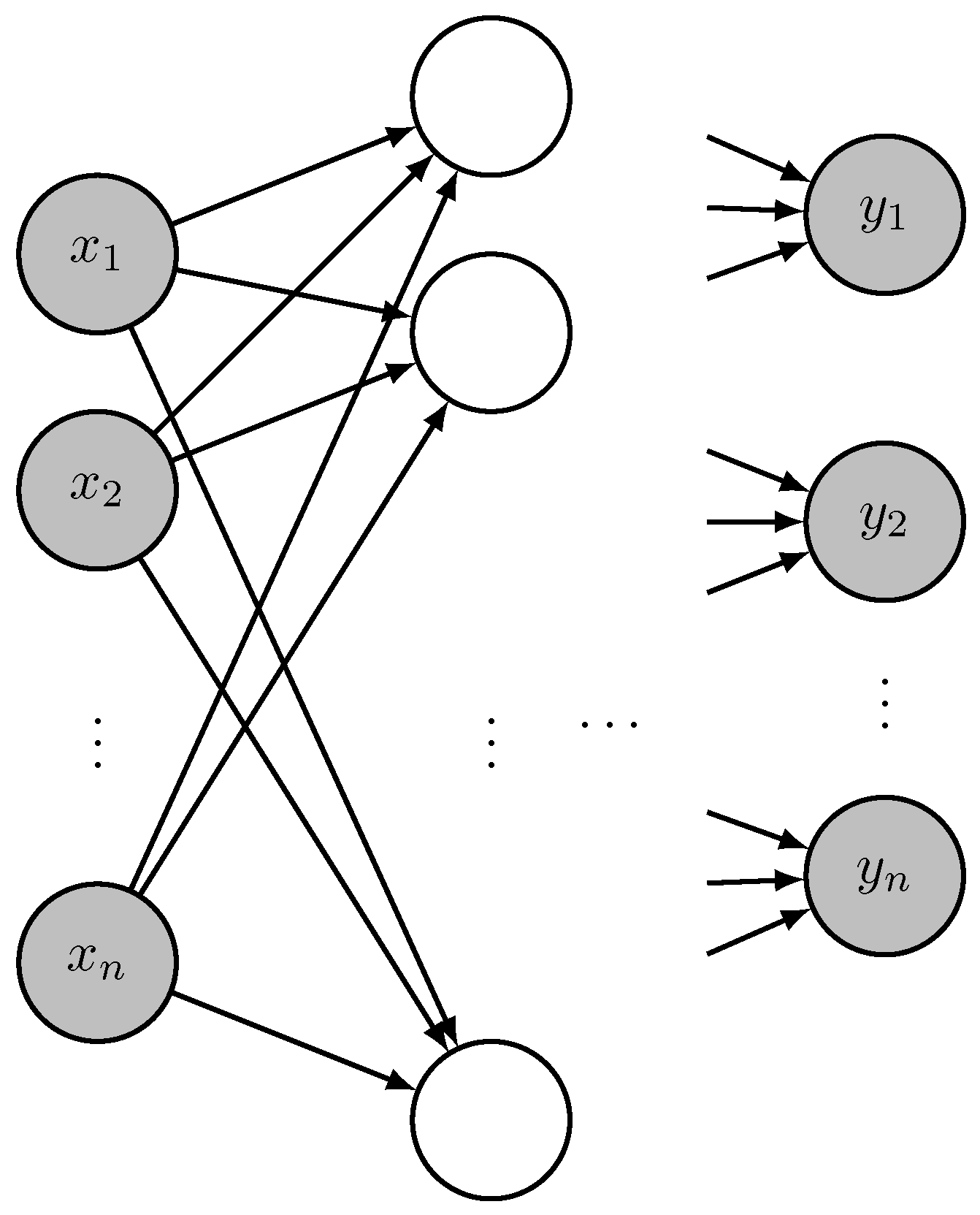
In neural networks, a set of inputs can feed a set of perceptrons, forming a layer. A feedforward neural network is composed of a series of layers, with the outputs of those layers being used as inputs for the following layer (see Figure 3).

The number of inputs and outputs of a neural network is defined by the data that are being modeled; however, the number of layers, number of nodes per layer, and activation functions are not so easily defined. Data scientists usually use previous experience to set an initial estimate that is improved in the training stage, as it is not the main goal of this study.

On “standard” neural networks, the results estimated by the neural network $Y_{NN}$ (see Figure 4) are compared with known results Y (e.g., obtained by numerical simulations or laboratory measurements) resulting in a loss, ${\mathcal{L}}_{data}$. This loss can be calculated in several ways, e.g., in this work, it was considered the mean square error.

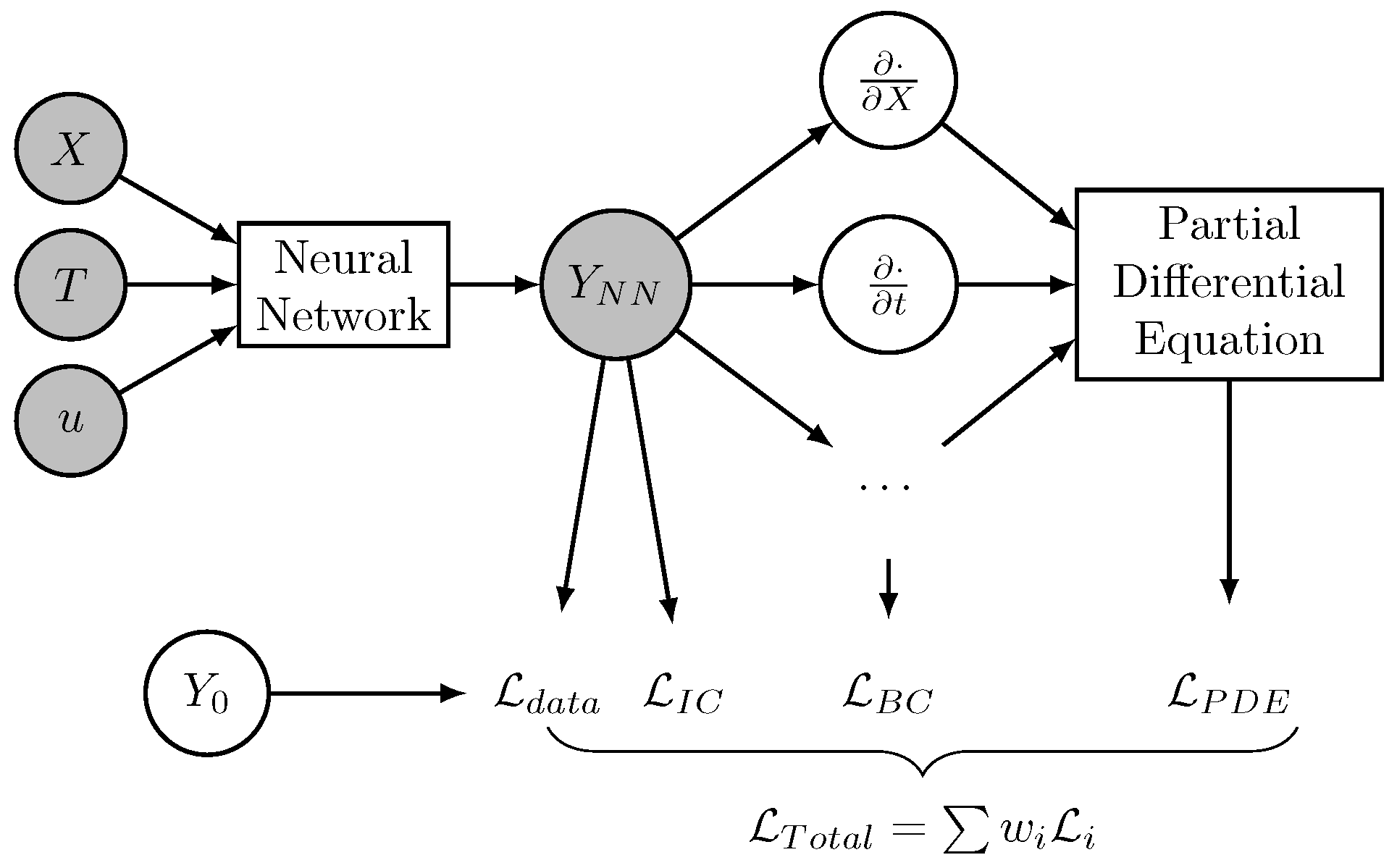
In Physics-Informed Neural Networks, the previously referred data can be used to estimate a total loss, or the train can be performed without any data, making this process much faster, especially when data come from time-consuming processes.

During PINN training, in addition to the estimation of $Y_{NN}$, its derivatives are also estimated using the automatic differentiation algorithm [29], and replaced on the differential equations to assess the resulting error, ${\mathcal{L}}_{PDE}$. The boundary conditions and initial conditions are assessed, leading to the losses ${\mathcal{L}}_{BC}$ and ${\mathcal{L}}_{IC}$, respectively. A total loss, ${\mathcal{L}}_{TOTAL}$, is calculated with the several partial losses multiplied by weights. In this work, the weights are defined as the inverse of the cardinality of each set.

This method comes in handy when the required data to train a neural network using the “standard” approach are too expensive to obtain, only requiring a number of collocation points, inside the problem’s domain, to be evaluated into the proposed neural network.

Algorithm 1 presents the PINN training algorithm to determine the neural network $Y_{NN}$ that receives the coordinates X, time t, and control u, as well the initial values $T\left(X,t=0\right)$ and returns the $T\left(X,t=t\right)$. During this training, the definition of a finite number of possibilities of each of these parameters is required. In this work, we do not consider the partitioning of the results and time marching to avoid convergence.

Algorithm 1 PINN algorithm.

1: set a set of initial conditions $Y(t=0)$ 2: set training data intervals to consider 3: define the neural network parameters: layers, nodes, and activation function 4: set learning parameters: learning rate, loss function 5: train the neural network aiming to minimize loss function

2.3. DQL

The objective of the control unit is to decide the best action for a given environment state, i.e., the action that maximizes the reward: at some stage, taking an action from a given state, or during an entire episode considering the expected future rewards available from the current state up to the episode end when the goal is achieved.

With a reinforcement learning strategy, each state, action taken and reward obtained is recorded in a table to support future decisions. When the set of possible states is too big or even infinite, one needs to make some kind of generalization, and neural networks can be used to perform this task. At Deep Q-Learning (DQL), instead of a function that looks at a table of previous results to decide the better action for a given state, an NN is used to evaluate the expected future reward (Q-value) as the sum of future rewards weighted with a discount factor ${\sum }_{t>0}{\gamma }^t{r}_t$ for a set of possible actions [28].

The use of such a supervised learning algorithm enables one to progressively improve the model (see Figure 5).

Q-Learning algorithm is based on the Bellman equation (Equation (1)):

$$Q_{new}\left(s_t,a_t\right)=Q_{main}\left(s_t,a_t\right)+\beta \left(r_t+\gamma \underset{a}{max}{Q}_{target}\left(s_{t+{\delta }_t},a\right)-Q_{main}\left(s_t,a_t\right)\right),$$

(1)

where $\beta$ is the learning rate, $r_t$ denotes the current reward obtained taking the action $a_t$ from state $s_t$, $\gamma$ is the discounting rate, and sa value in $\left[0,1\right]$ used to set the importance of immediate rewards compared with future ones.

During the DQL training algorithm, the estimate of $ma{x}_{a}Q\left(s_t,a_t\right)$ leads to systematic overestimation introducing a bias in the learning process. A solution to avoid this overestimation is to use two different estimators, $Q_{main}$ and $Q_{target}$, trained at different stages [30]. Whereas $Q_{main}$ is trained periodically every pre-determined number of iterations, $Q_{target}$ is updated, obtaining the values of $Q_{main}$ less frequently.

Algorithm 2 presents the DQL algorithm to determine the neural network Q that receives the environment state s and returns the reward Q-values (total discounted future rewards r) for each of the available actions a.

Algorithm  2 Deep Q-Learning algorithm.

1: initialize policy parameters 2: $ste{p}_{global}\leftarrow 0$ 3: for $episode=0$, $episod{e}_{max}$ do 4:    $ste{p}_{global}\leftarrow ste{p}_{global}+1$ 5:    for $step=0$, $ste{p}_{max}$ do 6:    Draw a random value $\omega \in \left[0,1\right]$ 7:    if $\omega <ϵ$ then 8:     choose a random action 9:    else 10:     choose the action (available from the current state) that maximizes Q 11:    end if 12:    execute the action and get a new state and reward (save on batch) 13:    if $ste{p}_{global}\equiv 0modstep{s}_{train}$ then 14:     train models 15:     update policy parameters 16:    end if 17:    if $ste{p}_{global}\equiv 0modstep{s}_{copy}$ then 18:     $Q_{target}\leftarrow Q_{main}$ 19:    end if 20:    end for 21: end for

3. Case Study

In this section, we present the details of the problem used to test the proposed methodology that aims to utilize a dimensionless model, compatible with neural networks.

3.1. Geometry, Boundary Conditions, and Mesh

The scenario under examination involves a 1D rod of length L, where natural convection occurs at its left end and a controlled heat source is present at its right end (see Figure 6).

The goal of this case is to reach a specific temperature in the center of the geometry, at $x=L/2$; this location ensures a positional induced delay in the heat transfer phenomena that is equally separated from the heat source ($x=L$) and the heat sink, in this case, convection ($x=0$), to better understand the effects of each control strategy. The governing equation is then the Energy Conservation Equation (2):

$${\displaystyle \frac{\partial T}{\partial t}}=\alpha {\displaystyle \frac{{\partial }^{2}T}{\partial x^2}},$$

(2)

where T is the temperature, t is the time, $\alpha$ is the thermal diffusivity, and x is the spatial coordinate.

The natural convection Equation (3) relies on the heat transfer coefficient h, which characterizes the heat convection condition at the surface of the rod, the thermal conductivity property of the rod material k, and the external temperature $T_{ext}$:

$$-k{\left[{\displaystyle \frac{\partial T}{\partial x}}\right]}_{x=0}=-h\left(T_{\mathrm{ext}}-{\left[T\right]}_{x=0}\right)$$

(3)

At the opposite end $x=L$, the heat source is controlled by a u function, leading to the condition shown in Equation (4):

$$-k{\left[{\displaystyle \frac{\partial T}{\partial x}}\right]}_{x=L}=u$$

(4)

As the initial conditions, we consider an initial temperature $T_{ini}$.

The above governing equation (Equation( 2)) can be adimensionalized by the following replacement of variables as presented in (5), (6) and (7):

$$\theta ={\displaystyle \frac{T-T_{\mathrm{ext}}}{T_{\mathrm{ini}}-T_{\mathrm{ext}}}},$$

(5)

$$\xi ={\displaystyle \frac{x}{L}},$$

(6)

$$\tau ={\displaystyle \frac{\alpha }{L^2}}t,$$

(7)

obtaining the equivalent Equation (8)

$${\displaystyle \frac{\partial \theta }{\partial \tau }}={\displaystyle \frac{{\partial }^2\theta }{\partial {\xi }^2}},$$

(8)

Alternatively, the normalized values were considered directly on Equation (2), thermal diffusivity $\alpha =1$, heat transfer coefficient $h=1[\mathrm{W}·{\mathrm{m}}^{-2}{\mathrm{K}}^{-1}]$, $T\in \left[T_{\mathrm{ext}},T_{\mathrm{ini}}\right]$ with $T_{\mathrm{ext}}=0$ and $T_{\mathrm{ini}}=1$, and $x\in \left[0,L\right]$ with $L=1$. The time step was defined as ${\delta }_t=0.1\mathrm{s}$.

For the space discretization, several meshes were considered, with 5, 11, 21, and 41 nodes.

3.2. Solution

For validation purposes, the analytical solution was an approximation for a numerical method, the Finite Volume Method, i.e., by integration on space $\left({\delta }_x\right)$ and time $\left({\delta }_t\right)$ at each mesh cell, leading to ${\delta }_x\left(T_i-T_i^{old}\right)={\delta }_t{\sum }_f\alpha {\displaystyle \frac{\partial T}{\partial \mathbf{n}}}$. The FVM discretization was performed considering a zero volume elements at both domain ends to tackle with boundary conditions and the remaining elements with length ${\delta }_x$.

3.3. PINN Parameters

In this case study, several PINN configurations were tested until acceptable results were achieved. A deeper analysis and optimization of such a model is not a goal of this work.

The $x\left[\mathrm{m}\right]$ values considered in this work were in $\left[0,1\right]$ with increment $0.1$, leading to 11 possible points to the reference case. The mesh studies were performed with 5, 11, 21, and 41 points with the corresponding increments. The initial values were defined considering a three-degree polynomial defined with the conditions ${\left[T\right]}_{x=0}=T_0$, ${\left[T\right]}_{x=L}=T_L$, ${\left[{\displaystyle \frac{\partial T}{\partial x}}\right]}_{x=0}=T_0-T_{ext}$ and ${\left[{\displaystyle \frac{\partial T}{\partial x}}\right]}_{x=L}=u$, where $T_0$ and $T_L$ are the temperatures at $x=0$ and $x=L$, respectively, with values in $\left[0,1\right]$ with an increment of $0.1$, and the random perturbation $rnd$ in $\left[-0.005,0.005\right]$. The time values $t\left[\mathrm{s}\right]$ were set in $[0,2]$ with an increment of $0.05$ and $u\in \left\{0,0.25,0.5,0.75,1\right\}$. Therefore, a training set with $11\times 21\times 5\times 11\times 11=139755$ rows of eleven $T_x$ values was set, and $10\%$ of its values randomly chosen were used to train the PINN.

Regarding the neural network, the input parameters are 14: the coordinate x, the time t, the control u, and the 11 initial temperatures ($T(x=0,t=0)$, $T(x=0.1,t=0)$, …, $T(x=1,t=0)$). The output is just one value, $T(x,t)$. The neural network was defined with 5 inner layers with $2\times 14$, $3\times 14$, $2\times 14$, 14 and 7 nodes, respectively. As activation functions, the hyperbolic tangent was chosen to activate the hidden layers, except the last layer, which was set with a linear activation function. The optimizer algorithm employed was Adam, and the train was performed with 200 iterations per each of the learning rates: ${10}^{-3},{10}^{-4},{10}^{-5},{10}^{-6},{10}^{-6}$.

3.4. DQL Parameters

As stated before, the input to DQL is a state s of the system at a given time t that should be enough to decide the action to take. However, it is possible to increase this information to feed the control with the data of previous time steps. Therefore, this study considered sending the temperature at each coordinate x not only at time t but the last $N_{s_t,h}$, and evaluating the difference control response.

The DQL neural network was set with $11\times N_{st,h}$ inputs for the defined number of previous time steps considered, multiplied by the number of temperatures of each time step (eleven): the 4 hidden layers with $2\times 11N_{st,h}$, $4\times 11N_{st,h}$, $2\times 11N_{st,h}$ and $1\times 11N_{st,h}$ nodes each, and sigmoid activation function. The last layer with activation function was set with softmax to return a probability distribution of the decision to make. The optimizer algorithm was set Adam with a learning rate of ${10}^{-3}$ and categorical cross-entropy as a loss function.

The DQL was trained with 400 episodes, with a 20 maximum steps per episode, saving the results in a 16 long batch before each training, with 4 iterations (epochs), copying $Q_{main}$ to $Q_{trarget}$ every 64 steps. The random actions were taken with an initial probability $1.0$, decreasing $1\%$ every steps until achieving a minimum probability $0.1$.

The learning rate $\beta$ was set as $0.9$, discount factor $\gamma =0.1$, and the space of actions (set of possible values of u) in $\{0,0.25,0.5,0.75,1\}$.

As initial values, we considered linear distribution between both ends with temperatures in $[0,1]$ plus a random perturbation in $[0,0.01]$.

Several possible $N{t}_{fw}$ future values were considered to evaluate the control system, to take into account the delay between the action and the system response.

4. Results

4.1. PINN Results

The training of the PINN was performed in an Intel^® Core^™ i7-7700K CPU at $4.20\mathrm{GHz}$ (4 cores, 8 threads) and $64\mathrm{GB}$ of RAM, and took approximately ${17}^{\prime }$ (with 5 elements), $2h{6}^{\prime }$ (with 11 elements), $11h{57}^{\prime }$ (with 21 elements), and $89h{21}^{\prime }$ (with 41 elements).

The prediction using the PINN was obtained almost instantaneously.

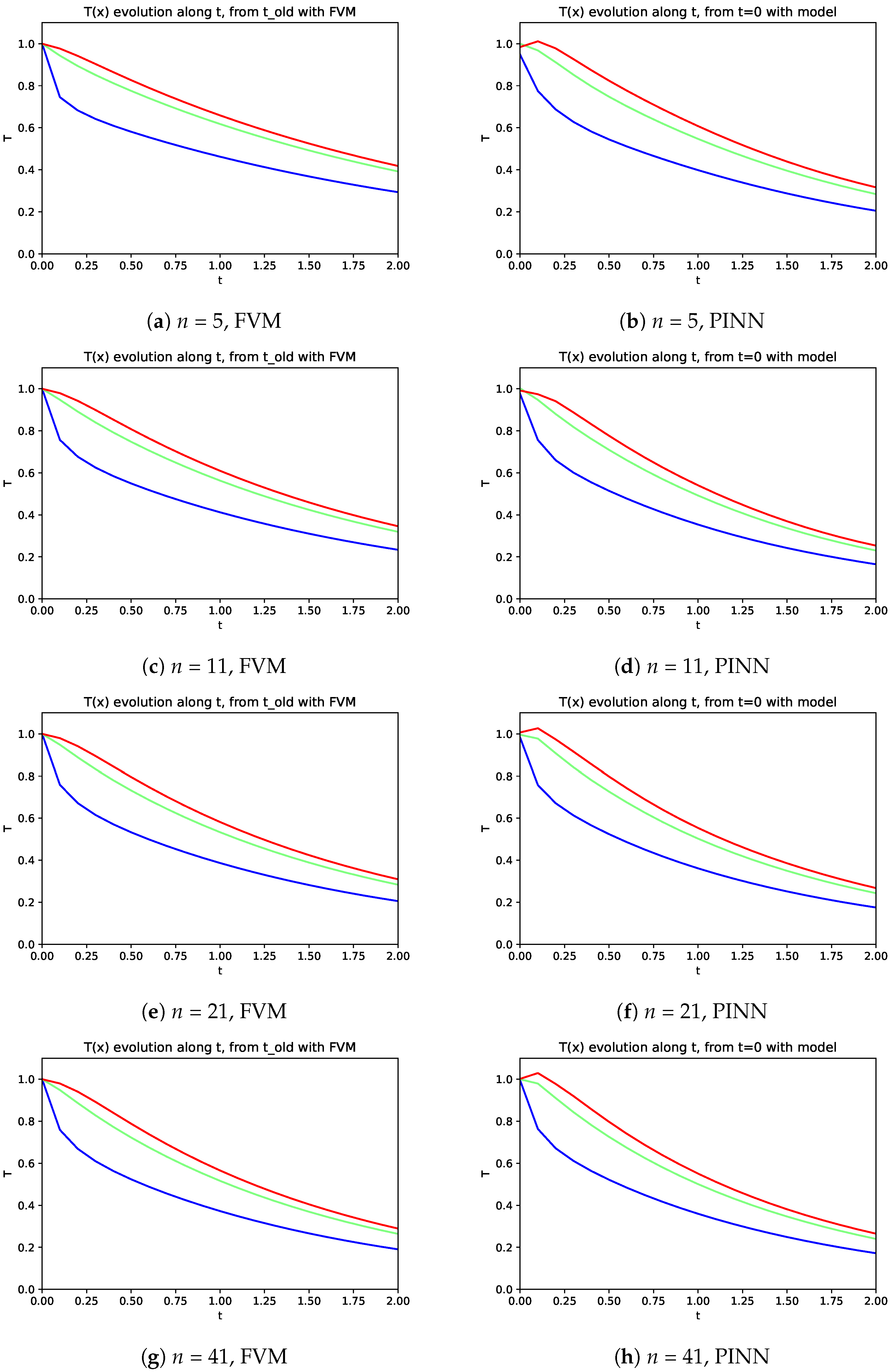
The PINN quality was evaluated through the analysis of its prediction to the temperature distribution for all (5, 11, 21 or 41) points homogeneously distributed along the range $\left[0,1\right]$, from the initial condition (at $t=0\mathrm{s}$) up to $t=2\mathrm{s}$ with a time step $0.1\mathrm{s}$.

Due to the integration interval, the FVM was employed considering the previous time step (old) values to evaluate the following one, whereas the PINN model is not limited by this issue.

When the initial conditions are defined at $t=0$, one can predict the evolution of the temperature at three points ($x=0\mathrm{m}$, $x=0.5\mathrm{m}$ and $x=1\mathrm{m}$) along the time (see Figure 7). The temperature decreases faster on the boundary with natural convection ($x=0\mathrm{m}$), whereas the two other places cool slower. The comparison of results obtained with the PINN model with those obtained with FVM enables one to note a good agreement, and consequently validate the PINN model (see Figure 7).

Regarding the mesh influence, from Figure 7, it can be noticed that similar results were obtained, with just some perturbation on the right boundary (red lines) temperatures obtained with PINN.

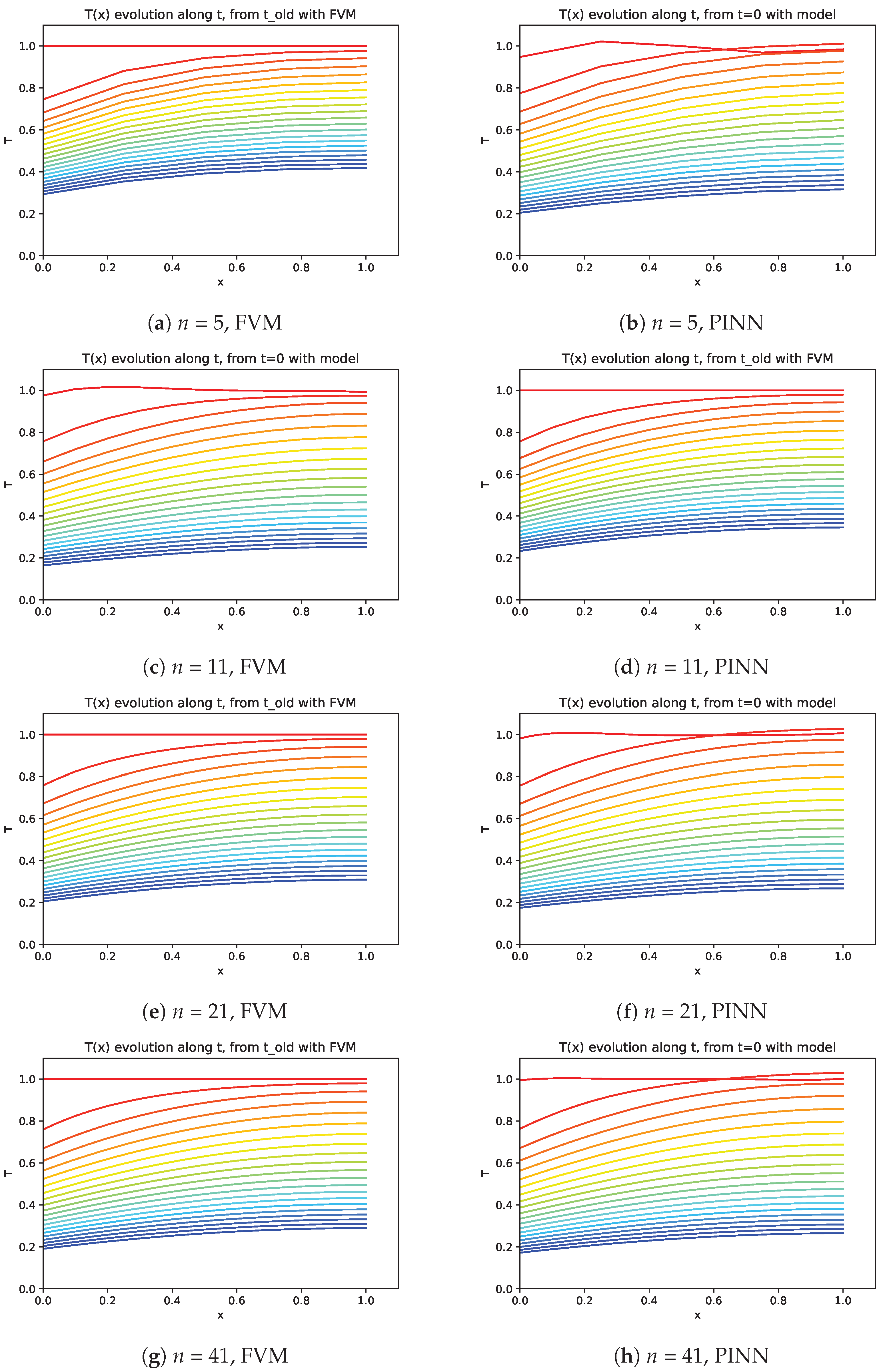
A similar analysis can be performed considering the evolution of the temperature distribution on the domain along the time (see Figure 8).

The comparison of the temperatures predicted by the PINN model and those obtained with FVM (see Figure 8) shows similarity with a slight difference for values to $t=0$, where the model seems to be affected by the boundary condition with natural convection. Several approaches were tried, namely, different weights to losses and more training iterations, leading to continuous improving of these results.

4.2. DQL Results

With the PINN defined, i.e., trained, it was possible to train the policy model, with the Deep Q-Learning algorithm. The training was performed on the same processor already referred and took about $18”$, $14”$, $11”$, and $11”$, respectively, for 5, 11, 21, and 41 nodes, using the FVM, whereas the PINN model took $51”$, $36”$, $27”$, and $27”$, respectively.

The simulation to test the DQL control took around $0.67”$ with FVM, whereas with the PINN, it took around $1.11”$.

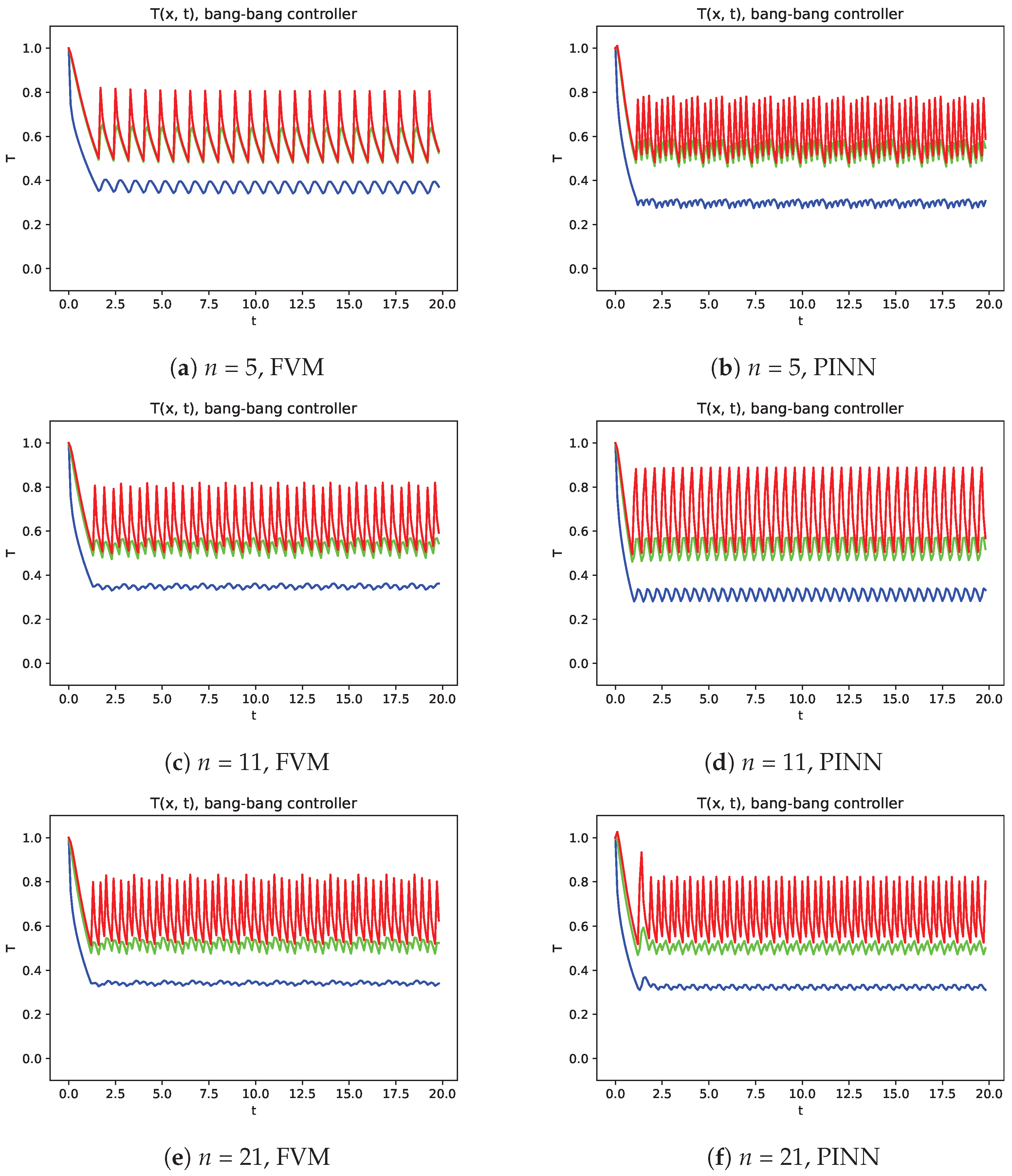
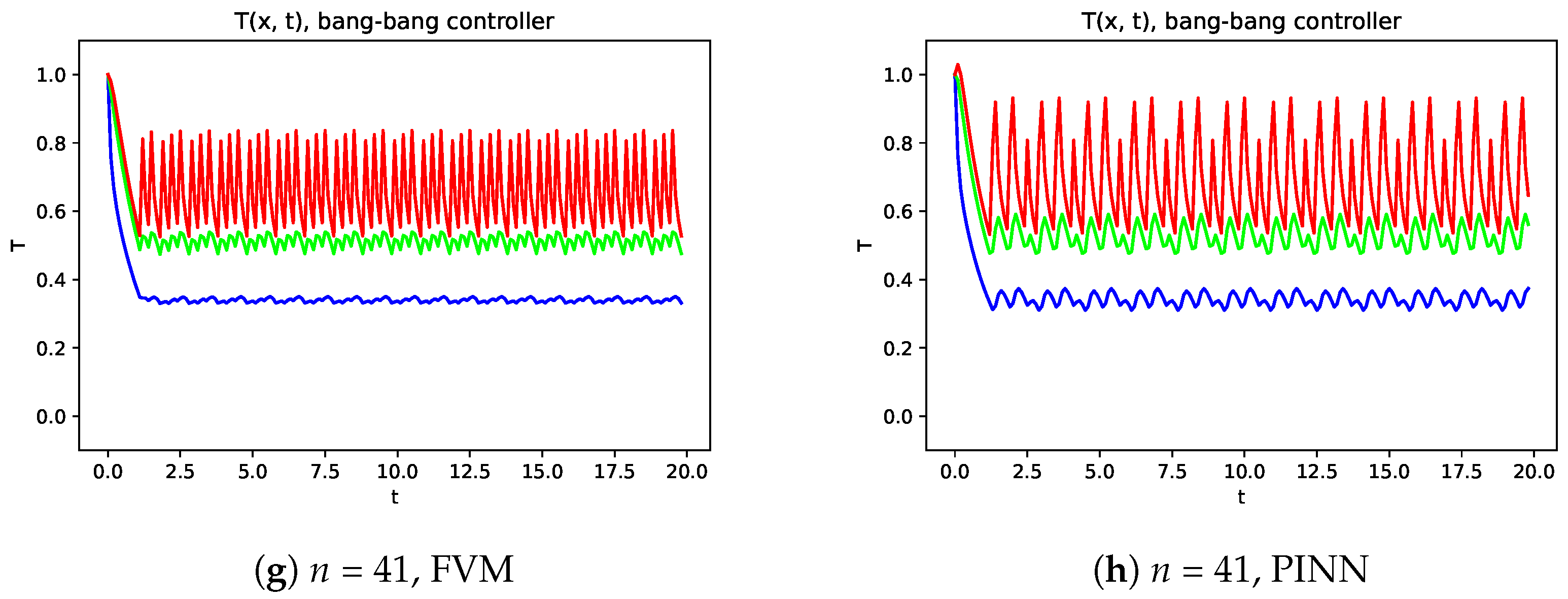
To set a baseline, we used a bang–bang controller, i.e., the heating is turned on always, then the temperature at $x=0.5$ is equal to or lower than the goal temperature $T=0.5$. The evolution of the temperatures at three points ($x=0$, $x=0.5$ and $x=1$) was monitored, and from this evolution with FVM versus the PINN model (see Figure 9), it seems that PINN enables a more stable control when coarser meshes are used, with FVM improving its performance with mesh refinement. However, it should be noted that the PINN hyperparameters can be changed with a deeper study to improve this behavior, which is not the goal of this study.

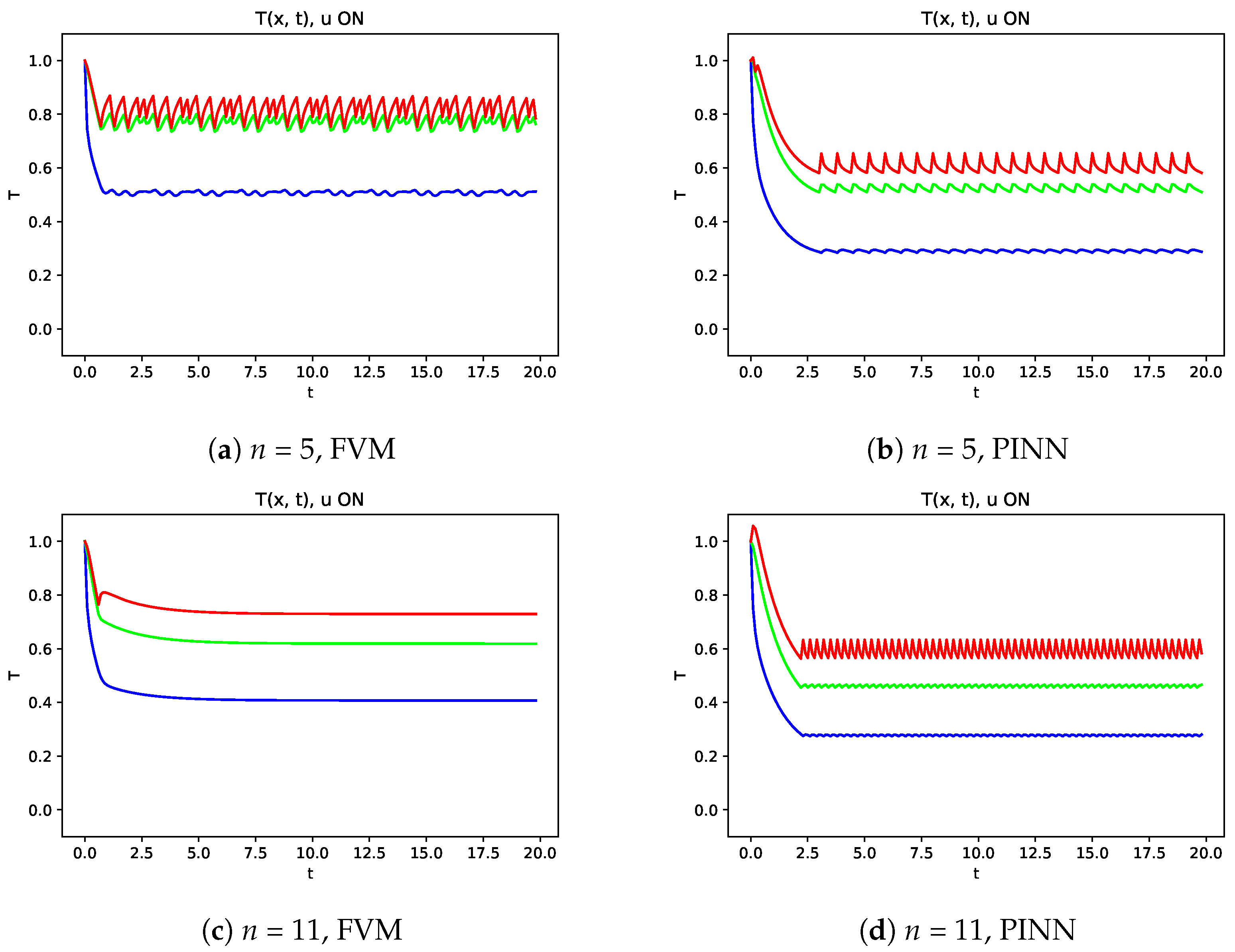
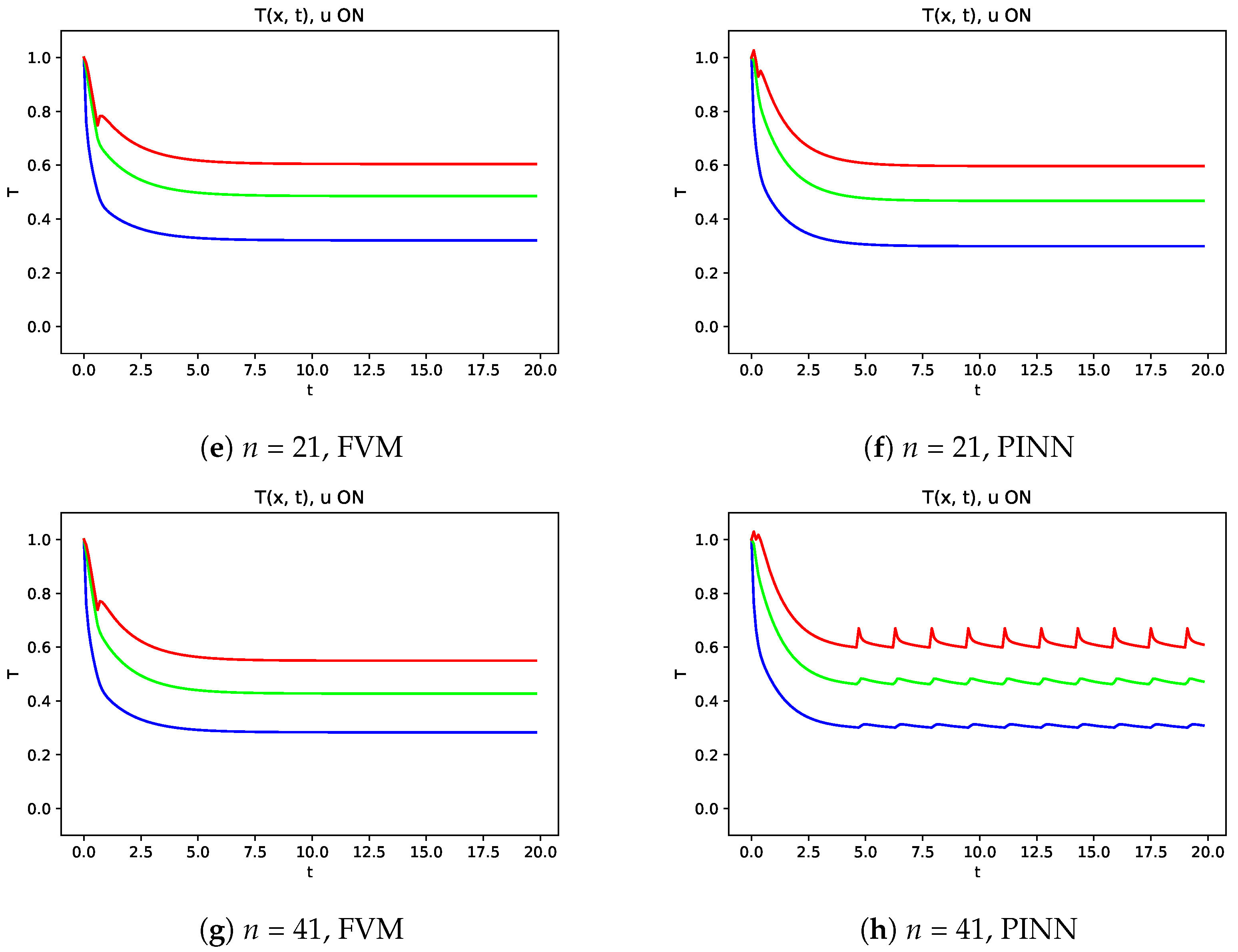
Aiming to evaluate the performance of the controller, the temperature evolutions along time at points $x=0$, $x=0.5$ and $x=1$ are represented in Figure 10, and it can be seen that the transition from the initial state to the oscillatory final state is smother when the controller defined with DQL was used. From the comparison of FVM and PINN, several hyperparameters of PINN were tested with better results obtained when the control considered a forecast on time 11 time steps in the future than the current value. However, it should be noted that these results can be improved with a deeper study, which is not the main goal of this work.

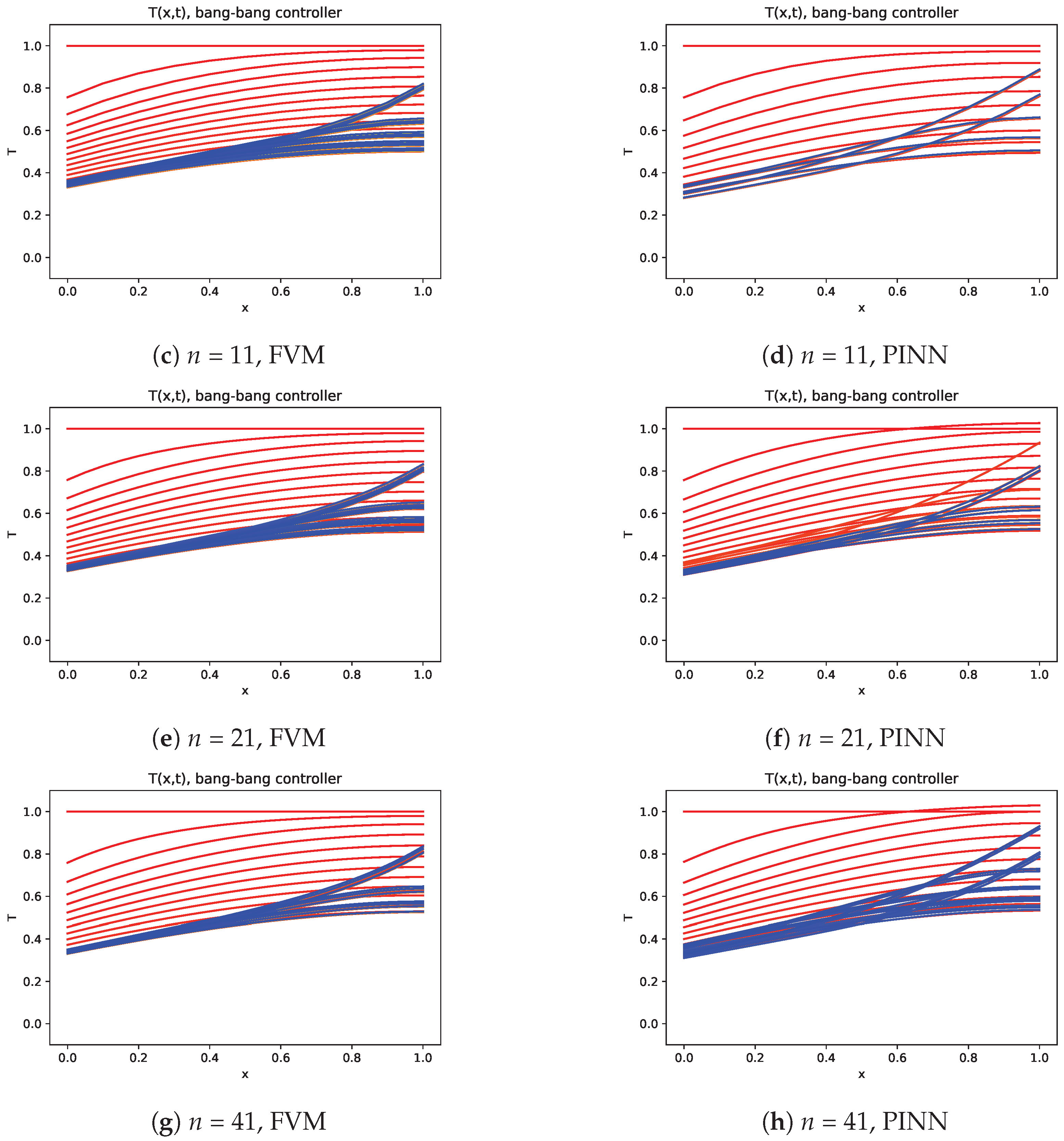
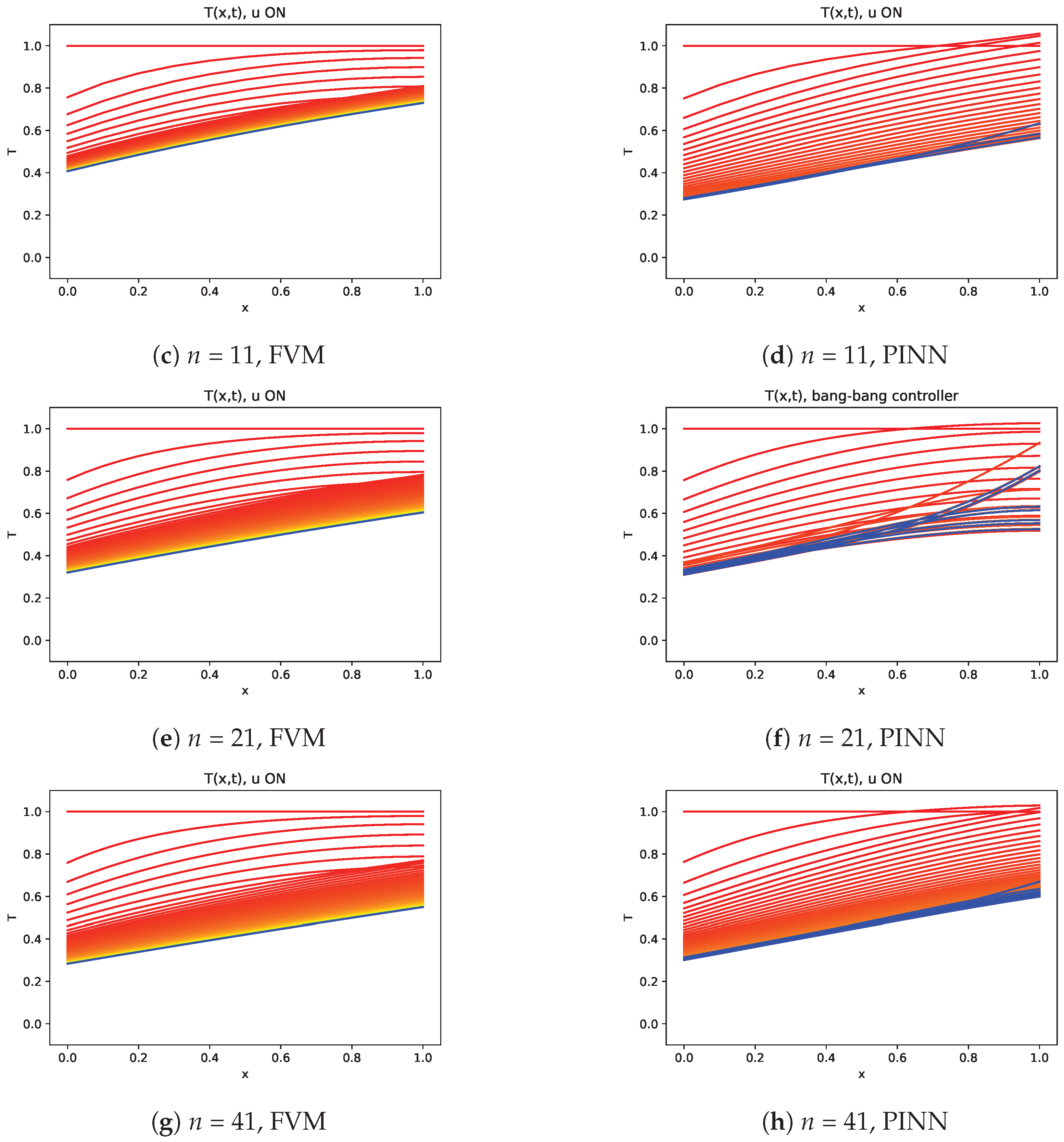
The evolution of the temperature on the domain along the time is presented in Figure 11 and Figure 12, respectively to the bang–bang controller and DQL controller, where the natural convection in the left boundary is identified by the characteristic temperature gradient and a progressive evolution to the final almost stationary state.

Since the bang–bang controller is not able to learn the time evolution of the temperature, it cannot produce a stable solution with strong variations in temperature distributions (see Figure 11). On the other hand, the control defined with the DQL strategy enables us to obtain much more stable solutions (see Figure 12).

5. Discussion

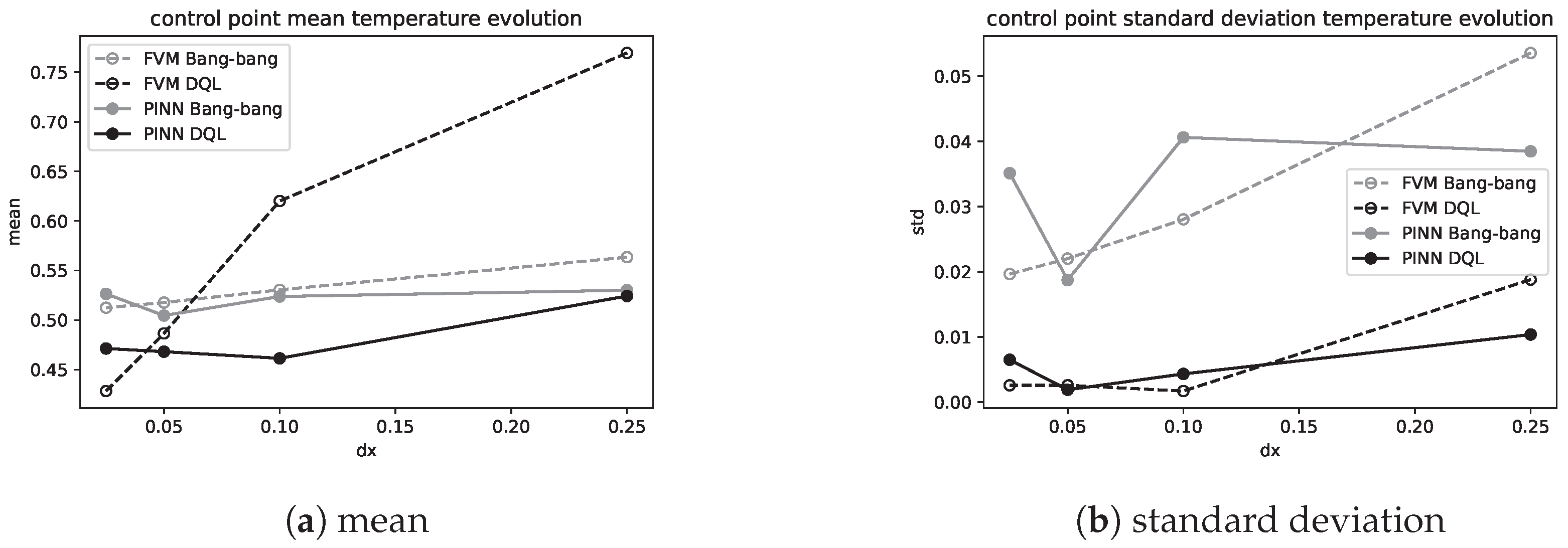
The temperature of the control point (at $x=0.5$) obtained with the different meshes was analyzed, considering its mean value and its standard deviation on the last 150 (of 200) time steps. These values (mean and standard deviation) are represented in Figure 13, against the mesh element size $dx$, i.e., lower values (when compared with bang–bang control strategy) to finer meshes, and it can be seen that the Deep Q-Learning applied to PINN model enables one to obtain mean values closer to the objective as the mesh is finer alongside the standard deviation diminishing. Regarding the PINN versus FVM model, it can be noted that the PINN enables one to obtain values closer to the goal and with lower variations.

In order to reach the desired temperature, two controller strategies were compared. As shown in Figure 9 for the bang–bang control strategy and for the DQL strategy as presented in Figure 10, they react in a different manner. This behavior is due to the reactive control action of the bang–bang control strategy, which only computes control actions based on the current measurement time. On the other hand, the DQL strategy computes its control action based on previous experience and combines the short-term effect of a particular control action, allowing it to foresee the error associated with such a control action, thus minimizing the fluctuations in temperature at the location of interest ($x=0.5$). Also, with the DQL proposal, the strategy can handle energy transport delays caused by the difference in location between the heat source ($x=1$) and the point of interest ($x=0.5$) due to the heat conduction limits of the proposed material.

6. Conclusions

In this work, a Physics-Informed Neural Network was trained to enable its use in edge computing hardware instead of more resource-demanding alternatives. This model was validated by comparison with a Finite Volume Method. The main advantage of this training strategy is that no data need to be gathered, making the training process much faster than the strategy that involves performing real measurements. Such data are created by defining the collocation points, and using the system governing equations, the data involving its boundary and initial conditions are generated.

A derived advantage of defining a process model using the PINN strategy is related to the concept of virtual sensors as stated in the work of Liu et al. [31]. This advantage states that a measurement can be taken indirectly by measuring a specific state of the system and, taking into account the boundary conditions, estimating the state of the system at a location where no probe can be placed due to impracticality or because such a probe could affect the performance of the system.

Since the presented methodology is based on PINN to model the phenomena, and the DQL to make the decisions are based on neural networks, therefore, based on matrix operations, it is easily scalable to more complex problems, with more mesh elements or more complex differential equations, without the consequent high increase in computation time. In additions, such operations are highly parallelizable.

Next, this implementation was used on a Deep Q-Learning algorithm to find a control policy aiming to attain a predefined temperature at a specific point. Such a control strategy was compared with the bang–bang control, analyzing a 1D problem. The results obtained enable one to show that this strategy is an interesting alternative implementation to use in more complex problems where there is a need for fast evaluations, which are required to make decisions.