Optimisation of Imaging Confocal Microscopy for Topography Measurements of Metal Additive Surfaces
Abstract
1. Introduction
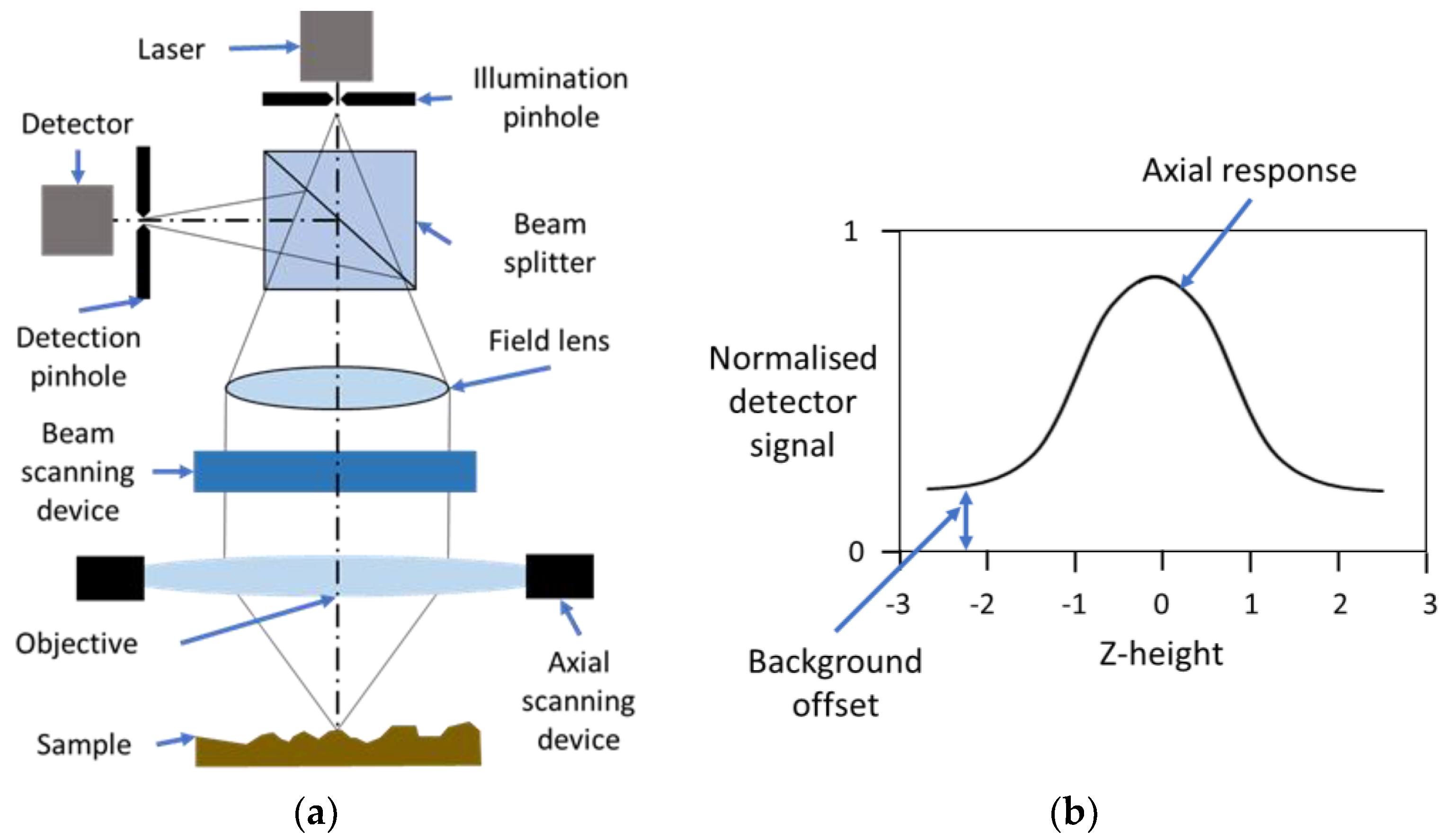
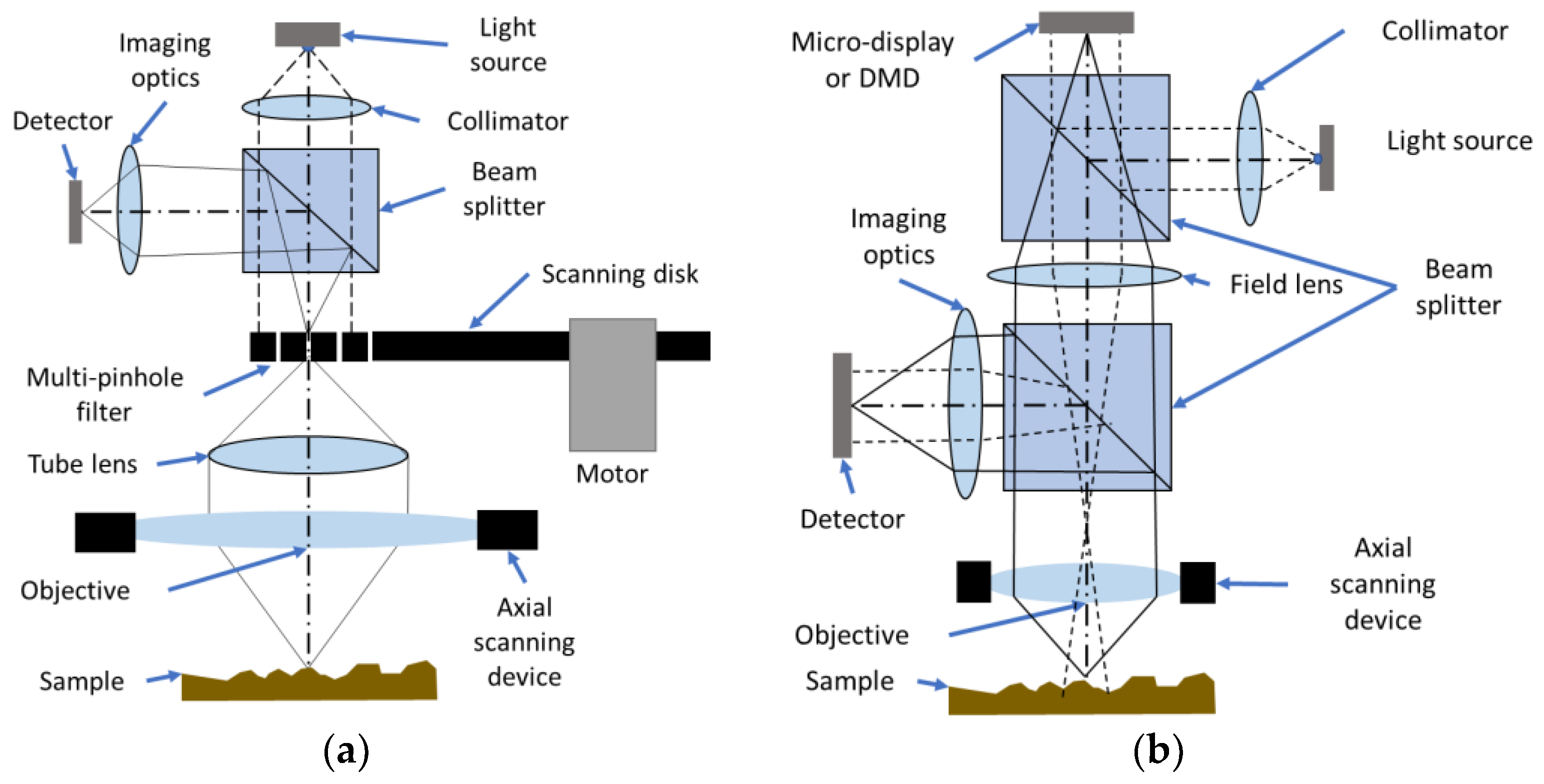
Background on Confocal Microscopy Techniques
2. Materials and Methods
2.1. Test Artefacts
2.2. Confocal Microscopy Measurement Process Parameters
- Coarse-shift single sampling (CSSS) creates projected slits in the programmable array, vertically spaced four pixels apart, that shift horizontally four times to produce each confocal image [17];
- Coarse-shift double sampling (CSDS) creates projected slits in the programmable array in two orientations (both four pixels apart) that scan in two directions: vertical slits that shift horizontally four times (as in CSSS), followed by horizontal slits that shift vertically four times. The responses for the horizontal and vertical scans are combined to produce the confocal image of intensities. Use of the CSDS setting results in increased measurement times but benefits from increased sampling within the same measurement [17].
2.3. Design of Experiments
2.4. Performance Metrics
- Measurement noise (noise) was quantified using the subtraction method (see [28] for details). This is computed by considering the subtraction of two topographies, after a subtraction of the least-squares mean plane—a form-removal operator (ISO 25178-3 [29] F-operator)—for all combinations of the three measured repeats (taken in quick succession). This resultant height map should be dominated by the difference in the noise component between two repeat measurements. The noise can be estimated by the ISO 25178 part 2 [30] parameter Sq—the root-mean-square height of the resultant subtracted topography map divided by the square root of 2. The lower this value for the same measurement time and lateral resolution, the better.
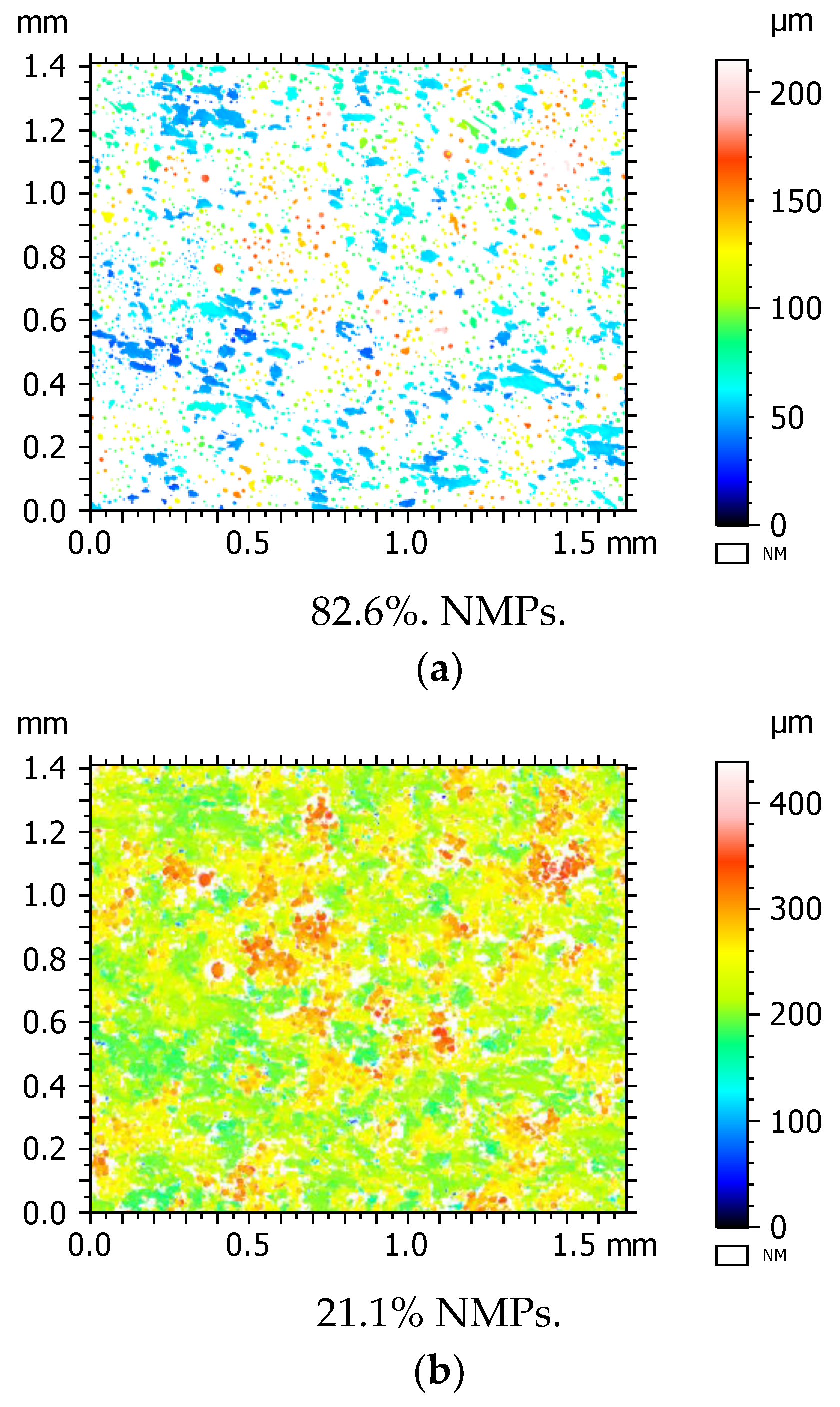
- Non-measured points (NMPs) were calculated as a percentage of the sum of NMPs over the total measured points of the surface topography within each height map. These are points for which the instrument does not acquire enough information, flagged by the instrument itself as non-measured. The lower this value, the better, provided no spikes appear and/or the noise is increased.
- The arithmetic mean height of the scale-limited surface Sa [30] was considered. To compute this parameter, only a least-squares mean plane by subtraction was used as a form-removal operator (ISO 25178-3 [29] F-operator). The parameter was computed with no further filtering applied (i.e., no separation of texture components at different spatial wavelengths), accepting the implicit operation of the lateral resolution and the NA of the objective as an S-filter [31].
2.5. Data Analysis
3. Results
3.1. Comparison between Stylus Instruments
3.2. Visualisation of the Influence of Measurement Parameters
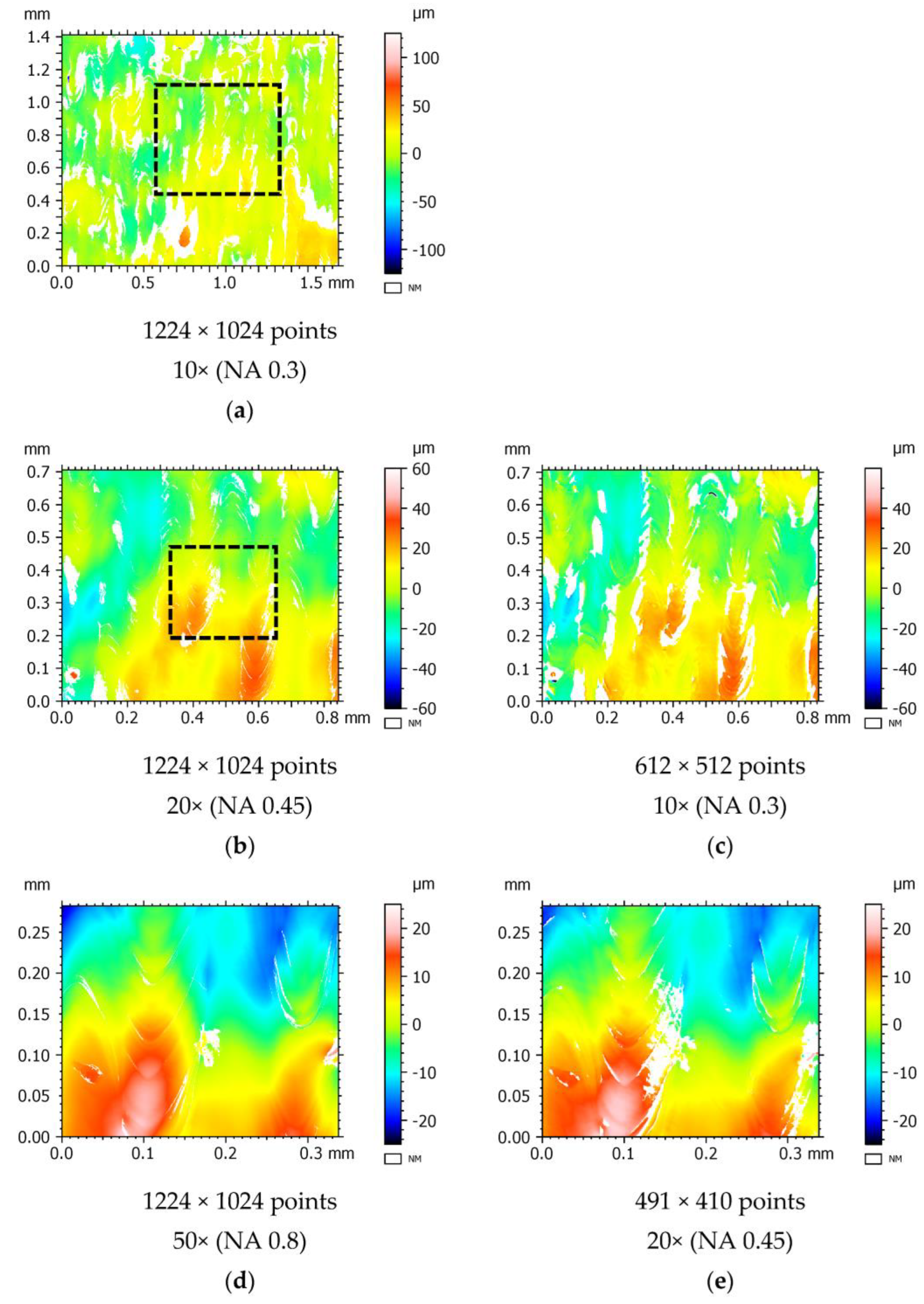
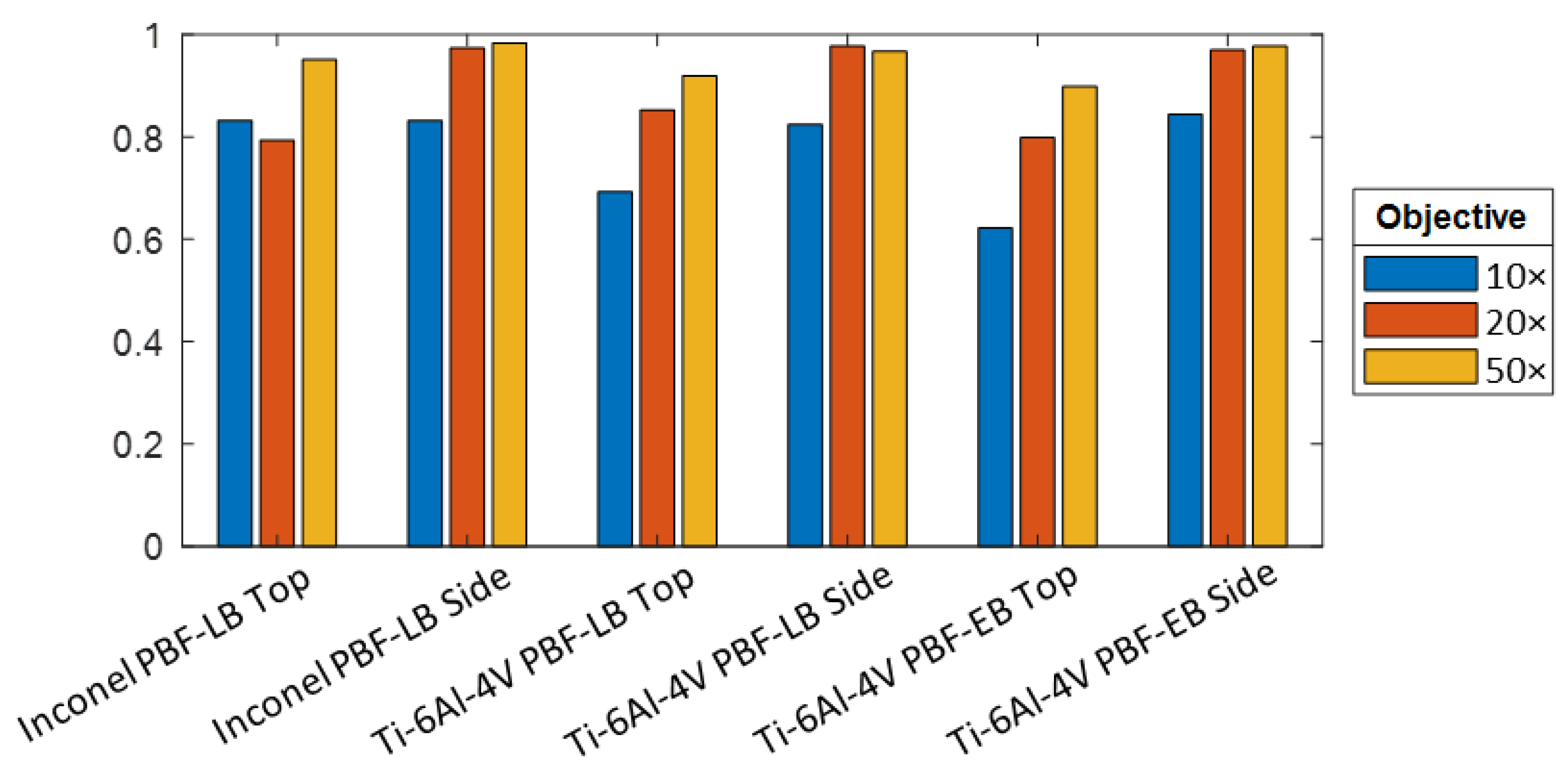
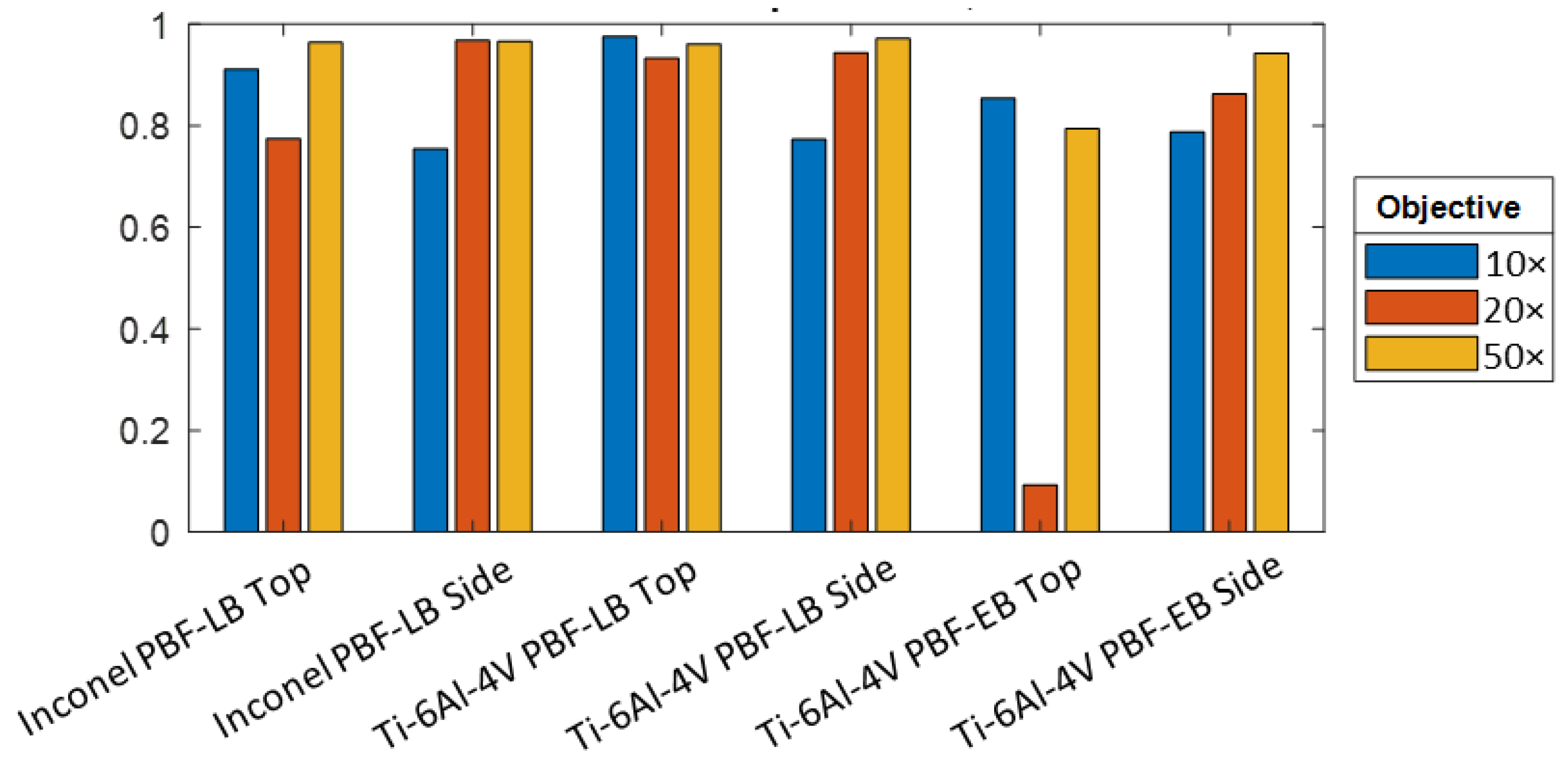
3.2.1. Effect of Changing Magnification on Surface Topography Measurement
3.2.2. Effect of Changing Scanning Mode on Surface Topography Measurement
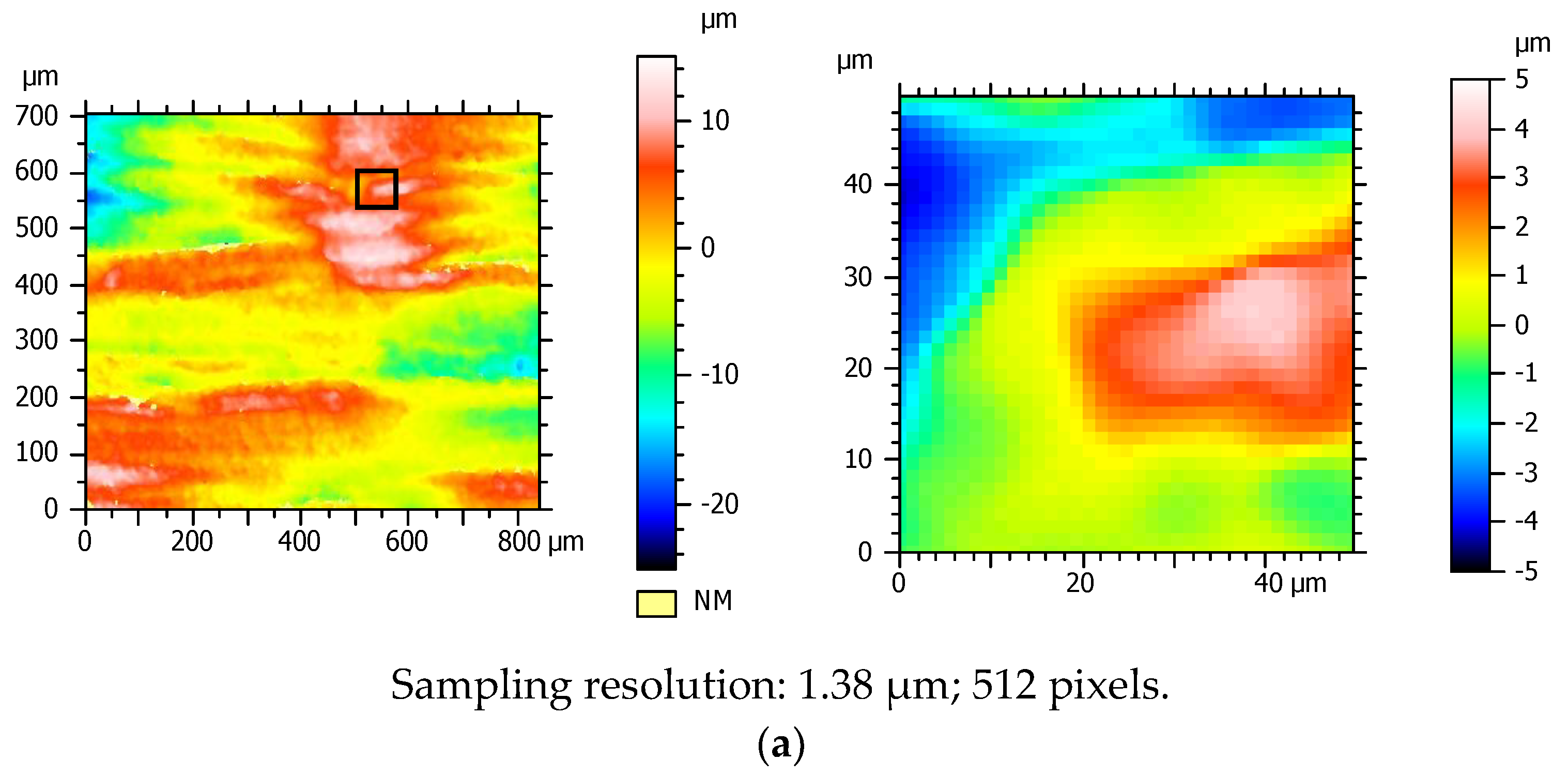
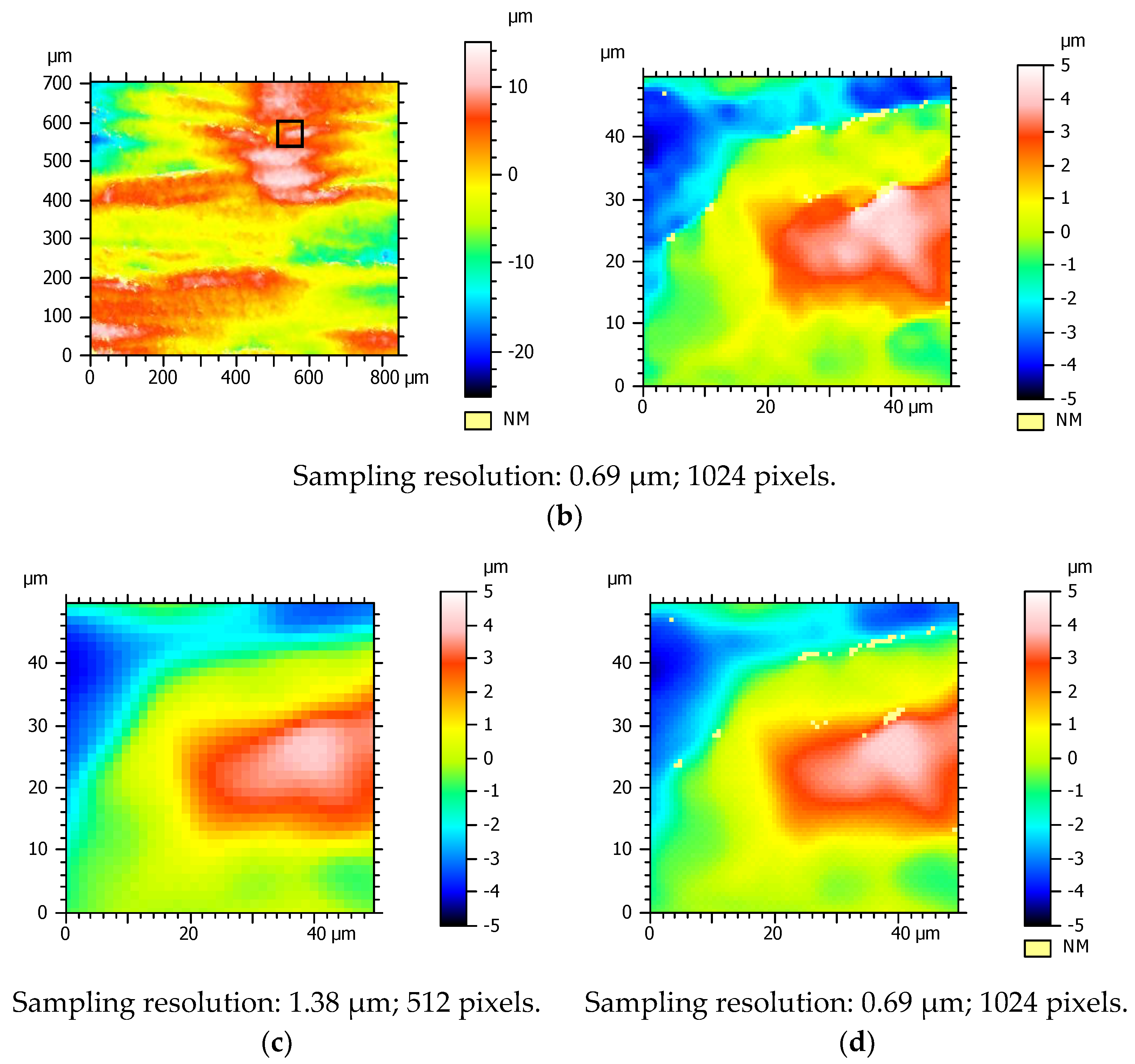
3.2.3. Effect of Changing Lateral Sampling Resolution on Surface Topography Measurement
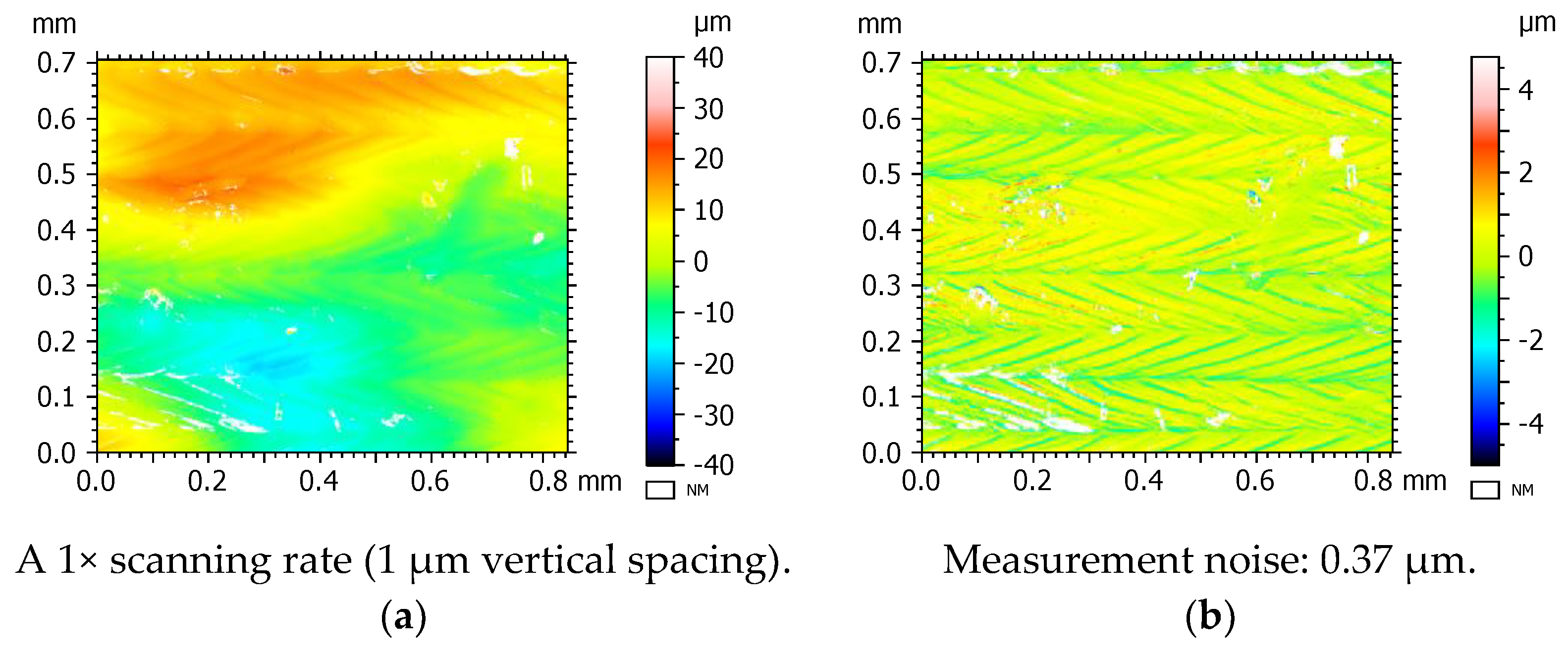
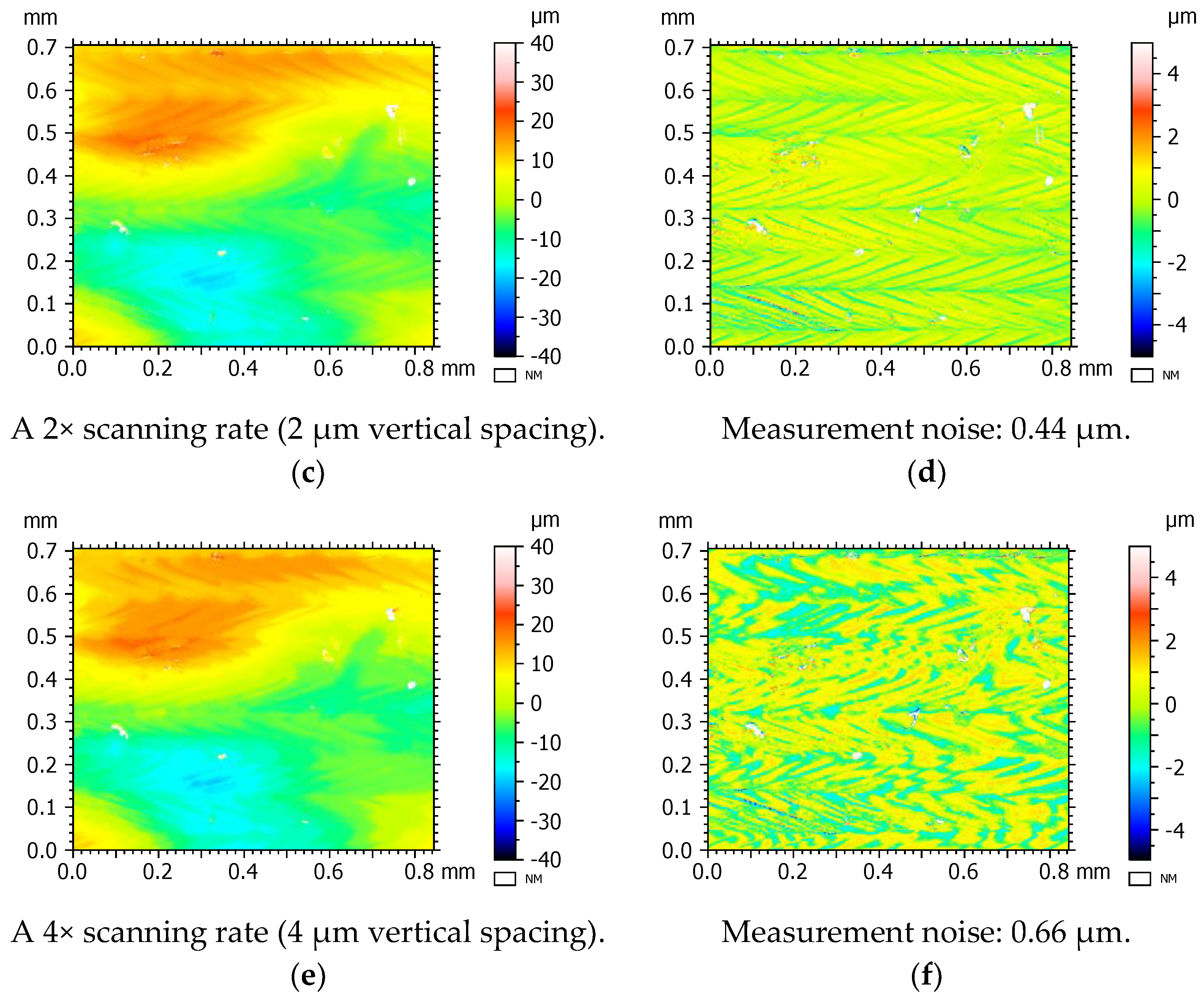
3.2.4. Effect of Changing Vertical Scanning Rate on Surface Topography Measurement
3.2.5. Effect of HDR on Surface Topography Measurement
3.2.6. Effect of Threshold Level on Surface Topography Measurement
3.3. Coefficient of Determination for Linear Models
3.4. Summary Tables for Main Effects Plots of Measurement Process Parameters
4. Discussion
5. Conclusions and Future Work
- AM surfaces vary significantly between surface orientation and material; therefore, a procedure to determine suitable measurement parameters should be performed for each new test case.
- Objective lens choice will depend on many things, such as the total measurement area required (which might use the largest field of view to reduce stitching), or the numerical aperture that might benefit the measurement of sloped regions or edges on the surface. It is often best to use a higher magnification with a larger numerical aperture on AM side surfaces over a large, stitched measurement region to measure the features with enough detail, rather than using an equally sized lower magnification over a single field measurement.
- Scanning modes can be optimised for AM surfaces, with the increased amount of sampling from the CSDS strategy offering increased measurement quality and more measured points—particularly for side surfaces.
- For the lateral sampling resolution on a single field of view, NMPs decrease with sampling size, although there is also an associated increase in noise of the measurement. For stitching, it is best to reduce the sampling size to have fewer data in the final file, at the expense of affecting the metrological performance studied in this work.
- Using smaller vertical step height sizes, more imaging planes are measured, allowing for reduced error in interpolation of the point of maximum intensity that represents the surface height. Decreasing the step size, however, comes at a cost of measurement time. For AM surfaces—especially side surfaces—it is better to use a smaller step height to reduce the measurement noise, but this must be balanced against increases in NMP.
- While light and gain should be adjusted to avoid saturation on smooth or reflective regions of the surface, the rough surfaces found on the AM side surfaces benefit from HDR being enabled, as it leads to greater coverage in the measurement (i.e., reduction in NMPs), because this setting allows for multiple captures with varied light levels sufficient to measure both deep recesses and the highly reflective regions on the top of spatter particles.
- Thresholding (within the internal algorithm) is chosen to remove or reduce artefacts (i.e., spike-like points) on the measurement result that would occur due to noise present on dark regions of the surface. Thresholding should be balanced to reduce noise in the measurement without an excessive increase in NMPs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Main Effects Plots and Process Parameter Significance for All Metrics and Surfaces
Appendix A.1. Non-Measured Points
Appendix A.1.1. 10× Objective Magnification
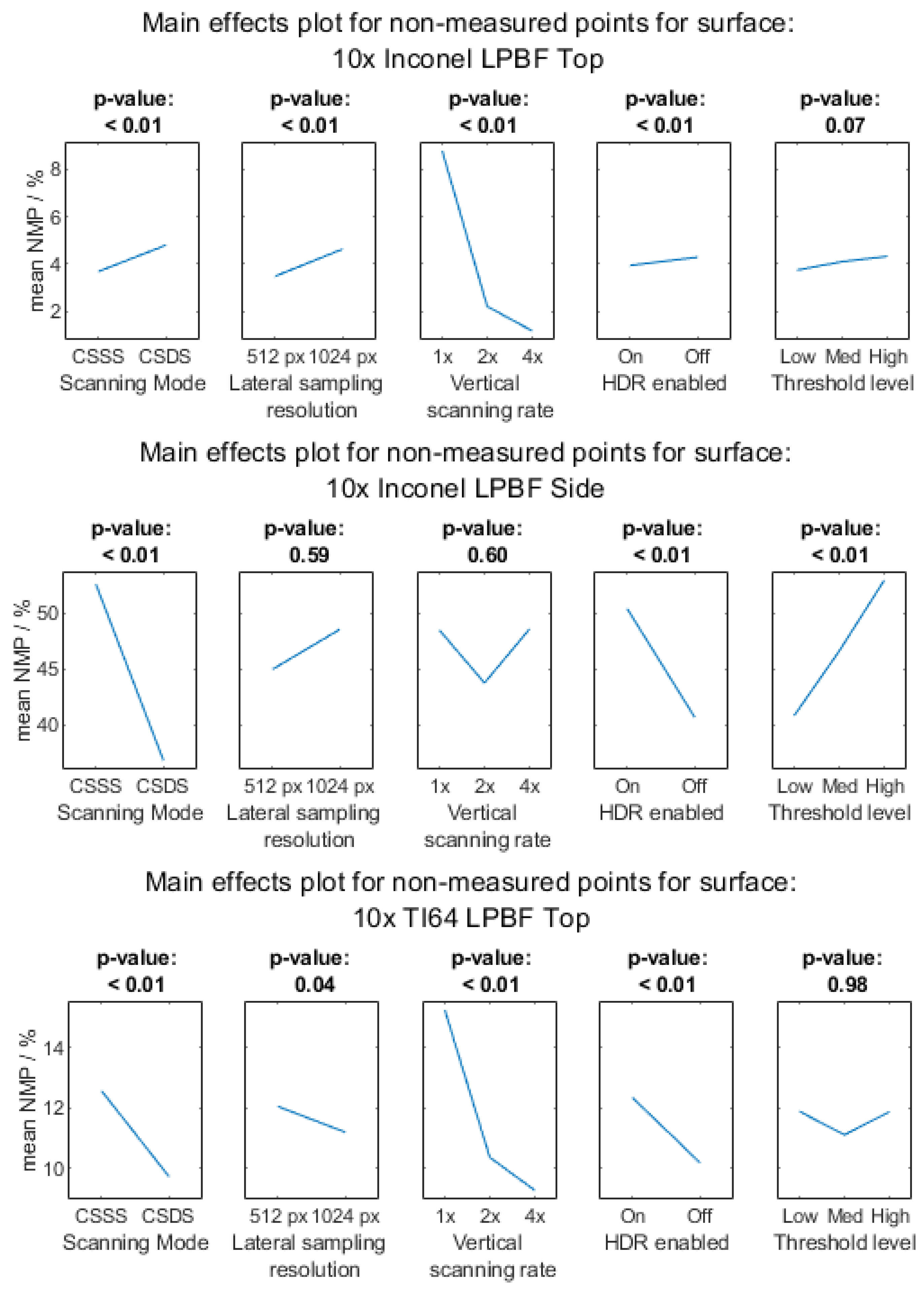
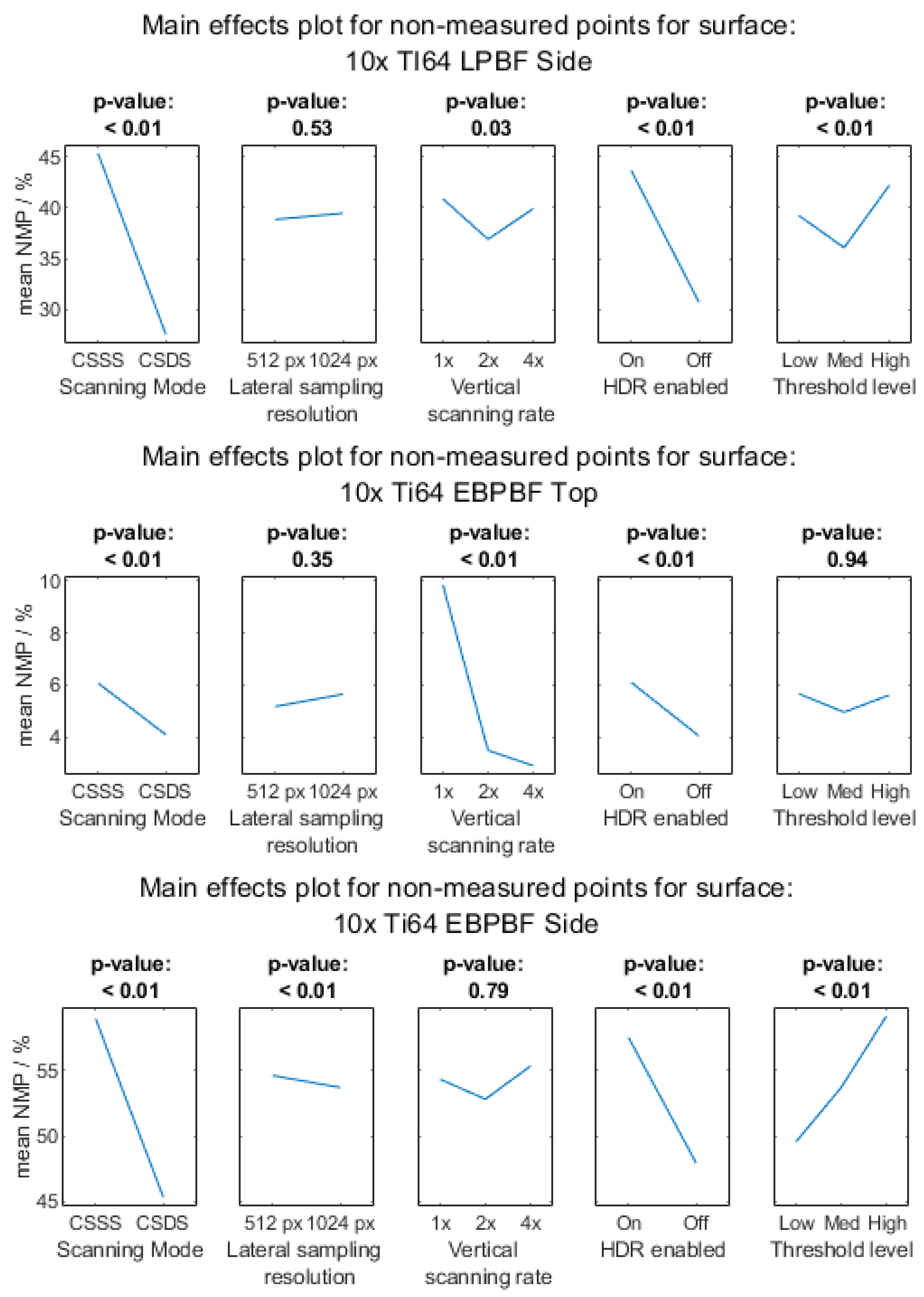
Appendix A.1.2. 20× Objective Magnification
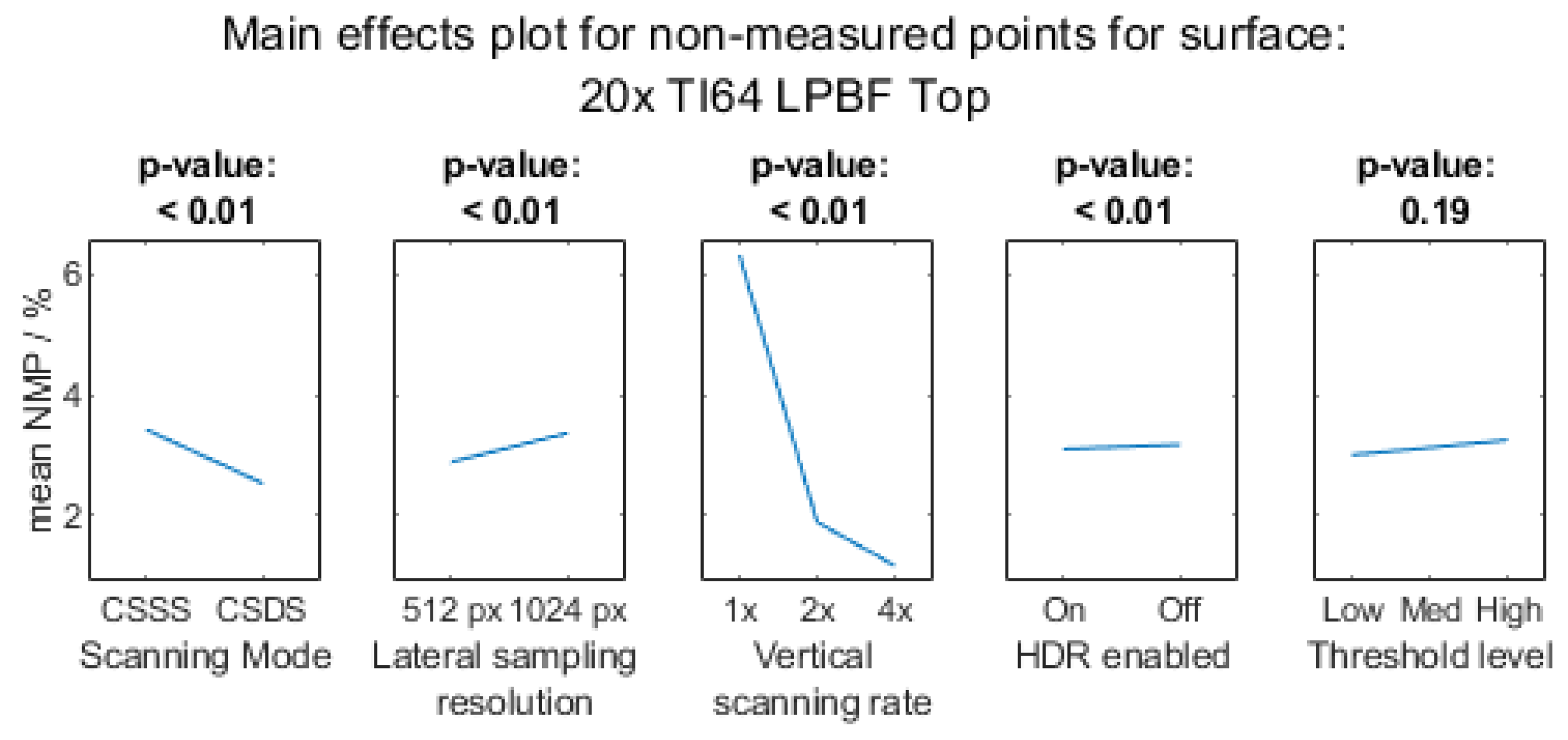

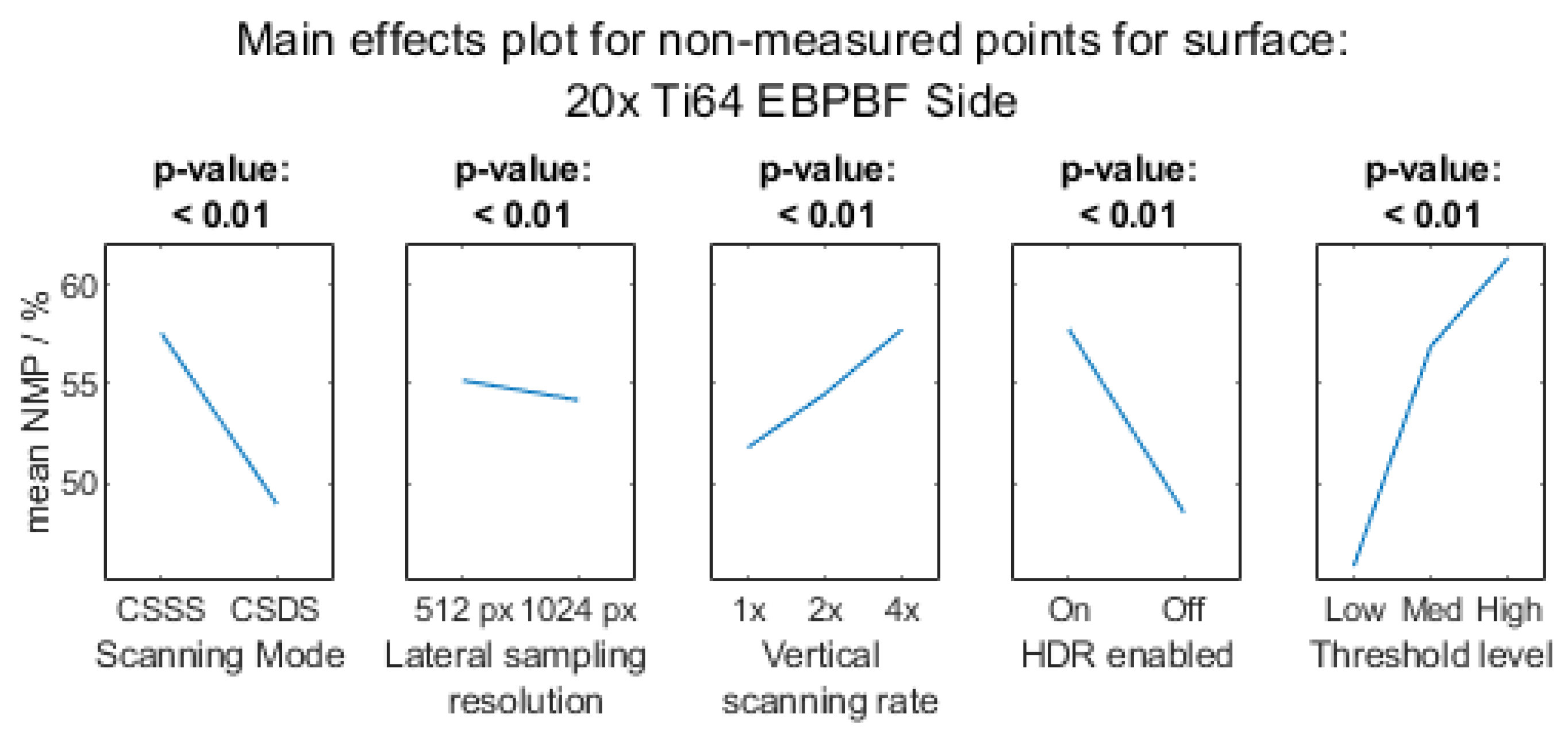
Appendix A.1.3. 50× Objective Magnification
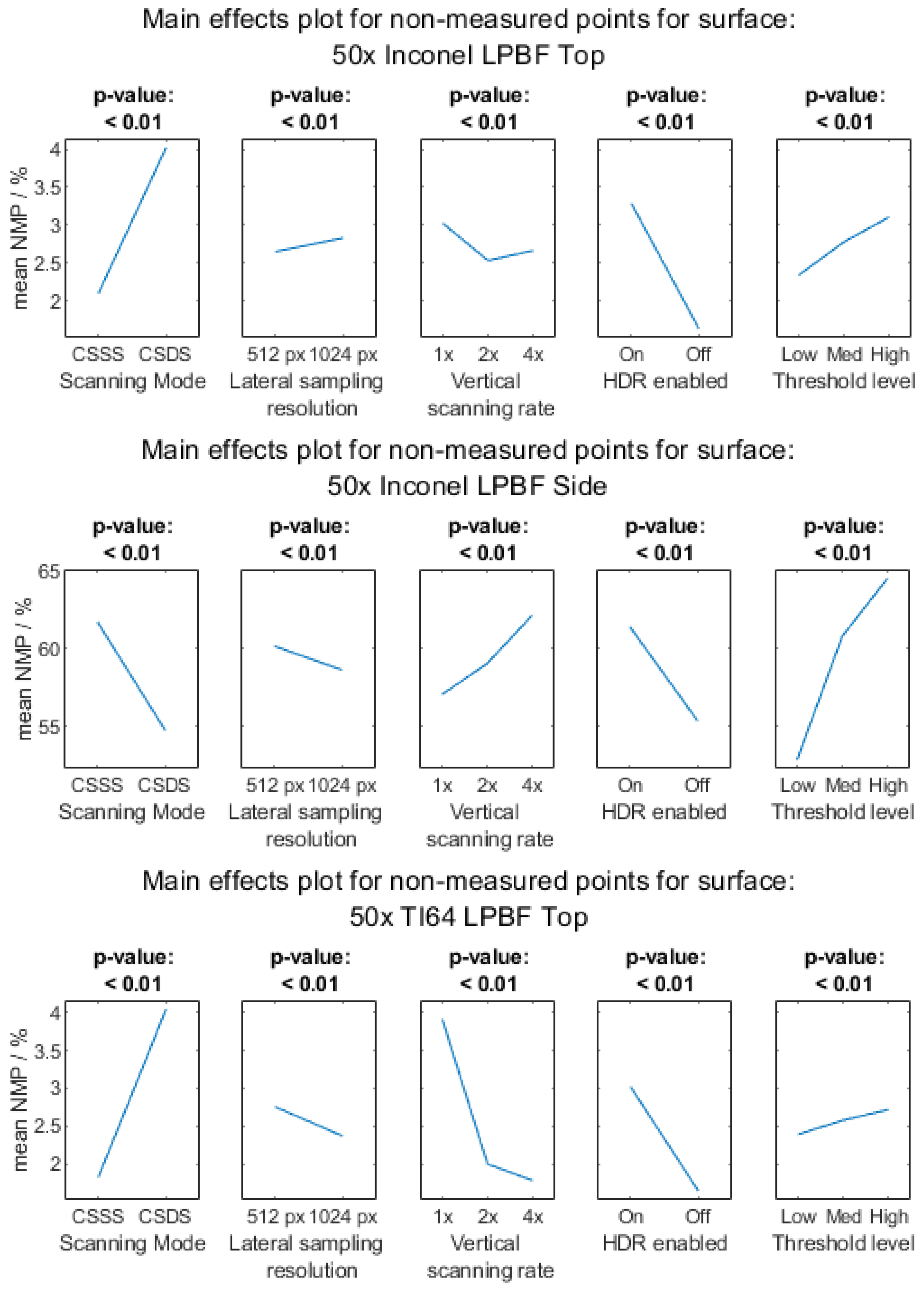
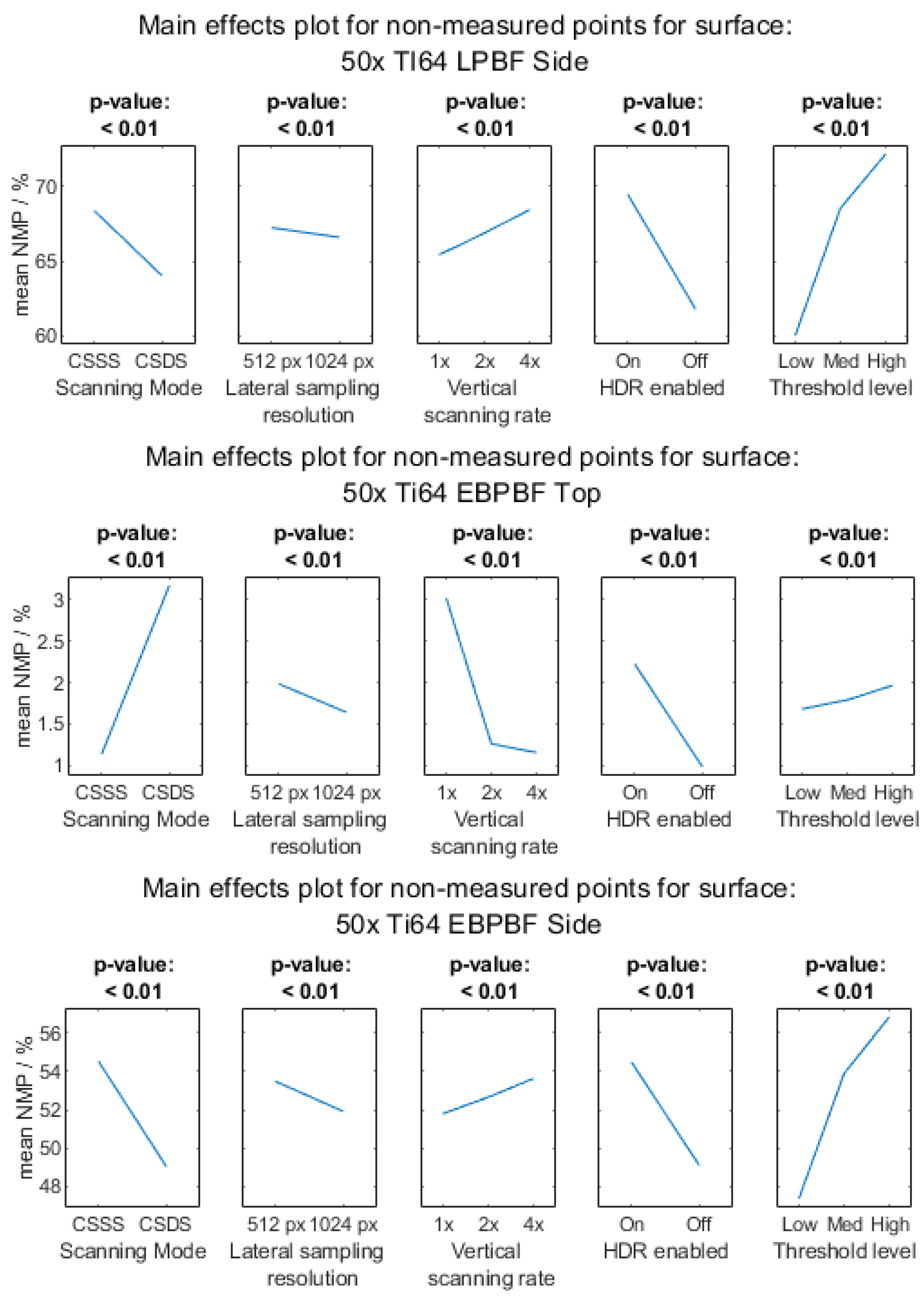
Appendix A.2. Measurement Noise
Appendix A.2.1. 10× Objective Magnification
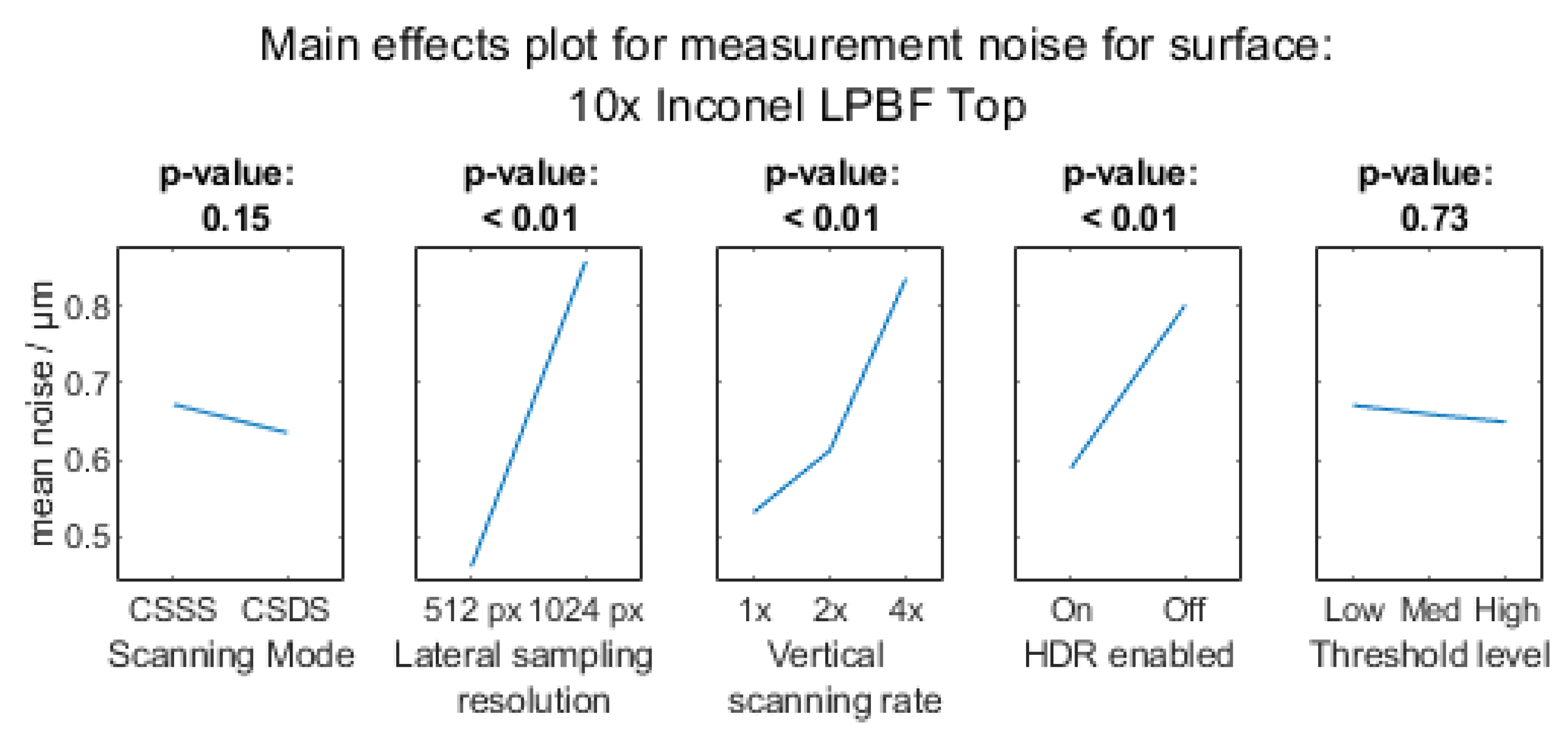

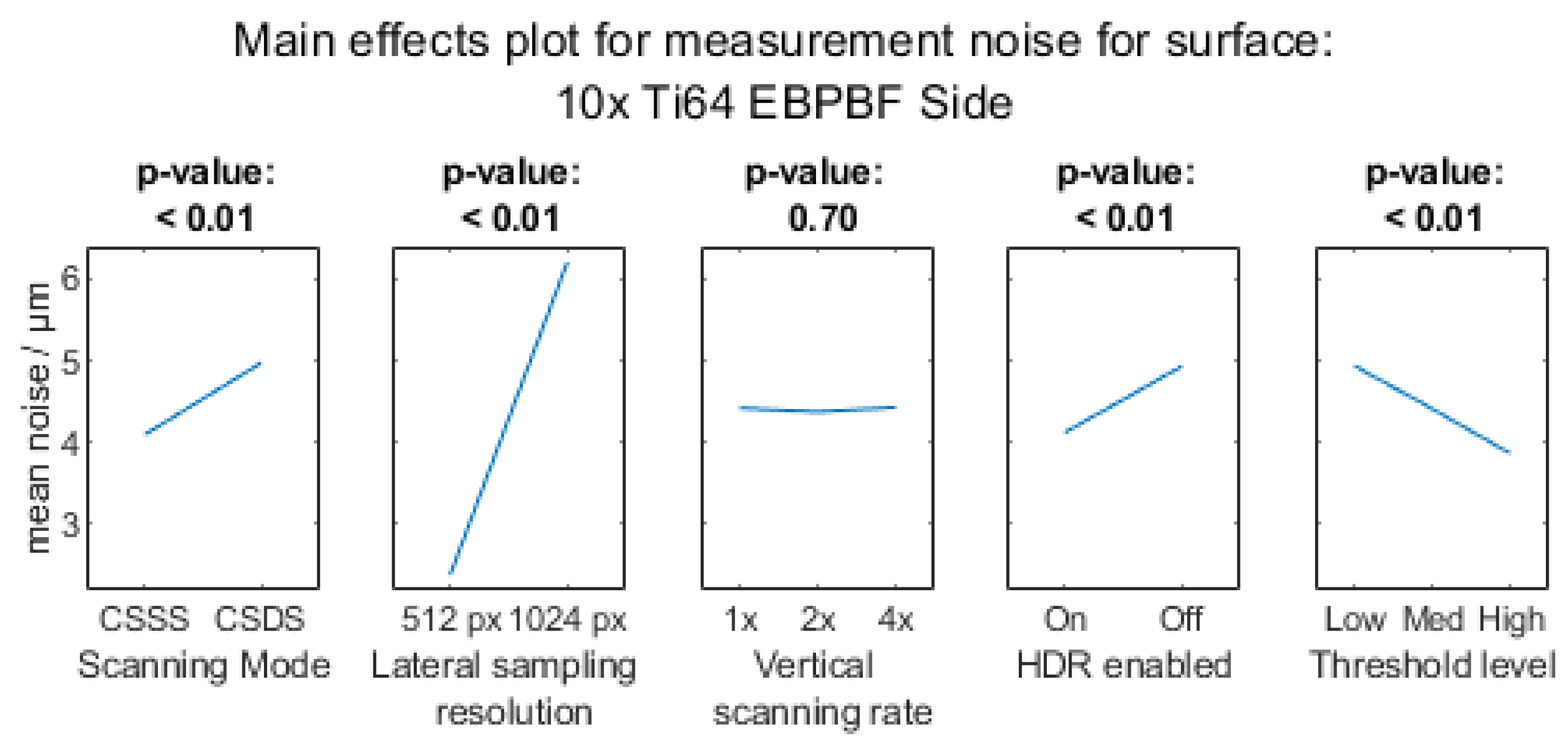
Appendix A.2.2. 20× Objective Magnification

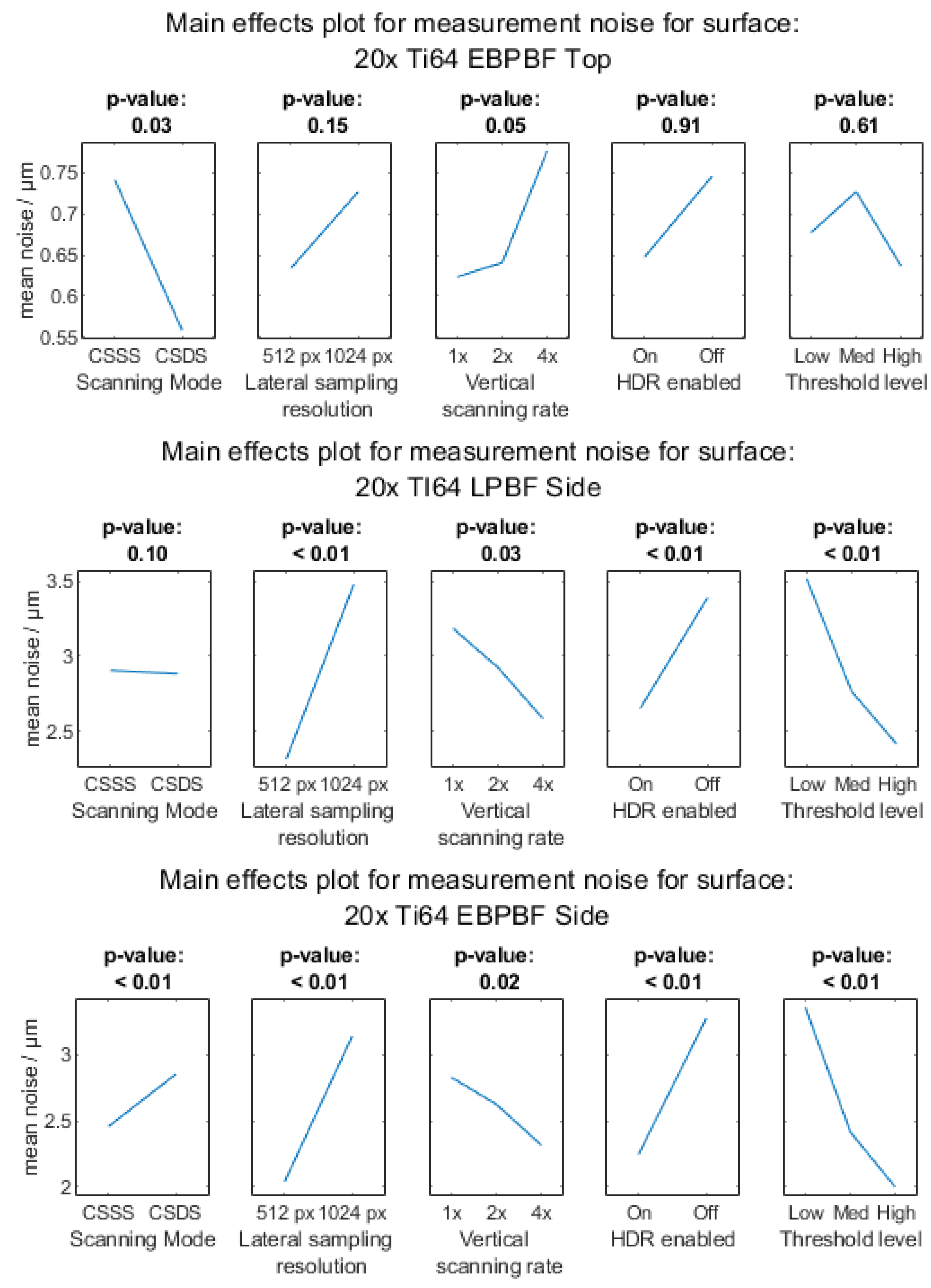
Appendix A.2.3. 50× Objective Magnification
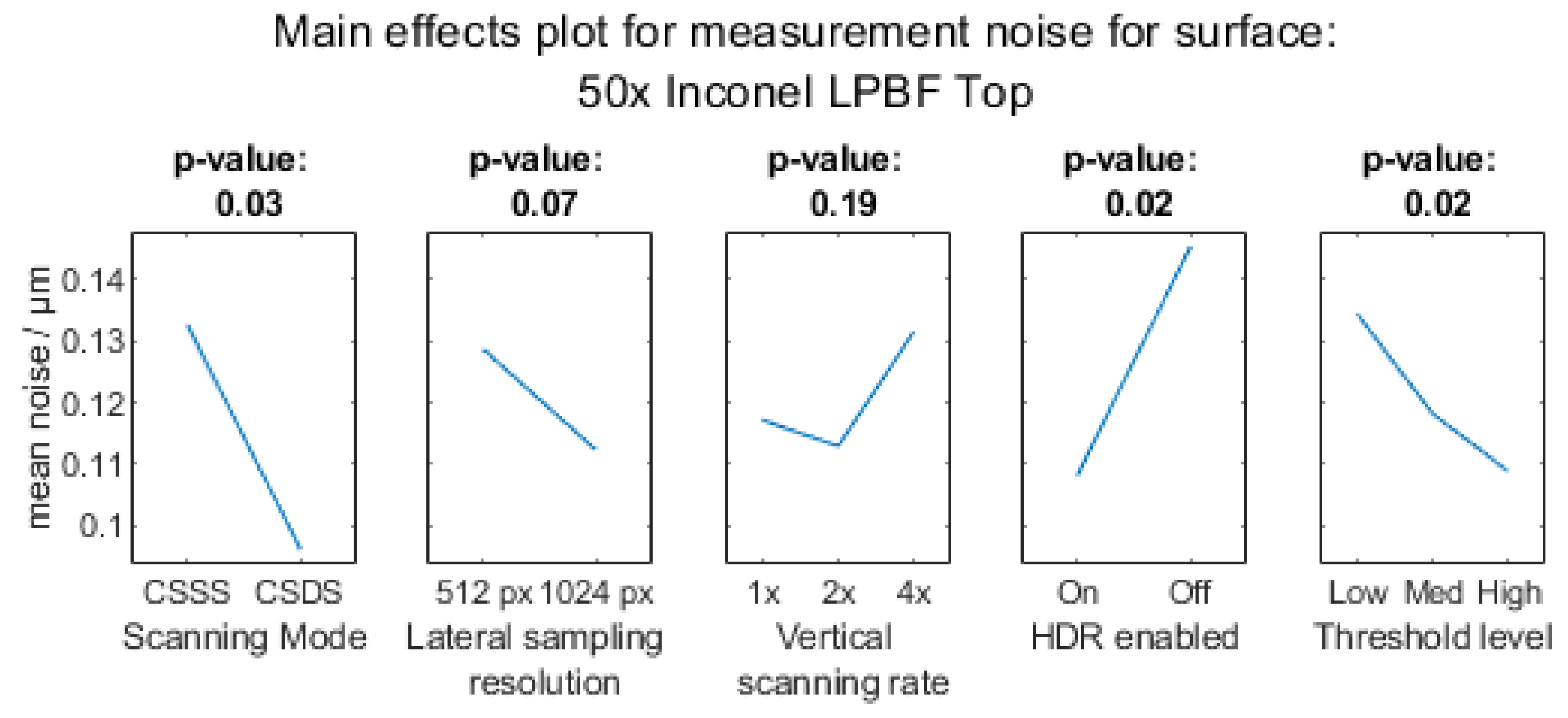
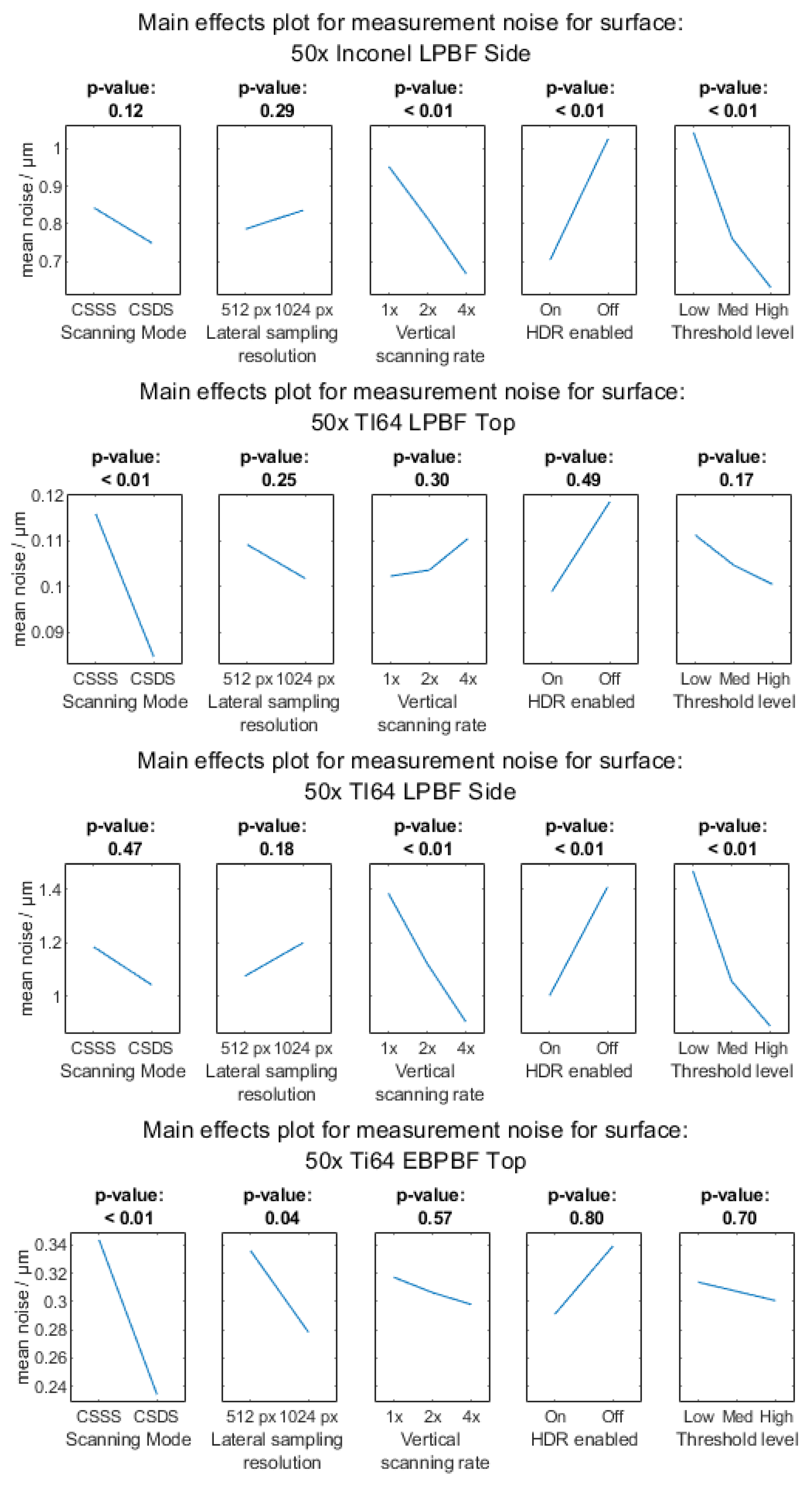

Appendix A.3. Surface Texture Parameter Sa
Appendix A.3.1. 10× Objective Magnification

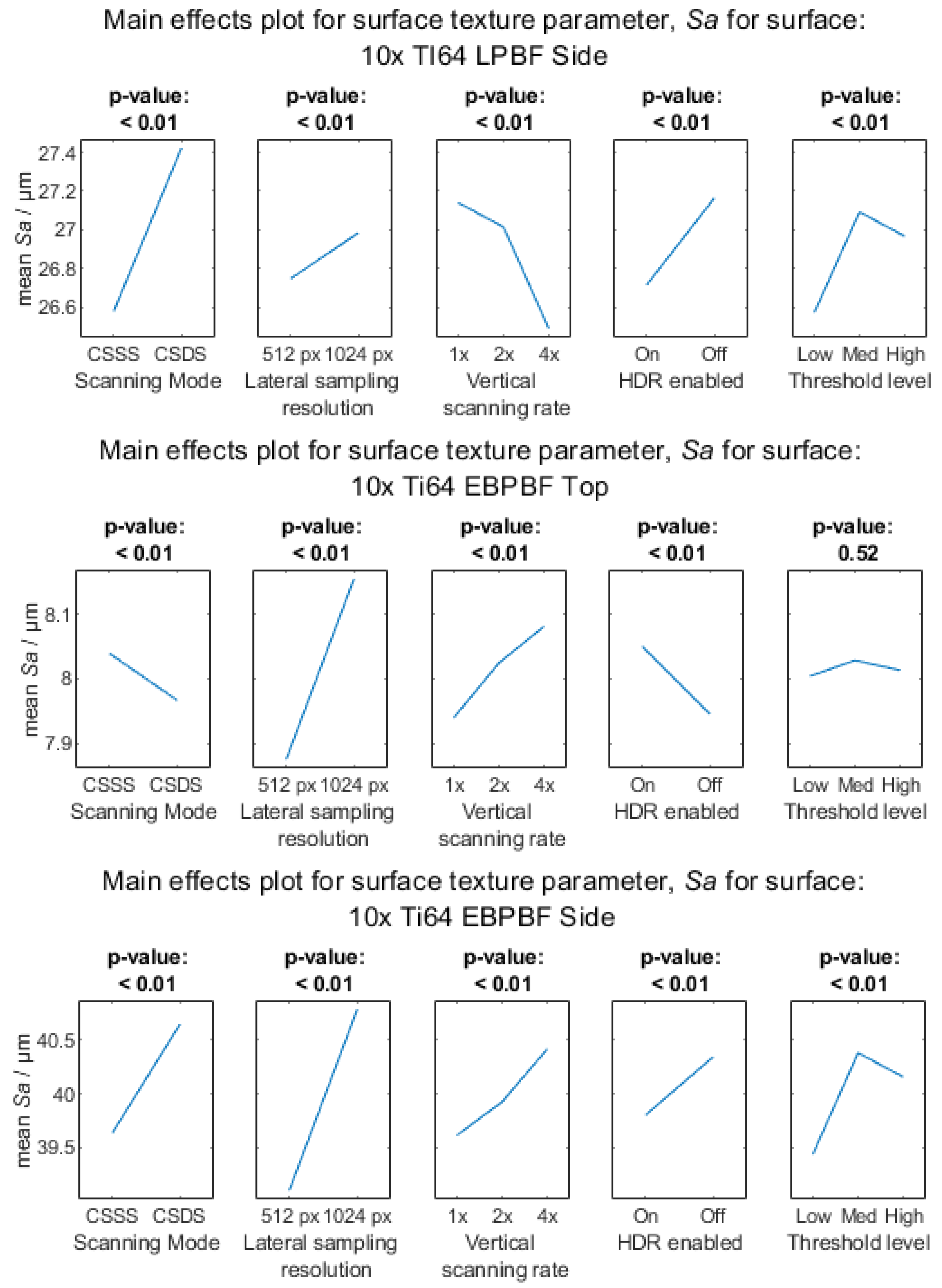
Appendix A.3.2. 20× Objective Magnification

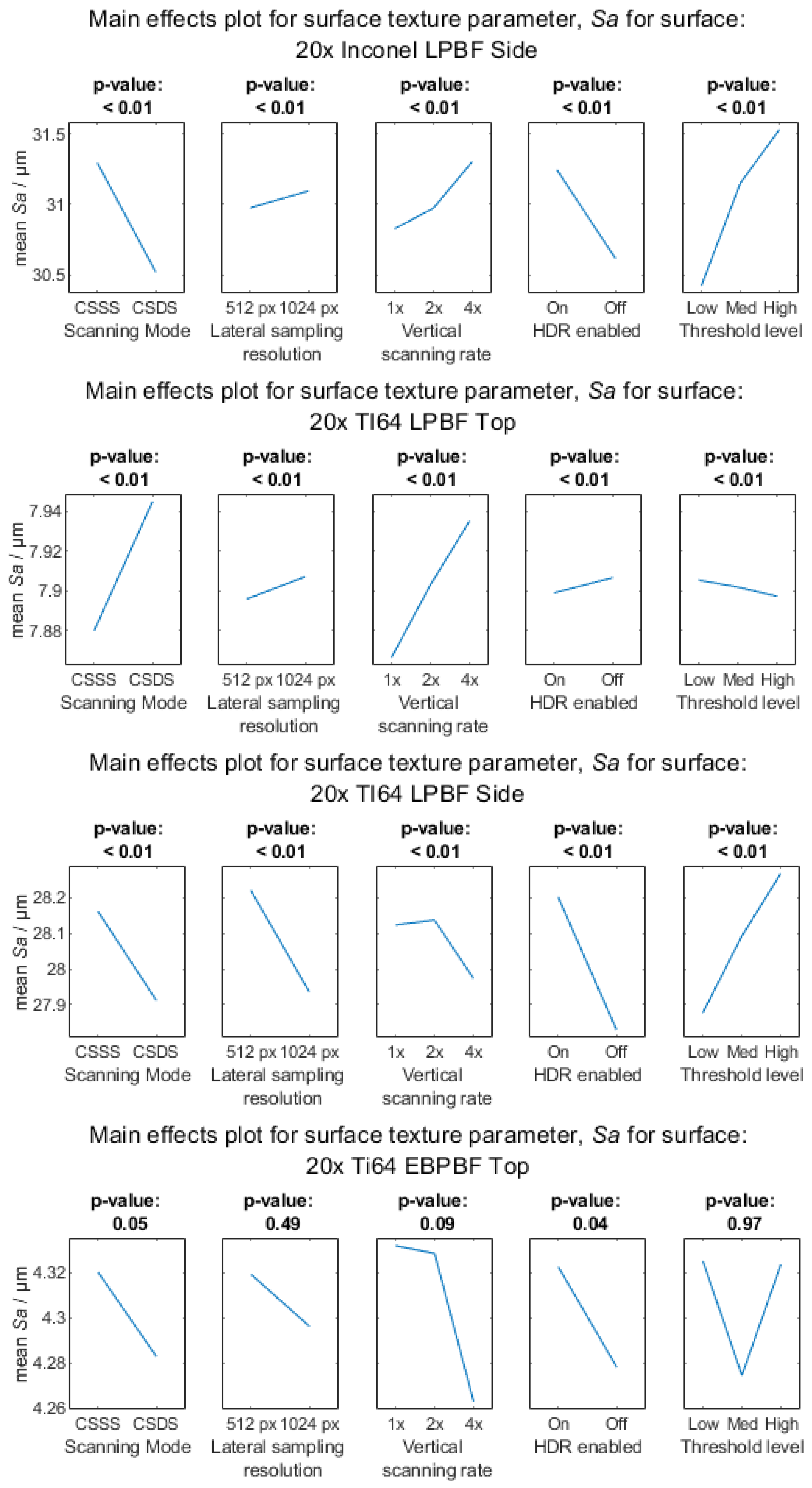
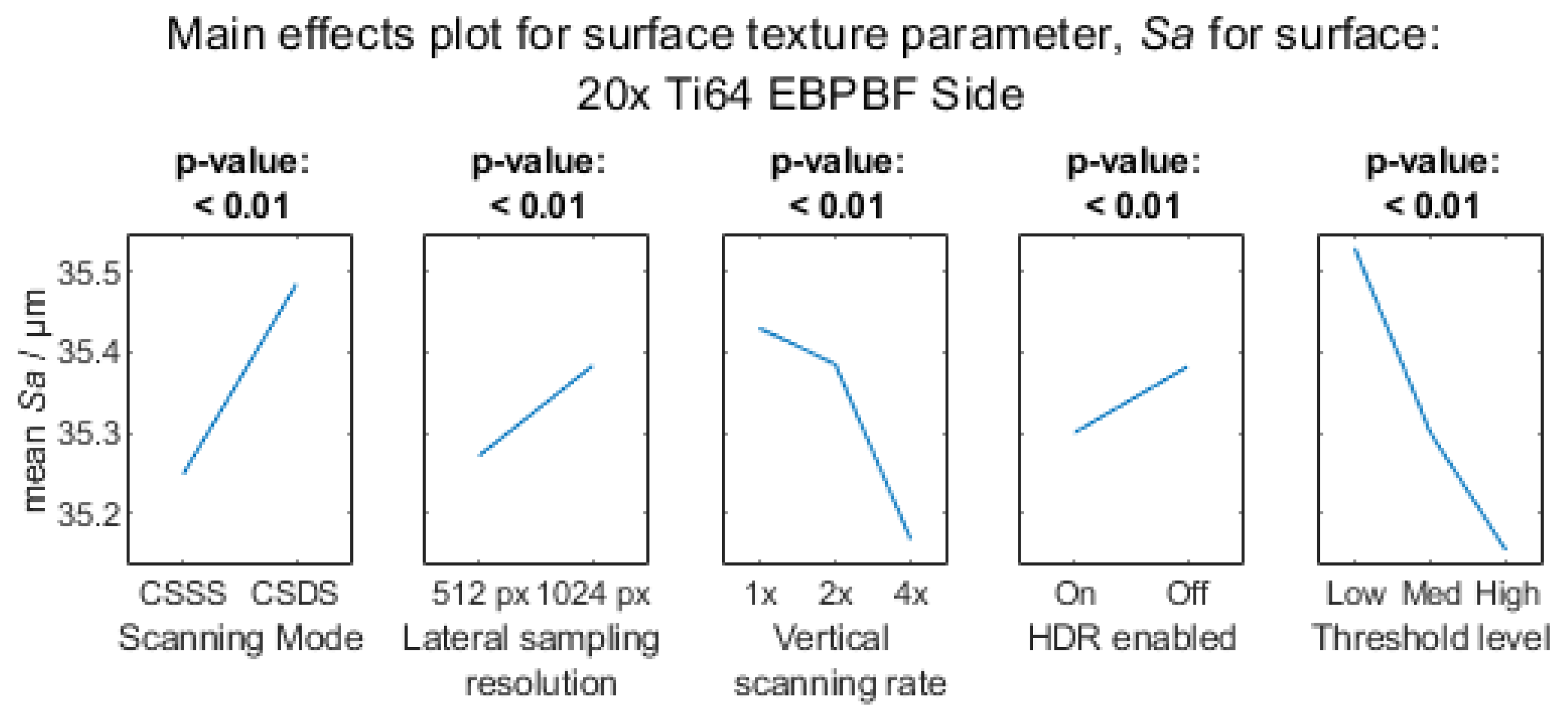
Appendix A.3.3. 50× Objective Magnification
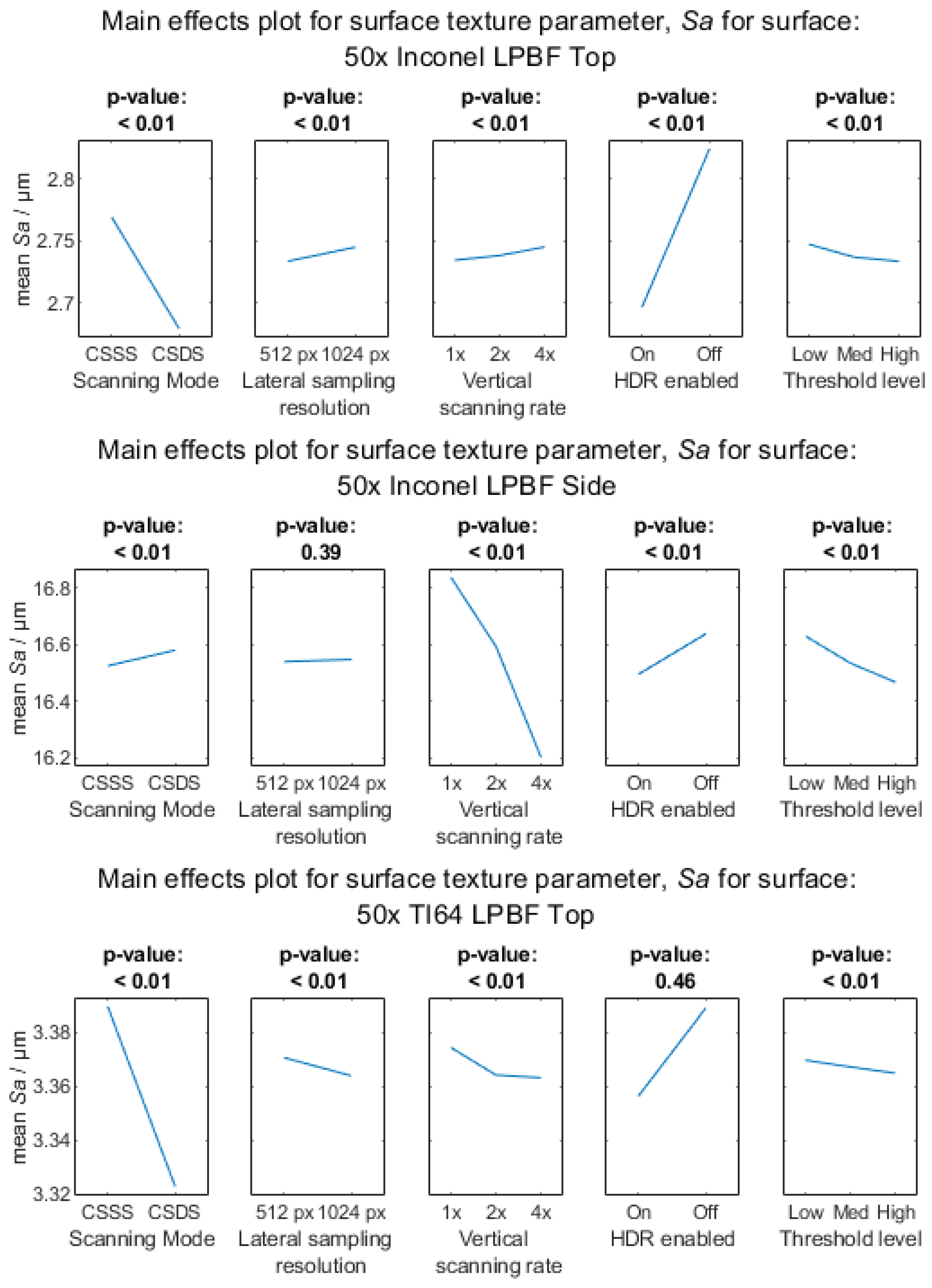
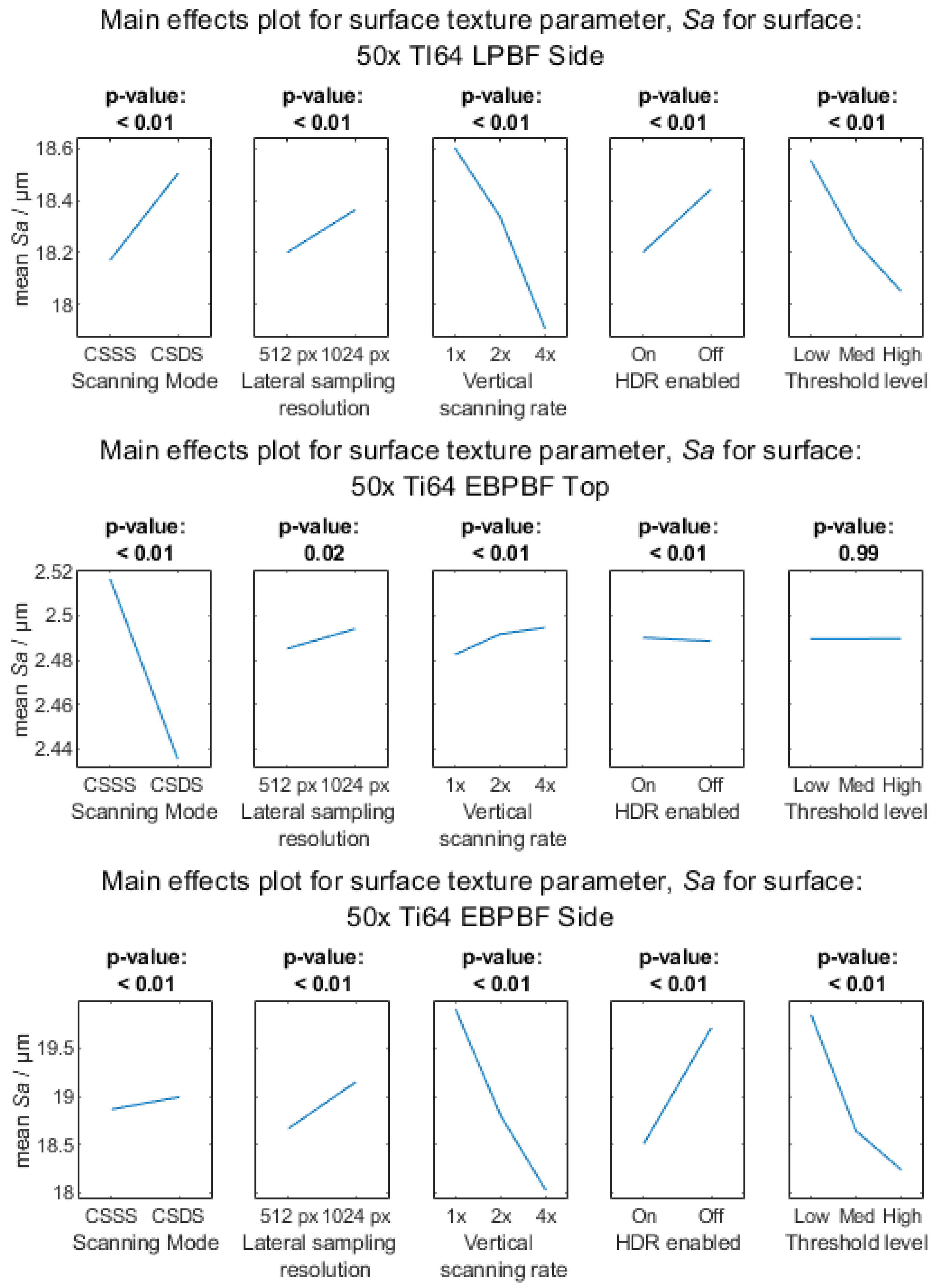
References
- Leach, R.K.; Bourell, D.; Carmignato, S.; Donmez, A.; Senin, N.; Dewulf, W. Geometrical metrology for metal additive manufacturing. Ann. CIRP 2019, 68, 677–700. [Google Scholar] [CrossRef]
- Townsend, A.; Senin, N.; Blunt, L.; Leach, R.; Taylor, J. Surface texture metrology for metal additive manufacturing: A review. Precis. Eng. 2016, 46, 34–47. [Google Scholar] [CrossRef]
- Senin, N.; Blunt, L. Characterisation of Individual Areal Features. In Characterisation of Areal Surface Texture; Leach, R.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 179–216. [Google Scholar]
- Lou, S.; Jiang, X.; Sun, W.; Zeng, W.; Pagani, L.; Scott, P.J. Characterisation methods for powder bed fusion processed surface topography. Precis. Eng. 2019, 57, 1–15. [Google Scholar] [CrossRef]
- Newton, L.; Senin, N.; Chatzivagiannis, E.; Smith, B.; Leach, R.K. Feature-based characterisation of Ti6Al4V electron beam powder bed fusion surfaces fabricated at different surface orientations. Addit. Manuf. 2020, 35, 101273. [Google Scholar] [CrossRef]
- Fox, J.C.; Allen, A.; Mullany, B.; Morse, E.; Isaacs, R.A.; Lata, M.; Sood, A.; Evans, C. Surface topography process signatures in nickel superalloy 625 additive manufacturing. In Proceedings of the 2021 SIG Additive Manufacturing: Advancing Precision in Additive Manufacturing, Online, 21 September 2021. [Google Scholar]
- Gomez, C.; Su, R.; Thompson, A.; DiSciacca, J.; Lawes, S.; Leach, R.K. Optimization of surface measurement for metal additive manufacturing using coherence scanning interferometry. Opt. Eng. 2017, 56, 111714. [Google Scholar] [CrossRef]
- Newton, L.; Senin, N.; Gomez, C.; Danzl, R.; Helmli, F.; Blunt, L.; Leach, R.K. Areal topography measurement of metal additive surfaces using focus variation microscopy. Addit. Manuf. 2019, 25, 365–389. [Google Scholar] [CrossRef]
- Thompson, A.; Senin, N.; Maskery, I.; Leach, R.K. Effects of magnification and sampling resolution in X-ray computed tomography for the measurement of additively manufactured metal surfaces. Precis. Eng. 2018, 53, 54–64. [Google Scholar] [CrossRef]
- Du Plessis, A.; Yadroitsev, I.; Yadroitsava, I.; Le Roux, S.G. X-ray microcomputed tomography in additive manufacturing: A review of the current technology and applications. 3D Print. Addit. Manuf. 2018, 5, 227–247. [Google Scholar] [CrossRef]
- Grimm, T.; Wiora, G.; Witt, G. Characterization of typical surface effects in additive manufacturing with confocal microscopy. Surf. Topogr. Metrol. Prop. 2015, 3, 014001. [Google Scholar] [CrossRef]
- Tato, W.; Blunt, L.; Llavori, I.; Aginagalde, A.; Townsend, A.; Zabala, A. Surface integrity of additive manufacturing parts: A comparison between optical topography measuring techniques. Proc. CIRP 2020, 87, 403–408. [Google Scholar] [CrossRef]
- Matilla, A.; Mariné, J.; Pérez, J.; Cadevall, C.; Artigas, R. Three-dimensional measurements with a novel technique combination of confocal and focus variation with a simultaneous scan. In Proceedings of the SPIE 9890 Optical Micro- and Nanometrology VI 98900B, Brussels, Belgium, 26 April 2016. [Google Scholar]
- Flys, O.; Berglund, J.; Rosén, B.G. Using confocal fusion for measurement of metal AM surface texture. Surf. Topogr. Metrol. Prop. 2020, 8, 024003. [Google Scholar] [CrossRef]
- Thompson, A.; Senin, N.; Giusca, C.; Leach, R.K. Topography of selectively laser melted surfaces: A comparison of different measurement methods. Ann. CIRP 2017, 66, 543–546. [Google Scholar] [CrossRef]
- Senin, N.; Thompson, A.; Leach, R.K. Characterisation of the topography of metal additive surface features with different measurement technologies. Meas. Sci. Technol. 2017, 28, 095003. [Google Scholar] [CrossRef]
- Artigas, R. Imaging confocal microscopy. In Optical Measurement of Surface Topography; Leach, R.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 237–286. [Google Scholar]
- Leach, R.K. (Ed.) Artigas R Imaging confocal microscopy. In Advances in Optical Surface Texture Metrology; IOP Publishing: Bristol, UK, 2020; pp. 4-1–4-33. [Google Scholar]
- ISO 25178-607; Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 607: Nominal Characteristics of Non-contact (Confocal Microscopy) Instruments. International Organization for Standardization: Geneva, Switzerland, 2019.
- Blateyron, F. Chromatic confocal microscopy. In Optical Measurement of Surface Topography; Leach, R.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 71–106. [Google Scholar]
- ISO 25178-602; 2010 Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 602: Nominal Characteristics of Non-Contact (Confocal Chromatic Probe) Instruments. International Organization for Standardization: Geneva, Switzerland, 2010.
- ISO 21920-2; Geometrical Product Specification (GPS)—Surface Texture: Profile—Part 2: Terms, Definitions and Surface Texture Parameters. International Organization for Standardization: Geneva, Switzerland, 1997.
- Sensofar: Non-Contact Surface Metrology and Device Inspection. Available online: https://www.sensofar.com/ (accessed on 29 March 2023).
- Thomas, M.; Su, R.; de Groot, P.J.; Leach, R.K. Optical topography measurement of steeply-sloped surfaces beyond the specular numerical aperture limit. In Proceedings of the Optics and Photonics for Advanced Dimensional Metrology, Online, 11 April 2020. [Google Scholar]
- de Groot, P.; Colonna de Lega, X.; Sykora, D.; Deck, L. The meaning and measure of lateral resolution for surface profiling interferometer. Opt. Photonice News 2012, 23, 10–13. [Google Scholar]
- de Groot, P. The meaning and measure of vertical resolution in surface metrology. In Proceedings of the 5th International Conference on Surface Metrology, Poznan, Poland, 4–7 April 2016. [Google Scholar]
- Fisher, R. The Design of Experiments, 5th ed.; Oliver & Boyd: Edinburgh, UK, 1949. [Google Scholar]
- Giusca, C.L.; Leach, R.K.; Helary, F.; Gutauskas, T.; Nimishakavi, L. Calibration of the scales of areal surface topography-measuring instruments: Part 1. Measurement noise and residual flatness. Meas. Sci. Technol. 2012, 23, 035008. [Google Scholar] [CrossRef]
- ISO 25178-3; 2012 Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 3: Specification Operators. International Organization for Standardization: Geneva, Switzerland, 2012.
- ISO 25178-2; 2021 Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions, and Surface Texture Parameters. International Organization for Standardization: Geneva, Switzerland, 2021.
- Digital Surf, Mountains® Surface Imaging & Metrology Software. Available online: http://www.digitalsurf.com/ (accessed on 29 March 2023).
- ISO 16610-21; Geometrical Product Specifications (GPS)—Filtration—Part 21: Linear Profile Filters: Gaussian Filters. International Organization for Standardization: Geneva, Switzerland, 2011.
- Sthle, L.; Wold, S. Analysis of variance (ANOVA). Chemometr. Intell. Lab. Syst. 1989, 6, 259–272. [Google Scholar] [CrossRef]
- Thompson, A.; Senin, N.; Leach, R.K. Feature-based characterisation of signature topography in laser powder bed fusion of metals. Meas. Sci. Technol. 2018, 29, 045009. [Google Scholar]
- de Groot, P. The instrument transfer function for optical measurements of surface topography. J. Phys. Photonics 2021, 3, 024004. [Google Scholar] [CrossRef]
- Dickins, A.; Widjanarko, T.; Sims-Waterhouse, D.; Thompson, T.; Lawes, S.; Senin, N.; Leach, R.K. Multi-view fringe projection system for surface topography measurement during metal powder bed fusion. J. Opt. Soc. Am. A 2020, 37, B93–B105. [Google Scholar] [CrossRef] [PubMed]
- Haitjema, H. Uncertainty in measurement of surface topography. Surf. Topogr. Metrol. Prop. 2015, 3, 035004. [Google Scholar] [CrossRef]




| Objective Magnification | 10× NA: 0.3 FoV: (1.6 × 1.4) mm Optical Resolution: 0.47 µm | 20× NA: 0.45 FoV: (0.8 × 0.7) mm Optical Resolution: 0.31 µm | 50× NA: 0.8 FoV: (0.3 × 0.3) mm Optical Resolution: 0.18 µm |
|---|---|---|---|
| Scanning modes | CSSS CSDS | CSSS CSDS | CSSS CSDS |
| Lateral sampling resolution | Low—512 pixel (2.76 µm) High—1024 pixel (1.38 µm) | Low—512 pixel (1.38 µm) High—1024 pixel (0.69 µm) | Low—512 pixel (0.55 µm) High—1024 pixel (0.28 µm) |
| Vertical scanning rate | Low—1× (2 µm) Medium—2× (4 µm) High—4× (8 µm) | Low—1× (1 µm) Medium—2× (2 µm) High—4× (4 µm) | Low—1× (0.2 µm) Medium—2× (0.4 µm) High—4× (0.8 µm) |
| HDR | On Off | On Off | On Off |
| Threshold level | Low—5% Medium—3% High—1% | Low—5% Medium—3% High—1% | Low—5% Medium—3% High—1% |
| Surface | Ra/μm |
|---|---|
| Inconel 718 PBF-LB top surface | 6.2 ± 1.3 |
| Inconel 718 PBF-LB side surface | 18.7 ± 1.8 |
| Ti-6Al-4V PBF-LB top surface | 25.6 ± 3.2 |
| Ti-6Al-4V PBF-LB side surface | 19.7 ± 2.9 |
| Ti-6Al-4V PBF-EB top surface | 6.7 ± 1.8 |
| Ti-6Al-4V PBF-EB side surface | 26.8 ± 3.2 |
| Magnification | Surface Orientation | Scanning Mode | Lateral Sampling Resolution | Vertical Scanning Rate | HDR Enabled | Threshold Level | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CSSS | CSDS | Low | High | Low | High | On | Off | Low | High | ||
| 10× | Top | Large negative | Small negative | Large negative | Small negative | - | |||||
| Side | Large negative | Small negative | - | Large negative | Large positive | ||||||
| 20× | Top | Small negative | Small positive | Large negative | - | - | |||||
| Side | Large negative | Small negative | Large positive | Large negative | Large positive | ||||||
| 50× | Top | Small Positive | Small negative | Large negative | Large negative | Small positive | |||||
| Side | Large Negative | Small negative | Small positive | Large negative | Large positive | ||||||
| Magnification | Surface Orientation | Scanning Mode | Lateral Sampling Resolution | Vertical Scanning Rate | HDR Enabled | Threshold Level | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CSSS | CSDS | Low | High | Low | High | On | Off | Low | High | ||
| 10× | Top | - | Large positive | Large positive | Large positive | - | |||||
| Side | Small positive | Large positive | - | Small positive | - | ||||||
| 20× | Top | - | - | Positive | - | - | |||||
| Side | - | Large positive | - | Large positive | Large negative | ||||||
| 50× | Top | Negative | - | - | - | - | |||||
| Side | - | - | Large negative | Large positive | Large negative | ||||||
| Magnification | Surface Orientation | Scanning Mode | Lateral Sampling Resolution | Vertical Scanning Rate | HDR Enabled | Threshold Level | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CSSS | CSDS | Low | High | Low | High | On | Off | Low | High | ||
| 10× | Top | Small negative | Large positive | Large positive | Small negative | - | |||||
| Side | Large negative | Small positive | - | Small negative | - | ||||||
| 20× | Top | - | - | - | Negative | - | |||||
| Side | Large negative | Large negative | Small negative | Large negative | Large positive | ||||||
| 50× | Top | Large negative | Small positive | Small positive | - | - | |||||
| Side | Small positive | Large negative | - | Small positive | Small negative | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Newton, L.; Thanki, A.; Bermudez, C.; Artigas, R.; Thompson, A.; Haitjema, H.; Leach, R. Optimisation of Imaging Confocal Microscopy for Topography Measurements of Metal Additive Surfaces. Metrology 2023, 3, 186-221. https://doi.org/10.3390/metrology3020011
Newton L, Thanki A, Bermudez C, Artigas R, Thompson A, Haitjema H, Leach R. Optimisation of Imaging Confocal Microscopy for Topography Measurements of Metal Additive Surfaces. Metrology. 2023; 3(2):186-221. https://doi.org/10.3390/metrology3020011
Chicago/Turabian StyleNewton, Lewis, Aditi Thanki, Carlos Bermudez, Roger Artigas, Adam Thompson, Han Haitjema, and Richard Leach. 2023. "Optimisation of Imaging Confocal Microscopy for Topography Measurements of Metal Additive Surfaces" Metrology 3, no. 2: 186-221. https://doi.org/10.3390/metrology3020011
APA StyleNewton, L., Thanki, A., Bermudez, C., Artigas, R., Thompson, A., Haitjema, H., & Leach, R. (2023). Optimisation of Imaging Confocal Microscopy for Topography Measurements of Metal Additive Surfaces. Metrology, 3(2), 186-221. https://doi.org/10.3390/metrology3020011








