Public Decision Policy for Controlling COVID-19 Outbreaks Using Control System Engineering
Abstract
1. Introduction
Humanity
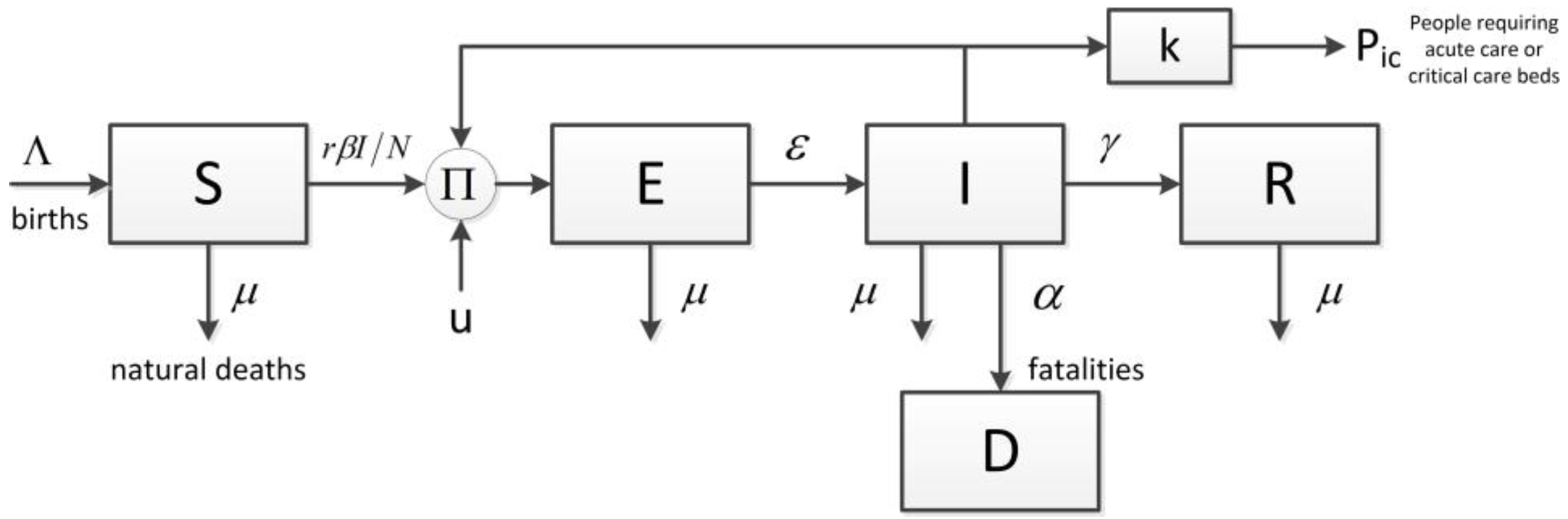
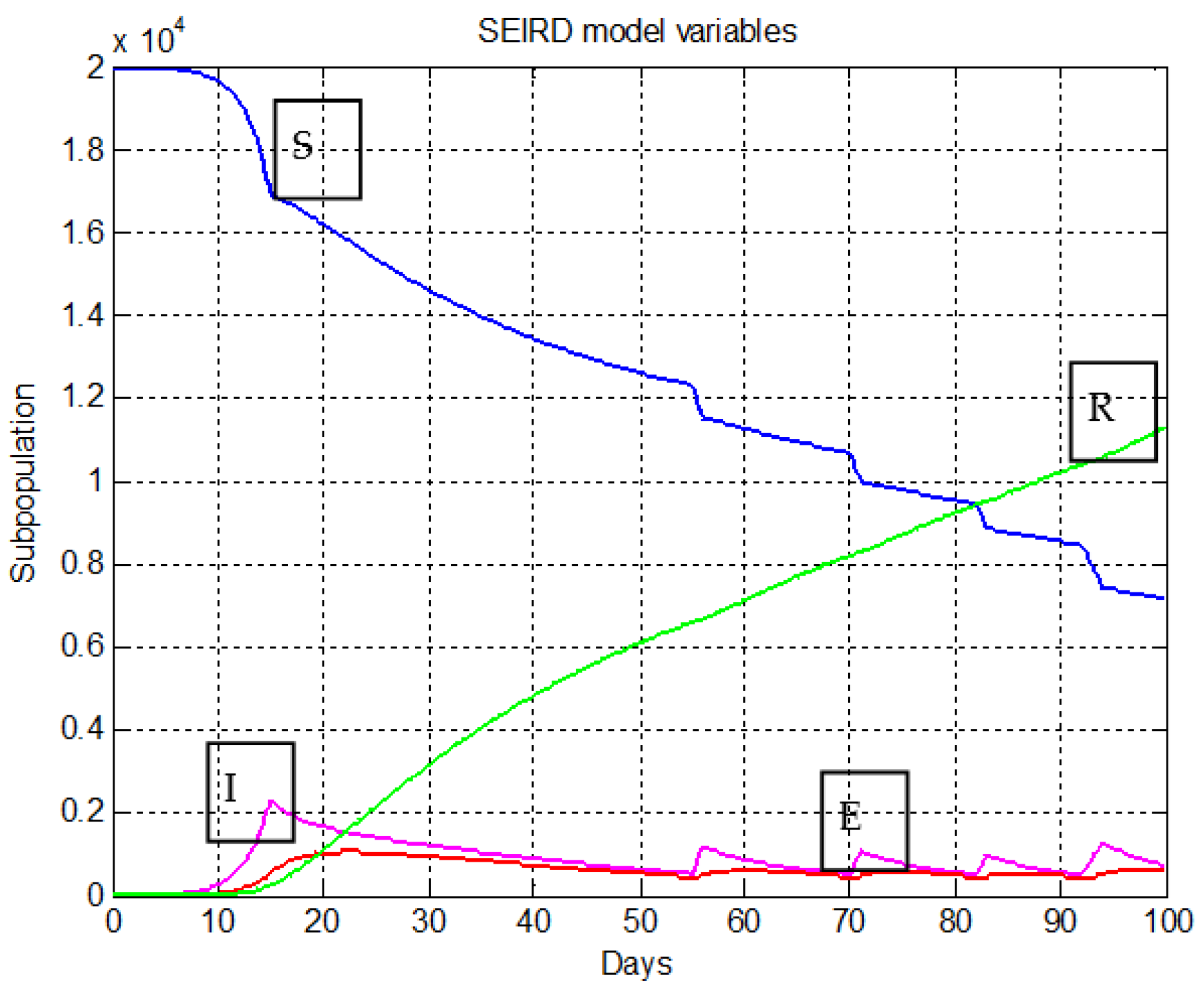
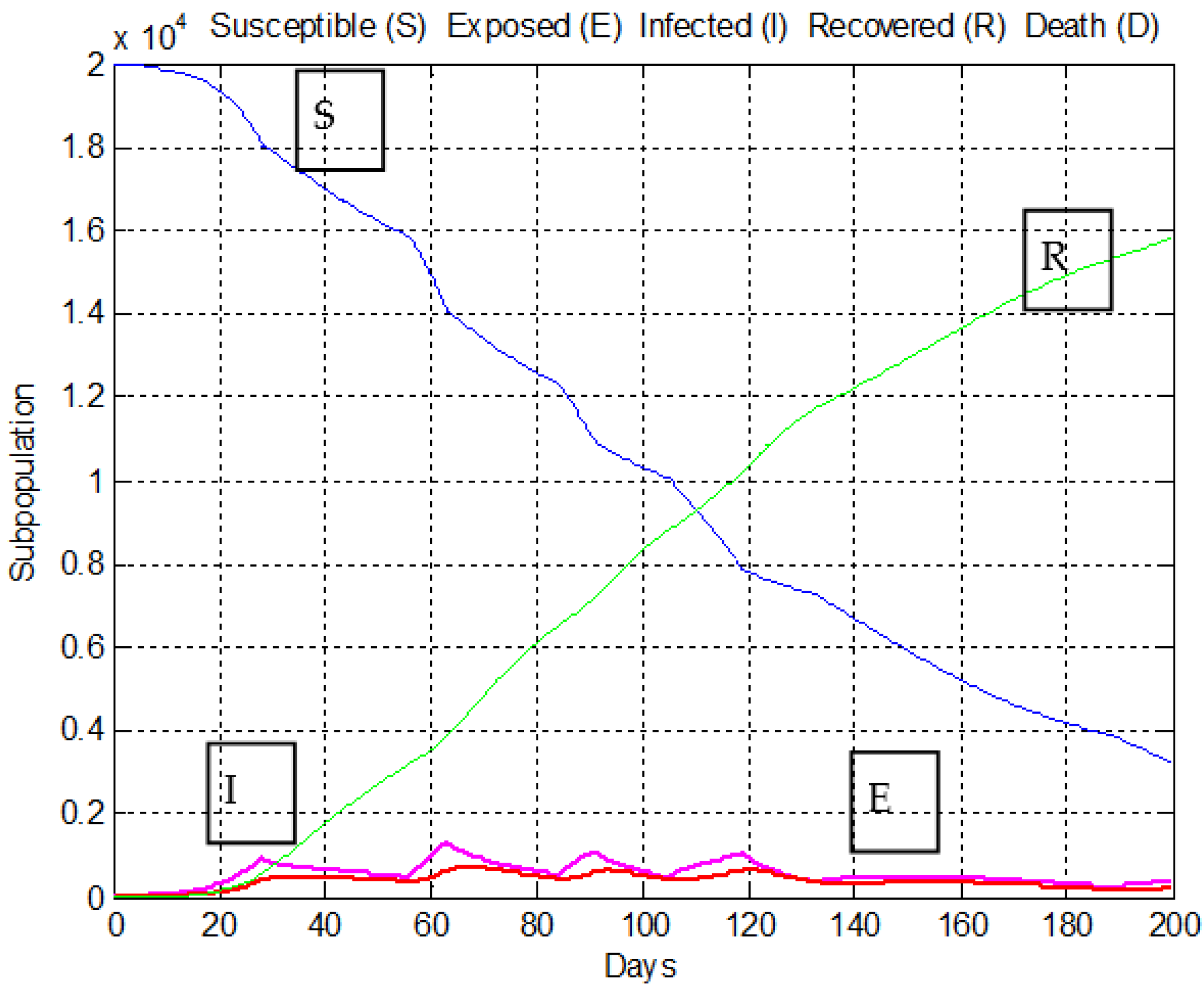
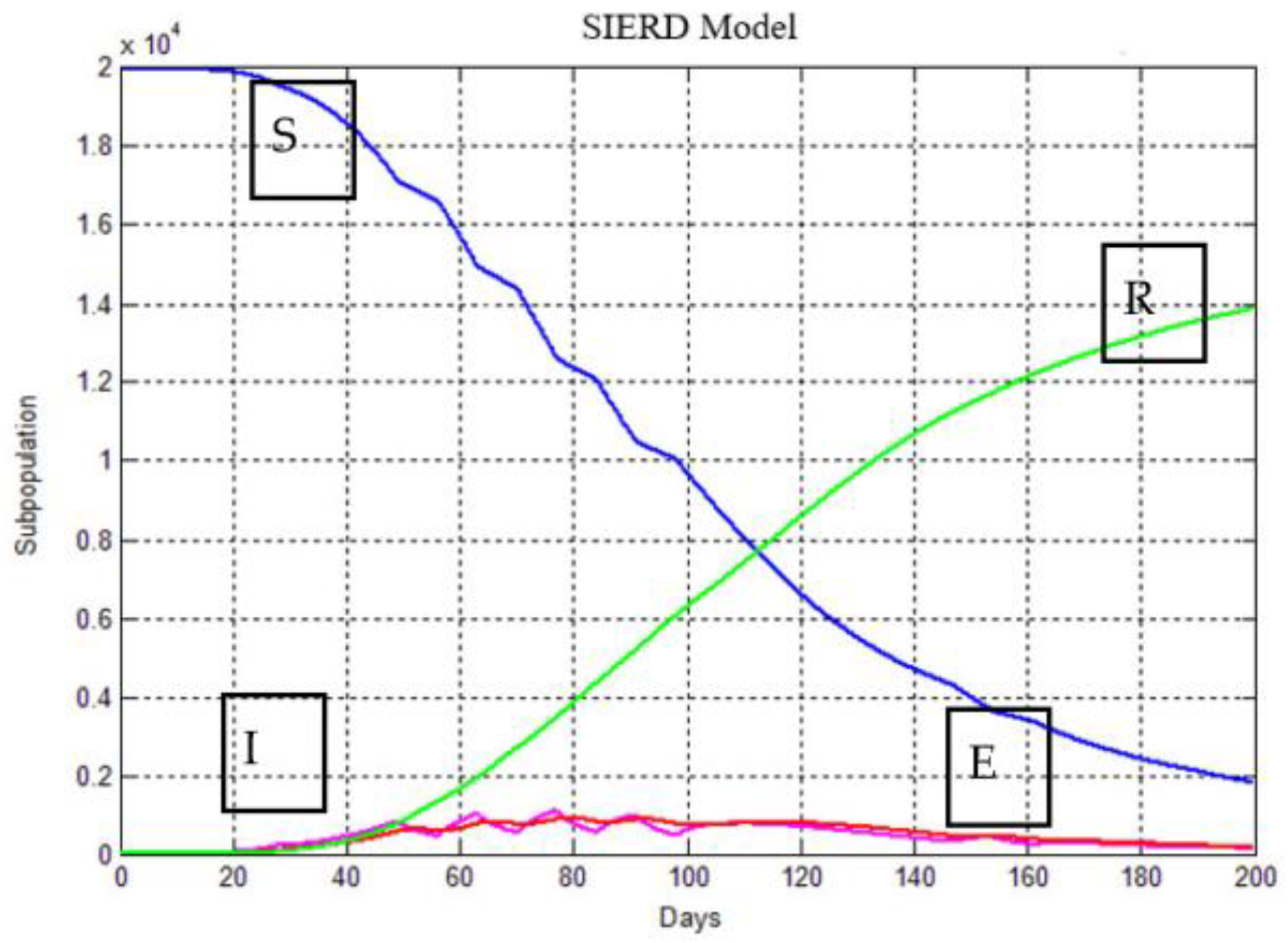
2. Mathematical Modeling of COVID-19 Epidemic
3. Proposal of a Public Decision Policy for Controlling COVID-19 Outbreaks Based on Control System Engineering
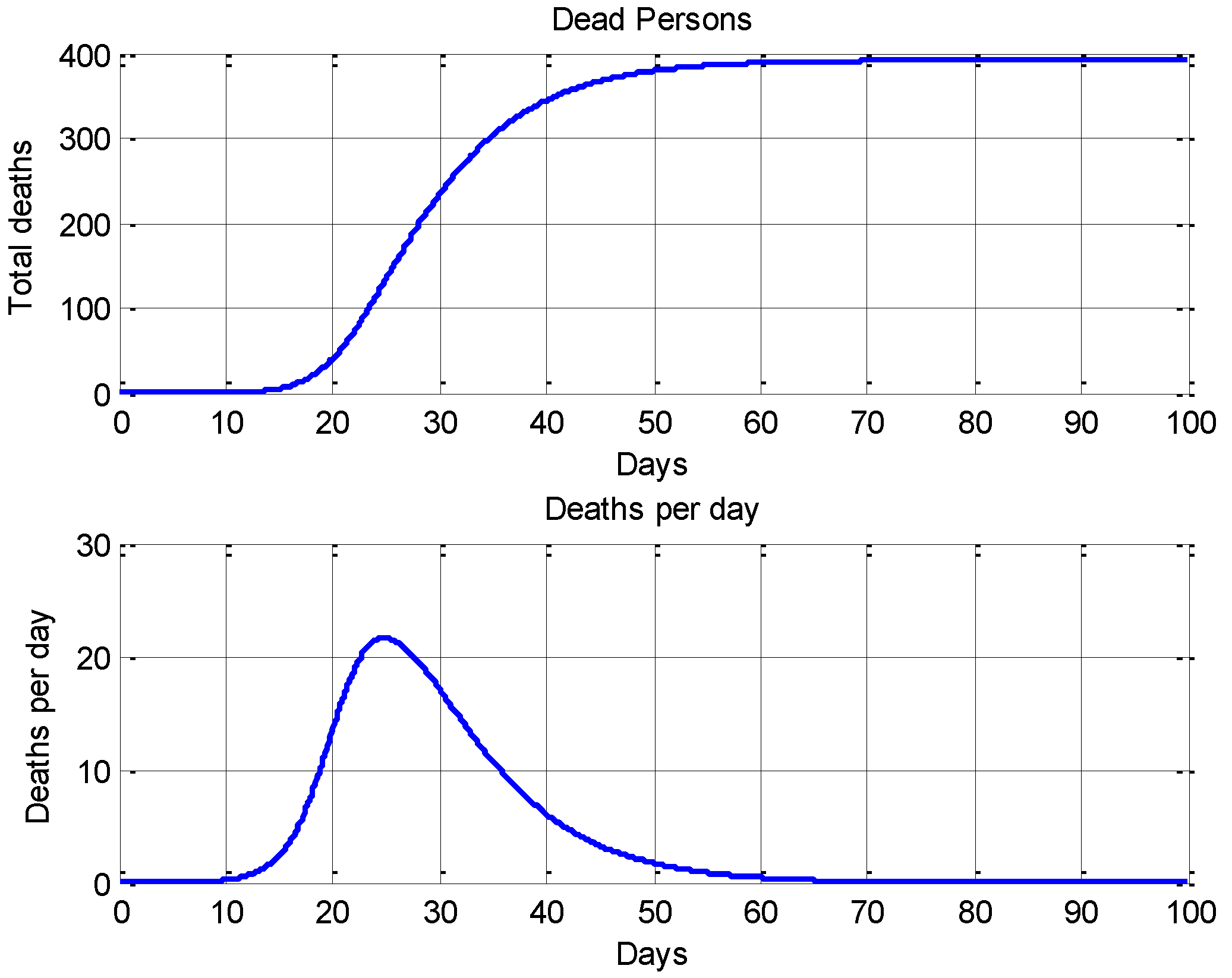
4. Simulations Analysis and Main Results
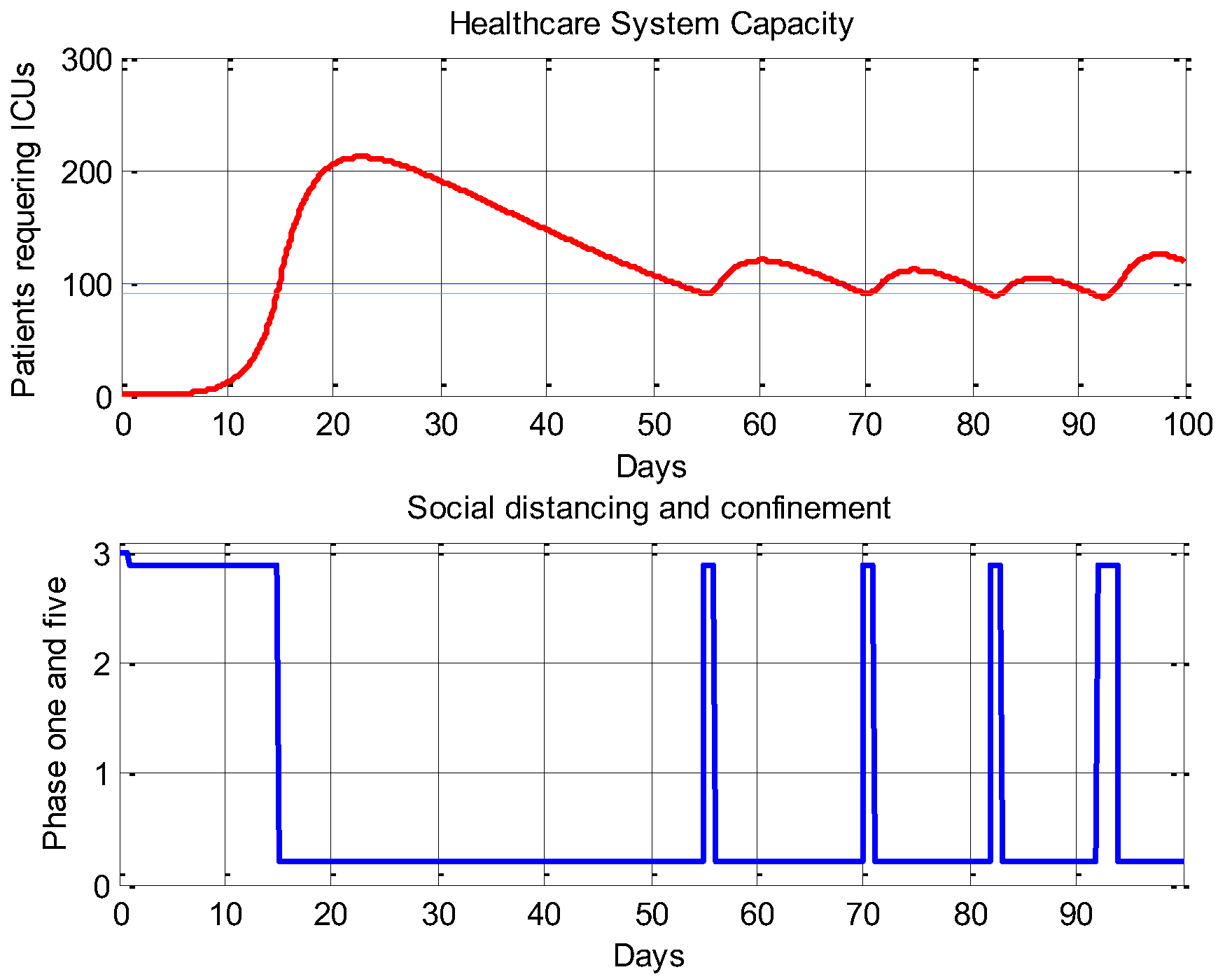
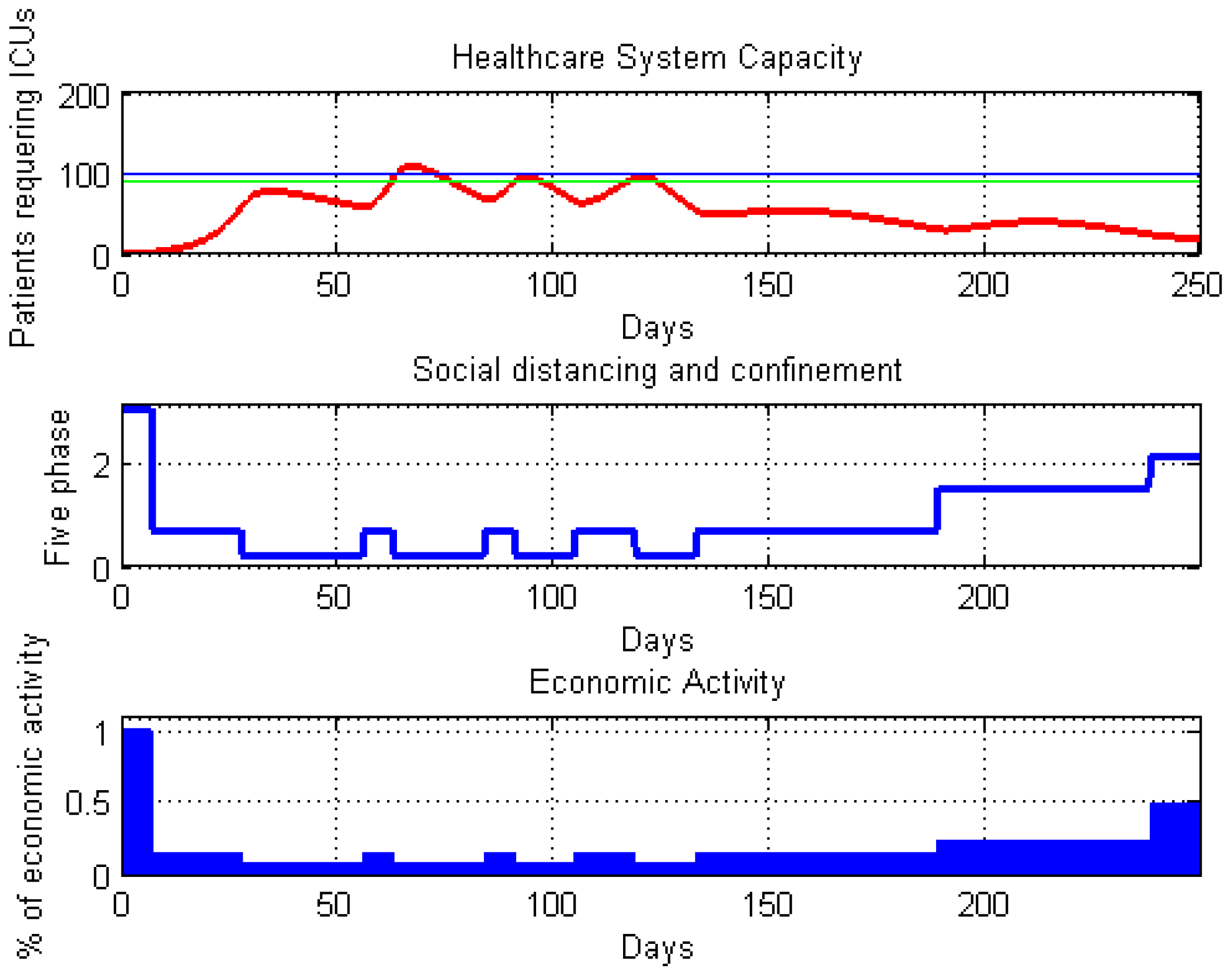
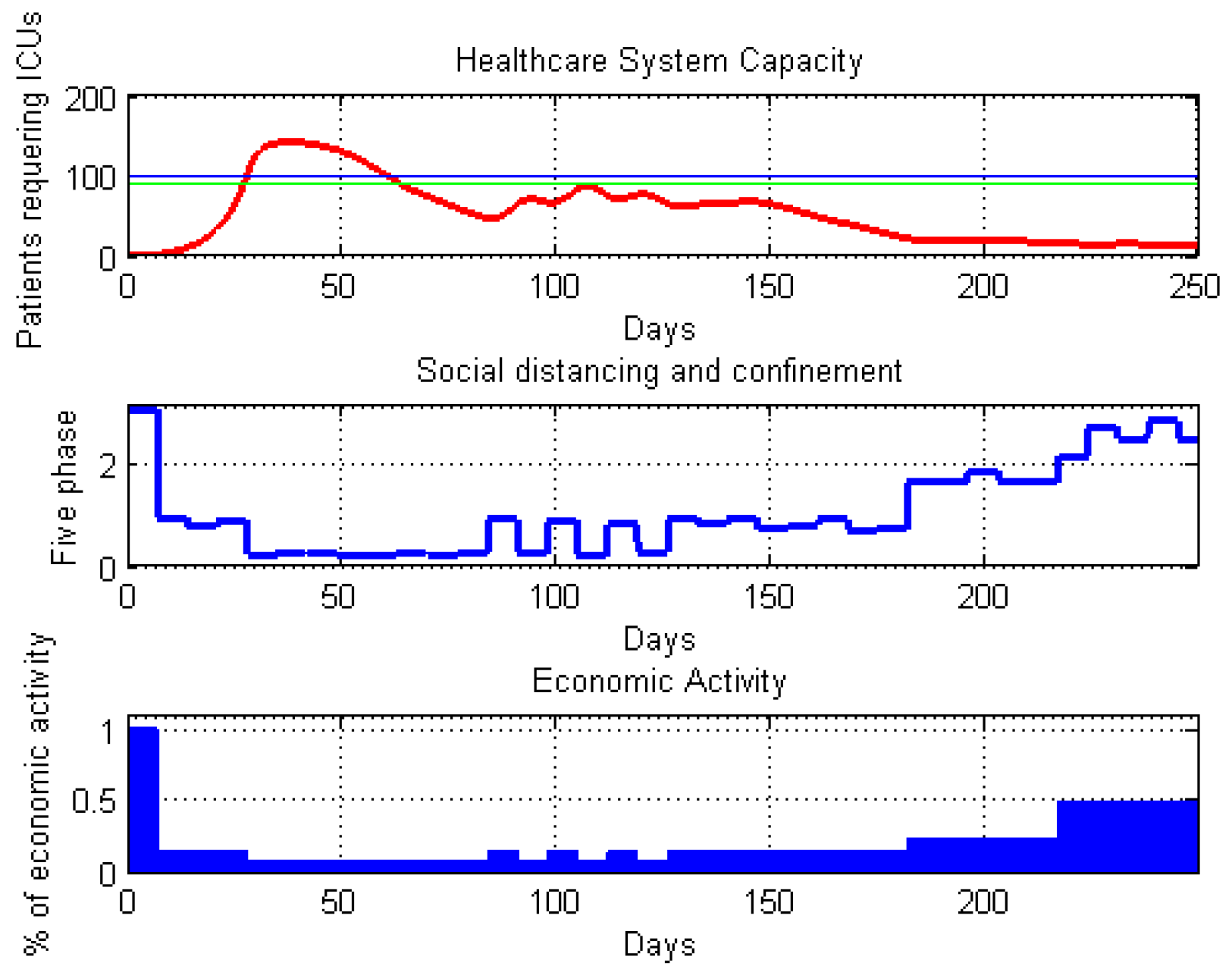
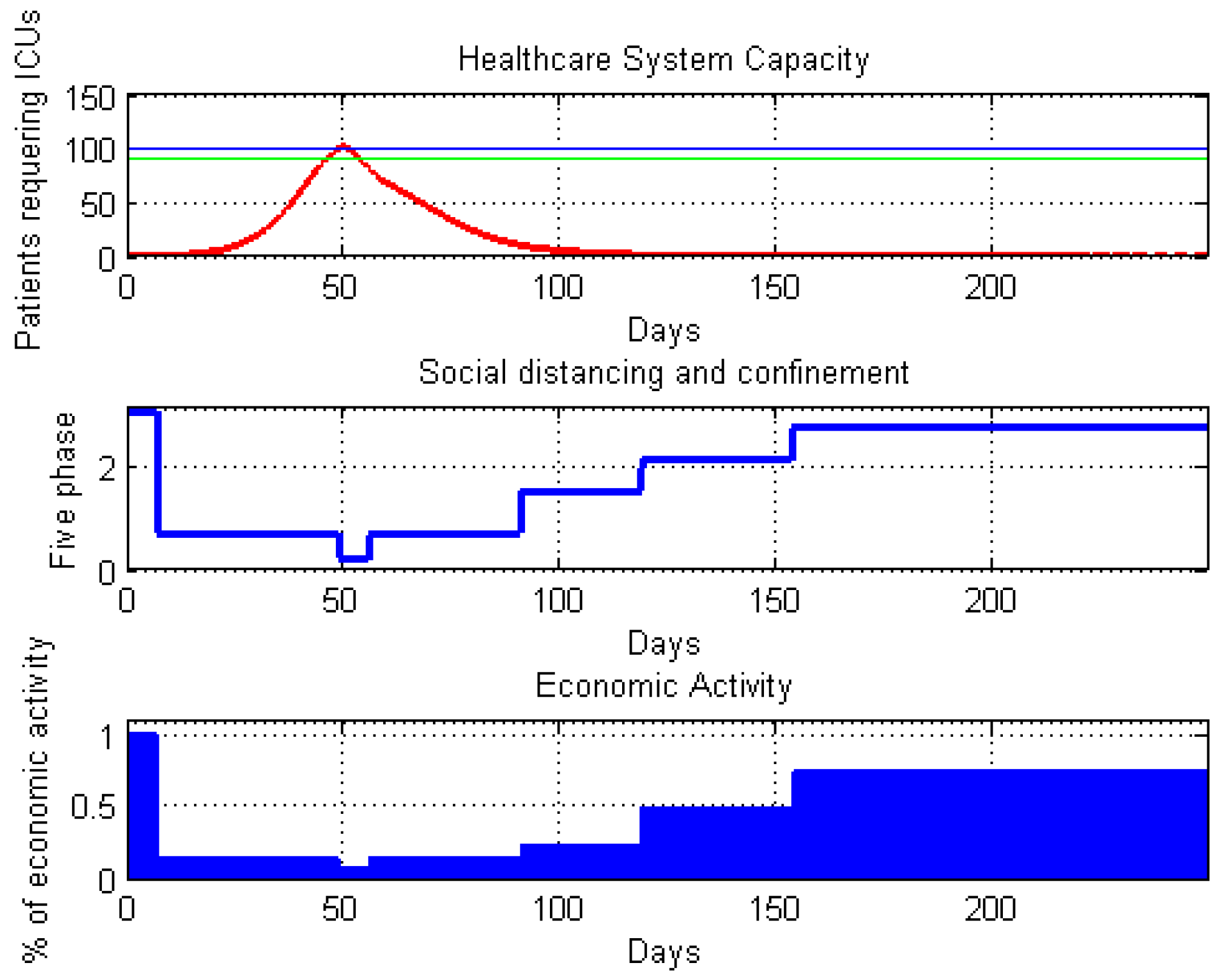
4.1. An Open-Loop Control System Strategy for Social Distancing and Confinement
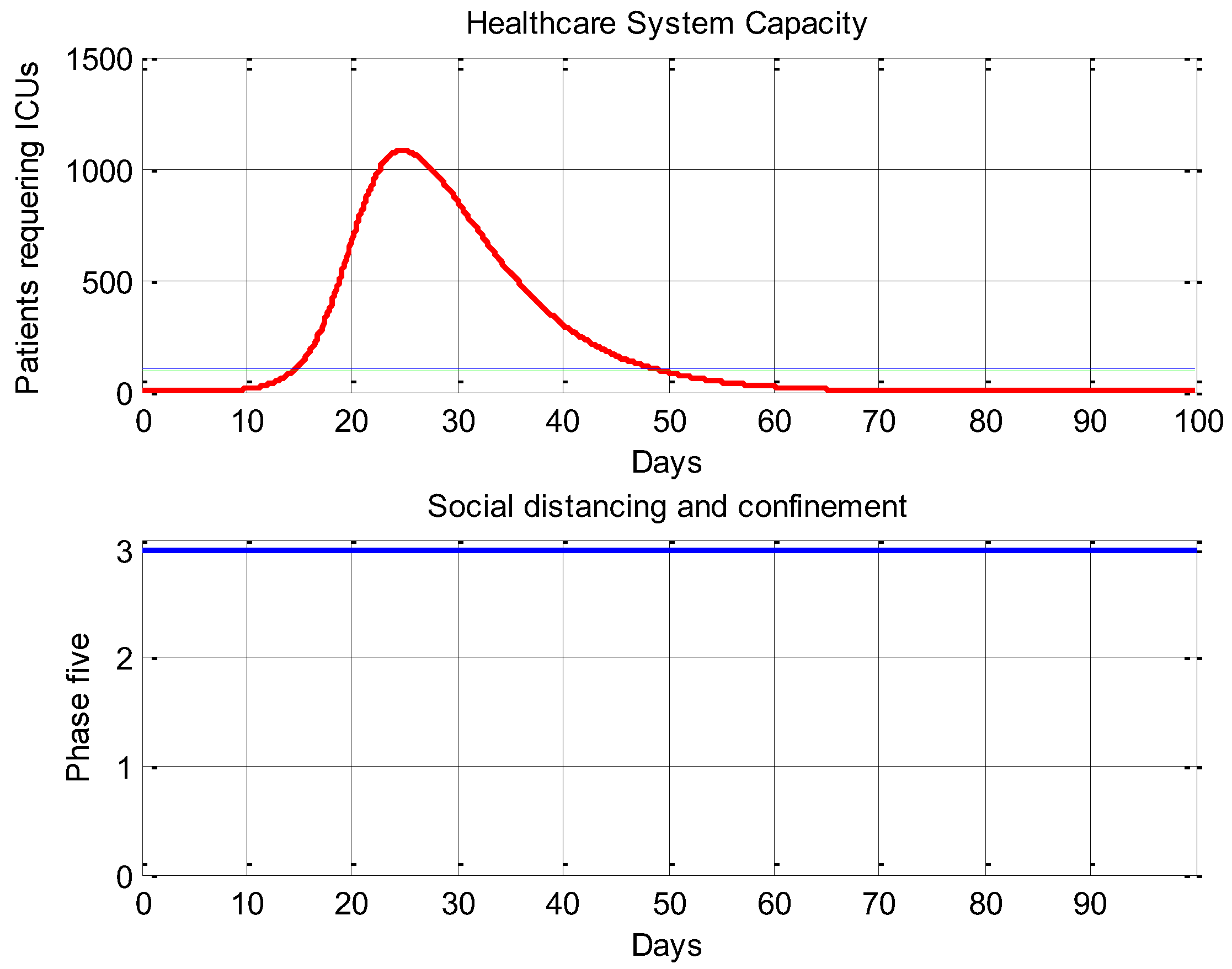
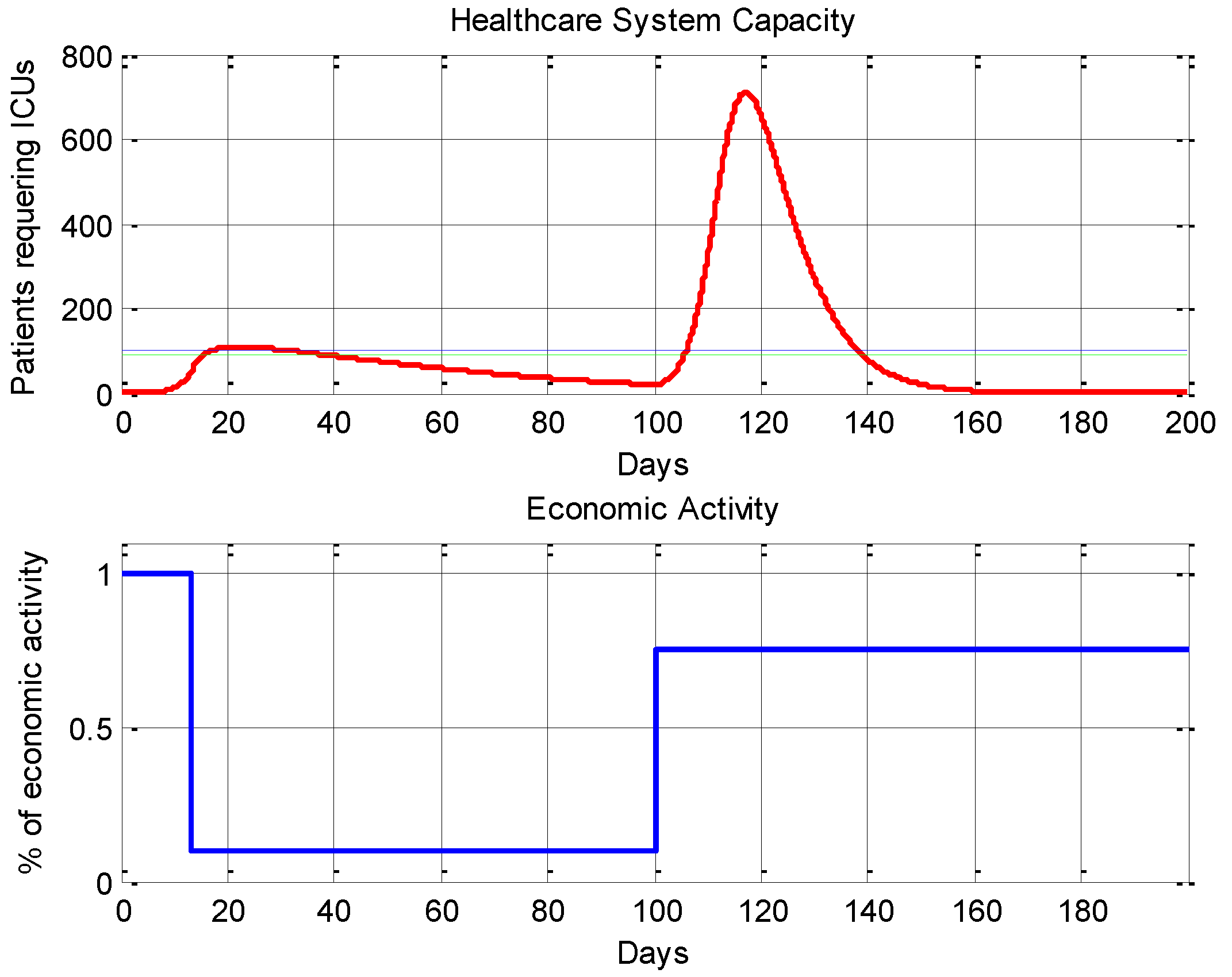
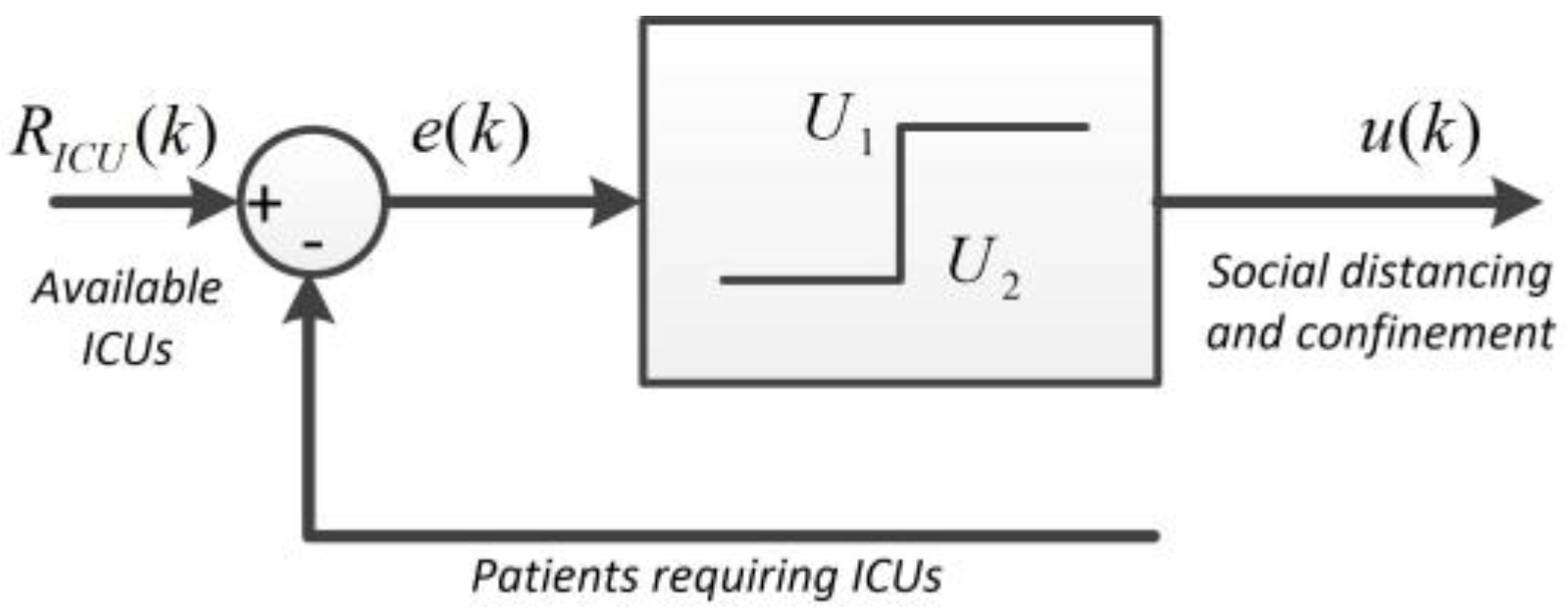
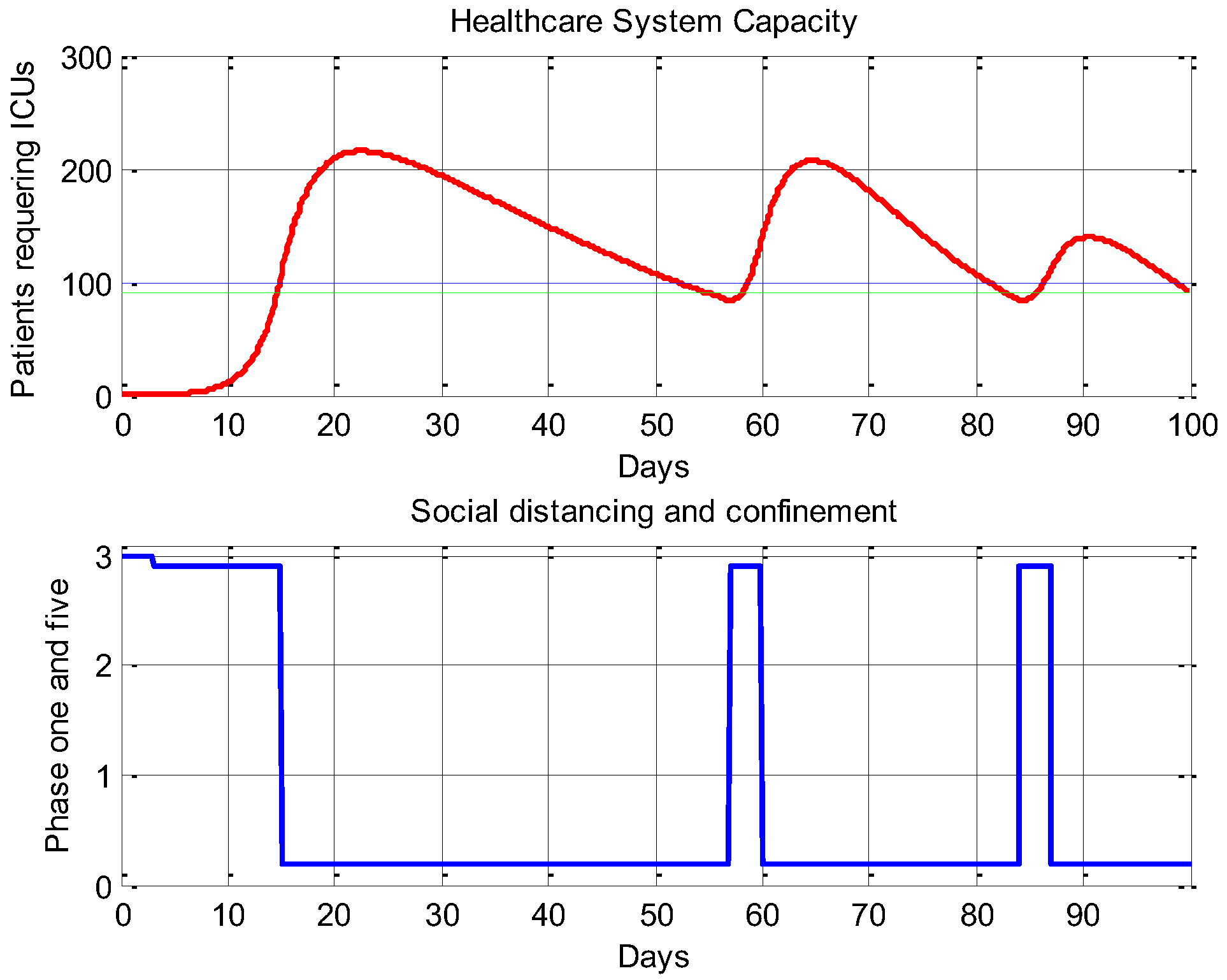
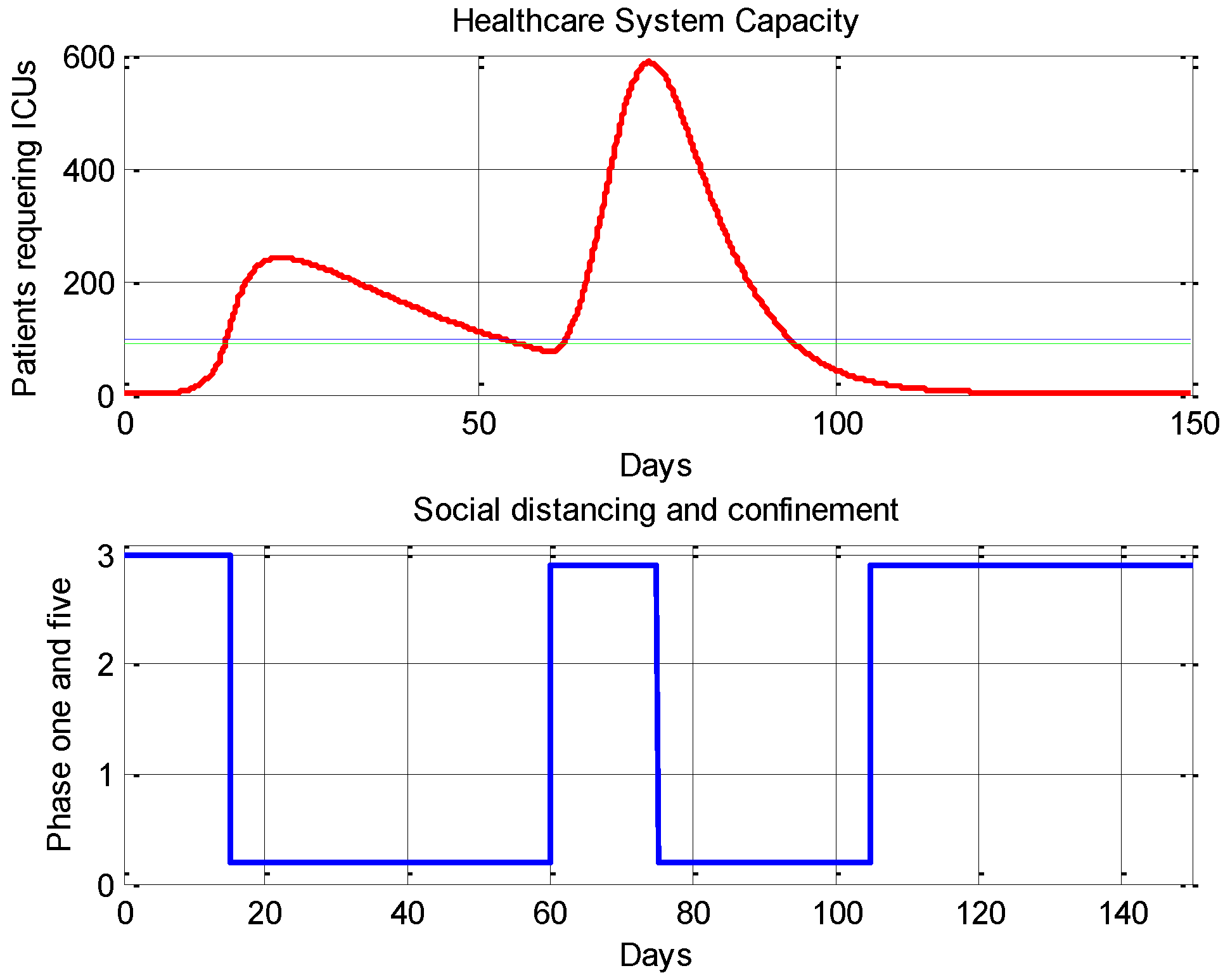
4.2. An On–off Control System Strategy
 |
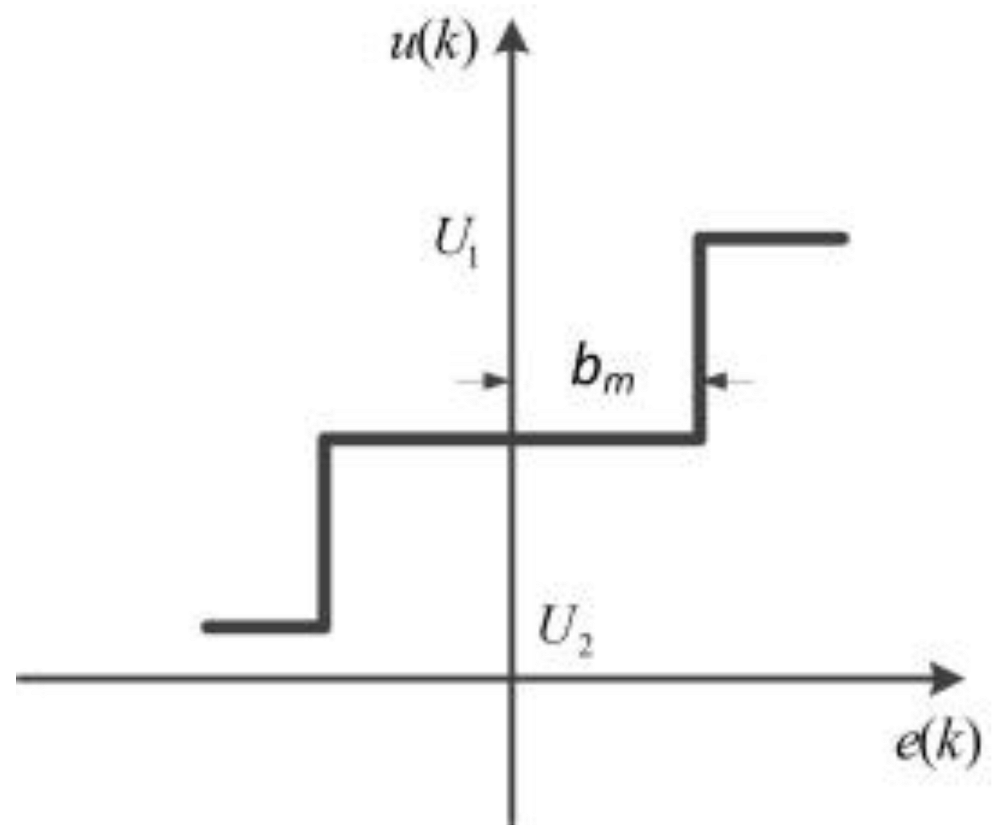 |
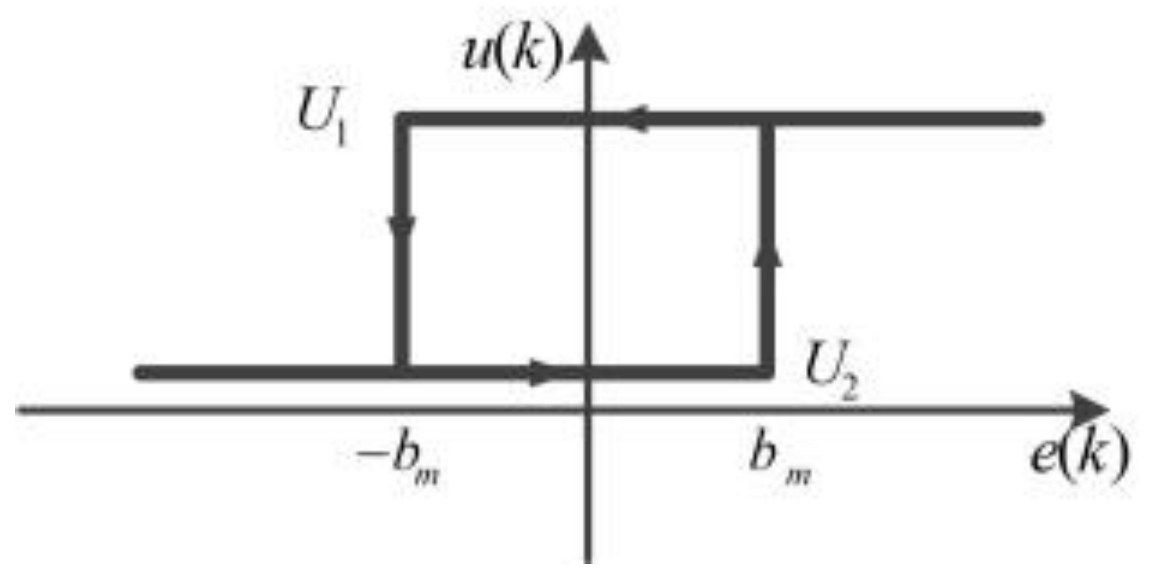 |
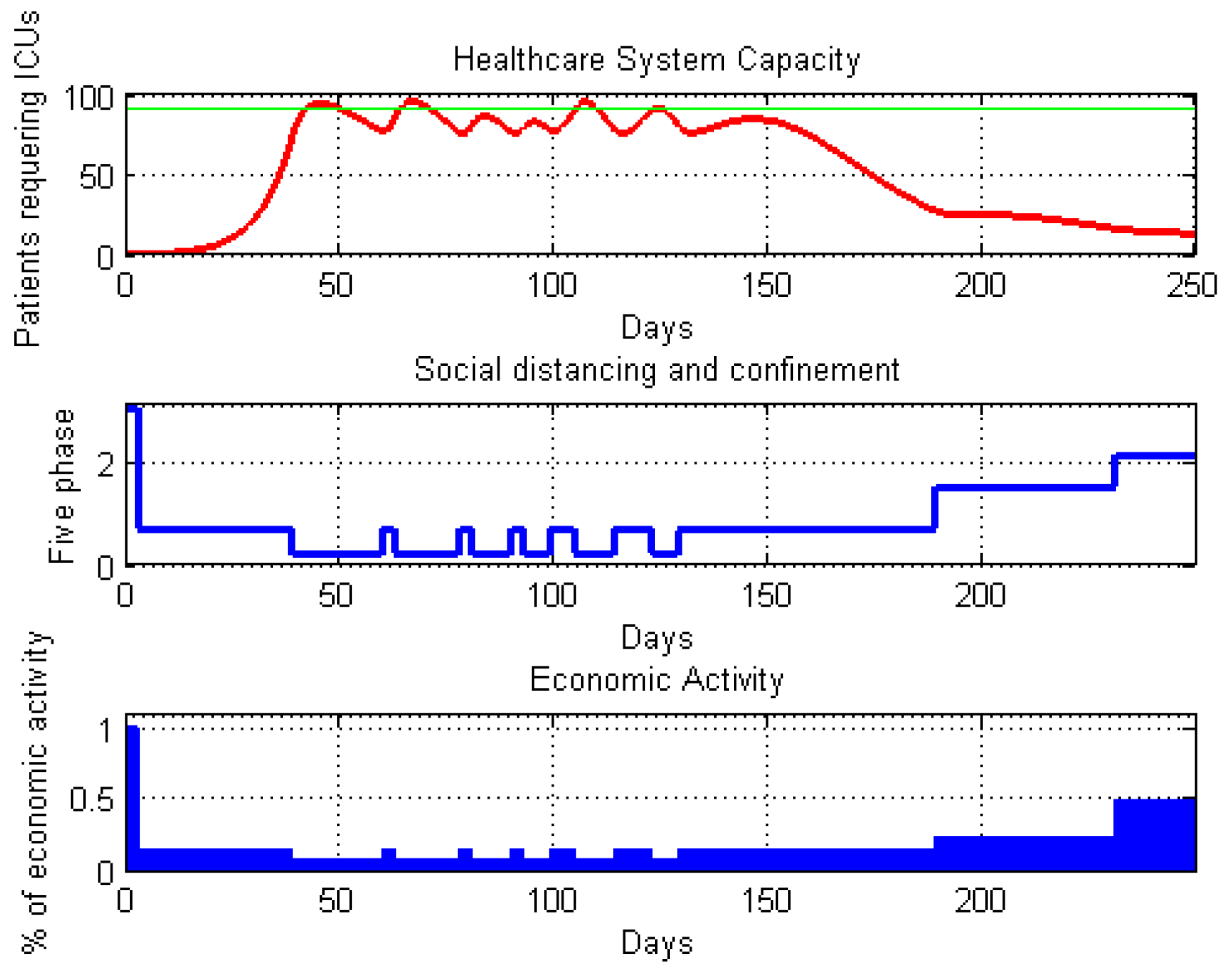
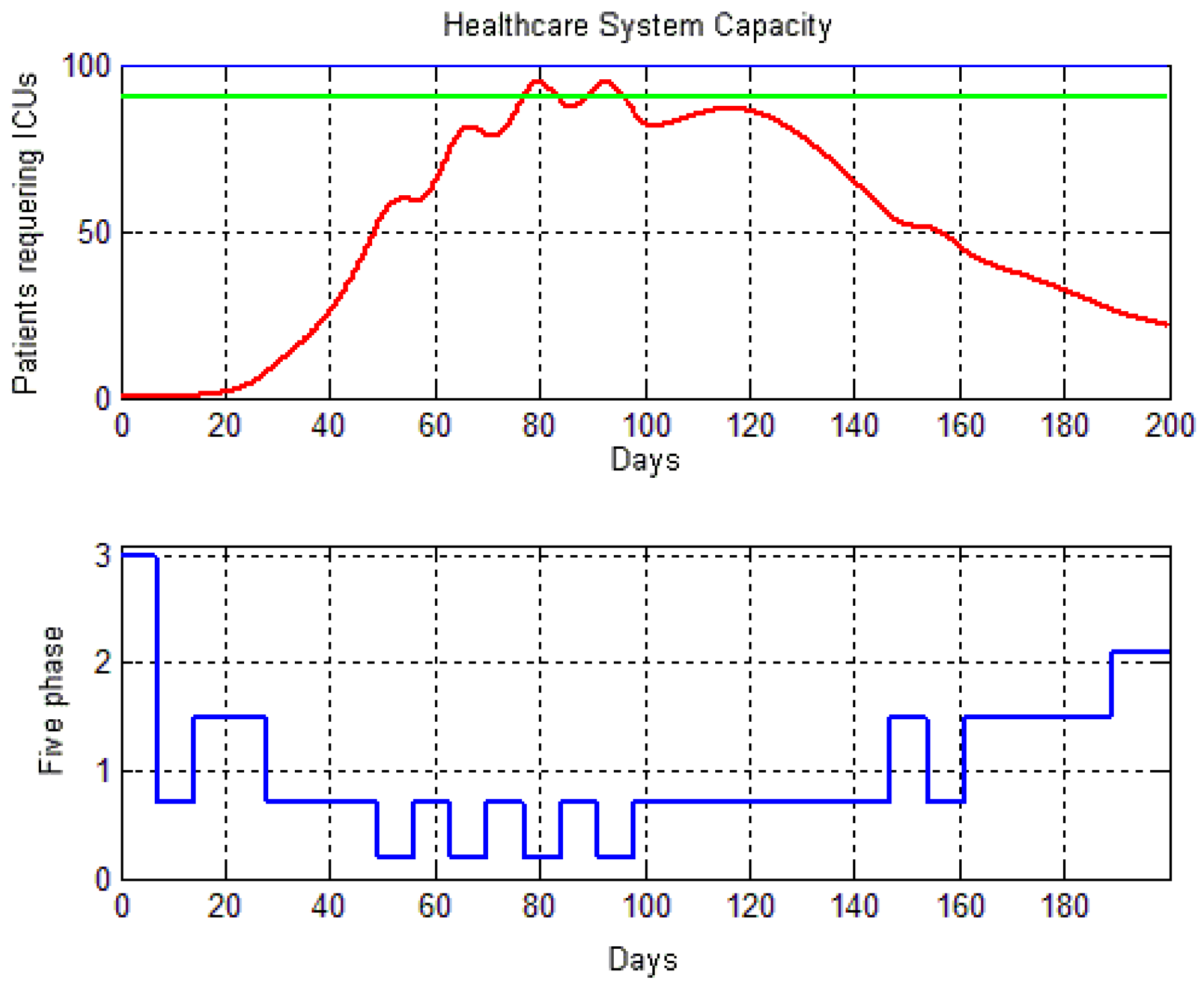
4.3. Main Results for the Proposed PID Control System
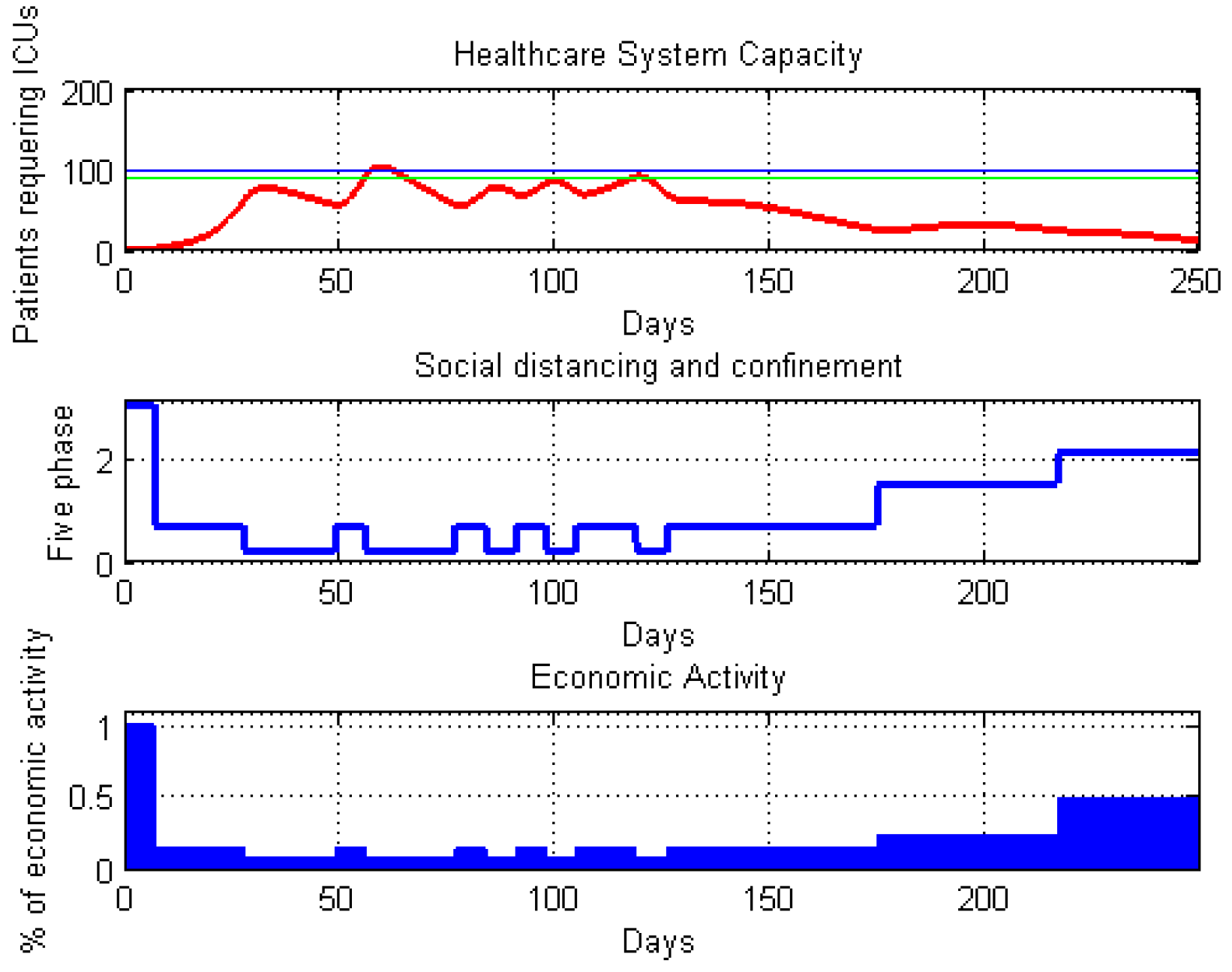
4.4. Modification of the SEIRD Model, Including the Testing of Asymptomatic and Presymptomatic Subjects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rutherford, A. Mathematical Modelling Techniques; Dover: New York, NY, USA, 1994. [Google Scholar]
- Bender, E.A. An Introduction to Mathematical Modeling; Dover: New York, NY, USA, 2000. [Google Scholar]
- Gershenfeld, N. The Nature of Mathematical Modeling; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Kuo, B. Automatic Control Systems, 9th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Bandekar, S.R.; Ghosh, M.; Bi, K. Impact of high-risk and low-risk population on COVID-19 dynamics considering antimicrobial resistance and control strategies. Eur. Phys. J. Plus. 2023, 138, 697. [Google Scholar] [CrossRef]
- Carcione, J.M.; Santos, J.E.; Bagaini, C.; Ba, J. A simulation of a COVID-19 epidemic based on a deterministic SEIR model. Front. Public Health 2020, 8, 230. [Google Scholar] [CrossRef] [PubMed]
- Brauer, F. Compartmental Models in Epidemiology. In Mathematical Epidemiology; Chapter in Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Willis, M.J.; Díaz, V.H.G.; Prado-Rubio, O.A.; von Stosch, M. Insights into the dynamics and control of COVID-19 infection rates. J. Chaos Solitons Fractal 2020, 138, 109937. [Google Scholar] [CrossRef] [PubMed]
- Sameni, R. Mathematical Modeling of Epidemic Diseases; A Case Study of the COVID-19 Coronavirus. In Quantitative Biology, Populations and Evolution; Draf Paper; Cornel University: Ithaca, NY, USA, 2020. [Google Scholar]
- Ferguson, N.; Laydon, D.; Nedjati Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunuba Perez, Z.; Cuomo-Dannenburg, G.; et al. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College COVID-19 Response Team: London, UK, 2020. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef] [PubMed]
- CTsay, C.; Lejarza, F.; Stadtherr, M.A.; Baldea, M. Modeling, state estimation, and optimal control for the US COVID-19 outbreak. Sci. Rep. 2020, 10, 10711. [Google Scholar] [CrossRef]
- Stewart, G.; van Heusden, K.; Dumont, G.A. Coronavirus: Policy Design for Stable Population Recovers: Using Feedback to Maximize Population Recovery Rate While Respecting Healthcare Capacity. IEEE Spectrum, 17 April 2020. Available online: https://spectrum.ieee.org/biomedical/diagnostics/how-control-theory-can-help-control-covid19 (accessed on 22 December 2023).
- Åström, K.J.; Hägglund, T. Advanced PID Control; International Society of Automation: Durham, NC, USA, 2006. [Google Scholar]
- Åström, K.J.; Hägglund, T. Control PID Avanzado; Pearson Educación, S.A.: Madrid, Spain, 2009. [Google Scholar]
- Cvejn, J. PID control of FOPDT plants with dominant dead time based on the modulus optimum criterion. Arch. Control. Sci. 2016, 26, 5–17. [Google Scholar] [CrossRef]
- Wang, C.; Li, D. Decentralized PID Controllers Based on Probabilistic Robustness. J. Dyn. Syst. Meas. Control 2011, 133, 61015. [Google Scholar] [CrossRef]
- Knospe, C. PID Control. IEEE Control. Syst. Mag. 2006, 26, 30–31. [Google Scholar] [CrossRef]
- Chitnis, N. Introduction to SEIR Models. In Workshop on Mathematical Models of Climate Variability, Environmental Change and Infectious Diseases; Department of Epidemiology and Public Health Systems Research and Dynamical Modelling: Trieste, Italy, 2017. [Google Scholar]
- Brauer, F. Chapter 2 Compartmental Models in Epidemiology; Department of Mathematics, University of British Columbia: Vancouver, BC, Canada, 1984. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: Berlin/Heidelberg, Germany, 2012; Volume 2. [Google Scholar]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamics; Princeton University Press: Princeton, NJ, USA, 2012; Volume 7. [Google Scholar]
- Das, A.; Dhar, A.; Goyal, S.; Kundu, A. COVID-19: Analysis of a modified SEIR model, a comparison of different intervention strategies and projections for India. Prepr. Serv. Health Sci. 2020, preprints. [Google Scholar] [CrossRef]
- Al-Sheikh, S.A. Modeling and Analysis of an SEIR Epidemic Model with a Limited Resource for Treatment. Glob. J. Sci. Front. Res. Math. Decis. Sci. 2012, 12, 56–66. [Google Scholar]
- Giannakeas, V.; Bhatia, D.; Warkentin, M.T.; Bogoch, I.; Stall, N.M. Estimating the Maximum Capacity of COVID-19 Cases Manageable per Day Given a Health Care System’s Constrained Resources. Am. Coll. Physicians J. Ann. Intern. Med. 2020, 173, 407–410. [Google Scholar] [CrossRef] [PubMed]
- Hadi, M.A.; Ali, H.I. Control of COVID-19 system using a novel nonlinear robust control algorithm. Biomed. Signal Process Control. 2021, 64, 102317. [Google Scholar] [CrossRef] [PubMed]
- Kuchen, B.; Carelli, R. Control Digital Directo; School of Engineering, Universidad Nacional de San Juan: San Juan, Argentina, 2010. [Google Scholar]
- Isermann, R. Digital Control System; Springer-Verlag: Berlin/Heidelberg, Germany, 1989; Volume 1. [Google Scholar]
- Arasteh, H.; Badi, A. A Study on Control of Novel corona-virus (2019-nCoV) Disease Process by Using PID Controller. medrxiv 2020, 23, 1–9. [Google Scholar] [CrossRef]
- Minorsky, N. Directional stability of automatically steered bodies. J. Am. Soc. Nav. Eng. 1922, 34, 280–309. [Google Scholar] [CrossRef]
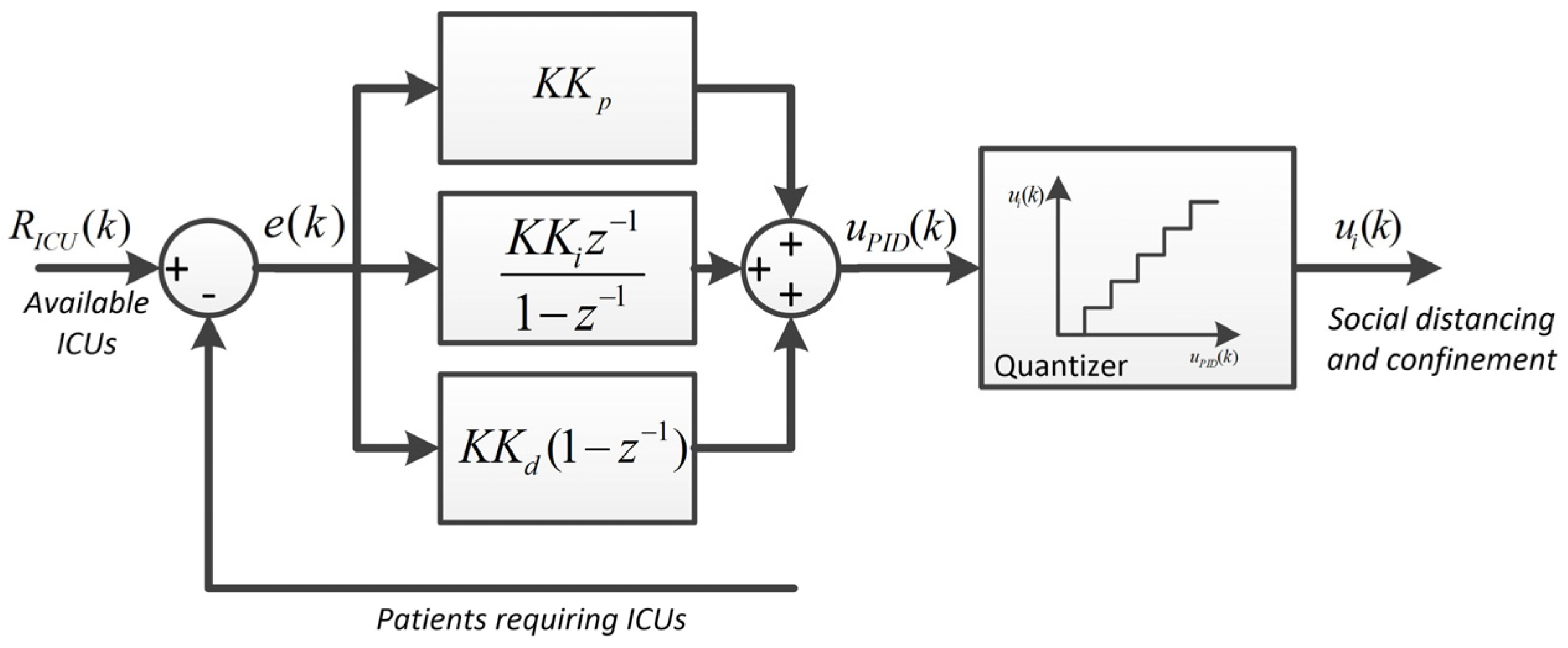



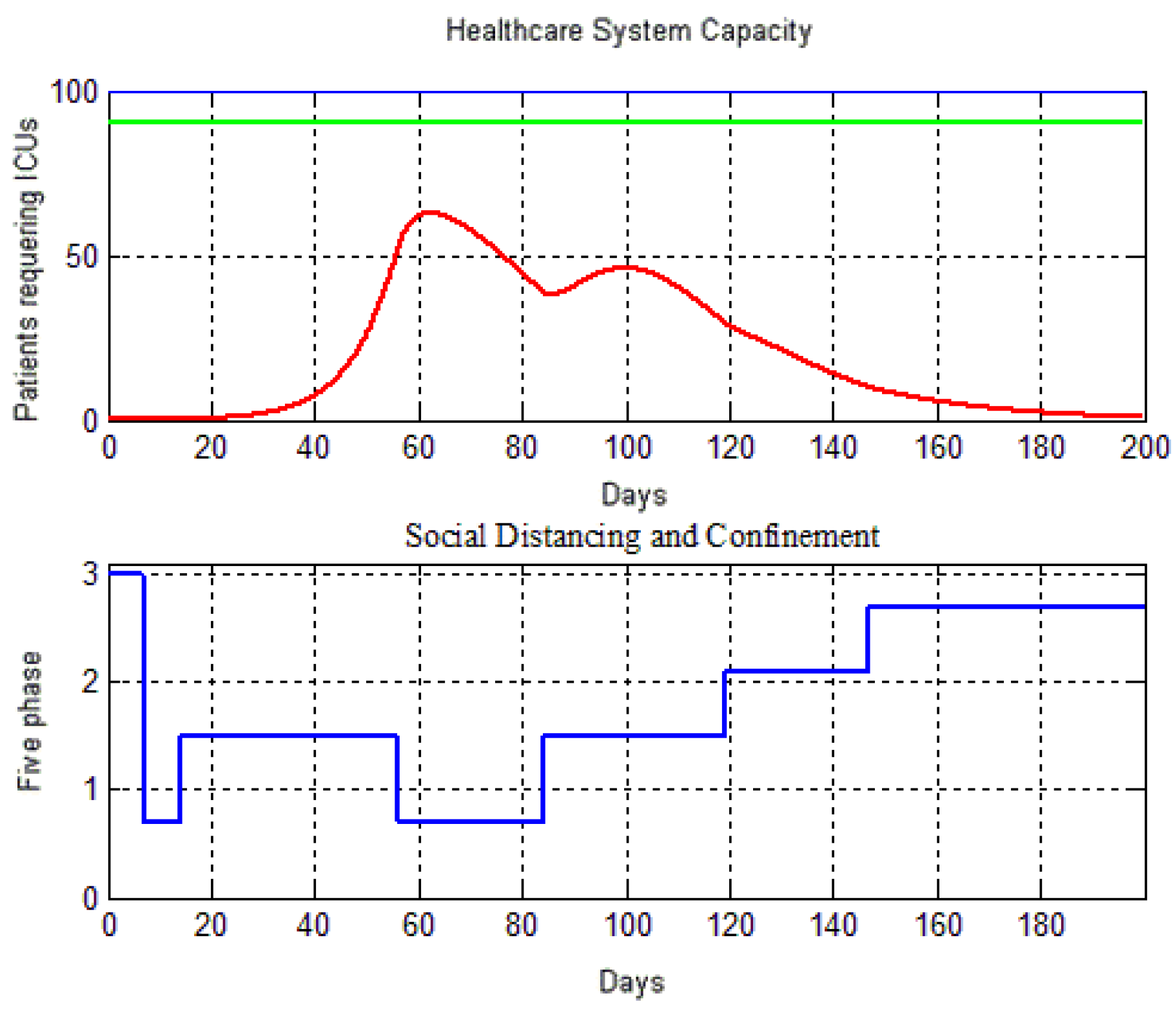
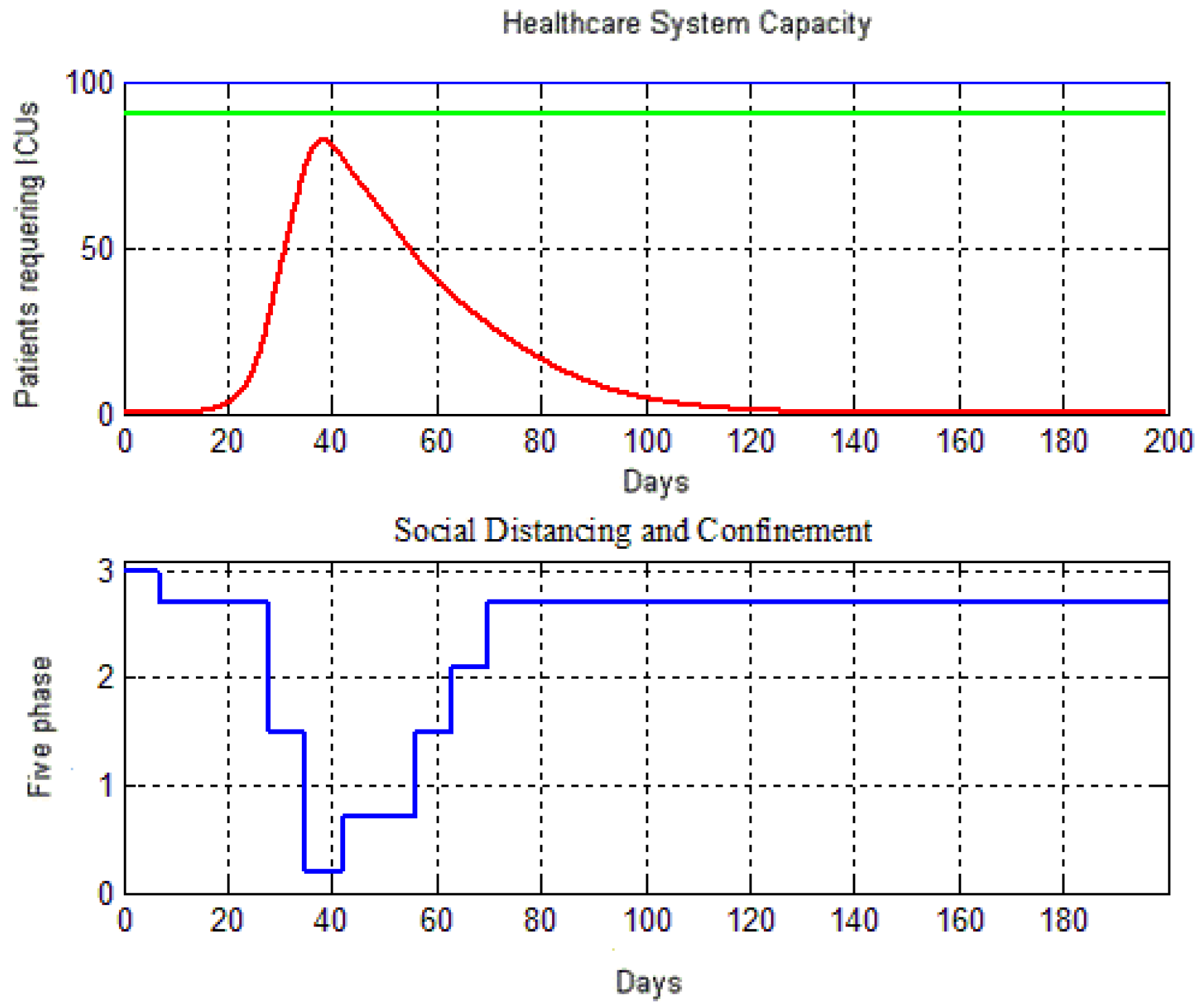
| Confinement Social Level | Proportion of Baseline Contact Rate | Control Action |
|---|---|---|
| Light | 70% | u1 = 2.7 |
| Weak | 50% | u2 = 2.1 |
| Medium | 30% | u3 = 1.5 |
| Strong | 20% | u4 = 0.7 |
| Extreme | 10% | u5 = 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patiño, H.D.; Pucheta, J.; Rivero, C.R.; Tosetti, S. Public Decision Policy for Controlling COVID-19 Outbreaks Using Control System Engineering. COVID 2024, 4, 44-62. https://doi.org/10.3390/covid4010005
Patiño HD, Pucheta J, Rivero CR, Tosetti S. Public Decision Policy for Controlling COVID-19 Outbreaks Using Control System Engineering. COVID. 2024; 4(1):44-62. https://doi.org/10.3390/covid4010005
Chicago/Turabian StylePatiño, H. Daniel, Julián Pucheta, Cristian Rodríguez Rivero, and Santiago Tosetti. 2024. "Public Decision Policy for Controlling COVID-19 Outbreaks Using Control System Engineering" COVID 4, no. 1: 44-62. https://doi.org/10.3390/covid4010005
APA StylePatiño, H. D., Pucheta, J., Rivero, C. R., & Tosetti, S. (2024). Public Decision Policy for Controlling COVID-19 Outbreaks Using Control System Engineering. COVID, 4(1), 44-62. https://doi.org/10.3390/covid4010005











