Advances in the Development of Representation Learning and Its Innovations against COVID-19
Abstract
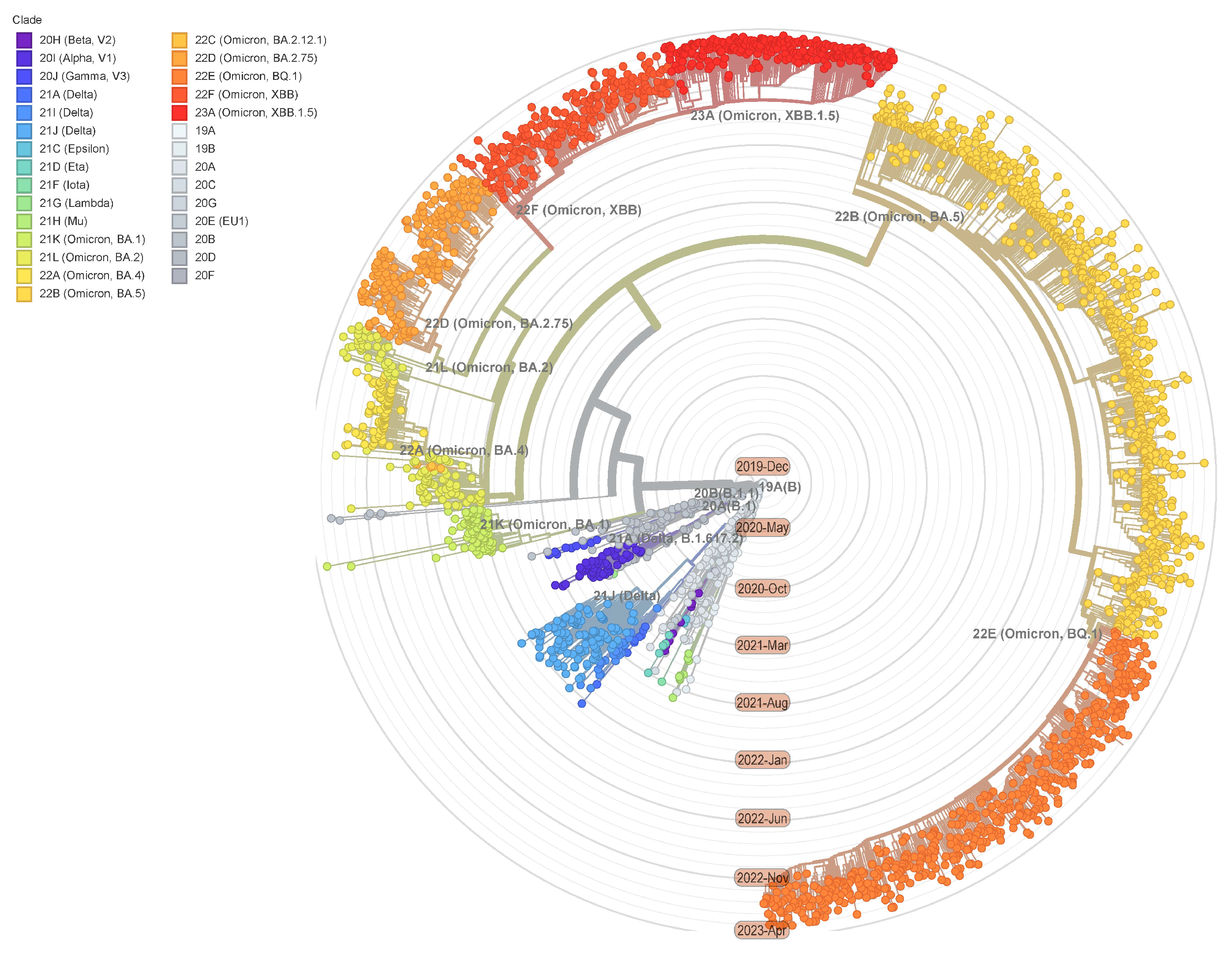
:1. Introduction
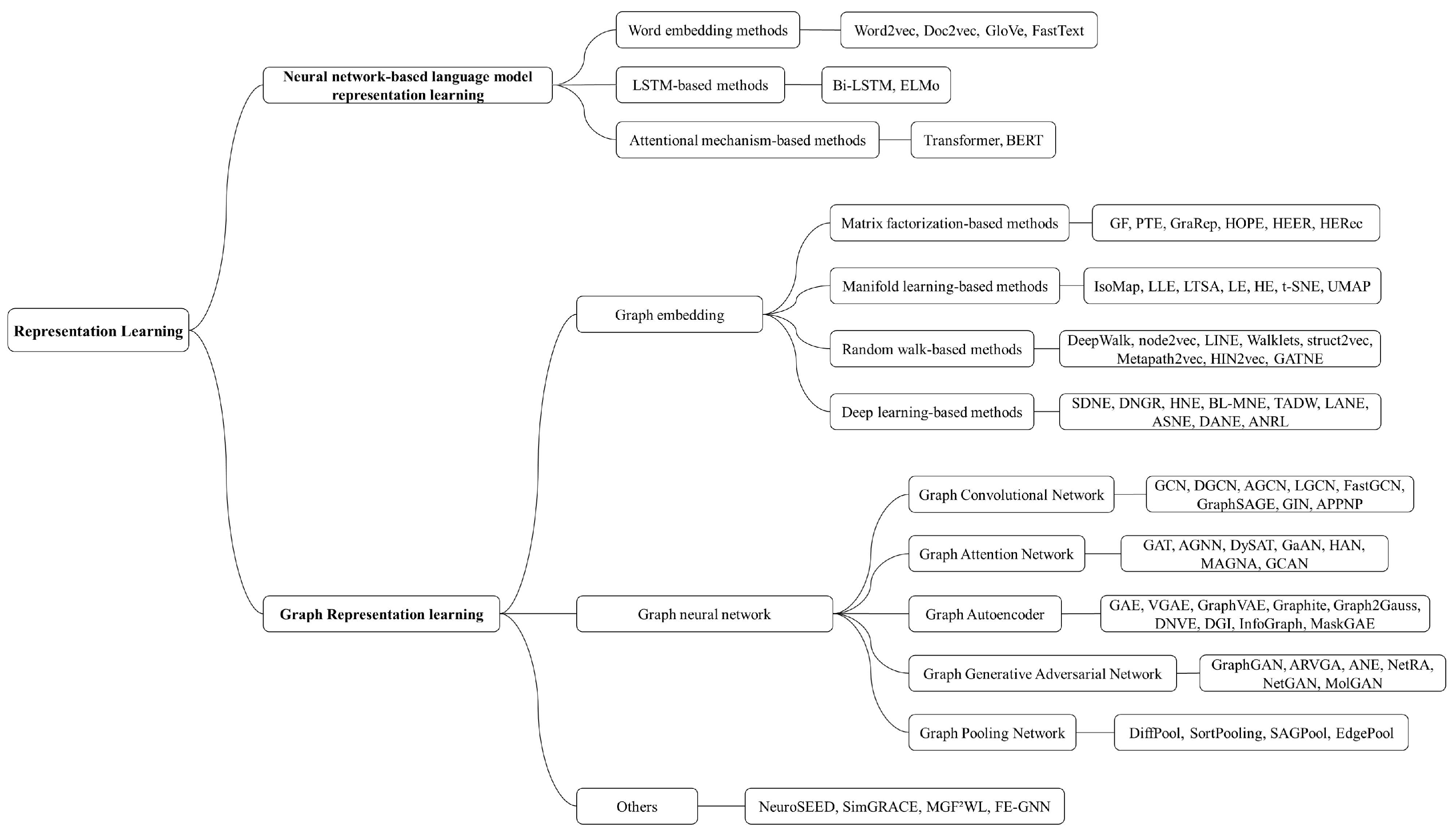
2. Representation Learning
3. Overview of Representation Learning Methods
3.1. Neural-Network-Based Language Model Representation Learning
3.2. Graph Representation Learning
3.2.1. Graph Embedding
3.2.2. Graph Neural Network-Based Methods
4. Representation Learning Methods for COVID-19
4.1. Pharmaceutical
4.1.1. Drug Discovery
4.1.2. Drug Repurposing
4.1.3. Drug–Target Interaction Prediction
4.1.4. Drug–Drug Interaction Prediction
4.1.5. Bio-Drug Interaction Prediction
4.2. Public Health and Healthcare
4.2.1. Case Prediction
4.2.2. Propagation Prediction
4.2.3. Analysis of EHRs and EMRs
5. Challenges and Prospects
5.1. Data Quality
5.2. Hyperparameters and Labels
5.3. Interpretability and Extensibility
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Harvey, W.T.; Carabelli, A.M.; Jackson, B.; Gupta, R.K.; Thomson, E.C.; Harrison, E.M.; Ludden, C.; Reeve, R.; Rambaut, A.; et al.; COVID-19 Genomics UK (COG-UK) Consortium; et al. SARS-CoV-2 variants, spike mutations and immune escape. Nat. Rev. Microbiol. 2021, 19, 409–424. [Google Scholar]
- Hadfield, J.; Megill, C.; Bell, S.M.; Huddleston, J.; Potter, B.; Callender, C.; Sagulenko, P.; Bedford, T.; Neher, R.A. Nextstrain: Real-time tracking of pathogen evolution. Bioinformatics 2018, 34, 4121–4123. [Google Scholar]
- Morens, D.M.; Folkers, G.K.; Fauci, A.S. The concept of classical herd immunity may not apply to COVID-19. J. Infect. Dis. 2022, 226, 195–198. [Google Scholar]
- Fu, L.; Wang, B.; Yuan, T.; Chen, X.; Ao, Y.; Fitzpatrick, T.; Li, P.; Zhou, Y.; Lin, Y.-f.; Duan, Q.; et al. Clinical characteristics of coronavirus disease 2019 (COVID-19) in china: A systematic review and meta-analysis. J. Infect. 2020, 80, 656–665. [Google Scholar]
- Williamson, E.J.; Walker, A.J.; Bhaskaran, K.; Bacon, S.; Bates, C.; Morton, C.E.; Curtis, H.J.; Mehrkar, A.; Evans, D.; Inglesby, P.; et al. Opensafely: Factors associated with COVID-19 death in 17 million patients. Nature 2020, 584, 430. [Google Scholar]
- Guo, Y.-R.; Cao, Q.-D.; Hong, Z.-S.; Tan, Y.-Y.; Chen, S.-D.; Jin, H.-J.; Tan, K.-S.; Wang, D.-Y.; Yan, Y. The origin, transmission and clinical therapies on coronavirus disease 2019 (COVID-19) outbreak—An update on the status. Mil. Med. Res. 2020, 7, 11. [Google Scholar]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in wuhan, china. Lancet 2020, 395, 497–506. [Google Scholar]
- Nguyen, T.T.; Abdelrazek, M.; Nguyen, D.T.; Aryal, S.; Nguyen, D.T.; Reddy, S.; Nguyen, Q.V.H.; Khatami, A.; Hsu, E.B.; Yang, S. Origin of novel coronavirus (COVID-19): A computational biology study using artificial intelligence. bioRxiv 2020. [Google Scholar] [CrossRef]
- Cascella, M.; Rajnik, M.; Aleem, A.; Dulebohn, S.C.; Napoli, R.D. Features, Evaluation, and Treatment of Coronavirus (COVID-19). In Statpearls [Internet]; 2022. Available online: https://www.ncbi.nlm.nih.gov/books/NBK554776/ (accessed on 10 July 2023).
- Jiang, S.; Hillyer, C.; Du, L. Neutralizing antibodies against SARS-CoV-2 and other human coronaviruses. Trends Immunol. 2020, 41, 355–359. [Google Scholar]
- Shrestha, L.B.; Foster, C.; Rawlinson, W.; Tedla, N.; Bull, R.A. Evolution of the SARS-CoV-2 omicron variants ba. 1 to ba. 5: Implications for immune escape and transmission. Rev. Med. Virol. 2022, 32, e2381. [Google Scholar]
- Korber, B.; Fischer, W.M.; Gnanakaran, S.; Yoon, H.; Theiler, J.; Abfalterer, W.; Hengartner, N.; Giorgi, E.E.; Bhattacharya, T.; Foley, B.; et al. Tracking changes in SARS-CoV-2 spike: Evidence that d614g increases infectivity of the COVID-19 virus. Cell 2020, 182, 812–827. [Google Scholar] [PubMed]
- Cao, Y.; Wang, J.; Jian, F.; Xiao, T.; Song, W.; Yisimayi, A.; Huang, W.; Li, Q.; Wang, P.; An, R.; et al. Omicron escapes the majority of existing SARS-CoV-2 neutralizing antibodies. Nature 2022, 602, 657–663. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, M.; Sharma, A.R.; Dhama, K.; Agoramoorthy, G.; Chakraborty, C. Omicron variant (b. 1.1. 529) of SARS-CoV-2: Understanding mutations in the genome, s-glycoprotein, and antibody-binding regions. GeroScience 2022, 44, 619–637. [Google Scholar] [CrossRef] [PubMed]
- Mannar, D.; Saville, J.W.; Zhu, X.; Srivastava, S.S.; Berezuk, A.M.; Tuttle, K.S.; Marquez, A.C.; Sekirov, I.; Subramaniam, S. SARS-CoV-2 omicron variant: Antibody evasion and cryo-em structure of spike protein–ace2 complex. Science 2022, 375, 760–764. [Google Scholar]
- Parums, D.V. The xbb. 1.5 (‘kraken’) subvariant of omicron SARS-CoV-2 and its rapid global spread. Med. Sci. Monit. 2023, 29, e939580-1. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Narayan, R.; Subramanian, A.; Xie, X. Gene expression inference with deep learning. Bioinformatics 2016, 32, 1832–1839. [Google Scholar] [CrossRef]
- Chen, H.; Engkvist, O.; Wang, Y.; Olivecrona, M.; Blaschke, T. The rise of deep learning in drug discovery. Drug Discov. Today 2018, 23, 1241–1250. [Google Scholar]
- Bakator, M.; Radosav, D. Deep learning and medical diagnosis: A review of literature. Multimodal Technol. Interact. 2018, 2, 47. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar]
- Xiong, J.; Xiong, Z.; Chen, K.; Jiang, H.; Zheng, M. Graph neural networks for automated de novo drug design. Drug Discov. Today 2021, 26, 1382–1393. [Google Scholar] [CrossRef]
- Yang, F.; Fan, K.; Song, D.; Lin, H. Graph-based prediction of protein–protein interactions with attributed signed graph embedding. BMC Bioinform. 2020, 21, 323. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Liang, L.; Liu, L.; Tang, M.-J. Graph neural networks and their current applications in bioinformatics. Front. Genet. 2021, 12, 690049. [Google Scholar] [CrossRef] [PubMed]
- Mercatelli, D.; Scalambra, L.; Triboli, L.; Ray, F.; Giorgi, F.M. Gene regulatory network inference resources: A practical overview. Biochim. Biophys. Acta (BBA)-Gene Regul. Mech. 2020, 1863, 194430. [Google Scholar]
- Cai, H.; Zheng, V.W.; Chang, K.C.-C. A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Trans. Knowl. Data Eng. 2018, 30, 1616–1637. [Google Scholar] [CrossRef]
- Xu, M. Understanding graph embedding methods and their applications. SIAM Rev. 2021, 63, 825–853. [Google Scholar] [CrossRef]
- Kotary, J.; Fioretto, F.; Hentenryck, P.V.; Wilder, B. End-to-end constrained optimization learning: A survey. arXiv 2021, arXiv:2103.16378. [Google Scholar]
- Wang, X.; Bo, D.; Shi, C.; Fan, S.; Ye, Y.; Philip, S.Y. A survey on heterogeneous graph embedding: Methods, techniques, applications and sources. IEEE Trans. Big Data 2022, 9, 415–436. [Google Scholar] [CrossRef]
- Muzio, G.; O’Bray, L.; Borgwardt, K. Biological network analysis with deep learning. Briefings Bioinform. 2021, 22, 1515–1530. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, L.; Zhong, F.; Wang, D.; Jiang, J.; Zhang, S.; Jiang, H.; Zheng, M.; Li, X. Graph neural network approaches for drug-target interactions. Curr. Opin. Struct. Biol. 2022, 73, 102327. [Google Scholar] [CrossRef]
- Ata, S.K.; Wu, M.; Fang, Y.; Ou-Yang, L.; Kwoh, C.K.; Li, X. Recent advances in network-based methods for disease gene prediction. Briefings Bioinform. 2021, 22, bbaa303. [Google Scholar] [CrossRef]
- Wieder, O.; Kohlbacher, S.; Kuenemann, M.; Garon, A.; Ducrot, P.; Seidel, T.; Langer, T. A compact review of molecular property prediction with graph neural networks. Drug Discov. Today Technol. 2020, 37, 1–12. [Google Scholar] [CrossRef] [PubMed]
- World. Statement on the Fifteenth Meeting of the IHR (2005) Emergency Committee on the COVID-19 Pandemic. May 2023. Available online: https://www.who.int/news/item/05-05-2023-statement-on-the-fifteenth-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-coronavirus-disease-(COVID-19)-pandemic (accessed on 10 July 2023).
- Feng, R.; Xie, Y.; Lai, M.; Chen, D.Z.; Cao, J.; Wu, J. Agmi: Attention-guided multi-omics integration for drug response prediction with graph neural networks. In Proceedings of the 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Houston, TX, USA, 9–12 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1295–1298. [Google Scholar]
- Zhu, Y.; Qian, P.; Zhao, Z.; Zeng, Z. Deep feature fusion via graph convolutional network for intracranial artery labeling. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, Scotland, 11–15 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 467–470. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Representation learning on graphs: Methods and applications. arXiv 2017, arXiv:1709.05584. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems; Burges, C.J., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2013; Volume 26. [Google Scholar]
- Le, Q.; Mikolov, T. Distributed representations of sentences and documents. In Proceedings of the 31st International Conference on Machine Learning, PMLR, Bejing, China, 22–24 June 2014; Xing,, E.P., Jebara, T., Eds.; Volume 32 of Proceedings of Machine Learning Research. pp. 1188–1196. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Bojanowski, P.; Grave, E.; Joulin, A.; Mikolov, T. Enriching word vectors with subword information. Trans. Assoc. Comput. Linguist. 2017, 5, 135–146. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, W.; Yu, K. Bidirectional lstm-crf models for sequence tagging. arXiv 2015, arXiv:1508.01991. [Google Scholar]
- Peters, M.E.; Neumann, M.; Iyyer, M.; Gardner, M.; Clark, C.; Lee, K.; Zettlemoyer, L. Deep contextualized word representations. arXiv 2018, arXiv:1802.05365. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Kim, Y.; Denton, C.; Hoang, L.; Rush, A.M. Structured attention networks. arXiv 2017, arXiv:1702.00887. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Gehring, J.; Auli, M.; Grangier, D.; Yarats, D.; Dauphin, Y.N. Convolutional sequence to sequence learning. In Proceedings of the 34th International Conference on Machine Learning, PMLR, International Convention Centre, Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; Volume 70 of Proceedings of Machine Learning Research. pp. 1243–1252. [Google Scholar]
- Sukhbaatar, S.; Szlam, A.; Weston, J.; Fergus, R. End-to-end memory networks. In Advances in Neural Information Processing Systems; Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28. [Google Scholar]
- Miller, A.; Fisch, A.; Dodge, J.; Karimi, A.-H.; Bordes, A.; Weston, J. Key-value memory networks for directly reading documents. arXiv 2016, arXiv:1606.03126. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Luong, M.-T.; Pham, H.; Manning, C.D. Effective approaches to attention-based neural machine translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Ahmed, A.; Shervashidze, N.; Narayanamurthy, S.; Josifovski, V.; Smola, A.J. Distributed large-scale natural graph factorization. In Proceedings of the 22nd International Conference on World Wide Web, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 37–48. [Google Scholar]
- Tang, J.; Qu, M.; Mei, Q. Pte: Predictive text embedding through large-scale heterogeneous text networks. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1165–1174. [Google Scholar]
- Cao, S.; Lu, W.; Xu, Q. Grarep: Learning graph representations with global structural information. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, Melbourne, Australia, 19–23 October 2015; pp. 891–900. [Google Scholar]
- Ou, M.; Cui, P.; Pei, J.; Zhang, Z.; Zhu, W. Asymmetric transitivity preserving graph embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1105–1114. [Google Scholar]
- Shi, Y.; Zhu, Q.; Guo, F.; Zhang, C.; Han, J. Easing embedding learning by comprehensive transcription of heterogeneous information networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2190–2199. [Google Scholar]
- Shi, C.; Hu, B.; Zhao, W.X.; Philip, S.Y. Heterogeneous information network embedding for recommendation. IEEE Trans. Knowl. Data Eng. 2018, 31, 357–370. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; de Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Zhang, Z.; Zha, H. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. SIAM J. Sci. Comput. 2004, 26, 313–338. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Donoho, D.L.; Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proc. Natl. Acad. Sci. USA 2003, 100, 5591–5596. [Google Scholar] [CrossRef]
- der Maaten, L.V.; Hinton, G. Visualizing data using t-sne. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Perozzi, B.; Kulkarni, V.; Chen, H.; Skiena, S. Do not walk, skip! online learning of multi-scale network embeddings. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2017, Sydney, Australia, 31 July–3 August 2017; pp. 258–265. [Google Scholar]
- Ribeiro, L.F.R.; Saverese, P.H.P.; Figueiredo, D.R. struc2vec: Learning node representations from structural identity. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 385–394. [Google Scholar]
- Dong, Y.; Chawla, N.V.; Swami, A. metapath2vec: Scalable representation learning for heterogeneous networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 135–144. [Google Scholar]
- Fu, T.; Lee, W.-C.; Lei, Z. Hin2vec: Explore meta-paths in heterogeneous information networks for representation learning. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 1797–1806. [Google Scholar]
- Cen, Y.; Zou, X.; Zhang, J.; Yang, H.; Zhou, J.; Tang, J. Representation learning for attributed multiplex heterogeneous network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1358–1368. [Google Scholar]
- Wang, D.; Cui, P.; Zhu, W. Structural deep network embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1225–1234. [Google Scholar]
- Cao, S.; Lu, W.; Xu, Q. Deep neural networks for learning graph representations. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Chang, S.; Han, W.; Tang, J.; Qi, G.-J.; Aggarwal, C.C.; Huang, T.S. Heterogeneous network embedding via deep architectures. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; pp. 119–128. [Google Scholar]
- Zhang, J.; Xia, C.; Zhang, C.; Cui, L.; Fu, Y.; Philip, S.Y. Bl-mne: Emerging heterogeneous social network embedding through broad learning with aligned autoencoder. In 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 605–914. [Google Scholar]
- Yang, C.; Liu, Z.; Zhao, D.; Sun, M.; Chang, E.Y. Network representation learning with rich text information. IJCAI 2015, 2015, 2111–2117. [Google Scholar]
- Huang, X.; Li, J.; Hu, X. Label informed attributed network embedding. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, Cambridge, UK, 6–10 February 2017; pp. 731–739. [Google Scholar]
- Liao, L.; He, X.; Zhang, H.; Chua, T.-S. Attributed social network embedding. IEEE Trans. Knowl. Data Eng. 2018, 30, 2257–2270. [Google Scholar] [CrossRef]
- Gao, H.; Huang, H. Deep attributed network embedding. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI), Stockholm, Sweden, 13–19 July 2018. [Google Scholar]
- Zhang, Z.; Yang, H.; Bu, J.; Zhou, S.; Yu, P.; Zhang, J.; Ester, M.; Wang, C. Anrl: Attributed network representation learning via deep neural networks. IJCAI 2018, 18, 3155–3161. [Google Scholar]
- Iuchi, H.; Matsutani, T.; Yamada, K.; Iwano, N.; Sumi, S.; Hosoda, S.; Zhao, S.; Fukunaga, T.; Hamada, M. Representation learning applications in biological sequence analysis. Comput. Struct. Biotechnol. J. 2021, 19, 3198–3208. [Google Scholar] [CrossRef]
- Yi, H.-C.; You, Z.-H.; Huang, D.-S.; Kwoh, C.K. Graph representation learning in bioinformatics: Trends, methods and applications. Briefings Bioinform. 2022, 23, bbab340. [Google Scholar] [CrossRef] [PubMed]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Zhuang, C.; Ma, Q. Dual graph convolutional networks for graph-based semi-supervised classification. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 499–508. [Google Scholar]
- Li, R.; Wang, S.; Zhu, F.; Huang, J. Adaptive graph convolutional neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Gao, H.; Wang, Z.; Ji, S. Large-scale learnable graph convolutional networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1416–1424. [Google Scholar]
- Chen, J.; Ma, T.; Xiao, C. Fastgcn: Fast learning with graph convolutional networks via importance sampling. arXiv 2018, arXiv:1801.10247. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Gasteiger, J.; Bojchevski, A.; Günnemann, S. Predict then propagate: Graph neural networks meet personalized pagerank. arXiv 2018, arXiv:1810.05997. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. Stat 2017, 1050, 10–21. [Google Scholar]
- Thekumparampil, K.K.; Wang, C.; Oh, S.; Li, L.-J. Attention-based graph neural network for semi-supervised learning. arXiv 2018, arXiv:1803.03735. [Google Scholar]
- Sankar, A.; Wu, Y.; Gou, L.; Zhang, W.; Yang, H. Dynamic graph representation learning via self-attention networks. arXiv 2018, arXiv:1812.09430. [Google Scholar]
- Zhang, J.; Shi, X.; Xie, J.; Ma, H.; King, I.; Yeung, D.-Y. Gaan: Gated attention networks for learning on large and spatiotemporal graphs. arXiv 2018, arXiv:1803.07294. [Google Scholar]
- Wang, X.; Ji, H.; Shi, C.; Wang, B.; Ye, Y.; Cui, P.; Yu, P.S. Heterogeneous graph attention network. In Proceedings of the The World Wide Web Conference, WWW ’19, San Francisco, CA, USA, 13–17 May 2019; pp. 2022–2032. [Google Scholar]
- Wang, G.; Ying, R.; Huang, J.; Leskovec, J. Multi-hop attention graph neural network. arXiv 2020, arXiv:2009.14332. [Google Scholar]
- Xu, H.; Zhang, S.; Jiang, B.; Tang, J. Graph context-attention network via low and high order aggregation. Neurocomputing 2023, 536, 152–163. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Simonovsky, M.; Komodakis, N. Graphvae: Towards generation of small graphs using variational autoencoders. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2018: 27th International Conference on Artificial N. Networks, Rhodes, Greece, 4–7 October 2018; Proceedings, Part I 27. Springer: Berlin/Heidelberg, Germany, 2018; pp. 412–422. [Google Scholar]
- Grover, A.; Zweig, A.; Ermon, S. Graphite: Iterative generative modeling of graphs. In Proceedings of the 36th International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; Chaudhuri, K., Salakhutdinov, R., Eds.; Volume 97 of Proceedings of Machine Learning Research. pp. 2434–2444. [Google Scholar]
- Bojchevski, A.; Günnemann, S. Deep gaussian embedding of graphs: Unsupervised inductive learning via ranking. arXiv 2017, arXiv:1707.03815. [Google Scholar]
- Zhu, D.; Cui, P.; Wang, D.; Zhu, W. Deep variational network embedding in wasserstein space. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2827–2836. [Google Scholar]
- Velickovic, P.; Fedus, W.; Hamilton, W.L.; Liò, P.; Bengio, Y.; Hjelm, R.D. Deep graph infomax. ICLR (Poster) 2019, 2, 4. [Google Scholar]
- Sun, F.-Y.; Hoffmann, J.; Verma, V.; Tang, J. Infograph: Unsupervised and semi-supervised graph-level representation learning via mutual information maximization. arXiv 2019, arXiv:1908.01000. [Google Scholar]
- Li, J.; Wu, R.; Sun, W.; Chen, L.; Tian, S.; Zhu, L.; Meng, C.; Zheng, Z.; Wang, W. Maskgae: Masked graph modeling meets graph autoencoders. arXiv 2022, arXiv:2205.10053. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Wang, J.; Zhao, M.; Zhang, W.; Zhang, F.; Xie, X.; Guo, M. Graphgan: Graph representation learning with generative adversarial nets. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Pan, S.; Hu, R.; Fung, S.; Long, G.; Jiang, J.; Zhang, C. Learning graph embedding with adversarial training methods. IEEE Trans. Cybern. 2019, 50, 2475–2487. [Google Scholar] [CrossRef] [PubMed]
- Dai, Q.; Li, Q.; Tang, J.; Wang, D. Adversarial network embedding. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Yu, W.; Zheng, C.; Cheng, W.; Aggarwal, C.C.; Song, D.; Zong, B.; Chen, H.; Wang, W. Learning deep network representations with adversarially regularized autoencoders. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2663–2671. [Google Scholar]
- Bojchevski, A.; Shchur, O.; Zügner, D.; Günnemann, S. NetGAN: Generating graphs via random walks. In Proceedings of the 35th International Conference on Machine Learning, PMLR, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; Volume 80 of Proceedings of Machine Learning Research. pp. 610–619. [Google Scholar]
- Cao, N.D.; Kipf, T. Molgan: An implicit generative model for small molecular graphs. arXiv 2018, arXiv:1805.11973. [Google Scholar]
- Ying, Z.; You, J.; Morris, C.; Ren, X.; Hamilton, W.; Leskovec, J. Hierarchical graph representation learning with differentiable pooling. Adv. Neural Inf. Process. Syst. 2018, 31, 1–11. [Google Scholar]
- Zhang, M.; Cui, Z.; Neumann, M.; Chen, Y. An end-to-end deep learning architecture for graph classification. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Lee, J.; Lee, I.; Kang, J. Self-attention graph pooling. In Proceedings of the International Conference on Machine Learning; PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 3734–3743. [Google Scholar]
- Diehl, F.; Brunner, T.; Le, M.T.; Knoll, A. Towards graph pooling by edge contraction. In ICML 2019 Workshop on Learning and Reasoning with Graph-Structured Data; Long Beach Convention Center: Long Beach, CA, USA, 2019. [Google Scholar]
- Corso, G.; Ying, Z.; Pándy, M.; Veličković, P.; Leskovec, J.; Liò, P. Neural distance embeddings for biological sequences. Adv. Neural Inf. Process. Syst. 2021, 34, 18539–18551. [Google Scholar]
- Xia, J.; Wu, L.; Chen, J.; Hu, B.; Li, S.Z. Simgrace: A simple framework for graph contrastive learning without data augmentation. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 1070–1079. [Google Scholar]
- Tang, C.; Zheng, X.; Zhang, W.; Liu, X.; Zhu, X.; Zhu, E. Unsupervised feature selection via multiple graph fusion and feature weight learning. Sci. China Inf. Sci. 2023, 66, 1–17. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, L.; Chen, G.; Zhang, K.; U, P.X.; Yang, Y. Feature expansion for graph neural networks. arXiv 2023, arXiv:2305.06142. [Google Scholar]
- Ton, A.-T.; Gentile, F.; Hsing, M.; Ban, F.; Cherkasov, A. Rapid identification of potential inhibitors of SARS-CoV-2 main protease by deep docking of 1.3 billion compounds. Mol. Inform. 2020, 39, 2000028. [Google Scholar] [CrossRef]
- Saravanan, K.M.; Zhang, H.; Hossain, M.T.; Reza, M.S.; Wei, Y. Deep learning-based drug screening for COVID-19 and case studies. In In Silico Modeling of Drugs against Coronaviruses: Computational Tools and Protocols; Humana: New York, NY, USA, 2021; pp. 631–660. [Google Scholar]
- Zhou, D.; Peng, S.; Wei, D.-Q.; Zhong, W.; Dou, Y.; Xie, X. Lunar: Drug screening for novel coronavirus based on representation learning graph convolutional network. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 1290–1298. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, M.; Luo, Y.; Xu, Z.; Xie, Y.; Wang, L.; Cai, L.; Qi, Q.; Yuan, Z.; Yang, T.; et al. Advanced graph and sequence neural networks for molecular property prediction and drug discovery. Bioinformatics 2022, 38, 2579–2586. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-S.; Liu, X.; Lu, L.; Hua, X.-S.; Chi, Y.; Xia, K. Multiphysical graph neural network (mp-gnn) for COVID-19 drug design. Briefings Bioinform. 2022, 23, bbac231. [Google Scholar] [CrossRef] [PubMed]
- Pi, J.; Jiao, P.; Zhang, Y.; Li, J. Mdgnn: Microbial drug prediction based on heterogeneous multi-attention graph neural network. Front. Microbiol. 2022, 13, 819046. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Tian, T.; Huang, S.; Wan, F.; Li, J.; Li, S.; Yang, H.; Hong, L.; Wu, N.; Yuan, E.; et al. A data-driven drug repositioning framework discovered a potential therapeutic agent targeting COVID-19. bioRxiv 2020. [Google Scholar] [CrossRef]
- Mall, R.; Elbasir, A.; Meer, H.A.; Chawla, S.; Ullah, E. Data-driven drug repurposing for COVID-19. ChemRxiv 2020. [Google Scholar] [CrossRef]
- Hooshmand, S.A.; Ghobadi, M.Z.; Hooshmand, S.E.; Jamalkandi, S.A.; Alavi, S.M.; Masoudi-Nejad, A. A multimodal deep learning-based drug repurposing approach for treatment of COVID-19. Mol. Divers. 2021, 25, 1717–1730. [Google Scholar] [CrossRef]
- Aghdam, R.; Habibi, M.; Taheri, G. Using informative features in machine learning based method for COVID-19 drug repurposing. J. Cheminform. 2021, 13, 70. [Google Scholar] [CrossRef]
- Hsieh, K.; Wang, Y.; Chen, L.; Zhao, Z.; Savitz, S.; Jiang, X.; Tang, J.; Kim, Y. Drug repurposing for COVID-19 using graph neural network with genetic, mechanistic, and epidemiological validation. Res. Sq. 2020, preprint. [Google Scholar]
- Pham, T.-H.; Qiu, Y.; Zeng, J.; Xie, L.; Zhang, P. A deep learning framework for high-throughput mechanism-driven phenotype compound screening and its application to COVID-19 drug repurposing. Nat. Mach. Intell. 2021, 3, 247–257. [Google Scholar] [CrossRef]
- Hsieh, K.; Wang, Y.; Chen, L.; Zhao, Z.; Savitz, S.; Jiang, X.; Tang, J.; Kim, Y. Drug repurposing for COVID-19 using graph neural network and harmonizing multiple evidence. Sci. Rep. 2021, 11, 23179. [Google Scholar] [CrossRef] [PubMed]
- Doshi, S.; Chepuri, S.P. A computational approach to drug repurposing using graph neural networks. Comput. Biol. Med. 2022, 150, 105992. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; You, Z.; Wang, L.; Hu, L.; Wong, L.; Ji, B.; Zhao, B. Sane: A sequence combined attentive network embedding model for COVID-19 drug repositioning. Appl. Soft Comput. 2021, 111, 107831. [Google Scholar] [CrossRef]
- Su, X.; Hu, L.; You, Z.; Hu, P.; Wang, L.; Zhao, B. A deep learning method for repurposing antiviral drugs against new viruses via multi-view nonnegative matrix factorization and its application to SARS-CoV-2. Briefings Bioinform. 2022, 23, bbab526. [Google Scholar] [CrossRef]
- Beck, B.R.; Shin, B.; Choi, Y.; Park, S.; Kang, K. Predicting commercially available antiviral drugs that may act on the novel coronavirus (SARS-CoV-2) through a drug-target interaction deep learning model. Comput. Struct. Biotechnol. J. 2020, 18, 784–790. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Chatterjee, P.; Halder, A.K.; Nasipuri, M.; Basu, S.; Plewczynski, D. Ml-dtd: Machine learning-based drug target discovery for the potential treatment of COVID-19. Vaccines 2022, 10, 1643. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, Q.; Liu, Y.; Du, Z.; Jin, R. Drug repositioning of COVID-19 based on mixed graph network and ion channel. Math. Biosci. Eng. 2022, 19, 3269–3284. [Google Scholar] [CrossRef]
- Zhang, P.; Wei, Z.; Che, C.; Jin, B. Deepmgt-dti: Transformer network incorporating multilayer graph information for drug–target interaction prediction. Comput. Biol. Med. 2022, 142, 105214. [Google Scholar] [CrossRef]
- Li, G.; Sun, W.; Xu, J.; Hu, L.; Zhang, W.; Zhang, P. Ga-ens: A novel drug–target interactions prediction method by incorporating prior knowledge graph into dual wasserstein generative adversarial network with gradient penalty. Appl. Soft Comput. 2023, 139, 110151. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, G.; Yang, H.; Zhong, W.; Chen, C.Y. Dsil-ddi: A domain-invariant substructure interaction learning for generalizable drug–drug interaction prediction. In IEEE Transactions on Neural Networks and Learning Systems; IEEE: Piscataway, NJ, USA, 2023; pp. 1–9. [Google Scholar]
- Sefidgarhoseini, S.; Safari, L.; Mohammady, Z. Drug-Drug Interaction Extraction Using Transformer-Based Ensemble Model. Res. Sq. 2023, preprint. [Google Scholar] [CrossRef]
- Ren, Z.-H.; You, Z.-H.; Yu, C.-Q.; Li, L.-P.; Guan, Y.-J.; Guo, L.-X.; Pan, J. A biomedical knowledge graph-based method for drug–drug interactions prediction through combining local and global features with deep neural networks. Briefings Bioinform. 2022, 23, bbac363. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ma, T.; Yang, X.; Wang, J.; Song, B.; Zeng, X. Muffin: Multi-scale feature fusion for drug–drug interaction prediction. Bioinformatics 2021, 37, 2651–2658. [Google Scholar] [CrossRef]
- Pan, D.; Quan, L.; Jin, Z.; Chen, T.; Wang, X.; Xie, J.; Wu, T.; Lyu, Q. Multisource attention-mechanism-based encoder–decoder model for predicting drug–drug interaction events. J. Chem. Inf. Model. 2022, 62, 6258–6270. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, S.; Shao, B.; Liu, T.-Y.; Zeng, X.; Wang, T. Multi-view substructure learning for drug-drug interaction prediction. arXiv 2022, arXiv:2203.14513. [Google Scholar]
- Ma, M.; Lei, X. A dual graph neural network for drug–drug interactions prediction based on molecular structure and interactions. PLoS Comput. Biol. 2023, 19, e1010812. [Google Scholar] [CrossRef] [PubMed]
- Dey, L.; Chakraborty, S.; Mukhopadhyay, A. Machine learning techniques for sequence-based prediction of viral–host interactions between SARS-CoV-2 and human proteins. Biomed. J. 2020, 43, 438–450. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Chen, F.; Liu, H.; Hong, P. Network-based virus–host interaction prediction with application to SARS-CoV-2. Patterns 2021, 2, 100242. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Ding, Y.; Tang, J.; Guo, F. Inferring human microbe–drug associations via multiple kernel fusion on graph neural network. Knowl.-Based Syst. 2022, 238, 107888. [Google Scholar] [CrossRef]
- Das, B.; Kutsal, M.; Das, R. A geometric deep learning model for display and prediction of potential drug-virus interactions against SARS-CoV-2. Chemom. Intell. Lab. Syst. 2022, 229, 104640. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. Predictions for COVID-19 with deep learning models of lstm, gru and bi-lstm. Chaos Solitons Fractals 2020, 140, 110212. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Paki, R. Prediction of COVID-19 confirmed cases combining deep learning methods and bayesian optimization. Chaos Solitons Fractals 2021, 142, 110511. [Google Scholar] [CrossRef] [PubMed]
- Sinha, T.; Chowdhury, T.; Shaw, R.N.; Ghosh, A. Analysis and prediction of COVID-19 confirmed cases using deep learning models: A comparative study. In Advanced Computing and Intelligent Technologies: Proceedings of the ICACIT 2021, New Delhi, India, 20–21 March 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 207–218. [Google Scholar]
- Gao, J.; Sharma, R.; Qian, C.; Glass, L.M.; Spaeder, J.; Romberg, J.; Sun, J.; Xiao, C. Stan: Spatio-temporal attention network for pandemic prediction using real-world evidence. J. Am. Med. Inform. Assoc. 2021, 28, 733–743. [Google Scholar] [CrossRef] [PubMed]
- Ntemi, M.; Sarridis, I.; Kotropoulos, C. An autoregressive graph convolutional long short-term memory hybrid neural network for accurate prediction of COVID-19 cases. IEEE Trans. Comput. Soc. Syst. 2022, 10, 724–735. [Google Scholar] [CrossRef]
- Li, D.; Ren, X.; Su, Y. Predicting COVID-19 using lioness optimization algorithm and graph convolution network. Soft Comput. 2023, 27, 5437–5501. [Google Scholar] [CrossRef]
- Skianis, K.; Nikolentzos, G.; Gallix, B.; Thiebaut, R.; Exarchakis, G. Predicting COVID-19 positivity and hospitalization with multi-scale graph neural networks. Sci. Rep. 2023, 13, 5235. [Google Scholar] [CrossRef]
- Malki, Z.; Atlam, E.-S.; Ewis, A.; Dagnew, G.; Ghoneim, O.A.; Mohamed, A.A.; Abdel-Daim, M.M.; Gad, I. The COVID-19 pandemic: Prediction study based on machine learning models. Environ. Sci. Pollut. Res. 2021, 28, 40496–40506. [Google Scholar] [CrossRef]
- Liu, D.; Ding, W.; Dong, Z.S.; Pedrycz, W. Optimizing deep neural networks to predict the effect of social distancing on COVID-19 spread. Comput. Ind. Eng. 2022, 166, 107970. [Google Scholar] [CrossRef]
- Ayris, D.; Imtiaz, M.; Horbury, K.; Williams, B.; Blackney, M.; See, C.S.H.; Shah, S.A.A. Novel deep learning approach to model and predict the spread of COVID-19. Intell. Syst. Appl. 2022, 14, 200068. [Google Scholar] [CrossRef]
- Gatta, V.L.; Moscato, V.; Postiglione, M.; Sperli, G. An epidemiological neural network exploiting dynamic graph structured data applied to the COVID-19 outbreak. IEEE Trans. Big Data 2020, 7, 45–55. [Google Scholar] [CrossRef]
- Hy, T.S.; Nguyen, V.B.; Tran-Thanh, L.; Kondor, R. Temporal multiresolution graph neural networks for epidemic prediction. In Workshop on Healthcare AI and COVID-19; PMLR: Baltimore, MD, USA, 22 July 2022; pp. 21–32. [Google Scholar]
- Geng, R.; Gao, Y.; Zhang, H.; Zu, J. Analysis of the spatio-temporal dynamics of COVID-19 in massachusetts via spectral graph wavelet theory. IEEE Trans. Signal Inf. Process. Over Netw. 2022, 8, 670–683. [Google Scholar] [CrossRef]
- Shan, B.; Yuan, X.; Ni, W.; Wang, X.; Liu, R.P. Novel graph topology learning for spatio-temporal analysis of COVID-19 spread. IEEE J. Biomed. Health Inform. 2023, 27, 2693–2704. [Google Scholar] [CrossRef]
- Izquierdo, J.L.; Ancochea, J.; Savana COVID-19 Research Group; Soriano, J.B. Clinical characteristics and prognostic factors for intensive care unit admission of patients with COVID-19: Retrospective study using machine learning and natural language processing. J. Med. Internet Res. 2020, 22, e21801. [Google Scholar] [CrossRef]
- Landi, I.; Glicksberg, B.S.; Lee, H.-C.; Cherng, S.; Landi, G.; Danieletto, M.; Dudley, J.T.; Furlanello, C.; Miotto, R. Deep representation learning of electronic health records to unlock patient stratification at scale. NPJ Digit. Med. 2020, 3, 96. [Google Scholar] [CrossRef] [PubMed]
- Wagner, T.; Shweta, F.N.U.; Murugadoss, K.; Awasthi, S.; Venkatakrishnan, A.J.; Bade, S.; Puranik, A.; Kang, M.; Pickering, B.W.; O’Horo, J.C.; et al. Augmented curation of clinical notes from a massive ehr system reveals symptoms of impending COVID-19 diagnosis. eLife 2020, 9, e58227. [Google Scholar] [CrossRef]
- Wanyan, T.; Honarvar, H.; Jaladanki, S.K.; Zang, C.; Naik, N.; Somani, S.; Freitas, J.K.D.; Paranjpe, I.; Vaid, A.; Zhang, J.; et al. Contrastive learning improves critical event prediction in COVID-19 patients. Patterns 2021, 2, 100389. [Google Scholar] [CrossRef] [PubMed]
- Wanyan, T.; Lin, M.; Klang, E.; Menon, K.M.; Gulamali, F.F.; Azad, A.; Zhang, Y.; Ding, Y.; Wang, Z.; Wang, F.; et al. Supervised pretraining through contrastive categorical positive samplings to improve COVID-19 mortality prediction. In Proceedings of the 13th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Northbrook, IL, USA, 7–10 August 2022; pp. 1–9. [Google Scholar]
- Ma, L.; Ma, X.; Gao, J.; Jiao, X.; Yu, Z.; Zhang, C.; Ruan, W.; Wang, Y.; Tang, W.; Wang, J. Distilling knowledge from publicly available online emr data to emerging epidemic for prognosis. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 3558–3568. [Google Scholar]
- Wanyan, T.; Vaid, A.; Freitas, J.K.D.; Somani, S.; Miotto, R.; Nadkarni, G.N.; Azad, A.; Ding, Y.; Glicksberg, B.S. Relational learning improves prediction of mortality in COVID-19 in the intensive care unit. IEEE Trans. Big Data 2020, 7, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Gan, Z.; Shi, X.; Patwari, A.; Rush, E.; Bonzel, C.-L.; Panickan, V.A.; Hong, C.; Ho, Y.-L.; Cai, T.; et al. Multiview incomplete knowledge graph integration with application to cross-institutional ehr data harmonization. J. Biomed. Inform. 2022, 133, 104147. [Google Scholar] [CrossRef]
- Gao, J.; Yang, C.; Heintz, J.; Barrows, S.; Albers, E.; Stapel, M.; Warfield, S.; Cross, A.; Sun, J. Medml: Fusing medical knowledge and machine learning models for early pediatric COVID-19 hospitalization and severity prediction. Iscience 2022, 25, 104970. [Google Scholar] [CrossRef]
- Ding, K.; Xu, Z.; Tong, H.; Liu, H. Data augmentation for deep graph learning: A survey. ACM SIGKDD Explor. Newsl. 2022, 24, 61–77. [Google Scholar] [CrossRef]
- Wu, Z.; Balloccu, S.; Kumar, V.; Helaoui, R.; Recupero, D.R.; Riboni, D. Creation, analysis and evaluation of annomi, a dataset of expert-annotated counselling dialogues. Future Internet 2023, 15, 110. [Google Scholar] [CrossRef]
- Ching, T.; Himmelstein, D.S.; Beaulieu-Jones, B.K.; Kalinin, A.A.; Do, B.T.; Way, G.P.; Ferrero, E.; Agapow, P.-M.; Zietz, M.; Hoffman, M.M.; et al. Opportunities and obstacles for deep learning in biology and medicine. J. R. Soc. Interface 2018, 15, 20170387. [Google Scholar] [CrossRef] [PubMed]
- Miotto, R.; Wang, F.; Wang, S.; Jiang, X.; Dudley, J.T. Deep learning for healthcare: Review, opportunities and challenges. Briefings Bioinform. 2018, 19, 1236–1246. [Google Scholar] [CrossRef] [PubMed]
- Zampieri, G.; Vijayakumar, S.; Yaneske, E.; Angione, C. Machine and deep learning meet genome-scale metabolic modeling. PLoS Comput. Biol. 2019, 15, e1007084. [Google Scholar] [CrossRef] [PubMed]


| Dataset | Dataset Type | Available Online |
|---|---|---|
| COVID-19db | Drug and target data | http://www.biomedical-web.com/covid19db/home |
| DrugBank | Drug data | https://go.drugbank.com/ |
| Ensembl | SARS-CoV-2 genomic data | https://COVID-19.ensembl.org/index.html |
| ESC | SARS-CoV-2 immune escape variants | http://clingen.igib.res.in/esc |
| GISAID | Genetic sequence; Clinical and epidemiological data | https://gisaid.org/ |
| NCBI | COVID-19 virus sequence | https://www.ncbi.nlm.nih.gov/datasets/taxonomy/2697049/ |
| Our World In Data | COVID-19 cases | https://ourworldindata.org/covid-cases |
| PDB | Protein Data | https://www.rcsb.org/ |
| RCoV19 | COVID-19 information integration | https://ngdc.cncb.ac.cn/ncov/?lang=en |
| SCoV2-MD | Molecular dynamics of SARS-CoV-2 proteins | https://submission.gpcrmd.org/covid19/ |
| SCovid | Single cell transcriptomics | http://bio-annotation.cn/scovid |
| T-cell COVID-19 Atlas | CD8 and CD4 T-cell epitopes | https://t-cov.hse.ru |
| VarEPS | SARS-CoV-2 variations evaluation | https://nmdc.cn/ncovn |
| World Health Organization | COVID-19 situation reports | https://www.who.int/emergencies/diseases/novel-coronavirus-2019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Parvej, M.M.; Zhang, C.; Guo, S.; Zhang, J. Advances in the Development of Representation Learning and Its Innovations against COVID-19. COVID 2023, 3, 1389-1415. https://doi.org/10.3390/covid3090096
Li P, Parvej MM, Zhang C, Guo S, Zhang J. Advances in the Development of Representation Learning and Its Innovations against COVID-19. COVID. 2023; 3(9):1389-1415. https://doi.org/10.3390/covid3090096
Chicago/Turabian StyleLi, Peng, Mosharaf Md Parvej, Chenghao Zhang, Shufang Guo, and Jing Zhang. 2023. "Advances in the Development of Representation Learning and Its Innovations against COVID-19" COVID 3, no. 9: 1389-1415. https://doi.org/10.3390/covid3090096
APA StyleLi, P., Parvej, M. M., Zhang, C., Guo, S., & Zhang, J. (2023). Advances in the Development of Representation Learning and Its Innovations against COVID-19. COVID, 3(9), 1389-1415. https://doi.org/10.3390/covid3090096






