Government Restriction Efficiency on Curbing COVID-19 Pandemic Transmission in Western Europe
Abstract
1. Introduction
1.1. Global Impact and Effectiveness of COVID-19 Restrictions
1.2. Methodologies Used for Evaluating Nonpharmaceutical Interventions against COVID-19
1.3. Proposed Research
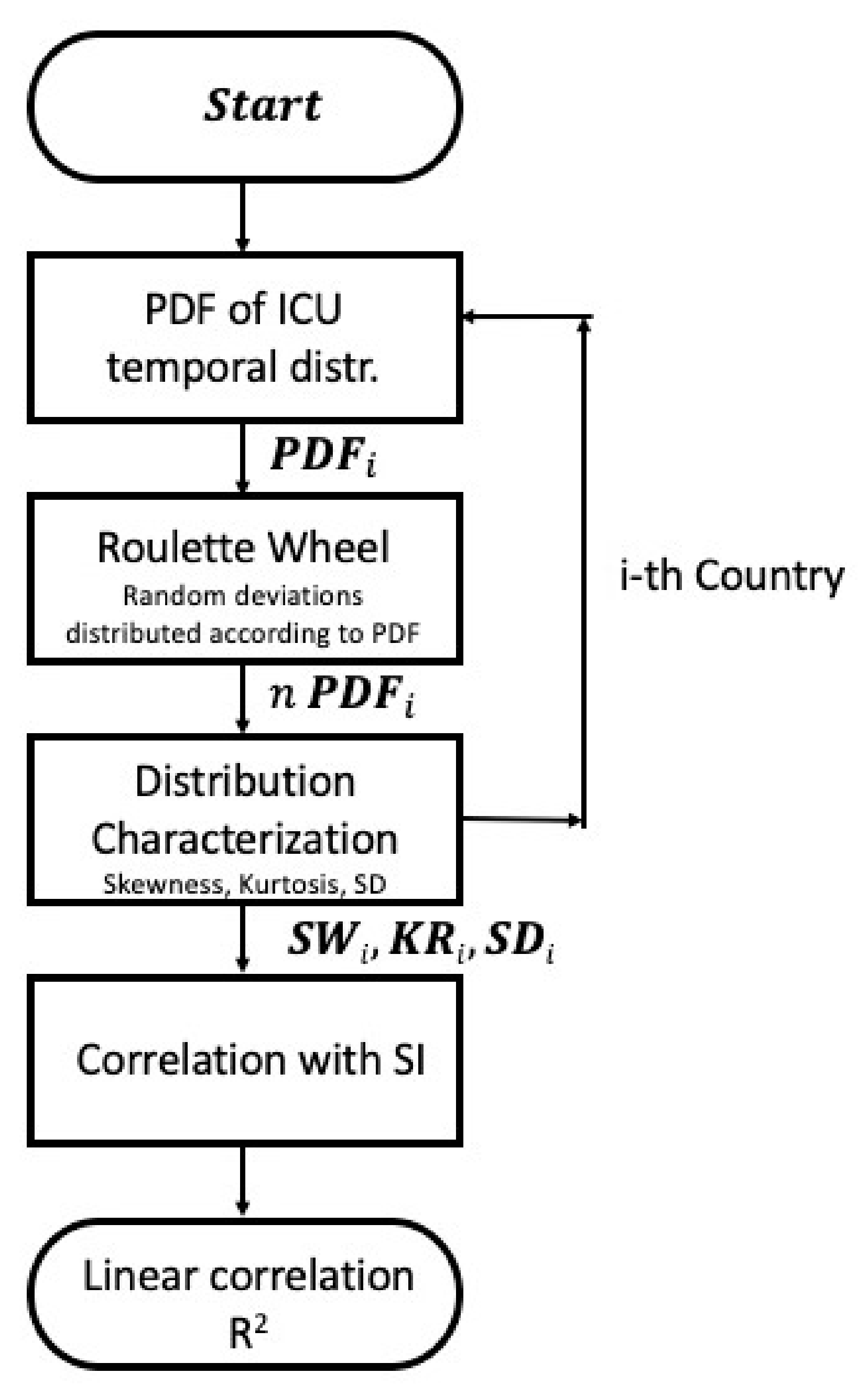
2. Methodology
2.1. Stringency Index
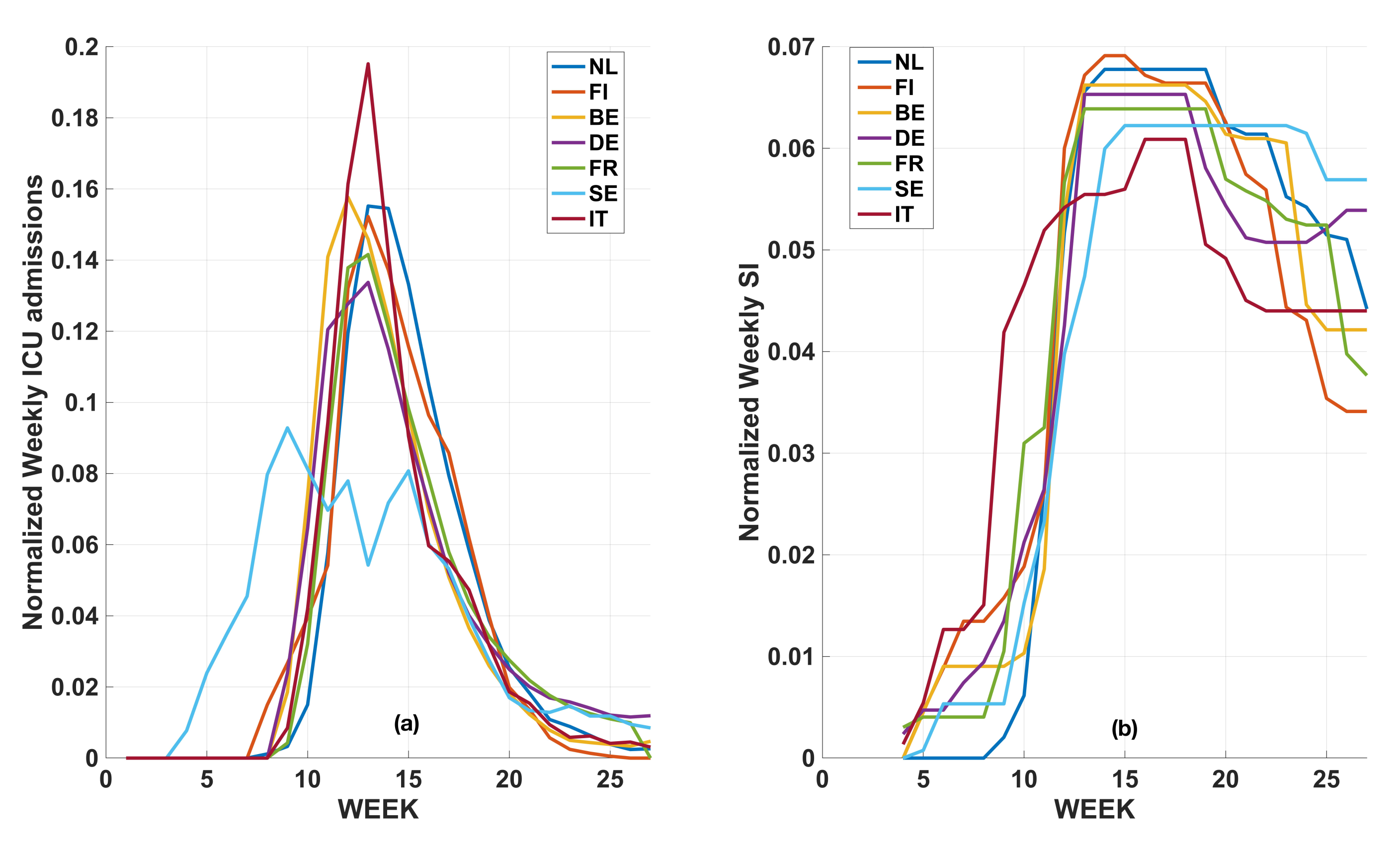
2.2. Temporal Distribution of Weekly ICU Admissions
2.3. Statistical Analysis
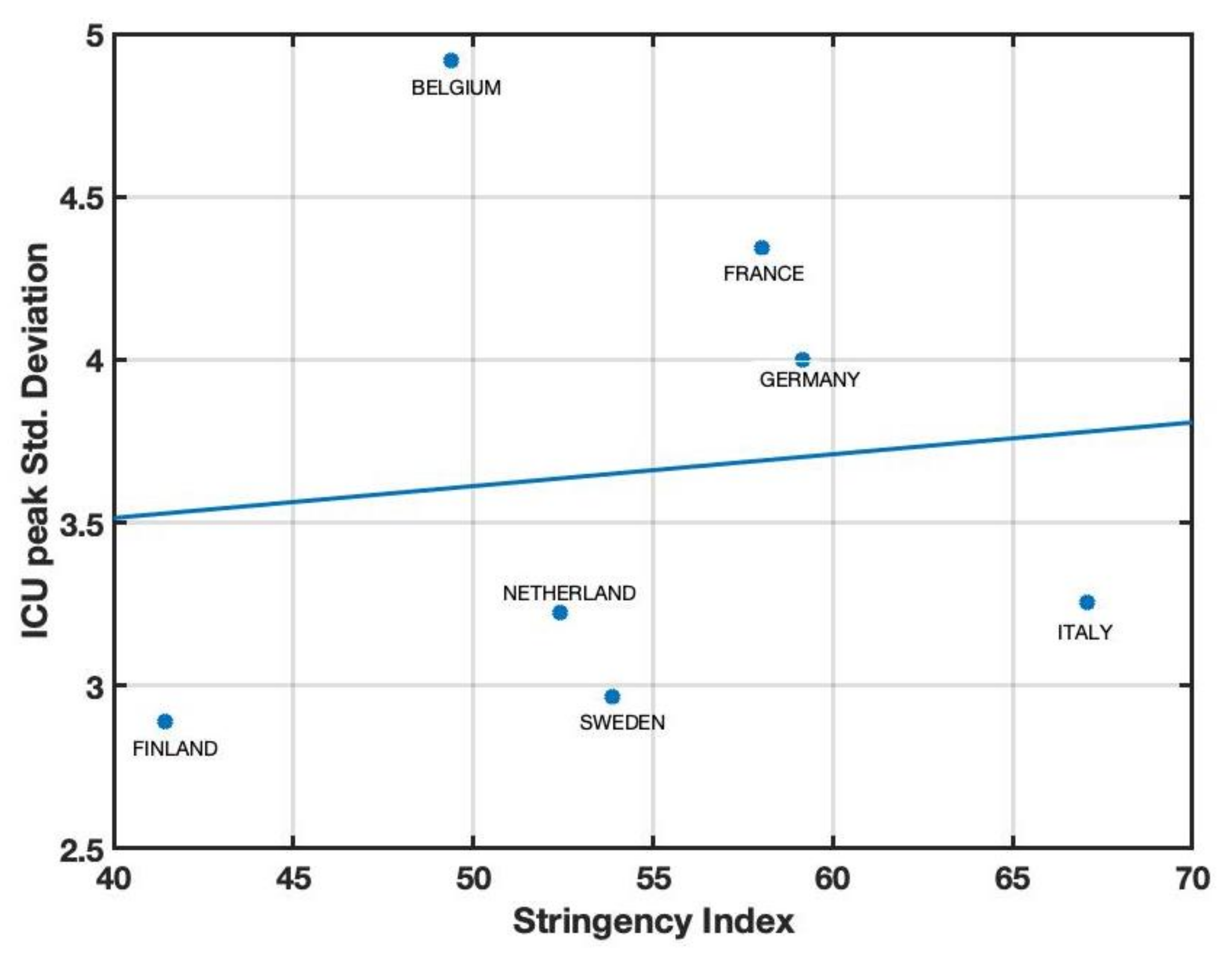
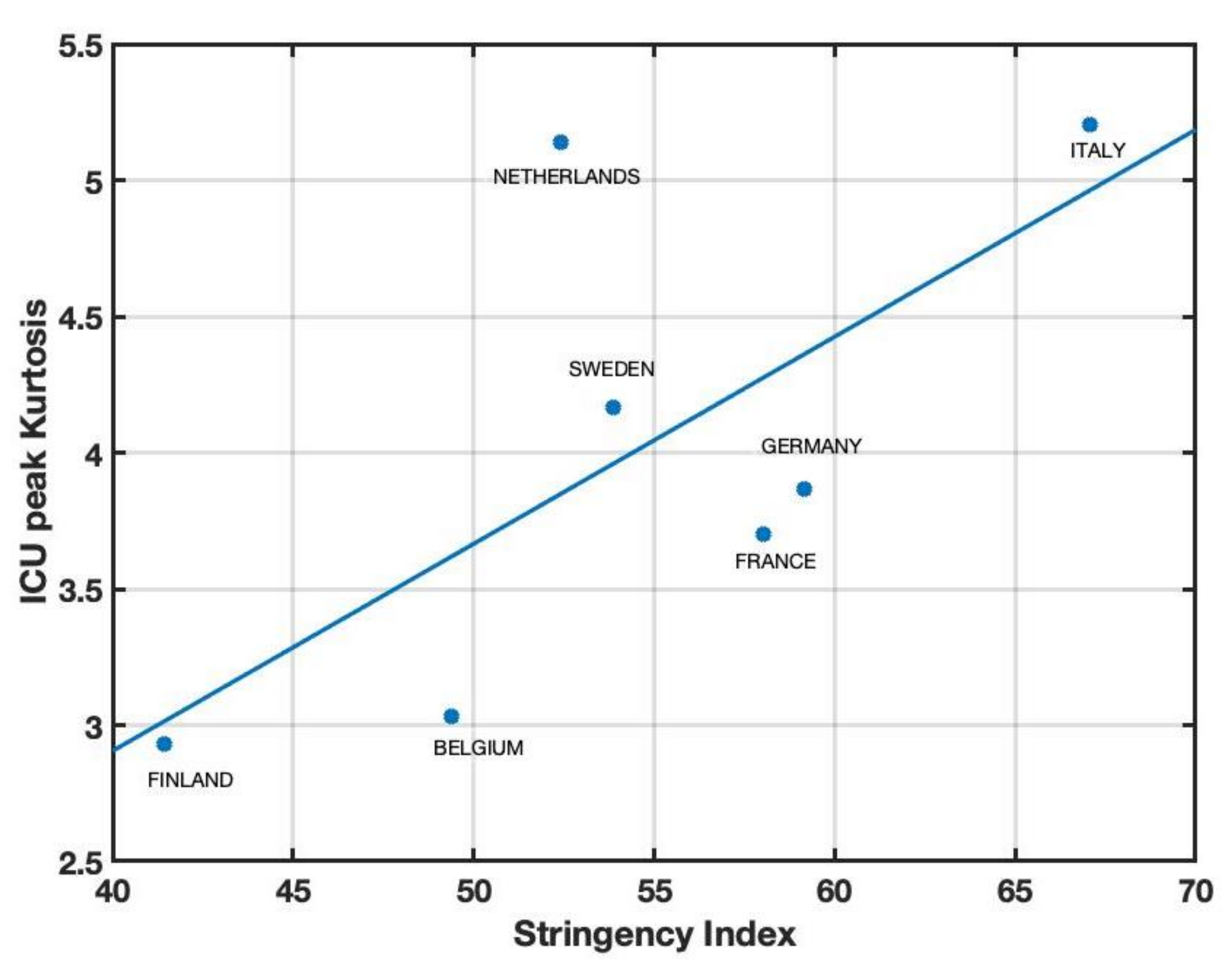
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lolli, S.; Chen, Y.C.; Wang, S.H.; Vivone, G. Impact of meteorological conditions and air pollution on COVID-19 pandemic transmission in Italy. Sci. Rep. 2020, 10, 16213. [Google Scholar] [CrossRef] [PubMed]
- Lolli, S.; Vivone, G. The role of tropospheric ozone in flagging COVID-19 pandemic transmission. Bull. Atmos. Sci. Technol. 2020, 1, 551–555. [Google Scholar] [CrossRef]
- Aslam, B.; Khalil, U.; Azam, U.; Maqsoom, A. A correlation study between weather and atmosphere with COVID-19 pandemic in Islamabad, Pakistan. Spat. Inf. Res. 2021, 29, 605–613. [Google Scholar] [CrossRef]
- Bar, S.; Parida, B.R.; Mandal, S.P.; Pandey, A.C.; Kumar, N.; Mishra, B. Impacts of COVID-19 lockdown on NO2 and PM2.5 levels in major urban cities of Europe and USA. Cities 2021, 117, 103308. [Google Scholar] [CrossRef] [PubMed]
- Bhawar, R.; Fadnavis, S.S.; Kumar, V.; Rahul, P.; Sinha, T.; Lolli, S. Radiative impacts of aerosols during COVID-19 lockdown period over the Indian region. Front. Environ. Sci. 2021, 9, 746090. [Google Scholar] [CrossRef]
- Meo, S.A.; Abukhalaf, A.A.; Sami, W.; Hoang, T.D. Effect of environmental pollution PM2.5, carbon monoxide, and ozone on the incidence and mortality due to SARS-CoV-2 infection in London, United Kingdom. J. King Saud Univ.-Sci. 2021, 33, 101373. [Google Scholar]
- Sangkham, S.; Thongtip, S.; Vongruang, P. Influence of air pollution and meteorological factors on the spread of COVID-19 in the Bangkok Metropolitan Region and air quality during the outbreak. Environ. Res. 2021, 197, 111104. [Google Scholar] [CrossRef]
- Lolli, S. Is the Air Too Polluted for Outdoor Activities? Check by Using Your Photovoltaic System as an Air-Quality Monitoring Device. Sensors 2021, 21, 6342. [Google Scholar] [CrossRef]
- Bontempi, E.; Vergalli, S.; Squazzoni, F. Understanding COVID-19 diffusion requires an interdisciplinary, multi-dimensional approach. Environ. Res. 2020, 188, 109814. [Google Scholar] [CrossRef]
- Tisdell, C.A. Economic, social and political issues raised by the COVID-19 pandemic. Econ. Anal. Policy 2020, 68, 17–28. [Google Scholar] [CrossRef]
- Yu, X.; Yang, R. COVID-19 transmission through asymptomatic carriers is a challenge to containment. Influenza Other Respir. Viruses 2020, 14, 474. [Google Scholar] [CrossRef]
- Flaxman, S.; Mishra, S.; Gandy, A.; Unwin, H.J.T.; Mellan, T.A.; Coupland, H.; Whittaker, C.; Zhu, H.; Berah, T.; Eaton, J.W.; et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature 2020, 584, 257–261. [Google Scholar] [CrossRef]
- Chaudhry, R.; Dranitsaris, G.; Mubashir, T.; Bartoszko, J.; Riazi, S. A country level analysis measuring the impact of government actions, country preparedness and socioeconomic factors on COVID-19 mortality and related health outcomes. EClinicalMedicine 2020, 25, 100464. [Google Scholar] [CrossRef]
- Hsiang, S.; Allen, D.; Annan-Phan, S.; Bell, K.; Bolliger, I.; Chong, T.; Druckenmiller, H.; Huang, L.Y.; Hultgren, A.; Krasovich, E.; et al. The effect of large-scale anti-contagion policies on the COVID-19 pandemic. Nature 2020, 584, 262–267. [Google Scholar] [CrossRef]
- Courtemanche, C.; Garuccio, J.; Le, A.; Pinkston, J.; Yelowitz, A. Strong Social Distancing Measures In The United States Reduced The COVID-19 Growth Rate: Study evaluates the impact of social distancing measures on the growth rate of confirmed COVID-19 cases across the United States. Health Aff. 2020, 39, 1237–1246. [Google Scholar] [CrossRef]
- Tian, H.; Liu, Y.; Li, Y.; Wu, C.H.; Chen, B.; Kraemer, M.U.; Li, B.; Cai, J.; Xu, B.; Yang, Q.; et al. An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science 2020, 368, 638–642. [Google Scholar] [CrossRef]
- Candido, D.S.; Claro, I.M.; De Jesus, J.G.; Souza, W.M.; Moreira, F.R.; Dellicour, S.; Mellan, T.A.; Du Plessis, L.; Pereira, R.H.; Sales, F.C.; et al. Evolution and epidemic spread of SARS-CoV-2 in Brazil. Science 2020, 369, 1255–1260. [Google Scholar] [CrossRef]
- Ferretti, L.; Wymant, C.; Kendall, M.; Zhao, L.; Nurtay, A.; Abeler-Dörner, L.; Parker, M.; Bonsall, D.; Fraser, C. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 2020, 368, eabb6936. [Google Scholar] [CrossRef]
- Hale, T.; Angrist, N.; Goldszmidt, R.; Kira, B.; Petherick, A.; Phillips, T.; Webster, S.; Cameron-Blake, E.; Hallas, L.; Majumdar, S.; et al. A global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker). Nat. Hum. Behav. 2021, 5, 529–538. [Google Scholar] [CrossRef]
- Nicola, M.; Alsafi, Z.; Sohrabi, C.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, M.; Agha, R. The socio-economic implications of the coronavirus pandemic (COVID-19): A review. Int. J. Surg. 2020, 78, 185–193. [Google Scholar] [CrossRef]
- Horton, R. The COVID-19 Catastrophe: What’s Gone Wrong and How to Stop It Happening Again; Polity Press: Cambridge, UK, 2020. [Google Scholar]
- Ioannidis, J.P. Coronavirus disease 2019: The harms of exaggerated information and non-evidence-based measures. Eur. J. Clin. Investig. 2020, 50, e13222. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Wang, D.; Abbas, J.; Duan, K.; Mubeen, R. Global financial crisis, smart lockdown strategies, and the COVID-19 spillover impacts: A global perspective implications from Southeast Asia. Front. Psychiatry 2021, 12, 643783. [Google Scholar] [CrossRef] [PubMed]
- Brooks, S.K.; Webster, R.K.; Smith, L.E.; Woodland, L.; Wessely, S.; Greenberg, N.; Rubin, G.J. The psychological impact of quarantine and how to reduce it: Rapid review of the evidence. Lancet 2020, 395, 912–920. [Google Scholar] [CrossRef] [PubMed]
- Bambra, C.; Riordan, R.; Ford, J.; Matthews, F. COVID-19 and the gender health paradox. Scand. J. Public Health 2020, 49, 19–27. [Google Scholar] [CrossRef]
- Haug, N.; Geyrhofer, L.; Londei, A.; Dervic, E.; Desvars-Larrive, A.; Loreto, V.; Pinior, B.; Thurner, S.; Klimek, P. Ranking the effectiveness of worldwide COVID-19 government interventions. Nat. Hum. Behav. 2020, 4, 1303–1312. [Google Scholar] [CrossRef]
- Evans, M.; Hastings, N.; Peacock, B.; Forbes, C. Statistical Distributions; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Di Domenico, L.; Pullano, G.; Sabbatini, C.E.; Boëlle, P.Y.; Colizza, V. Impact of lockdown on COVID-19 epidemic in Île-de-France and possible exit strategies. BMC Med. 2020, 18, 240. [Google Scholar] [CrossRef]
| Indicator |
|---|
| School Closing |
| Workplace Closing |
| Canceling Public Events |
| Restriction on gathering size |
| Close Public Transport |
| Stay at Home Requirements |
| Restrictions on Internal Movements |
| Restrictions on International Travels |
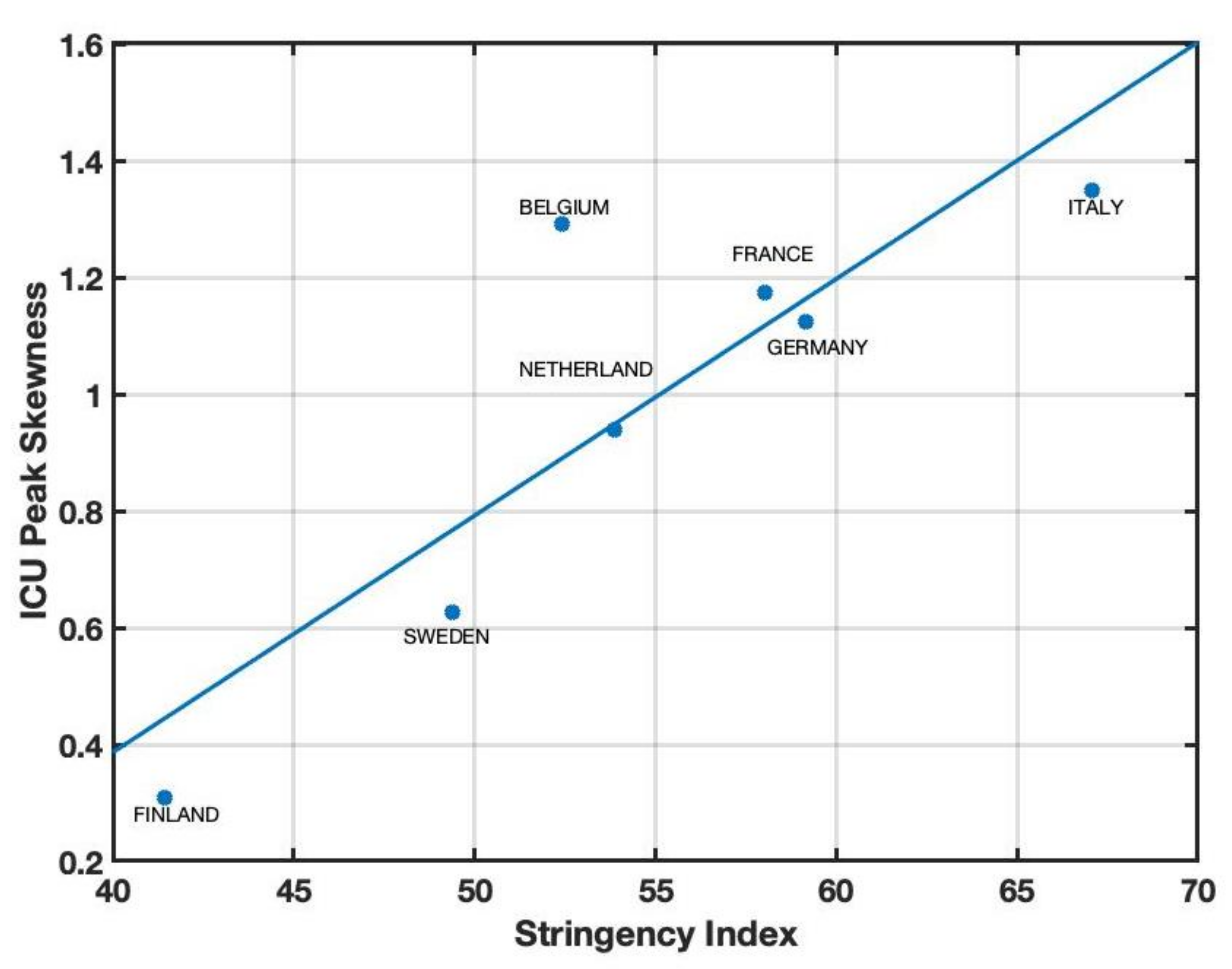
| Country | Skewness | Kurtosis | Std. Dev. | SI |
|---|---|---|---|---|
| Belgium | 1.29 | 5.14 | 3.22 | 52.40 |
| Finland | 0.30 | 2.92 | 2.89 | 41.45 |
| France | 1.17 | 3.70 | 4.34 | 58.02 |
| Germany | 1.12 | 3.87 | 4.00 | 59.14 |
| Italy | 1.34 | 5.20 | 3.25 | 67.06 |
| Sweden | 0.62 | 3.03 | 4.92 | 49.40 |
| The Netherlands | 0.93 | 4.16 | 2.96 | 53.88 |
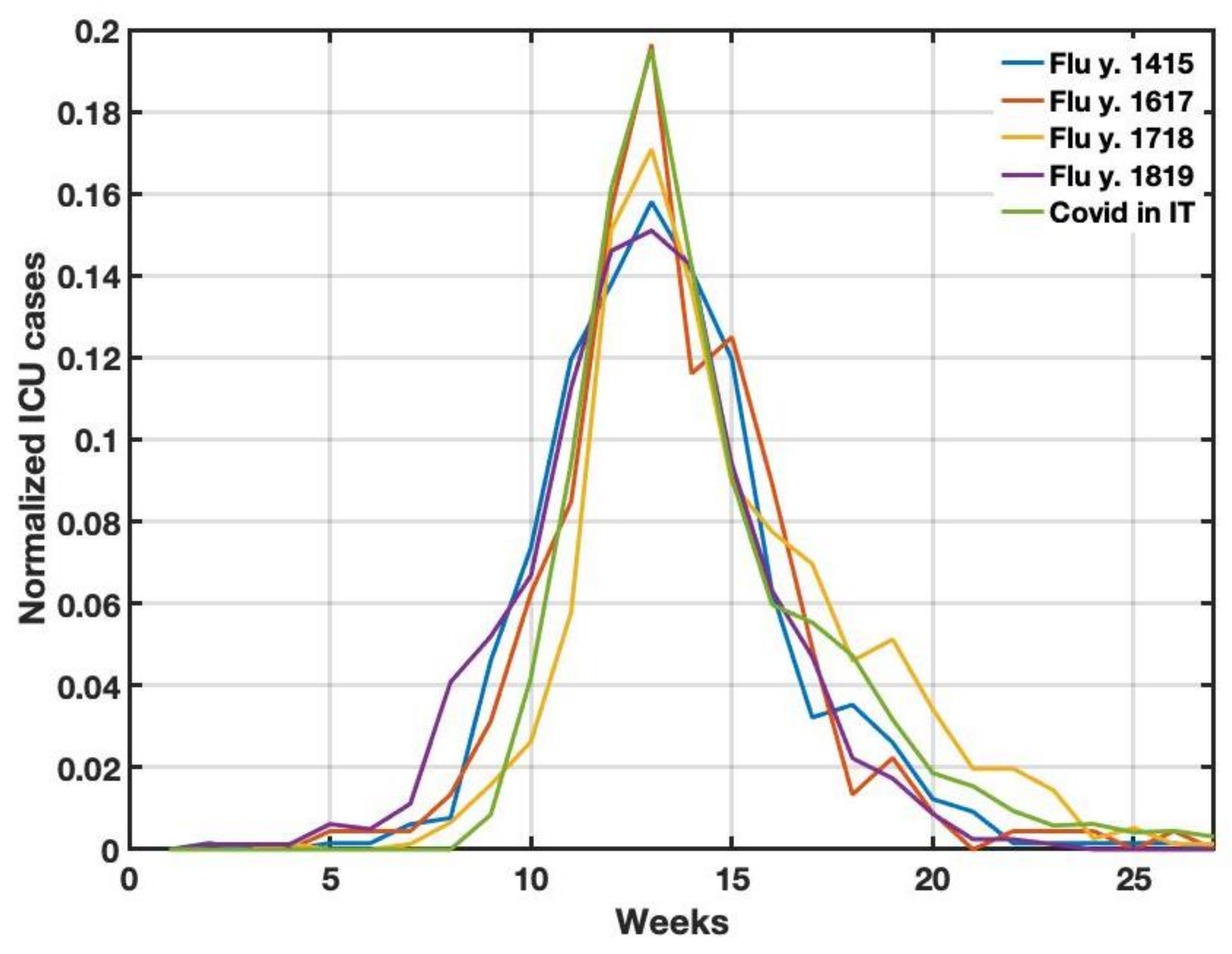
| Year | Skewness |
|---|---|
| 2014–2015 | 0.53 |
| 2016–2017 | 0.58 |
| 2017–2018 | 0.77 |
| 2018–2019 | 0.39 |
| COVID-19 2020 | 1.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lolli, S.; Piazza, F.; Vivone, G. Government Restriction Efficiency on Curbing COVID-19 Pandemic Transmission in Western Europe. COVID 2023, 3, 1079-1091. https://doi.org/10.3390/covid3080079
Lolli S, Piazza F, Vivone G. Government Restriction Efficiency on Curbing COVID-19 Pandemic Transmission in Western Europe. COVID. 2023; 3(8):1079-1091. https://doi.org/10.3390/covid3080079
Chicago/Turabian StyleLolli, Simone, Francesco Piazza, and Gemine Vivone. 2023. "Government Restriction Efficiency on Curbing COVID-19 Pandemic Transmission in Western Europe" COVID 3, no. 8: 1079-1091. https://doi.org/10.3390/covid3080079
APA StyleLolli, S., Piazza, F., & Vivone, G. (2023). Government Restriction Efficiency on Curbing COVID-19 Pandemic Transmission in Western Europe. COVID, 3(8), 1079-1091. https://doi.org/10.3390/covid3080079








