Abstract
Non-pharmaceutical interventions have been implemented intermittently for more than a year in most countries of the world to mitigate the COVID-19 epidemic. In France, while the vaccination campaign is progressing, the French government has decided to remove many public health restrictions such as business closure, lockdowns, and curfews. Nonetheless, social distancing, mask wearing, and hand washing (also called barrier gestures) are still recommended. We utilize an age-structured compartmental SEIR model that takes into account the SARS-CoV-2 waning immunity, vaccination, and increased transmissibility from variants of concern to estimate if barrier gestures can be relaxed without causing a resurgence of severe infections. This model assumes that the susceptibility to infection is a function of immunity status, which depends on initial infection severity and vaccination status. It is calibrated on confirmed COVID-19 cases from the French surveillance database, and accounts for changes in contact behaviors due to the implementation of nation-wide public health policies. We study the partial and full relaxation of barrier gestures occurring from August to December 2021 under various immunity duration assumptions. Maintaining the application of barrier gestures appears essential to avoid a resurgence of severe infections that would exceed French health care capacities, while surmounting vaccine hesitancy represents the key to consider their relaxation. Immunity duration assumptions significantly influence the short-term dynamic of the epidemic, which should be considered for further modelling.
1. Introduction
Causing more than 200 million infections and at least 4.4 million deaths worldwide, the COVID-19 epidemic is a global health, economic, and social crisis. The causative agent, SARS-CoV-2, emerged in China’s Hubei province in December 2019. Various non-pharmaceutical measures, in particular lockdown and social distancing, have been implemented around the world to effectively control the spread of the virus [1,2]. Nevertheless, all of these measures have negative economic and social consequences, as well as repercussions on the mental health of populations. Considerable efforts in vaccine research have resulted in the development of several effective vaccines against COVID-19 in a few months. As of 30 August 2021, more than 5 billion doses of the vaccine have been administered worldwide [3].
Numerous studies have used compartmental models to either estimate the parameters of the epidemic dynamics [4,5], measure the impact of social distancing [6,7,8], or evaluate different vaccine strategies [9]. Many of these studies assumed that immunity acquired after an infection was definitive. Indeed, it has been shown that immunity acquired after a first infection protects against reinfection for at least 6 months [10,11]. Nevertheless, several immunological studies have shown that, following natural infection, the anti-SARS-CoV2 antibody titer declines over time [12,13,14,15] even though it remains detectable in more than 90% of cases at 7 months [14]. A study suggests that anti-SARS-CoV-2 CD4+ and CD8+ specific T cells decline with a half-life of 3 to 5 months [15], while another study found that they were maintained 10 months post-infection [16]. With regard to other coronaviruses, reinfections are frequent in the year following a seasonal coronavirus infection (common cold) [17], while immunity appears to be prolonged after infection with SARS-CoV or MERS [18,19,20]. Concerning vaccination, a significant trend of the decline in anti-SARS-CoV2 antibodies was demonstrated with both BNT162b2 and ChAdOx1 nCoV-19 [21]. The latest study endpoint of the BNT162b2 clinical trial suggests that vaccine efficacy against symptomatic infections may decline over time [22]. However, to date, the exact duration of the protection anti-SARS-CoV-2 conferred by an infection or by vaccination remains unknown. As the epidemic has lasted for more than a year, it seems necessary to take this parameter into account to model the epidemic. Indeed, several studies have shown that the future evolution of the epidemic would depend on the duration of immunity, from extinction after a large epidemic wave to the transition to an endemic mode [23,24,25,26].
The French government, similar to many others, has successively implemented many restrictions in order to mitigate the epidemic, such as travel restrictions, lockdowns, curfews, obligation to work from home, and the closure of bars, restaurants, cinemas, or schools. In addition to these measures, barrier gestures have been promoted. These barrier gestures include mask wearing, washing hands regularly, using single-use disposable tissues, keeping a distance of at least 2 m between individuals, and avoiding gatherings of more than six people with the aim to reducing human-to-human viral transmission.
Four vaccines are currently licensed in France: two messenger RNA vaccines (BNT162b2 and mRNA-1273), and two viral vector vaccines (ChAdOx1 nCoV-19 and Ad26.COV2.S). The vaccination campaign began on January 2021, targeting first the elderly and the subpopulation with comorbidities at risk for severe COVID-19. The program was then progressively extended to the entire adult population over a few months, and then to children over 12 years old. As of 24 August 2021, 71.1% of the French population have received at least one dose of the vaccine, and 62.7% have completed the vaccination schedule [27].
A French modelling study estimated that it would be necessary to vaccinate 90% of individuals over 65 years old and 89% of the 18–64 year olds before all social distancing measures could be relaxed [28]. This study assumes that immunity does not wane over time, which could lead to an underestimation of these thresholds. In addition, Europe is facing the breakthrough of the delta variant, which is estimated to be 1.97 times more transmissible than the historical strain, and is predicted to represent 90% of COVID-19 cases in August 2021 [29]. However, the vaccine coverage reached at the end of the vaccination campaign is uncertain. A survey conducted among the French population estimates that 16% of adults do not want to be vaccinated and that only 74% of parents would agree to have their child under 17 vaccinated [30]. Finally, because immune responses following vaccination are lower in the elderly [31], a booster campaign for this population is being considered by the authorities.
While the vaccine rollout is progressing, the French government has removed public health restrictions, but the application of barrier gestures is recommended [32]. In this study, we aim to estimate the consequences of a barrier gesture relaxation on the evolution of the epidemic in France, taking into account vaccination, the emergence of variants of concern, in particular, the delta variant, and waning immunity. In addition, we aim to investigate in a preliminary analysis the impact of a booster vaccine campaign for the elderly.
2. Materials and Methods
2.1. Model
We used a compartmental age-structured model of COVID-19 infection previously developed by Childs et al. [33] which is adapted from a model of vaccination and waning immunity applied to pertussis [34]. A flow diagram of the model is shown in Figure 1 for a single age group. The model is based on a Susceptible-Exposed-Infected-Vaccinated-Susceptible model structure (SEIVS) with age structure (i.e., groups 0–4, 5–9, …, 75+ years). As in Childs et al. [33], we use Sim, Ekjm, Ijm, and Vlim to denote the number of susceptible, exposed, infectious, and vaccinated individuals in each age group m (1 ≤ m ≤ 16), where i (1 ≤ i ≤ 4) denotes immune status, j (2 ≤ j ≤ 4) denotes symptom severity, k (1 ≤ k ≤ 3) represents stages in the exposed class, and l (1 ≤ l ≤ 2) denotes the number of vaccine doses that individuals have received.
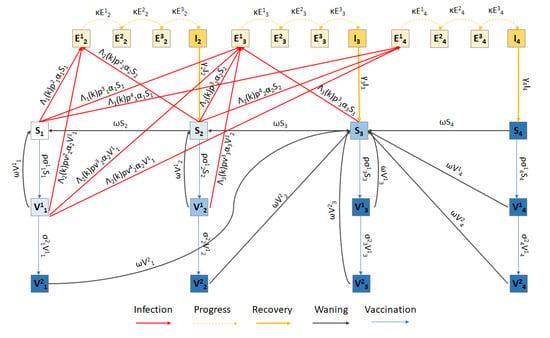
Figure 1.
Schematic of the age-structured SEIVS model for one age group, derived from Childs et al. [33]. Here, S1, S2, S3, and S4 (blue shaded boxes) represent susceptible individuals who are fully susceptible, have some low and moderate immunity, and full immunity, respectively. I2, I3, and I4 (yellow boxes) represent infected individuals with mild, moderate, and severe symptoms, respectively, who will develop some low, moderate, or full immunity once recovered (yellow lines), respectively. V1i and V2i represent vaccinated individuals from the Si classes (1 ≤ i ≤ 4) after 1 and 2 doses of vaccine, respectively. Ekj (2 ≤ j ≤ 4) represent exposed individuals (infected but not-yet-infectious) with progressive stages k (1 ≤ k ≤ 3) that will experience mild I2, moderate I3, and severe I4 symptoms. Susceptible and vaccinated individuals can be infected and move to the exposed classes (red lines). Immunity gained from infection and vaccination can wane (black lines). Susceptible and vaccinated classes in the same shade of blue have similar protection.
A full description of the model is available in Childs et al. [33]. Briefly, the base model consists of an immune continuum, distinguishing four states of susceptibility (fully susceptible (S1), somewhat immune (S2), moderately immune (S3), and fully resistant to infection (S4)); three infectious states with mild (I2), moderate (I3), and severe (I4) symptoms (i.e., infections requiring at least one medical consultation); and three infected but not-yet-infectious states (Ekj, j = 2,3,4, k = 1,2,3). It is assumed that individuals of higher immune status are less susceptible to infection than those of lower status. Co-morbidity statuses by age [35] determine the probability of mild, moderate, and severe symptoms for each age group. Immunity develops after infection. It is assumed that people with mild, moderate, and severe symptoms move to immune classes S2, S3, and S4, respectively, upon recovery (i.e., the severity of symptoms is proportional to neutralizing immunity development [14,36,37,38]). Vaccination is implemented into the model using a two-dose structure, where compartments V1i and V2i denote those with one and two doses, respectively, where i is the level of susceptibility. It is assumed that two doses of the vaccine, or one dose of the vaccine administered to individuals in immune states S3 and S4, provide the same level of immunity or protection from infection as S4; i.e., full resistance to infection. Additionally, it is assumed that one dose of the vaccine given to individuals in S1 and S2 provides protection similar to states S2 and S3, respectively, where protective efficacies against infection and/or severe disease decrease with a lower level of immunity. Finally, it is assumed that the immunity gained from infection or vaccination wanes over time (Figure 1, black lines).
Detailed descriptions of the equations are provided in Appendix A.
2.2. Parameters
Parameter values and references are provided in Table 1.

Table 1.
Parameter definitions, values, and references for the age-structured SEIVS model.
Susceptibility is assumed to decrease with increasing immunity, but does not depend on age. Thus, the susceptibility α of an individual somewhat immune (S2) or moderately immune (S3) corresponds respectively to 1/3 and 2/3 of that of an individual fully susceptible (S1). Infectivity (β) is assumed to vary by the severity of the disease and is chosen to produce a basic reproduction number, R0, equal to 2.9 [4] using the Next Generation Matrix method [48]. By immunity status, we assume that the infectivity of individuals with mild (I2) or severe (I4) infections is 0.5 and 0.1 times the infectivity of moderate infections (I3). Indeed, people with milder symptoms are expected to have lower infectivity [39]. Simultaneously, more severe disease outcomes are expected to induce behavioral changes that lower infectivity, such as limiting mobility,. Infectivity is considered in the calculation of the infection force λ, which takes into account the average number of contacts between age classes and the proportion of the population infected and infectious (Appendix A—Model equations). Susceptible individuals Si, upon infection, move to the mild, moderate, and severe symptom classes with probabilities pjim for each age group m and each immune status i. These probabilities are determined by the prevalence of zero, one, and two or more co-morbidities that increase the risk of severe COVID-19 disease within each age group, informed by [35]. pj1m is directly derived from these prevalences, whereas pj2m and pj3m are modified in order to assume that people in the S2 and S3 compartments are, respectively, 70% protected and fully protected against moving to the severe disease class I4 (Table S2). The incubation period lasts on average 4.5 days. Therefore, it is assumed that the progression rates through the pre-infectious period κ is equal to 1/1.5. The contagious period is estimated to last 7 to 8 days [41,49,50] and depends on symptom severity, with milder disease associated with shorter infectious periods [51,52]. Thus, we assumed that the recovery rate is respectively equal to 1/5, 1/10, and 1/15 for mild (I2), moderate (I3), and severe infections (I4). Given the short period considered, we assume the absence of natality, mortality, and aging. Finally, we assume that immunity lasts on average 3 years between successive stages, which means that it takes 9 years to pass from a fully resistant to a fully susceptible compartment. For vaccinated classes, we assume that immunity in V11 wanes to S1, V12 wanes to S2, and that of all other vaccinated classes wanes to S3.
Vaccination is implemented from 1 January 2021 and takes into account the different age groups that are successively eligible in France, starting first from the elderly (Table S3). In order to take into account vaccine hesitancy, we assume that 10% of the over-75s, 20% of the (20–74) year olds, and 30% of the (10–19) year olds will not be vaccinated [30]. We determine the first dose vaccination rate σ1i given the desired coverage at the end of each month of the vaccination program. From January to June 2021, the monthly coverage is derived from the VAC-SI (Système d’Informations pour le suivi de la VACcination) database (Table S4). From July, we assume that 15 million doses (including first and second doses) will be administrated each month, which corresponds to the average distribution in the previous 3 months. Monthly coverage is scaled to a daily rate accounting for the portion of the population in the current vaccine-eligible age groups in each eligible compartment (S1, S2, S3, and S4). Individuals receive a second dose 28 days after the first one and acquire immunity immediately. The vaccine’s efficacy against all infections is assumed to be 50% after 1 dose and 80% after 2 doses. The vaccine’s efficacy against severe infections is assumed to be 70% after 1 dose. Given the model architecture, the efficacy against severe infections after 2 doses is equal to the efficacy against all infections after 2 doses.
In order to take into account the emergence of the variants of concern (alpha, beta, gamma, and delta), we use the SI-DEP database (Système d’Informations de DEPistage), which provides information about the distribution of these variants among all confirmed COVID-19 cases over time (Figures S1 and S2). For the delta variant, we assume that it will represent 90% of the reported cases at the end of August 2021 [29]. We assume that alpha-beta-gamma variants and the delta variant are, respectively, 50% [53,54] and 97% [55] more transmissible than the historical strain.
2.3. Contact Matrices and Public Health Mitigation Strategies
Age-specific daily contacts for the French population are obtained from pre-pandemic estimations [40]. The model incorporates the contact-rates, cma, the governmental measures taken to mitigate the epidemic such as lockdowns, curfews, the closing of schools, businesses, bars, restaurants, or working from home. The schedule of these governmental measures is available at https://www.gouvernement.fr/info-coronavirus/les-actions-du-gouvernement [56]. Specific modifications to the contact matrices are provided in the Supplementary Material (Tables S5–S8).
2.4. Calibration
The model is calibrated using daily reported COVID-19 cases from the SI-DEP database, from 13 May 2020 to 1 July 2021. SI-DEP is the French surveillance system that gathers all COVID-19 infections confirmed by Polymerase Chain Reaction or antigenic tests at the national level. We assume that reported COVID-19 cases correspond to all severe cases (I4) and 3/5 of the moderate cases (I3). The k-value is the only model parameter that is fit to COVID-19 data, and reflects the population compliance to barrier gestures. Given that climatic conditions are not implemented in the model, the k-value also captures part of the influence of the climate on the transmission [57]. This parameter lies between 0 and 1 (1 being pre-pandemic value; i.e., no barrier gesture application), and it linearly scales contact-rates from the contact matrices. Thus, the force of infection λim depends on the k-value (Appendix A).
2.5. Barrier Gesture Relaxation Scenarios
After 1 August 2021, we formulate different hypotheses for the relaxation of barrier gestures based on the evolution of the k-value. The baseline scenario corresponds to no relaxation. For this scenario, we chose to set the k-value for July–August 2021 to those estimated during the same period in the previous year, assuming that barrier gestures will be applied at the same level. After August 2021, we maintain the k-value at this level until it is modified to reflect a relaxation scenario.
Different scenarios of barrier gesture relaxation are formulated according to the timing of the relaxation (August, September, October, November, or December) and its magnitude (k-value raised to 0.7, 0.8, 0.9, or 1, i.e., the pre-pandemic level). For each relaxation scenario, the k-value set before the relaxation is identical to the no relaxation scenario. We chose to evaluate the impact of each relaxation scenario on the evolution of severe cases I4, i.e., infections requiring at least one medical consultation, and on the number of prevalent intensive care units’ (ICU) hospitalizations. Due to the fact that our model does not directly incorporate a hospitalized compartment, we extrapolated the predictive number of ICU hospitalizations by estimating the mean ratio between the past ICU hospitalizations from the SI-VIC database (Système d’Information pour le suivi des VICtimes d’attentats et de situations sanitaires exceptionnelles) and the past I4 cases.
2.6. Sensitivity Analyses
We successively explored a pessimistic immunity duration hypothesis, assuming that immunity wanes totally over 3 years instead of 9, and an optimistic hypothesis assuming that immunity does not wane. We also study one scenario without vaccine hesitancy, thus allowing the vaccination of 100% of each eligible age class, and one analysis with a better vaccine efficacy (Table 1). The model was refitted to estimate the retrospective k-value for all of these analyses except for the no vaccine hesitancy hypothesis.
Finally, we implemented (crudely) a booster vaccination campaign for people over 75 in order to estimate the upper bound effect of this strategy. In this analysis, we assumed that on 1 September 2021, a fraction of the people over 75 move from the S compartments to the corresponding V2 compartments, ultimately returning all 75+ individuals that were previously protected by vaccination back to the V2 protective classes.
3. Results
3.1. Calibration
Figure 2a and Figure 3 show the k-value (reflecting the population compliance to barrier gestures) estimation and the model fit from 13 May 2020 to 1 July 2021 for the main analysis, respectively. Figures showing the k-value and the fit of the model to the data for the sensitivity analyses are shown in the Supplementary Materials (Figures S3–S5). In addition, Figure 2b plots the reduction in the average number of contacts for the entire population over time, given the combined effect of the modifications in the contact matrices and the fitted k-value. We note qualitative similarities between this figure and the time-dependent transmission rate of COVID-19 in the French population [8].
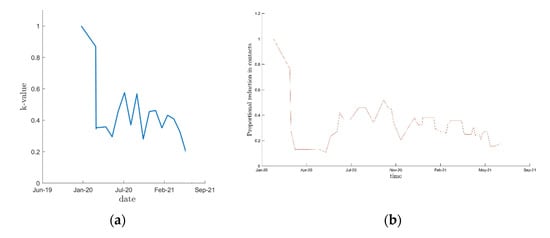
Figure 2.
(a) Main analysis k-value estimation (reflecting the population compliance to barrier gestures) in France from 13 May 2020 to 1 July 2021; (b) Main analysis estimation of reduction in the average number of contacts consecutively to non-pharmaceutical interventions given the combined effect of the modifications in the contact matrices and the fitted k-value in France from 13 May 2020 to 1 July 2021.
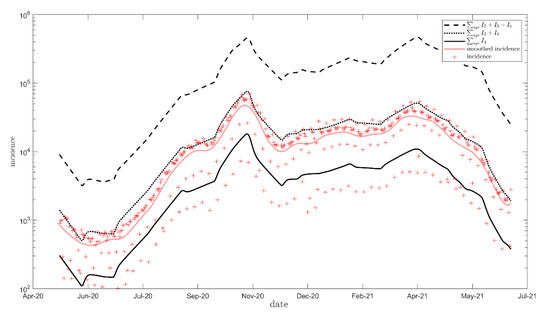
Figure 3.
Main analysis model fit. Daily incidence of severe (I4, solid line), moderate and severe (I3 + I4, dotted line), and all infections (I2 + I3 + I4, dashed line) from the model and reported COVID-19 cases from French surveillance database (red crosses show daily incidence data, red line shows smoothed incidence data) from May 2020 to 1 July 2021 (logarithmic scale).
3.2. Impact of Barrier Gesture Relaxation, Main Analysis
The predicted evolution of the severe case I4 incidence for each relaxation scenario are presented in Figure 4 from 1 July 2021. Regardless of the timing, the complete relaxation of barrier gestures (setting k-value to 1, pink curve) is followed by an epidemic resurgence whose peak systematically exceeds that of the 2nd and 3rd epidemic waves in France. However, even in the optimistic scenario of no relaxation (defined as a barrier gesture applying at an equivalent level to that of the same period in 2020), we do observe a significant rebound (black curve).
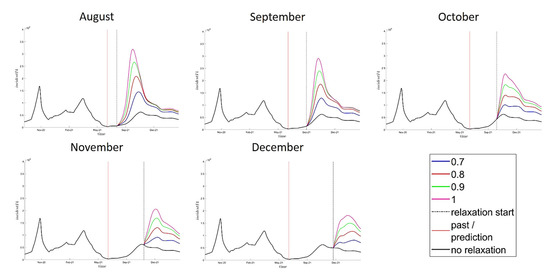
Figure 4.
Evolution of incident COVID-19 severe cases (I4) in France for each barrier gesture relaxation scenario in the main analysis (i.e., 9 years waning immunity assumption). Relaxation scenarios: k-value (barrier gesture compliance index) raised either to 0.7, 0.8, 0.9, or 1 in August, September, October, November, or December. The start of relaxation is indicated by the vertical dashed black line. No relaxation: k-value equal to previous year estimates at the same period (black line). Prediction starts from 1 July 2021 (vertical red line).
To focus on ICU hospitalizations, we estimated the ratio between ICU hospitalizations (from the SI-VIC database) and prevalent I4 cases in the past history of the pandemic (Figure S7), which is on average 3.62%. Whatever the scenario (Figure 5), the complete relaxation of barrier gestures leads to a predicted increase of prevalent ICU hospitalizations, and the peak consistently exceeds French health care capacities (which is estimated at a maximum of about 5000 ICU beds at the national level [58]).
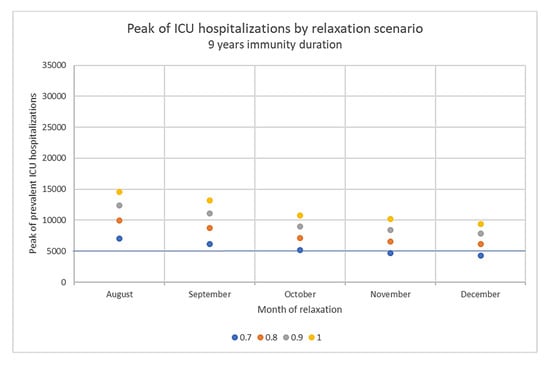
Figure 5.
Peak of Intensive Care Units’ hospitalizations (ICU) predicted in France from July 2021 following each relaxation scenario, assuming that immunity wanes in 9 years. Relaxation scenarios: k-value (barrier gesture compliance index) raised either to 0.7, 0.8, 0.9, or 1 in August, September, October, November, or December.
As expected, people over 75 years old represent the major part of severe infections I4 (Figure S8). While 90% of the 75+ have been vaccinated at least once by the end of June 2021 (Figure S6), about 25% of them are fully susceptible in September 2021 (Figure S9) due both to waning immunity and to the vaccine efficacy hypothesis. Nevertheless, in a sensitivity analysis assuming a 90% vaccine efficacy against infections after two doses, even though the predicted peak ICU hospitalizations following each relaxation scenario is on average 41.0% lower than in the main analysis, a complete relaxation of barrier gestures still overwhelms health care system (Table S10 and Figure S10).
3.3. Impact of Immunity Duration Hypothesis
As shown in Figure 6, our predictions are particularly sensitive to changes in our immunity duration assumptions. Assuming that immunity completely wanes over 3 years, we find that the ICU hospitalization peak is, on average, 86.1% higher than the same result when a 9-year immunity duration is assumed. In contrast, ICU hospitalizations peak at an average 46.1% lower when immunity is not allowed to wane (Table S11).
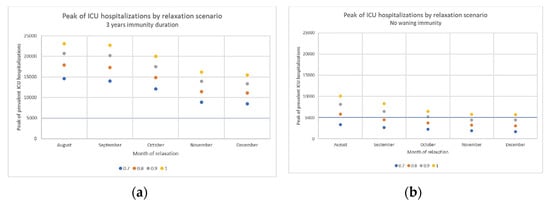
Figure 6.
Peak of Intensive Care Units’ hospitalizations (ICU) predicted in France from July 2021 following each relaxation scenario, assuming that immunity wanes in 3 years (a), or assuming that immunity does not wane (b). Relaxation scenarios: k-value (barrier gesture compliance index) raised either to 0.7, 0.8, 0.9 or 1 in August, September, October, November or December.
3.4. Impact of Vaccine Hesitancy
In the absence of vaccine hesitancy, the vaccine coverage of at least one dose reaches 100% of the over 10 years old population at the end of November 2021 (Figure S11 and Table S12). Under this assumption, ICU hospitalizations peak at, on average, 47.7% lower than in the main analysis, which includes vaccine hesitancy. This effect is particularly strong for the November and December relaxation scenarios, for which assuming no vaccine hesitancy reduces the hospitalization peak by about 65% (Table S13). In that case, a complete relaxation of barrier gestures would be possible in November and December 2021 without exceeding the French ICU hospitalization capacities (Figure 7).
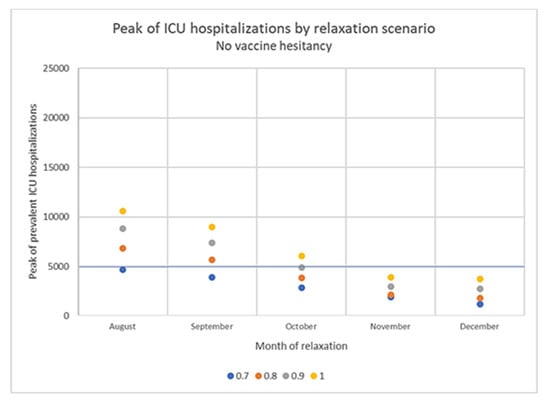
Figure 7.
Peak of Intensive Care Units’ hospitalizations (ICU) predicted in France from July 2021 following each relaxation scenario assuming no vaccine hesitancy with a 9 years immunity duration assumption. Relaxation scenarios: k-value (barrier gesture compliance index) raised either to 0.7, 0.8, 0.9 or 1 in August, September, October, November or December.
3.5. Booster Campaign
Finally, we explored a crude implementation of a booster vaccination campaign for people over 75 years of age on 1 September 2021. In this analysis, we find a 16.3% average reduction in ICU peak hospitalization following barrier gesture relaxation (Table S14 and Figure S12). Even though this analysis is optimistic in that it assumes that all but the vaccine hesitant people over 75+ will receive their booster dose on this date, this crude implementation of a booster dose allows us to estimate the best expected benefit from a booster vaccination campaign among the elderly.
4. Discussion
We used an age-structured compartmental model of COVID-19 that takes into account the waning and boosting of immunity from vaccination and infection [33]. We first showed that, considering the context of vaccine hesitancy in France and the delta variant breakthrough, maintaining the application of barrier gestures appears essential to avoid a resurgence of severe infections that would exceed French health care capacities. Our study particularly highlighted the influence of immunity duration assumptions on the future short-term dynamic of the epidemic, which should not be neglected for further modelling. In addition, we reasserted the necessity to strengthen the vaccine rollout whereas current vaccines are effective (at least for severe disease) against the predominant delta variant [59]. Indeed, among our sensitivity analyses, the only scenario that would allow a complete barrier gesture relaxation without overwhelming ICU bed capacities is relaxation occurring from November with a 100% vaccine coverage of the eligible population. Finally, according to our very preliminary analysis, the strategy consisting of the revaccination of people over 75 would not allow us to relax barrier gestures safely, in particular in the context of vaccine hesitancy. Nevertheless, further modelling is needed to evaluate more accurately this last statement.
Our work is consistent with other French modelling, having estimated that, given the current vaccine rollout and the progression of the delta variant, barrier gesture application will be necessary to maintain severe cases under health care capacities’ limits [60,61]. Nevertheless, our predictions tend to be more pessimistic. One explication is that we took into account the greater transmissibility of the delta variant at the level that has been estimated by ECDC [29], whereas these studies explored an inferior range of effective reproductive numbers. In addition, these studies assumed that the immunity acquired after an infection or vaccination is definitive. Finally, our model, incorporating contact patterns, takes into account both school re-opening and the recovery of on-site work, which leads to increased transmission rates in September. Similar to our findings, a very high vaccination coverage was estimated to be required to allow a complete relaxation of control measures [28], and a high vaccine hesitancy was related to a prolonged need for non-pharmaceutical-interventions [62]. On the other hand, our work highlighted the influence of the immunity duration on the short-term dynamic of the epidemic. Few other studies chose to modelling the COVID-19 epidemic incorporating waning immunity [23,24,25,26,33]. Giannitsarou et al. estimated that given the population turnover, the disease would become endemic in the long term with recurrent waves, and its magnitude would depend on how fast immunity wanes [26]. Saad-Roy et al. showed that the shorter immunity duration conferred by vaccination, the higher the vaccine coverage required to achieve herd immunity [25].
Measuring the compliance of the population to barrier gestures is challenging. Our model is fit using a single parameter: the k-value. Due to the fact that we incorporated the changes in contact patterns consequently to governmental measures directly in the contact matrices, this k-value reflects the population compliance to barrier gestures. Nevertheless, it also incorporates temporal variations in testing and variations in climatic conditions which influence transmission [8]. However, even though the detection rate increased significantly during the first months of the epidemic, it remained relatively stable during our calibration period [63]. Concerning climatic conditions, we estimated in another modelling study that transmission is increased on average by 10% during the winter period and decreased by 22% during the summer period [8]. Due to the fact that we did not account for these variations, we expect our predictions to be somewhat overestimated in the summer and underestimated in the winter. However, one can notice that our model indirectly accounts for quarantine using a reduced transmission rate in the severely infected class I4, and by using reduced contact rates using the k-value, which can moderate these over- and under-estimations. Another limitation of our model is that it underestimates vaccine efficacy against severe infections after two doses, assuming that it is equal to vaccine efficacy against all infections (which is set to 80% in the main analysis). However, assuming an optimistic 90% vaccine efficacy after two doses against infections and severe cases leads to similar conclusions with no possibility to fully relax barrier gestures safely. In addition, it ignores the fact that both mRNA and vectored vaccines have been used in France, which may have different immunogenicity. Nevertheless, 90% of the administrated vaccines in France are mRNA vaccines, in great majority BNT162b2 [64], for which we calibrated the model. Thus, we believe it may not have a significant impact on our results. Also, we did not account for the increased risk of hospitalization related to the alpha variant compared to the historical strain [65] which could explain that our ICU hospitalizations/prevalent I4 ratio tends to increase over the calibration period. This could lead to an underestimation of the ICU hospitalizations rebound. We also did not account for the age-related immune response heterogeneity to the SARS-CoV2 infection and vaccine, which will have to be considered in the future to investigate more accurately the impact of a booster vaccination campaign among the elderly. Finally, although it would require more data on the dynamic of the epidemic at a finer level and individual mobility data, the extension of this work from a national to a regional or local level, in the line of Viguerie et al. work [66], could be considered. This would be particularly interesting with respect to the questions of removing the barrier gestures locally when incidence is low, or vaccination uptake is high.
In conclusion, while the durability of immunity provided by an infection or by vaccination remains uncertain, we provide an insight on the predictable dynamic of the epidemic in France assuming that immunity wanes. To date, maintaining the application of barrier gestures seems unavoidable in the French context as to not overwhelm health care capacities. While the possibility of a booster campaign among the elderly is being considered, scientific evidences on its potential benefit are lacking.
Supplementary Materials
The following are available online at www.mdpi.com/article/10.3390/covid1020041/s1. Table S1. Size of the population in each age group. Table S2. Proportions of mild, moderate, and severe infections by age and by immune status. Table S3. Eligible age classes to vaccination by month. Table S4. Desired vaccine coverage with at least one dose at the end of each month informed by VAC-SI (Système d’Informations pour le suivi de la VACcination). Table S5. Contact matrices for pre-pandemic contacts at home, at school, at work and other contacts. Table S6. Definitions of perturbation matrices for contacts at school, at work and other contacts. Table S7. Percentage reduction in contacts by each perturbation matrices. Table S8. Application periods of perturbation matrices. Table S9. Proportion of the population vaccinated with at least one dose and vaccinated with 2 doses at the end of each month taking into account vaccine hesitancy. Table S10. Average variation of ICU hospitalizations peak assuming a better vaccine efficacy compared to the main analysis. Table S11. Average variation of ICU hospitalizations peak for each hypothesis of immunity duration compared to the main analysis. Table S12. Proportion of the population vaccinated with at least one dose and vaccinated with 2 doses at the end of each month assuming no vaccine hesitancy. Table S13. Average variation of ICU hospitalizations peak assuming no vaccine hesitancy compared to the main analysis with vaccine hesitancy. Table S14. Average variation of ICU hospitalizations peak assuming a booster vaccination campaign on 1 September 2021 for the 75+ compared to the main analysis. Figure S1. Proportion of alpha, beta or gamma Variants Of Concern (VOC) infections among all COVID-19 infections. Figure S2. Proportion of delta VOC infections among all COVID-19 infections. Figure S3. Calibration’s plot for the 3 years immunity duration analysis. Figure S4. Calibration’s plot for the no waning immunity analysis. Figure S5. Calibration’s plot for the 9 years waning immunity analysis with a better vaccine efficacy. Figure S6. Proportion of the population vaccinated with at least one dose by age class, taking into account vaccine hesitancy. Figure S7. Ratio between ICU hospitalizations from SI-VIC database and prevalent I4 cases. Figure S8. Prevalent I4 cases by age class in the no barrier gesture relaxation scenario, main analysis. Figure S9. Proportion of fully susceptible individuals (S1) by age class in the no barrier gesture relaxation scenario, main analysis. Figure S10. Peak of ICU hospitalizations predicted following each relaxation scenario assuming a better vaccine efficacy. Figure S11. Proportion of the population vaccinated with at least one dose by age class assuming no vaccine hesitancy. Figure S12. Peak of ICU hospitalizations predicted following each relaxation scenario assuming a booster vaccination campaign for the 75+.
Author Contributions
Methodology, J.M.H., M.P., L.W. and R.T.; software, D.W.D.; formal analysis, C.V.; writing—original draft preparation, C.V.; writing—review and editing, C.V., D.W.D., J.M.H., L.W., M.P. and R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by NSERC (J.M.H).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Lauren Childs, Jing Li, Zhilan Feng, John Glasser, and Gergely Rost for their discussions and input on this project.
Variants of Concern Data for France Are Publicly Available on
https://www.data.gouv.fr/fr/datasets/donnees-de-laboratoires-pour-le-depistage-indicateurs-sur-les-variants/—Reported COVID-19 cases data for France are available on: https://www.data.gouv.fr/fr/datasets/donnees-relatives-aux-resultats-des-tests-virologiques-covid-19/—Prevalent intensive care unit’s hospitalization data are for France are publicly available on: https://geodes.santepubliquefrance.fr/#c=indicator&f=0&i=covid_hospit.rea&s=2021-08-03&t=a01&view=map2.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Our model tracks age, infection and immune status. Susceptible individuals of status i and age m are denoted by Sim. Infectious individuals of symptom severity j and age m are denoted by Ijm. Infected but not-yet-infectious individuals of symptom severity j, age m and stage k are denoted by Ekjm. Vaccinated individuals of initial immune status i, age m and dose l are denoted by Vlim. Parameter descriptions are found in Table 1 in the main test. The system of ODEs for age group m is given by the following set of equations:
Susceptible compartments
Vaccinated compartments
Exposed compartments
where,
Infectious compartments
where for 1 ≤ m ≤ 16,
References
- Kraemer, M.U.G.; Yang, C.-H.; Gutierrez, B.; Wu, C.H.; Klein, B.; Pigott, D.M.; Open COVID-19 Data Working Group; du Plessis, L.; Faria, N.R.; Li, R.; et al. The Effect of Human Mobility and Control Measures on the COVID-19 Epidemic in China. Science 2020, 368, 493–497. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pei, S.; Kandula, S.; Shaman, J. Differential Effects of Intervention Timing on COVID-19 Spread in the United States. Sci. Adv. 2020, 6, eabd6370. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Weekly Operational Update on COVID-19. 30 August 2021. Issue No 70. Available online: https://www.who.int/publications/m/item/weekly-operational-update-on-covid-19---30-august-2021 (accessed on 7 October 2021).
- Salje, H.; Kiem, C.T.; Lefrancq, N.; Courtejoie, N.; Bosetti, P.; Paireau, J.; Andronico, A.; Hozé, N.; Richet, J.; Dubost, C.L.; et al. Estimating the Burden of SARS-CoV-2 in France. Science 2020, 369, 208–211. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.G.; Klepac, P.; Liu, Y.; Prem, K.; Jit, M.; CMMID COVID-19 Working Group; Eggo, R.M. Age-Dependent Effects in the Transmission and Control of COVID-19 Epidemics. Nat. Med. 2020, 26, 1205–1211. [Google Scholar] [CrossRef]
- Davies, N.G.; Kucharski, A.J.; Eggo, R.M.; Gimma, A.; Edmunds, W.J.; Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group. Effects of Non-Pharmaceutical Interventions on COVID-19 Cases, Deaths, and Demand for Hospital Services in the UK: A Modelling Study. Lancet Public Health 2020, 5, e375–e385. [Google Scholar] [CrossRef]
- Di Domenico, L.; Pullano, G.; Sabbatini, C.E.; Boëlle, P.Y.; Colizza, V. Impact of Lockdown on COVID-19 Epidemic in Île-de-France and Possible Exit Strategies. BMC Med. 2020, 18, 240. [Google Scholar] [CrossRef]
- Collin, A.; Hejblum, B.P.; Vignals, C.; Lehot, L.; Thiebaut, R.; Moireau, P.; Prague, M. Using Population Based Kalman Estimator to Model COVID-19 Epidemic in France: Estimating the Effects of Non-Pharmaceutical Interventions on the Dynamics of Epidemic. MedRxiv 2021. submitted. [Google Scholar] [CrossRef]
- Bubar, K.M.; Reinholt, K.; Kissler, S.M.; Lipsitch, M.; Cobey, S.; Grad, Y.H.; Larremore, D.B. Model-Informed COVID-19 Vaccine Prioritization Strategies by Age and Serostatus. Science 2021, 371, 916–921. [Google Scholar] [CrossRef]
- Harvey, R.A.; Rassen, J.A.; Kabelac, C.A.; Turenne, W.; Leonard, S.; Klesh, R.; Meyer, W.A., 3rd; Kaufman, H.W.; Anderson, S.; Cohen, O.; et al. Association of SARS-CoV-2 Seropositive Antibody Test with Risk of Future Infection. JAMA Intern. Med. 2021, 181, 672–679. [Google Scholar] [CrossRef]
- Lumley, S.F.; O’Donnell, D.; Stoesser, N.E.; Matthews, P.C.; Howarth, A.; Hatch, S.B.; Marsden, B.D.; Cox, S.; James, T.; Warren, F.; et al. Antibody Status and Incidence of SARS-CoV-2 Infection in Health Care Workers. N. Engl. J. Med. 2021, 384, 533–540. [Google Scholar] [CrossRef]
- Seow, J.; Graham, C.; Merrick, B.; Acors, S.; Pickering, S.; Steel, K.J.A.; Hemmings, O.; O’Byrne, A.; Kouphou, N.; Galao, R.P.; et al. Longitudinal Observation and Decline of Neutralizing Antibody Responses in the Three Months Following SARS-CoV-2 Infection in Humans. Nat. Microbiol. 2020, 5, 1598–1607. [Google Scholar] [CrossRef]
- Long, Q.-X.; Tang, X.-J.; Shi, Q.L.; Li, Q.; Deng, H.J.; Yuan, J.; Hu, J.L.; Xu, W.; Zhang, Y.; Lv, F.J.; et al. Clinical and Immunological Assessment of Asymptomatic SARS-CoV-2 Infections. Nat. Med. 2020, 26, 1200–1204. [Google Scholar] [CrossRef]
- den Hartog, G.; Vos, E.R.A.; van den Hoogen, L.L.; van Boven, M.; Schepp, R.M.; Smits, G.; van Vliet, J.; Woudstra, L.; Wijmenga-Monsuur, A.J.; van Hagen, C.C.E.; et al. Persistence of Antibodies to SARS-CoV-2 in Relation to Symptoms in a Nationwide Prospective Study. Clin. Infect. Dis. 2021. [Google Scholar] [CrossRef]
- Dan, J.M.; Mateus, J.; Kato, Y.; Hastie, K.M.; Yu, E.D.; Faliti, C.E.; Grifoni, A.; Ramirez, S.I.; Haupt, S.; Frazier, A.; et al. Immunological Memory to SARS-CoV-2 Assessed for up to 8 Months after Infection. Science 2021, 371, eabf4063. [Google Scholar] [CrossRef]
- Jung, J.H.; Rha, M.-S.; Sa, M.; Choi, H.K.; Jeon, J.H.; Seok, H.; Park, D.W.; Park, S.H.; Jeong, H.W.; Choi, W.S.; et al. SARS-CoV-2-Specific T Cell Memory Is Sustained in COVID-19 Convalescent Patients for 10 Months with Successful Development of Stem Cell-like Memory T Cells. Nat. Commun. 2021, 12, 4043. [Google Scholar] [CrossRef]
- Edridge, A.W.D.; Kaczorowska, J.; Hoste, A.C.; Bakker, M.; Klein, M.; Loens, K.; Jebbink, M.F.; Matser, A.; Kinsella, C.M.; Rueda, P.; et al. Seasonal Coronavirus Protective Immunity Is Short-Lasting. Nat. Med. 2020, 26, 1691–1693. [Google Scholar] [CrossRef]
- Sariol, A.; Perlman, S. Lessons for COVID-19 Immunity from Other Coronavirus Infections. Immunity 2020, 53, 248–263. [Google Scholar] [CrossRef]
- Liu, W.; Fontanet, A.; Zhang, P.H.; Zhan, L.; Xin, Z.T.; Baril, L.; Tang, F.; Lv, H.; Cao, W.C. Two-Year Prospective Study of the Humoral Immune Response of Patients with Severe Acute Respiratory Syndrome. J. Infect. Dis. 2006, 193, 792–795. [Google Scholar] [CrossRef] [Green Version]
- Le Bert, N.; Tan, A.; Kunasegaran, K.; Tham, C.Y.; Hafezi, M.; Chia, A.; Chng, M.H.Y.; Lin, M.; Tan, N.; Linster, M.; et al. SARS-CoV-2-Specific T Cell Immunity in Cases of COVID-19 and SARS, and Uninfected Controls. Nature 2020, 584, 457–462. [Google Scholar] [CrossRef]
- Shrotri, M.; Navaratnam, A.M.D.; Nguyen, V.; Byrne, T.; Geismar, C.; Fragaszy, E.; Beale, S.; Fong, W.L.E.; Patel, P.; Kovar, J.; et al. Spike-Antibody Waning after Second Dose of BNT162b2 or ChAdOx1. Lancet 2021, 398, 385–387. [Google Scholar] [CrossRef]
- Thomas, S.J.; Moreira, E.D.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Gonzalo Pérez, M.; Polack, F.P.; Zerbini, C.; et al. Six Month Safety and Efficacy of the BNT162b2 MRNA COVID-19 Vaccine. MedRxiv 2021. to be submitted. [Google Scholar] [CrossRef]
- Kissler, S.M.; Tedijanto, C.; Goldstein, E.; Grad, Y.H.; Lipsitch, M. Projecting the Transmission Dynamics of SARS-CoV-2 through the Postpandemic Period. Science 2020, 368, 860–868. [Google Scholar] [CrossRef]
- Lavine, J.S.; Bjornstad, O.N.; Antia, R. Immunological Characteristics Govern the Transition of COVID-19 to Endemicity. Science 2021, 371, 741–745. [Google Scholar] [CrossRef]
- Saad-Roy, C.M.; Wagner, C.E.; Baker, R.E.; Morris, S.E.; Farrar, J.; Graham, A.L.; Levin, S.A.; Mina, M.J.; Metcalf, C.J.E.; Grenfell, B.T. Immune Life History, Vaccination, and the Dynamics of SARS-CoV-2 over the next 5 Years. Science 2020, 370, 811–818. [Google Scholar] [CrossRef]
- Giannitsarou, C.; Kissler, S.; Toxvaerd, F. Waning Immunity and the Second Wave: Some Projections for SARS-CoV-2. University of Cambridge, Faculty of Economics, Centre for Economic Policy Research Discussion Paper No. DP14852. 2020. Available online: https://ssrn.com/abstract=3628172 (accessed on 7 October 2021).
- Santé Publique France. Point Epidémiologique n°78 du 26 aout 2021. Available online: https://www.santepubliquefrance.fr/maladies-et-traumatismes/maladies-et-infections-respiratoires/infection-a-coronavirus/documents/bulletin-national/covid-19-point-epidemiologique-du-26-aout-2021 (accessed on 7 October 2021).
- Kiem, C.T.; Massonnaud, A.; Levy-Bruhl, D.; Poletto, C.; Colizza, V.; Bosetti, P.; Fontanet, A.; Gabet, A.; Olié, V.; Zanetti, L.; et al. modelling study investigating short and medium-term challenges for COVID-19 vaccination: From prioritisation to the relaxation of measures. EClinicalMedicine 2021, 38, 101001. [Google Scholar] [CrossRef] [PubMed]
- European Center for Disease Prevention and Controle. Implications for the EU-EEA on the Spread of SARS-CoV-2 Delta-VOC; ECDC: Stockholm, Sweden, 2021. [Google Scholar]
- Santé Publique France. Résultats de la vague 26 de l’enquête CoviPrev (15–21 juillet 2021). Available online: https://www.santepubliquefrance.fr/etudes-et-enquetes/coviprev-une-enquete-pour-suivre-l-evolution-des-comportements-et-de-la-sante-mentale-pendant-l-epidemie-de-covid-19 (accessed on 7 October 2021).
- Collier, D.A.; Ferreira, I.A.T.M.; Kotagiri, P.; Datir, R.; Lim, E.; Touizer, E.; Meng, B.; Abdullahi, A.; CITIID-NIHR BioResource COVID-19 Collaboration; Elmer, A.; et al. Age-Related Immune Response Heterogeneity to SARS-CoV-2 Vaccine BNT162b2. Nature 2021, 596, 417–422. [Google Scholar] [CrossRef] [PubMed]
- Avis Relatif au Contact Tracing et à L’application des Mesures Barrières Chez les Personnes Totalement Vaccinées Contre le Covid-19. Haut Conseil de Santé Publique, France. Available online: https://www.hcsp.fr/Explore.cgi/AvisRapportsDomaine?clefr=1069 (accessed on 7 October 2021).
- Childs, L.; Dick, D.W.; Feng, Z.; Heffernan, J.M.; Li, J.; Röst, G. Modeling Waning and Boosting of COVID-19 in Canada with Vaccination. medRxiv 2021. to be submitted. [Google Scholar] [CrossRef]
- Carlsson, R.-M.; Childs, L.M.; Feng, Z.; Glasser, J.W.; Heffernan, J.M.; Li, J.; Röst, G. Modeling the Waning and Boosting of Immunity from Infection or Vaccination. J. Theor. Biol. 2020, 497, 110265. [Google Scholar] [CrossRef] [PubMed]
- Clark, A.; Jit, M.; Warren-Gash, C.; Guthrie, B.; Wang, H.H.; Mercer, S.W.; Sanderson, C.; McKee, M.; Troeger, C.; Ong, K.L.; et al. Global, Regional, and National Estimates of the Population at Increased Risk of Severe COVID-19 Due to Underlying Health Conditions in 2020: A Modelling Study. Lancet Glob. Health 2020, 8, e1003–e1017. [Google Scholar] [CrossRef]
- Crawford, K.H.D.; Dingens, A.S.; Eguia, R.; Wolf, C.R.; Wilcox, N.; Logue, J.K.; Shuey, K.; Casto, A.M.; Fiala, B.; Wrenn, S.; et al. Dynamics of Neutralizing Antibody Titers in the Months After Severe Acute Respiratory Syndrome Coronavirus 2 Infection. J. Infect. Dis. 2021, 223, 197–205. [Google Scholar] [CrossRef]
- Dufloo, J.; Grzelak, L. Asymptomatic and Symptomatic SARS-CoV-2 Infections Elicit Polyfunctional Antibodies. Cell Rep. Med. 2021, 2, 100275. [Google Scholar] [CrossRef]
- Piccoli, L.; Park, Y.-J.; Tortorici, M.A.; Czudnochowski, N.; Walls, A.C.; Beltramello, M.; Silacci-Fregni, C.; Pinto, D.; Rosen, L.E.; Bowen, J.E.; et al. Mapping Neutralizing and Immunodominant Sites on the SARS-CoV-2 Spike Receptor-Binding Domain by Structure-Guided High-Resolution Serology. Cell 2020, 183, 1024–1042.e21. [Google Scholar] [CrossRef]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial Undocumented Infection Facilitates the Rapid Dissemination of Novel Coronavirus (SARS-CoV-2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef] [Green Version]
- Prem, K.; Zandvoort, K.V.; Klepac, P.; Eggo, R.M.; Davies, N.G.; Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group; Cook, A.R.; Jit, M. Projecting contact matrices in 177 geographical regions: An update and comparison with empirical data for the COVID-19 era. PLoS Comput. Biol. 2021, 17, e1009098. [Google Scholar] [CrossRef]
- He, X.; Lau, E.H.Y.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal Dynamics in Viral Shedding and Transmissibility of COVID-19. Nat. Med. 2020, 26, 672–675. [Google Scholar] [CrossRef] [Green Version]
- Bi, Q.; Wu, Y.; Mei, S.; Ye, C.; Zou, X.; Zhang, Z.; Liu, X.; Wei, L.; Truelove, S.A.; Zhang, T.; et al. Epidemiology and Transmission of COVID-19 in 391 Cases and 1286 of Their Close Contacts in Shenzhen, China: A Retrospective Cohort Study. Lancet Infect. Dis. 2020, 20, 911–919. [Google Scholar] [CrossRef]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Hall, V.J.; Foulkes, S.; Saei, A.; Andrews, N.; Oguti, B.; Charlett, A.; Wellington, E.; Stowe, J.; Gilson, N.; Atti, A.; et al. Effectiveness of BNT162b2 MRNA Vaccine Against Infection and COVID-19 Vaccine Coverage in Healthcare Workers in England, Multicentre Prospective Cohort Study (the SIREN Study). SSRN Electron. J. 2021. Available online: https://ssrn.com/abstract=3790399 (accessed on 7 October 2021). [CrossRef]
- Dagan, N.; Barda, N.; Kepten, E.; Miron, O.; Perchik, S.; Katz, M.A.; Hernán, M.A.; Lipsitch, M.; Reis, B.; Balicer, R.D. BNT162b2 MRNA Covid-19 Vaccine in a Nationwide Mass Vaccination Setting. N. Engl. J. Med. 2021, 384, 1412–1423. [Google Scholar] [CrossRef]
- Pritchard, E.; Matthews, P.C.; Stoesser, N.; Eyre, D.W.; Gethings, O.; Vihta, K.D.; Jones, J.; House, T.; VanSteenHouse, H.; Bell, I.; et al. Impact of Vaccination on New SARS-CoV-2 Infections in the United Kingdom. Nat. Med. 2021, 27, 1370–1378. [Google Scholar] [CrossRef]
- Charmet, T.; Schaeffer, L.; Grant, R.; Galmiche, S.; Chény, O.; Von Platen, C.; Maurizot, A.; Rogoff, A.; Omar, F.; David, C.; et al. Impact of Original, B.1.1.7, and B.1.351/P.1 SARS-CoV-2 Lineages on Vaccine Effectiveness of Two Doses of COVID-19 MRNA Vaccines: Results from a Nationwide Case-Control Study in France. Lancet Reg. Health-Eur. 2021, 8, 100171. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The Construction of Next-Generation Matrices for Compartmental Epidemic Models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [Green Version]
- Van Vinh Chau, N.; Lam, V.T.; Dung, N.T.; Yen, L.M.; Minh, N.; Hung, L.M.; Ngoc, N.M.; Dung, N.T.; Man, D.N.H.; Nguyet, L.A.; et al. The Natural History and Transmission Potential of Asymptomatic Severe Acute Respiratory Syndrome Coronavirus 2 Infection. Clin. Infect. Dis. 2020, 71, 2679–2687. [Google Scholar] [CrossRef]
- Cheng, H.-Y.; Jian, S.-W.; Liu, D.P.; Ng, T.C.; Huang, W.T.; Lin, H.H.; Taiwan COVID-19 Outbreak Investigation Team. Contact Tracing Assessment of COVID-19 Transmission Dynamics in Taiwan and Risk at Different Exposure Periods Before and After Symptom Onset. JAMA Intern. Med. 2020, 180, 1156. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, L.-M.; Wan, L.; Xiang, T.X.; Le, A.; Liu, J.M.; Peiris, M.; Poon, L.L.M.; Zhang, W. Viral Dynamics in Mild and Severe Cases of COVID-19. Lancet Infect. Dis. 2020, 20, 656–657. [Google Scholar] [CrossRef] [Green Version]
- Zheng, S.; Fan, J.; Yu, F.; Feng, B.; Lou, B.; Zou, Q.; Xie, G.; Lin, S.; Wang, R.; Yang, X.; et al. Viral Load Dynamics and Disease Severity in Patients Infected with SARS-CoV-2 in Zhejiang Province, China, January-March 2020: Retrospective Cohort Study. BMJ 2020, 369, m1443. [Google Scholar] [CrossRef] [Green Version]
- Davies, N.G.; Abbott, S.; Barnard, R.C.; Jarvis, C.I.; Kucharski, A.J.; Munday, J.D.; Pearson, C.A.B.; Russell, T.W.; Tully, D.C.; Washburne, A.D.; et al. Estimated Transmissibility and Impact of SARS-CoV-2 Lineage B.1.1.7 in England. Science 2021, 372, eabg3055. [Google Scholar] [CrossRef]
- Gaymard, A.; Bosetti, P.; Feri, A.; Destras, G.; Enouf, V.; Andronico, A.; Burrel, S.; Behillil, S.; Sauvage, C.; Bal, A.; et al. Early Assessment of Diffusion and Possible Expansion of SARS-CoV-2 Lineage 20I/501Y.V1 (B.1.1.7, Variant of Concern 202012/01) in France, January to March 2021. Eurosurveillance 2021, 26, 2100133. [Google Scholar] [CrossRef]
- Campbell, F.; Archer, B.; Laurenson-Schafer, H.; Jinnai, Y.; Konings, F.; Batra, N.; Pavlin, B.; Vandemaele, K.; Van Kerkhove, M.D.; Jombart, T.; et al. Increased Transmissibility and Global Spread of SARS-CoV-2 Variants of Concern as at June 2021. Eurosurveillance 2021, 26, 2100509. [Google Scholar] [CrossRef]
- Les Actions du Gouvernement. Available online: https://www.gouvernement.fr/info-coronavirus/les-actions-du-gouvernement (accessed on 7 October 2021).
- Liu, X.; Huang, J.; Li, C.; Zhao, Y.; Wang, D.; Huang, Z.; Yang, K. The Role of Seasonality in the Spread of COVID-19 Pandemic. Environ. Res. 2021, 195, 110874. [Google Scholar] [CrossRef]
- Nombre de Lits de Réanimation, de Soins Intensifs et de Soins Continus En France, Fin 2013 et 2019. DRESS. 2021. Available online: https://drees.solidarites-sante.gouv.fr/article/nombre-de-lits-de-reanimation-de-soins-intensifs-et-de-soins-continus-en-france-fin-2013-et (accessed on 6 August 2021).
- Lopez Bernal, J.; Andrews, N.; Gower, C.; Gallagher, E.; Simmons, R.; Thelwall, S.; Stowe, J.; Tessier, E.; Groves, N.; Dabrera, G.; et al. Effectiveness of Covid-19 Vaccines against the B.1.617.2 (Delta) Variant. N. Engl. J. Med. 2021, 385, 585–594. [Google Scholar] [CrossRef]
- Kiem, C.T.; Bosetti, P.; Hozé, N.; Paireau, J.; Cauchemez, S. Impact de L’accélération de la Vaccination sur L’épidémie du Variant Delta en France Métropolitaine; Institut Pasteur: Paris, France, 2021; Available online: https://modelisation-covid19.pasteur.fr/variant/Institut_Pasteur_Acceleration_vaccination_et_Delta_20210726.pdf (accessed on 7 October 2021).
- Bosetti, P.; Kiem, C.T.; Andronico, A.; Colizza, V.; Yazdanpanah, Y.; Fontanet, A.; Benamouzig, D.; Cauchemez, S. Epidemiology and Control of SARS-CoV-2 Epidemics in Partially Vaccinated Populations: A Modeling Study Applied to France; Institut Pasteur: Paris, France, 2021; to be submitted; Available online: https://hal-pasteur.archives-ouvertes.fr/pasteur-03272638 (accessed on 7 October 2021).
- Mesa, D.O.; Hogan, A.B.; Watson, O.J.; Charles, G.D.; Hauck, K.; Ghani, A.C.; Winskill, P. Report 43: Quantifying the Impact of Vaccine Hesitancy in Prolonging the Need for Non-Pharmaceutical Interventions to Control the COVID-19 Pandemic. Imp. Coll. Lond. 2021. to be submitted. [Google Scholar] [CrossRef]
- Hozé, N.; Paireau, J.; Lapidus, N.; Kiem, C.T.; Salje, H.; Severi, G.; Touvier, M.; Zins, M.; de Lamballerie, X.; Lévy-Bruhl, D.; et al. Monitoring the Proportion of the Population Infected by SARS-CoV-2 Using Age-Stratified Hospitalisation and Serological Data: A Modelling Study. Lancet Public Health 2021, 6, e408–e415. [Google Scholar] [CrossRef]
- Les Données de la Vaccination Contre la COVID, Assurance Maladie. Available online: https://datavaccin-covid.ameli.fr/pages/type-vaccins/ (accessed on 7 October 2021).
- Nyberg, T.; Twohig, K.A.; Harris, R.J.; Seaman, S.R.; Flannagan, J.; Allen, H.; Charlett, A.; De Angelis, D.; Dabrera, G.; Presanis, A.M. Risk of Hospital Admission for Patients with SARS-CoV-2 Variant B.1.1.7: Cohort Analysis. BMJ 2021, 373, n1412. [Google Scholar] [CrossRef] [PubMed]
- Viguerie, A.; Lorenzo, G.; Auricchio, F.; Baroli, D.; Hughes, T.J.; Patton, A.; Reali, A.; Yankeelov, T.E.; Veneziani, A. Simulating the spread of COVID-19 via a spatially-resolved susceptible–exposed–infected–recovered–deceased (SEIRD) model with heterogeneous diffusion. Appl. Math. Lett. 2021, 111, 106617. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).