Pandemic Growth and Benfordness: Empirical Evidence from 176 Countries Worldwide
Abstract
:1. Introduction
Pandemic Growth
2. Materials and Methods
2.1. Hypothesis Testing
2.2. COVID-19 Data Sampling
3. Results
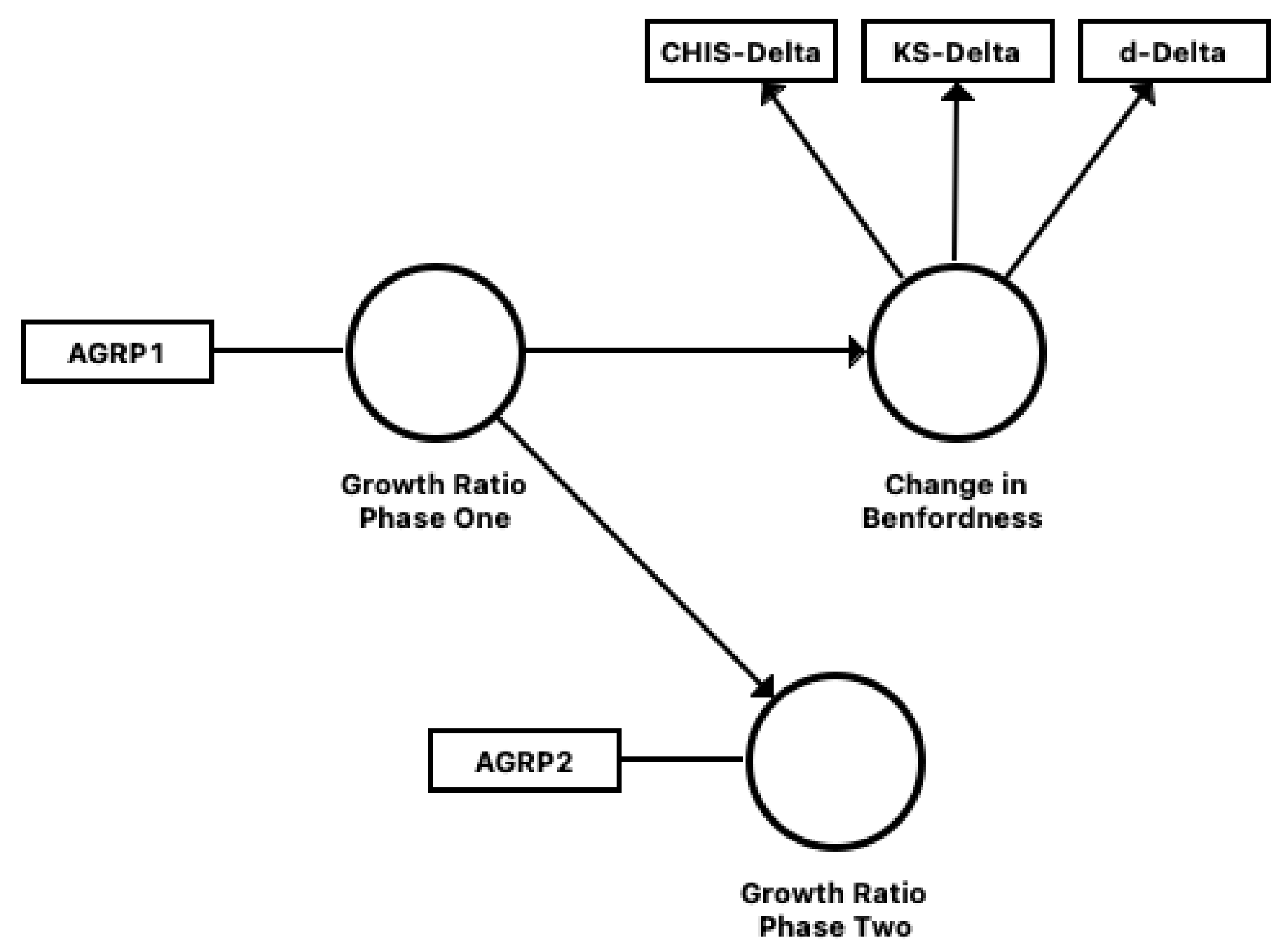
3.1. Measurement Model
3.2. Structural Model
4. Conclusions
4.1. Findings
4.2. Limitation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Coronavirus Disease (COVID-19) Outbreak. Geneva: WHO. 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 13 June 2021).
- Koch, C.; Okamura, K. Benford’s Law and COVID-19 Reporting. 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3586413 (accessed on 20 August 2021).
- Idrovo, A.J.; Manrique-Hernandez, E.F. Data Quality of Chinese Surveillance of 270 COVID-19: Objective Analysis Based on WHO’s Situation Reports. Asia. Pac. J. Public Health 2020, 32, 165–167. [Google Scholar] [CrossRef]
- Wie, A.; Vellwock, A.E. Is COVID-19 Data Reliable? A Statistical Analysis with Benford’s Law. 2020. Available online: https://www.researchgate.net/publication/344164702_Is_COVID-19_data_reliable_A_statistical_analysis_with_Benford%27s_Law (accessed on 13 June 2021).
- Lee, K.-B.; Han, S.; Jeong, Y. COVID-19 Flattening the Curve, and Benford’s Law. Phys. A Stat. Mech. Its Appl. 2020, 559, 125090. [Google Scholar] [CrossRef]
- Isea, R. How Valid are the Reported Cases of People Infected with Covid-19 in the World? Int. J. Coronaviruses 2020, 1, 53–56. [Google Scholar] [CrossRef]
- Sambridge, M.; Jackson, A. National COVID numbers—Benford’s law looks for errors. Nature 2020, 581, 384–385. [Google Scholar] [CrossRef]
- Farhadi, N. Can we rely on Covid-19 data? An assessment of data from over 200 countries. Sci. Prog. 2021, 104, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Farhadi, N.; Lahooti, H. Are COVID-19 Data Reliable? A Quantitative Analysis of Pandemic Data from 182 Countries. COVID 2021, 1, 137–152. [Google Scholar] [CrossRef]
- Newcomb, S. Note on the Frequency of Use of the Different Digits in Natural 242 Numbers. Am. J. Math. 1881, 4, 39–40. [Google Scholar] [CrossRef] [Green Version]
- Benford, F. The Law of Anomalous Numbers. Proc. Am. Philos. Soc. 1938, 78, 551–572. [Google Scholar]
- Durtschi, C.; Hillison, W.; Pacini, C. The Effective Use of Benford’s law to Assist in Detecting Fraud in Accounting Data. J. Forensic Account. 2004, 5, 17–34. [Google Scholar]
- Grammatikos, T.; Papanikolaou, N.I. Applying Benford’s law to Detect Accounting 250 Data Manipulation in the Banking Industry. J. Financ. Serv. Res. 2020, 59, 115–142. [Google Scholar] [CrossRef]
- Roukema, B.F. A first-digit anomaly in the 2009 Iranian presidential election. J. Appl. Stat. 2014, 41, 164–199. [Google Scholar] [CrossRef] [Green Version]
- Castorina, P.; Iorio, A.; Lanteri, D. Data analysis on CoronavirusCoronavirus spreading by macroscopic growth Laws. Int. J. Mod. Phys. C 2020, 31, 2050103. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Kurkin, A.; Kurkina, O.; Kokoulina, M.; Epifanova, A. Logistic equation and COVID-19. Chaos Solitons Fractals 2020, 140, 110241. [Google Scholar] [CrossRef]
- World Health Organization. Severe Acute Respiratory Syndrome (SARS). Available online: https://www.who.int/health-topics/severe-acute-respiratory-syndrome#tab=tab_1 (accessed on 4 August 2021).
- Ma, J. Estimating epidemic exponential growth rate and basic reproduction number. Infect. Dis. Model. 2020, 5, 129–141. [Google Scholar] [CrossRef] [PubMed]
- US Department of Health & Human Services. 1918 Pandemic (H1N1 Virus). Available online: https://www.cdc.gov/flu/pandemic-resources/1918-pandemic-h1n1.html (accessed on 4 August 2021).
- Sanderson, G. Exponential Growth and Epidemics. 2020. Available online: https://www.youtube.com/watch?v=Kas0tIxDvrg (accessed on 3 September 2021).
- Putz, C. If Only It Were That Easy: Tajikistan Declares Itself COVID-19 Free. The Diplomat. 2021. Available online: https://thediplomat.com/2021/01/if-only-it-were-that-easy-tajikistan-declares-itself-covid-19-free (accessed on 13 June 2021).
- Vector, D. What’s Happening in Belarus? Here Are the Basics. New York Times. 2021. Available online: https://www.nytimes.com/2021/05/26/world/europe/whats-happening-in-belarus.html (accessed on 13 June 2021).
- Deutsche Welle. Why Bangladesh is No Longer Fear the Coronavirus. 2021. Available online: https://www.dw.com/en/bangladesh-coronavirus-no-fear/a-55091050 (accessed on 13 June 2021).
- Yackley, A.J. Dollar Blow for Turkey as Tourism Season Runs into the Sand. Financial Times. 2021. Available online: https://www.ft.com/content/f7f4f65f-400d-437d-9ffa-e50fec485942 (accessed on 13 June 2021).
- Jarvis, S.B.; MacKenzie, S.B.; Podsakoff, P.M. A critical review of construct indicators and measurement model misspecification in marketing and consumer research. J. Consum. Res. 2003, 30, 199–218. [Google Scholar] [CrossRef]
- Hair, J.F.; Risher, J.J.; Sarstedt, M.; Ringle, C.M. When to use and how to report the results of PLS-SEM. Eur. Bus. Rev. 2019, 31, 2–24. [Google Scholar] [CrossRef]
- Hult, J.F.; Ringle, C.M.; Sarstedt, M. A Primer on Partial Least Squares Structural Equation Modeling (PLS-SEM); Sage Publications: Thousand Oaks, CA, USA, 2017. [Google Scholar]
- Rönkkö, M.; Cho, E. An Updated Guideline for Assessing Discriminant Validity. Organ. Res. Methods 2020, 1094428120968614. [Google Scholar] [CrossRef]
- Brown, W. Some experimental results in the correlation of mental abilities. Br. J. Psychol. 1910, 3, 296–322. [Google Scholar] [CrossRef]
- Reinartz, W.J.; Haenlein, M.; Henseler, J. An empirical comparison of the efficacy of covariance-based and variance-based SEM. Int. J. Res. Mark. 2009, 26, 332–344. [Google Scholar] [CrossRef] [Green Version]
- Hair, J.F.; Hult, G.T.M.; Ringle, C.M.; Sarstedt, M.; Thiele, K.O. Mirror, Mirror on the wall: A comparative evaluation of composite-based structural equation modeling methods. J. Acad. Mark. Sci. 2017, 45, 616–632. [Google Scholar] [CrossRef]
- Jöreskog, K.G. Simultaneous factor analysis in several populations. Psychometrika 1971, 36, 409–426. [Google Scholar] [CrossRef]
- Chin, W. Issues and Opinion on Structural Equation Modeling. Manag. Inf. Syst. Q. 1988, 22, 1–11. [Google Scholar]
- Voorhees, C.M.; Brady, M.K.; Calantone, R.; Ramirez, E. Discriminant validity testing in marketing: An analysis, causes for concern, and proposed remedies. J. Acad. Mark. Sci. 2016, 44, 119–134. [Google Scholar] [CrossRef]
- Shmueli, G.; Ray, S.; Velasquez Estrada, J.M.; Shatla, S.B. The elephant in the room: Evaluating the predictive performance of PLS models. J. Bus. Res. 2016, 69, 4552–4564. [Google Scholar] [CrossRef]
- Chornokondratenko, M. Treated Like a ‘Toy’: Another Belarusian Athlete on Life under Lukashenko. 2021. Available online: https://www.reuters.com/world/europe/treated-like-toy-another-belarusian-athlete-life-under-lukashenko-2021-08-09 (accessed on 3 September 2021).
- BBC. Coronavirus: Iran Cover-Up of Deaths Revealed by Data Leak. Available online: https://www.bbc.com/news/world-middle-east-53598965 (accessed on 15 August 2021).
- Johns Hopkins University. Global Health Security Index. 2019. Available online: https://www.ghsindex.org/ (accessed on 13 June 2021).

| Researcher | Variables | Deadline | Number of Countries |
|---|---|---|---|
| Idrovo and Manrique-Hernándlockez | Confirmed cases, suspected cases, and deaths, cumulated confirmed cases, and cumulated confirmed deaths | 21 January 2020–15 March 2020 | 1 |
| Koch and Okamura | Daily cases, deaths | 20 January 2020–10 April 2020 | 3 |
| Lee, Han, and Jeong | Daily cases, deaths | 22 January 2020–6 April 2020 | 10 |
| Wei and Vellwock | Daily cases, deaths | Not stated–1 September 2020 | 20 |
| Isea | Daily cases, deaths | 29 December 2019–30 April 2020 | 23 |
| Jackson and Sambridge | Cumulated confirmed cases and deaths | 16 January 2020–9 April 2020 | 51 |
| Farhadi | Daily cases, deaths, tests | 31 December 2019–24 September 2020 | 182 |
| Farhadi and Lahooti | Daily cases, deaths, tests, vaccination | 21 January 2020–6 June 2021 | 154 |
| First Digit | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Benford’s frequency | 0.301 | 0.176 | 0.125 | 0.097 | 0.079 | 0.067 | 0.058 | 0.051 | 0.046 |
| Location | Total Growth | Total STDEV | Phase1 Growth | STDEV Phase1 | Phase2 Growth | STDEV Phase2 |
|---|---|---|---|---|---|---|
| Afghanistan | 1.38 | 2.14 | 1.48 | 2.85 | 1.29 | 1.29 |
| Germany | 1.37 | 1.59 | 1.34 | 1.63 | 1.40 | 1.55 |
| Australia | 1.26 | 1.51 | 1.30 | 2.02 | 1.22 | 0.90 |
| Israel | 1.25 | 2.16 | 1.23 | 1.43 | 1.26 | 2.62 |
| Belgium | 1.10 | 0.58 | 1.11 | 0.67 | 1.09 | 0.50 |
| Pakistan | 1.09 | 1.01 | 1.21 | 1.51 | 1.00 | 0.21 |
| Kuwait | 1.06 | 0.54 | 1.11 | 0.78 | 1.02 | 0.18 |
| Turkey | 1.05 | 0.59 | 1.09 | 0.82 | 1.02 | 0.29 |
| Netherlands | 1.04 | 0.31 | 1.07 | 0.42 | 1.01 | 0.18 |
| Bangladesh | 1.04 | 0.27 | 1.07 | 0.35 | 1.02 | 0.19 |
| Iraq | 1.04 | 0.36 | 1.07 | 0.51 | 1.01 | 0.16 |
| Russia | 1.04 | 0.49 | 1.08 | 0.74 | 1.00 | 0.05 |
| Indonesia | 1.04 | 0.35 | 1.07 | 0.49 | 1.01 | 0.16 |
| Iran | 1.03 | 0.21 | 1.06 | 0.30 | 1.01 | 0.09 |
| Belarus | 1.03 | 0.67 | 1.04 | 0.98 | 1.02 | 0.27 |
| Tajikistan | 0.96 | 0.28 | 0.96 | 0.28 | 0.95 | 0.26 |
| Sweden | 0.95 | 1.19 | 1.21 | 1.43 | 0.57 | 0.48 |
| d* | CHI | K-S | Growth | Phase1 | Phase2 | ||||
|---|---|---|---|---|---|---|---|---|---|
| d-Factor | 100% | ||||||||
| CHI | 49% | 100% | |||||||
| K-S | 73% | 45% | 100% | ||||||
| Growth | 12% | 58% | 15% | 100% | |||||
| Phase1 | 26% | 75% | 28% | 78% | 100% | ||||
| Phase2 | 7% | 46% | 10% | 98% | 64% | 100% | |||
| 9% | 53% | 9% | 98% | 70% | 99% | 100% | |||
| 21% | 76% | 19% | 78% | 96% | 65% | 73% | 100% | ||
| 8% | 50% | 8% | 98% | 67% | 99% | 100% | 69% | 100% |
| Variable | Definition | N | Mean | Std. Deviation | Minimum | Maximum |
|---|---|---|---|---|---|---|
| d-Delta | d* improvement between Phase One and Phase Two : d-factor for Period B from 21 January 2020 to 6 June2021; : d-factor for Period A from 31 December 2019 to 24 September 2020 | 174 | 0.890 | 0.442 | 0.260 | 2.537 |
| 102 | 0.972 | 0.491047 | 0.293 | 2.538 | ||
| KS-Delta | K-S change between Phase One and Phase Two : K-S statistic for the period B from 21 january 2020 to 6 June 2021 : K-S statistic for period A from 31 December 2019 to 24 September 2020 | 174 | 4.377 | 6.5230 | 0.248 | 36.530 |
| 102 | 24.990 | 14.625 | 6.410 | 71.117 | ||
| CHI-Delta | Chi-square change between Phase One and Phase Two : Chi-square for Period B from 21 January 2020 to 6 June 2021 : Chi-square for Period A from 31 December 2019 to 24 September 2020 | 174 | 4.782 | 13.063 | 0.006 | 137.382 |
| 104 | 6.256 | 16.730 | 0.006 | 137.382 | ||
| AGRP1 | Average growth ratio for the period from 21 January 2020 to 24 September 2020 | 176 | 1.202 | 0.798 | 0.056 | 10.546 |
| 102 | 1.311 | 0.952 | 0.188 | 10.546 | ||
| AGRP2 | Average growth ratio for the period from 25 September 2020 to 6 June 2021 | 176 | 1.242 | 1.668 | 0.000 | 17.901 |
| 102 | 1.382 | 2.154 | 0.000 | 17.901 |
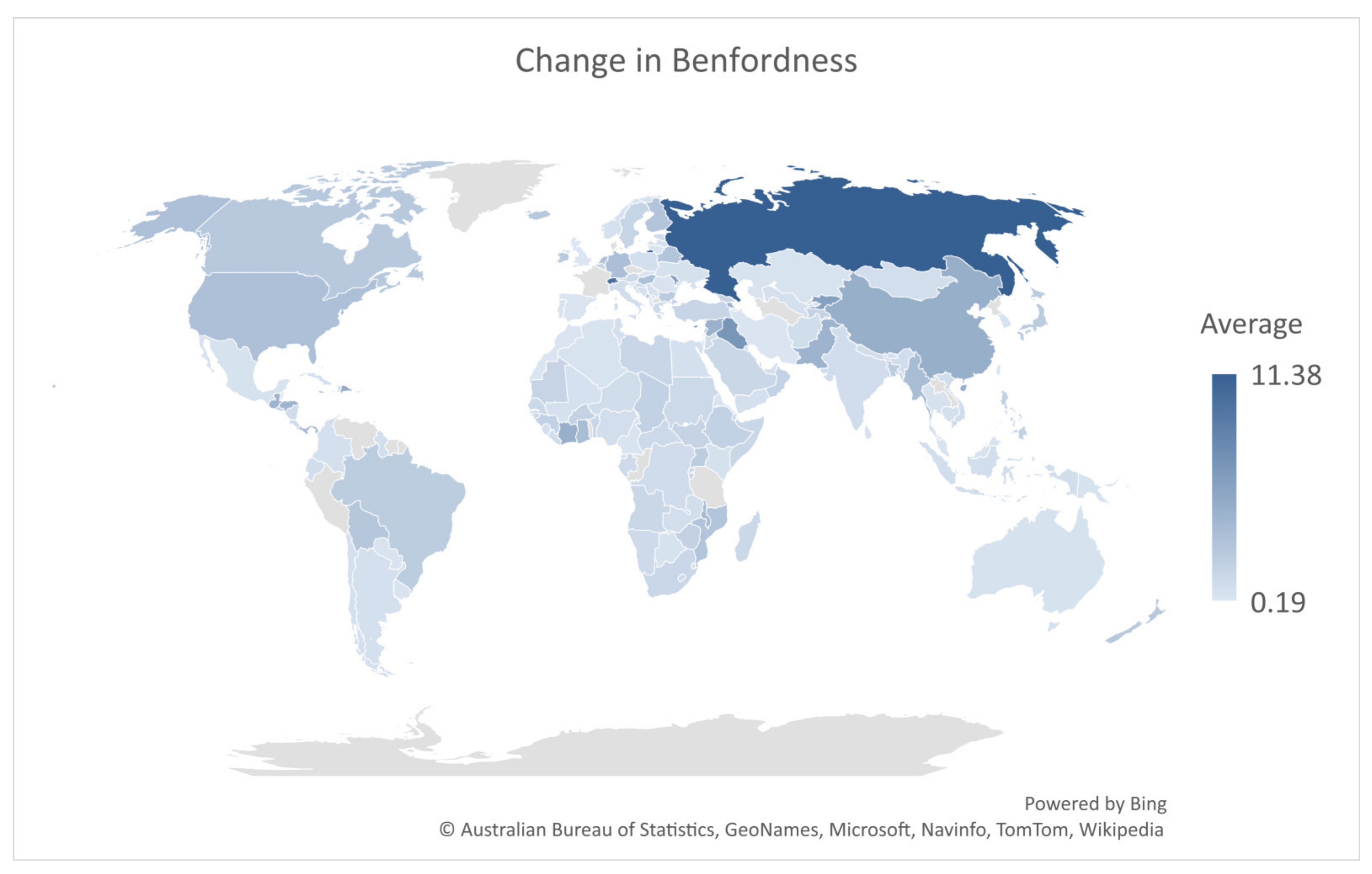
| Location | Sample Size | CHI-Delta | KS-Delta | d-Delta | AGRP1 | AGRP2 |
|---|---|---|---|---|---|---|
| Afghanistan | 814 | 1.01 | 2.51 | 0.40 | 1.48 | 1.29 |
| Albania | 1281 | 0.03 | 3.95 | 0.01 | 1.20 | 1.04 |
| Algeria | 897 | 0.41 | 2.28 | 0.18 | 1.11 | 1.01 |
| Andorra | 394 | 0.62 | 2.81 | 0.22 | 1.83 | 0.95 |
| Angola | 677 | 2.67 | 3.39 | 0.79 | 1.26 | 1.18 |
| Antigua and Barbuda | 167 | 5.60 | 5.76 | 0.97 | 0.12 | 0.59 |
| Argentina | 1369 | 0.67 | 2.36 | 0.28 | 1.09 | 1.04 |
| Armenia | 1063 | 11.01 | 2.93 | 3.76 | 1.21 | 1.13 |
| Australia | 878 | 0.05 | 1.77 | 0.03 | 1.30 | 1.22 |
| Austria | 1265 | 1.65 | 2.37 | 0.70 | 1.28 | 1.02 |
| Azerbaijan | 888 | 11.01 | 2.52 | 4.37 | 1.03 | 1.10 |
| Bahamas | 368 | 1.14 | 2.36 | 0.49 | 1.14 | 0.79 |
| Bahrain | 1115 | 1.00 | 2.49 | 0.40 | 1.44 | 1.02 |
| Bangladesh | 1332 | 4.11 | 2.37 | 1.73 | 1.07 | 1.02 |
| Barbados | 318 | 0.97 | 3.83 | 0.25 | 0.74 | 1.14 |
| Belarus | 916 | 7.03 | 2.22 | 3.17 | 1.04 | 1.02 |
| Belgium | 1341 | 3.57 | 2.21 | 1.62 | 1.11 | 1.09 |
| Belize | 395 | 0.56 | 4.11 | 0.14 | 0.79 | 1.00 |
| Benin | 168 | 2.16 | 1.66 | 1.30 | 0.37 | 0.06 |
| Bhutan | 636 | 1.21 | 8.05 | 0.15 | 0.70 | 1.25 |
| Bolivia | 1267 | 6.21 | 2.30 | 2.70 | 1.17 | 1.06 |
| Bosnia and Herzegovina | 1030 | 1.13 | 2.97 | 0.38 | 1.20 | 0.83 |
| Botswana | 180 | 0.60 | 3.46 | 0.17 | 0.08 | 0.05 |
| Brazil | 888 | 4.31 | 2.25 | 1.92 | 1.16 | 1.09 |
| Bulgaria | 1194 | 5.12 | 2.58 | 1.98 | 1.32 | 1.46 |
| Burkina Faso | 464 | 3.25 | 2.38 | 1.37 | 1.33 | 1.06 |
| Burundi | 255 | 3.72 | 4.40 | 0.85 | 0.48 | 1.45 |
| Cambodia | 300 | 1.15 | 5.36 | 0.21 | 0.92 | 0.96 |
| Cameroon | 247 | 0.08 | 1.43 | 0.06 | 1.06 | 0.20 |
| Canada | 1373 | 5.84 | 2.37 | 2.47 | 1.27 | 1.17 |
| Cape Verde | 883 | 0.20 | 4.31 | 0.05 | 1.67 | 1.23 |
| The Central African Republic | 211 | 1.63 | 1.56 | 1.04 | 1.07 | 0.45 |
| Chad | 468 | 3.70 | 2.94 | 1.26 | 1.19 | 1.35 |
| Chile | 1310 | 0.54 | 2.29 | 0.24 | 1.07 | 1.03 |
| China | 572 | 10.19 | 1.46 | 6.98 | 1.53 | 1.15 |
| Colombia | 1247 | 0.70 | 2.15 | 0.32 | 1.11 | 1.02 |
| Comoros | 243 | 0.13 | 4.76 | 0.03 | 0.49 | 2.51 |
| Congo | 1145 | 1.76 | 2.17 | 0.81 | 0.19 | 0.00 |
| Costa Rica | 1081 | 1.51 | 2.25 | 0.67 | 1.20 | 0.70 |
| Cote d’Ivoire | 985 | 9.45 | 2.40 | 3.94 | 1.20 | 1.78 |
| Croatia | 1216 | 1.54 | 2.44 | 0.63 | 1.13 | 1.31 |
| Cuba | 1117 | 0.59 | 2.54 | 0.23 | 1.23 | 1.07 |
| Cyprus | 1029 | 16.56 | 5.44 | 3.04 | 1.22 | 1.06 |
| Dem. Rep. of Congo | 992 | 4.15 | 2.40 | 1.73 | 1.34 | 1.26 |
| Denmark | 1256 | 1.11 | 2.42 | 0.46 | 1.76 | 17.90 |
| Djibouti | 432 | 3.32 | 2.53 | 1.32 | 1.33 | 1.66 |
| Dominican Republic | 1205 | 11.41 | 2.21 | 5.17 | 1.10 | 1.14 |
| Ecuador | 1284 | 1.08 | 2.31 | 0.47 | 1.52 | 1.70 |
| Egypt | 901 | 0.66 | 2.35 | 0.28 | 1.28 | 1.01 |
| El Salvador | 1155 | 4.22 | 2.54 | 1.66 | 1.06 | 0.88 |
| Equatorial Guinea | 155 | 0.72 | 2.77 | 0.26 | 0.20 | 0.02 |
| Eritrea | 180 | 0.28 | 4.00 | 0.07 | 0.15 | 0.81 |
| Estonia | 1145 | 0.91 | 2.68 | 0.34 | 1.39 | 1.11 |
| Ethiopia | 1222 | 2.54 | 2.63 | 0.97 | 1.20 | 1.05 |
| Finland | 1121 | 5.57 | 2.32 | 2.40 | 1.33 | 1.05 |
| France | 1281 | 137.38 | 2.47 | 55.66 | 10.55 | 14.79 |
| Gabon | 293 | 1.56 | 2.06 | 0.76 | 0.59 | 0.04 |
| The Gambia | 614 | 2.09 | 5.20 | 0.40 | 0.68 | 0.94 |
| Georgia | 740 | 3.40 | 3.56 | 0.96 | 1.32 | 1.22 |
| Germany | 911 | 7.44 | 2.23 | 3.33 | 1.34 | 1.40 |
| Ghana | 793 | 8.42 | 2.29 | 3.67 | 0.91 | 0.73 |
| Greece | 1233 | 2.02 | 2.54 | 0.79 | 1.51 | 1.07 |
| Guatemala | 1295 | 11.21 | 3.82 | 2.93 | 1.33 | 1.49 |
| Guinea | 1044 | 3.85 | 2.53 | 1.52 | 0.97 | 1.10 |
| Guinea-Bissau | 209 | 2.89 | 2.40 | 1.20 | 0.75 | 0.93 |
| Guyana | 577 | 1.16 | 3.14 | 0.37 | 1.20 | 1.49 |
| Haiti | 440 | 1.38 | 1.81 | 0.76 | 1.40 | 0.84 |
| Honduras | 803 | 10.53 | 2.27 | 4.63 | 1.33 | 1.12 |
| Hong Kong | 574 | 2.51 | 2.23 | 1.12 | 1.19 | 1.24 |
| Hungary | 1299 | 7.19 | 2.47 | 2.91 | 1.21 | 1.05 |
| Iceland | 797 | 5.85 | 2.18 | 2.69 | 1.11 | 0.91 |
| India | 1320 | 1.20 | 2.30 | 0.52 | 1.21 | 1.00 |
| Indonesia | 1242 | 1.05 | 2.30 | 0.46 | 1.07 | 1.01 |
| Iran | 1127 | 0.12 | 2.06 | 0.06 | 1.05 | 1.01 |
| Iraq | 1231 | 16.20 | 2.40 | 6.75 | 1.07 | 1.01 |
| Ireland | 1208 | 5.31 | 2.35 | 2.26 | 1.35 | 1.04 |
| Israel | 1335 | 0.21 | 2.24 | 0.10 | 1.23 | 1.26 |
| Italy | 1401 | 1.13 | 2.39 | 0.47 | 1.06 | 1.02 |
| Jamaica | 911 | 9.20 | 4.38 | 2.10 | 1.14 | 1.15 |
| Japan | 1403 | 3.99 | 3.32 | 1.20 | 1.09 | 1.05 |
| Jordan | 904 | 1.35 | 4.28 | 0.32 | 1.23 | 1.01 |
| Kazakhstan | 1160 | 0.51 | 2.53 | 0.20 | 1.54 | 2.65 |
| Kenya | 999 | 0.50 | 2.13 | 0.23 | 1.13 | 1.21 |
| Kosovo | 613 | 0.71 | 2.05 | 0.35 | 1.53 | 0.63 |
| Kuwait | 1236 | 1.49 | 2.47 | 0.60 | 1.11 | 1.02 |
| Kyrgyzstan | 677 | 15.50 | 2.57 | 6.02 | 1.45 | 0.99 |
| Latvia | 1154 | 0.66 | 2.77 | 0.24 | 1.66 | 1.19 |
| Lebanon | 807 | 6.62 | 2.78 | 2.38 | 1.36 | 1.04 |
| Lesotho | 241 | 1.98 | 3.95 | 0.50 | 0.29 | 1.82 |
| Liberia | 281 | 1.12 | 1.46 | 0.77 | 1.29 | 0.53 |
| Libya | 1032 | 1.71 | 2.61 | 0.66 | 1.15 | 0.88 |
| Liechtenstein | 686 | 1.50 | 13.72 | 0.11 | 0.47 | 1.62 |
| Lithuania | 1190 | 0.38 | 3.25 | 0.12 | 1.30 | 1.08 |
| Luxembourg | 1027 | 6.30 | 2.31 | 2.72 | 1.39 | 0.84 |
| Macedonia | 1273 | - | - | - | 1.39 | 0.84 |
| Madagascar | 625 | 2.13 | 2.47 | 0.86 | 1.32 | 0.93 |
| Malawi | 739 | 10.13 | 2.14 | 4.73 | 1.70 | 1.28 |
| Malaysia | 1195 | 0.32 | 2.61 | 0.12 | 1.40 | 1.05 |
| Maldives | 936 | 0.92 | 2.57 | 0.36 | 1.26 | 1.12 |
| Mali | 641 | 0.98 | 2.68 | 0.37 | 1.60 | 1.54 |
| Malta | 1081 | 1.86 | 2.77 | 0.67 | 1.35 | 1.11 |
| Mauritania | 621 | 3.14 | 4.78 | 0.66 | 1.33 | 1.21 |
| Mauritius | 188 | 0.92 | 3.62 | 0.25 | 1.08 | 0.98 |
| Mexico | 1412 | 0.37 | 2.18 | 0.17 | 1.08 | 1.16 |
| Moldova | 884 | 14.04 | 2.37 | 5.92 | 1.12 | 1.10 |
| Monaco | 335 | 1.38 | 4.04 | 0.34 | 0.85 | 1.31 |
| Mongolia | 528 | 1.56 | 8.38 | 0.19 | 1.05 | 1.16 |
| Montenegro | 707 | 4.33 | 3.29 | 1.32 | 1.23 | 1.03 |
| Morocco | 1308 | 0.20 | 2.40 | 0.08 | 1.21 | 1.20 |
| Mozambique | 1046 | 5.67 | 2.83 | 2.01 | 1.46 | 1.11 |
| Myanmar | 897 | 7.56 | 5.86 | 1.29 | 1.38 | 1.10 |
| Namibia | 951 | 1.91 | 3.37 | 0.56 | 1.43 | 1.21 |
| Nepal | 1170 | 1.40 | 2.61 | 0.54 | 1.03 | 1.04 |
| Netherlands | 889 | 6.36 | 2.38 | 2.67 | 1.07 | 1.01 |
| New Zealand | 711 | 5.32 | 2.01 | 2.65 | 0.95 | 1.38 |
| Nicaragua | 132 | 1.43 | 2.13 | 0.67 | 0.06 | 0.00 |
| Niger | 423 | 1.63 | 2.60 | 0.63 | 0.94 | 1.26 |
| Nigeria | 922 | 0.89 | 2.02 | 0.44 | 1.16 | 1.17 |
| Norway | 1066 | 0.65 | 2.37 | 0.27 | 1.27 | 1.07 |
| Oman | 695 | 3.12 | 1.93 | 1.61 | 1.01 | 0.63 |
| Pakistan | 1286 | 10.48 | 2.29 | 4.58 | 1.21 | 1.00 |
| Palestine | 1025 | 1.77 | 3.96 | 0.45 | 1.25 | 0.99 |
| Panama | 1327 | 6.91 | 2.30 | 3.00 | 1.83 | 1.04 |
| Papua New Guinea | 212 | 0.55 | 3.59 | 0.15 | 1.20 | 0.61 |
| Paraguay | 1228 | 0.19 | 2.61 | 0.07 | 1.49 | 1.04 |
| Peru | 1216 | 53.13 | 2.16 | 24.56 | 1.15 | 0.71 |
| Philippines | 1329 | 3.80 | 2.38 | 1.60 | 1.28 | 1.04 |
| Poland | 1296 | 1.42 | 2.41 | 0.59 | 1.08 | 1.05 |
| Portugal | 1343 | 0.53 | 2.26 | 0.23 | 1.07 | 1.07 |
| Qatar | 1114 | 1.51 | 2.26 | 0.67 | 1.23 | 1.30 |
| Romania | 1251 | 0.21 | 2.20 | 0.10 | 1.11 | 1.04 |
| Russia | 1297 | 30.11 | 2.28 | 13.23 | 1.08 | 1.00 |
| Rwanda | 917 | 1.95 | 2.45 | 0.80 | 1.43 | 1.25 |
| Saint Lucia | 236 | 1.08 | 14.75 | 0.07 | 0.27 | 0.91 |
| St Vincent and Grenadines | 162 | 1.04 | 5.59 | 0.19 | 0.27 | 0.91 |
| San Marino | 290 | 1.10 | 2.59 | 0.43 | 1.53 | 0.93 |
| Sao Tome and Principe | 279 | 1.72 | 2.76 | 0.62 | 3.06 | 1.59 |
| Saudi Arabia | 1345 | 1.63 | 2.31 | 0.71 | 1.13 | 1.01 |
| Senegal | 1219 | 2.05 | 2.34 | 0.88 | 1.17 | 1.15 |
| Serbia | 1318 | 0.46 | 3.60 | 0.13 | 1.08 | 1.01 |
| Seychelles | 173 | 2.44 | 7.52 | 0.32 | 0.41 | 1.25 |
| Sierra Leone | 399 | 0.75 | 1.95 | 0.39 | 1.48 | 1.15 |
| Singapore | 516 | 1.94 | 1.99 | 0.97 | 1.06 | 1.22 |
| Slovakia | 1150 | 0.25 | 2.99 | 0.08 | 1.91 | 1.31 |
| Slovenia | 1231 | 0.22 | 2.78 | 0.08 | 1.22 | 1.26 |
| Somalia | 331 | 1.74 | 2.14 | 0.82 | 0.85 | 1.12 |
| South Africa | 1307 | 2.41 | 2.32 | 1.04 | 1.00 | 1.03 |
| South Korea | 1299 | 0.10 | 2.25 | 0.04 | 1.00 | 1.03 |
| South Sudan | 384 | 3.06 | 3.00 | 1.02 | 1.00 | 1.03 |
| Spain | 690 | 0.07 | 1.95 | 0.04 | 1.02 | 0.64 |
| Sri Lanka | 1105 | 0.57 | 2.70 | 0.21 | 1.68 | 1.17 |
| Sudan | 847 | 2.00 | 2.49 | 0.80 | 0.85 | 0.99 |
| Suriname | 521 | - | - | - | 1.22 | 1.43 |
| Sweden | 919 | 2.08 | 1.94 | 1.07 | 1.21 | 0.57 |
| Switzerland | 1132 | 27.69 | 1.99 | 13.94 | 1.14 | 0.70 |
| Syria | 704 | 10.73 | 3.76 | 2.85 | 1.10 | 1.01 |
| Taiwan | 853 | 0.33 | 2.34 | 0.14 | 0.75 | 1.37 |
| Tajikistan | 301 | 3.01 | 1.66 | 1.81 | 0.96 | 0.95 |
| Thailand | 1028 | 0.74 | 2.68 | 0.28 | 1.34 | 1.29 |
| Timor | 139 | 2.11 | 11.58 | 0.18 | 0.79 | 1.00 |
| Togo | 951 | 81.66 | 2.37 | 34.43 | 1.52 | 1.18 |
| Trinidad and Tobago | 853 | 3.82 | 6.37 | 0.60 | 1.33 | 1.56 |
| Tunisia | 741 | 0.47 | 1.79 | 0.27 | 1.22 | 0.98 |
| Turkey | 1325 | 2.71 | 2.45 | 1.11 | 1.09 | 1.02 |
| Uganda | 819 | 4.60 | 3.16 | 1.45 | 1.08 | 1.12 |
| Ukraine | 1178 | 0.68 | 2.34 | 0.29 | 1.12 | 1.03 |
| UAE | 1313 | 0.98 | 2.34 | 0.42 | 1.04 | 1.03 |
| UK | 1358 | 0.01 | 2.29 | 0.00 | 1.04 | 1.03 |
| USA | 1389 | 6.56 | 1.87 | 3.51 | 1.04 | 1.03 |
| Uruguay | 1013 | 0.37 | 2.80 | 0.13 | 1.43 | 1.12 |
| Uzbekistan | 655 | 1.23 | 2.22 | 0.56 | 1.20 | 1.06 |
| Venezuela | 793 | 1.39 | 2.88 | 0.48 | 1.18 | 1.00 |
| Vietnam | 452 | 1.07 | 2.69 | 0.40 | 1.18 | 1.89 |
| Yemen | 548 | 0.70 | 2.08 | 0.34 | 1.40 | 0.93 |
| Zambia | 1010 | 0.01 | 2.90 | 0.00 | 1.76 | 1.22 |
| Zimbabwe | 1004 | 3.71 | 2.99 | 1.24 | 1.44 | 1.39 |
| Sample | Chi-Square | K-S | d-Factor |
|---|---|---|---|
| 176 countries, full sample | 0.920 p-Value: 0.000 | 0.760 p-Value: 0.000 | 0.767 p-Value: 0.000 |
| 102 countries with significant data | 1.000 p-Value: 0.000 | 1.000 p-Value: 0.000 | 1.000 p-Value: 0.000 |
| Sample | Cronbach’s Alpha | Composite Reliability | AVE |
|---|---|---|---|
| 176 countries, total sample | 0.808 | 1.213 | 0.858 |
| 102 countries with a large sample size | 1.000 | 1.000 | 1.000 |
| Construct | Size | Change in Benfordness | Growth Ratio Phase One | Growth Ratio Phase Two |
|---|---|---|---|---|
| Change in Benfordness | 176 | 0 | 0 | 0 |
| 102 | 0 | 0 | 0 | |
| Growth Ratio Phase One | 176 | 0.710 | 0 | 0 |
| 102 | 0.768 | 0 | 0 | |
| Growth Ratio Phase Two | 176 | 0.461 | 0.623 | 0 |
| 102 | 0.464 | 0.661 | 0 |
| Items | 176 Countries (Full Sample) | 102 Countries with a Large Sample Size |
|---|---|---|
| CHIDelta | 1.359 | 1.000 |
| KSDelta | 2.653 | - |
| Phase1 | 1.000 | 1.000 |
| Phase2 | 1.000 | 1.000 |
| dDelta | 2.724 | - |
| Sample | R2 |
|---|---|
| 176 countries (total sample) | |
| Change in Benfordness | 0.370 |
| Growth Ratio Phase Two | 0.388 |
| 102 countries with a large sample size | |
| Change in Benfordness | 0.590 |
| Growth Ratio Phase Two | 0.437 |
| N | Original Sample (O) | Sample Mean (M) | Standard Deviation (STDEV) | T Statistics (|O/STDEV|) | p Values | |
|---|---|---|---|---|---|---|
| Growth Ratio Phase One -> Change in Benfordness | 176 | 0.609 | 0.503 | 0.236 | 2.582 | 0.01 |
| 102 | 0.623 | 0.57 | 0.266 | 2.344 | 0.019 | |
| Growth Ratio Phase One -> Growth Ratio Phase Two | 176 | 0.768 | 0.55 | 0.387 | 1.986 | 0.048 |
| 102 | 0.661 | 0.643 | 0.246 | 2.687 | 0.007 |
| Items | RMSE | |
|---|---|---|
| LM | PLS | |
| KSDelta | 13.662 | 13.343 |
| dDelta | 0.437 | 0.443 |
| CHIDelta | 12.458 | 11.681 |
| Phase2 | 1.479 | 1.479 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhadi, N.; Lahooti, H. Pandemic Growth and Benfordness: Empirical Evidence from 176 Countries Worldwide. COVID 2021, 1, 366-383. https://doi.org/10.3390/covid1010031
Farhadi N, Lahooti H. Pandemic Growth and Benfordness: Empirical Evidence from 176 Countries Worldwide. COVID. 2021; 1(1):366-383. https://doi.org/10.3390/covid1010031
Chicago/Turabian StyleFarhadi, Noah, and Hooshang Lahooti. 2021. "Pandemic Growth and Benfordness: Empirical Evidence from 176 Countries Worldwide" COVID 1, no. 1: 366-383. https://doi.org/10.3390/covid1010031
APA StyleFarhadi, N., & Lahooti, H. (2021). Pandemic Growth and Benfordness: Empirical Evidence from 176 Countries Worldwide. COVID, 1(1), 366-383. https://doi.org/10.3390/covid1010031






