Reasonable Limiting of 7-Day Incidence per Hundred Thousand and Herd Immunization in Germany and Other Countries
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
3.1. MSDIHT Value
- 1.
- Germany has already experienced very high values of the SDIHT during the second wave without a breakdown of hospital capacity and without any triage decisions. A maximum death rate of 1100 per day has been reported, which with a fatality rate of corresponds to per day and an SDIHT of .
- 2.
- If in the future one would stick to an MSDIHT value of 50, it means that only about one third of the medical capacity in Germany would be used for the intensive treatment of COVID-19 SIPs, even with a low percentage of breathing apparati used for these persons.
- 3.
- Only with more accurate and complete testing of the population could the dark number of be reduced. In this case a higher MSDIHT value would be possible, which at most equals the SDIHT value of Equation (1). Such a high limiting value would spare Germany from its currently imposed strict lockdown. The costs for such extensive and complete testing campaigns are highly justified, as they are orders of magnitude below the estimated economical costs of each lockdown day of about 444 million euros.
- 4.
- The adopted fatality rate of implies that in the worst case (without the now available vaccination campaigns of the population), the total number of COVID-19 fatalities is million persons in Germany. This large number is about half of the typical annual number of deaths in Germany, and it is getting reduced further not only by the ongoing vaccination program [8], but also by the obvious advantage that comes with the decrease of the dark number, the knowledge of being infected or not.
- 5.
- A significantly higher SDIHT-value is possible if a greater than 20 percent fraction of breathing apparati can be made available for the treatment of seriously infected persons (SIPs). E.g., a value of 43 percent, so that , results in an SDIHT-value of 600. The greatest hindrance for such an enhancement in is the lack of enough suitably trained nursing staff caused by the inattractive pay for these personel. We suggest enhancing the attractiveness of these jobs by paying an annual COVID-bonus of euros per year for nursing personel treating SIPs. With one nurse taking care of two SIPs in an 8 h working shift, for around-the-clock treatment nurses per SIP are needed, so for SIPS in total, nurses are needed. The annual cost for their COVID-bonus would be 630 million euros per year or million euros per day, corresponding to less than percent of the daily lockdown costs of 444 million euros. From an economical point of view, this would be a very wise investment in the German health system.
3.2. Herd Immunization
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dorn, F.; Fuest, C.; Göttert, M.; Krolage, C.; Lautenbacher, S.; Link, S.; Peichl, A.; Reif, M.; Sauer, S.; Stöckli, M.; et al. Die Volkswirtschaftlichen Kosten des Corona-Shutdown für Deutschland: Eine Szenarienrechnung; ifo-Schnelldienst; Ifo-Institute: Munich, Germany, 2020; Volume 4, p. 29. [Google Scholar]
- Beznoska, M.; Hentze, T.; Hüther, M. Zum Umgang mit den Corona Schulden; IW-Policy paper 7/21; Institut der Deutschen Wirtschaft: Cologne, Germany, 2021. [Google Scholar]
- Schlickeiser, R.; Kröger, M. Dark numbers and herd immunity of the first Covid-19 wave and future social interventions. Epidem. Int. J. 2020, 4, 000152. [Google Scholar]
- Schlickeiser, R.; Schlickeiser, F. A gaussian model for the time development of the Sars-Cov-2 corona pandemic disease. Prrdictions for Germany made on March 30. Physics 2020, 2, 164–170. [Google Scholar] [CrossRef]
- Schüttler, J.; Schlickeiser, R.; Schlickeiser, F.; Kröger, M. Covid-19 predictions using a Gauss model, based on data from April 2. Physics 2020, 2, 197–202. [Google Scholar] [CrossRef]
- Estrada, E. COVID-19 and SARS-CoV-2. Modeling the present, looking at the future. Phys. Rep. 2020, 869, 1–51. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Schlickeiser, R.; Kröger, M. Analytical modeling of the temporal evolution of epidemics outbreaks accounting for vaccinations. Physics 2021, 3, 386–426. [Google Scholar] [CrossRef]
- John, T.J.; Samuel, R. Herd immunity and herd effects: New insights and definitions. Eur. J. Epidemiol. 2000, 16, 601. [Google Scholar] [CrossRef] [PubMed]
- Garnett, G.P. Role of herd immunity in determining the effect of vaccines against sexually transmitted disease. J. Infect. Dis. 2005, 191 (Suppl. 1), 97–106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perisic, A.; Bauch, C.T. Social contact networks and disease eradicability under voluntary vaccination. PLoS Comput. Biol. 2009, 5, e1000280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodpothong, P.; Auewarakul, P. Viral evolution and transmission effectiveness. World J. Virol. 2012, 1, 131–134. [Google Scholar] [CrossRef] [PubMed]
- Britton, T.; Ball, F.; Trapman, P. A mathematical model reveals the influence of population heterogeneity on herd immunization to SARS-CoV-2. Science 2020, 369, 846–849. [Google Scholar] [CrossRef] [PubMed]
- Ganasegeran, K.; Ch’ng, A.S.H.; Looi, I. What is the estimated COVID-19 reproduction number and the proportion of the population that needs to be immunized to achieve herd immunity in Malaysia? A mathematical epidemiology synthesis. Covid 2021, 1, 13–19. [Google Scholar] [CrossRef]
- Kwok, K.O.; Lai, F.; Wei, W.I.; Wong, S.Y.S.; Tang, J.W.T. Herd immunity—Estimating the level required to halt the COVID-19 epidemics in affected countries. J. Infect. 2020, 80, e32–e33. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M.; Schlickeiser, R. Gaussian doubling times and reproduction factors of the COVID-19 pandemic disease. Front. Phys. 2020, 8, 276. [Google Scholar] [CrossRef]
- Schlickeiser, R.; Kröger, M. Analytical solution of the SIR-model for the temporal evolution of epidemics: Part B. Semi-time case. J. Phys. A 2021, 54, 175601. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Delamater, P.L.; Street, E.J.; Leslie, T.F.; Yang, Y.T.; Jacobsen, K.H. Complexity of the basic reproduction number (R0). Emerg. Inf. Dis. 2019, 25, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schlickeiser, R.; Kröger, M. First consistent determination of the basic reproduction number for the first Covid-19 wave in 71 countries from the SIR-epidemics model with a constant ratio of recovery to infection rate. Glob. J. Sci. Front. Res. 2020, 20, 37–43. [Google Scholar] [CrossRef]
- Fraser, C. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS ONE 2007, 2, e758. [Google Scholar] [CrossRef] [PubMed]
- Kadkhoda, K. Herd Immunity to COVID-19. Alluring and Elusive. Am. J. Clin. Pathol. 2021, 155, 471–472. [Google Scholar] [CrossRef] [PubMed]
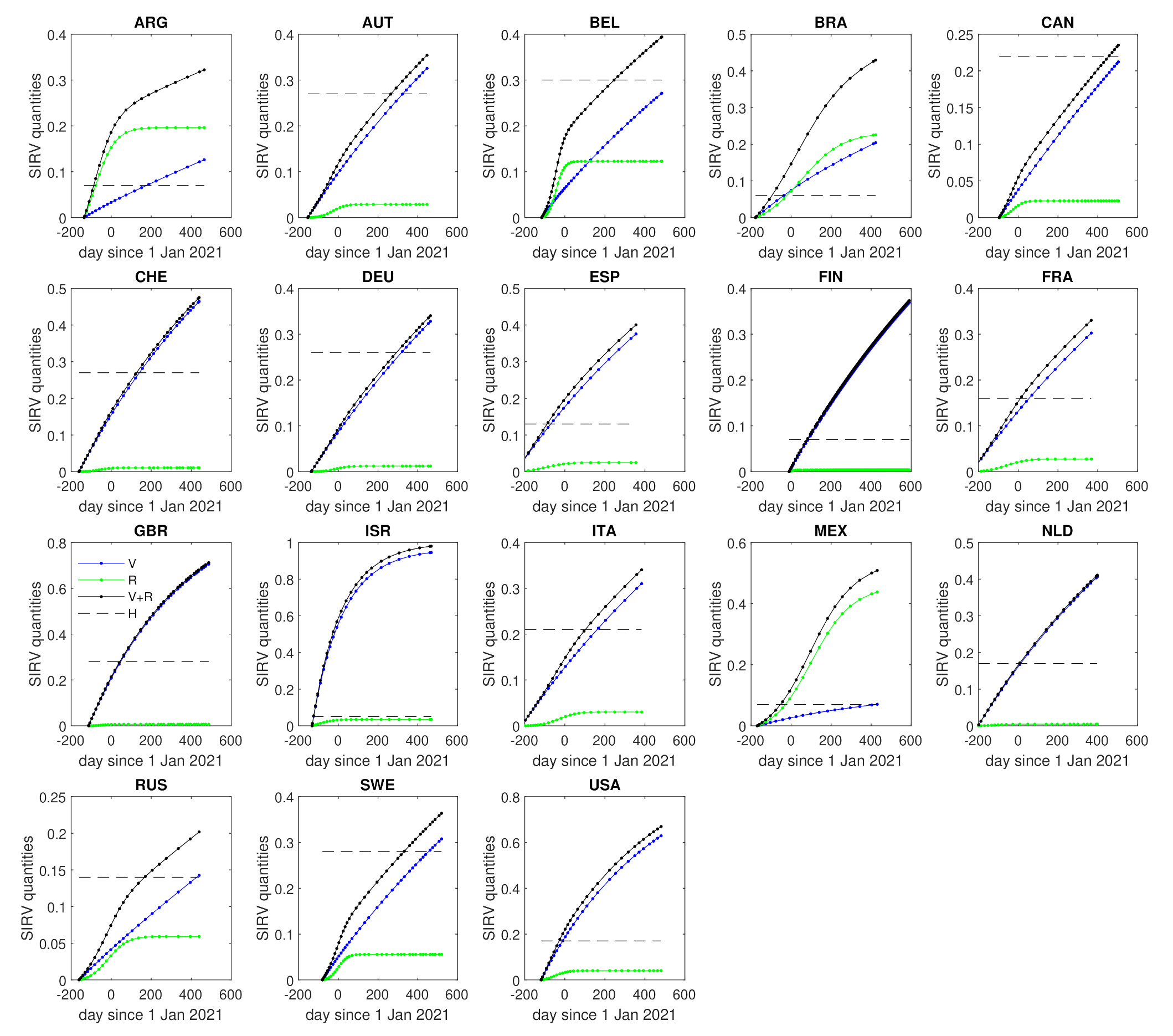
| Country | k | b | x | H | |||
|---|---|---|---|---|---|---|---|
| ARG | 0.125 | 0.912 | 0.0022 | 0.15 | 1.08 | 0.07 | −78 |
| AUT | 0.520 | 0.905 | 0.0013 | 0.67 | 1.37 | 0.27 | 291 |
| BEL | 0.551 | 0.896 | 0.0011 | 0.77 | 1.44 | 0.30 | 265 |
| BRA | 0.046 | 0.790 | 0.0099 | 0.13 | 1.07 | 0.06 | −71 |
| CAN | 1.018 | 0.962 | 0.0004 | 0.52 | 1.28 | 0.22 | 458 |
| CHE | 0.458 | 0.894 | 0.0023 | 0.66 | 1.36 | 0.27 | 157 |
| DEU | 0.559 | 0.915 | 0.0012 | 0.64 | 1.35 | 0.26 | 322 |
| ESP | 0.175 | 0.876 | 0.0046 | 0.29 | 1.15 | 0.13 | −84 |
| FIN | 3.858 | 0.997 | 0.0002 | 0.16 | 1.08 | 0.07 | 83 |
| FRA | 0.228 | 0.886 | 0.0027 | 0.35 | 1.19 | 0.16 | 17 |
| GBR | 0.389 | 0.867 | 0.0053 | 0.70 | 1.39 | 0.28 | 63 |
| ISR | 0.050 | 0.855 | 0.1283 | 0.10 | 1.05 | 0.05 | −124 |
| ITA | 0.289 | 0.873 | 0.0022 | 0.50 | 1.27 | 0.21 | 130 |
| MEX | 0.038 | 0.712 | 0.0044 | 0.15 | 1.08 | 0.07 | −43 |
| NLD | 0.397 | 0.929 | 0.0022 | 0.38 | 1.20 | 0.17 | 8 |
| RUS | 0.337 | 0.933 | 0.0008 | 0.30 | 1.16 | 0.14 | 171 |
| SWE | 0.652 | 0.922 | 0.0010 | 0.69 | 1.38 | 0.28 | 332 |
| USA | 0.218 | 0.868 | 0.0081 | 0.39 | 1.21 | 0.17 | −25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlickeiser, R.; Kröger, M. Reasonable Limiting of 7-Day Incidence per Hundred Thousand and Herd Immunization in Germany and Other Countries. COVID 2021, 1, 130-136. https://doi.org/10.3390/covid1010012
Schlickeiser R, Kröger M. Reasonable Limiting of 7-Day Incidence per Hundred Thousand and Herd Immunization in Germany and Other Countries. COVID. 2021; 1(1):130-136. https://doi.org/10.3390/covid1010012
Chicago/Turabian StyleSchlickeiser, Reinhard, and Martin Kröger. 2021. "Reasonable Limiting of 7-Day Incidence per Hundred Thousand and Herd Immunization in Germany and Other Countries" COVID 1, no. 1: 130-136. https://doi.org/10.3390/covid1010012
APA StyleSchlickeiser, R., & Kröger, M. (2021). Reasonable Limiting of 7-Day Incidence per Hundred Thousand and Herd Immunization in Germany and Other Countries. COVID, 1(1), 130-136. https://doi.org/10.3390/covid1010012







