Chemical Synthesis of Nanostructured Topological Pb1−xSnxSe (x = 0–1) Alloy Films—A Study of Their Structural, Optical, and Thermopower Properties
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis and Deposition
2.2. Sample Characterization
3. Results and Discussion
3.1. Structural and Composition Results
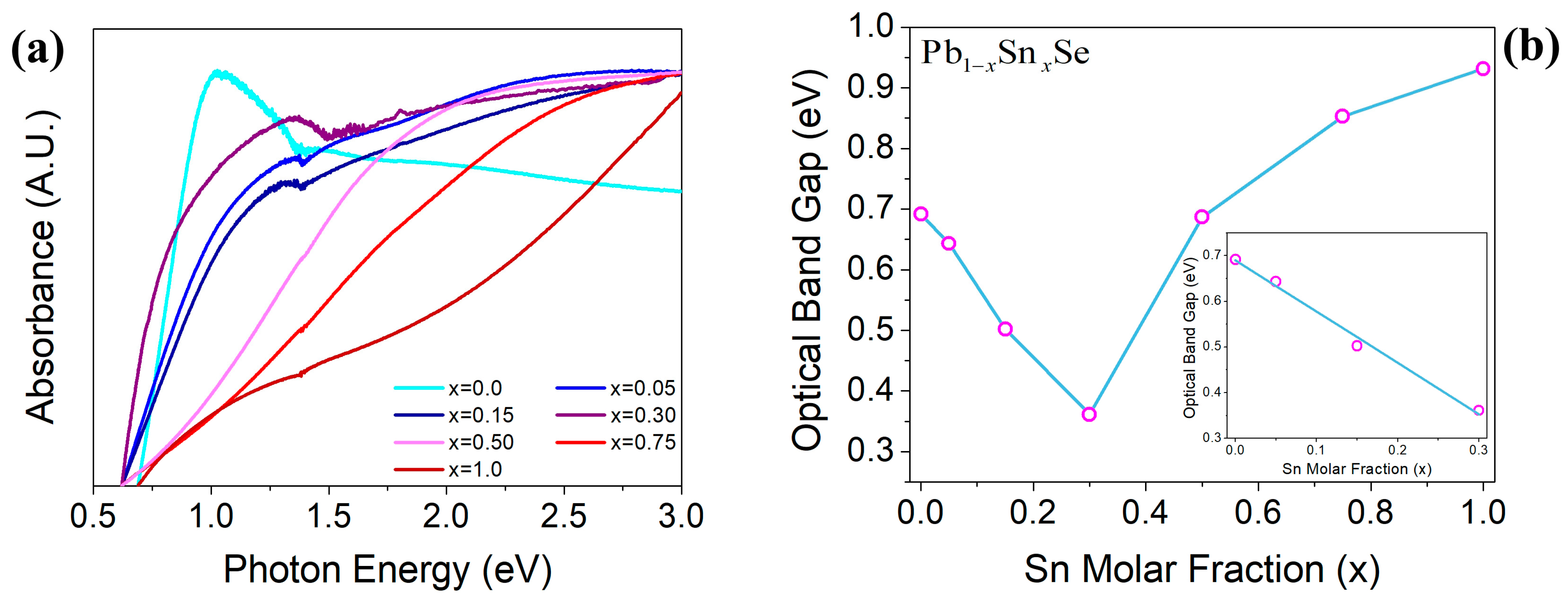
3.2. Optical Properties Results
3.3. Morphology Results
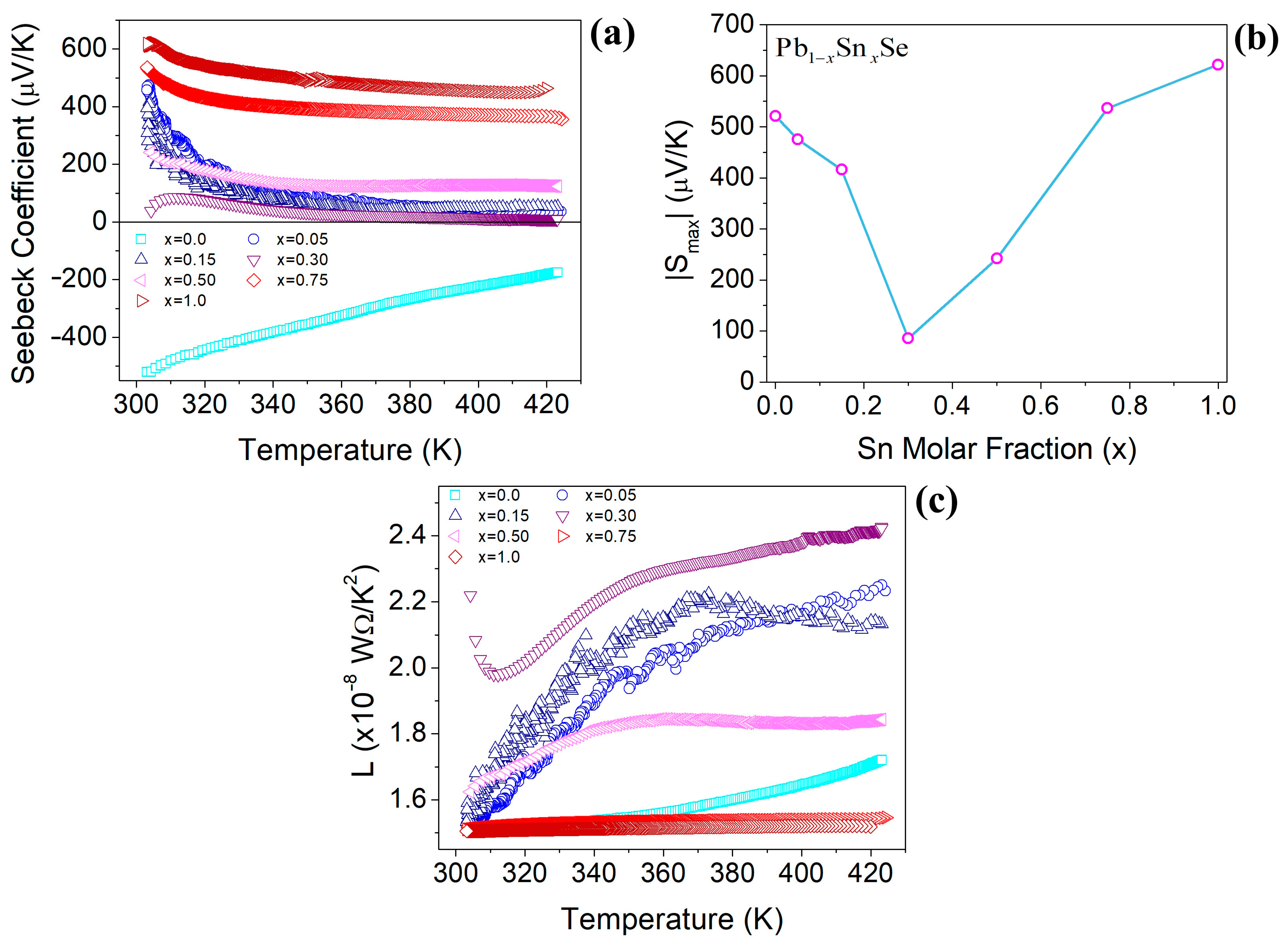
3.4. Seebeck Coefficient Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, G.; Zhao, L.-D.; Kanatzidis, M.G. Rationally designing high-performance bulk thermoelectric materials. Chem. Rev. 2016, 116, 12123–12149. [Google Scholar] [CrossRef]
- Dalven, R. A review of the semiconductor properties of PbTe, PbSe, PbS and PbO. Infrared Phys. 1969, 9, 141–184. [Google Scholar] [CrossRef]
- Sun, Y.; Zhong, Z.; Shirakawa, T.; Franchini, C.; Li, D.; Li, Y.; Yunoki, S.; Chen, X.-Q. Rocksalt SnS and SnSe: Native topological crystalline insulators. Phys. Rev. B 2013, 88, 235122. [Google Scholar] [CrossRef]
- Dziawa, P.; Kowalski, B.J.; Dybko, K.; Buczko, R.; Szczerbakow, A.; Szot, M.; Łtusakowska, E.; Balasubramanian, T.; Wojek, B.M.; Berntsen, M.H.; et al. Topological crystalline insulator states in Pb1-xSnxSe. Nat. Mater. 2012, 11, 1023–1027. [Google Scholar] [CrossRef]
- Guo, C.; Wang, D.; Zhang, X.; Zhao, L.-D. One-One Correspondence between n-Type SnTe Thermoelectric and Topological Phase Transition. Chem. Mater. 2022, 34, 3423–3429. [Google Scholar] [CrossRef]
- Wu, C.-F.; Wei, T.-R.; Li, J.-F. Electrical and thermal transport properties of Pb1-xSnxSe solid solution thermoelectric materials. Phys. Chem. Chem. Phys. 2015, 17, 13006–13012. [Google Scholar] [CrossRef]
- Woolley, J.C.; Berolo, O. Phase Studies of the Pb1-xSnxSe Alloys. Mater. Res. Bull. 1968, 3, 445–450. [Google Scholar] [CrossRef]
- Hoff, G.F.; Dixon, J.R. Electrical Properties of Pb1-xSnxSe Semiconductor Alloys. Solid State Commun. 1972, 10, 433–437. [Google Scholar] [CrossRef]
- Strauss, A.J. Inversion of Conduction and Valence Bands in Pb1-xSnxSe Alloys. Phys. Rev. 1967, 157, 608–611. [Google Scholar] [CrossRef]
- Reddy, P.D.; Nordin, L.J.; Hughes, L.B.; Preidl, A.-K.; Mukherjee, K. Expanded Stability of Layered SnSe-PbSe Alloys and Evidence of Displacive Phase Transformation from Rocksalt in Heteroepitaxial Thin Films. ACS Nano 2024, 18, 13437–13449. [Google Scholar] [CrossRef]
- Neupane, M.; Xu, S.-Y.; Sankar, R.; Gibson, Q.; Wang, Y.J.; Belopolski, I.; Alidoust, N.; Bian, G.; Shibayev, P.P.; Sanchez, D.S.; et al. Topological phase diagram and saddle point singularity in a tunable topological crystalline insulator. Phys. Rev. B 2015, 92, 075131. [Google Scholar] [CrossRef]
- Saghir, M.; Sanchez, A.M.; Hindmarsh, S.A.; York, S.J.; Balakrishnan, G. Nanomaterials of the Topological Crystalline Insulators, Pb1-xSnxTe and Pb1-xSnxSe. Cryst. Growth Des. 2015, 15, 5202–5206. [Google Scholar] [CrossRef]
- Markov, V.F.; Tretyakova, N.A.; Maskaeva, L.N.; Bakanov, V.M.; Mukhamedzyanov, H.N. Hydrochemical synthesis, structure, semiconductor properties of films of substitutional Pb1-xSnxSe solid solutions. Thin Solid Films 2012, 520, 5227–5231. [Google Scholar] [CrossRef]
- Liu, Y.; Lee, S.; Fiedler, C.; Spadaro, M.C.; Chang, C.; Li, M.; Hong, M.; Arbiol, J.; Ibáñez, M. Enhancing thermoelectric performance of solution-processed polycrystalline SnSe with PbSe nanocrystals. Chem. Eng. J. 2024, 490, 151405. [Google Scholar] [CrossRef]
- Pei, Y.; Shi, X.; LaLonde, A.; Wang, H.; Chen, L.; Snyder, G.J. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 2011, 473, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhang, G.; Fan, S.; Li, Y. Hydrothermal synthesis of PbSe, PbTe semiconductor nanocrystals. J. Phys. Chem. Sol. 2001, 62, 1957–1960. [Google Scholar] [CrossRef]
- Tomm, J.W.; Sumpf, B.; Herrmann, K.; Szczerbakow, A. Some aspects of the technology of lead salt diode lasers used in gas monitoring systems. Cryst. Res. Technol. 1987, 22, 981. [Google Scholar] [CrossRef]
- Ravich, Y.I.; Efimova, B.A.; Smirnov, I.A. Semiconducting Lead Chalcogenides. In Monographs in Semiconductor Physics, 1st ed.; Stil’bans, L.S., Ed.; Springer: New York, NY, USA, 1970; Volume 5, pp. 15–377. [Google Scholar]
- Chen, P.; Wu, Z.; Shi, Y.; Li, C.; Wang, J.; Yang, J.; Dong, X.; Gou, J.; Wang, J.; Jiang, Y. High-performance silicon-based PbSe-CQDs infrared photodetector. J. Mater Sci. Mater. Electron. 2021, 32, 9452–9462. [Google Scholar] [CrossRef]
- Feng, W.; Li, Z.; Chen, Y.; Chen, J.; Lang, H.; Wan, J.; Gao, Y.; Dong, H. Enhanced photoelectric properties of PbSnSe thin films via quick oxygen ion-implantation sensitization. J. Mater Sci. 2022, 57, 1881–1889. [Google Scholar] [CrossRef]
- Nishimura, Y.; He, X.; Katase, T.; Tadano, T.; Ide, K.; Kitani, S.; Hanzawa, K.; Ueda, S.; Hiramatsu, H.; Kawaji, H.; et al. Electronic and Lattice Thermal Conductivity Switching by 3D-2D Crystal Structure Transition in Nonequilibrium (Pb1−xSnx)Se. Adv. Electron. Mater. 2022, 8, 2200024. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, D.; Li, C.; Wang, J.; Wang, G.; Zhao, L.-D. Improving the thermoelectric performance of p-type PbSe. J. Mater. Chem. A 2020, 8, 4931–4937. [Google Scholar] [CrossRef]
- Qin, B.; He, W.; Zhao, L.-D. Estimation of the potential performance in p-type SnSe crystals through evaluating weighted mobility and effective mass. J. Materiomics 2020, 6, 671–676. [Google Scholar] [CrossRef]
- McCann, P.J. Thermoelectric Materials. US Patent 0055528 A1, 8 March 2012. [Google Scholar]
- Webber, D.H.; Buckley, J.J.; Antunez, P.D.; Brutchey, R.L. Facile dissolution of selenium and tellurium in a thiol-amine solvent mixture under ambient conditions. Chem. Sci. 2014, 5, 2498–2502. [Google Scholar] [CrossRef]
- Díaz-Torres, E.; Roque, J.; Arreola-Pina, A.S.; Pérez-Guzmán, M.A.; Ortega-Amaya, R.; Ortega-López, M. Nanostructured PbSe Films Deposited by Spray Pyrolysis Using PbSe Colloidal Solutions. Nanomaterials 2023, 13, 2595. [Google Scholar] [CrossRef]
- Burkov, A.T. Measurements of Resistivity and Thermopower. In Thermoelectrics Handbook: Micro to Nano, 1st ed.; Rowe, D.M., Ed.; CRC Press Taylor and Francis: Boca Raton, FL, USA, 2006; pp. 22-1–22-12. [Google Scholar]
- Patterson, A.L. The Scherrer formula for X-ray particle size determination. Phys. Rev. 1939, 56, 978–982. [Google Scholar] [CrossRef]
- Katase, T.; Takahashi, Y.; He, X.; Tadano, T.; Ide, K.; Yoshida, H.; Kawachi, S.; Yamaura, J.; Sasase, M.; Hiramatsu, H.; et al. Reversible 3D-2D structural phase transition and giant electronic modulation in nonequilibrium alloy semiconductor, lead-tin-selenide. Sci. Adv. 2021, 7, eabf2725. [Google Scholar] [CrossRef]
- Díaz-Torres, E.; Ortega-López, M.; Matsumoto, Y.; Santoyo-Salazar, J. Simple synthesis of PbSe nanocrystals and their self-assembly into 2D ‘flakes’ and 1D ‘ribbons’ structures. Mater. Res. Bull. 2016, 80, 96–101. [Google Scholar] [CrossRef]
- Liu, Y.; You, L.; Wang, C.; Zhang, J.; Yang, J.; Guo, K.; Luo, J.; Zhang, W. Enhancing Thermoelectric Performance of PbSe by Se Vacancies. J. Electron. Mater. 2018, 47, 2584–2590. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, C.; Chen, X.; Zhuo, D.; Du, J.; Wang, S.; Ning, L. First-principles study on intrinsic defects of SnSe. RSC Adv. 2017, 7, 27612–27618. [Google Scholar] [CrossRef]
- Gibbs, Z.M.; Kim, H.-S.; Wang, H.; Snyder, G.J. Band gap estimation from temperature dependent Seebeck measurement–Deviations from the 2e|S|maxTmax relation. Appl. Phys. Lett. 2015, 106, 022112. [Google Scholar] [CrossRef]
- Chen, C.-L.; Wang, H.; Chen, Y.-Y.; Day, T.; Snyder, G.J. Thermoelectric properties of p-type polycrystalline SnSe doped with Ag. J. Mater. Chem. A 2014, 2, 11171–11176. [Google Scholar] [CrossRef]
- Rogacheva, E.I.; Tavrina, T.V.; Grigorov, S.N.; Nashchekina, O.N.; Volobuev, V.V.; Fedorov, A.G.; Nasedkin, K.A.; Dresselhaus, M.S. Effect of Oxidation on the Thermoelectric Properties of PbSe Thin Films. J. Electron. Mater. 2002, 31, 298–303. [Google Scholar] [CrossRef]
- Kim, H.-S.; Gibbs, Z.M.; Tang, Y.; Wang, H.; Snyder, G.J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef]
- Chen, Y.-X.; Li, F.; Li, D.; Zheng, Z.; Luo, J.; Fan, P. Thermoelectric Properties of Tin Telluride Quasi Crystal Grown by Vertical Bridgman Method. Materials 2019, 12, 3001. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Torres, E.; Flores-Conde, A.; García-Ávila, A.; Ortega-López, M. Electronic transport study of PbSe pellets prepared from self-assembled 2D-PbSe nanostructures. Curr. Appl. Phys. 2018, 18, 226–230. [Google Scholar] [CrossRef]
- Matsuura, H.; Riss, A.; Garmroudi, F.; Parzer, M.; Bauer, E. Cooperative Nernst effect of multilayer systems: Parallel circuit model study. Phys. Rev. Res. 2024, 6, 043071. [Google Scholar] [CrossRef]


| Material | S (µV/K) | L (WΩ/K2) |
|---|---|---|
| PbTe | 310–360 [5] | 1.57–1.55 × 10−8 [5] |
| Pb0.70Sn0.30Te | 70–150 [5] | 2.05–1.77 × 10−8 [5] |
| Pb0.30Sn0.70Te | 50–80 [5] | 2.15–2.00 × 10−8 [5] |
| SnTe | 35–39 [37] | 2.29–2.22 × 10−8 [37] |
| PbSe | −520–(−175) | 1.51–1.72 × 10−8 |
| Pb0.70Sn0.30Se | 87–10 | 1.97–2.42 × 10−8 |
| Pb0.25Sn0.75Te | 538–357 | 1.51–1.55 × 10−8 |
| SnSe | 627–449 | ~1.51 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Torres, E.; Guillén-Cervantes, Á.; Ortega-López, M. Chemical Synthesis of Nanostructured Topological Pb1−xSnxSe (x = 0–1) Alloy Films—A Study of Their Structural, Optical, and Thermopower Properties. Micro 2025, 5, 13. https://doi.org/10.3390/micro5010013
Díaz-Torres E, Guillén-Cervantes Á, Ortega-López M. Chemical Synthesis of Nanostructured Topological Pb1−xSnxSe (x = 0–1) Alloy Films—A Study of Their Structural, Optical, and Thermopower Properties. Micro. 2025; 5(1):13. https://doi.org/10.3390/micro5010013
Chicago/Turabian StyleDíaz-Torres, Esteban, Ángel Guillén-Cervantes, and Mauricio Ortega-López. 2025. "Chemical Synthesis of Nanostructured Topological Pb1−xSnxSe (x = 0–1) Alloy Films—A Study of Their Structural, Optical, and Thermopower Properties" Micro 5, no. 1: 13. https://doi.org/10.3390/micro5010013
APA StyleDíaz-Torres, E., Guillén-Cervantes, Á., & Ortega-López, M. (2025). Chemical Synthesis of Nanostructured Topological Pb1−xSnxSe (x = 0–1) Alloy Films—A Study of Their Structural, Optical, and Thermopower Properties. Micro, 5(1), 13. https://doi.org/10.3390/micro5010013






