Droplets Sliding Down Partially Wetted (Non-Superhydrophobic) Surfaces: A Review
Abstract
1. Introduction
2. Sliding Down a Homogeneous Surface
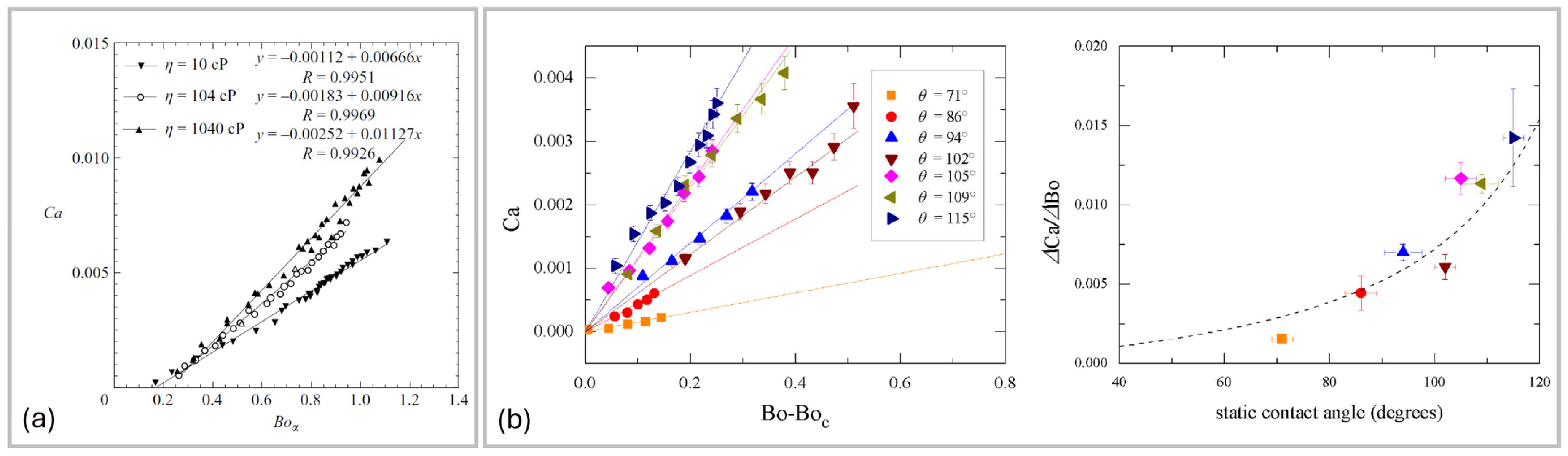
2.1. Onset of Sliding
2.2. Sliding Dynamics
- Gravitational pull along the plane: ρVgsinα;
- Viscous drag on the surface: −ηUV1/3;
- Interfacial forces: σV1/3Δθ.
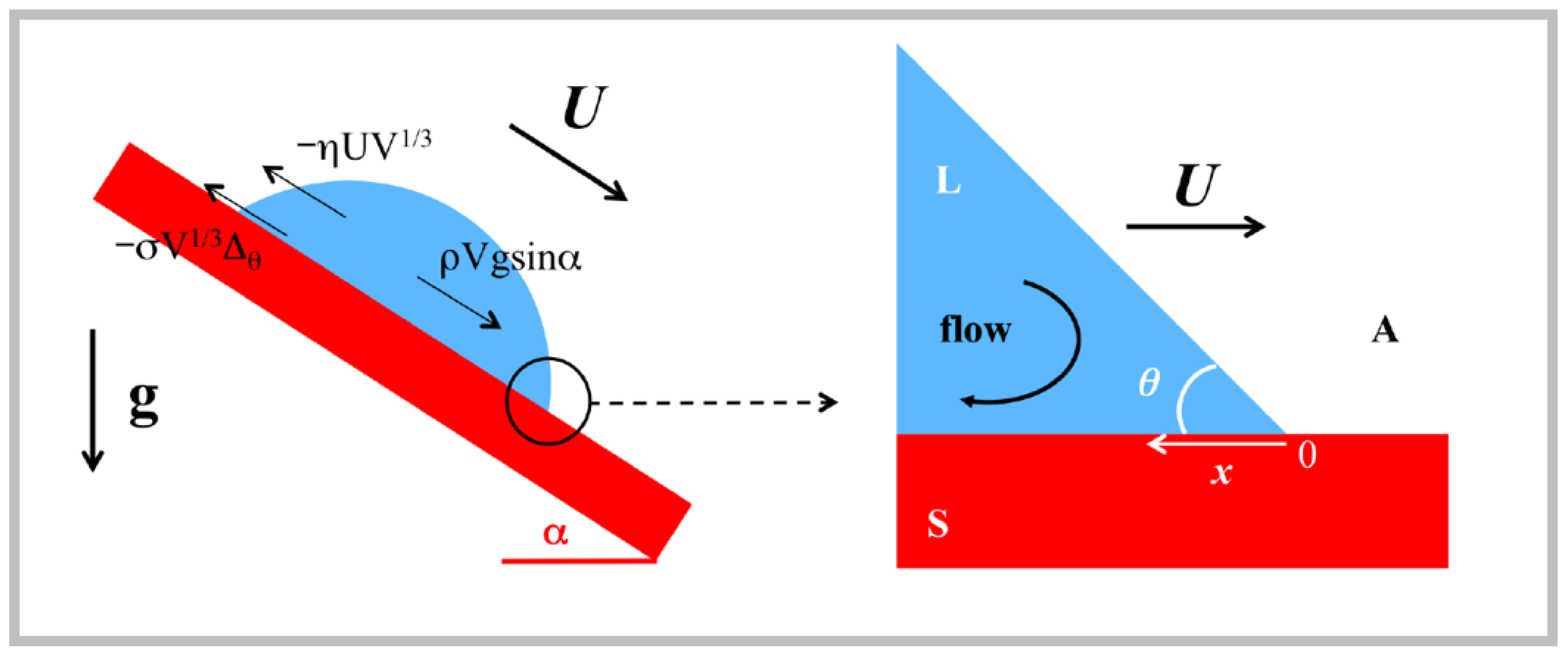
- is the capillary number;
- is the effective Bond number based on the component of the gravity force parallel to the plane;
- is a constant depending on the wetting hysteresis through Dθ.
2.2.1. Theoretical/Numerical Studies
- w is the width of the contact area;
- Λ is the length scale where the wedge flow approximation;
- λ is a cutoff length introduced to prevent a blowup of the dissipation;
- L is the peripheral length of the drop/solid contact area;
2.2.2. Experimental Studies
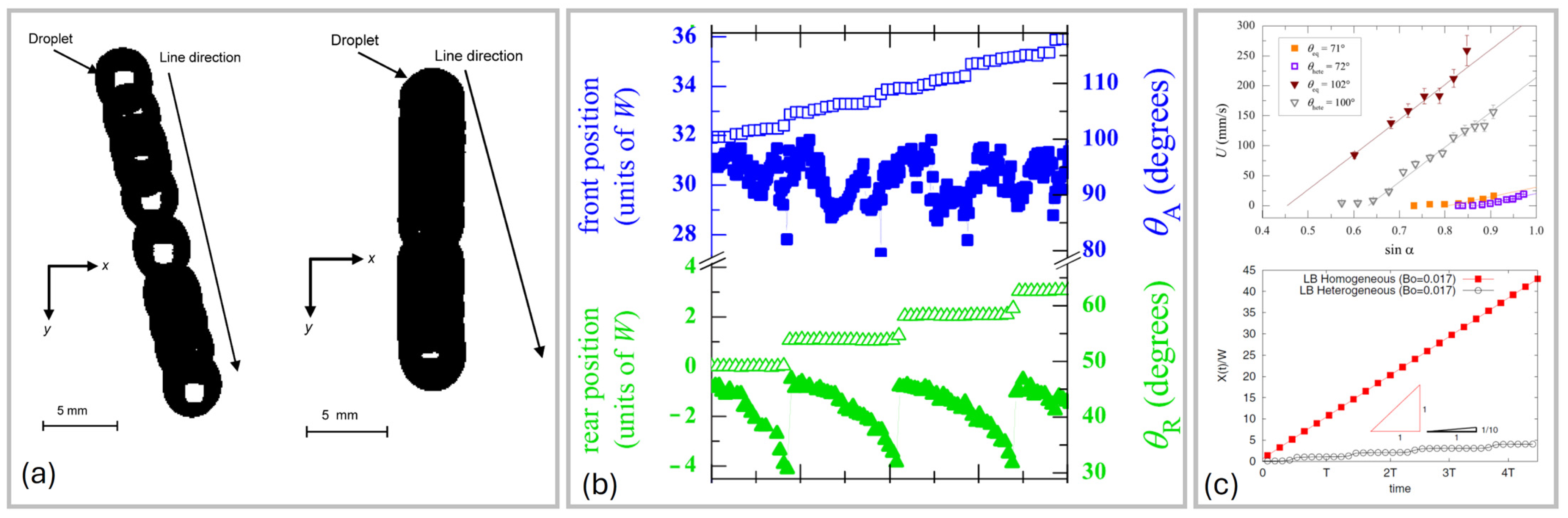
2.3. Droplet Shape
- For small angles, the drop is round;
- For bigger angles, the rear forms a corner;
- For further higher angles, corners become cusps emitting smaller droplets (pearling), and the shape is no longer constant.
- Drops elongate and flatten as the sliding velocity increases;
- The shape of the rear depends on the Capillary number;
- The advancing angle increases as the Ca increases with a power law dependence, while the receding contact angle decreases for increasing Ca with a similar power law.

2.4. Flow Inside the Drop During Sliding
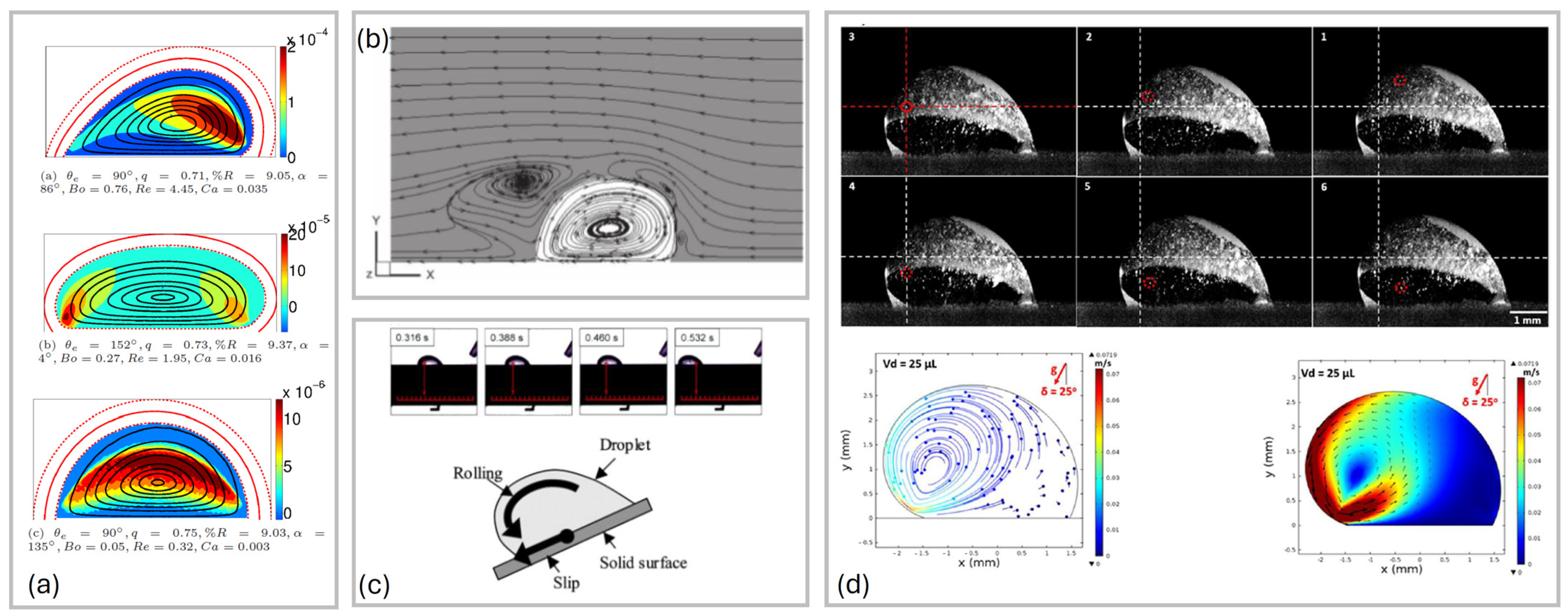
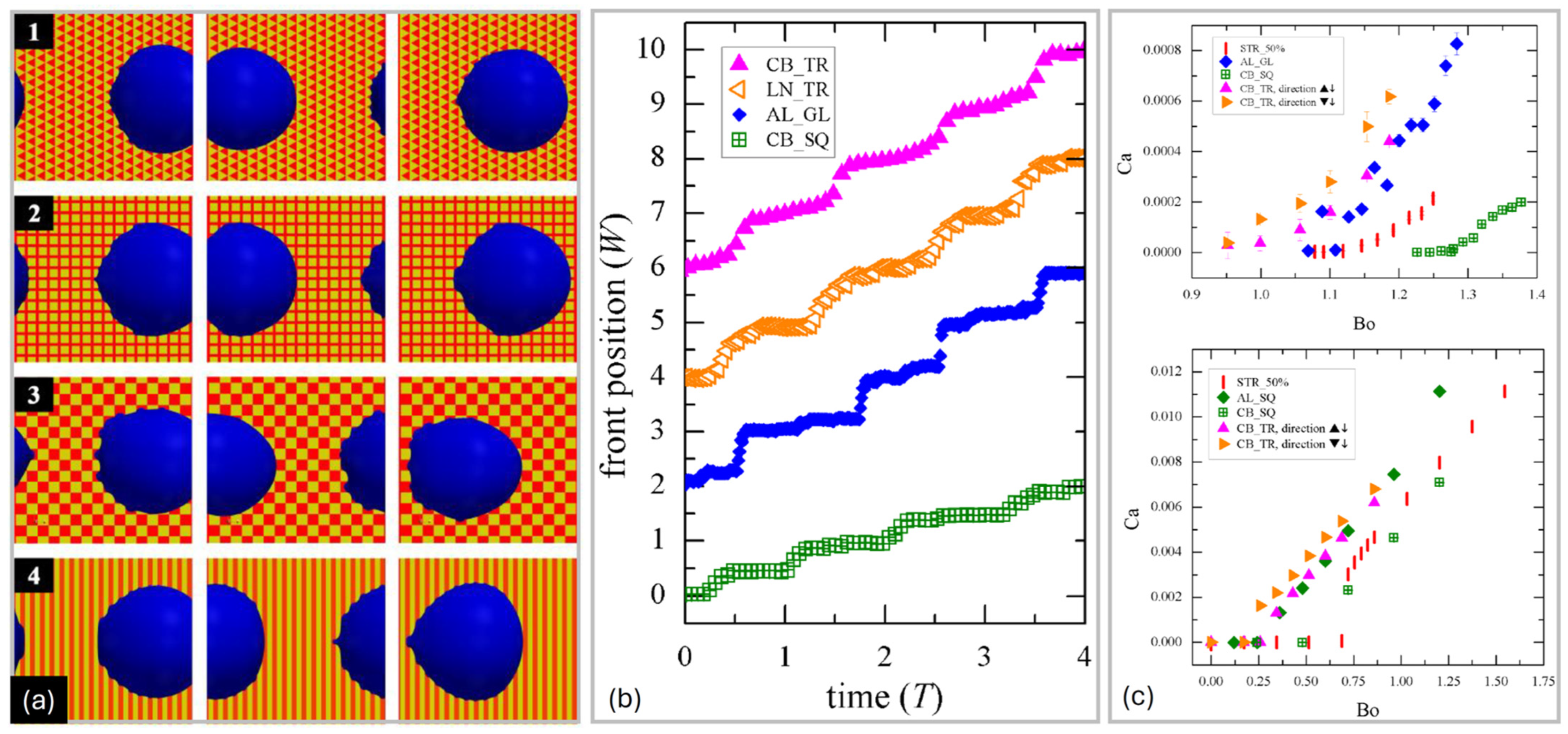
3. Sliding Down a Chemically Heterogeneous Surface
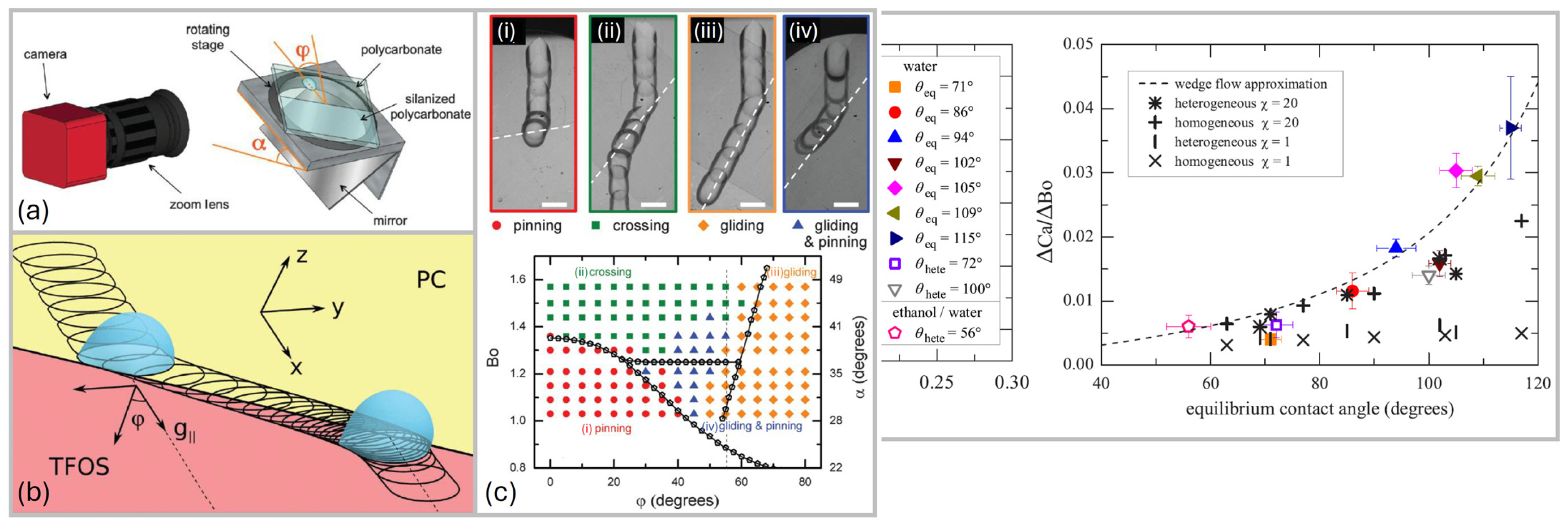
3.1. Single Chemical Step
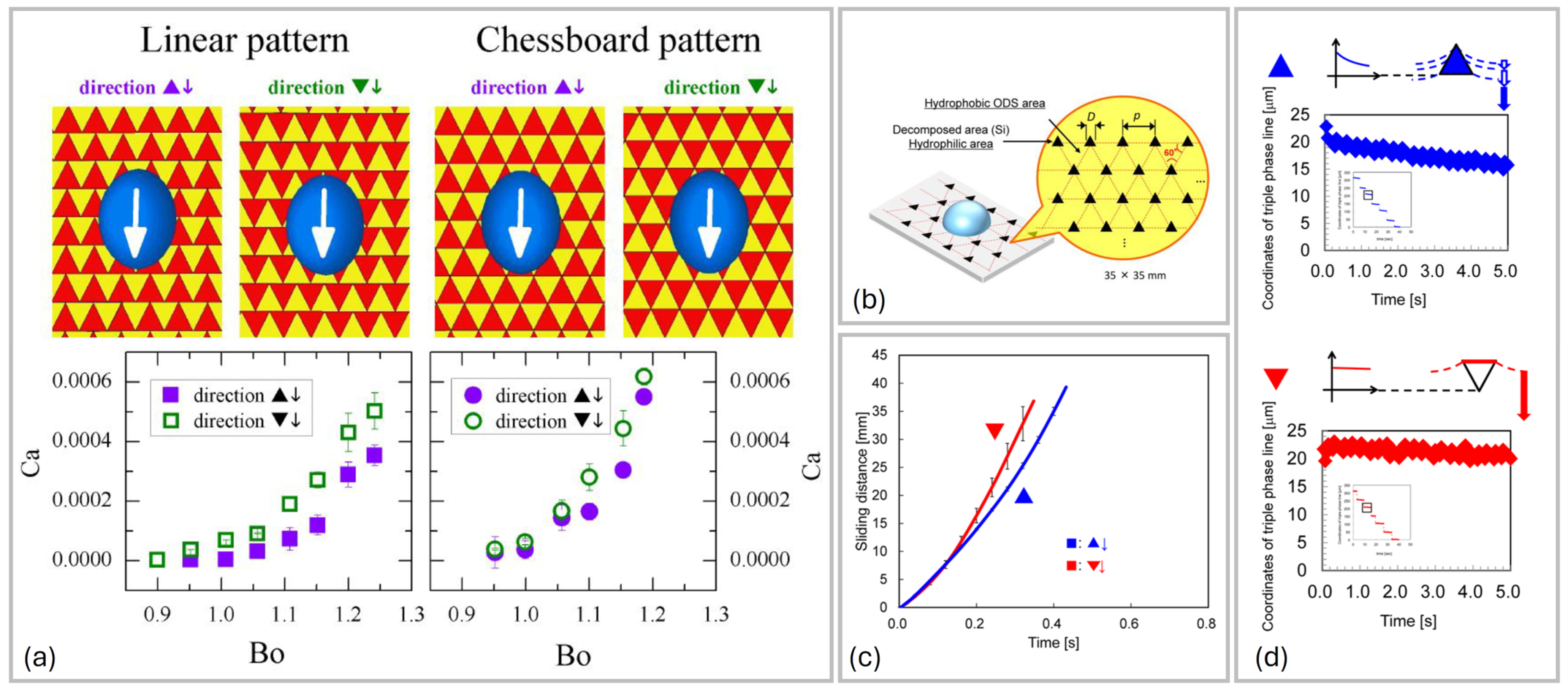
3.2. Striped Surfaces
3.3. Surfaces Formed by Geometrical Tiles
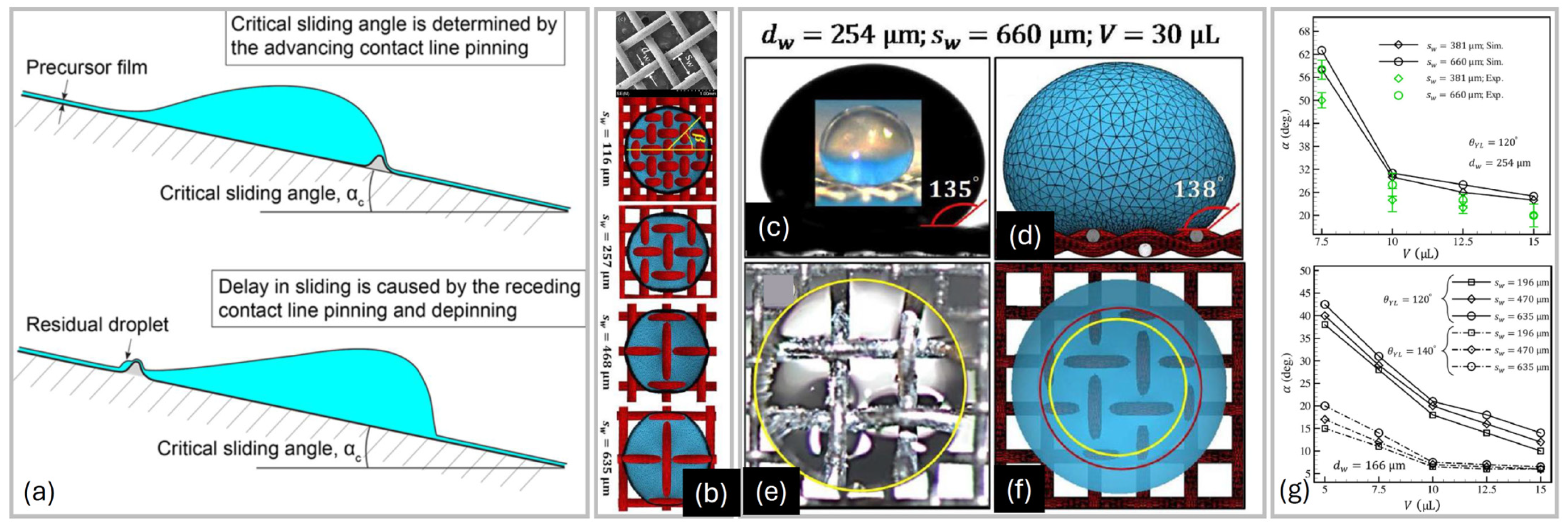
4. Sliding Down Geometrically Patterned Surfaces
5. Sliding of Droplets Made of Complex Fluids
6. Conclusions and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Butt, H.J.; Berger, R.; De Coninck, J.; Tadmor, R. Drop Friction. Nat. Rev. Phys. 2025, 7, 425–438. [Google Scholar] [CrossRef]
- Eral, H.B.; ’T Mannetje, D.J.C.M.; Oh, J.M. Contact Angle Hysteresis: A Review of Fundamentals and Applications. Colloid Polym. Sci. 2012, 291, 247–260. [Google Scholar] [CrossRef]
- de Gennes, P.-G.; Brochard-Wyart, F.; Quéré, D. Capillarity and Wetting Phenomena; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Li, X.; Bodziony, F.; Yin, M.; Marschall, H.; Berger, R.; Butt, H.J. Kinetic Drop Friction. Nat. Commun. 2023, 14, 4571. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Lee, T.R. Contact Angle and Wetting Properties. Springer Ser. Surf. Sci. 2013, 51, 3–34. [Google Scholar] [CrossRef]
- Wen, Q.; Guo, Z. Recent Advances in the Fabrication of Superhydrophobic Surfaces. Chem. Lett. 2016, 45, 1134–1149. [Google Scholar] [CrossRef]
- Jiang, Z.; Sun, Y.; Yan, M.; Qian, B.; Jiang, A.; Zhang, X.; Bi, J.; Tong, Y.; Yu, L.; Li, W. Recent Advancements in Fabrication Strategies and Applications of Superhydrophobic Coatings. J. Mater. Sci. 2025, 60, 7826–7858. [Google Scholar] [CrossRef]
- Podgorski, T.; Flesselles, J.M.; Limat, L. Corners, Cusps, and Pearls in Running Drops. Phys. Rev. Lett. 2001, 87, 036102. [Google Scholar] [CrossRef]
- Le Grand, N.; Daerr, A.; Limat, L. Shape and Motion of Drops Sliding down an Inclined Plane. J. Fluid Mech. 2005, 541, 293–315. [Google Scholar] [CrossRef]
- Varagnolo, S.; Ferraro, D.; Fantinel, P.; Pierno, M.; Mistura, G.; Amati, G.; Biferale, L.; Sbragaglia, M. Stick-Slip Sliding of Water Drops on Chemically Heterogeneous Surfaces. Phys. Rev. Lett. 2013, 111, 066101. [Google Scholar] [CrossRef]
- Semprebon, C.; Varagnolo, S.; Filippi, D.; Perlini, L.; Pierno, M.; Brinkmann, M.; Mistura, G. Deviation of Sliding Drops at a Chemical Step. Soft Matter 2016, 12, 8268–8273. [Google Scholar] [CrossRef]
- Puthenveettil, B.A.; Hopfinger, E.J. Motion and Shape of Partially Non-Wetting Drops on Inclined Surfaces. J. Fluid Mech. 2013, 726, 26–61. [Google Scholar] [CrossRef]
- Nakajima, A.; Nakagawa, Y.; Furuta, T.; Sakai, M.; Isobe, T.; Matsushita, S. Sliding of Water Droplets on Smooth Hydrophobic Silane Coatings with Regular Trianglehydrophilic Regions. Langmuir 2013, 29, 9269–9275. [Google Scholar] [CrossRef] [PubMed]
- Furuta, T.; Sakai, M.; Isobe, T.; Matsushita, S.; Nakajima, A. Sliding of Water Droplets on Hydrophobic Surfaces with Various Hydrophilic Region Sizes. Langmuir 2011, 27, 7307–7313. [Google Scholar] [CrossRef] [PubMed]
- Swift, M.R.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann Simulation of Nonideal Fluids. Phys. Rev. Lett. 1995, 75, 830. [Google Scholar] [CrossRef] [PubMed]
- Briant, A.J.; Wagner, A.J.; Yeomans, J.M. Lattice Boltzmann Simulations of Contact Line Motion. I. Liquid-Gas Systems. Phys. Rev. E 2004, 69, 031602. [Google Scholar] [CrossRef]
- Briant, A.J.; Yeomans, J.M. Lattice Boltzmann Simulations of Contact Line Motion. II. Binary Fluids. Phys. Rev. E 2004, 69, 031603. [Google Scholar] [CrossRef]
- Varagnolo, S.; Mistura, G.; Pierno, M.; Sbragaglia, M. Sliding Droplets of Xanthan Solutions: A Joint Experimental and Numerical Study. Eur. Phys. J. E 2015, 38, 126. [Google Scholar] [CrossRef]
- Huang, J.; Wang, X.P. A Lattice Boltzmann Model for Multiphase Flows with Moving Contact Line and Variable Density. J. Comput. Phys. 2018, 353, 26–45. [Google Scholar] [CrossRef]
- Guo, G.; Ji, B.; Zhang, P.; Chen, B.; Galindo-Torres, S.A. A Hybrid Diffuse Boundary Approach for Modeling Contact-Line Dynamics within the Framework of Phase-Field Lattice Boltzmann Method. Comput. Fluids 2025, 291, 106575. [Google Scholar] [CrossRef]
- Semprebon, C.; Brinkmann, M. On the Onset of Motion of Sliding Drops. Soft Matter 2014, 10, 3325–3334. [Google Scholar] [CrossRef]
- Chou, T.H.; Hong, S.J.; Sheng, Y.J.; Tsao, H.K. Drops Sitting on a Tilted Plate: Receding and Advancing Pinning. Langmuir 2012, 28, 5158–5166. [Google Scholar] [CrossRef]
- Venkateshan, D.G.; Tafreshi, H.V. Modelling Droplet Sliding Angle on Hydrophobic Wire Screens. Colloids Surf. A Physicochem. Eng. Asp. 2018, 538, 310–319. [Google Scholar] [CrossRef]
- Sartori, P.; Quagliati, D.; Varagnolo, S.; Pierno, M.; Mistura, G.; Magaletti, F.; Casciola, C.M. Drop Motion Induced by Vertical Vibrations. New J. Phys. 2015, 17, 113017. [Google Scholar] [CrossRef]
- Qian, T.; Wu, C.; Lei, S.L.; Wang, X.P.; Sheng, P. Modeling and Simulations for Molecular Scale Hydrodynamics of the Moving Contact Line in Immiscible Two-Phase Flows. J. Phys. Condens. Matter 2009, 21, 464119. [Google Scholar] [CrossRef]
- Schwartz, L.W.; Eley, R.R. Simulation of Droplet Motion on Low-Energy and Heterogeneous Surfaces. J. Colloid Interface Sci. 1998, 202, 173–188. [Google Scholar] [CrossRef]
- Snoeijer, J.H.; Le Grand-Piteira, N.; Limat, L.; Stone, H.A.; Eggers, J. Cornered Drops and Rivulets. Phys. Fluids 2007, 19. [Google Scholar] [CrossRef]
- Benilov, E.S.; Benilov, M.S. A Thin Drop Sliding down an Inclined Plate. J. Fluid Mech. 2015, 773, 75–102. [Google Scholar] [CrossRef]
- Furmidge, C.G.L. Studies at Phase Interfaces. I. The Sliding of Liquid Drops on Solid Surfaces and a Theory for Spray Retention. J. Colloid Sci. 1962, 17, 309–324. [Google Scholar] [CrossRef]
- ElSherbini, A.I.; Jacobi, A.M. Liquid Drops on Vertical and Inclined Surfaces: I. An Experimental Study of Drop Geometry. J. Colloid Interface Sci. 2004, 273, 556–565. [Google Scholar] [CrossRef]
- Xu, Z. An Inclined Plane Based Dynamic Contact Angle Algorithm and Its Validity in Application of Hydrophobicity Measurement for Insulating Materials. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 1832–1835. [Google Scholar] [CrossRef]
- Gao, N.; Geyer, F.; Pilat, D.W.; Wooh, S.; Vollmer, D.; Butt, H.J.; Berger, R. How Drops Start Sliding over Solid Surfaces. Nat. Phys. 2018, 14, 191–196. [Google Scholar] [CrossRef]
- Extrand, C.W.; Kumagai, Y. Liquid Drops on an Inclined Plane: The Relation between Contact Angles, Drop Shape, and Retentive Force. J. Colloid Interface Sci. 1995, 170, 515–521. [Google Scholar] [CrossRef]
- Extrand, C.W.; Gent, A.N. Retention of Liquid Drops by Solid Surfaces. J. Colloid Interface Sci. 1990, 138, 431–442. [Google Scholar] [CrossRef]
- Stern, Y.; Tadmor, R.; Miron, A.; Vinod, A. Furmidge Equation Revisited. Langmuir 2025, 41, 11785–11793. [Google Scholar] [CrossRef]
- Frenkel, Y.I. On the Behavior of Liquid Drops on a Solid Surface. 1. The Sliding of Drops on an Inclined Surface. arXiv 2005. [Google Scholar] [CrossRef]
- Antonim, C.; Carmona, F.J.; Pierce, E.; Marengo, M.; Amirfazli, A. General Methodology for Evaluating the Adhesion Force of Drops and Bubbles on Solid Surfaces. Langmuir 2009, 25, 6143–6154. [Google Scholar] [CrossRef]
- Berejnov, V.; Thorne, R.E. Effect of Transient Pinning on Stability of Drops Sitting on an Inclined Plane. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2007, 75, 066308. [Google Scholar] [CrossRef]
- Tadmor, R.; Bahadur, P.; Leh, A.; N’Guessan, H.E.; Jaini, R.; Dang, L. Measurement of Lateral Adhesion Forces at the Interface between a Liquid Drop and a Substrate. Phys. Rev. Lett. 2009, 103, 266101. [Google Scholar] [CrossRef]
- Lagubeau, G.; Le Merrer, M.; Clanet, C.; Quéré, D. Leidenfrost on a Ratchet. Nat. Phys. 2011, 7, 395–398. [Google Scholar] [CrossRef]
- Pilat, D.W.; Papadopoulos, P.; Schäffel, D.; Vollmer, D.; Berger, R.; Butt, H.J. Dynamic Measurement of the Force Required to Move a Liquid Drop on a Solid Surface. Langmuir 2012, 28, 16812–16820. [Google Scholar] [CrossRef]
- Mannetje, D.; Banpurkar, A.; Koppelman, H.; Duits, M.H.G.; Van Den Ende, D.; Mugele, F. Electrically Tunable Wetting Defects Characterized by a Simple Capillary Force Sensor. Langmuir 2013, 29, 9944–9949. [Google Scholar] [CrossRef]
- Timonen, J.V.I.; Latikka, M.; Ikkala, O.; Ras, R.H.A. Free-Decay and Resonant Methods for Investigating the Fundamental Limit of Superhydrophobicity. Nat. Commun. 2013, 4, 2398. [Google Scholar] [CrossRef]
- Olin, P.; Lindström, S.B.; Pettersson, T.; Wågberg, L. Water Drop Friction on Superhydrophobic Surfaces. Langmuir 2013, 29, 9079–9089. [Google Scholar] [CrossRef]
- Pierce, E.; Carmona, F.J.; Amirfazli, A. Understanding of Sliding and Contact Angle Results in Tilted Plate Experiments. Colloids Surfaces A Physicochem. Eng. Asp. 2008, 323, 73–82. [Google Scholar] [CrossRef]
- Jena, A.K.; Bhimavarapu, Y.V.R.; Tang, S.; Liu, J.; Das, R.; Gulec, S.; Vinod, A.; Yao, C.W.; Cai, T.; Tadmor, R. Stages That Lead to Drop Depinning and Onset of Motion. Langmuir 2021, 38, 92–99. [Google Scholar] [CrossRef] [PubMed]
- Santos, M.J.; Velasco, S.; White, J.A. Simulation Analysis of Contact Angles and Retention Forces of Liquid Drops on Inclined Surfaces. Langmuir 2012, 28, 11819–11826. [Google Scholar] [CrossRef] [PubMed]
- Janardan, N.; Panchagnula, M.V. Effect of the Initial Conditions on the Onset of Motion in Sessile Drops on Tilted Plates. Colloids Surfaces A Physicochem. Eng. Asp. 2014, 456, 238–245. [Google Scholar] [CrossRef]
- Janardan, N.; Panchagnula, M.V. Onset of Sliding Motion in Sessile Drops with Initially Non-Circular Contact Lines. Colloids Surfaces A Physicochem. Eng. Asp. 2016, 498, 146–155. [Google Scholar] [CrossRef]
- Suzuki, S.; Nakajima, A.; Sakai, M.; Song, J.H.; Yoshida, N.; Kameshima, Y.; Okada, K. Sliding Acceleration of Water Droplets on a Surface Coated with Fluoroalkylsilane and Octadecyltrimethoxysilane. Surf. Sci. 2006, 600, 2214–2219. [Google Scholar] [CrossRef]
- Annapragada, S.R.; Murthy, J.Y.; Garimella, S.V.; Annapragada, S.R.; Murthy, J.Y.; Garimella, S. V Prediction of Droplet Dynamics on an Incline. Int. J. Heat Mass Transf. 2012, 55, 1466–1474. [Google Scholar] [CrossRef]
- Koh, Y.Y.; Lee, Y.C.; Gaskell, P.H.; Jimack, P.K.; Thompson, H.M. Droplet Migration: Quantitative Comparisons with Experiment. Eur. Phys. J. Spec. Top. 2009, 166, 117–120. [Google Scholar] [CrossRef]
- Huh, C.; Scriven, L.E. Hydrodynamic Model of Steady Movement of a Solid/Liquid/Fluid Contact Line. J. Colloid Interface Sci. 1971, 35, 85–101. [Google Scholar] [CrossRef]
- Cox, R.G. The Dynamics of the Spreading of Liquids on a Solid Surface. Part 1. Viscous Flow. J. Fluid Mech. 1986, 168, 169–194. [Google Scholar] [CrossRef]
- De Gennes, P.G. Wetting: Statics and Dynamics. Rev. Mod. Phys. 1985, 57, 827. [Google Scholar] [CrossRef]
- Jacqmin, D. Contact-Line Dynamics of a Diffuse Fluid Interface. J. Fluid Mech. 2000, 402, 57–88. [Google Scholar] [CrossRef]
- Hocking, L.M. Sliding and Spreading of Thin Two-Dimensional Drops. Q. J. Mech. Appl. Math. 1981, 34, 37–55. [Google Scholar] [CrossRef]
- Dussan, E.B.; Chow, R.T.-P. On the Ability of Drops or Bubbles to Stick to Non-Horizontal Surfaces of Solids. J. Fluid Mech. 1983, 137, 1–29. [Google Scholar] [CrossRef]
- Dussan, E.B.V. On the Ability of Drops or Bubbles to Stick to Non-Horizontal Surfaces of Solids. Part 2. Small Drops or Bubbles Having Contact Angles of Arbitrary Size. J. Fluid Mech. 1985, 151, 1–20. [Google Scholar] [CrossRef]
- Kim, H.Y.; Lee, H.J.; Kang, B.H. Sliding of Liquid Drops Down an Inclined Solid Surface. J. Colloid Interface Sci. 2002, 247, 372–380. [Google Scholar] [CrossRef]
- Varagnolo, S.; Schiocchet, V.; Ferraro, D.; Pierno, M.; Mistura, G.; Sbragaglia, M.; Gupta, A.; Amati, G. Tuning Drop Motion by Chemical Patterning of Surfaces. Langmuir 2014, 30, 2401–2409. [Google Scholar] [CrossRef]
- Ahmed, G.; Sellier, M.; Jermy, M.; Taylor, M. Modeling the Effects of Contact Angle Hysteresis on the Sliding of Droplets down Inclined Surfaces. Eur. J. Mech.-B/Fluids 2014, 48, 218–230. [Google Scholar] [CrossRef]
- Yilbas, B.S.; Al-Sharafi, A.; Ali, H.; Al-Aqeeli, N. Dynamics of a Water Droplet on a Hydrophobic Inclined Surface: Influence of Droplet Size and Surface Inclination Angle on Droplet Rolling. RSC Adv. 2017, 7, 48806–48818. [Google Scholar] [CrossRef]
- Sbragaglia, M.; Biferale, L.; Amati, G.; Varagnolo, S.; Ferraro, D.; Mistura, G.; Pierno, M. Sliding Drops across Alternating Hydrophobic and Hydrophilic Stripes. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2014, 89, 012406. [Google Scholar] [CrossRef] [PubMed]
- Engelnkemper, S.; Wilczek, M.; Gurevich, S.V.; Thiele, U. Morphological Transitions of Sliding Drops: Dynamics and Bifurcations. Phys. Rev. Fluids 2016, 1, 073901. [Google Scholar] [CrossRef]
- Schwartz, L.W.; Roux, D.; Cooper-White, J.J. On the Shapes of Droplets That Are Sliding on a Vertical Wall. Phys. D Nonlinear Phenom. 2005, 209, 236–244. [Google Scholar] [CrossRef]
- Peschka, D. Thin-Film Free Boundary Problems for Partial Wetting. J. Comput. Phys. 2015, 295, 770–778. [Google Scholar] [CrossRef]
- Ben Amar, M.; Cummings, L.J.; Pomeau, Y. Transition of a Moving Contact Line from Smooth to Angular. Phys. Fluids 2003, 15, 2949–2960. [Google Scholar] [CrossRef]
- Mognetti, B.M.; Kusumaatmaja, H.; Yeomans, J.M. Drop Dynamics on Hydrophobic and Superhydrophobic Surfaces. Faraday Discuss. 2010, 146, 153–165. [Google Scholar] [CrossRef]
- Thampi, S.P.; Adhikari, R.; Govindarajan, R. Do Liquid Drops Roll or Slide on Inclined Surfaces? Langmuir 2013, 29, 3339–3346. [Google Scholar] [CrossRef]
- Gao, L.; McCarthy, T.J. Contact Angle Hysteresis Explained. Langmuir 2006, 22, 6234–6237. [Google Scholar] [CrossRef]
- Sauer, R.A. A Frictional Sliding Algorithm for Liquid Droplets. Comput. Mech. 2016, 58, 937–956. [Google Scholar] [CrossRef]
- Clarke, A. The Application of Particle Tracking Velocimetry and Flow Visualisation to Curtain Coating. Chem. Eng. Sci. 1995, 50, 2397–2407. [Google Scholar] [CrossRef]
- Chen, Q.; Ramé, E.; Garoff, S. The Velocity Field near Moving Contact Lines. J. Fluid Mech. 1997, 337, 49–66. [Google Scholar] [CrossRef]
- Shikhmurzaev, Y.D. Capillary Flows with Forming Interfaces; CRC Press: Boca Raton, FL, USA, 2007; ISBN 9781584887492. [Google Scholar]
- Mahrous, E.; Roy, R.V.; Jarauta, A.; Secanell, M. A Two-Dimensional Numerical Model for the Sliding Motion of Liquid Drops by the Particle Finite Element Method. Phys. Fluids 2021, 33, 032117. [Google Scholar] [CrossRef]
- Mahrous, E.; Valéry Roy, R.; Jarauta, A.; Secanell, M. A Three-Dimensional Numerical Model for the Motion of Liquid Drops by the Particle Finite Element Method. Phys. Fluids 2022, 34, 052120. [Google Scholar] [CrossRef]
- Suzuki, S.; Nakajima, A.; Sakai, M.; Sakurada, Y.; Yoshida, N.; Hashimoto, A.; Kameshima, Y.; Okada, K. Slipping and Rolling Ratio of Sliding Acceleration for a Water Droplet Sliding on Fluoroalkylsilane Coatings of Different Roughness. Chem. Lett. 2008, 37, 58–59. [Google Scholar] [CrossRef]
- Furuta, T.; Nakajima, A.; Sakai, M.; Isobe, T.; Kameshima, Y.; Okada, K. Evaporation and Sliding of Water Droplets on Fluoroalkylsilane Coatings with Nanoscale Roughness. Langmuir 2009, 25, 5417–5420. [Google Scholar] [CrossRef]
- Al-Sharafi, A.; Yilbas, B.S.; Ali, H.; Alaqeeli, N. A Water Droplet Pinning and Heat Transfer Characteristics on an Inclined Hydrophobic Surface. Sci. Rep. 2018, 8, 3061. [Google Scholar] [CrossRef]
- Sakai, M.; Song, J.H.; Yoshida, N.; Suzuki, S.; Kameshima, Y.; Nakajima, A. Direct Observation of Internal Fluidity in a Water Droplet during Sliding on Hydrophobic Surfaces. Langmuir 2006, 22, 4906–4909. [Google Scholar] [CrossRef]
- Xie, J.; Xu, J.; Shang, W.; Zhang, K. Mode Selection between Sliding and Rolling for Droplet on Inclined Surface: Effect of Surface Wettability. Int. J. Heat Mass Transf. 2018, 122, 45–58. [Google Scholar] [CrossRef]
- Maglio, M.; Legendre, D. Numerical Simulation of Sliding Drops on an Inclined Solid Surface. Environ. Sci. Eng. 2014, 47–69. [Google Scholar] [CrossRef]
- Limat, L. Drops Sliding down an Incline at Large Contact Line Velocity: What Happens on the Road towards Rolling? J. Fluid Mech. 2014, 738, 1–4. [Google Scholar] [CrossRef]
- Léopoldès, J.; Bucknall, D.G. Droplet Spreading on Microstriped Surfaces. J. Phys. Chem. B 2005, 109, 8973–8977. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, S.; Nakajima, A.; Tanaka, K.; Sakai, M.; Hashimoto, A.; Yoshida, N.; Kameshima, Y.; Okada, K. Sliding Behavior of Water Droplets on Line-Patterned Hydrophobic Surfaces. Appl. Surf. Sci. 2008, 254, 1797–1805. [Google Scholar] [CrossRef]
- Morita, M.; Koga, T.; Otsuka, H.; Takahara, A. Macroscopic-Wetting Anisotropy on the Line-Patterned Surface of Fluoroalkylsilane Monolayers. Langmuir 2005, 21, 911–918. [Google Scholar] [CrossRef]
- Xing, L.; Zhang, Y.; Zhao, Y. Many-Body Dissipative Particle Dynamics Simulation of Droplet Dynamic Behavior on Stripe-Patterned Surfaces. Phys. Fluids 2025, 37, 092007. [Google Scholar] [CrossRef]
- Omidian, F.; Foroutan, M. Investigation of the Dynamic Behavior of a Water Nanodroplet on an Inclined Au(100) Surface Using Molecular Dynamics Simulation. Comput. Mater. Sci. 2025, 259, 114169. [Google Scholar] [CrossRef]
- Herde, D.; Thiele, U.; Herminghaus, S.; Brinkmann, M. Driven Large Contact Angle Droplets on Chemically Heterogeneous Substrates. Europhys. Lett. 2012, 100, 16002. [Google Scholar] [CrossRef]
- Savva, N.; Kalliadasis, S. Droplet Motion on Inclined Heterogeneous Substrates. J. Fluid Mech. 2013, 725, 462–491. [Google Scholar] [CrossRef]
- Moosavi, A.; Rauscher, M.; Dietrich, S. Size Dependent Motion of Nanodroplets on Chemical Steps. J. Chem. Phys. 2008, 129, 044706. [Google Scholar] [CrossRef]
- Rauscher, M.; Dietrich, S. Nano-Droplets on Structured Substrates. Soft Matter 2009, 5, 2997–3001. [Google Scholar] [CrossRef]
- Thiele, U.; Knobloch, E. Driven Drops on Heterogeneous Substrates: Onset of Sliding Motion. Phys. Rev. Lett. 2006, 97, 204501. [Google Scholar] [CrossRef] [PubMed]
- Thiele, U.; Knobloch, E. On the Depinning of a Driven Drop on a Heterogeneous Substrate. New J. Phys. 2006, 8, 313. [Google Scholar] [CrossRef]
- Kusumaatmaja, H.; Léopoldès, J.; Dupuis, A.; Yeomans, J.M. Drop Dynamics on Chemically Patterned Surfaces. Europhys. Lett. 2006, 73, 740–746. [Google Scholar] [CrossRef]
- Kusumaatmaja, H.; Yeomans, J.M. Modeling Contact Angle Hysteresis on Chemically Patterned and Superhydrophobic Surfaces. Langmuir 2007, 23, 6019–6032. [Google Scholar] [CrossRef]
- Wang, X.P.; Qian, T.; Sheng, P. Moving Contact Line on Chemically Patterned Surfaces. J. Fluid Mech. 2008, 605, 59–78. [Google Scholar] [CrossRef]
- Beltrame, P.; Hänggi, P.; Thiele, U. Depinning of Three-Dimensional Drops from Wettability Defects. Europhys. Lett. 2009, 86, 24006. [Google Scholar] [CrossRef]
- He, B.; Qin, C.; Zhou, S.; Wen, B. Analysis of Depinning Behavior of Drop on Chemically Heterogeneous Surface. Phys. Rev. Fluids 2020, 5, 114003. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Zhu, Q.; Wu, K.; Chen, Z.; Wang, Z. Simulation of Droplet Dynamics in an Inclined Channel Considering Contact Angle Hysteresis Using the Cascade Lattice Boltzmann Method. Phys. Fluids 2024, 36, 012130. [Google Scholar] [CrossRef]
- Chen, J.W.; Zhang, C.Y.; Gao, P.; Liu, H.R.; Ding, H. Droplet Sliding on an Inclined Substrate with Chemical Defects. Int. J. Multiph. Flow 2025, 194, 105445. [Google Scholar] [CrossRef]
- Demou, A.D.; Savva, N. Hybrid AI-Analytical Modeling of Droplet Dynamics on Inclined Heterogeneous Surfaces. Mathematics 2024, 12, 1188. [Google Scholar] [CrossRef]
- Anantharaju, N.; Panchagnula, M.; Neti, S. Evaporating Drops on Patterned Surfaces: Transition from Pinned to Moving Triple Line. J. Colloid Interface Sci. 2009, 337, 176–182. [Google Scholar] [CrossRef] [PubMed]
- Shanahan, M.E.R. Simple Theory of “Stick-Slip” Wetting Hysteresis. Langmuir 2002, 11, 1041–1043. [Google Scholar] [CrossRef]
- Bormashenko, E.; Musin, A.; Zinigrad, M. Evaporation of Droplets on Strongly and Weakly Pinning Surfaces and Dynamics of the Triple Line. Colloids Surfaces A Physicochem. Eng. Asp. 2011, 385, 235–240. [Google Scholar] [CrossRef]
- Orejon, D.; Sefiane, K.; Shanahan, M.E.R. Stick–Slip of Evaporating Droplets: Substrate Hydrophobicity and Nanoparticle Concentration. Langmuir 2011, 27, 12834–12843. [Google Scholar] [CrossRef]
- Oksuz, M.; Erbil, H.Y. Comments on the Energy Barrier Calculations during “Stick–Slip” Behavior of Evaporating Droplets Containing Nanoparticles. J. Phys. Chem. C 2014, 118, 9228–9238. [Google Scholar] [CrossRef]
- Dong, B.; Wang, F.; Zhang, X.; Jiang, X. 3D Lattice Boltzmann Simulation of Droplet Evaporation on Patterned Surfaces: Study of Pinning–Depinning Mechanism. Int. J. Multiph. Flow 2020, 125, 103218. [Google Scholar] [CrossRef]
- Ding, Y.; Jia, L.; Peng, Q.; Guo, J. Critical Sliding Angle of Water Droplet on Parallel Hydrophobic Grooved Surface. Colloids Surfaces A Physicochem. Eng. Asp. 2020, 585, 124083. [Google Scholar] [CrossRef]
- Hao, P.; Lv, C.; Yao, Z.; He, F. Sliding Behavior of Water Droplet on Superhydrophobic Surface. Europhys. Lett. 2010, 90, 66003. [Google Scholar] [CrossRef]
- Reyssat, M.; Richard, D.; Clanet, C.; Quéré, D. Dynamical Superhydrophobicity. Faraday Discuss. 2010, 146, 19–33. [Google Scholar] [CrossRef]
- Sakai, M.; Kono, H.; Nakajima, A.; Zhang, X.; Sakai, H.; Abe, M.; Fujishima, A. Sliding of Water Droplets on the Superhydrophobic Surface with Zno Nanorods. Langmuir 2009, 25, 14182–14186. [Google Scholar] [CrossRef]
- Miwa, M.; Nakajima, A.; Fujishima, A.; Hashimoto, K.; Watanabe, T. Effects of the Surface Roughness on Sliding Angles of Water Droplets on Superhydrophobic Surfaces. Langmuir 2000, 16, 5754–5760. [Google Scholar] [CrossRef]
- Yoshimitsu, Z.; Nakajima, A.; Watanabe, T.; Hashimoto, K. Effects of Surface Structure on the Hydrophobicity and Sliding Behavior of Water Droplets. Langmuir 2002, 18, 5818–5822. [Google Scholar] [CrossRef]
- Park, J.; Kumar, S. Droplet Sliding on an Inclined Substrate with a Topographical Defect. Langmuir 2017, 33, 7352–7363. [Google Scholar] [CrossRef] [PubMed]
- Mhatre, N.V.; Kumar, S. Pinning–Depinning Transition of Droplets on Inclined Substrates with a Three-Dimensional Topographical Defect. Soft Matter 2024, 20, 3529–3540. [Google Scholar] [CrossRef] [PubMed]
- Bao, Q.; Kang, H. Numerical Simulation of Droplet Impacting and Sliding on Hydrophobic Granular Surfaces. Math. Probl. Eng. 2021, 2021, 5534003. [Google Scholar] [CrossRef] [PubMed]
- Chamakos, N.T.; Kavousanakis, M.E.; Boudouvis, A.G.; Papathanasiou, A.G. Droplet Spreading on Rough Surfaces: Tackling the Contact Line Boundary Condition. Phys. Fluids 2016, 28, 022105. [Google Scholar] [CrossRef]
- Bird, J.C.; Mandre, S.; Stone, H.A. Short-Time Dynamics of Partial Wetting. Phys. Rev. Lett. 2008, 100, 234501. [Google Scholar] [CrossRef]
- Wu, M.; Cubaud, T.; Ho, C.-M.; Wu, M.; Cubaud, T.; Ho, C.-M. Scaling Law in Liquid Drop Coalescence Driven by Surface Tension. Phys. Fluids 2004, 16, L51–L54. [Google Scholar] [CrossRef]
- Stapelbroek, B.B.J.; Jansen, H.P.; Kooij, E.S.; Snoeijer, J.H.; Eddi, A. Universal Spreading of Water Drops on Complex Surfaces. Soft Matter 2014, 10, 2641–2648. [Google Scholar] [CrossRef]
- Du, J.; Chamakos, N.T.; Papathanasiou, A.G.; Min, Q. Initial Spreading Dynamics of a Liquid Droplet: The Effects of Wettability, Liquid Properties, and Substrate Topography. Phys. Fluids 2021, 33, 042118. [Google Scholar] [CrossRef]
- Bellantoni, E.; Guglietta, F.; Pelusi, F.; Desbrun, M.; Um, K.; Nicolaou, M.; Savva, N.; Sbragaglia, M. Immersed Boundary-Lattice Boltzmann Mesoscale Method for Wetting Problems. Phys. Rev. E 2025, 112, 025305. [Google Scholar] [CrossRef]
- Kim, U.; Lee, J.; Kim, J.H. Role of Droplet Viscosity on the Formation of Residual Droplets on Grooved Hydrophobic Surfaces. Phys. Fluids 2023, 35, 122116. [Google Scholar] [CrossRef]
- Larson, R.G. The Structure and Rheology of Complex Fluids, 1999th ed.; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Ahmed, G.; Sellier, M.; Lee, Y.C.; Jermy, M.; Taylor, M. Modeling the Spreading and Sliding of Power-Law Droplets. Colloids Surfaces A Physicochem. Eng. Asp. 2013, 432, 2–7. [Google Scholar] [CrossRef]
- Varagnolo, S.; Filippi, D.; Mistura, G.; Pierno, M.; Sbragaglia, M. Stretching of Viscoelastic Drops in Steady Sliding. Soft Matter 2017, 13, 3116–3124. [Google Scholar] [CrossRef] [PubMed]
- Sartori, P.; Ferraro, D.; Dassie, M.; Meggiolaro, A.; Filippi, D.; Zaltron, A.; Pierno, M.; Mistura, G. Oscillatory Motion of Viscoelastic Drops on Slippery Lubricated Surfaces. Commun. Phys. 2022, 5, 81. [Google Scholar] [CrossRef]
- Carneri, M.; Ferraro, D.; Azarpour, A.; Meggiolaro, A.; Cremaschini, S.; Filippi, D.; Pierno, M.; Zanchetta, G.; Mistura, G. Sliding and Rolling of Yield Stress Fluid Droplets on Highly Slippery Lubricated Surfaces. J. Colloid Interface Sci. 2023, 644, 487–495. [Google Scholar] [CrossRef]
- Luo, M.; Gupta, R.; Frechette, J. Modulating Contact Angle Hysteresis to Direct Fluid Droplets along a Homogenous Surface. ACS Appl. Mater. Interfaces 2012, 4, 890–896. [Google Scholar] [CrossRef]
- ’T Mannetje, D.; Ghosh, S.; Lagraauw, R.; Otten, S.; Pit, A.; Berendsen, C.; Zeegers, J.; Van Den Ende, D.; Mugele, F. Trapping of Drops by Wetting Defects. Nat. Commun. 2014, 5, 3559. [Google Scholar] [CrossRef]
- Imani, G.; Zhang, L.; Xu, C.; Sun, H.; Yang, Y.; Yao, J. Study of the Trapping Mechanism of Merging Drops Moving under Thermocapillary Migration on a Surface with Wettability Contrast. J. Pet. Sci. Eng. 2023, 220, 111172. [Google Scholar] [CrossRef]
- Mistura, G.; Pierno, M. Drop Mobility on Chemically Heterogeneous and Lubricant-Impregnated Surfaces. Adv. Phys. X 2017, 2, 591–607. [Google Scholar] [CrossRef]
- Chang, B.; Zhou, Q.; Ras, R.H.A.; Shah, A.; Wu, Z.; Hjort, K. Sliding Droplets on Hydrophilic/Superhydrophobic Patterned Surfaces for Liquid Deposition. Appl. Phys. Lett. 2016, 108, 154102. [Google Scholar] [CrossRef]
- Lai, Y.; Pan, F.; Xu, C.; Fuchs, H.; Chi, L. In Situ Surface-Modification-Induced Superhydrophobic Patterns with Reversible Wettability and Adhesion. Adv. Mater. 2013, 25, 1682–1686. [Google Scholar] [CrossRef]
- Sharma, M.; Gupta, S.; Bhatt, B.; Bhatt, G.; Bhattacharya, S.; Khare, K. Anisotropic Motion of Aqueous Drops on Lubricated Chemically Heterogenous Slippery Surfaces. Adv. Mater. Interfaces 2021, 8, 2001916. [Google Scholar] [CrossRef]
- Rigoni, C.; Ferraro, D.; Carlassara, M.; Filippi, D.; Varagnolo, S.; Pierno, M.; Talbot, D.; Abou-Hassan, A.; Mistura, G. Dynamics of Ferrofluid Drops on Magnetically Patterned Surfaces. Langmuir 2018, 34, 8917–8922. [Google Scholar] [CrossRef]


| Method | Assumptions | Advantages | Limitations | Treatment of Dynamic Contact Angles | Inclusion of Hysteresis | Computational Cost | Typical Applications |
|---|---|---|---|---|---|---|---|
| Lattice Boltzmann | Mesoscopic kinetic model; discrete lattice; fluid as particle distributions | Efficient for complex geometries; parallelizable; handles multiphase flows well | Requires careful tuning of interface parameters; limited by lattice resolution | Geometric wetting boundary models; can prescribe advancing/receding angles | Yes, via hysteresis windows and boundary conditions | Moderate to high, depending on resolution and dimensionality | Droplet impact, microfluidics, evaporation, wetting on patterned surfaces |
| Surface Evolver | Minimization of surface energy; quasi-static equilibrium; no inertia | Accurate equilibrium shapes; flexible geometry; low computational cost | Dynamics can be described as collection of quasi-static states; neglects inertia and viscous effects | Not inherently dynamic; static contact angles only | No, direct modeling; hysteresis must be manually encoded | Low | Static droplet shapes, pendant drops, wetting morphologies |
| Cahn–Hilliard/Navier–Stokes | Diffuse interface; phase-field model; coupled partial differential equations (PDEs) | Captures interface dynamics and phase separation; thermodynamically consistent | High computational cost; sensitive to mobility and interface thickness parameters | Coupled with Navier slip and dynamic contact angle models | Yes, via boundary conditions and mobility tuning | High | Droplet impact, phase separation, active fluids, turbulent multiphase flows |
| Molecular Dynamics | Atomistic interactions; Newtonian mechanics; Lennard-Jones potentials | Captures nanoscale physics; includes thermal fluctuations and molecular detail | Limited to small systems and short timescales; expensive | Emerges naturally from molecular interactions | Yes, observed at nanoscale; matches macroscale models like Cox–Voinov | Very high | Nanoscale wetting, contact line friction, droplet nucleation |
| Lubrication Theory | Thin film approximation; low Reynolds number; small slopes | Analytical tractability; low computational cost; good for spreading flows | Not valid for large contact angles or inertial effects; limited to thin films | Often uses Cox–Voinov or matched asymptotic models | Yes, via advancing/receding angle models | Low | Coating flows, spreading, contact line motion |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varagnolo, S. Droplets Sliding Down Partially Wetted (Non-Superhydrophobic) Surfaces: A Review. Liquids 2025, 5, 29. https://doi.org/10.3390/liquids5040029
Varagnolo S. Droplets Sliding Down Partially Wetted (Non-Superhydrophobic) Surfaces: A Review. Liquids. 2025; 5(4):29. https://doi.org/10.3390/liquids5040029
Chicago/Turabian StyleVaragnolo, Silvia. 2025. "Droplets Sliding Down Partially Wetted (Non-Superhydrophobic) Surfaces: A Review" Liquids 5, no. 4: 29. https://doi.org/10.3390/liquids5040029
APA StyleVaragnolo, S. (2025). Droplets Sliding Down Partially Wetted (Non-Superhydrophobic) Surfaces: A Review. Liquids, 5(4), 29. https://doi.org/10.3390/liquids5040029







