Previous Article in Journal
Mesoscopic Liquids Emit Thermal Waves Under Shear Strain or Microflow
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Liquids
Volume 5
Issue 4
10.3390/liquids5040028
liquids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Tuning of the Viscosity Maximum and the Temperature Effect on Wormlike Micelle Solutions Using Hydrotropic and Inorganic Salts

by
Kamilla B. Shishkhanova
*,
Vyacheslav S. Molchanov
and
Olga E. Philippova
*
Physics Department, Lomonosov Moscow State University, 119991 Moscow, Russia
*
Authors to whom correspondence should be addressed.
Liquids 2025, 5(4), 28; https://doi.org/10.3390/liquids5040028
Submission received: 19 August 2025 / Revised: 16 October 2025 / Accepted: 21 October 2025 / Published: 26 October 2025
(This article belongs to the Section Chemical Physics of Liquids)
Browse Figures
Versions Notes

Abstract

The rheological properties of aqueous solutions of wormlike micelles (WLMs) of cationic surfactant erucyl bis(hydroxyethyl)methylammonium chloride (EHAC) in the presence of hydrotropic salt sodium salicylate (NaSal) and inorganic salt sodium chloride (NaCl) have been studied. The conditions for maximum zero-shear viscosity at fixed surfactant concentration were investigated. It has been shown that charged WLMs in the presence of NaSal have higher viscosities than well-screened micelles in the presence of NaCl. This is because the adsorption of hydrophobic salicylate ions onto the micelles increases their length more significantly than the presence of a large amount of sodium ions in the solution. It was discovered that the effect of temperature on the rheological properties depends on both the type of salt used and the salt/surfactant molar ratio. An unusual increase in zero-shear viscosity and elastic modulus was observed at a NaSal concentration that corresponds to the maximum zero-shear viscosity when the WLMs are linear, charged, and “unbreakable”. These results expand the possibilities of using hydrotropic salts to create stable, highly viscous systems in various fields, and opening up new horizons for applications in oil production, cosmetics, and household chemicals.

1. Introduction

Molecules of ionic surfactants in an aqueous solution can self-organize into wormlike micelles (WLMs) when salt is added to the solution. Salt ions screen the repulsion between similarly charged surfactant head groups on the micelle surface, bringing them closer together. This increases the molecular packing parameter, and the cylindrical shape becomes more favorable compared to a spherical one [1]. In the presence of salt, surfactants with long hydrophobic tails can form very long cylindrical micelles known as WLMs. When entangled, WLMs form a network that provides a solution with high viscoelastic properties such as viscosity, modulus of elasticity, and relaxation time [1,2,3,4,5]. These characteristics vary depending on the salt concentration [6,7,8], type of surfactant [4,9], pH, and temperature [8,10]. Due to this, WLMs are widely used as thickeners with controlled viscoelastic properties in oil production, cosmetics, and household chemicals. The high viscoelastic properties of WLM solutions are typically achieved at high surfactant concentrations and relatively low temperatures, which limits their practical applications.
At a fixed concentration of surfactant, the viscosity of the solution varies significantly depending on the amount of salt. Typically, the viscosity passes through the maximum with increasing salt concentration [11,12,13]. The initial increase in viscosity is explained by the increasing length of the micelles. The maximum viscosity corresponds to the formation of the longest linear WLMs. At higher salt concentrations, the viscosity significantly decreases due to the branching of micelles [7].
The viscoelastic properties of WLMs also depend on the type of salt used. Most studies have shown that the effect of salt is determined by the efficiency of binding of salt ions to micelles [14,15,16,17,18]. The stronger the binding, the lower the salt concentration required to form longer micelles and obtain more viscous solutions [19,20]. For non-penetrating ions of inorganic salts, it has been shown that the polarization effect and, therefore, the binding efficiency are consistent with the Hofmeister series [14,15,16,17,18,19,20,21]. Penetrating ions of hydrotropic salts have a stronger binding affinity for micelles due to their hydrophobicity [22]. These ions induce greater structural changes in micelles compared to non-penetrating ions [22]. Isabettini et al. [21] demonstrated that an increase in the hydrophobicity of the salt counterion leads to an increase in the viscosity of WLM solutions. Pleines et al. [23] developed a thermodynamic model to predict the viscosity of solutions of WLMs in both linear and branched forms. It was shown that the maximum zero-shear viscosity for different salts corresponds to the longest linear WLMs and the highest binding efficiency.
WLM solutions with ordinary inorganic salts exhibit a decrease in viscosity at heating, as described in existing theory-based papers [24,25]. This is because the thermal motion of surfactant molecules hinders their aggregation. Therefore, it is difficult to create highly viscous solutions of WLMs at elevated temperatures. In some studies, aromatic salts with a hydrophobic penetrating ion have been used to change the temperature effect on WLMs [22,26,27]. Unlike ordinary salts, the ions of a hydrotropic salt not only bind to the charged head of the surfactant through electrostatic interactions, but they can also integrate into the surface of the micelle through hydrophobic interactions. At the same time, some studies have shown that the temperature dependence of viscosity in these systems is unusual compared to standard solutions of WLMs: with increasing temperature, the viscosity of a surfactant solution with a hydrotropic salt can pass through the maximum. For example, such behavior has been observed in EHAC/sodium hydroxynaphthalene carboxylate (SHNC) solutions with an excess of hydrotropic salt (salt/surfactant molar ratio of 9/1), which causes the micelles to be recharged and their length to be forcibly reduced. The authors explained the increase in micelle length, and hence, viscosity, by the desorption of the penetrating ions and the decrease in the micelle’s charge [27]. Cao et al. [28] have examined a similar system of cationic surfactant docosyl(trimethyl)azanium chloride (DCTAC) and hydrotropic salt SHNC. At an SHNC/DCTAC molar ratio of 1:2, this system forms ultra-stable WLMs whose viscosities do not change up to 130 °C. The authors have found that SHNC strongly binds with DCTAC micelles through multiple interactions, including hydrophobic, π–cation, and π-π interactions, which decreases the dynamic exchange of SHNC between micelles. At the same time, Raghavan and co-authors have shown that solutions containing 40 mM EHAC and 450 mM sodium salicylate (NaSal) demonstrate a regular decrease in the zero-shear viscosity at heating [26]. In another article by Raghavan [29], for a similar system containing 60 mM EHAC and NaSal, with NaSal/EHAC molar ratios ranging from 0.2 to 0.7, a maximum was observed on the temperature dependences for viscosity. However, the exact cause of this behavior was not explained. In addition, it has been shown that these solutions can have very high viscosities over a wide range of temperatures [29]. Thus, WLMs containing hydrotropic salts can exhibit temperature resistance or exhibit a regular decrease in viscoelastic properties. However, this phenomenon is still poorly studied.
In this study, we used hydrotropic NaSal and the inorganic salt NaCl to investigate the conditions required to obtain high values of viscoelastic properties at a fixed EHAC surfactant concentration. Unlike previous works on this topic, we study micelle solutions with different types of salts and the same surfactant. This allows us to directly compare the effects of adding hydrotropic and inorganic salts on the maximum value of viscosity and the temperature dependence of viscosity. We found that hydrotropic salt can induce higher viscosity, corresponding to longer linear WLMs. The effect of temperature on viscoelastic properties was also studied at various salt concentrations, using both hydrotropic and inorganic salts. The conditions for temperature resistance in the presence of hydrotropic salts were determined, and explanations for these results were proposed.
The practical significance of these findings lies in the potential application of WLM/hydrotropic salt solutions as thickeners for fracturing fluids in the oil industry. Specifically, it is crucial that these solutions maintain high viscosities at elevated temperatures, as WLM solutions typically lose their viscoelastic characteristics in such conditions.

2. Materials and Methods

2.1. Materials

EHAC, C22 surfactant with a cis unsaturation at the 13-carbon position [11,29,30] containing 25 wt% 2-propanol was provided by AkzoNobel. To obtain a pure surfactant, the commercial solution was diluted by deionized water (1:10) and freeze-dried as described elsewhere [30]. Sodium chloride from Sigma-Aldrich (>99.8% purity) and sodium salicylate from Sigma-Aldrich (>99.5% purity) were used without further purification. Water was purified by Millipore Milli-Q system.

2.2. Sample Preparation

Surfactant solutions were prepared by mixing appropriate quantities of aqueous stock solutions of the surfactant and the salt with distilled−deionized water. The samples were stirred for 1 day and left for equilibration at room temperature for another 1 day. In the resulting solutions, the concentrations of EHAC, NaCl, and NaSal were varied within the following ranges: 0.9–19 mM for EHAC, 100–520 mM for NaCl, and 0.5–10 mM for NaSal. All prepared solutions are summarized in Table 1.

2.3. Rheometry

Rheometry was used to determine the viscosity as a function of shear rate and the storage modulus G′ and loss modulus G″ as a function of frequency. Steady and dynamic experiments were carried out on stress control, using an Anton Paar Physica MCR301 rheometer (Graz, Austria). Cone-plane cell CP50-1 with a diameter of cone 50 mm and angle 1 was used in the experiments. The sample volume was 0.59 mL. Shear stress was applied to a sample, and shear deformation was measured as a function of time. Amplitudes of deformation for dynamic experiments were chosen from linear viscoelastic response range according to preliminary amplitude sweep tests. Special care was taken to provide the sample with enough time to relax completely before each measurement.

3. Results and Discussion

3.1. Rheological Properties of EHAC/NaSal Solutions at Room Temperature

At 25 °C, EHAC/NaSal solutions were investigated at two fixed EHAC concentrations of 13 and 18 mM, with different salt/surfactant molar ratios ranging from 0.25 to 0.7 (Table 1).

3.1.1. Effect of Salt Concentration

At both concentrations of EHAC, there is a maximum in the dependence of viscosity on the EHAC/NaSal molar ratio (or, in other words, on the salt concentration). This effect is observed in many surfactant solutions with salt [11,12,13], and the increase in zero-shear viscosity is explained by an increase in micelle length, and a further decrease is due to the transition from linear micelles to branched ones [22,26,31,32]. Branching points can move along the cylindrical part of the micelle, relieving the applied mechanical stress and thereby reducing viscosity [7]. So, the maximum value of zero-shear viscosity (all quantities are mentioned and expressed in SI units in the nomenclature section in the Appendix A) is associated with the longest linear WLMs. Such behavior has been observed in many experimental studies of surfactants, both with ordinary and hydrotropic salts [33,34]. The hydrotropic ion has a hydrophobic part, so it is adsorbed onto the micelle’s surface to minimize contact with water. The hydrotropic ion, being adsorbed between the hydrophilic heads of surfactant molecules on the surface of a micelle reduces both the repulsion between oppositely charged surfactant heads and the penetration of water to the hydrophobic core of the micelles.
The contour length of charged WLMs L increases with increasing end-cap energy Ec and decreasing electrostatic energy Ee in accordance with the following formula [35,36]:
L   ~   ϕ 1 2 e x p ( E c − E e 2 k T )
where ϕ is the volume fraction of surfactant and k is the Boltzmann constant. Ee, in turn, is related to the degree of charge of the micelle and the concentration of free ions in the solution [36]:
E e ≅ k T l B r v 2 ϕ − 1 2 ,
where lB is the Bjerrum length, r is the micelle radius, and v is the effective charge per unit micelle length.
The use of a hydrophobic ion makes it possible to simultaneously increase Ec by reducing the contacts of the hydrophobic core of the micelle with water and reduce Ee, thus greatly increasing the length of the micelles [22]. This leads to an increase in viscosity with an increase in the NaSal/EHAC ratio by more than five orders of magnitude (Figure 1a).
At both EHAC concentrations, the maximum viscosity is observed at the EHAC/NaSal molar ratio of ~0.5 (Figure 1a). Approximately the same ratio of salt and surfactant (0.5) for different concentrations of surfactants indicates the optimal ratio between EHAC and NaSal, and creates the longest linear WLMs. Figure 1a shows that the increase in viscosity (and hence the length of the micelles) is sharper at a lower concentration of surfactant, since in this case the micelles are initially shorter and thus the increase in their length is more noticeable. At the same time, at an EHAC concentration of 18 mM, the viscosity is an order of magnitude higher than at 13 mM EHAC with the same salt ratio, which indicates a significantly longer micelle length. This can be due to an increase in the number and in the length of micelles according to Equation (1). In addition, at a higher concentration of surfactant, there are more free ions in the solution. This leads to a decrease in the Ee value, which also contributes to the increase in the length of micelles.
At a low NaSal/EHAC molar ratio, the solutions have almost no elastic response. As the salt/surfactant molar ratio increases, the solutions start to exhibit viscoelastic behavior (Figure 1b). The relaxation time trel, which is inversely proportional to the crossover frequency wc at which the storage G′ and loss G″ moduli intersect [37], varies from 0.03 to more than 50 s when the NaSal/EHAC molar ratio changes from 0.4 to 0.5. For solutions with NaSal/EHAC molar ratios of 0.5 and 0.6, one can observe that G′ > G″ for the entire range of the frequency. This is typical for viscoelastic solutions of WLMs, and this phenomenon is associated with the formation of a network of WLMs and an increase in the number of entanglements, which occurs when the length of the micelles increases [22,38].

3.1.2. Effect of Surfactant Concentration

Figure 2a shows the dependence of viscosity on surfactant concentration at a fixed NaSal/EHAC molar ratio of 0.5, which corresponds to the point of maximum viscosity. One can see that viscosity remains quite low until the concentration of the surfactant is around 6 mM, then a sharp increase in viscosity is observed. This is due to the transition from a dilute to a semi-dilute regime. Therefore, a concentration of 6 mM can be considered as the crossover concentration c* for surfactant micelles. The observed concentration dependence of viscosity is typical for WLM solutions [5,30,32,39,40,41,42].
Above c*, the viscosity η0 follows a power-law dependence on the surfactant concentration: η0~c10. Its exponent (10) is significantly higher than the predicted value of 3.5 for living WLMs at the fast-breaking limit (breaking time tbr << reptation time trep) [12], which is commonly observed experimentally [9]. Furthermore, it exceeds the 5.25–5.7 range predicted for uncharged short WLMs at the slow-breaking limit (tbr >> trep), where micelles do not break during reptation (so-called “unbreakable” micelles) [30,41,43]. Such a sharp increase in viscosity, as observed in the present system, most probably corresponds to very long, charged micelles in a slow-breaking regime [5]. Previously, such high values of the exponent were only observed in a few systems, including cationic surfactants (exponents of 9.5 [40] and 10.5 [34]) and mixtures of cationic and anionic surfactants (exponent of 9.1 [44]). Therefore, the power-law behavior of the viscosity dependence on EHAC concentration indicates the formation of charged “unbreakable” WLMs. Since the surfactant concentration is actually twice that of NaSal, the resulting micelles are charged. Typically, at higher surfactant concentrations, the “unbreakable” chain mode transitions to fast-breaking mode due to the increased micelle length [30,33,41], and as the reptation time (trep) increases and the breaking time (tbr) decreases for longer micelles, the fast-breaking limit (tbr << trep) is approached. However, in our system, “unbreakable” chains persisted across the entire concentration range, correlating with increased viscosity (Figure 2a).
These “unbreakable” WLMs have a long relaxation time, as seen in Figure 2b, indicating a large micelle contour length. Additionally, the frequency dependence in Figure 2b demonstrates that as surfactant concentration increases, the storage modulus G′ reaches a plateau, and the system transitions to a gel-like state, which has previously been observed in long-lived WLMs [33,38]. So, we can assume that the WLMs at NaSal/EHAC molar ratio of 0.5 are also long-lived.

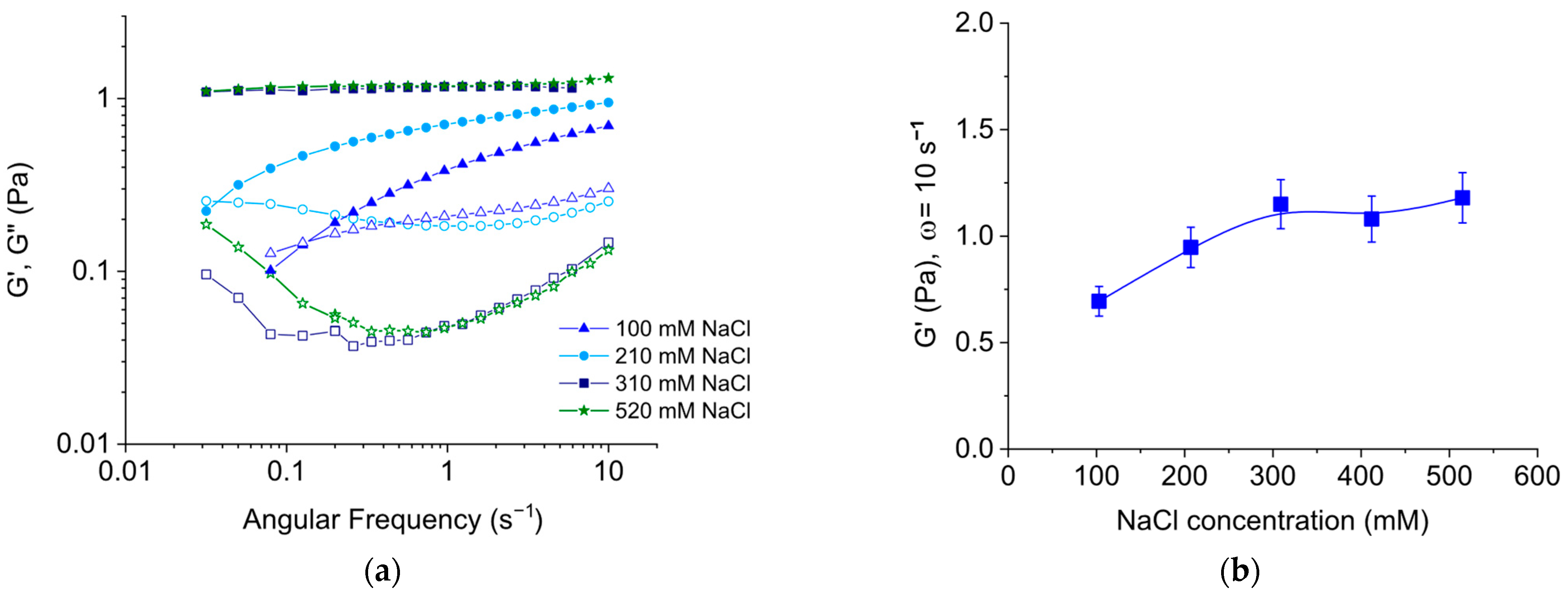
3.2. Comparison of Rheological Properties of EHAC/NaSal and EHAC/NaCl Solutions at Room Temperature

For a comparative study on the effect of hydrotropic (NaSal) and inorganic (NaCl) salts on the rheological properties of EHAC solutions, the concentration of EHAC was fixed at 18 mM. In the case of NaCl, the plot for viscosity as a function of salt concentration passes through the maximum around 310 mM NaCl (Figure 3b), demonstrating a typical dependence that reflects the transition from linear to branched micelles [7,33,34].
For the comparison of NaCl and NaSal salts, we used salt concentrations corresponding to the region of linear micelles: 100 and 210 mM for NaCl, and 6.5 mM for NaSal. Note that in the case of NaCl, the viscosity maximum has been observed at salt/surfactant molar ratios (5.5, 11.7) which are one order of magnitude higher than those for NaSal (0.36). Frequency dependences of storage G′ and loss G″ and Cole–Cole plots are presented in Figure 4b. One can see that, for solution with 210 mM NaCl, Cole–Cole plot is closer to a semicircle. An ideal semicircle is characteristic for solutions that exhibit Maxwellian behavior with a single relaxation time [7,45,46]. This behavior is typical for micelles in the fast-breaking regime when tbr << trep. The deviation of the graphs from the semicircle indicates an increase in the ratio of tbr/trep [7,45,46,47]. Therefore, solutions with 210 mM NaCl are closer to the fast-breaking regime (tbr << trep) and have the lowest tbr/trep ratio, which usually corresponds to well-screened, long WLMs. This is consistent with a high concentration of NaCl. In contrast, solutions with a lower concentration of NaCl and with the hydrotropic salt NaSal demonstrate non-Maxwellian behavior that is characteristic of “unbreakable” micelles (tbr >> trep). This observation is consistent with the earlier conclusions concerning the concentration dependence of the viscosities of EHAC/NaSal solutions.
Despite the unscreened charge of EHAC/NaSal micelles, the value of maximum viscosity of solutions with NaSal is an order of magnitude higher than that of solutions with NaCl (Figure 3b). Therefore, at the same concentration of surfactant, an order of magnitude lower amount of hydrotropic penetrating salt is required to create highly viscous solutions compared to non-penetrating salt, and the resulting viscosity of these solutions is also approximately one order of magnitude higher. The higher viscosities of the solutions suggest that in the presence of NaSal salt, the micelles are longer. Thus, branching, which leads to a decrease in viscosity, occurs with longer micelles; that is, micelles with NaSal are less prone to branching. It could be explained by the higher charge of these micelles compared to the micelles in the presence of NaCl [22,48]. This makes the use of salts with a penetrating ion the most promising in applications requiring high viscosities.
Viscoelastic solutions of 18 mM EHAC at a NaCl concentration higher than 310 mM are characterized by the presence of a plateau in the storage modulus, G0, which is related to the density of crosslinks or the size of cells in an entangled network [22,38]. One can compare elastic modulus G0 near the maximum viscosity for two different salts. For the system NaCl/EHAC, at 310 mM NaCl, G0 is equal to 1 Pa (Figure 5a), which is about two times more than the value for the system with 9 mM NaSal (Figure 6b). As is known, the G0 is proportional to the entanglement density and almost does not depend on the WLM length in dense networks [8,27]. G0 can be expressed in terms of the correlation length ξ by the expression [49]:
G 0 ≈ k T ξ 3 ,
and the correlation length ξ, in turn, is related to the contour length between the entanglement points le and the persistence length lp and is written as follows [49]:
ξ ≈ l e 3 5 · l p 2 5 ,
Thus, the increase in G0 can be explained by a decrease in le or lp. So, we can assume that the lp is longer in the presence of NaSal than in the presence of NaCl. It can be explained by the differences in ionic strength: the greater the ionic strength, the shorter the lp value, as the electrostatic repulsion on the surface of the micelles is well screened [50]. The concentration of NaSal (9 mM) is more than an order of magnitude smaller than the NaCl concentration (310 mM).

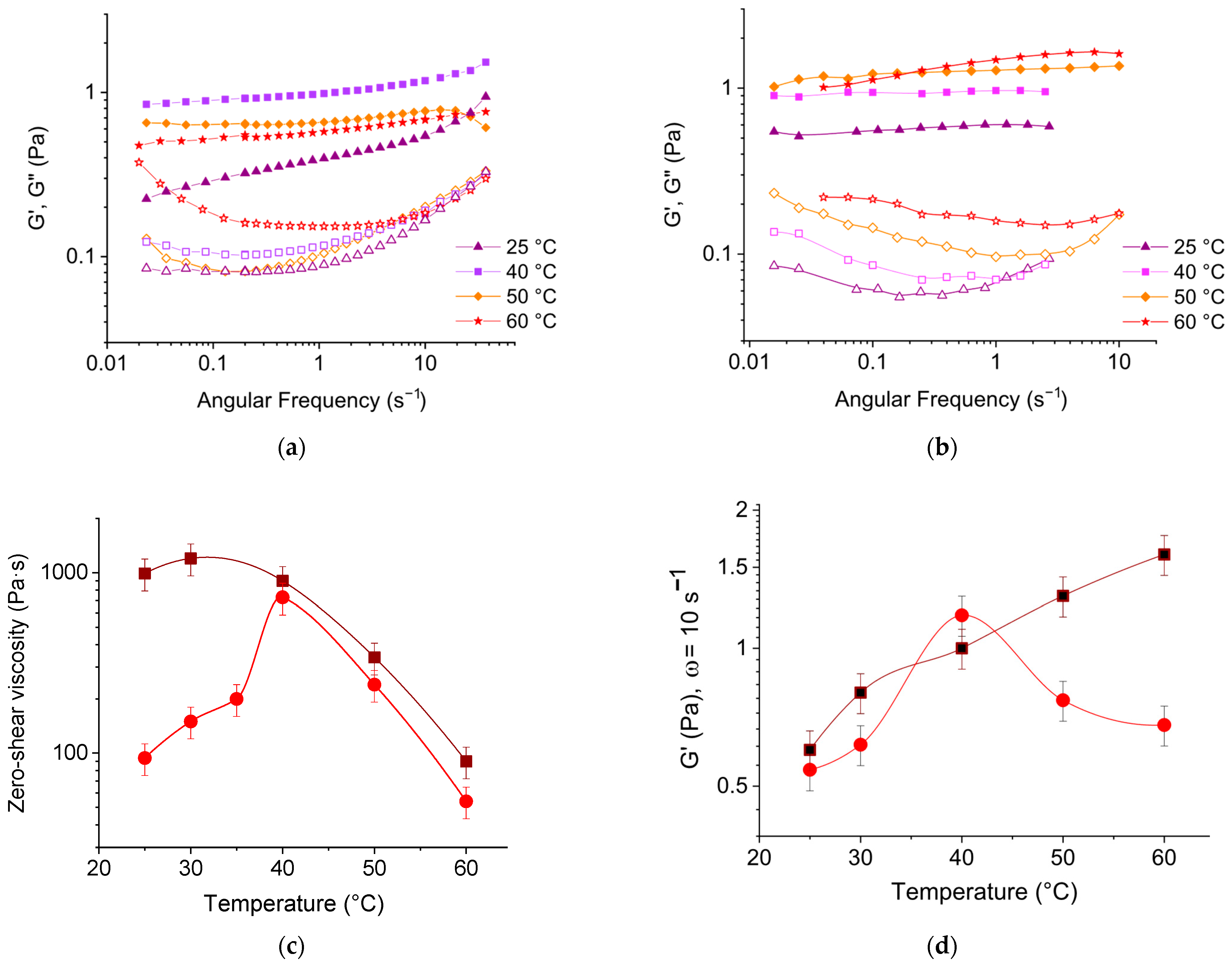
3.3. Effect of Temperature on Rheological Properties of EHAC/NaSal Solutions

The temperature dependence of the rheological properties of EHAC/NaSal solutions was studied by varying the temperature from 25 to 60 °C at two EHAC concentrations—13 and 18 mM—and a fixed NaSal/EHAC molar ratio of 0.5, which corresponds to the region near the viscosity maximum, where long and linear cylindrical micelles are formed.
At both EHAC concentrations, over the entire measured temperature range, the systems behave as viscoelastic solutions. Their storage modulus G′ prevails over the loss modulus G″ and the relaxation time trel is more than 100 s (the crossover point is not reached within the measured frequency range) (Figure 6a,b). As the temperature increases, the system with 13 mM EHAC transitions to a gel-like state, where a plateau appears at the frequency dependences of the storage modulus G′ (Figure 6a). At 18 mM EHAC, the system is in a gel-like state at all studied temperatures (Figure 6b).
At heating, one can observe an increase in zero-shear viscosity η0 (Figure 6c). However, with a further rise in temperature, the viscosity passes through the maximum, and at T > 40 °C it decreases. This effect was observed in similar systems containing EHAC/hydrotropic salt [27]; however, unlike our system, these systems used a high salt/surfactant molar ratio of 9. The authors explained this effect by the desorption of the hydrophobic counterions. Due to their high hydrophobicity, the salt counterions penetrate the hydrophobic part of the micelles. At a high salt/surfactant ratio, the micelles of the cationic surfactant acquire a high negative charge because of the large amount of adsorbed counterions. As the temperature increases, some counterions desorb and the charge of the micelle decreases, resulting in the growth of the micelles in length. However, in our case, the salt/surfactant molar ratio is only 0.5, and the micelles cannot be recharged by adsorbed counterions; therefore, the mechanism described above cannot be exactly applicable to our system.
One of the assumptions that can explain the observed temperature effect on viscosity in our case is as follows. As the temperature increases, the salicylate ions are partially desorbed from the micelles. This increases the charge of the micelles, but also increases the ionic strength of the solution screening the repulsion between similarly charged head groups. As a result, Ee could drop so much that it would lead to an increase in the length of micelles (Equation (1)). At the same time, the micelles of surfactants themselves are known to shorten exponentially with increasing temperature [24,35,47,51]. At T > 40 °C, the second effect becomes dominant, and we observe a decrease in viscosity. The viscosity decrease with increasing temperature can be described empirically by the Arrhenius equation [24,25]:
η 0 =   A ∗ e x p ( E a / R T )
where Ea is the activation energy and R is the gas constant. Using this formula, Ea = 110 ± 5 and 100 ± 4 kJ/mol was obtained from the slopes of the straight lines ln η0 vs. 1/T at high temperatures for solutions with 13 and 18 mM EHAC, respectively (NaSal/EHAC = 0.5) (Figure S1). The values obtained are the same as those in the literature for typical WLMs, which become shorter when heated [34,52,53,54].
The temperature dependences of the storage modulus demonstrate that at 13 mM EHAC, G′ values (at 10 s−1) pass through the maximum at heating (Figure 6d). In contrast, at 18 mM EHAC, G′ (at 10 s−1) increases with heating over the entire measured temperature range (Figure 6d). A similar increase in plateau modulus and the passing through of the maximum was observed for NaSal/EHAC (60 mM/18 mM) solutions [30] and for long-tailed zwitterionic surfactant solutions [39]. In both cases these WLM solutions demonstrated gel-like rheological behavior, but the effect has not been explained. In our system, G′ at 10 s−1 corresponds to the plateau modulus G0 (Figure 6b). According to Equations (3) and (4), the increase in G0, which indicates an increase in the density of the network of entangled WLMs, can be explained by a decrease in the entanglement length le and/or the persistence length lp. The decrease in the persistence length can be due to the increase in ionic strength accompanying the desorption of salicylate ions upon heating, which reduces the electrostatic contribution to the persistence length [50]. At 13 mM EHAC, the temperature dependence of G′ passes through the maximum at higher temperatures because one more effect influencing G′ comes into play: the shortening of WLMs, which leads to an increase in entanglement length le. At 18 mM EHAC, the amount of NaSal salt and therefore the ionic strength of the solution are higher so that the effect of the decrease in lp predominates.
For viscoelastic liquids with a pronounced elastic modulus G0 and a minimum of G″, the contour length L refers to le in accordance with the following equation [47]:
L l e   =   G 0 G ″ m i n ,
This ratio was estimated for solutions of 18 mM EHAC at a NaSal/EHAC molar ratio of 0.5 (the temperature dependence of L/le is given in Figure S2). If typical values for le for similar systems are 80–150 nm [12,55], then the L micelles in this system will vary approximately from 8 to 28 µm. At temperatures above 30 °C, the length decreases, which is consistent with the empirical Arrhenius relationships for WLMs with electrostatic repulsion shielding [35] (Equation (1)). However, as the temperature increases from 25 to 30 °C, the length increases. This observation is consistent with the fact that viscosity increases in this temperature range, which is also not typical for micellar chains with increasing temperature. Thus, depending on the viscosity and length of the micelles, two effects can contribute to the temperature: (1) the above-described effect of desorption of binding counterions, which increases the length of micelles, and (2) the standard effect of chain shortening upon heating for micellar chains, as described in the literature.
At 18 mM EHAC, the frequency dependences of G′ and G″ were obtained also at a lower NaSal/EHAC molar ratio of 0.36 (Figure 7). At this ratio, the micelles are linear, but they are shorter than at a NaSal/EHAC molar ratio of 0.5, because they are more charged. As a result, there is no plateau on the frequency dependence of storage modulus G′(ω), and the curves G′(ω) and G″(ω) cross each other. So, these WLM solutions exhibit a viscoelastic state rather than a gel-like one. As the temperature increases, the crossover point shifts to the right; that is, the relaxation time decreases, and the viscosity of the systems also decreases. No maximum on the temperature dependence of viscosity is observed at the studied temperature range. It can be assumed that at a NaSal/EHAC molar ratio of 0.36, the maximum may occur at lower temperatures than for a NaSal/EHAC molar ratio of 0.5. A shift in the viscosity maximum to the lower temperatures with a decrease in the salt/surfactant ratio was also observed at high concentrations of surfactants [27]. It could be related to an increase in the number of adsorbed sodium ions with decreasing temperature [28]. In our case, we can suggest that the desorption of a small number of salicylate ions may not be sufficient to induce length growth.
Thus, it was discovered that the temperature effect on the rheological properties of EHAC in the presence of NaSal can be tuned by the salt/surfactant ratio and the total surfactant concentration.

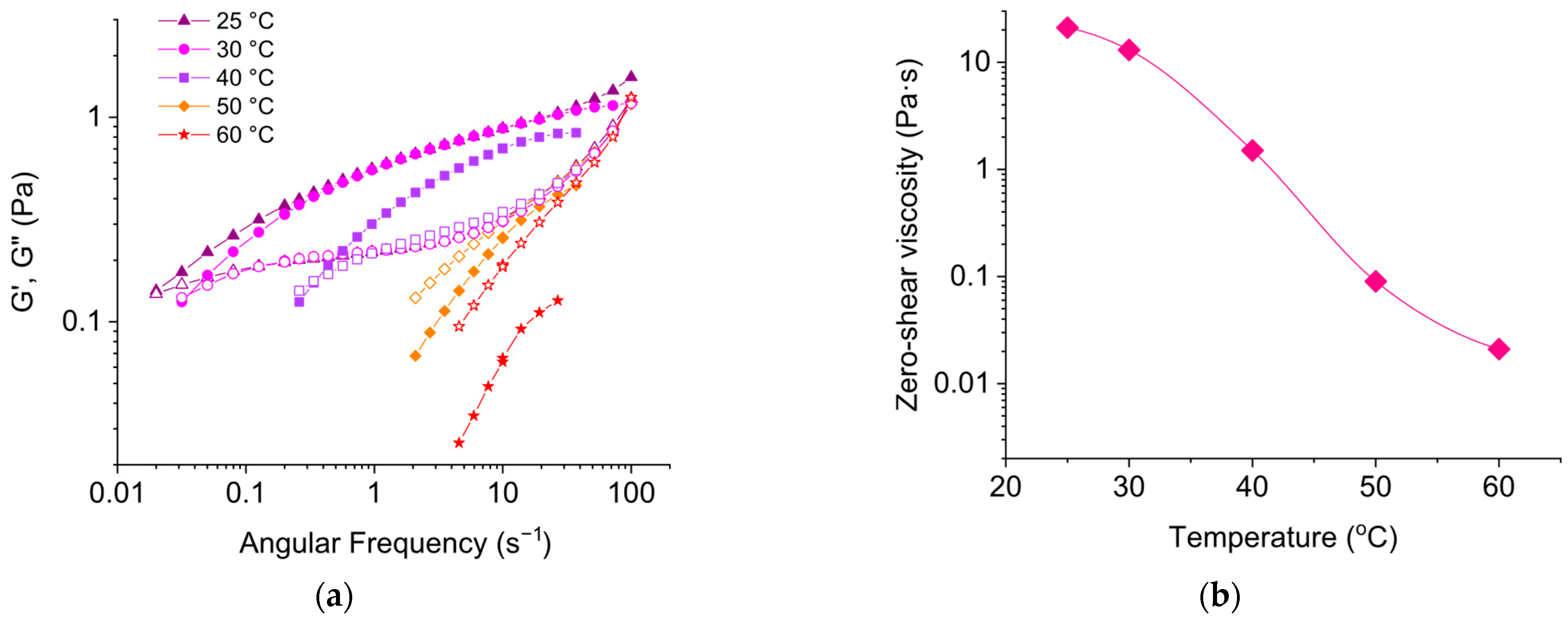
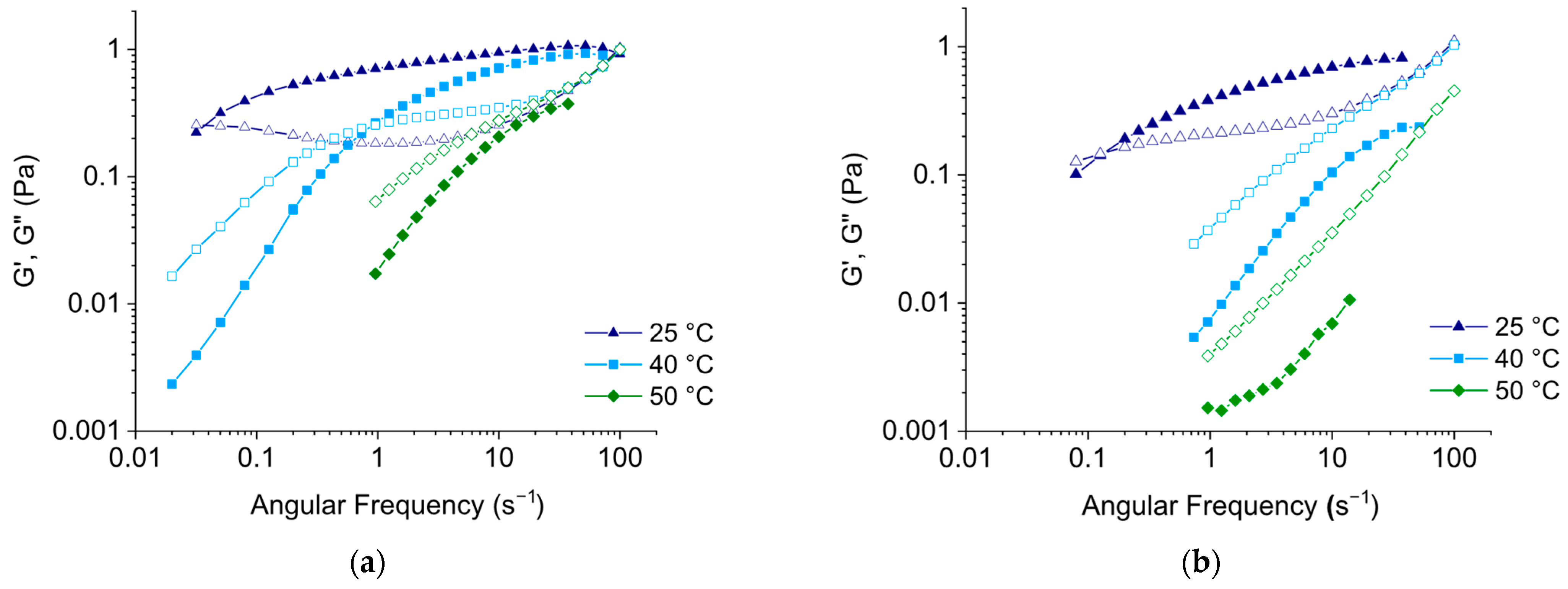
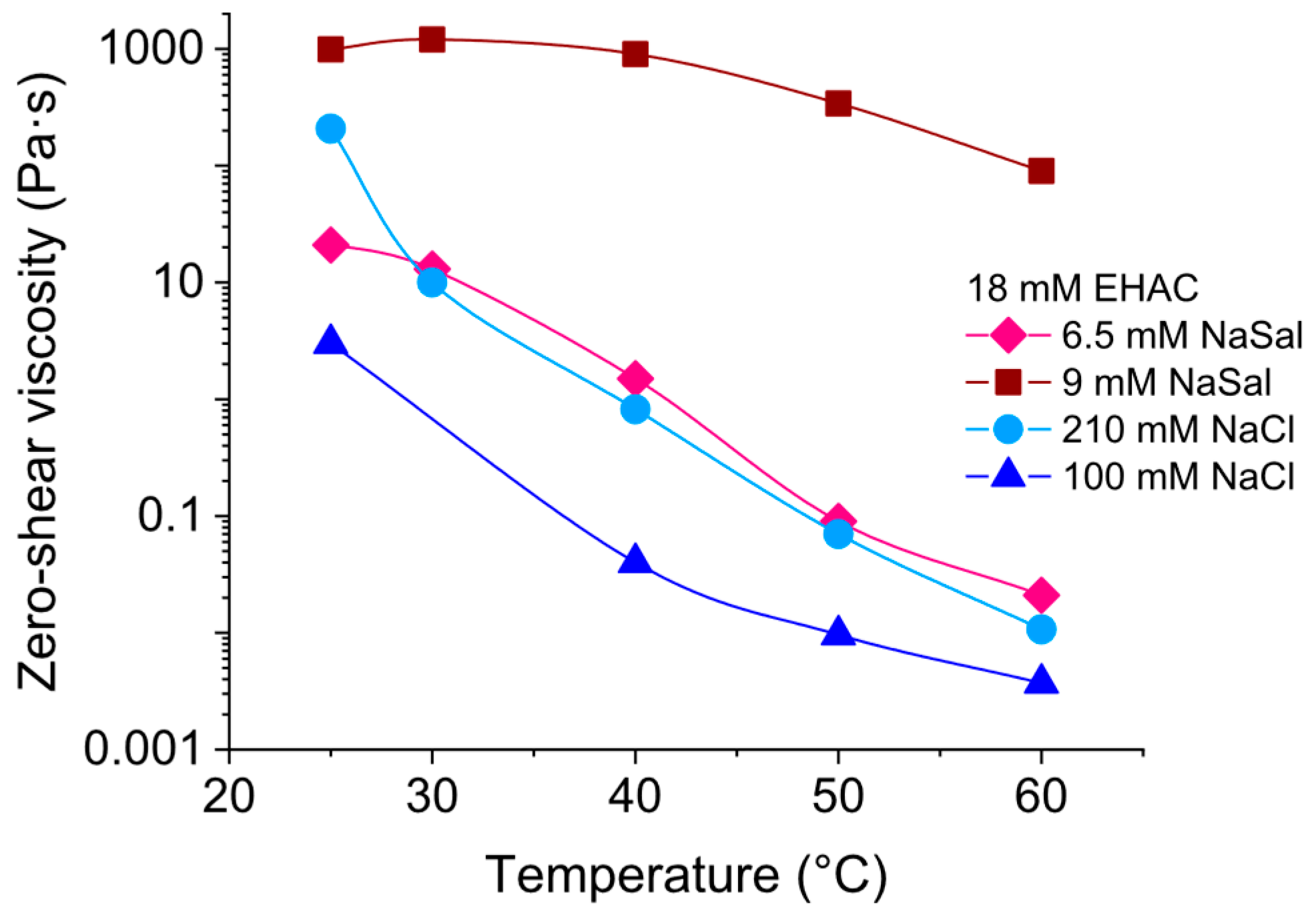
3.4. Comparison of Rheological Properties of EHAC/NaSal and EHAC/NaCl Solutions at Elevated Temperatures

For the comparison with EHAC/NaSal systems described above, the EHAC/NaCl solutions with 18 mM EHAC and 100 and 210 mM NaCl were used. These solutions contain linear WLMs with different degrees of screened electrostatic repulsion on the surface of the WLMs. Figure 8 shows that the G′ and G″ decrease with increasing temperature. At room temperature the solutions demonstrated a wide range of elastic responses (G′ > G″). In the presence of 210 mM NaCl, the range is wider due to longer WLMs and relaxation times as a result of the screened electrostatic repulsion on the surface of the micelles. The relaxation time in the WLM network decreases significantly with increasing temperature until 40 °C (Figure 8a), while for a shorter WLM solution (100 mM NaCl), only a viscous response (G′ > G″) has been observed at all frequencies, meaning disruption of the WLM network. These changes in rheological properties due to temperature are a typical effect observed in many WLM solutions when inorganic salts are present [30,45,56]. It is explained by the shortening of micelles until the disruption of the network because the WLM length becomes shorter than the entanglement length le. It should be noted that in many WLM solutions with hydrotropic salts, the temperature effects are similar to those observed with inorganic salts [57,58]. This means that in order to achieve an increase in viscosity and elasticity as in the EHAC/NaSal systems described above, it is not enough to just use hydrotropic salts. One also needs to find the right concentration of surfactant and the right salt/surfactant ratio.
Thus, as the temperature increases, the zero-shear viscosity of EHAC/NaCl solutions decreases, which is typical for WLM solutions according to Equation (5) (Figure 9). As expected, at lower salt concentrations, the viscosity is lower over the entire temperature range, since the micelles are shorter. One can compare (Figure 9) the zero-shear viscosity behavior with heating in case-fixed surfactant concentrations (18 mM EHAC) and both different types of salts and different salt-to-surfactant ratios. It should be noted that the entangled linear WLMs are formed in these solutions. The difference in zero-shear viscosity between the solutions with hydrotropic and inorganic salts can be less than an order of magnitude at 25 °C. However, at 60 °C, the solution with NaSal exhibits high viscoelasticity, while the solution with NaCl has low viscosity. The difference becomes four orders of magnitude. In addition, if we decrease the salt-to-surfactant ratio in the solution containing NaSal from 0.5 to 0.36, at 60 °C, it shows a transition from a viscoelastic fluid to a low-viscosity fluid.
Figure S1 shows the dependence of viscosity on the inverse temperature on a semilogarithmic scale. From these dependencies, the activation energy values Ea were estimated from the Arrhenius relationships (Equation (5)). For solutions of 18 mM EHAC and 9 mM NaSal, the viscosity dependence passed through the maximum, and this system Ea was estimated from an approximation in the high temperature range. The estimation gives the activation energy values of 170 and 220 kJ/mol for solutions with 100 and 210 mM NaCl, respectively, and 190 and 100 kJ/mol for solutions with 6.5 and 9 mM NaSal, respectively. These values are in the range of 70–300 kJ/mol, which is similar to the values obtained for other WLM systems [5,29,35,59,60].
As can be seen, the Ea can be lowered when using a certain amount of hydrotropic salt. This makes it more favorable for the formation of long WLMs at high temperatures. Therefore, as can be seen from our results, when using a hydrotropic salt and a salt/surfactant ratio near the maximum viscosity, one can obtain highly viscous solutions that maintain high viscosity values even at elevated temperatures. This is their incomparable advantage over solutions with inorganic salts.

4. Conclusions

In this work, WLM solutions of cationic surfactant EHAC in the presence of the hydrotropic salt NaSal and inorganic salt NaCl were studied at different concentrations of surfactants and salts. It was shown that in the presence of hydrotropic salt, maximum zero-shear viscosity corresponds to the formation of long “unbreakable” linearly charged WLMs. The salycilate ion can interact with the micelle of a cationic surfactant not only through electrostatic interactions, but also through hydrophobic interaction with the core of the micelle. We suggest that it provides a formation of long-lived WLMs. The formation of long linear “unbreakable” charged WLMs in some cases even demonstrated the transition of viscoelastic solutions to a gel-like state.
The comparison of EHAC solutions with the penetrating ions of NaSal salts and the non-penetrating ions of NaCl salts shows that the former exhibit much greater viscoelastic properties. The maximum viscosity of solutions with NaSal is an order of magnitude higher than that of solutions with NaCl, and the required concentrations of salt to achieve maximum viscosity are of an order of magnitude lower. This makes systems with hydrotropic ions more attractive for applications requiring high viscosities.
Hydrotropic salts also provide the possibility to obtain WLM solutions that maintain their viscosities even when heated. The conditions for the formation of temperature-resistant WLM solutions are determined. They correspond to the near maximum value of WLM length at low temperatures, showing gel-like consistency. Thus, the use of a hydrotropic salt instead of an inorganic one, and the use of a correct salt/surfactant ratio makes it possible to obtain highly viscoelastic solutions even at elevated temperatures. These results make WLM/hydrotropic salt solutions promising for use in fracturing fluids in the oilfield industry, especially at elevated temperatures, where WLM solutions usually lose their viscoelastic properties.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/liquids5040028/s1. Figure S1: Zero-shear viscosity as a function of inverse temperature of the aqueous solutions of 18 mM EHAC at the different salt concentrations: 6.5 mM NaSal (diamonds), 9 mM NaSal (squares), 100 mM NaCl (triangles), 210 mM NaCl (circles) and of 13 mM EHAC, 6.5 mM NaSal (open squares); Figure S2: The dependence of L/le on the inverse temperature for solutions of 18 mM EHAC with a ratio of NaSal/EHAC = 0.5/1.

Author Contributions

Conceptualization, V.S.M. and O.E.P.; formal analysis, V.S.M. and O.E.P.; investigation, K.B.S.; resources, O.E.P.; writing—original draft preparation, K.B.S.; writing—review and editing, V.S.M. and O.E.P.; supervision, O.E.P.; funding acquisition, K.B.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Foundation for the Advancement of Theoretical Physics and Mathematics “BASIS” (project no. 23-2-2-10-1).

Data Availability Statement

Data are available from the authors upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
WLMWormlike micelle
EHACErucyl bis(hydroxyethyl)methylammonium chloride
NaSalSodium salicylate
DCTACDocosyl(trimethyl)azanium chloride
SHNC3-hydroxy naphthalene-2-carboxylate

Appendix A

This is a nomenclature section indicating the different quantities expressed in SI units.
Table A1. Nomenclature of quantities.
Table A1. Nomenclature of quantities.
QuantitySymbolUnit
(SI)		Description
Zero-shear viscosityη0Pa·s Viscosity plateau measured at low shear rate.
Storage modulusG′PaElastic part of the sample response from dynamic rheological measurements.
Loss modulusG′′Pa Inelastic part of the sample response from dynamic rheological measurements.
Shear rate-s−1 Rate of shear applied during rheology tests.
Salt concentration-mol/L Concentration of salt in solution.
Surfactant concentration-mol/L Concentration of surfactant in solution.
Salt-to-surfactant molar ratio--Molar ratio of salt to surfactant.
Frequencyωs−1Frequency of oscillatory rheological measurement.
Relaxation timeτrelsCharacteristic time for network relaxation.
Activation energyEakJ/mol Energy barrier for temperature-related processes.
End-cap energyEckJ/molEnergy required to create two end-caps from a semi-infinite cylinder for neutral micelles.
Electrostatic energyEekJ/molEnergy related to the degree of charge of the micelle and the concentration of free ions in the solution.
TemperatureTK or °CTemperature of the system during experiments.
Contour length of
micelles		Lnm Length of micelle chain.
Persistence lengthlpnm Persistence length describing micelle stiffness.
Entanglement lengthlenm Contour length between entanglements in the micelle network.

References

  1. Philippova, O. Wormlike Micelles: Advances in Systems, Characterisation and Applications; Dreiss, C., Ed.; Soft Matter Series; Royal Society of Chemistry: London, UK, 2017; Volume 6. [Google Scholar]
  2. Holmberg, K.; Jönsson, B.; Kronberg, B.; Lindman, B. Surfactants and Polymers in Aqueous Solution; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
  3. Richtering, W. The Colloidal Domain—Where Physics, Chemistry, Biology and Technology Meet. Appl. Rheol. 2019, 11, 177. [Google Scholar] [CrossRef]
  4. Khatory, A.; Kern, F.; Lequeux, F.; Appell, J.; Porte, G.; Morie, N.; Ott, A.; Urbach, W. Entangled versus Multiconnected Network of Wormlike Micelles. Langmuir 1993, 9, 933–939. [Google Scholar] [CrossRef]
  5. Kern, F.; Lequeux, F.; Zana, R.; Candau, S.J. Dynamical Properties of Salt-Free Viscoelastic Micellar Solutions. Langmuir 1994, 10, 1714–1723. [Google Scholar] [CrossRef]
  6. Han, Y.X.; Zhou, H.; Wei, Y.Q.; Mei, Y.J.; Wang, H. Effect of TBAB/KCl on Constructing Anionic Wormlike Micelles. Wuli Huaxue Xuebao/Acta Phys.-Chim. Sin. 2015, 31, 2124–2130. [Google Scholar] [CrossRef]
  7. Khatory, A.; Lequeux, F.; Kern, F.; Candau, S.J. Linear and Nonlinear Viscoelasticity of Semidilute Solutions of Wormlike Micelles at High Salt Content. Langmuir 1993, 9, 1456–1464. [Google Scholar] [CrossRef]
  8. Molchanov, V.S.; Philippova, O.E. Effects of Concentration and Temperature on Viscoelastic Properties of Aqueous Potassium Oleate Solutions. Colloid J. 2009, 71, 239–245. [Google Scholar] [CrossRef]
  9. Molchanov, V.S.; Shashkina, Y.A.; Philippova, O.E.; Khokhlov, A.R. Viscoelastic Properties of Aqueous Anionic Surfactant (Potassium oleate) Solutions. Colloid J. 2005, 67, 606–609. [Google Scholar] [CrossRef]
  10. Pletneva, V.A.; Molchanov, V.S.; Philippova, O.E. Effect of Polymer on Rheological Behavior of Heated Solutions of Potassium Oleate Cylindrical Micelles. Colloid J. 2010, 72, 716–722. [Google Scholar] [CrossRef]
  11. Croce, V.; Cosgrove, T.; Maitland, G.; Hughes, T.; Karlsson, G. Rheology, Cryogenic Transmission Electron Spectroscopy, and Small-Angle Neutron Scattering of Highly Viscoelastic Wormlike Micellar Solutions. Langmuir 2003, 19, 8536–8541. [Google Scholar] [CrossRef]
  12. Magid, L.J. The Surfactant-Polyelectrolyte Analogy. J. Phys. Chem. B 1998, 102, 4064–4074. [Google Scholar] [CrossRef]
  13. Cappelaere, E.; Cressely, R. Rheological Behavior of an Elongated Micellar Solution at Low and High Salt Concentrations. Colloid Polym. Sci. 1998, 276, 1050–1056. [Google Scholar] [CrossRef]
  14. Kang, B.; Tang, H.; Zhao, Z.; Song, S. Hofmeister Series: Insights of Ion Specificity from Amphiphilic Assembly and Interface Property. ACS Omega 2020, 5, 6229–6239. [Google Scholar] [CrossRef]
  15. Maiti, K.; Mitra, D.; Guha, S.; Moulik, S.P. Salt Effect on Self-Aggregation of Sodium Dodecylsulfate (SDS) and Tetradecyltrimethylammonium Bromide (TTAB): Physicochemical Correlation and Assessment in the Light of Hofmeister (Lyotropic) Effect. J. Mol. Liq. 2009, 146, 44–51. [Google Scholar] [CrossRef]
  16. Vlachy, N.; Jagoda-Cwiklik, B.; Vácha, R.; Touraud, D.; Jungwirth, P.; Kunz, W. Hofmeister Series and Specific Interactions of Charged Headgroups with Aqueous Ions. Adv. Colloid Interface Sci. 2009, 146, 42–47. [Google Scholar] [CrossRef] [PubMed]
  17. Boström, M.; Williams, D.R.M.; Ninham, B.W. Ion Specificity of Micelles Explained by Ionic Dispersion Forces. Langmuir 2002, 18, 6010–6014. [Google Scholar] [CrossRef]
  18. Koroleva, S.V.; Korchak, P.; Victorov, A.I. Molecular Thermodynamic Modeling of the Specific Effect of Salt on the Aggregation of Nonionic Surfactants. J. Chem. Eng. Data 2020, 65, 987–992. [Google Scholar] [CrossRef]
  19. Warmbier-Wytykowska, E.; Williams, A.P.; Rozanski, J.; Fischer, P.; Lutz-Bueno, V.; Handschin, S.; Baraldi, L.; Warmbier, J.; Wagner, P.; Różańska, S. How Do the Valency and Radii of Cations Affect the Rheological Properties of Aqueous Solutions of Zwitterionic and Anionic Surfactant Mixtures? Langmuir 2025, 41, 3561–3571. [Google Scholar] [CrossRef]
  20. Abezgauz, L.; Kuperkar, K.; Hassan, P.A.; Ramon, O.; Bahadur, P.; Danino, D. Effect of Hofmeister Anions on Micellization and Micellar Growth of the Surfactant Cetylpyridinium Chloride. J. Colloid Interface Sci. 2010, 342, 83–92. [Google Scholar] [CrossRef]
  21. Isabettini, S.; Böni, L.J.; Baumgartner, M.; Saito, K.; Kuster, S.; Fischer, P.; Lutz-Bueno, V. Higher Salt Hydrophobicity Lengthens Ionic Wormlike Micelles and Stabilizes Them upon Heating. Langmuir 2021, 37, 132–138. [Google Scholar] [CrossRef]
  22. Oelschlaeger, C.; Suwita, P.; Willenbacher, N. Effect of Counterion Binding Efficiency on Structure and Dynamics of Wormlike Micelles. Langmuir 2010, 26, 7045–7053. [Google Scholar] [CrossRef]
  23. Pleines, M.; Kunz, W.; Zemb, T.; Benczédi, D.; Fieber, W. Molecular Factors Governing the Viscosity Peak of Giant Micelles in the Presence of Salt and Fragrances. J. Colloid Interface Sci. 2019, 537, 682–693. [Google Scholar] [CrossRef]
  24. Makhloufi, R.; Cressely, R. Temperature Dependence of the Non-Newtonian Viscosity of Elongated Micellar Solutions. Colloid Polym. Sci. 1992, 270, 1035–1041. [Google Scholar] [CrossRef]
  25. Candau, S.J.; Hirsch, E.; Zana, R.; Delsanti, M. Rheological Properties of Semidilute and Concentrated Aqueous Solutions of Cetyltrimethylammonium Bromide in the Presence of Potassium Bromide. Langmuir 1989, 5, 1225–1229. [Google Scholar] [CrossRef]
  26. Raghavan, S.R.; Edlund, H.; Kaler, E.W. Cloud-Point Phenomena in Wormlike Micellar Systems Containing Cationic Surfactant and Salt. Langmuir 2002, 18, 1056–1064. [Google Scholar] [CrossRef]
  27. Kalur, G.C.; Frounfelker, B.D.; Cipriano, B.H.; Norman, A.I.; Raghavan, S.R. Viscosity Increase with Temperature in Cationic Surfactant Solutions Due to the Growth of Wormlike Micelles. Langmuir 2005, 21, 10998–11004. [Google Scholar] [CrossRef] [PubMed]
  28. Cao, X.; Guo, W.; Zhu, Q.; Ge, H.; Yang, H.; Ke, Y.; Shi, X.; Lu, X.; Feng, Y.; Yin, H. Supramolecular Self-Assembly of Robust, Ultra-Stable, and High-Temperature-Resistant Viscoelastic Worm-like Micelles. J. Colloid Interface Sci. 2023, 649, 403–415. [Google Scholar] [CrossRef]
  29. Raghavan, S.R.; Kaler, E.W. Highly Viscoelastic Wormlike Micellar Solutions Formed by Cationic Surfactants with Long Unsaturated Tails. Langmuir 2001, 17, 300–306. [Google Scholar] [CrossRef]
  30. Shashkina, J.A.; Philippova, O.E.; Zaroslov, Y.D.; Khokhlov, A.R.; Pryakhina, T.A.; Blagodatskikh, I.V. Rheology of Viscoelastic Solutions of Cationic Surfactant. Effect of Added Associating Polymer. Langmuir 2005, 21, 1524–1530. [Google Scholar] [CrossRef]
  31. Hassan, P.A.; Candau, S.J.; Kern, F.; Manohar, C. Rheology of Wormlike Micelles with Varying Hydrophobicity of the Counterion. Langmuir 1998, 14, 6025–6029. [Google Scholar] [CrossRef]
  32. Rehage, H.; Hoffmann, H. Rheological Properties of Viscoelastic Surfactant Systems. J. Phys. Chem. 1988, 92, 4712–4719. [Google Scholar] [CrossRef]
  33. Molchanov, V.S.; Kuklin, A.I.; Orekhov, A.S.; Arkharova, N.A.; Philippova, O.E. Temporally Persistent Networks of Long-Lived Mixed Wormlike Micelles of Zwitterionic and Anionic Surfactants. J. Mol. Liq. 2021, 342, 116955. [Google Scholar] [CrossRef]
  34. Molchanov, V.S.; Rostovtsev, A.V.; Shishkhanova, K.B.; Kuklin, A.I.; Philippova, O.E. Strong Viscosity Increase in Aqueous Solutions of Cationic C22-Tailed Surfactant Wormlike Micelles. Fluids 2022, 7, 8. [Google Scholar] [CrossRef]
  35. Cates, M.E.; Candau, S.J. Statics and Dynamics of Worm-like Surfactant Micelles. J. Phys. Condens. Matter 1990, 2, 6869–6892. [Google Scholar] [CrossRef]
  36. Safran, S.A.; Pincus, P.A.; Cates, M.E.; MacKintosh, F.C. Growth of Charged Micelles. J. Phys. Paris 1990, 51, 503–510. [Google Scholar] [CrossRef]
  37. Butler, P.D.; Magid, L.J.; Hayter, J.B. Structure and Flow in Surfactant Solutions; Herb, C.A., Prud’homme, R.K., Eds.; American Chemical Society: Washington, DC, USA, 1994; ISBN 0841230544/9780841230545. [Google Scholar]
  38. Kumars, R.; Kalur, G.C.; Ziserman, L.; Danino, D.; Raghavan, S.R. Wormlike Micelles of a C22-Tailed Zwitterionic Betaine Surfactant: From Viscoelastic Solutions to Elastic Gels. Langmuir 2007, 23, 12849–12856. [Google Scholar] [CrossRef]
  39. Fischer, P.; Rehage, H.; Grüning, B. Linear Flow Properties of Dimer Acid Betaine Solutions with and without Changes Ionic Strength. J. Phys. Chem. B 2002, 106, 11041–11046. [Google Scholar] [CrossRef]
  40. Molchanov, V.S.; Pletneva, V.A.; Kuklin, A.I.; Philippova, O.E. Nanocomposite Composed of Charged Wormlike Micelles and Magnetic Particles. J. Phys. Conf. Ser. 2017, 848, 012013. [Google Scholar] [CrossRef]
  41. Molchanov, V.S.; Philippova, O.E.; Khokhlov, A.R.; Kovalev, Y.A.; Kuklin, A.I. Self-Assembled Networks Highly Responsive to Hydrocarbons. Langmuir 2007, 23, 105–111. [Google Scholar] [CrossRef]
  42. Cates, M.E.; Fielding, S.M. Rheology of Giant Micelles. Adv. Phys. 2006, 55, 799–879. [Google Scholar] [CrossRef]
  43. Turner, M.S.; Marques, C.; Cates, M.E. Dynamics of Wormlike Micelles: The “Bond-Interchange” Reaction Scheme. Langmuir 1993, 9, 695–701. [Google Scholar] [CrossRef]
  44. Koehlcr, R.D.; Raghavan, S.R.; Kaier, E.W. Microstructure and Dynamics of Wormlike Micellar Solutions Formed by Mixing Cationic and Anionic Surfactants. J. Phys. Chem. B 2000, 104, 11035–11044. [Google Scholar] [CrossRef]
  45. Fischer, P.; Rehage, H. Rheological Master Curves of Viscoelastic Surfactant Solutions by Varying the Solvent Viscosity and Temperature. Langmuir 1997, 13, 7012–7020. [Google Scholar] [CrossRef]
  46. Turner, M.S.; Cates, M.E. Linear Viscoelasticity of Living Polymers: A Quantitative Probe of Chemical Relaxation Times. Langmuir 1991, 7, 1590–1594. [Google Scholar] [CrossRef]
  47. Granek, R.; Cates, M.E. Stress Relaxation in Living Polymers: Results from a Poisson Renewal Model. J. Chem. Phys. 1992, 96, 4758–4767. [Google Scholar] [CrossRef]
  48. Wang, P.; Pei, S.; Wang, M.; Yan, Y.; Sun, X.; Zhang, J. Study on the Transformation from Linear to Branched Wormlike Micelles: An Insight from Molecular Dynamics Simulation. J. Colloid Interface Sci. 2017, 494, 47–53. [Google Scholar] [CrossRef] [PubMed]
  49. de Gennes, P.G.; Witten, T.A. Scaling Concepts in Polymer Physics. Phys. Today 1980, 33, 6. [Google Scholar] [CrossRef]
  50. Jerke, G.; Pedersen, J.S.; Egelhaaf, S.U.; Schurtenberger, P. Flexibility of Charged and Uncharged Polymer-like Micelles. Langmuir 1998, 14, 6013–6024. [Google Scholar] [CrossRef]
  51. Ponton, A.; Schott, C.; Quemada, D. Rheological Behavior of Flexible Elongated Micelles: Temperature Effect in an Isotropic Phase. Colloids Surf. A Physicochem. Eng. Asp. 1998, 145, 37–45. [Google Scholar] [CrossRef]
  52. Sarmiento-Gomez, E.; Lopez-Diaz, D.; Castillo, R. Microrheology and Characteristic Lengths in Wormlike Micelles Made of a Zwitterionic Surfactant and SDS in Brine. J. Phys. Chem. B 2010, 114, 12193–12202. [Google Scholar] [CrossRef] [PubMed]
  53. Rózańska, S. Rheology of Wormlike Micelles in Mixed Solutions of Cocoamidopropyl Betaine and Sodium Dodecylbenzenesulfonate. Colloids Surf. A Physicochem. Eng. Asp. 2015, 482, 394–402. [Google Scholar] [CrossRef]
  54. Kuryashov, D.A.; Philippova, O.E.; Molchanov, V.S.; Bashkirtseva, N.Y.; Diyarov, I.N. Temperature Effect on the Viscoelastic Properties of Solutions of Cylindrical Mixed Micelles of Zwitterionic and Anionic Surfactants. Colloid J. 2010, 72, 230–235. [Google Scholar] [CrossRef]
  55. Carver, M.; Smith, T.L.; Gee, J.C.; Delichere, A.; Caponetti, E.; Magid, L.J. Tuning of Micellar Structure and Dynamics in Aqueous Salt-Free Solutions of Cetyltrimethylammonium Mono- and Dichlorobenzoates. Langmuir 1996, 12, 691–698. [Google Scholar] [CrossRef]
  56. Kern, F.; Zana, R.; Candau, S.J. Rheological Properties of Semidilute and Concentrated Aqueous Solutions of Cetyltrimethylammonium Chloride in the Presence of Sodium Salicylate and Sodium Chloride. Langmuir 1991, 7, 1344–1351. [Google Scholar] [CrossRef]
  57. Oelschlaeger, C.; Schopferer, M.; Scheffold, F.; Willenbacher, N. Linear-to-Branched Micelles Transition: A Rheometry and Diffusing Wave Spectroscopy (DWS) Study. Langmuir 2009, 25, 716–723. [Google Scholar] [CrossRef]
  58. Tung, S.H.; Huang, Y.E.; Raghavan, S.R. Contrasting Effects of Temperature on the Rheology of Normal and Reverse Wormlike Micelles. Langmuir 2007, 23, 372–376. [Google Scholar] [CrossRef]
  59. Oda, R.; Narayanan, J.; Hassan, P.A.; Manohar, C.; Salkar, R.A.; Kern, F.; Candau, S.J. Effect of the Lipophilicity of the Counterion on the Viscoelasticity of Micellar Solutions of Cationic Surfactants. Langmuir 1998, 14, 4364–4372. [Google Scholar] [CrossRef]
  60. Shrestha, R.G.; Shrestha, L.K.; Aramaki, K. Wormlike Micelles in Mixed Amino Acid-Based Anionic/Nonionic Surfactant Systems. J. Colloid Interface Sci. 2008, 322, 596–604. [Google Scholar] [CrossRef]
Liquids 05 00028 g001
Figure 1. (a) Zero-shear viscosity as a function of NaSal/EHAC molar ratio at two different EHAC concentrations: 13 mM (circles) and 18 mM (squares) at 25 °C. (b) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for 13 mM aqueous solutions of EHAC at increasing molar ratios of NaSal/EHAC: 0.4 (triangles), 0.5 (circles), and 0.6 (squares) at 25 °C.
Figure 1. (a) Zero-shear viscosity as a function of NaSal/EHAC molar ratio at two different EHAC concentrations: 13 mM (circles) and 18 mM (squares) at 25 °C. (b) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for 13 mM aqueous solutions of EHAC at increasing molar ratios of NaSal/EHAC: 0.4 (triangles), 0.5 (circles), and 0.6 (squares) at 25 °C.
Liquids 05 00028 g001
Liquids 05 00028 g002
Figure 2. (a) Zero-shear viscosity as a function of EHAC concentration at the fixed NaSal/EHAC molar ratio of 0.5 at 25 °C. (b) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions of 8.7 mM EHAC (diamonds), 11 mM EHAC (squares), and 14 mM (circles) at the fixed NaSal/EHAC molar ratio of 0.5 at 25 °C.
Figure 2. (a) Zero-shear viscosity as a function of EHAC concentration at the fixed NaSal/EHAC molar ratio of 0.5 at 25 °C. (b) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions of 8.7 mM EHAC (diamonds), 11 mM EHAC (squares), and 14 mM (circles) at the fixed NaSal/EHAC molar ratio of 0.5 at 25 °C.
Liquids 05 00028 g002
Liquids 05 00028 g003
Figure 3. (a) Flow curves for 18 mM aqueous solutions of EHAC at different concentrations of salt NaCl: 210 mM (circles), 310 mM (squares), and 520 mM (stars) at 25 °C. (b) Zero-shear viscosity as a function of salt concentration for 18 mM aqueous solutions of EHAC in the presence of NaSal salt (squares) or NaCl salt (circles) at 25 °C.
Figure 3. (a) Flow curves for 18 mM aqueous solutions of EHAC at different concentrations of salt NaCl: 210 mM (circles), 310 mM (squares), and 520 mM (stars) at 25 °C. (b) Zero-shear viscosity as a function of salt concentration for 18 mM aqueous solutions of EHAC in the presence of NaSal salt (squares) or NaCl salt (circles) at 25 °C.
Liquids 05 00028 g003
Liquids 05 00028 g004
Figure 4. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli and (b) the normalized dependences of loss modulus G″ on the storage modulus G′ (Cole–Cole plots) for 18 mM aqueous solutions of EHAC at different concentrations of salts: 6.5 mM NaSal (triangles), 100 mM NaCl (circles), and 210 mM NaCl (squares) at 25 °C.
Figure 4. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli and (b) the normalized dependences of loss modulus G″ on the storage modulus G′ (Cole–Cole plots) for 18 mM aqueous solutions of EHAC at different concentrations of salts: 6.5 mM NaSal (triangles), 100 mM NaCl (circles), and 210 mM NaCl (squares) at 25 °C.
Liquids 05 00028 g004
Liquids 05 00028 g005
Figure 5. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for 18 mM aqueous solutions of EHAC at different concentrations of salt NaCl: 100 mM (triangles), 210 mM (circles), 310 mM (squares), and 520 mM (stars) at 25 °C. (b) Storage modulus G′ (at the frequency of 10 s−1) as a function of the NaCl concentration for 18 mM aqueous solutions of EHAC at 25 °C.
Figure 5. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for 18 mM aqueous solutions of EHAC at different concentrations of salt NaCl: 100 mM (triangles), 210 mM (circles), 310 mM (squares), and 520 mM (stars) at 25 °C. (b) Storage modulus G′ (at the frequency of 10 s−1) as a function of the NaCl concentration for 18 mM aqueous solutions of EHAC at 25 °C.
Liquids 05 00028 g005
Liquids 05 00028 g006
Figure 6. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions containing 13 mM EHAC and 6.5 mM NaSal at different temperatures: 25 °C (triangles), 40 °C (squares), 50 °C (diamonds), and 60 °C (stars). (b) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions containing 18 mM EHAC and 9 mM NaSal at different temperatures: 25 °C (triangles), 40 °C (squares), 50 °C (diamonds), and 60 °C (stars). (c) Zero-shear viscosity and (d) storage modulus G′ (at a frequency of 10 s−1) as a function of temperature for 13 mM EHAC (circles) and 18 mM EHAC (squares) aqueous solutions at a fixed NaSal/EHAC molar ratio of 0.5.
Figure 6. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions containing 13 mM EHAC and 6.5 mM NaSal at different temperatures: 25 °C (triangles), 40 °C (squares), 50 °C (diamonds), and 60 °C (stars). (b) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions containing 18 mM EHAC and 9 mM NaSal at different temperatures: 25 °C (triangles), 40 °C (squares), 50 °C (diamonds), and 60 °C (stars). (c) Zero-shear viscosity and (d) storage modulus G′ (at a frequency of 10 s−1) as a function of temperature for 13 mM EHAC (circles) and 18 mM EHAC (squares) aqueous solutions at a fixed NaSal/EHAC molar ratio of 0.5.
Liquids 05 00028 g006
Liquids 05 00028 g007
Figure 7. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions of 18 mM EHAC and 6.5 mM NaSal at different temperatures: 25 °C (triangles), 30 °C (circles), 40 °C (squares), 50 °C (diamonds), and 60 °C (stars), and (b) zero-shear viscosity as a function of temperature of the aqueous solutions of 18 mM EHAC, 6.5 mM NaSal.
Figure 7. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions of 18 mM EHAC and 6.5 mM NaSal at different temperatures: 25 °C (triangles), 30 °C (circles), 40 °C (squares), 50 °C (diamonds), and 60 °C (stars), and (b) zero-shear viscosity as a function of temperature of the aqueous solutions of 18 mM EHAC, 6.5 mM NaSal.
Liquids 05 00028 g007
Liquids 05 00028 g008
Figure 8. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions containing 18 mM EHAC and 210 mM NaCl at different temperatures: 25 °C (triangles), 40 °C (squares), and 50 °C (diamonds). (b) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions containing 18 mM EHAC and 100 mM NaCl at different temperatures: 25 °C (triangles), 40 °C (squares), 50 °C (diamonds).
Figure 8. (a) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions containing 18 mM EHAC and 210 mM NaCl at different temperatures: 25 °C (triangles), 40 °C (squares), and 50 °C (diamonds). (b) Frequency dependences of storage G′ (filled symbols) and loss G″ (open symbols) moduli for aqueous solutions containing 18 mM EHAC and 100 mM NaCl at different temperatures: 25 °C (triangles), 40 °C (squares), 50 °C (diamonds).
Liquids 05 00028 g008
Liquids 05 00028 g009
Figure 9. Zero-shear viscosity as a function of temperature for 18 mM aqueous solutions of EHAC at different salt concentrations: 6.5 mM NaSal (diamonds), 9 mM NaSal (squares), 100 mM NaCl (triangles), and 210 mM NaCl (circles).
Figure 9. Zero-shear viscosity as a function of temperature for 18 mM aqueous solutions of EHAC at different salt concentrations: 6.5 mM NaSal (diamonds), 9 mM NaSal (squares), 100 mM NaCl (triangles), and 210 mM NaCl (circles).
Liquids 05 00028 g009
Table 1. Description of surfactant solutions and the temperature ranges they were tested at.
Table 1. Description of surfactant solutions and the temperature ranges they were tested at.
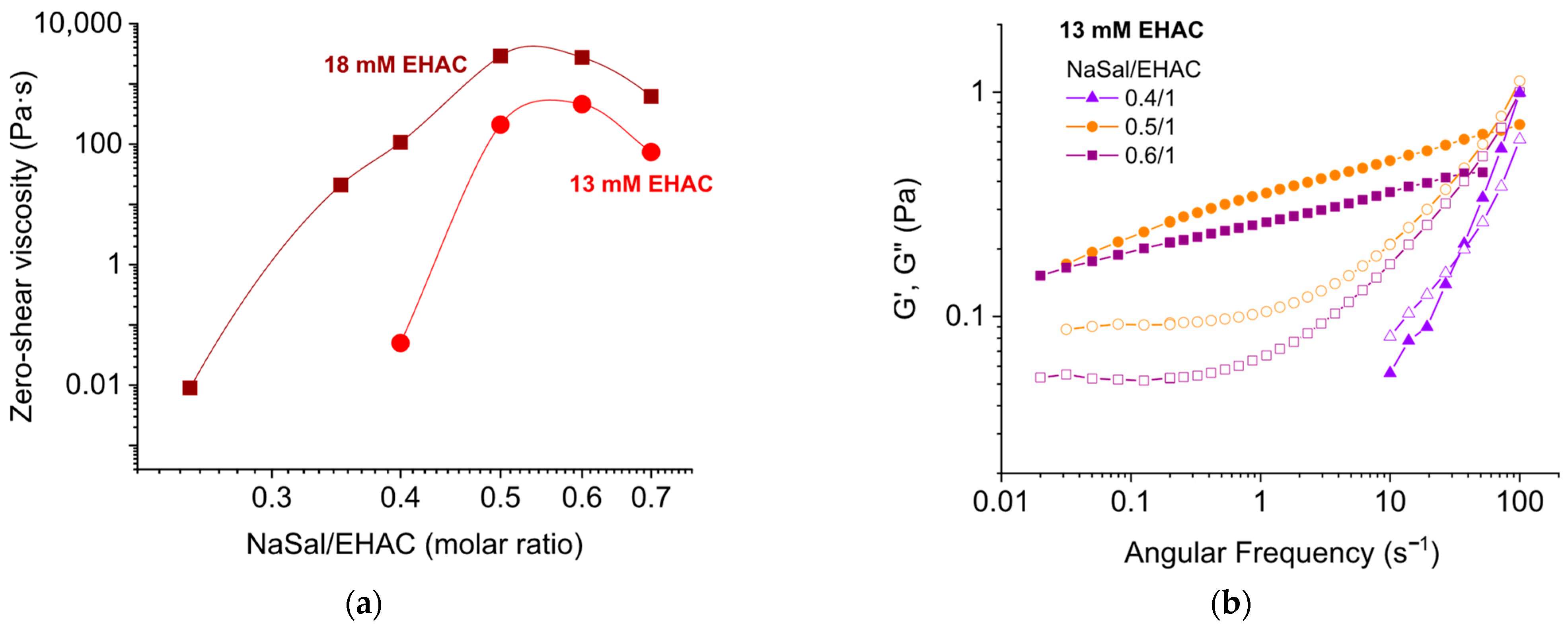
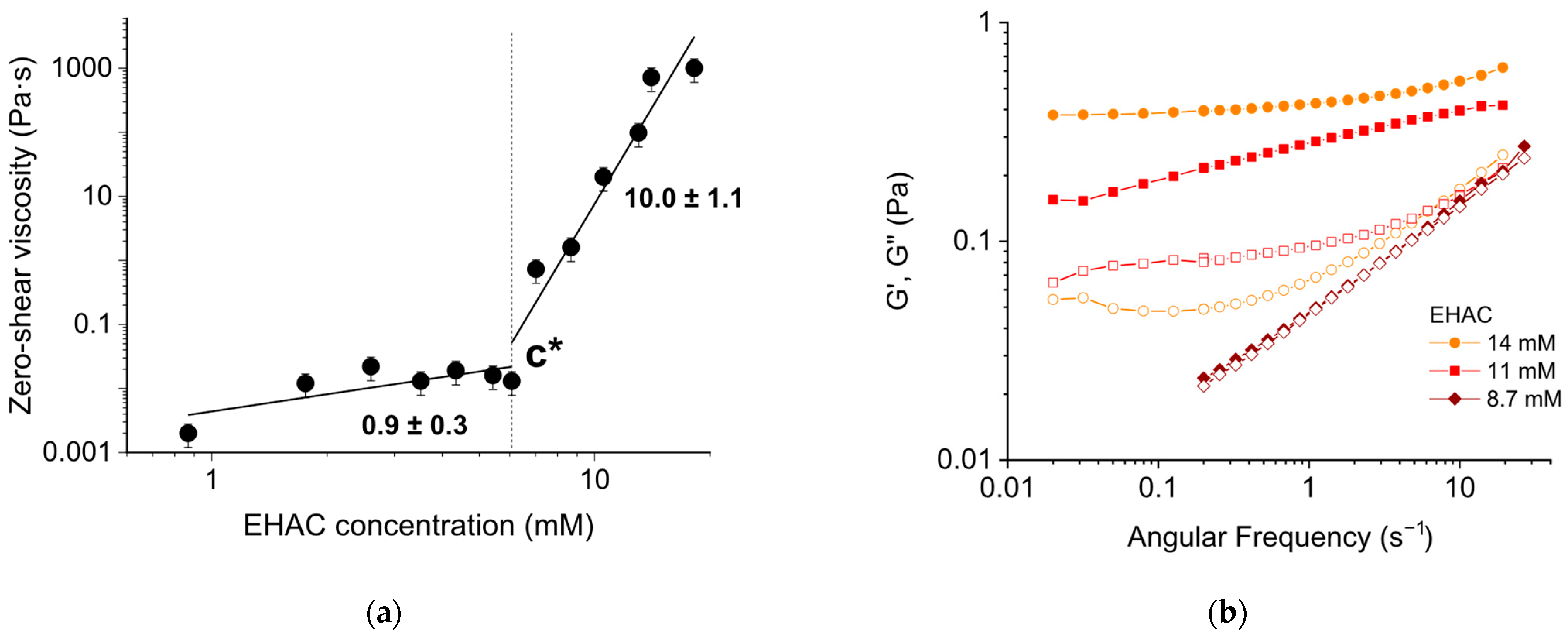
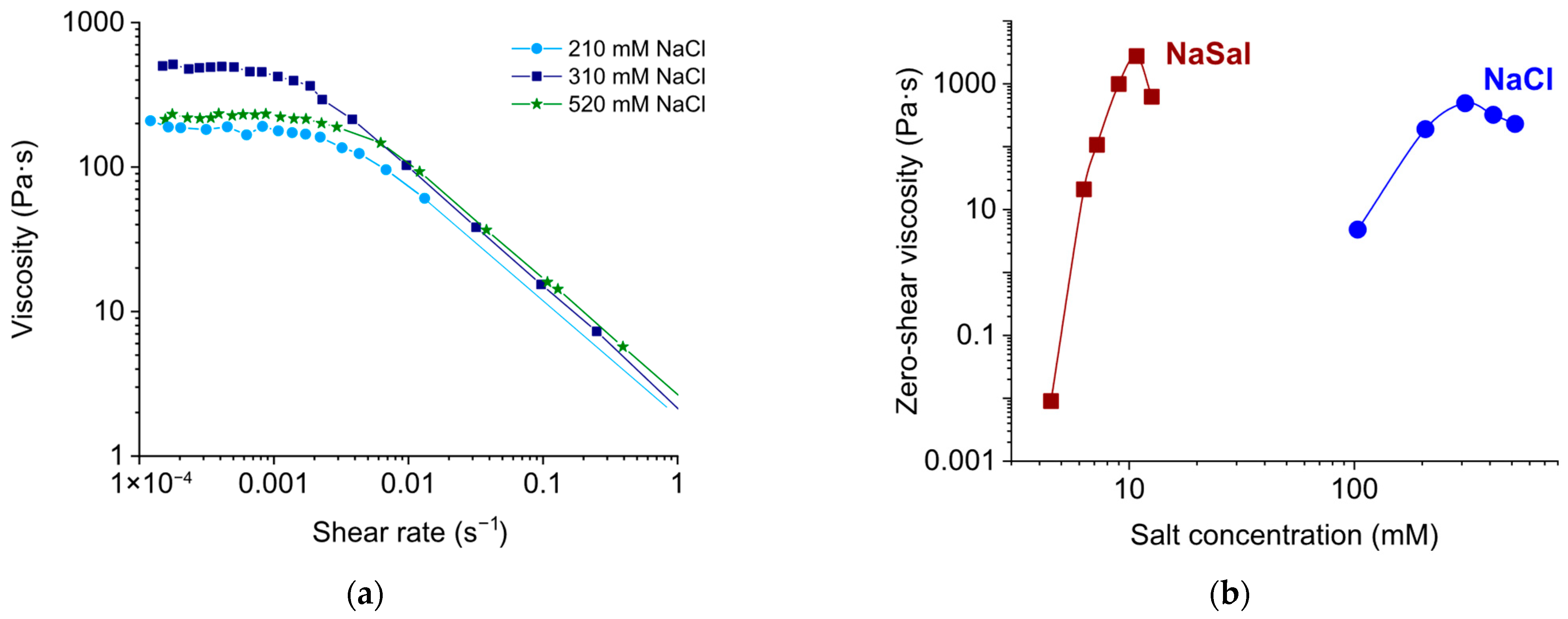
Surfactant
Concentration (mM)		Salt
Type		Salt-to-Surfactant
Molar Ratio		Temperature (°C)
13NaSal0.4–0.725
18NaSal0.25–0.725
0.9–19 NaSal0.525
18NaCl5.6–29 25
13NaSal0.525–60
18NaSal0.36; 0.525–60
18NaCl5.6; 11.725–60
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Shishkhanova, K.B.; Molchanov, V.S.; Philippova, O.E. Tuning of the Viscosity Maximum and the Temperature Effect on Wormlike Micelle Solutions Using Hydrotropic and Inorganic Salts. Liquids 2025, 5, 28. https://doi.org/10.3390/liquids5040028

AMA Style

Shishkhanova KB, Molchanov VS, Philippova OE. Tuning of the Viscosity Maximum and the Temperature Effect on Wormlike Micelle Solutions Using Hydrotropic and Inorganic Salts. Liquids. 2025; 5(4):28. https://doi.org/10.3390/liquids5040028

Chicago/Turabian Style

Shishkhanova, Kamilla B., Vyacheslav S. Molchanov, and Olga E. Philippova. 2025. "Tuning of the Viscosity Maximum and the Temperature Effect on Wormlike Micelle Solutions Using Hydrotropic and Inorganic Salts" Liquids 5, no. 4: 28. https://doi.org/10.3390/liquids5040028

APA Style

Shishkhanova, K. B., Molchanov, V. S., & Philippova, O. E. (2025). Tuning of the Viscosity Maximum and the Temperature Effect on Wormlike Micelle Solutions Using Hydrotropic and Inorganic Salts. Liquids, 5(4), 28. https://doi.org/10.3390/liquids5040028

Article Metrics

Back to TopTop