Solubility of Deferiprone in Non-Aqueous Mixtures of Polyethylene Glycol 400 and 1-Propanol at 293.2–323.2 K
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Measurement of Deferiprone Solubility
2.3. Computational Section
2.3.1. van’t Hoff Equation
2.3.2. λh Equation
2.3.3. Yalkowsky Model
2.3.4. The Modified Wilson Model
2.3.5. Jouyban–Acree Model
2.3.6. Jouyban–Acree–van’t Hoff Model
2.4. Thermodynamic Parameters
3. Results and Discussion
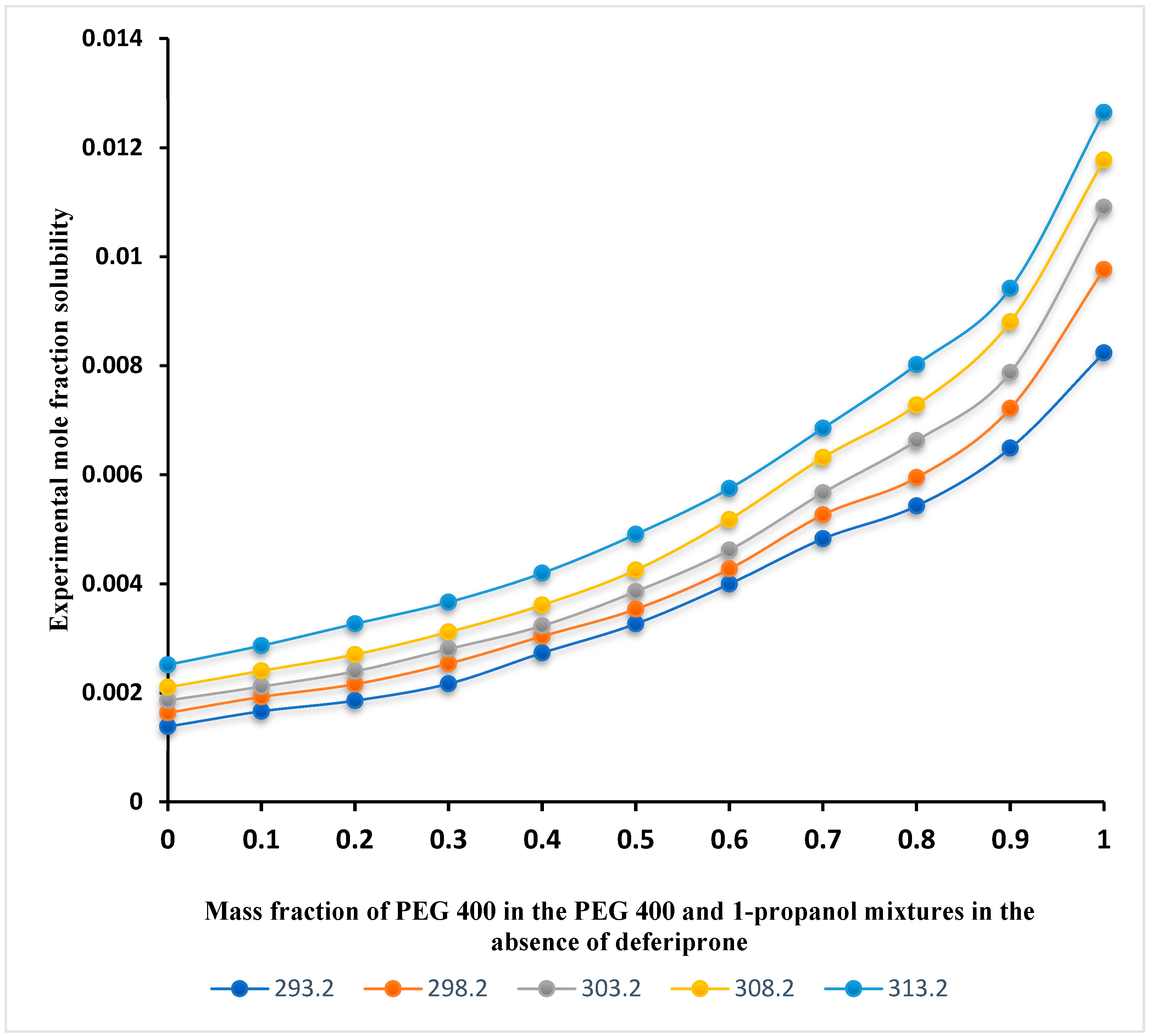
3.1. Solubility Profile of Deferiprone and Data Modeling
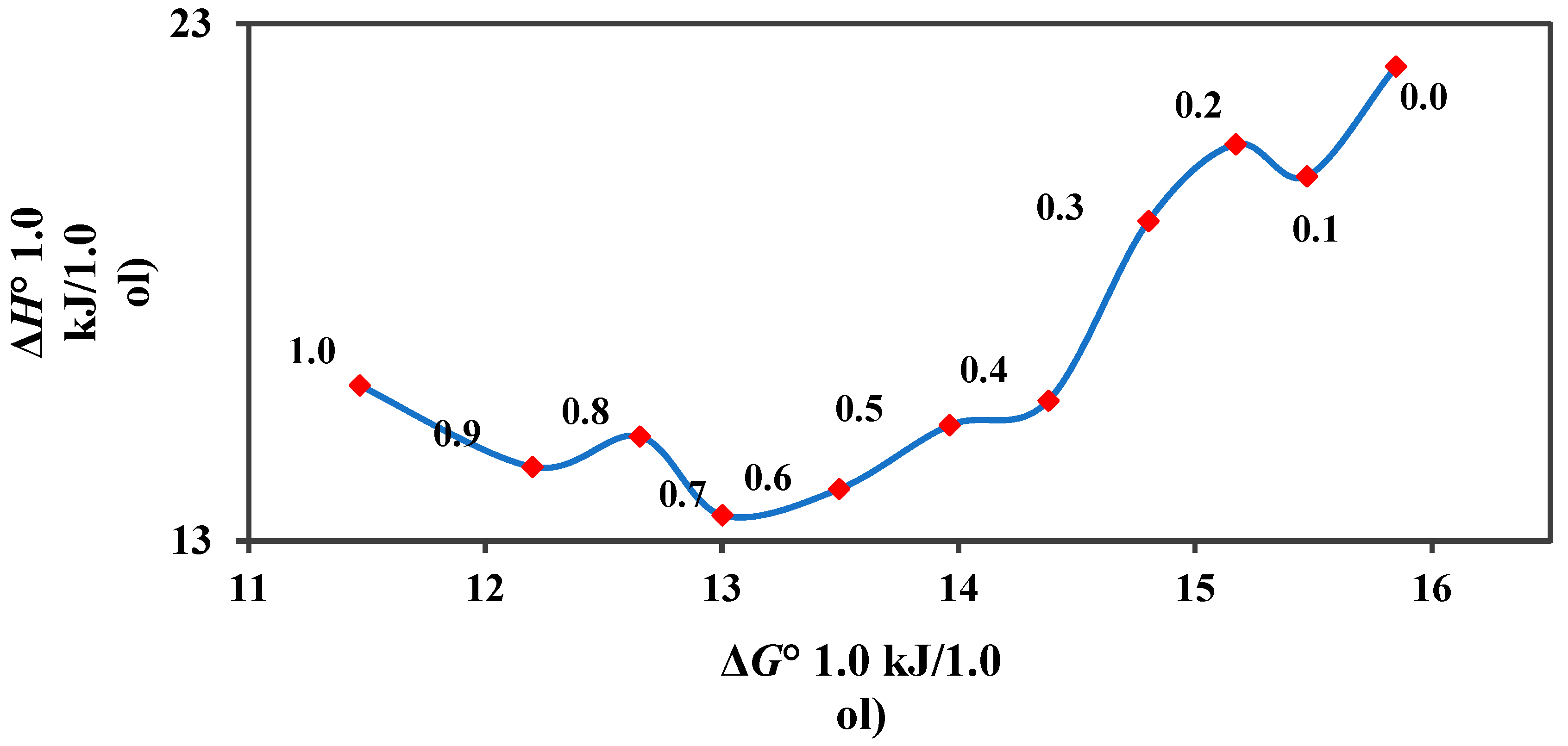
3.2. Calculation of Thermodynamic Parameters of Deferiprone Dissolution
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thachil, J.; Owusu-Ofori, S.; Bates, I. Haematological diseases in the tropics. In Manson’s Tropical Infectious Diseases; W.B. Saunders: Philadelphia, PA, USA, 2014; p. 894. [Google Scholar]
- Vij, R.; Machado, R.F. Pulmonary complications of hemoglobinopathies. Chest 2010, 138, 973–983. [Google Scholar] [CrossRef] [PubMed]
- Taher, A.T.; Saliba, A.N. Iron overload in thalassemia: Different organs at different rates. Hematology 2017, 2017, 265–271. [Google Scholar] [CrossRef] [PubMed]
- Iuliano, L.; Violi, F.; Pedersen, J.Z.; Praticò, D.; Rotilio, G.; Balsano, F. Free radical-mediated platelet activation by hemoglobin released from red blood cells. Arch. Biochem. Biophys. 1992, 299, 220–224. [Google Scholar] [CrossRef] [PubMed]
- Panigrahi, I.; Agarwal, S. Thromboembolic complications in β-thalassemia: Beyond the horizon. Thromb. Res. 2007, 120, 783–789. [Google Scholar] [CrossRef] [PubMed]
- Timoshnikov, V.A.; Kobzeva, T.V.; Polyakov, N.E.; Kontoghiorghes, G.J. Redox interactions of vitamin C and iron: Inhibition of the pro-oxidant activity by deferiprone. Int. J. Mol. Sci. 2020, 21, 3967. [Google Scholar] [CrossRef] [PubMed]
- Jouyban, A.; Abbasi, M.; Rahimpour, E.; Barzegar-Jalali, M.; Vaez-Gharamaleki, J. Deferiprone solubility in some non-aqueous mono-solvents at different temperatures: Experimental data and thermodynamic modelling. Phys. Chem. Liq. 2018, 56, 619–626. [Google Scholar] [CrossRef]
- Savjani, K.T.; Gajjar, A.K.; Savjani, J.K. Drug solubility: Importance and enhancement techniques. Int. Sch. Res. Not. 2012, 2012, 195727. [Google Scholar] [CrossRef] [PubMed]
- Jouyban, A. Review of the cosolvency models for predicting solubility of drugs in water-cosolvent mixtures. J. Pharm. Pharm. Sci. 2008, 11, 32–58. [Google Scholar] [CrossRef] [PubMed]
- Gheitasi, N.; Nazari, A.H.; Haghtalab, A. Thermodynamic modeling and solubility measurement of cetrizine hydrochloride and deferiprone in pure solvents of acetonitrile, ethanol, acetic acid, sulfolane, and ethyl acetate and their mixtures. J. Chem. Eng. Data 2019, 64, 5486–5496. [Google Scholar] [CrossRef]
- Chahiyan-Broujeni, H.; Gharib, F. Thermodynamic study on solubility of deferiprone at different ionic strengths and various temperatures. Montash Chem. 2016, 147, 1177–1181. [Google Scholar] [CrossRef]
- Zhou, C.; Shi, X.; Wang, H.; An, N. Measurement and correlation of solubilities of trans-ferulic acid in solvents. J. Chem. Ind. Eng. 2007, 58, 2705. [Google Scholar]
- Buchowski, H.; Ksiazczak, A.; Pietrzyk, S. Solvent activity along a saturation line and solubility of hydrogen-bonding solids. J. Phys. Chem. 1980, 84, 975–979. [Google Scholar] [CrossRef]
- Yalkowsky, S.H. (Ed.) Solubility and Solubilization in Aqueous Media, Techniques of Solubilization of Drugs; Marcel Dekker: New York, NY, USA, 1981. [Google Scholar]
- Perlovich, G.L.; Kurkov, S.V.; Bauer-Brandl, A. Thermodynamics of solutions: II. Flurbiprofen and diflunisal as models for studying solvation of drug substances. Eur. J. Pharm. Sci. 2003, 19, 423–432. [Google Scholar] [CrossRef] [PubMed]
- Jouyban, A.; Acree, W.E. A single model to represent physico-chemical properties of liquid mixtures at various temperatures. J. Mol. Liq. 2021, 323, 115054. [Google Scholar] [CrossRef]
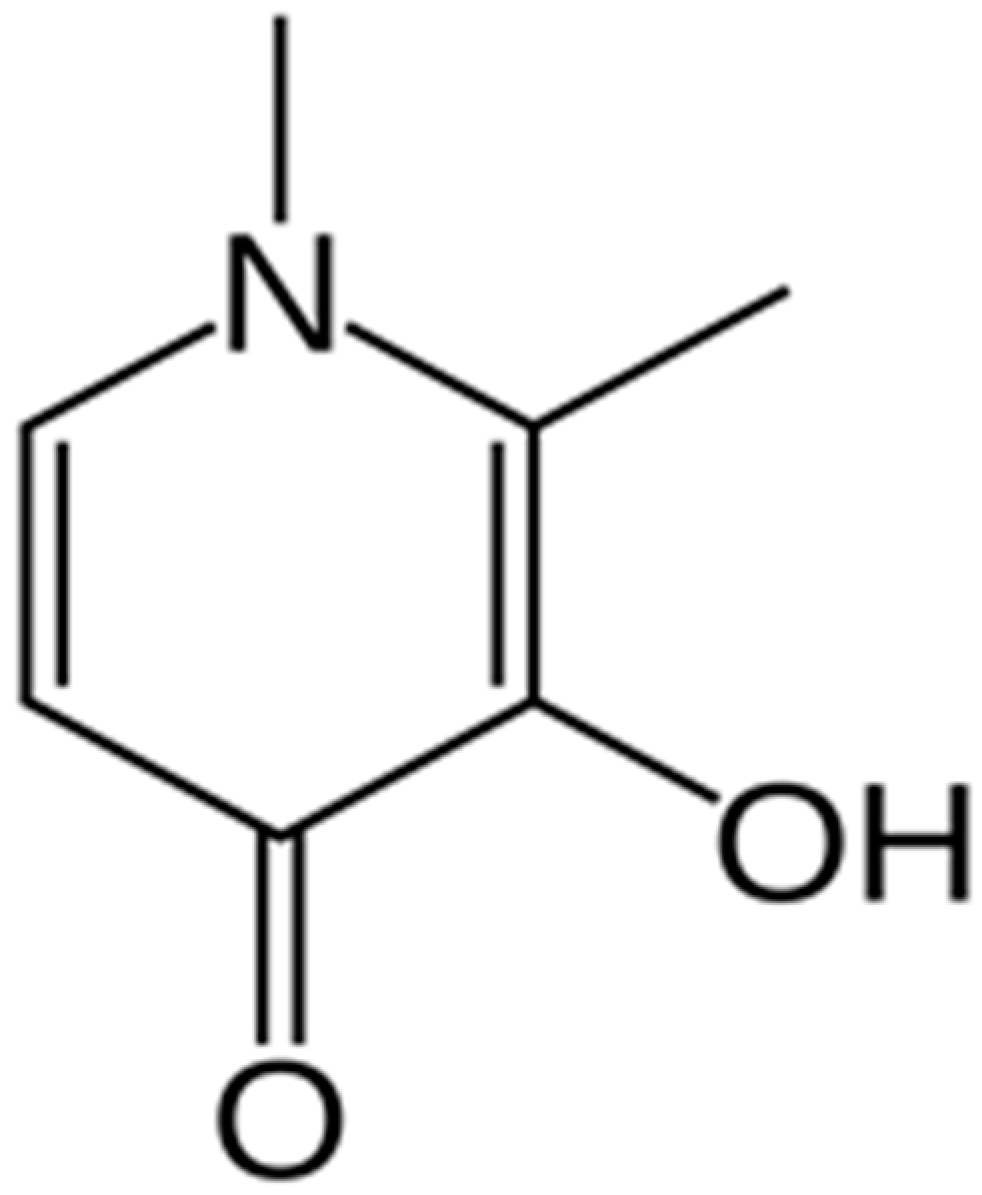
| Chemical Name | CAS No. | Molecular Formula | Molar Mass (g·mole−1) | Source | Purity (Percentage) | Analysis Method |
|---|---|---|---|---|---|---|
| Deferiprone | 30652-11-0 | C7H9NO2 | 139.15 | Arasto Pharmaceutical Chemicals Inc., Tehran, Iran | ≥99.7% | HPLC a |
| 1-Propanol | 71-23-8 | C3H8O | 60.10 | Merck, Darmstadt, Germany | ≥99.5% | GC b |
| Polyethylene glycol 400 | 25322-68-3 | C2nH4n+2On+1, n = 8.2 to 9.1 | 380–420 | Merck, Darmstadt, Germany | ≥99.0% | GC b |
| Distilled deionized water | 7732-18-5 | H2O | 18.02 | Shahid Ghazi Pharmaceutical Co., Tabriz, Iran | ≥99.9% | GC b |
| Ethanol | 64-17-5 | C2H6O | 46.07 | Jahan Alcohol Teb, Arak, Iran | ≥93.5% | GC b |
| w1 | A | B | MRD% |
|---|---|---|---|
| 0.00 | 2.512 | −2667.448 | 1.2 |
| 0.10 | 1.819 | −2412.151 | 1.9 |
| 0.20 | 2.185 | −2486.642 | 2.0 |
| 0.30 | 1.741 | −2307.875 | 1.5 |
| 0.40 | 0.530 | −1890.212 | 2.2 |
| 0.50 | 0.506 | −1832.665 | 1.8 |
| 0.60 | 0.202 | −1684.222 | 1.4 |
| 0.70 | 0.196 | −1623.279 | 0.6 |
| 0.80 | 0.940 | −1806.659 | 0.3 |
| 0.90 | 0.886 | −1736.001 | 0.7 |
| 1.00 | 1.802 | −1925.654 | 2.4 |
| Overall | 1.4 | ||
| w1 | λ | h | MRD% |
|---|---|---|---|
| 0.00 | 0.505 | 20.103 | 2.4 |
| 0.10 | 0.505 | 21.213 | 3.0 |
| 0.20 | 0.506 | 24.680 | 3.2 |
| 0.30 | 0.506 | 26.219 | 2.2 |
| 0.40 | 0.506 | 25.626 | 2.9 |
| 0.50 | 0.507 | 29.263 | 2.7 |
| 0.60 | 0.508 | 32.185 | 2.1 |
| 0.70 | 0.510 | 37.305 | 1.1 |
| 0.80 | 0.512 | 47.553 | 1.0 |
| 0.90 | 0.514 | 54.231 | 0.6 |
| 1.00 | 0.520 | 78.629 | 1.5 |
| Overall | 2.0 | ||
| ln x | |||||
|---|---|---|---|---|---|
| w1 | 293.2 K | 298.2 K | 303.2 K | 308.2 K | 313.2 K |
| 0.00 | −6.59 | −6.42 | −6.29 | −6.17 | −5.99 |
| 0.10 | −6.41 | −6.24 | −6.11 | −5.99 | −5.83 |
| 0.20 | −6.23 | −6.06 | −5.94 | −5.82 | −5.66 |
| 0.30 | −6.05 | −5.88 | −5.76 | −5.65 | −5.50 |
| 0.40 | −5.87 | −5.70 | −5.58 | −5.48 | −5.34 |
| 0.50 | −5.69 | −5.52 | −5.40 | −5.30 | −5.18 |
| 0.60 | −5.51 | −5.35 | −5.23 | −5.13 | −5.02 |
| 0.70 | −5.34 | −5.17 | −5.05 | −4.96 | −4.86 |
| 0.80 | −5.16 | −4.99 | −4.87 | −4.79 | −4.69 |
| 0.90 | −4.98 | −4.81 | −4.70 | −4.61 | −4.53 |
| 1.00 | −4.80 | −4.63 | −4.52 | −4.44 | −4.37 |
| MRD% | 3.2 | 8.2 | 11.1 | 10.1 | 9.7 |
| Overall MRD% | 8.5 | ||||
| T (K) | λ12 | λ21 | MRD% |
|---|---|---|---|
| 293.2 | 0.711 | 1.221 | 2.4 |
| 298.2 | 0.756 | 1.323 | 2.1 |
| 303.2 | 1.462 | 0.684 | 1.6 |
| 308.2 | 1.433 | 0.698 | 1.4 |
| 313.2 | 1.455 | 0.687 | 1.6 |
| Overall | 1.8 | ||
| Jouyban–Acree | Jouyban–Acree–van’t Hoff | ||
|---|---|---|---|
| J0 | −131.586 | A1 | 1.802 |
| J1 | −56.892 | B1 | −1925.654 |
| J2 | −144.322 | A2 | 2.512 |
| B2 | −2667.448 | ||
| J0 | −131.235 | ||
| J1 | −56.563 | ||
| J2 | −143.446 | ||
| MRD% 2.8 | 3.0 | ||
| w1 | 293.2 K | 298.2 K | 303.2 K | 308.2 K | 313.2 K |
|---|---|---|---|---|---|
| 0.00 | 0.802 ± 0.001 | 0.798 ± 0.001 | 0.796 ± 0.001 | 0.794 ± 0.001 | 0.788 ± 0.001 |
| 0.10 | 0.823 ± 0.001 | 0.823 ± 0.001 | 0.822 ± 0.001 | 0.820 ± 0.001 | 0.819 ± 0.001 |
| 0.20 | 0.853 ± 0.002 | 0.851 ± 0.001 | 0.849 ± 0.000 | 0.847 ± 0.001 | 0.845 ± 0.003 |
| 0.30 | 0.879 ± 0.001 | 0.877 ± 0.001 | 0.877 ± 0.000 | 0.875 ± 0.001 | 0.874 ± 0.001 |
| 0.40 | 0.907 ± 0.001 | 0.906 ± 0.001 | 0.906 ± 0.001 | 0.905 ± 0.001 | 0.904 ± 0.001 |
| 0.50 | 0.940 ± 0.002 | 0.938 ± 0.001 | 0.937 ± 0.001 | 0.936 ± 0.001 | 0.936 ± 0.001 |
| 0.60 | 0.971 ± 0.001 | 0.971 ± 0.001 | 0.969 ± 0.002 | 0.967 ± 0.002 | 0.967 ± 0.001 |
| 0.70 | 1.007 ± 0.001 | 1.006 ± 0.001 | 1.005 ± 0.001 | 1.003 ± 0.001 | 1.002 ± 0.001 |
| 0.80 | 1.042 ± 0.001 | 1.042 ± 0.001 | 1.039 ± 0.001 | 1.038 ± 0.001 | 1.038 ± 0.001 |
| 0.90 | 1.082 ± 0.000 | 1.080 ± 0.001 | 1.079 ± 0.001 | 1.075 ± 0.002 | 1.074 ± 0.001 |
| 1.00 | 1.123 ± 0.001 | 1.120 ± 0.001 | 1.119 ± 0.001 | 1.116 ± 0.002 | 1.114 ± 0.001 |
| w1 a | ΔG° (kJ·mol−1) | ΔH° (kJ·mol−1) | ΔS° (J·K−1·mol−1) | TΔS° (kJ·mol−1) | ζH | ζTΔS |
|---|---|---|---|---|---|---|
| 0.00 | 15.85 | 22.18 | 20.88 | 6.33 | 0.778 | 0.222 |
| 0.10 | 15.47 | 20.06 | 15.13 | 4.58 | 0.814 | 0.186 |
| 0.20 | 15.17 | 20.67 | 18.16 | 5.50 | 0.790 | 0.210 |
| 0.30 | 14.80 | 19.19 | 14.47 | 4.39 | 0.814 | 0.186 |
| 0.40 | 14.38 | 15.72 | 4.41 | 1.34 | 0.922 | 0.078 |
| 0.50 | 13.96 | 15.24 | 4.20 | 1.27 | 0.923 | 0.077 |
| 0.60 | 13.49 | 14.00 | 1.68 | 0.51 | 0.965 | 0.035 |
| 0.70 | 13.00 | 13.50 | 1.63 | 0.49 | 0.965 | 0.035 |
| 0.80 | 12.65 | 15.02 | 7.82 | 2.37 | 0.864 | 0.136 |
| 0.90 | 12.20 | 14.43 | 7.37 | 2.23 | 0.866 | 0.134 |
| 1.00 | 11.47 | 16.01 | 14.99 | 4.54 | 0.779 | 0.221 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaei, H.; Jouyban, A. Solubility of Deferiprone in Non-Aqueous Mixtures of Polyethylene Glycol 400 and 1-Propanol at 293.2–323.2 K. Liquids 2025, 5, 5. https://doi.org/10.3390/liquids5010005
Rezaei H, Jouyban A. Solubility of Deferiprone in Non-Aqueous Mixtures of Polyethylene Glycol 400 and 1-Propanol at 293.2–323.2 K. Liquids. 2025; 5(1):5. https://doi.org/10.3390/liquids5010005
Chicago/Turabian StyleRezaei, Homa, and Abolghasem Jouyban. 2025. "Solubility of Deferiprone in Non-Aqueous Mixtures of Polyethylene Glycol 400 and 1-Propanol at 293.2–323.2 K" Liquids 5, no. 1: 5. https://doi.org/10.3390/liquids5010005
APA StyleRezaei, H., & Jouyban, A. (2025). Solubility of Deferiprone in Non-Aqueous Mixtures of Polyethylene Glycol 400 and 1-Propanol at 293.2–323.2 K. Liquids, 5(1), 5. https://doi.org/10.3390/liquids5010005








