Visualization of the 3D Structure of Subcritical Aqueous Ca(NO3)2 Solutions at 25~350 °C and 40 MPa by Raman and X-Ray Scattering Combined with Empirical Potential Structure Refinement Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation and Compositions
2.2. Raman Scattering Measurements
2.3. X-Ray Scattering Measurements
2.4. Data Correction and Analysis
2.4.1. Energy Correction
2.4.2. Escape Peak Correction
2.4.3. Absorption Correction
2.4.4. The Incident Spectral Intensity I0
2.4.5. EPSR Modeling
3. Results and Discussion
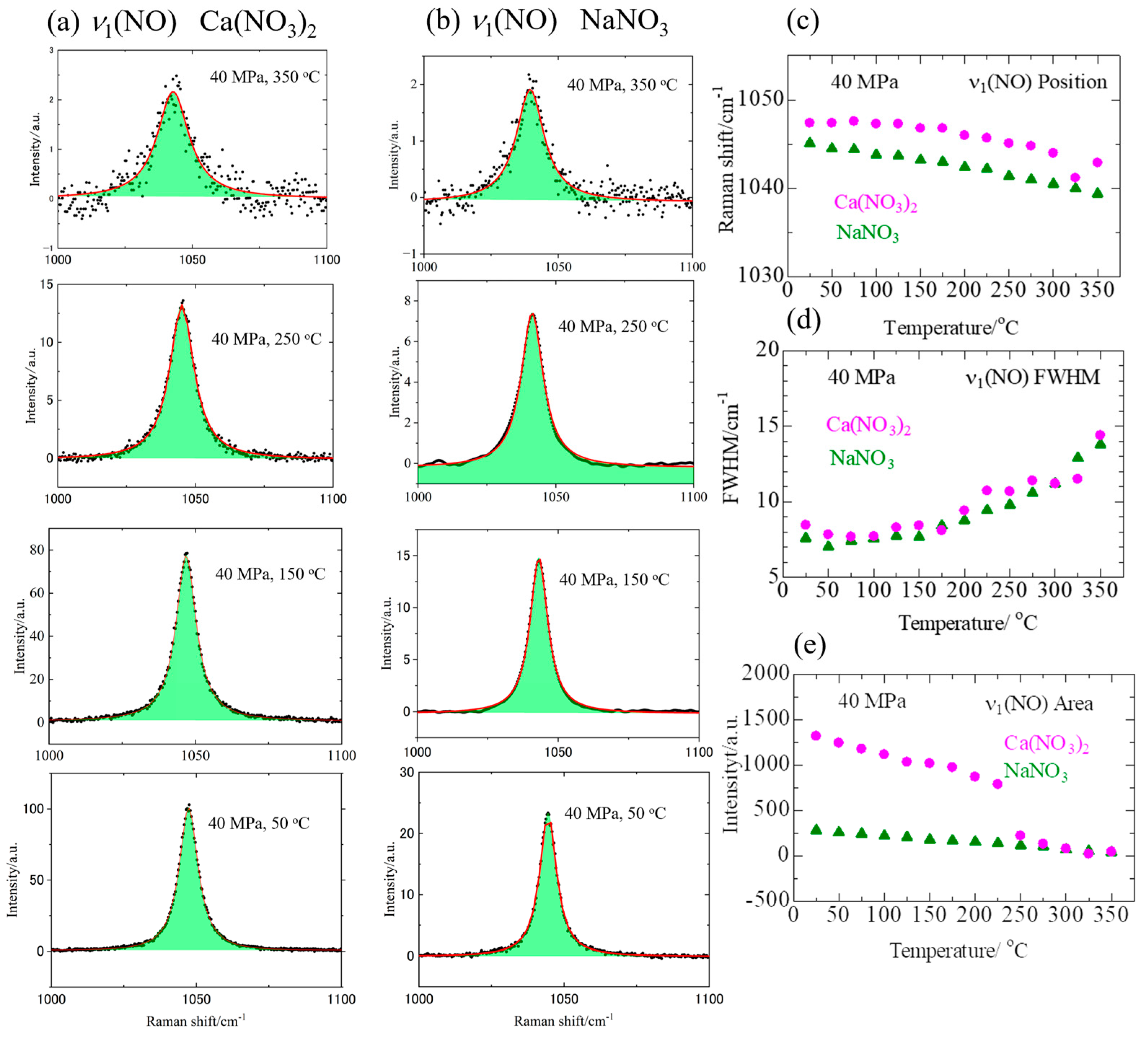
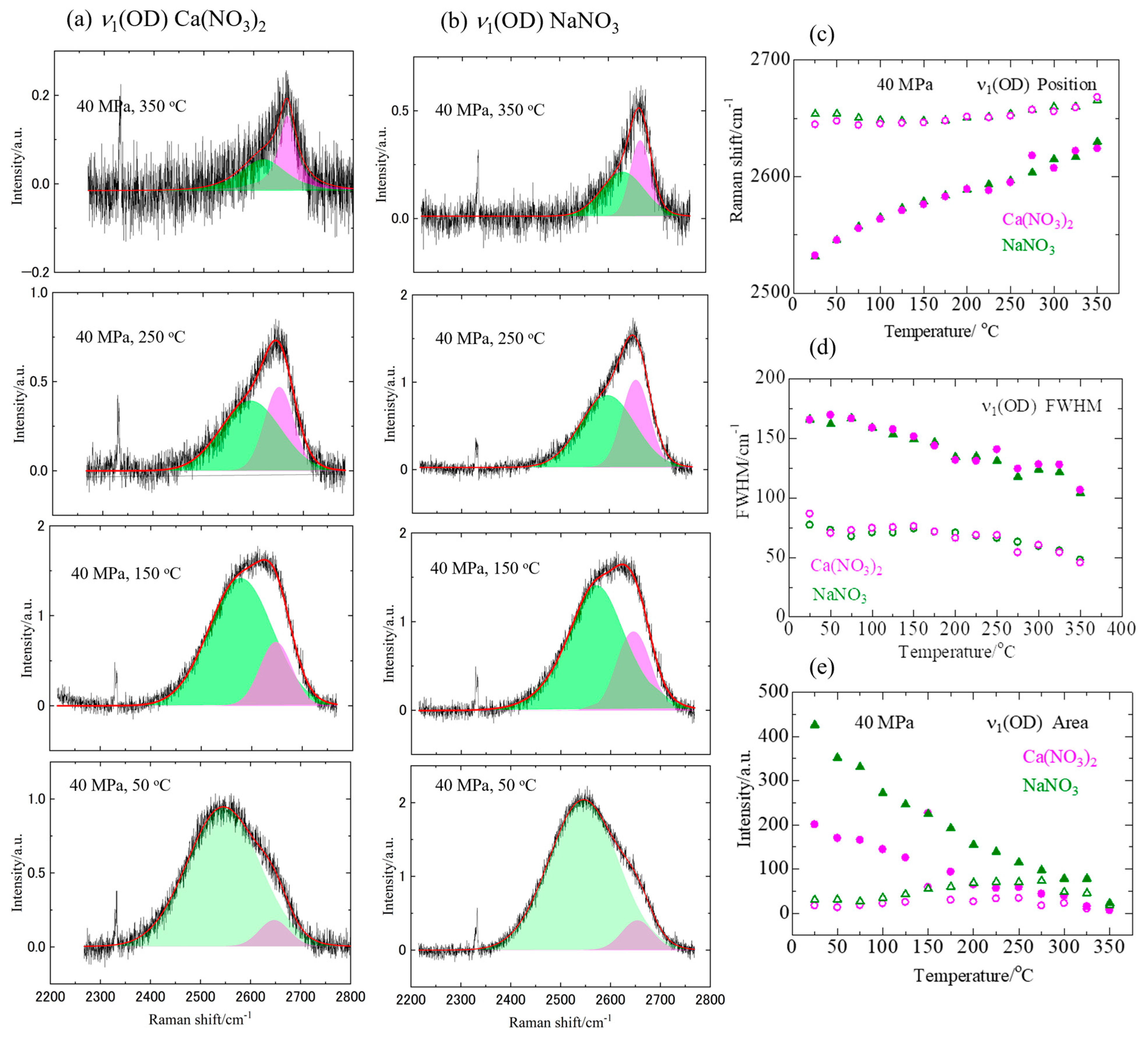
3.1. Raman Spectra
3.2. X-Ray Scattering and EPSR Modeling
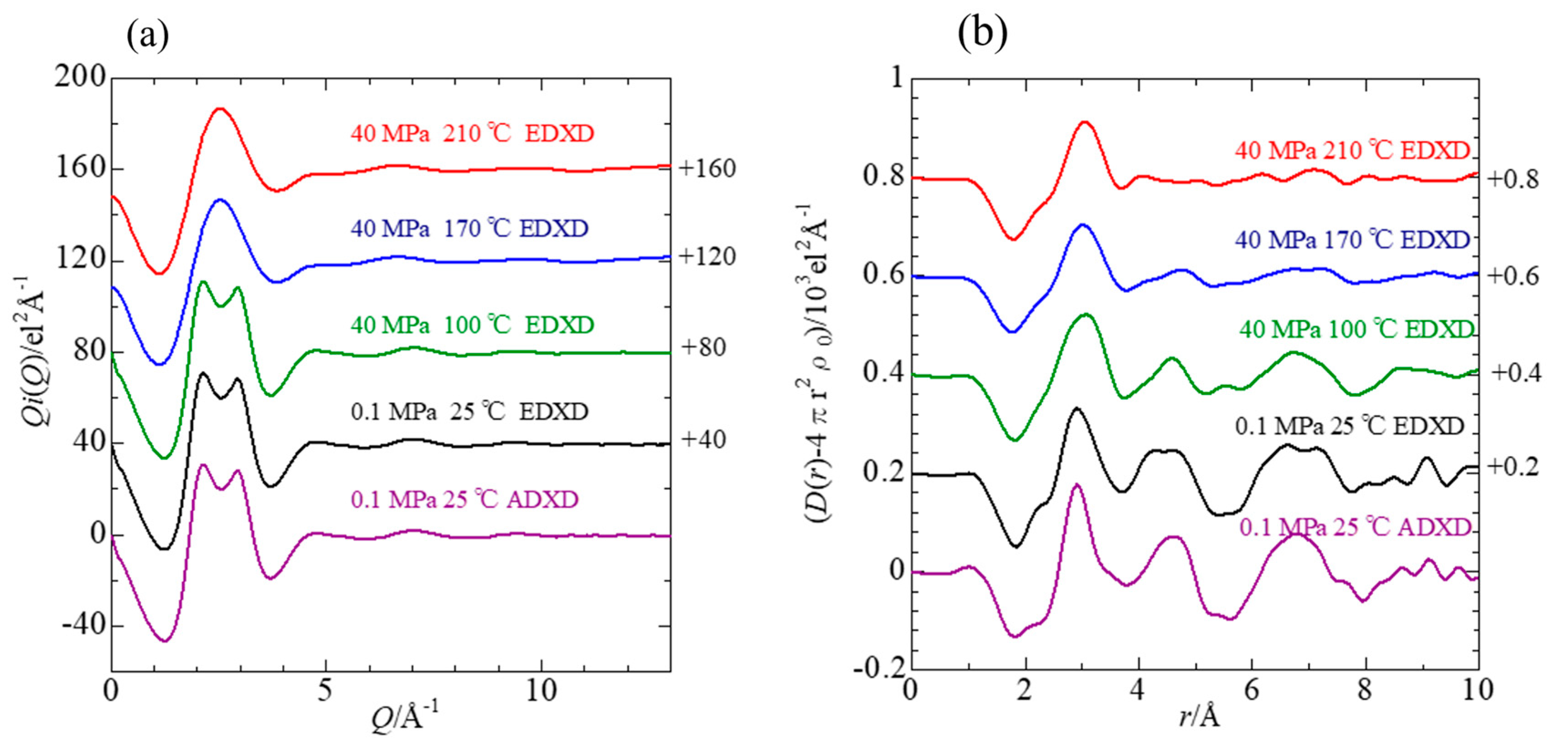
3.2.1. Total Interference Functions and Radial Distribution Functions
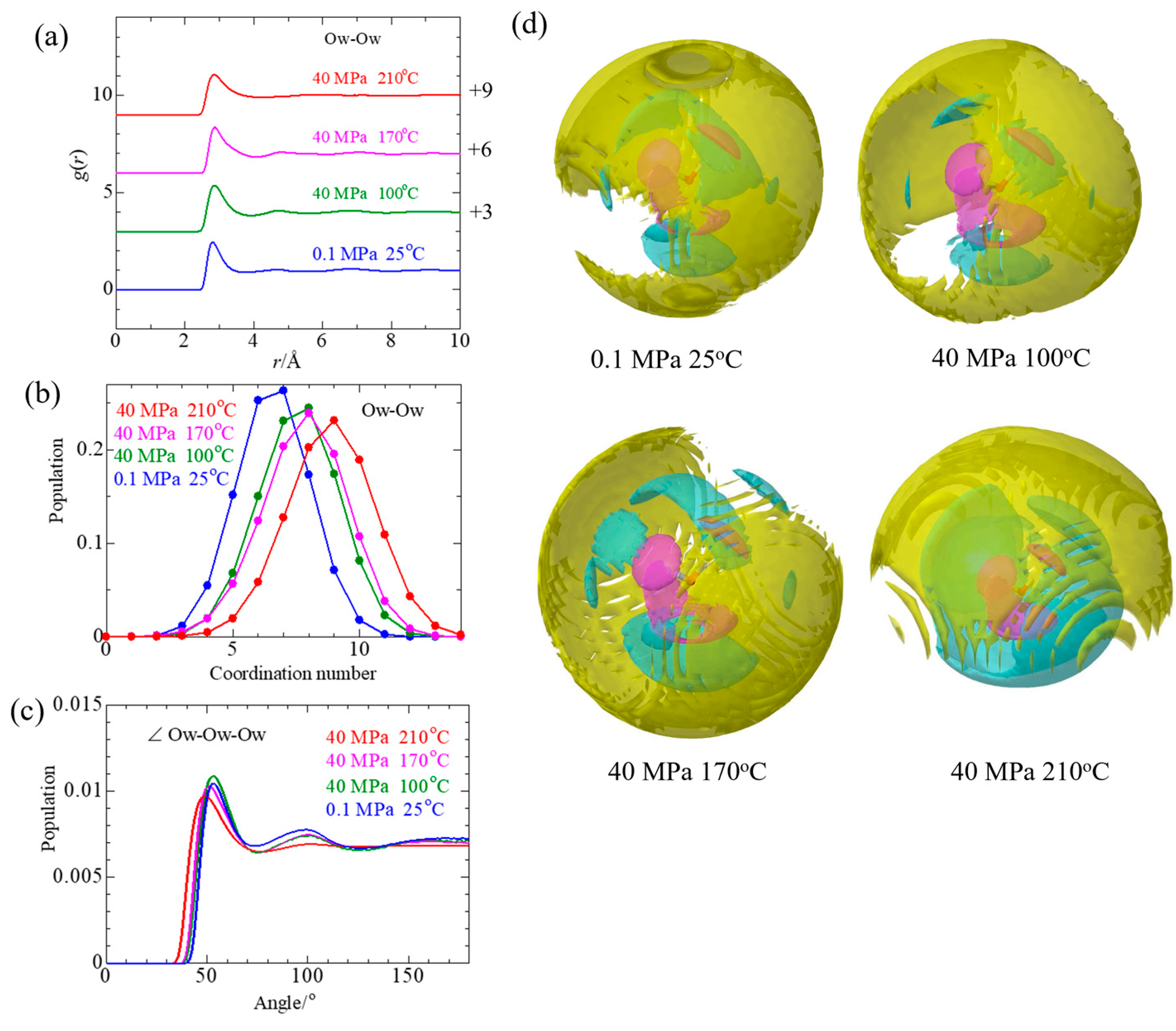
3.2.2. Solvent Water
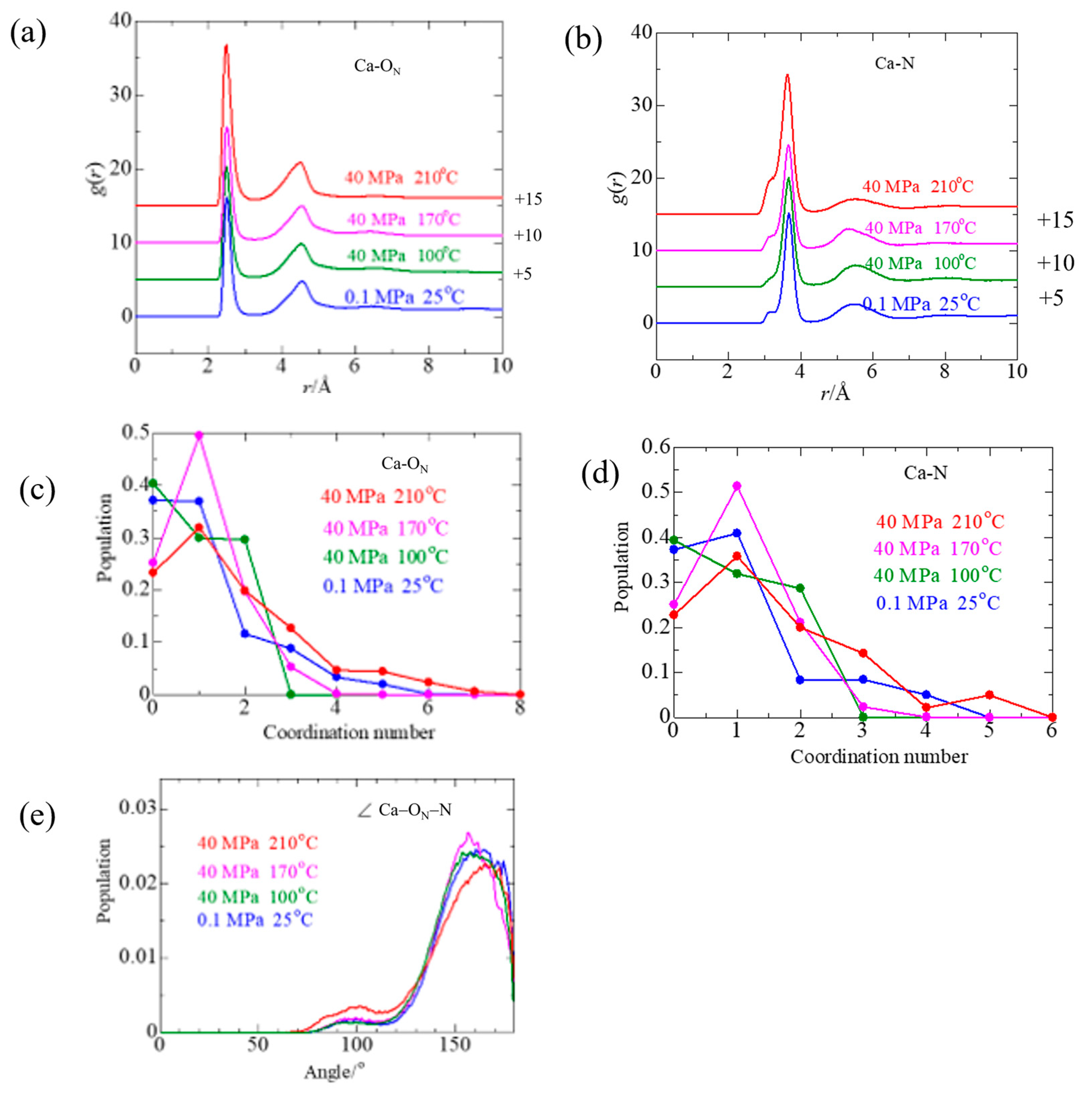
3.2.3. Ca2+ Solvation
3.2.4. Ca2+–NO3− Ion Pair
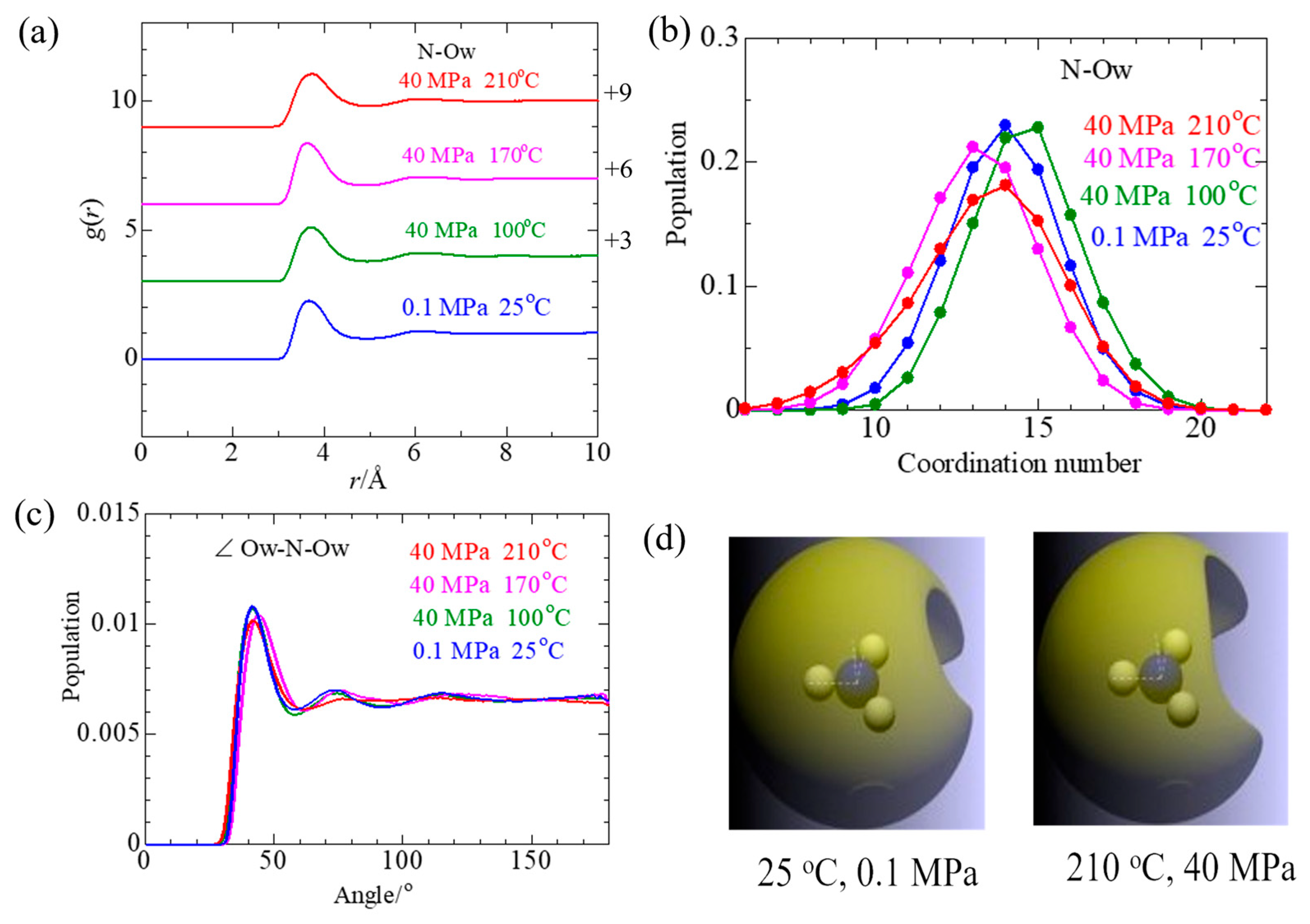
3.2.5. NO3− Solvation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sako, T.; Sugeta, T.; Otake, K.; Sato, M.; Tsugumi, M.; Hiaki, T.; Hongo, M. Decomposition of Dioxins in Fly Ash with Supercritical Water Oxidation. J. Chem. Eng. Jpn. 1997, 30, 744–747. [Google Scholar] [CrossRef][Green Version]
- Brunner, G. Applications of Supercritical Fluids. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 321–342. [Google Scholar] [CrossRef]
- Supercritical Fluids: Fundamentals and Applications; Kiran, E., Debenedetti, P.G., Peters, C.J., Eds.; Springer: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Ohara, S.; Mousavand, T.; Sasaki, T.; Umetsu, M.; Naka, T.; Adschiri, T. Continuous production of fine zinc oxide nanorods by hydrothermal synthesis in supercritical water. J. Mater. Sci. 2008, 43, 2393–2396. [Google Scholar] [CrossRef]
- Uematsu, M.; Franck, E.U. Static dielectric constant of water and steam. J. Phys. Chem. Ref. Data 1980, 9, 1291–1306. [Google Scholar] [CrossRef]
- Yamaguchi, T. Historical development of a study of the structure and dynamics of liquids and solutions. J. Mol. Liq. 2024, 395, 123919. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Persson, I. (Eds.) Coordination Chemistry: Metal Ions and Complexes in Solution; Royal Society of Chemistry: London, UK, 2023. [Google Scholar]
- Soper, A.K. Computer simulation as a tool for the interpretation of total scattering data from glasses and liquids. Mol. Simul. 2012, 38, 1171–1185. [Google Scholar] [CrossRef]
- Soper, A.K. Empirical potential Monte Carlo simulation of fluid structure. Chem. Phys. 1996, 202, 295–306. [Google Scholar] [CrossRef]
- Soper, A.K. Partial structure factors from disordered materials diffraction data: An approach using empirical potential structure refinement. Phys. Rev. B. 2005, 72, 104204. [Google Scholar] [CrossRef]
- Hess, P.; Tsien, R.W. Mechanism of ion permeation through calcium channels. Nature 1984, 309, 453–456. [Google Scholar] [CrossRef]
- Dudev, T.; Lim, C. Importance of Metal Hydration on the Selectivity of Mg2+ and Ca2+ in Magnesium Ion Channels. J. Am. Chem. Soc. 2013, 135, 17200–17208. [Google Scholar] [CrossRef]
- Irish, D.E.; Walrafen, G.E. Raman and Infrared Spectral Studies of Aqueous Calcium Nitrate Solutions. J. Chem. Phys. 1967, 46, 378–384. [Google Scholar] [CrossRef]
- Spohn, P.D.; Brill, T.B. Raman Spectroscopy of the Species in Concentrated Aqueous Solutions of Zn(NO3)2, Ca(NO3)2, Cd(NO3)2, LiNO3, and NaNO3 up to 450 °C and 30 MPa. J. Phys. Chem. 1989, 93, 6224–6231. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, F.; Yamaguchi, T.; Yoshida, K.; Wang, G.; Liu, R.; Song, L.; Zhou, Y.; Liu, H. Structure of phase change energy storage material Ca(NO3)2.4H2O. J. Mol. Liq. 2022, 356, 119010. [Google Scholar] [CrossRef]
- Licheri, G.; Piccaluga, G.; Pinna, G. X-ray diffraction study of the average solute species in CaCl2 aqueous solutions. J. Chem. Phys. 1976, 64, 2437–2441. [Google Scholar] [CrossRef]
- Probst, M.M.; Radnai, T.; Heinzinger, K.; Bopp, P.; Rode, B.M. Molecular dynamics and X-ray investigation of an aqueous calcium chloride solution. J. Phys. Chem. 1985, 89, 753–759. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Hayashi, S.; Ohtaki, H. X-Ray diffraction study of calcium(II) chloride hydrate melts: CaCl2·RH2O (R = 4.0, 5.6, 6.0, and 8.6). Inorg. Chem. 1989, 28, 2434–2439. [Google Scholar] [CrossRef]
- Megyes, T.; Grósz, T.; Radnai, T.; Bakó, I.; Pálinkás, G. Solvation of Calcium Ion in Polar Solvents: An X-ray Diffraction and ab initio Study. J. Phys. Chem. A 2004, 108, 7261–7271. [Google Scholar] [CrossRef]
- Takamuku, T.; Umecky, T.; Yagafarov, O.F.; Katayama, Y.T. Structures of aqueous calcium chloride solutions by energy-dispersive-ray diffraction under high temperatures and high pressures. Bunseki Kagaku 2015, 64, 203–210. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Wang, G.; Zhou, Y.; Yamaguchi, T.; Liu, H.; Zhu, F.; Wu, Z. Structure of Aqueous CaCl2 solutions by X-ray Scattering and Density Functional Theory. Russ. J. Phys. Chem. A 2022, 96, S68–S76. [Google Scholar] [CrossRef]
- Cummings, S.; Enderby, J.E.; Howe, R.A. Ion hydration in aqueous CaCl2 solutions. J. Phys. C Solid State Phys. 1980, 13, 1. [Google Scholar] [CrossRef]
- Hewish, N.A.; Neilson, G.W.; Enderby, J.E. Environment of Ca2+ ions in aqueous solvent. Nature 1982, 297, 138. [Google Scholar] [CrossRef]
- Badyal, Y.S.; Barnes, A.C.; Cuello, J.J.; Simonson, J.M. Understanding the effects of Concentration on the Solvation Structure of Ca2+ in Aqueous Solution. II: Insights into Longer Range Order from Neutron Diffraction Isotope Substitution. J. Phys. Chem. A 2004, 108, 11819–11827. [Google Scholar] [CrossRef]
- Bruni, F.; Imberti, S.; Mancinelli, R.; Ricci, M.A. Aqueous solutions of divalent chlorides; ions hydration shell and water structure. J. Chem. Phys. 2012, 136, 064520. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Nishio, M.; Yoshida, K.; Takumi, M.; Nagata, K.; Hattori, T. Ion Hydration and Association in an Aqeous Calcium Chloride Solution in the GPa Range. Eur. J. Inorg. Chem 2019, 1170–1177. [Google Scholar] [CrossRef]
- Spångberg, D.; Hermansson, K.; Lindqvist-Reis, P.; Jalilehvand, F.; Sandström, M.; Persson, I. Model Extended X-Ray Absorption Fine Structure (EXAFS) Spectra from Molecular Dynamics Data for Ca2+ and Al3+ Aqueous Solutions. J. Phys. Chem. B 2000, 104, 10467–10472. [Google Scholar] [CrossRef]
- Jalilehvand, F.; Spångberg, D.; Lindqvist-Reis, P.; Hermansson, K.; Persson, I.; Sandström, M. Hydration of the Calcium Ion. An EXAFS, Large-Angle X-Ray Scattering, and Molecular Dynamics Simulation Study. J. Am. Chem. Soc. 2001, 123, 431–441. [Google Scholar] [CrossRef] [PubMed]
- Fulton, J.L.; Heald, M.S.; Badyal, Y.S.; Simonson, J.M. Understanding the effects of concentration on the Solvation Structure of Ca2+ in Aqueous Solution. I: The Perspective on Local Structure from EXAFS and XANES. J. Phys. Chem. A 2003, 107, 4688–4696. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Li, K.; Yamauchi, M.; Fukuyama, N.; Yoshida, K. Visualization of 3D structure of aqueous magnesium nitrate solution at 25~350 °C and 40 MPa as revealed by Raman scattering, X-ray diffraction and Empirical Potential, Structure Refinement Modeling. Bunseki Kagaku 2015, 64, 295–308. [Google Scholar] [CrossRef][Green Version]
- Yamaguchi, T.; Fujimura, K.; Uchi, K.; Yoshida, K.; Katayama, Y. Structure of water from ambient to 4 GPa revealed by energy-dispersive X-ray diffraction combined with empirical potential structure refinement modeling. J. Mol. Liq. 2012, 176, 44–51. [Google Scholar] [CrossRef]
- Fujimoto, T.; Yoshida, K.; Yamaguchi, T. Energy dispersive X-ray diffractometer designed for measurements of solution under extreme condition and its performance. Fukuoka Univ. Sci. Rep. 2003, 33, 55–63. [Google Scholar]
- Nishikawa, K.; Iijima, T. Corrections for Intensity Data in Energy-dispersive X-Ray Diffractometry of Liquids. Application to Carbon Tetrachloride. Bull. Chem. Soc. Jpn. 1984, 57, 1750–1759. [Google Scholar] [CrossRef]
- Hosokawa, S.; Tamura, G. Structural Studies on the Meal-Nonmetal Transition in Expanded Mercury-X-ray Diffraction Measurements by the Energy-Dispersive Method. Mem. Fac. Integr. Art Sci. Hiroshima Univ. Ser. IV 1992, 17, 1–34. [Google Scholar]
- Ibers, J.A.; Hamilton, W.C. (Eds.) International Tables for X-Ray Crystallography; The Kynoch Press: Birmingham, UK, 1962; Volume IV. [Google Scholar]
- Mitsuhashi, T.; Nagao, J.; Iijima, T. In Proceedings of the Annual Meeting of the Crystallographic Society of Japan, Tokyo, Japan, 1982.
- Paalman, H.H.; Pings, C.J. Numerical evaluation of X-Ray Absorption Factors for Cylindrical Samples and Annular Sample Cells. J. Appl. Phys. 1962, 33, 2635–2639. [Google Scholar] [CrossRef]
- XCYLABS; Laboratory of Solution Chemistry, Department of Chemistry, Fukuoka University: Jonan, Fukuoka, Japan.
- International Tables for X-Ray Crystallography; MacGillavry, C.H., Rieck, G.D., Eds.; The Kynoch Press: Birmingham, UK, 1962; Volume III. [Google Scholar]
- Funakoshi, K. Energy-Dispersive X-Ray Diffraction for Binary Alkali Silicate Melts Using Synchrotron Radiation Under High Pressure and Temperature. Ph.D. Thesis, Tokyo Institute of Technology, Meguro, Japan, 1997. [Google Scholar]
- Johansson, G.; Sandström, M. Computer Programs for the Analysis of Data on X-Ray Diffraction by Liquids. Chem. Scr. 1973, 4, 195–198. [Google Scholar]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.R. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Mamatkulov, S.; Fyta, M.; Netz, R.R. Force fields for monovalent and divalent metal cations in TIP3P water based on thermodynamic and kinetic properties. J. Chem. Phys. 2013, 138, 024505. [Google Scholar] [CrossRef] [PubMed]
- Megyes, T.; Balint, S.; Peter, E.; Grosz, T.; Bako, I.; Krienke, H.; Bellissent-Funel, M.C. Solution Structure of NaNO3 in Water; Diffraction and Molecular Dynamics Simulation Study. J. Phys. Chem. B 2009, 113, 4054–4064. [Google Scholar] [CrossRef]
- Soper, A.K. EPSR25, Empirical Potential Structure Refinement–EPSR Shell: A User’s Guide ISIS; Rutherford Appleton Laboratory: Didcot, UK, 2009. [Google Scholar]
- Walrafen, G.E. Raman spectral studies of HDO in H2O. J. Chem. Phys. 1968, 48, 244–251. [Google Scholar] [CrossRef]
- Yamanaka, K.; Yamaguchi, T.; Wakita, H. Structure of water in the liquid and supercritical states by rapid X-ray diffractometry using an imaging plate detector. J. Chem. Phys. 1994, 101, 9830–9836. [Google Scholar] [CrossRef]
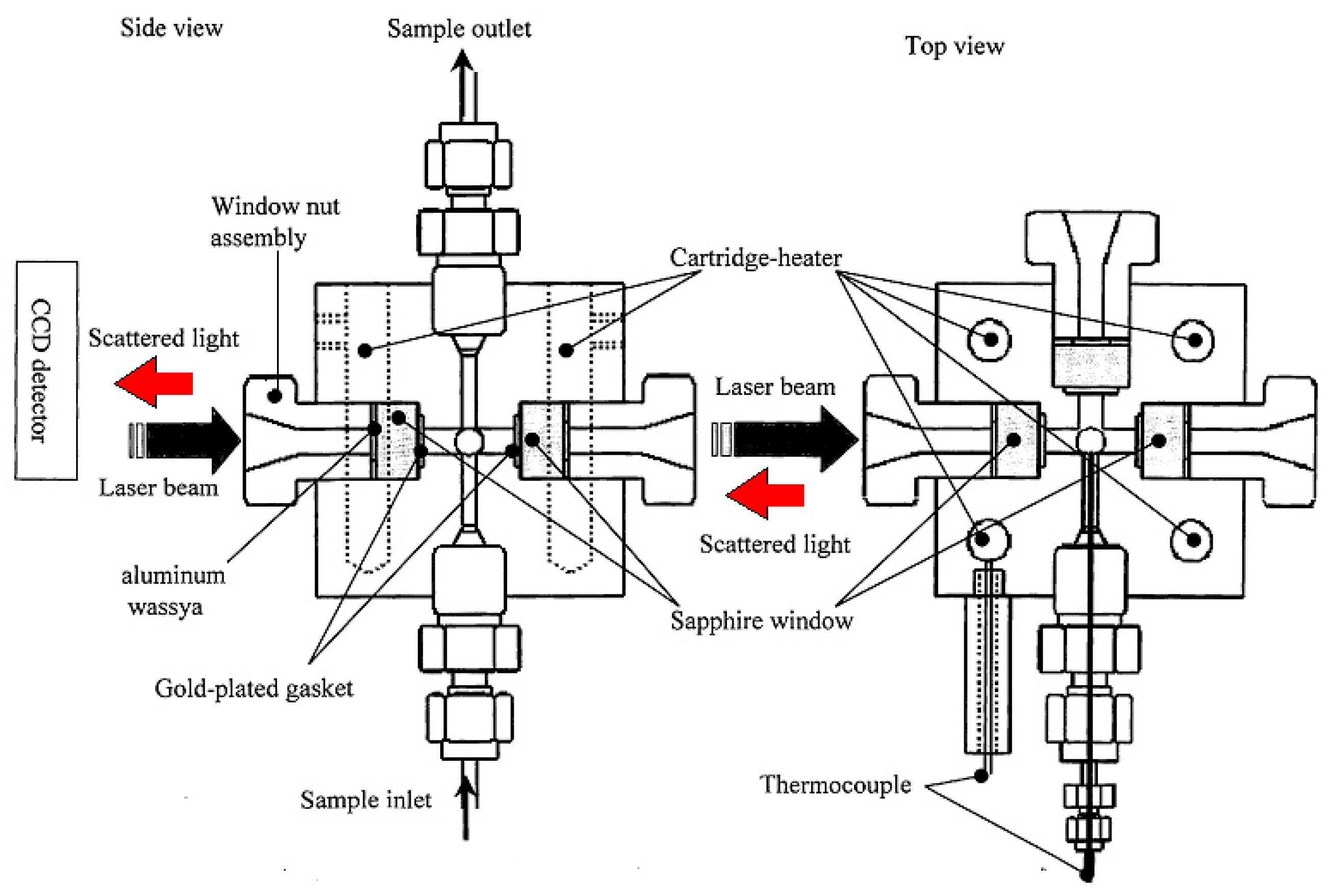
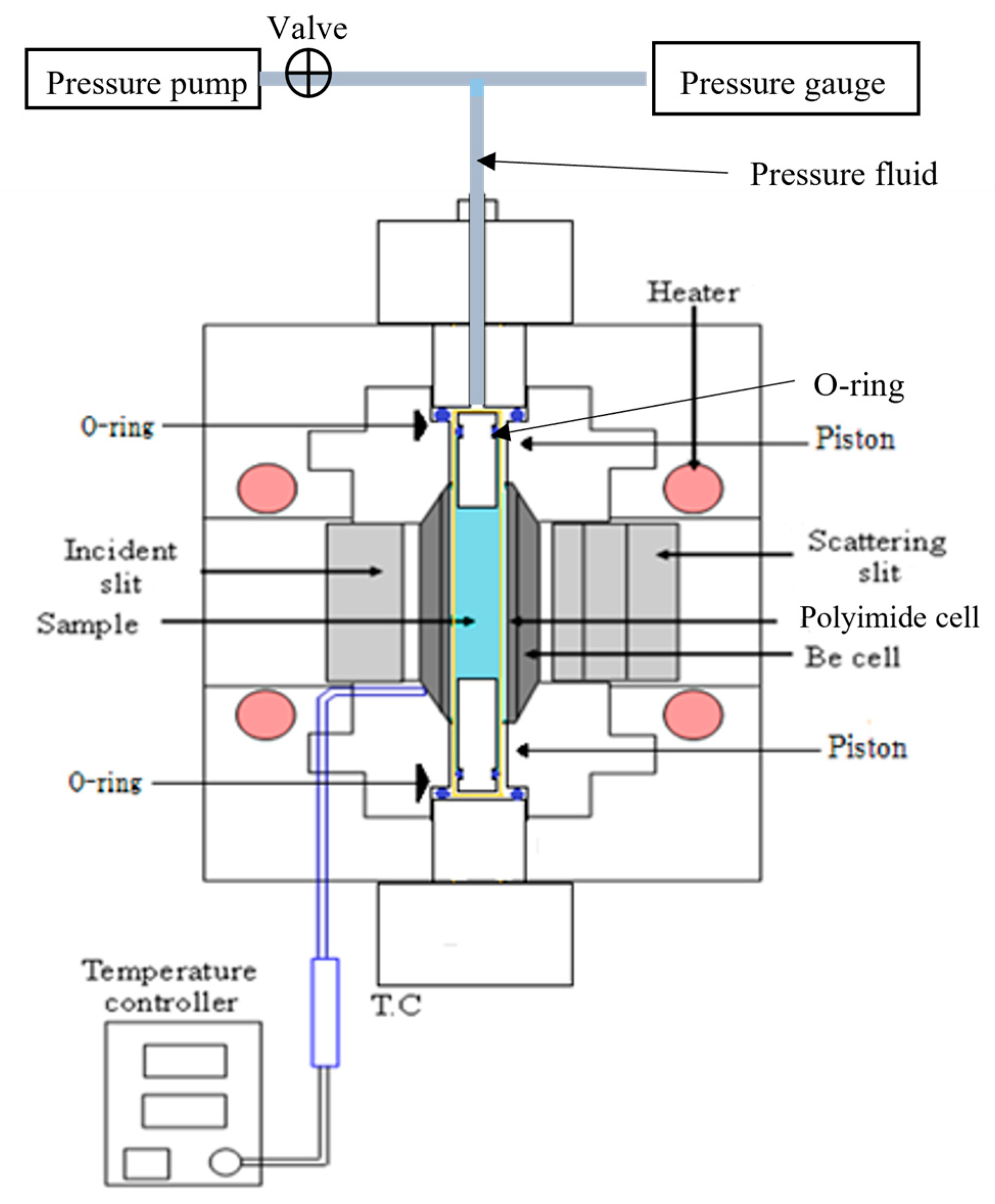

| Concentration/mol dm−3 | Density/g cm−3 | |||
|---|---|---|---|---|
| M | NO3− | H2O | ||
| Na+ | 0.936 | 0.936 | 54.1 | 1.052 |
| Ca2+ | 0.944 | 1.89 | 53.2 | 1.113 |
| Ow | Hw | Ca | N | O | |
|---|---|---|---|---|---|
| ε (kJ/mol) | 0.650 | 0.00 | 0.780 | 0.837 | 0.649 |
| σ (Å) | 3.165 | 0.00 | 2.790 | 3.900 | 3.154 |
| Atomic mass | 16 | 1 | 40 | 14 | 16 |
| Coulomb Charge q (e) | −0.848 | 0.424 | 2.000 | 0.860 | −0.620 |
| Atom Pair | Thermodynamic Condition | r1 (Å) | r2 (Å) | CN | rmin (Å) | rmax (Å) |
|---|---|---|---|---|---|---|
| Ca2+–Ow | 25 °C, 0.1 MPa | 2.48 | 4.72 | 6.9 ± 1.3 | 2.22 | 3.22 |
| 100 °C, 40 MPa | 2.48 | 4.89 | 7.2 ± 1.1 | 2.22 | 3.36 | |
| 170 °C, 40 MPa | 2.48 | 4.83 | 6.8 ± 1.0 | 2.24 | 3.36 | |
| 210 °C, 40 MPa | 2.46 | 4.86 | 6.1 ± 1.6 | 2.18 | 3.40 | |
| Ca2+–ON | 25 °C, 0.1 MPa | 2.47 | 4.54 | 1.1 ± 1.2 | 2.22 | 3.36 |
| 100 °C, 40 MPa | 2.48 | 4.52 | 0.89 ± 0.83 | 2.22 | 3.12 | |
| 170 °C, 40 MPa | 2.51 | 4.62 | 1.1 ± 0.8 | 2.22 | 3.12 | |
| 210 °C, 40 MPa | 2.48 | 4.50 | 1.7 ± 1.6 | 2.18 | 3.32 | |
| Ca2+–N | 25 °C, 0.1 MPa | 3.66 | 5.48 | 1.0 ± 1.1 | 2.86 | 4.14 |
| 100 °C, 40 MPa | 3.16sh 3.65 | 5.27 | 0.89 ± 0.82 | 2.84 | 4.18 | |
| 170 °C, 40 MPa | 3.16sh 3.65 | 5.32 | 1.0 ± 0.7 | 2.84 | 4.18 | |
| 210 °C, 40 MPa | 3.16sh 3.63 | 5.52 | 1.5 ± 1.3 | 2.72 | 4.36 | |
| 25 °C, 0.1 MPa | 3.65 | 6.12 | 13.9 ± 1.7 | 2.88 | 4.78 | |
| N–Ow | 100 °C, 40 MPa | 3.60 | 6.18 | 14.5 ± 1.7 | 2.94 | 4.80 |
| 170 °C, 40 MPa | 3.54 | 6.28 | 13.1 ± 1.9 | 2.94 | 4.80 | |
| 210 °C, 40 MPa | 3.72 | 6.26 | 13.4 ± 2.2 | 2.82 | 4.98 | |
| Ow–Ow | 25 °C, 0.1 MPa | 2.81 | 4.66 | 6.6 ± 1.4 | 2.34 | 3.74 |
| 100 °C, 40 MPa | 2.86 | 4.70 | 7.6 ± 1.6 | 2.40 | 3.92 | |
| 170 °C, 40 MPa | 2.86 | 4.79 | 7.8 ± 1.7 | 2.44 | 4.04 | |
| 210 °C, 40 MPa | 2.84 | 4.76sh 5.72 | 8.8 ± 1.7 | 2.34 | 4.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaguchi, T.; Li, K.; Matsumoto, Y.; Fukuyama, N.; Yoshida, K. Visualization of the 3D Structure of Subcritical Aqueous Ca(NO3)2 Solutions at 25~350 °C and 40 MPa by Raman and X-Ray Scattering Combined with Empirical Potential Structure Refinement Modeling. Liquids 2025, 5, 1. https://doi.org/10.3390/liquids5010001
Yamaguchi T, Li K, Matsumoto Y, Fukuyama N, Yoshida K. Visualization of the 3D Structure of Subcritical Aqueous Ca(NO3)2 Solutions at 25~350 °C and 40 MPa by Raman and X-Ray Scattering Combined with Empirical Potential Structure Refinement Modeling. Liquids. 2025; 5(1):1. https://doi.org/10.3390/liquids5010001
Chicago/Turabian StyleYamaguchi, Toshio, Kousei Li, Yuki Matsumoto, Nami Fukuyama, and Koji Yoshida. 2025. "Visualization of the 3D Structure of Subcritical Aqueous Ca(NO3)2 Solutions at 25~350 °C and 40 MPa by Raman and X-Ray Scattering Combined with Empirical Potential Structure Refinement Modeling" Liquids 5, no. 1: 1. https://doi.org/10.3390/liquids5010001
APA StyleYamaguchi, T., Li, K., Matsumoto, Y., Fukuyama, N., & Yoshida, K. (2025). Visualization of the 3D Structure of Subcritical Aqueous Ca(NO3)2 Solutions at 25~350 °C and 40 MPa by Raman and X-Ray Scattering Combined with Empirical Potential Structure Refinement Modeling. Liquids, 5(1), 1. https://doi.org/10.3390/liquids5010001









