A Basic Approach to Equations of States for Studying the Real Behavior of Noble Gases

Abstract

The relation between the pressure and molar concentration (in mol/L) of real gases in a low- to medium-pressure range is precisely described by a logarithmic two-parameter equation. Increasing the concentration caused an increase in pressure and also the weakening of the effect due to intermolecular interactions, forming the basis for an equation with an adjusted parameter. Exceeding a critical concentration by a further increase caused a switch to another set of parameters in the same equation. At high pressure, a second switch to an exponential term was observed. This equation of state, defined segment by segment, was attributed to three different structures of the medium. The validity of the equations found was verified with experimental data reported in the literature for helium, neon, argon, krypton, and xenon and is discussed in more detail for argon. The temperature dependence of the parameters of the equations is reported and the formation of a liquid phase is discussed.

1. Introduction

The dependence of the volume of a gas (v) on pressure (p) has been of general interest for a long time [1]. Reference is made to various applications, such as the detection of the influence of intermolecular interactions. In principle, equations of states allow quantitative descriptions of such interactions. A complete absence of interactions would lead to the equation for ideal gases being supported by the kinetic gas theory and realized by highly diluted permanent gases. Real gases exhibit more complex behavior caused by noticeable interactions where suitable equations of state are still under discussion. The van der Waals equation is one of the most established; however, it requires a Maxwell construction as a further assumption to cover the two-phase region of real systems and is still under discussion [2]. This creates a general problem, as there are no analytic functions consisting of curved and linear segments. Thus, even the introduction of more parameters in more complex functions maintains them as approximations, such as in the Clausius [3], Dieterici, Redlich–Kwong [4], Redlich–Kwong–Soave [5], Peng–Robinson [6], Benedict–Webb–Rubin [7], Bertholet [8], and Wohl [9] equations. More recent concepts have applied a perturbation theory of intermolecular interactions, such as the Statistical Association Fluid Theory (SAFT), considering various types of such interactions [10,11,12,13]. A global uniform treatment of these intermolecular interactions would bring about further progress.

2. General Intermolecular Interactions

The pressure p of a gas or liquid depends on the number of particles in a volume. This is more conveniently indicated by the applied molar concentration c (the inverse of volume/mol), widely applied in chemistry. Starting from highly diluted gases with essentially independent, non-interacting particles, the pressure p is expected to be proportional to the concentration c. This results in the differential Equation (1), where const₁ is a constant for the proportionality between the effect of concentration and pressure, considering the different dimensions of c and p.

dp = const₁·dc

(1)

The intermolecular interactions of particles become increasingly important at higher concentrations of c. Only a fraction of the effects of c on p remains, whereby this becomes smaller at higher concentrations of c so that an inverse proportionality becomes an approach [14]. Accordingly, the differential Equation (2), with a different constant const₂ for proportionality, was obtained for higher concentrations.

dp = const_2/c ·dc

(2)

A scaling factor c* is defined as the shift from ideal behavior, according to Equation (1), to more real behavior in (2); for experimental verification and further details, see below. Equation (2) was divided by this scaling factor c*, multiplied by c, and added to Equation (1). A separation of variables resulted in the differential Equation (3), in which the denominator is dimensionless.

$$dp={\displaystyle \frac{{const}_1+{const}_2/c*}{\left(\frac{c}{c*}+1\right)}} dc$$

(3)

Equation (4) was obtained by integrating Equation (3) with the integration constant p_o.

$$p=(c^{*}· {const}_1+{const}_2)· \ln \left({\displaystyle \frac{c}{c*}}+1\right)+p_o$$

(4)

All constants of the pre-factor were combined to form the constant E for simplification, which characterized the energetic effect of concentration c on pressure p [E = $(c^{*}· {const}_1+{const}_2)]$) to obtain Equation (5). Finally, p_o was expected to be close to zero because of infinite diluted gases.

$$p=E· \ln \left({\displaystyle \frac{c}{c*}}+1\right)+p_o$$

(5)

Equation (5) had to be tested for practical applications. Firstly, Equation (5) was converted into the Ideal Gas Equation for diluted gases by a Taylor series expansion and truncation after the linear term, resulting in Equation (6), where c << c* and the concentration c is the number of moles n over the volume V.

$$p\approx {\displaystyle \frac{E}{\left(c+c*\right)}} · c \approx {\displaystyle \frac{E}{c*}} · c={\displaystyle \frac{E n}{c* V}} c<<c^{*}$$

(6)

This resulted in the Ideal Gas Equation (7) with R·T = E/c*.

$$p·V\approx n · {\displaystyle \frac{E}{c*}}=n · R·T c<<c^{*}$$

(7)

Secondly, the application of Equation (5) to the description of the behavior of real gases will be tested. The noble gas argon was used as a model based on the precise measurements of Michels, Levelt, and De Graaff [15] (compare also Refs. [16,17]) because its atoms form spherically symmetrical simple spheres with no tendency to form any chemical bonds. An isotherm at −120 °C, just above the critical point [18] of about −122 °C, was used for the test, since appreciable real behavior could be expected.

3. Argon

The linear correlation between the pressure p of Ar at −120 °C and the function of the concentration c represented by Equation (5) are shown in Figure 1 (performance of target to actual comparison, where r means the correlation number [19] and σ the standard deviation. r² means the measure of determination) and indicates a good accordance with the real system because of statistical scatter within the limits of experimental error. The standard deviation of 0.3 atm corresponds to a relative error of 1.6% at the medium pressure of 19.3 atm. The calculated function compared to the experimental data is shown in the inset of Figure 1. The limiting concentration c of 5.4 mol/L corresponds to a permanent contact of argon atoms (see below). The agreement of Equation (5) with the experimental data is not limited to the isotherm near the critical point, but also applies for all reported isotherms above and below the critical point: see Figure 2 where the data of all linear correlation are given in the caption.

4. Further Noble Gases

Equation (5) also applies to the other noble gases for similar concentration ranges as for the heavier noble gas krypton until 3.5 mol/L, as shown in Figure 3. The correlations according to Equation (5) are even better than for argon, where an almost ideal behavior is observed for temperatures of 200 °C and more. The even heavier noble gas xenon also fulfills Equation (5) and can be seen in Figure 4; the statistical data are given the caption.

The application of Equation (5) can be verified for the lighter neon and is shown in Figure 5; the smaller size of the atoms includes increased concentrations until 5.5 mol/L.

The application of Equation (5) can even be extended to the very light helium and is verified by a linear correlation of the precise measurement of the isotherm at 4.245 K (Leyden isotherm), see Figure 6. The application of Equation (5) to the isotherm at 4.245 K is shown in Figure 7, where the given function closely follows the experimental data. The application for even lower temperatures is shown in the inset.

5. Exceeding Limiting Concentrations

The concentration dependence of the argon pressure below the limiting concentration c of 5.4 mol/L is shown in Figure 1 and essentially corresponds to the individual movement of atoms with occasional contact with other atoms. The dependence of p on the concentration c can be realized by means of Equation (5) up to about 8.6 mol/L, as is shown in Figure 8. Exceeding this concentration leads to an abrupt change in the parameters E and c* of Equation (5) and a non-zero intercept p_o. This change is shown in Figure 8 by the solid curve up to 8.6 mol/L and the dotting continued in the extrapolation to higher concentrations. The function for higher concentration corresponds to the experimental data up to 18 mol/L and is indicated by the solid curve and the dashed extrapolation to higher concentrations. For even higher concentrations, the pressure p increases exponentially with the concentration c, according to Equation (8), with the parameters E and p_o and the intercept p*.

p = p_o·e^E·c + p*

(8)

No further deviations were found. The isotherms of argon for lower temperatures were investigated to obtain more information, since the influence of the interactions on p is significantly stronger, as is shown in the inset of Figure 8. Equations (5) and (8) are valid for the entire range of measured temperatures from 25 until −140 °C and cover even the range below the critical point of −122.3 °C for both monophasic branches; detailed information on the parameters of Equations (5) and (8) as well as statistical data can be found in

Table 1. Parameters of Equation (5) (region i and ii) and Equation (8) (region iii) for argon. E, p_o, p* and σ in atm, c* in mol/L. Nine points for the correlation numbers r in region (i) except six for −135 °C and seven for −140 °C; seven points for the correlation numbers r in region (ii) and (iii). E and c* were divided by 10 000 000 for better visualization.

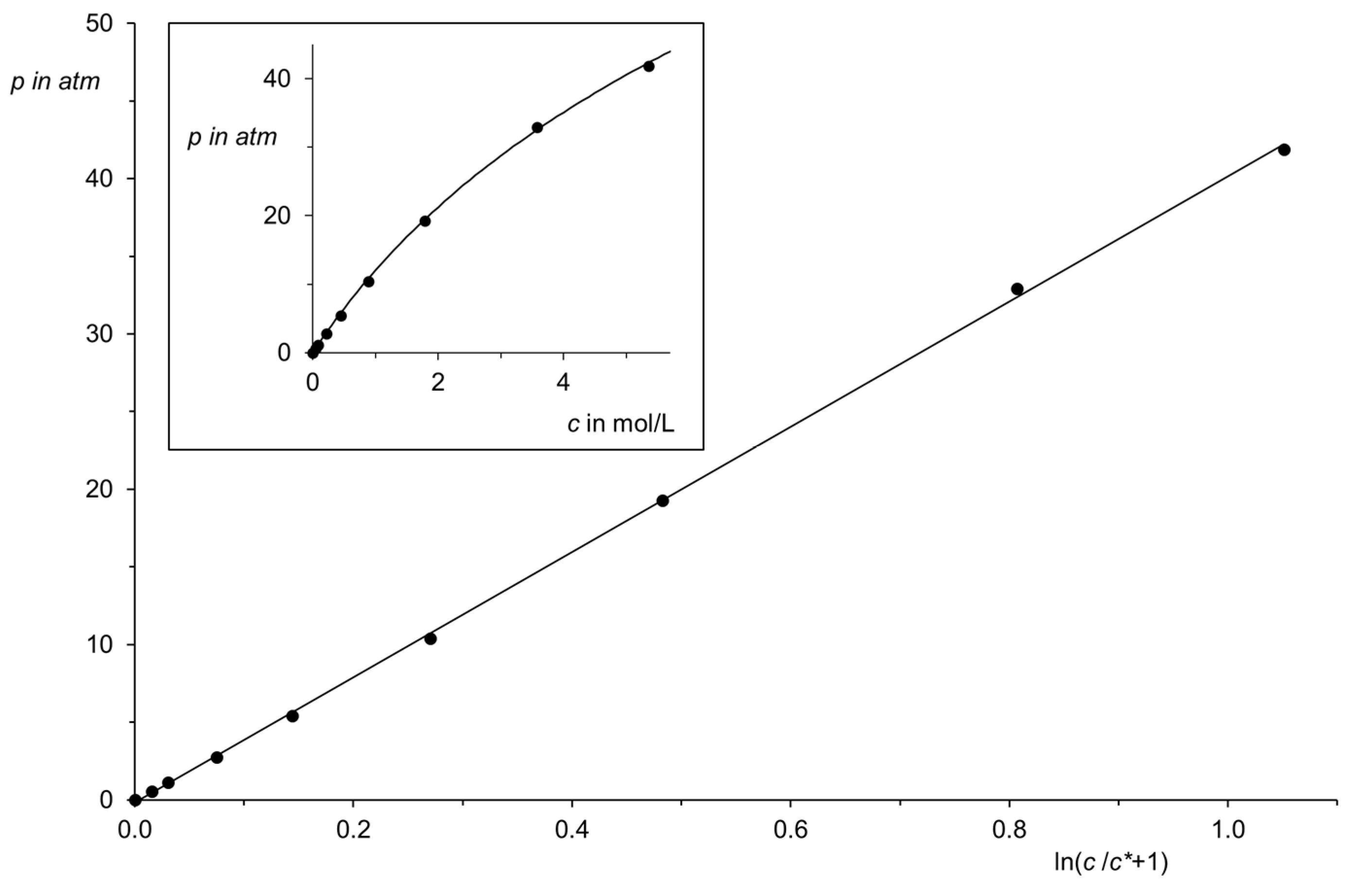
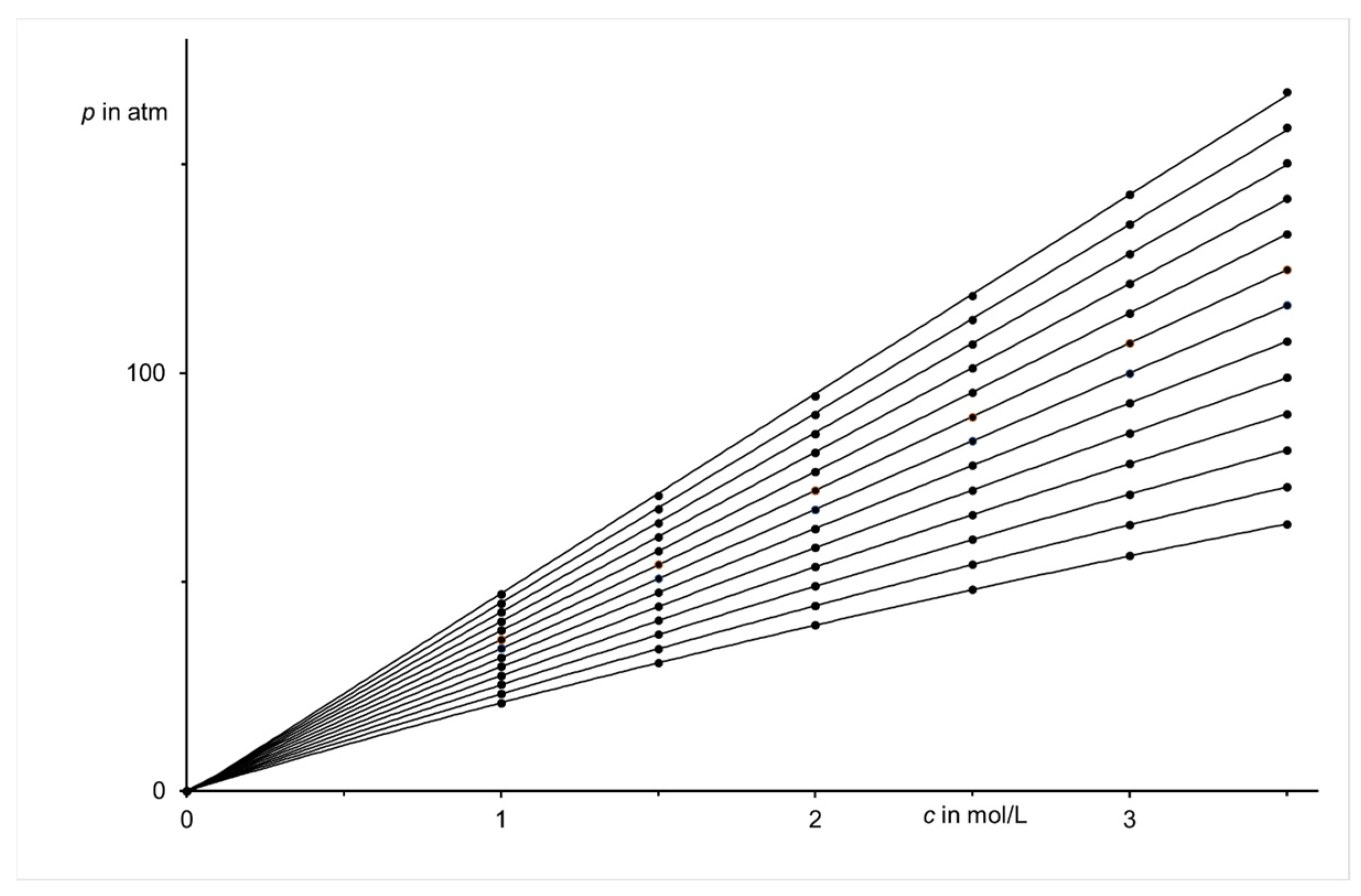
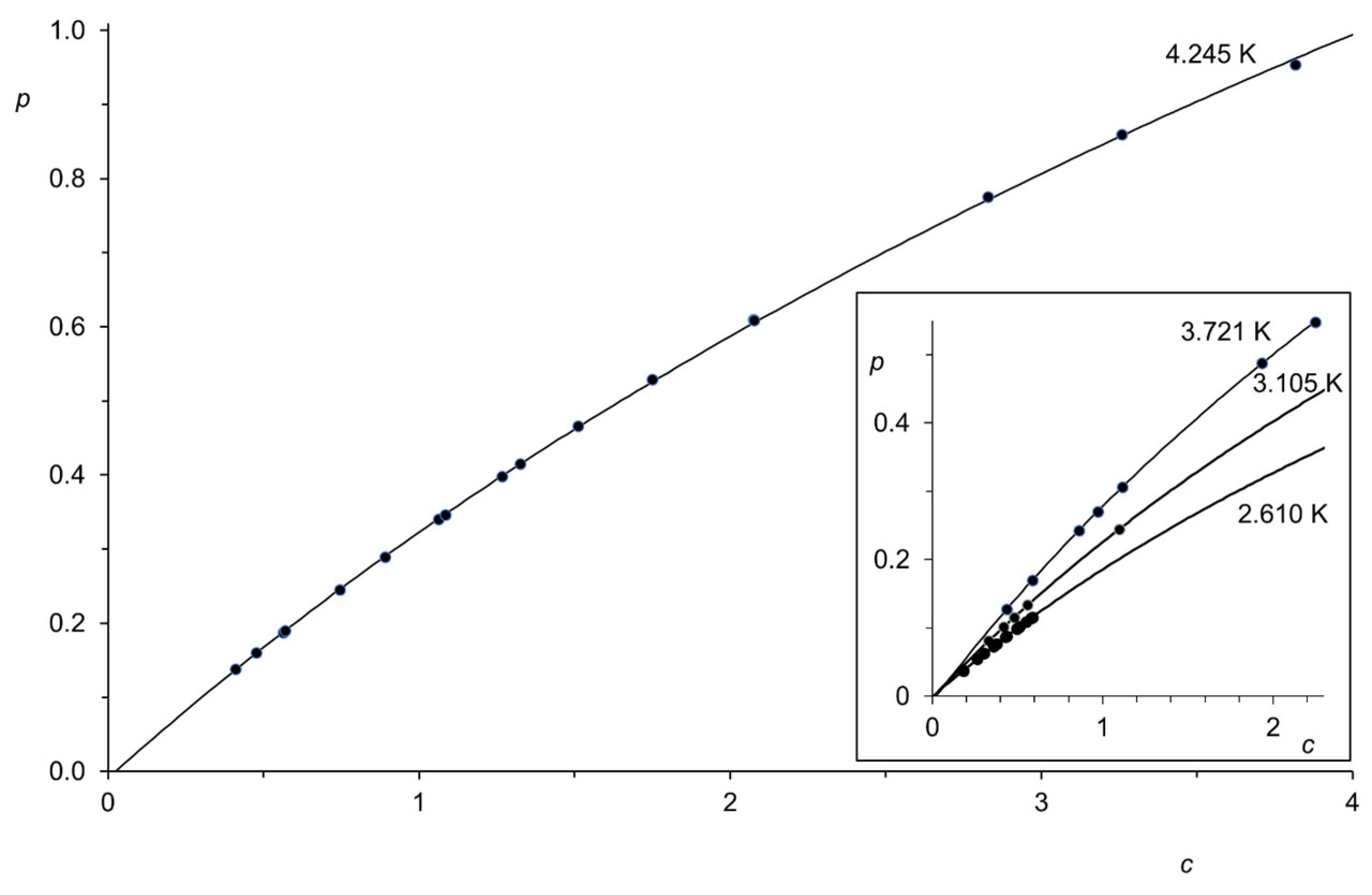
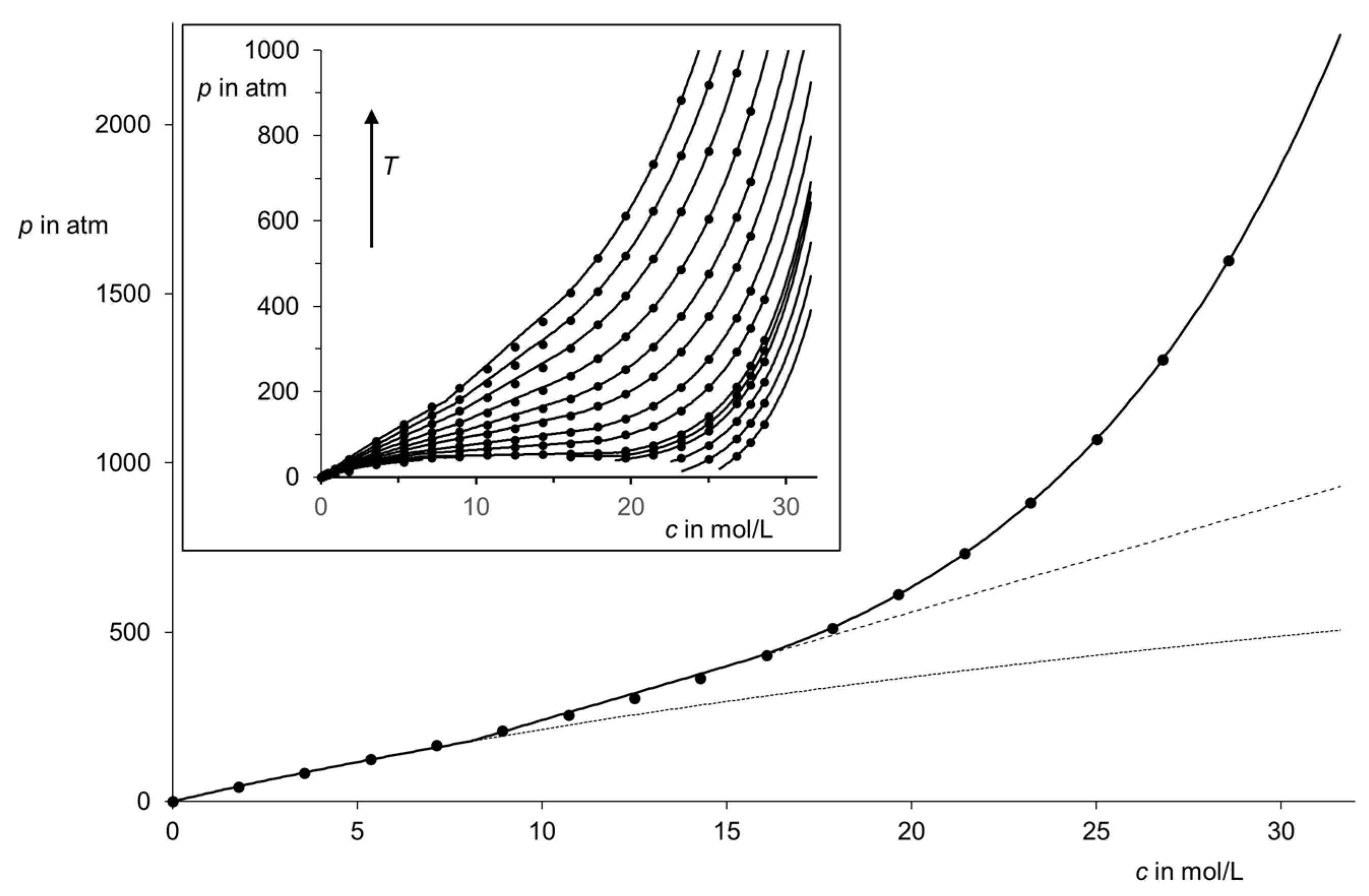
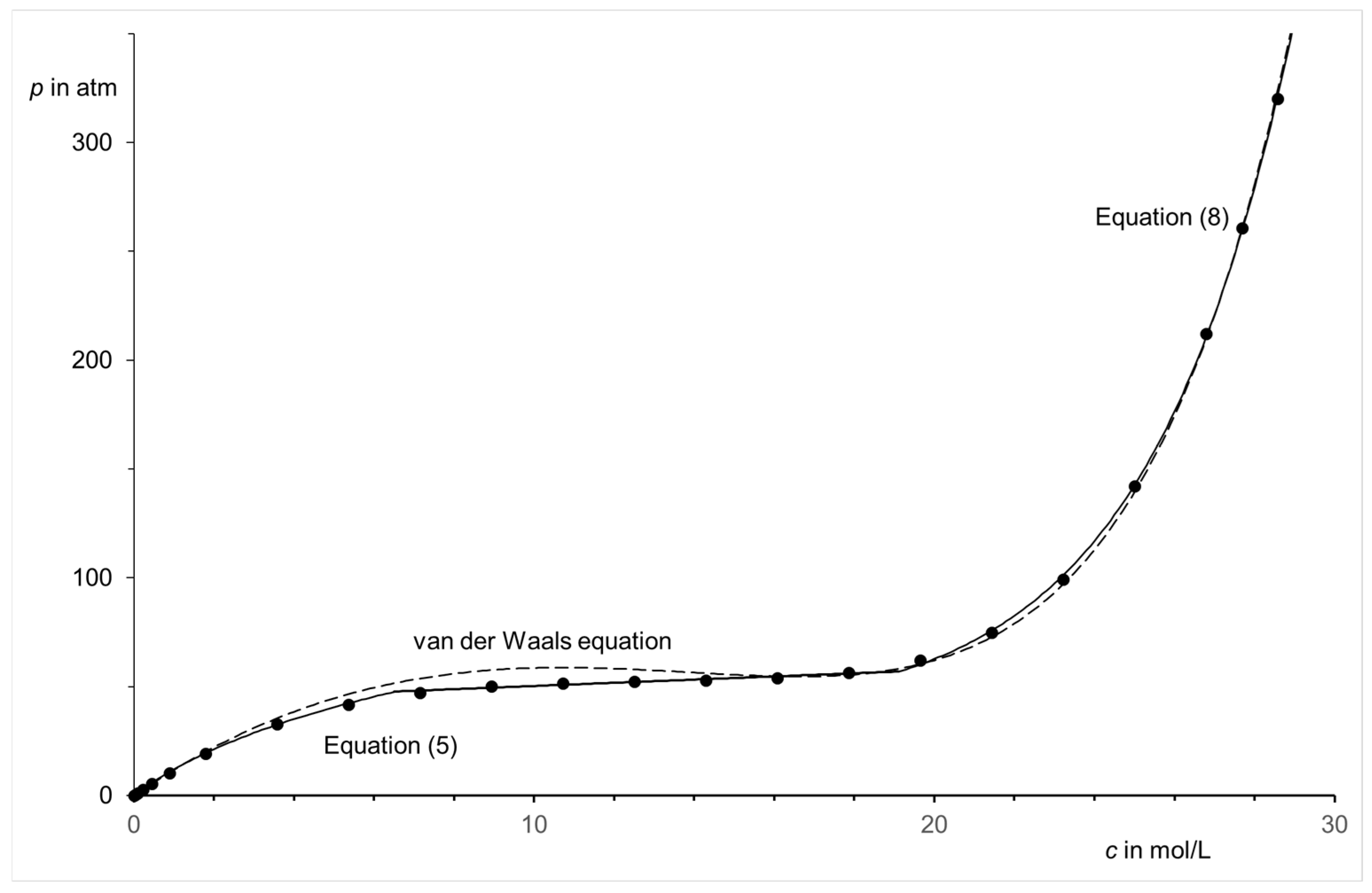
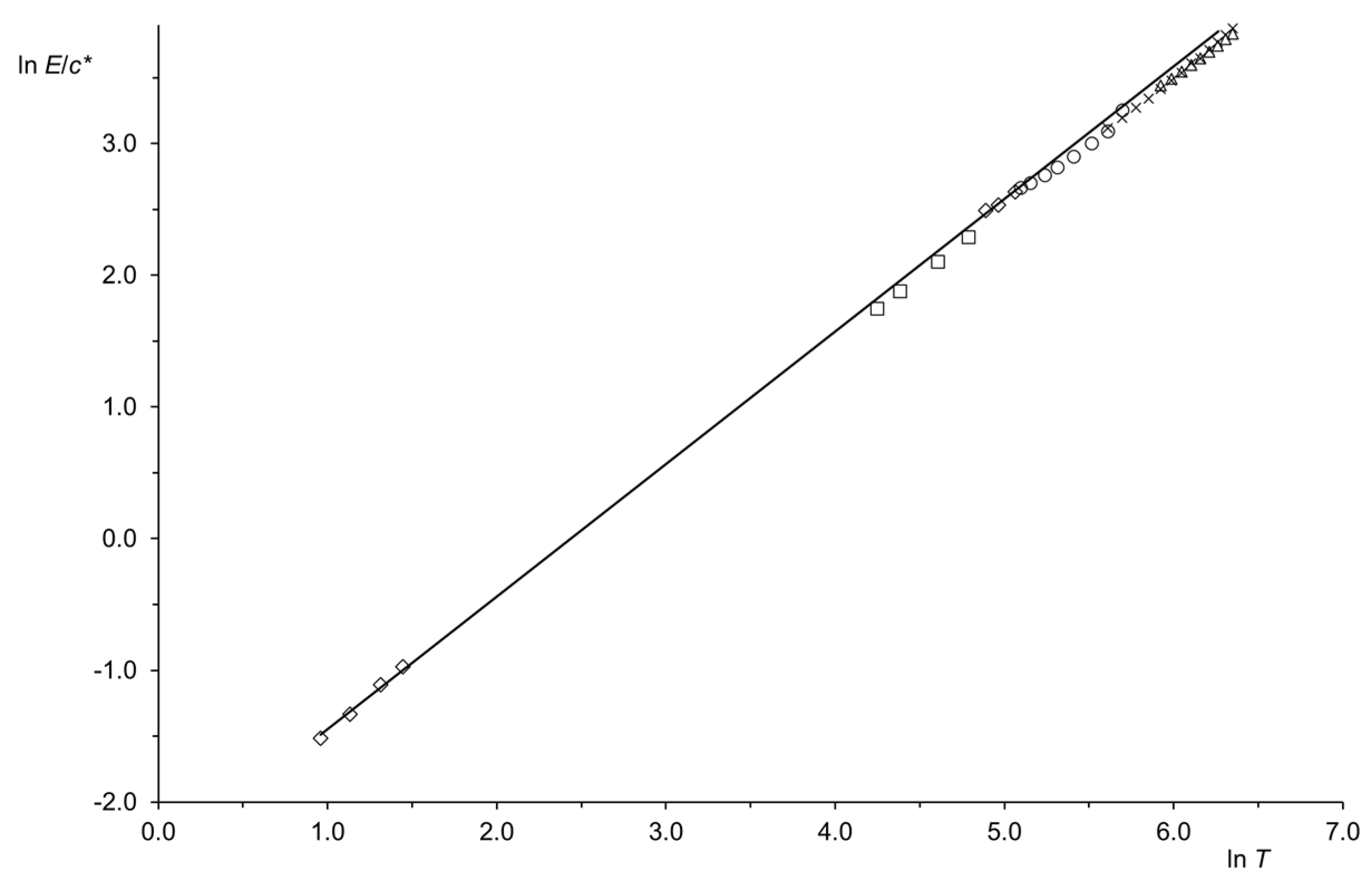
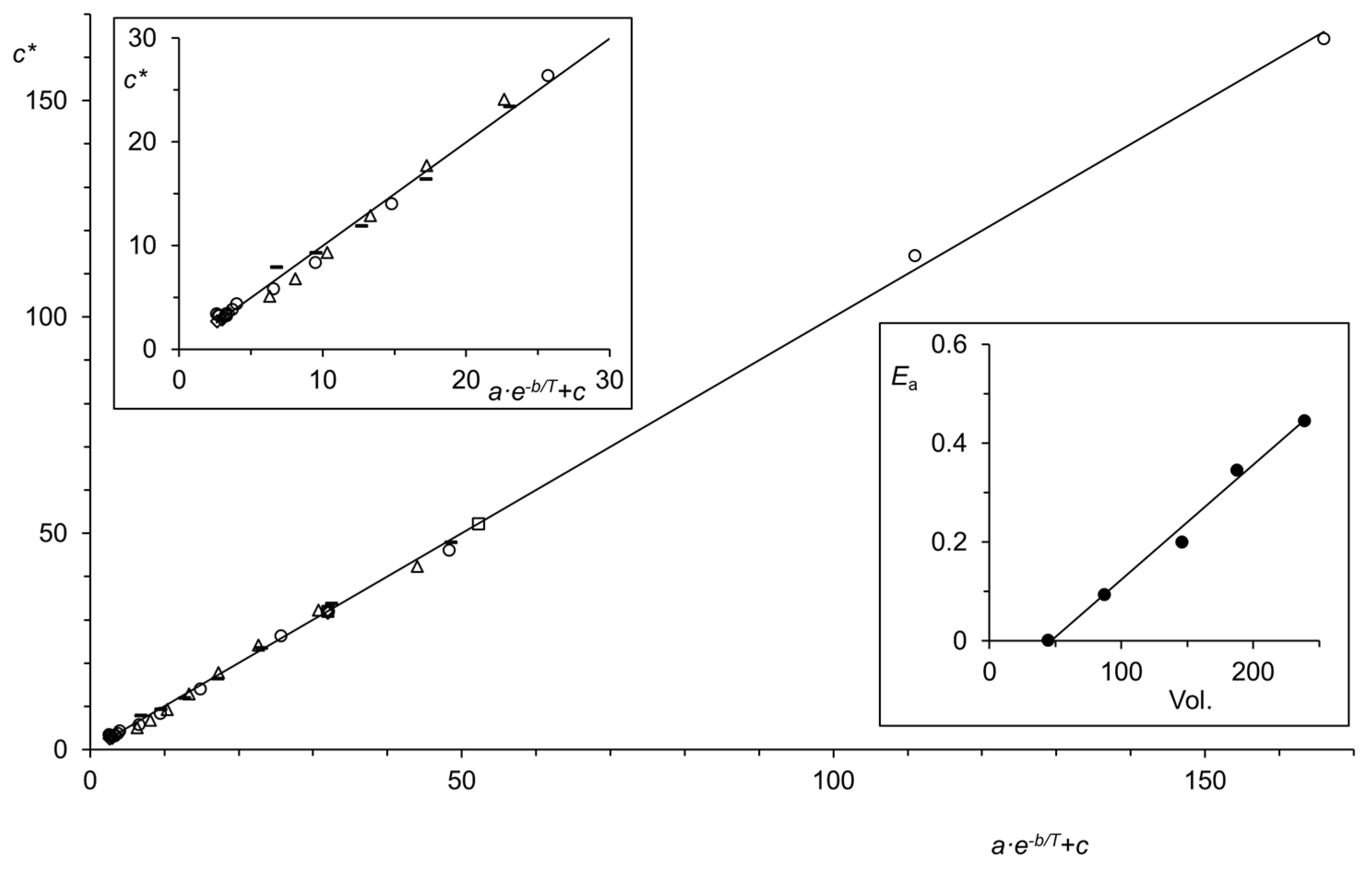
	Region (i)					Region (ii)					Region (iii)
T in °C	E	c*	po	r	s	E	c*	po	r	s	E	p*	po	r	s
25	564.9	21.8	−0.931	0.9997645	1.42	907.9	28.4	−79.2	0.993	15.6	43.35	0.123	121.4	0.9999998	0.2
0	791.3	35.8	0.055	0.9999980	0.08	795.6	29.9	−57.5	0.993	12.9	29.75	0.131	126.4	1	0.1
−25	439.2	21.8	0.037	0.9999987	0.06	601.0	28.4	−35.6	0.993	10.3	18.32	0.142	127.0	0.9999999	0.1
−50	250.7	13.7	0.012	0.9999997	0.02	445.6	28.4	−13.5	0.994	7.5	9.79	0.156	119.0	0.9999999	0.1
−70	158.7	9.45	−0.017	0.9999997	0.02	321.0	28.4	4.1	0.994	5.3	5.02	0.172	105.3	0.9999993	0.2
−85	110.1	6.97	−0.049	0.9999958	0.07	240.0	29.9	17.1	0.994	3.7	2.45	0.190	92.0	0.9999974	0.4
−100	74.1	4.98	−0.092	0.9999773	0.14	143.1	29.9	29.4	0.995	2.1	0.88	0.217	73.6	0.9999904	0.6
−110	55.5	3.86	−0.129	0.9999399	0.21	80.7	29.9	36.9	0.994	1.2	0.41	0.237	54.4	0.9999529	1.3
−120	40.3	2.88	−0.178	0.9998387	0.30	22.5	30.8	43.0	0.970	0.8	0.11	0.275	35.6	0.9998646	1.8
−122.5	36.9	2.65	−0.193	0.9997909	0.33	9.4	30.8	43.5	0.915	0.9	0.07	0.287	30.4	0.9998158	2.0
−125	33.8	2.43	−0.209	0.9997282	0.36						0.04	0.302	25.1	0.9997335	2.2
−130	27.9	2.00	−0.246	0.9995254	0.44						0.05	0.296	−2.1	0.9999351	0.9
−135	19.5	1.67	−0.005	0.9999901	0.02						0.04	0.301	−27.0	0.9999923	0.3
−140	36.3	3.25	−0.015	0.9999958	0.02						0.03	0.300	−57.5	1	0.0

.

The application of Equation (5) and (8), respectively, was compared with the well-established van der Waals equation p = n·R·T/(V-n·b) − a·n²/V²) where p means the pressure, V the volume, n the moles, T the absolute temperature, and R the universal gas constant. a and b are adjustable coefficients. The van der Waals equation was transformed to use the concentration c = n/V to obtain p = c·R·T/(1-c·b) − c²·a. The parameters a and b were adapted to the experimental values of the isotherm at −120 °C by means of the least squares, as is shown in Figure 9. The segmental adaptation using Equations (5) and (8) (solid curves) gives appreciably better results than the van der Waals equation (dashed curve).

The results shown in Figure 8 are interpreted in relation to the atomic contacts. At low concentrations, there are only random sporadic interactions between the particles, which can essentially still enable their free movement. As the concentration increases, the distance between the particles decreases until permanent contact is achieved and a comparably abrupt transition to a changed structure of the medium occurs. The concentration c_k(i–ii) of about 8.62 mol/L observed for this transition corresponds to a cube of 5.78 Å for the volume for one atom. The statistical average distance [27,28] is smaller by a factor of about 0.55 and is 3.20 Å; this indicates an effective diameter of one argon atom. A further increase in the concentration c reduces the distance between the particles more and more until a dense packing at c_k(ii–iii) of 18 mol/L is achieved; this corresponds to a cube of 4.52 Å for one atom. The most dense are hexagonal or cubic faced packings. Thus, a dense cubic-face-centered packing can be used for an approximation to c_k(ii–iii) where the lattice constant is larger by a factor of √2 than the interatomic distance so that 3.19 Å is obtained; this is in good agreement with the distance 3.20 Å found for c_k(i–ii).

For comparison, the reported [29] van der Waals radius for argon of 1.88 Å gives a diameter of 3.76 Å for argon atoms. This value is in acceptable agreement with the distance of 3.2 Å found, for which the application of a completely different model has to be considered.

A further increase in concentration c results in a strong repulsion of the electron shell of the atoms, verified by the exponential Equation (8) and the right branch in Figure 8, with a strong increase in pressure p.

6. The Two-Phasic Region

Figure 8 represents the isotherm of argon at 25 °C, which is appreciable above the critical point of 150.87 K and −122.28 °C, respectively. Similar isotherms are obtained for lower temperatures up to the critical point; see the inset of Figure 8 and Table 1. Even below the critical point, Equations (5) and (8) can be applied to the branches in region (i) with low concentration and region (iii) with high concentration, indicating a generally similar behavior of the medium. The formation of two phases is interpreted as limited miscibility of the two structures of the medium, the densely packed arrangement in region (iii) and the less densely arrangement in region (i) and (ii), respectively. As a consequence, a surface between these phases is formed which is characterized by the surface tension. The surface tension between these structures decreases with increasing temperatures and vanishes at the critical point.

7. Isotherms of Other Noble Gases

Isotherms similar to those interpreted for argon were found for the other noble gases. The critical concentration c_k(i–ii) of krypton was found at about 5.0 mol/L and corresponds to the larger dimension of krypton atoms, while xenon reaches the transition at 3.2 mol/L. The smaller homologue neon requires 15 mol/L. The relative concentrations of transition are approximately proportional to the relative volume of the elementary cells of crystalline noble gases because they present the volumes of the atoms and are given in Figure 10 (all noble gases form cubic face centered crystal lattices). The c_k(i–ii) value of helium can be estimated from the lattice constant of crystalline material by extrapolation and would require more than 30 mol/L and a very high pressure, respectively.

The c_k(i–ii) values of argon were only slightly temperature-dependent, as shown in the inset in Figure 10; the concentration may be essentially determined by the atomic dimensions of argon. There was a sufficiently large experimental basis for the determination at various temperatures, where there seems to be a slight increase at lower temperatures. However, considerable experimental uncertainties stand in the way of an exact determination.

8. The Temperature Dependence of Parameters

A linear temperature dependence of the quotient E/c* is to be expected according to Equation (7) based on the comparison of the coefficients with the equation of ideal gases. To check this, the ln E/c* of the experimental values were plotted against ln T in Figure 11. Slopes were found close to 1. The slope of 0.939 was found for argon for region (i) above the critical point (see Figure 11); the slope decreases slightly to 0.87 with stronger scattering of the points when lower temperatures are included. The slope for the heavier Kr was 1.022 and for Xe 0.922. Similar results were obtained for the less heavy Ne of 1.01 and for He of 1.007. The approximation to the slope to 1 is remarkable because this means an extrapolation to ideal gases from dense gases with strong real behavior.

The temperature dependence of the parameter c* is completely different from the quotient E/c* as there is initially a strong increase with the temperature and finally a plateau is reached at very high temperatures. The primary increase can be described by an Arrhenius diagram, which is shown in Figure 12. Remarkably, the data for all noble gases cover the same linear correlation. Apparently, activation is involved in the atomic interactions where the activation energy (E_a) can be calculated from the Arrhenius diagram (b/R) and is 1.8 J/mol for He, 95 J/mol for Ne, 201 J/mol for Ar, 346 J/mol for Kr, and 447 J/mol for Xe. These small values of activation energy correspond approximately to the volume of the elementary cells of crystalline noble gases, as can be seen in the inset lower right in Figure 12. This could be due to the fact that the electron shell becomes softer as the diameter of the atoms increases, allowing more interactions at atomic contacts.

9. Conclusions

The concept that the pressure of gases increases with the concentration, where the increase is gradually damped by intermolecular interactions, led to a logarithmic two-parameter equation for pressure and concentration. A continuous increase in the concentration led to a critical concentration bring exceeded with a switch to a second set of the parameters for the same equation. A further continuous increase in concentration causes a second critical value and switch to an exponential dependency of the pressure on concentration. This was verified by experimental data for the noble gases He, Ne, Ar, Kr, and Xe. The behavior was interpreted in terms of three different structures of media in which (i) at low concentrations only random contacts exist, which (ii) after exceeding a critical concentration form a structure with permanent contacts, and which (iii) after exceeding a second critical concentration form densely packed particles with increasing repulsion of the electron shell. No further change could be detected (it would be of interest whether the exponential Equation (8) remains suitable for extremely high pressure). The formation of liquid phases was attributed to a limited miscibility of structure with free particles and densely packed particles. Investigation of the temperature dependence of the parameter yielded the law for ideal gases at high dilution and a verification of the Arrhenius equation for the critical concentration c* of the two-parameter equation. This was interpreted as a contribution of an activated process to the temperature dependence of parameters, whereby only small activation energies of a few to several hundred J/mol were found. The activation energies correlate linearly with the volume of the elementary cells of crystalline noble gases, indicating the importance of increasing size-dependent softening of the atoms for their interaction.

The developed equations for the state of gases and liquids can be useful for determining the concentration of gases by pressure measurements [30], whereby the high precision of the developed equations is of particular advantage.