Abstract
Catalan’s SPPN, a measure of solvent polarity/polarizability has been analysed in terms of molecular properties derived from computational chemistry. The results show that SPPN correlates positively with the molecular dipole moment and quadrupolar amplitude and negatively with the molecular polarizability. These correlations are shared with Kamet and Taft’s π* and Reichardt and Dimroth’s ET(30). Thus, one can associate the solvent polarity with non-specific interactions involving the permanent charges on solvent molecules. It is also noted that the opposite correlations, all three parameters increasing with increasing solvent polarity but decreasing with increasing solvent polarizability, creates an ambiguity in their use, for example, in linear free energy relationships.
Keywords:
solvent parameters; polarity; polarizability; ET(30); Catalan SPP; computational chemistry 1. Introduction
Understanding and predicting the effects of changes in solvent on chemical processes are among the classical problems of solution chemistry. Thus, virtually all thermodynamic, kinetic and spectroscopic properties of chemical systems are sensitive to changes in the solvent, some changing by orders of magnitude.
The use of linear free energy relationships to explore or predict the effect of changes in solvent on chemical processes is well established. The principle is straightforward and one writes:
where SP is some property, such as the log of the solubility of a solute, the Pi are experimental parameters reflecting properties of the solvent (or solute) and that ci are coefficients reflecting the response of the solute (or solvent). In effect each ciPi term represents the effect of a different intermolecular interaction on SP.
Generally the parameters Pi are derived from experiments that are designed to isolate a particular interaction. In general Pi values represent specific, acid–base interactions: (1) the basicity of the solvent (Kamlet and Taft’s β [1], Catalan’s SB [2], Gutmann’s DN [3]); (2) the acidity of the solvent (Kamlet and Taft’s α [4], Catalan’s SA [5], Gutmann’s AN [3]) or non-specific interactions that are collected together in parameters that are measures of the polarity/polarizability of the solvent (Kamlet and Taft’s π* [6], Catalan’s SPP [7], Reichardt and Dimroth’s ET(30) [8]).
The range of experimental parameters raises several interesting questions, including (1) the extent to which these parameters simply reflect properties of the solvent molecules, (2) which molecular properties contribute to the experimental parameters and (3) whether different parameters, for basicity say, reflect the same molecular properties.
These have been explored in a series of papers where experimental parameters have been correlated with a set of molecular properties derived from computational chemistry. These have shown that measures of solvent basicity (β, DN [9] and SB [10]) reflect the partial charge on the most negative atom of the solvent molecule and the energy of the donor orbital, while measures of the solvent acidity (α [11], AN and SA [10]) reflect only the partial charge on the most positive hydrogen atom of the solvent molecule.
In the present paper, a similar analysis of Catalan’s SPPN, a measure of solvent polarity and polarizability, is reported and the results compared to those reported previously for Kamlet and Tafts’s π* and Reichardt and Dimroth’s ET(30) [12,13].
2. Methods and Materials
2.1. Computational Details
The computational methods have been discussed in some detail previously [9,11,12,13]. Since the calculated molecular properties can depend on the method used, calculations were carried out using both the Hartree–Fock and density functional (B3LYP functional) methods using the 6-311+g(3df,2p) basis set. For the molecular dipole moments, quadrupolar amplitudes and polarizabilities, plots of the values calculated using the two methods against each other are linear and so the choice of method is immaterial [9]. This isn’t the case for orbital energies, for which such plots show scatter around a straight line [9]. The situation for partial atomic charges is more complex, since these are not quantum mechanical observables and require a model that ascribes the electronic charge density to the individual atoms. Partial charges based on Mullican’s model are highly dependent on the basis set and appear not to converge as the basis set is increased. Those based on the Hirshfeld [14], Natural bond order [15] and the CM5 [16] model do converge as the basis set is improved [9] and all have been used previously. It was fond that the Hirshfeld and NBO models gave very similar results [12] and, in a recent paper considering Abraham parameters it was recognized that the CM5 model overestimates the partial charges on nitrogen atoms, for amides at least [17]. Thus the analyses reported here use partial charges derived using Hirshfeld’s model.
All calculations were carried out using the Gaussian 9 software [18].
2.2. Analyses of Parameters
As in previous work, the normalized parameter, SPPN in this case, has been considered. The use of normalized scales allows relatively direct comparison of the results of the analyses. Values of SPPN were taken from [7].
The approach used is a simple [9], multivariable regression of the experimental parameter, P, against molecular descriptors, Qi, representing different molecular properties. Thus:
where P0 is the value of P when all of the aiQi terms are zero and the ai are the coefficients recovered from the regression. In essence each aiQi term represents the contribution of a particular interaction to P.
The molecular descriptors are normalized and calculated from the calculated molecular properties, qi, as:
where and are the minimum and maximum values of . With the exception of the orbital energies, the values of are taken to be zero.
Seven molecular properties: the partial charges on the most negative atom and on the most positive hydrogen atom, the molecular dipole moments, quadrupolar amplitudes (see Appendix A) and polarizabilities and the energies of electron donor and acceptor orbitals are considered. In general, the orbital energies are taken to be those of the highest occupied and lowest unoccupied molecular orbitals; the exception to this is the case of solvents with aromatic groups. This was discussed previously [9] but, briefly, solvents with a common functional group have, for example, similar basicity parameters, whether they are aliphatic or aromatic, although for aromatic solvents, the high energy π-bonds of the aromatic ring are clearly the HOMOs, while for aliphatic solvents the HOMO is associated with the basic functional group. The fact that the basicity parameters are similar argues for the use of the energies of the orbitals at the interacting functional group rather than those of the aromatic ring.
In applying Equation (1), the experimental parameter, P, was initially correlated with all seven molecular descriptors; subsequently, descriptors making negligible contributions (typically ai ≤ 0.03) or with standard deviations comparable to the value of the coefficient, were excluded and the correlation repeated with the remaining descriptors. Since both the calculated properties and experimental parameters for solvents with a common functional group are similar, the distributions of these can’t be represented by statistics based on the normal distribution. Thus, the decision as to whether a descriptor was making a significant contribution to P was decided on the basis of the increase in the standard deviation between the calculated and experimental values of P, when the descriptor was excluded from the correlation.
3. Results
Catalan’s SPPN is based on the differences in the solvatochromism of 2-(dimethylamino)-7-nitrofluorine and its homomorph, 2-fuoro-7-nitrofluorine (Figure 1), which show similar solvatochromism with that of 2-(dimethylamino)-7-nitrofluorine being substantially larger. This assumes that specific interactions, such as hydrogen bonding to the NO2 moiety will be removed by the subtraction, leaving only effects from solvent polarity and polarizability.
Figure 1.
Structures of 2-(dimethylamino)-7-nitrofluorine and 2-fuoro-7-nitrofluorine.
In the analysis of SPPN polychlorinated alkanes, flexible esters and pyridine were outliers and were excluded from the analysis. The analyses showed that only three solvent molecular properties: the dipole moment, quadrupolar amplitude and polarizability, showed significant correlations with SPPN. The coefficients recovered from the analyses are listed in Table 1. Also listed in Table 1 are the corresponding coefficients for Kamlet, Abboud and Taft’s π and Reichardt and Dimroth’s normalized . The SPPN values calculated using the coefficients in Table 1 and solvent descriptors, Qi, recovered from properties calculated using the density functional method are compared with experimental values in Figure 2 (the dashed lines are one standard deviation above and below the line representing perfect agreement); the plot using properties recovered from Hartree–Fock calculations is similar. The values for pyridine (brown circle below the line) and the polychloroalkanes (grey triangles) are included in Figure 2.

Table 1.
Comparison of the ai values for Catalan SPP, Kamlet, Abboud and Taft’s π* and Reichardt and Dimroth’s .
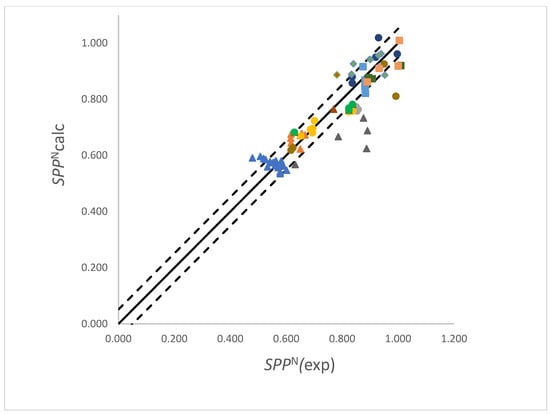
Figure 2.
Comparison of the experimental SPPN values and values calculated using the coefficients in Table 1 (for density functional calculations). The symbols represent: blue triangles, alkanes; dark grey triangles, chloro-alkanes; orange triangles, aromatics; yellow circles, ethers; green circles, nitriles; light grey circles, alcohols; brown circles, amines and pyridine; dark blue circles, esters; light blue squares, ketones; grey diamonds, amides; beige squares, S=O and P=O compounds. The solid line represents perfect agreement and the dashed lines are 1 standard deviation above and below this.
The values for the esters provide a cautionary example for the use of computational methods. For rigid molecules the molecular properties recovered from computational calculations are essentially determined by the method and basis set but for flexible molecules the properties may also vary depending on the assumed molecular structure. This was discussed previously [12] with regard to the variation of calculated properties of carboxylic acids with rotation around the C−OH bond of the acid group. It was found that the dipole moments and quadrupolar amplitudes of the acids depended strongly on the conformation but that the other properties did not. It was also found that all molecular properties were relatively insensitive to coiling of the alkyl chain of longer chain carboxylic acids.
In the case of the esters, the O=CR−O moiety will be planar while rotation around the C−O bond is relatively free. The variations in the calculated molecular properties with rotation around the C−O bond are shown, as normalized molecular descriptors, in Table 2; also shown are the corresponding SPP values calculated using the descriptors and the coefficients reported in Table 1.

Table 2.
Solvent descriptors a for esters with different molecular geometries.
Again, it can be seen that, while the variations are much smaller than those for the carboxylic acids, it is only the dipole moments and quadrupolar amplitudes that vary significantly with rotation around the C−O bond while the other molecular properties are relatively constant.
Results for methylsalicylate are included in Table 2, since rotation of the benzene ring progressively moves the O−H in the 2 position on the benzene ring away from the C−O−C oxygen to the C=O oxygen. In this case, the dipole moment essentially doubles between the 0° and 180° rotamers but, in the calculation of SPPN, this is almost exactly compensated by the corresponding increase in the quadrupolar amplitude.
4. Discussion
Like SPPN, both π* and show positive dependences on the solvent dipole mements and quadrupolar amplitudes and a negative dependence on the solvent molecule’s polarizability. Each, however, shows an additional contribution.
In the case of , the additional contribution is from the charge on the most positive hydrogen atom on the solvent molecule and reflects hydrogen bonding at the pendant oxygen atom of the betaine dye used to define the scale. Of course, this is well known and was used by Kamlet and Taft to define their α scale of hydrogen bond acidity [4].
The reason for dependence of π* on the energy of the electron donor orbital of the solvent molecule is less clear. Both Catalan and Kamlet and Taft considered the possibility of hydrogen bonding to the NO2 group on the aromatic probe molecules, but if this were the case one would expect a correlation with the charge on the most negative atom of the solvent molecule, which is the dominant contribution to measures of hydrogen bond basicity (Kamlet and Taft’s β [9,12], Gutmann’s donor number [9], Abraham’s B [17] and Catalan’s SB [10]).
Leaving these aside, it is interesting that all three parameters show positive correlations with the solvent’s molecular dipole moment and quadrupolar amplitude and a negative correlation with the solvent molecule’s polarizability.
Since these are intended as measures of a solvent’s polarity and polarizability, it is reasonable to associate the polarity with the dipole moment and quadrupolar amplitude. That is, the polarity is related to the intensity of the permanent charges imbedded in the solvent.
The basis of solvent parameters based on solvatochromism is that the equilibrium solvation of the ground state interacts with the excited state of the probe (By the Franck–Condon principle, the time scale of the electronic transition is vastly less than the time scale of molecular motions, so that, initially, the excited state interacts with the ground state solvation shells.) and so, if, for example. the excited state of the probe has greater charge separation than the ground state (This situation leads to an inverse relationship between the solvent parameter and the energy of the electronic transition; that is, the larger the energy gap the smaller the solvent parameter. The reverse situation, where the ground state has greater charge separation leads to a direct relationship; that is, to parameters that increase as the transition energy increases.), it will interact more strongly with the surrounding solvation shells, lowering the excitation energy.
It is implicit in the design of all based on solvatochromism, that all solute–solvent interactions will be stronger with the form of the solute with the greatest charge separation. This assumption is generally found to be correct; thus, basicity scales are positively correlated with the partial charge on the most negative atom and the energy of the donor orbital [9,10,12,17] and acidity parameters are positively correlated with the partial charge on the most positive hydrogen atom [10,11].
As is clear from Table 1, the polarity/polarizability parameters show positive correlations with the dipole moment and quadrupolar amplitude, measures of the intensity of charges imbedded in the surrounding solvent, but negative correlations with the molecular polarizability of the solvent. That is, increasing polarizability leads to decreases in SPPN, π* and .
The expectation that polarizability should correlate positively with these experimental parameters essentially arises from the assumption that charge–induced dipole interactions will dominate. However, solvent molecules may also interact with the probe molecules by London forces, in which case the stronger interaction is likely to be with the form with the lower charge separation, the ground state in the above case, where the excited state has the greater dipole moment. The observed negative correlation between SPPN, π* and the polarizability of the solvent molecules, argues that this latter interaction dominates.
Whatever the explanation, SPPN, π* and all show the same negative correlation with the solvent molecular polarizability, which makes their use in linear free energy relationships problematic. Thus, solvents with equal values of SPPN, for example, can have quite different polarizabilities, compensated by differences in the dipole moments and/or quadrupolar amplitudes.
5. Conclusions
The analysis of SPPN shows that, like Kamlet and Taft’s π* and Reichardt’s , shows positive correlations with the molecular dipole moment and quadrupolar amplitude of solvent molecules and a negative correlation with the molecular polarizability.
Since these parameters are measures of the solvent polarity and polarizability it is reasonable to ascribe the solvent polarity to the permanent charges on the solvent molecules. In the approach used here, the dipole moment and quadrupolar amplitude are used as measures of the intensity of these charges. Thus, the solvent polarity is determined by the permanent charges in the solvent molecule and acts by non-specific interactions of these permanent charges with permanent charges on the solute. In contrast, solvent polarizability is determined by the polarizability of the individual solvent molecules and involves interactions with the non-polar parts of the solute through London forces.
It seems surprising that these experimental parameters reflect London rather than the expected charge/dipole–induced dipole interactions. However, the experimental parameters are based largely on probe molecules containing one or more aromatic rings, generally one for π* [6], two for SPPN [7] and six for [8], and so are likely to interact well through London forces.
The observation that the polarity and polarizability act on the experimental parameters in opposite directions, increasing polarity increasing the values of the parameter while increasing polarizability decreases the values creates an obvious difficulty in the use of these parameters in linear free energy relationships, for example.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
The quadrupolar amplitude is calculated as I = x, y, z and j = x, y, z, where the qij are the components of the traceless quadrupole. Complex charge distribu-tions, such as those of polyatomic molecules, are commonly represented by a series of superimposed point objects. The first is a point charge (the net charge), which is a scalar quantity, the second is the dipole, which is a vector and the third is the quadrupole, which is a tensor. Just as the dipole has no net charge, the quadrupole has no net moment. The dipole moment and quadrupolar amplitude are used here simply as quantitative measures of the scale of charge centers imbedded in the bulk solvent, the “intensity” of embedded charges. The simplest way to see the necessity for both the dipolar and quadrupolar contributions is to consider CO2, which, despite having partial charges on the O and C atoms has a zero dipole moment, but a nonzero quadrupolar amplitude.
References
- Kamlet, M.J.; Taft, R.W. The solvatochromic comparison method. I. The β-scale of solvent hydrogen-bond acceptor (HBA) basicities. J. Am. Chem. Soc. 1976, 98, 377–383. [Google Scholar] [CrossRef]
- Catalán, J.; Díaz, C.; López, V.; Pérez, P.; de Paz, J.-L.G.; Rodriguez, J.G. A generalized solvent basicity scale: The solvatochromism of 5-nitroindoline and its homomorph 1-methyl-5-nitroindoline. Liebigs Ann. 1996, 1996, 1785–1794. [Google Scholar] [CrossRef]
- Gutmann, V. Empirical parameters for donor and acceptor properties of solvents. Electrochim. Acta 1976, 21, 661–670. [Google Scholar] [CrossRef]
- Taft, R.W.; Kamlet, M.J. The solvatochromic comparison method. 2. The α-scale of solvent hydrogen-bond donor (HBD) acidities. J. Am. Chem. Soc. 1976, 98, 2886–2894. [Google Scholar] [CrossRef]
- Catalán, J.; Díaz, C. A generalized solvent acidity scale: The solvatochromism of o-tert-butylstilbazolium betaine dye and its homomorph o,o′-di-tert-butylstilbazolium betaine dye. Liebigs Ann. 1997, 1997, 1941–1949. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Abboud, J.L.; Taft, R.W. The solvatochromic comparison method. 6. The π* scale of solvent polarities. J. Am. Chem. Soc. 1977, 99, 6027–6038. [Google Scholar] [CrossRef]
- Catalán, J.; López, V.; Pérez, P.; Martín-Villamil, R.; Rodriguez, J.G. Progress towards a generalized solvent polarity scale: The solvatochromism of 2-(dimethylamino)-7-nitrofluorene and its homomorph 2-fluoro-7-nitrofluorene. Liebigs Ann. 1995, 1995, 241–252. [Google Scholar] [CrossRef]
- Dimroth, K.; Reichardt, C.; Siepmann, T.; Bohlmann, F. Über pyridinium-N-phenol-betaine und ihre verwendung zur charakterisierung der polarität von lösungsmitteln. Justus Liebigs Ann. Chem. 1963, 661, 1–37. [Google Scholar] [CrossRef]
- Waghorne, W.E.; O’Farrell, C. Solvent basicity, a study of Kamlet–Taft β and Gutmann DN values using computationally derived molecular properties. J. Solution Chem. 2018, 47, 1609–1625. [Google Scholar] [CrossRef]
- Waghorne, W.E. Solvent Acidity and Basicity Scales: Analysis of Catalan’s SB and SA scales and Gutmann’s Acceptor Number and Comparison with Kamlet and Taft’s β and α Solvent Scales and Abraham’s B and A Solute Scales. 2024, in preparation. 2024; in preparation. [Google Scholar]
- Waghorne, E. A Study of Abraham’s effective hydrogen bond acidity and polarity/polarizability parameters, A and S, using computationally derived molecular properties. J. Solution Chem. 2023. [Google Scholar] [CrossRef]
- Waghorne, W.E. A study of Kamlet–Taft β and π* scales of solvent basicity and polarity/polarizability using computationally derived molecular properties. J. Solution Chem. 2020, 49, 466–485. [Google Scholar] [CrossRef]
- Waghorne, W.E. A study of the Reichardt parameter using solvent molecular properties derived from computational chemistry and consideration of the Kamlet and Taft α scale of solvent hydrogen bond acidities. J. Solution Chem. 2020, 49, 1360–1372. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Foster, J.P.; Weinhold, F. Natural hybrid orbitals. J. Amer. Chem. Soc. 1980, 102, 7211–7218. [Google Scholar] [CrossRef]
- Marenich, A.V.; Jerome, S.V.; Craner, C.J.; Truhlar, D.G. Charge Model 5: An extension of Hirshfeld population analysis for the accurate description of molecular interactions in gaseous and condensed phases. J. Chem. Theory Comput. 2012, 6, 527–541. [Google Scholar] [CrossRef] [PubMed]
- Waghorne, W.E. A study of the Abraham effective solute hydrogen bond basicity parameter using computationally derived molecular properties. J. Solution Chem. 2023, 51, 1133–1147. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; Nakatsuji, H.; Caricato, M.; Li, X.; et al. Gaussian, 9th ed.; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).