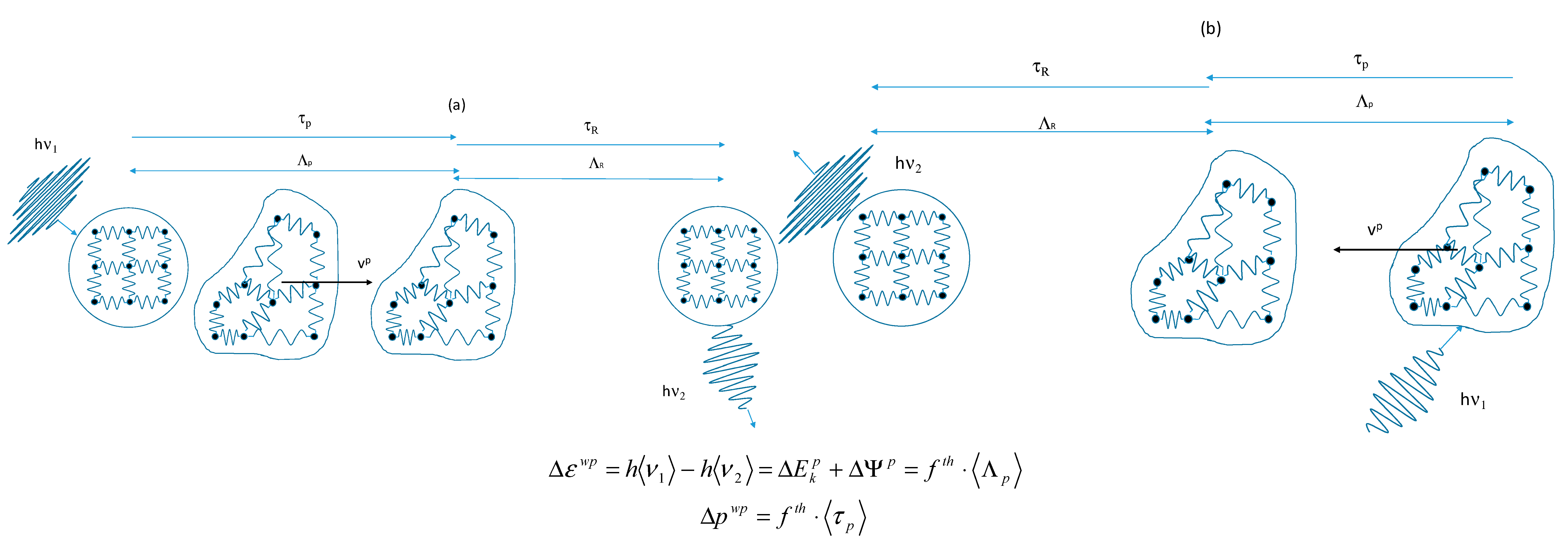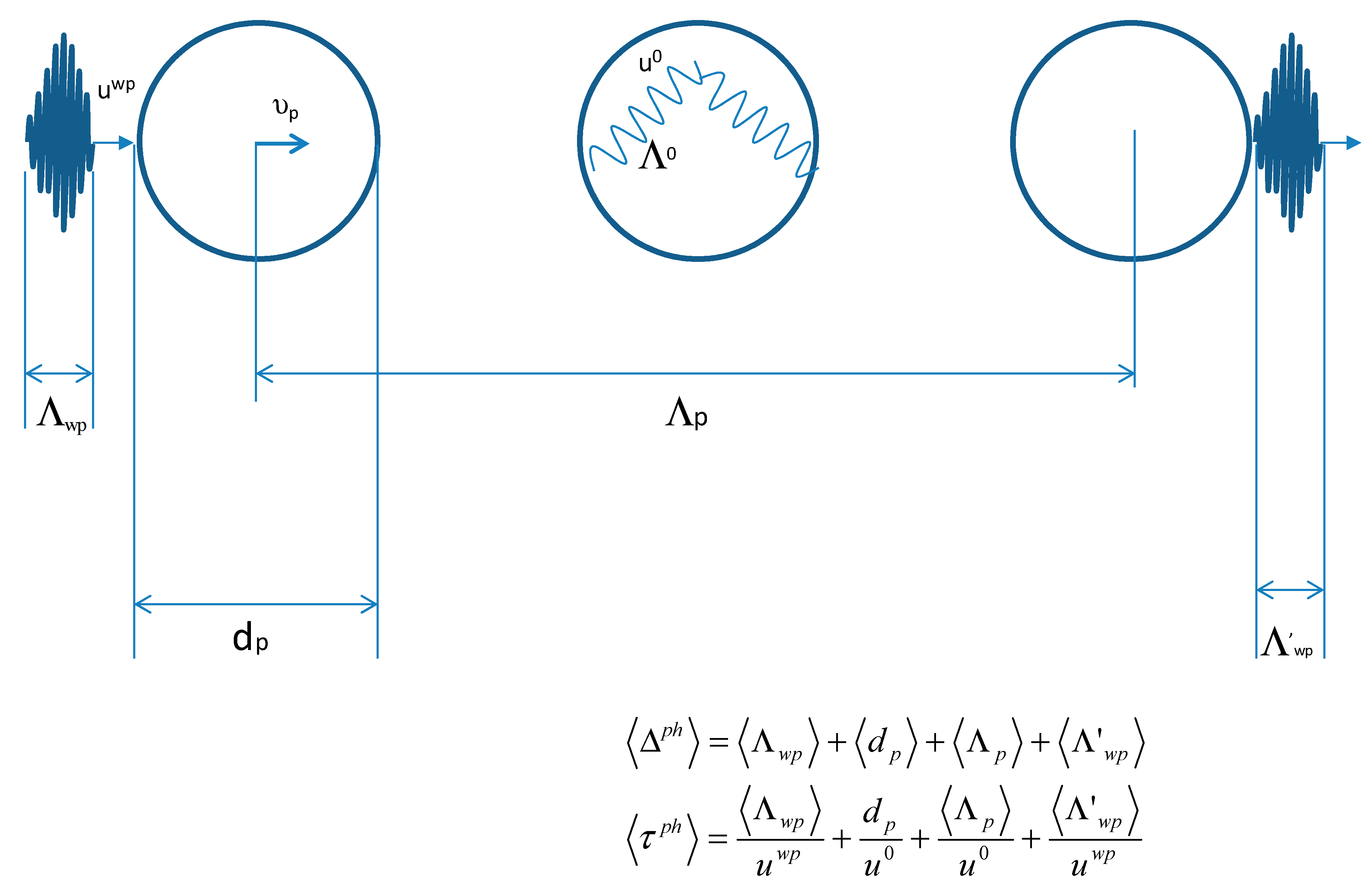1. Introduction
The paradox of the equations that describe the diffusion of energy, mass, or something else in physics has been known for some time now [
1,
2,
3,
4,
5,
6]. This paradox consists in the fact that the equations which mathematically describe the diffusion, those of the parabolic type (e.g., Fourier, Fick, Dufour), are characterized by an infinite diffusion velocity: if, at the initial instant, there is a disturbance on one edge of the system, this disturbance is instantaneously present “at the same time” in every other point of the system, although with different intensity. This paradox, as is also known, is due to the fact that the parabolic equations normally used to describe the phenomenon of propagation of signals in material media are rather suitable to describe the phenomenon of diffusion, and as such are strictly valid only in stationary conditions, i.e., when every transient effect has been overcome in the dynamics of the system at microscopic level. It is also well known that the hyperbolic-type equations are among those suitable for describing the propagation of mass and/or energy in a material medium even in the transient phase. In fact, these equations, also known as the “telegrapher’s equations” [
7,
8], when the proper initial and boundary conditions are given, provide solutions that have an initial undulatory nature without back front, present only in the transient, and become then of diffusive type, or parabolic, when the observation time of the phenomenon is much longer than the transient characteristic time, making the memory term negligible. Hyperbolic equations indeed allow to correctly describe those systems characterized by a “memory effect”, i.e., traditionally those for which the response to a thermodynamic force is subsequent to the application of the force.
The physical reason for the above resides in the fact that the equilibrium state is not achieved instantaneously because thermal energy is carried microscopically by molecular interactions and proceeds with a finite velocity. The classical Fourier law describing heat conduction
has the characteristic of instantaneity. In Equation (1),
Jq is the heat flux,
K is the thermal conductivity and
T is the temperature. Equation (1) contains the information asserting that if a uniform temperature gradient is established throughout a homogeneous fluid, then the heat flow is everywhere and every time proportional to the temperature gradient. Equations such as (1) are very common in Irreversible Thermodynamics [
9] because they express the Onsager’s theory property that the response of a system to an applied force is
simultaneous with the application of the force [
10,
11]. As a general rule, such
simultaneity in a macroscopic theory turns out to be an approximation to a
causal behavior, where the response to a force comes
after the application of the force. To account for the
causality behavior, it is necessary to modify the equation for heat conduction to take into consideration a relaxation time,
τ, not present in Equation (1).
Cattaneo [
1] was the first to propose that a term linear in the derivative of the heat flux be added to Fourier law to account for the relaxation behavior. In this way, he obtained a hyperbolic equation in the form of the so-called “telegrapher equation”. Few years after Cattaneo, Vernotte [
2,
3] proposed the same equation to remove the paradox, although the term was added by him ad hoc into the Fourier equation on a pure mathematical basis. Whatever of the two formalisms is taken as example, that of Cattaneo or that of Vernotte, what matters is that Nettleton [
12] has demonstrated that (i) the telegrapher equation may be viewed formally, from the point of view of the Onsager Irreversible Thermodynamics [
10,
11], as a force-flux equation linking two irreversible processes, and (ii) a linear relaxation equation for liquids is consistent with the assumption that thermal energy is carried by elastic waves of very high frequencies. Very interestingly, Nettleton uses the Debye/Brillouin model for heat conduction [
13,
14,
15,
16], although he voluntary neglects the shear waves due to the supposed smallness of their contribution to the total balance.
The mechanism classically believed to occur at the base of heat conduction in fluids is that of molecular collisions: the thermal energy content is distributed among molecules proportionally to their degrees of freedom (DoF); the higher the energy content, the higher the number of DoF excited. By applying a heat flux to one edge of a fluid medium, the energy transferred to the system is distributed to the molecules from the hot to the cold side by means of avalanches of energetic particles that redistribute the excess of thermal energy by means of collisions. However, such a mechanism has a weak point just in the quasi-instantaneous character of the collision among molecules, making the identification and the calculation of the relaxation time a hard exercise. In addition, it does not provide the physical mechanism requested for the telegrapher equation to work.
In a series of recent papers [
17,
18], we have presented a model of organization of the liquid state at mesoscopic level, dubbed Dual Model of Liquids (DML); it was even applied to calculate several liquid specific quantities, in particular the thermal conductivity, the order-of-magnitude of the relaxation times governing the interaction process and the liquid specific heat, finding good correspondence with the experimental data and with other theoretical model. In few words, DML assumes that liquid molecules are arranged at mesoscopic level on solid-like local lattices. Propagation of perturbations occurs at characteristic timescales typical of solids within these local domains of coherence, while mutual interactions of local clusters with inelastic wave packets allow exchanging energy and momentum with them. The liquid is then a Dual System, the two subsystems being the
liquid particles—i.e., the clusters of molecules—and the
lattice particles—i.e., the wave packets (through the manuscript, we will use the terms lattice particle, wave packet, phonon, collective excitation on one side, or liquid particle, molecular cluster and iceberg on the other, interchangeably, as synonyms). The purpose of the present work is to show that if the propagation of heat in liquids is due to the mutual interactions of these two subsystems constituting the liquid, it is suitably described by a Cattaneo-like equation. Indeed, it is just the presence of two interacting populations to justify the presence of the relaxation term in the equation for heat transport that we propose to be linear as well in the relaxation time as early proposed by Cattaneo and Vernotte. The tunnel effect characterizing the interaction and the interaction itself are the physical mechanisms allowing for the interpretation of the heat transport to be of a dynamical nature, thus excluding also the dilemma of infinite diffusion velocity. The additional time derivative term characterizing the hyperbolic equations originates in the energy balance equation where the intrinsically negative term
τ ∂Jq/∂t is added to the Fourier law:
It accounts for that part of the energy temporary stored in the system for the time interval τ, i.e., the relaxation time, in a non-propagating form. During such time lapse, the linear relationship between the heat flux and the temperature gradient does not hold (even if the presence of τ·∂Jq/∂t makes Jq and ∇T no more proportional everywhere and every time).
The problem is certainly not new, with many texts and scientific works written about it (see
Section 2). However, they have mainly been focused on the mathematical problem, only estimating, on the one hand, the extent of the “delay” in the propagation of the signal, i.e., the relaxation time, and on the other assuming that there should be a mechanism of “inelastic” type at its base. Nevertheless, the most important ingredient to complete the recipe has always been lacking, namely the identification of such a physical mechanism underlying the propagation phenomenon and therefore capable of allowing a calculation of relaxation times on a physical basis at the mesoscopic level. It is precisely in this framework that this work is placed, by providing the missing link through the DML.
Another important aspect correlated with the use of hyperbolic equations typical of systems made of two interacting subsystems is the emergence of a gap in the momentum space, usually known as the “
k-gap” or
Gapped Momentum States (GMS) [
19,
20,
21,
22]. We will show that the DML is even characterized by a
k-gap, whose importance is crucial in the identification of the relaxation times typical of a dual system [
17]. Recently, a thorough analysis has allowed to recognize also the presence of a Gapped Energy States (GES) in dual systems [
23].
In the following sections, although what was stated is equally valid both for mass or energy propagation, reference will preferentially be given to energy propagation in the form of heat. The term “propagation” is used here to specify that the equation (and the phenomenon) that we deal with is of hyperbolic “propagation” type instead of the classical parabolic “diffusive” one. In addition, effects due to internal friction among molecules such as viscosity are neglected because the system is supposed at rest and in a stable configuration to avoid convection; the presence of external field force that may couple with the temperature gradient giving rise to convection is not considered as well. In the same way, any effect of thermal expansion is also not considered. DML is in fact not a macroscopic model of liquids, but rather a micro/mesoscopic model aimed at modeling the energy and momentum exchange between molecules and lattice in a liquid matrix on the base of experimental evidence. Finally, dispersionless systems are considered for simplicity, and any variation with temperature or pressure of the several quantities is neglected.
The paper is organized as follows.
Section 2 is dedicated to an historical excursus of the adoption and modifications of the equation for the heat conduction.
Section 3.1 is dedicated to a brief recall of the DML (the complete description is available elsewhere, [
17,
18]).
Section 3.2 is dedicated to the derivation of the heat propagation equation in the form of the Cattaneo equation. In particular, the physical meaning of the relaxation time characteristic of the
lattice particle ↔
liquid particle elementary interactions of DML is discussed. In the
Section 4, the consequences of the approach are illustrated as well as the physical interpretation of the several parameters characterizing the heat propagation equation. Finally, in the
Section 5, future developments of the DML are anticipated.
2. Historical Background
The history of Fourier law modification is very long; without claim to completeness, it could be interesting to bring to light the most salient points of the slow rise to prominence of the most widely used modification in mathematical physics, namely that of the Cattaneo equation, or of the use of an equation with a linear term in the first-time derivative of the heat flux in general. Still, currently, the most referenced source, which collects most of the developments of the phenomenon of heat propagation (or diffusion), is represented by the two reviews by Joseph and Preziosi [
5,
6], which the reader is referred to if interested in detailed historical developments.
As historical note, the telegrapher equation was officially proposed for the first time by Oliver Heaviside [
24,
25]. His formulation of the telegrapher’s equations became commercially important during his own lifetime, after their significance went unremarked for a long while. The telegrapher’s equations are actually two coupled differential equations describing current and voltage in an electric line with distributed loads. Interestingly, it is believed that W. Thomson first, and Kirchhoff [
8] later, wrote the telegraph equation before Heaviside; both were, in fact, very active in the effort to lay the trans-Atlantic telegraph cable as commitment to the UK government. Heaviside sometime later was the first to realize that physical constants could be adjusted to eliminate the dispersion on the transmission line.
The telegrapher equation was obtained [
1,
2,
3,
4,
26,
27] or used [
28,
29,
30,
31,
32,
33] by many authors in the past to describe the heat conduction in liquids. In the same way, many authors [
30,
31,
32,
33] have studied the diffusion of “something” in condensed media, but they were usually interested in the behavior in stationary conditions, so the paradox of the infinite velocity of energy diffusion has never emerged and discussed at physical level before Cattaneo. If the first to explicitly highlight the paradox was Cattaneo in his 1948 article, the same issue was apparently addressed independently by Morse and Feshbach [
34]. Surprisingly, the telegrapher’s equation was, however, obtained for the first time by J.C. Maxwell [
26] to describe the diffusion of heat in a material medium. Because he was interested in the diffusion phenomenon, he voluntarily did not consider the term containing the time derivative with the justification that “The first term of this equation may be neglected, as the rate of conduction will rapidly establish itself” (see [
26], page 86 after Equation (143), and [
27]). For this reason, no attention was paid to its importance in describing the diffusion process in its initial stages (as is known, the same equation can also be used to describe the diffusion of matter and not only of energy, giving rise to the Fick’ equation). Maxwell was certainly right in his assumption; nevertheless, his approach contributed to keeping the issue hidden for quite a long time afterward.
Einstein, in his 1905 articles on Brownian motion [
31,
32], starting from a thermodynamic–statistical approach, establishes the relations that describe the diffusion coefficient in terms of known parameters of a solution; he is not concerned with the transient phase, but once again demonstrates that his model leads to the classical equation of steady-state diffusion.
In the early 1920s, Taylor [
33] tackled the mathematical model of diffusion. He also deduces the classic Fick equation since his goal is, once again, to describe the diffusion of particles at equilibrium, starting from a “discrete” model of the way in which each individual particle advances.
To highlight the absurdity of the infinite velocity of propagation, Cattaneo [
1] refers his analysis to the Boltzmann’ description [
27] of a diffusive process. Cattaneo introduces the concept of correlation between collisional events for the first time, and defines the relaxation time <
τC> in connection with the collision integral of the system, doing so to demonstrate that the equation that correctly describes the diffusion is the one that will then take his name, and that he himself defines as an equation with “memory”. Solutions of the hyperbolic equation for heat transport predict a phenomenology of the diffusive type, after an initial short-lived undulatory phase consisting in a wave propagation with velocity
(see Equation (37)). However, no hint on the physical nature of these waves comes from the Cattaneo approach, although by digging into the depths of the literature, one can discover that already in 1946 Peshkov [
35] had hypothesized that in low-temperature liquids, “a gas of thermal quanta capable of performing vibrations similar to those of sound should exist”.
The inconsistency of the Fourier’ law with the Irreversible Thermodynamics was already highlighted by Onsager [
10] (page 419) because of the lacking of an acceleration term. A theory in which a “thermal inertia” is postulated is due to Kaliski [
36], who generalized the Onsager relations and arrived at a telegraph equation after some simplifications. In 1951, Goldstein [
28] retrieved Taylor’s results [
33] and Boltzmann’s approach [
27], and proceeded, like Maxwell [
26] and Cattaneo [
1], to write a “telegrapher’” equation (without and with leakage) to describe the heat diffusion also in the transient phase.
It is also interesting to highlight that the various authors mentioned above did not have a clear and full vision of the works of all their predecessors. Goldstein, for example, cites only Taylor in his work, and seems to ignore those of Maxwell, Boltzmann and Cattaneo. Cattaneo expressly cites Boltzmann’s work, reusing it also in part, but ignores that of Maxwell. Boltzmann himself does not mention Maxwell’s work in the literature of his book.
In 1958, Grad [
37] unearthed the additional time derivative term (see Equation (15)) plus a number of other corrections to the Fourier law. In 1963, M. Chester [
29] resumed Maxwell’s work, and he was the first to quote both Vernotte [
2,
3] and Cattaneo [
4], but only the 1958 work of the latter (written in contrast to first Vernotte’s paper) and curiously not the original one [
1]. In his interesting paper on the relaxation theory for thermal conduction in liquids, Nettleton [
12] seems to know only the two papers by Vernotte, although he is well aware of the pioneering works by Frenkel [
38], Brillouin [
16] and Lucas [
39]. Chester nevertheless uses Cattaneo’s results to demonstrate that in dielectrics, or in solids without free electrons, there is a relationship between the speed of propagation of thermal energy deduced from the coefficients of the equation and that of phonons, a relationship for which he provides a precise theoretical justification. In fact, Chester went much deeper in his reasoning about the heat propagation in condensed media. He indeed pointed out that the presence of “second sound” [
40] in solids was due to the presence of phonons in the medium. Consequently, if second sound was foreseen and then revealed in HeII [
41,
42], it could be detectable also in other media in which propagation of elastic and thermal energy was due to phonon propagation, such as non-metallic solids, as well as liquids. The difference with HeII could only be the presence of a critical frequency for the appearance of second sound.
In 1982, Coleman, Fabrizio and Owen [
30], in dealing with the consequences of using the Cattaneo equation to describe the propagation of the second sound in crystals, correctly quoted Maxwell [
26], Cattaneo [
1] and Chester [
29]. Joseph and Preziosi [
5,
6] collected in their articles a wide bibliography dedicated to the implications deriving from the various diffusive and propagative models. Very recently, Ozorio Cassol and Dubljevic [
43] compared parabolic and hyperbolic partial differential equations for heat diffusion. They cite both the 1958 work of Cattaneo [
4] and that of Vernotte [
2]. In this frame, it is important to mention also the paper by Gandolfi et al. [
44], who provided an empirical solution to the paradoxical instantaneousness of the heat equation called Dual-Phase-Lag (DPL) model.
A paper by Nettleton [
45] deserves special mention; in it, the author deals with the density fluctuations in pure liquids by modeling the heat flux as made by two components, one carried by sound waves of very high frequency like elastic waves in a solid,
ψ1, and the other by molecules,
ψ2, so that
q =
ψ1 +
ψ2. Both
ψ1 and
ψ2 will each obey a relaxation equation relating the time derivatives
ψi (
i = 1,2) to
ψi and ∇
T. At this point, the author claims that the inertia of molecules justifies the fact that a sudden appearance of a temperature gradient will initially affect only
but not
ψi. Then he builds a very general relaxation equation that he uses to obtain the density fluctuation and temperature-dependence in the system. What matters of this approach is that i) Nettleton assumes the liquid thermal content as made of two components, and that ii) these two components interact among themselves in a similar way to the two-field potential representing displacements and velocities,
ϕ1 and
ϕ2, introduced in Equation (30), or, alternatively, the two sub-systems described by Equation (31).
4. Discussion
Let us first point out that, as is well known, Equation (15) is a truncated form of a more extensive expression which includes pressure and density spatial variations of the several quantities present in it and that may be derived from kinetic theory in the case of an ideal gas [
26,
27,
28,
33]. In addition, many additional terms are present in the complete form if one considers the spatial variations of mechanical properties of the medium. These corrections, however, are not germane to the matters which follow, so they have been ignored as specified in the
Section 1 (they should be taken into account in a careful treatment dealing with a practical experimental situation).
Equation (15) is the simplest equation combining diffusion and waves, obtaining energy propagation. In addition, and this is not secondary, it allows for dissipation to take place. Its meaning is well known: it states that there is a physical mechanism by means of which energy is not freely flowing through the liquid, but is temporarily subtracted for a time <
ϑ>; this effect has an influence during the transient phase but not at the steady state (although still present at microscopic level), because it becomes irrelevant when a time interval larger than <
ϑ> has elapsed. Hence, <
ϑ> represents the finite build-up time for the onset of a thermal current once a temperature gradient is applied to a system. The heat flow does not start instantaneously but rather grows gradually with the delay time <
ϑ>. Conversely, if a thermal gradient is suddenly removed, there is a lag in the disappearance of the heat current, and Equation (15) exhibits just such a delay, whereas the classical Fourier diffusive equation does not [
43]. To the best of the author’s knowledge, in the present manuscript, it is shown, for the first time, that in DML that is a dual system the interaction represented in
Figure 1 allows to build a Cattaneo-type equation for the heat diffusion in liquids. The additional term in such equation is now supported just by the energy exchange mechanism shown in
Figure 1 between particles and phonons, the latter being the carriers of elastic (thermal) energy, and not added ad hoc as in the past. It accounts for the energy stored in non-propagating form. The combination of Cattaneo Equation (11) with the energy conservation Equation (14) provides a hyperbolic Equation (15), namely the telegraphist equation, whose solutions are in line with the phenomenology observed in liquids. The presence of the two interacting populations,
lattice particles and
liquid particles, justifies the presence of the relaxation term in the equation for heat transport (11) that we have even proposed to be linear in the relaxation time. These interactions are characterized by a (classic) tunnel effect which is the physical mechanism allowing the interpretation of the heat transport to be of a dynamical nature, thus avoiding the dilemma of infinite diffusion velocity. Incidentally, the fact that the tunnel effect produces a mesoscopic lattice redistribution of the energy content is reminiscent of the Interstitial Theory of Granato [
63] for the liquid specific heat. In his model, Granato determined that the linear temperature-dependent component of the specific heat at low temperature is identified as occurring due to the interstitialcy tunneling between different orientations of the interstitialcies themselves.
Very recently, Gandolfi et al. [
44] pointed out the attention to the Cattaneo–Vernotte equation solving the paradox of infinite velocity proposing the DPL model. Comparing Equation (15) of the present paper with Equation (4) of that paper, the time lag there is reminiscent of the relaxation time causing the memory term here.
Further discussing Equation (15), it is interesting to note that the quantity
is the fraction of the heat flux carried by wave packets transformed into energy of molecular modes of the
liquid particles; dividing it by
uwp, we obtain the momentum flux
transferred from the heat current to the
liquid particles
corresponding to the kinetic energy density of
liquid particles. Dimensionally,
is also a pressure, and as such it represents the radiation pressure exerted by the current of wave-packets on the
liquid particles following the interaction. This pressure may also be regarded as a sort of osmotic pressure determining the displacement of
liquid particles following the collisions with the wave packets. Indeed, to a pressure difference
, the liquid responds with the self-diffusion of the
liquid particles. This interpretation could be used to explain the selective diffusion of solute (or solvent) in a solution, either in thermal equilibrium or in presence of a gradient. The tunnel effect could be regarded as a semi-permeable membrane that works allowing only the passage of
liquid particles and preventing that of
lattice particles [
62]. A similar argument was raised by Ward and Wilks [
64,
65] in dealing with the mechano-thermal effect observed in HeII.
It is worth highlighting that the presence of something like second sound in liquids was assumed by some authors approximately 25 years ago [
46,
47,
48,
49,
50,
51,
52,
53,
54,
55,
56,
57,
58,
59,
60,
61]. In 1996, the presence of a “fast sound” propagating on a short length scale, of the order of some molecular diameters, was discovered in water and other liquids. Its velocity, approximately 3200 m/s, is very close to that of the ordinary sound in solid water, 4000 m/s. Therefore, in ordinary liquids, second sound, faster than the ordinary one, is present. Incidentally, the wave vector
km introduced with Equation (20) provides, through the relation ν
m=
km·uϕ/2π, the critical frequency for the appearance of second sound (see
Section 2), while in [
17], it has been shown that DML is able to justify such a (second) fast sound both on a physical base and numerically.
The delay time <ϑ> is associated with the “communication time” between phonons and molecule clusters for the commencement of resistive flow. Fourier equation may be considered indeed as the thermal counterpart (at steady state) of the first Ohm’s law, the flow of electrical charges being replaced by the resistive flow of thermal charges, the phonons. If, on one hand, <ϑ> is the time necessary for the establishment of the resistive flow, Φ = 1/<ϑ> is proportional to the frequency of occurrence of the phonon ↔ particle collisions. Φ is therefore a measure of how fast the phonons are able to transmit the thermal signal in the liquid as a result of their interactions with the clusters.
It is intriguing to compare Equation (15) with that obtained by Frenkel upon the generalization of the Navier–Stokes equation to viscoelastic media [
19,
20,
21,
22,
23,
38] when he considered the Maxwell relaxation theory of elasticity, namely
where
u is the fluid velocity component normal to
z and
ηl is its viscosity. Such a comparison shows that the ratio
is dimensionally a viscosity,
ηwp, that has a similar role for the temperature as
does for the fluid current. Therefore, we could speculate that if
represents the capability of a fluid to transmit momentum,
ηwp represents the same capability for the wave-packet current. Indeed, bartering Equation (13) for
, the ratio
is just the momentum per unit of surface carried by wave packets.
Very instructive is the comparison of Equation (15) with the analog in electromagnetism represented by the telegraphy equation [
24]. The comparison with electromagnetism is indeed the most suitable because of the presence of flowing electrical charges, such as the wave packets in the DML. Let us indeed suppose to have a circuitry in which
L represents the uniformly distributed inductance of the line,
I is the electrical current flowing through the line,
V is the electrical potential and
R is the uniformly distributed electrical resistance of the line. By excluding sources and sinks along the line, the equation that relates the voltage to the current in terms of properties per unit length of the conductor is
and the charge conservation equation is
where
C is the uniformly distributed capacity of the line. Combining Equations (25) and (26),
is the well-known equation of telegraphy where we easily recognize Equation (15) by replacing
V,
R,
L/R and
C with
T,
, <
ϑ> and
, respectively. Similarly, we may recognize Equation (11) by replacing even
I with
in Equation (25). We can conclude that considering the heat in a liquid as carried by the wave packet current, is equivalent to considering an electric line affected by inductance.
An interesting aspect of Equation (15) is its behaviour in the high frequency limit of fast thermal fluctuations. To fix the ideas, let us suppose that the external temperature
T varies at a rate
f = (1/
T)·(
∂T/
∂t), much faster than Φ = 1/<
ϑ> introduced before; then, Equation (15) predicts a wave propagation of temperature instead of diffusion. The frequency Φ is also a critical frequency for the onset of thermal waves; if the external temperature varies with time at a rate higher than Φ, the temperature signal has no way to stabilize, and the diffusive regime does not take place. This frequency is directly proportional to the thermal resistivity, being zero if the thermal resistivity is zero. The order of magnitude of the relaxation time has been calculated [
17,
18] amounting to several picoseconds, in agreement with experiments; consequently, Φ ≈ 10
11 ÷ 10
12 Hz.
Following the previous reasoning, we could affirm that Equation (15) also takes into account the capability of a medium to dissipate the thermal energy carried by the (anharmonic) wave packets, a circumstance not considered by the classical Fourier equation that is formally the extension of Equation (15) to the steady state. In fact, neglecting dissipation in Equation (15) leads to consider the limit <
ϑ>→0. From the physical point of view, a finite value of <
ϑ> means that the thermal wave has a finite propagation range, and here we come to comment on Equations (17), (20) and (21) in further detail. The first observation is related to Equation (17) that represents a dispersion relation for the wave-packet frequency (or at least for those wave packets interacting with the
liquid particles). It represents a fingerprint of Dual Systems, i.e., of closed systems made of two distinct and interacting populations. In fact, as indicated in Equation (20), not all wave packets are allowed to interact but only those with momentum above
km revealing the so-called
k-gap. This aspect has been extensively discussed elsewhere [
17,
19,
20,
21,
22,
23]; here, we want, however, to also focus the attention on Equation (21) and on the following expression that provides the gap in terms of wavelength instead of momentum:
The reader has certainly recognized the Einstein relation [
31] in the last equality. The same expression for <Λ
C> as Equation (28) is obtained by observing that it holds
As before, substituting Equation (12) into Equation (28), one obtains an expression for in terms of relaxation time and wave-packet parameters, .
In discussing the solutions of Equation (24) in [
21], the authors rightly wondered how large might the
k-gap be. Here, we shift the attention to the <Λ
C>-gap or the <
ϑ>-gap rather than the
k-gap. Recalling that a wave is well defined only if its wavelength is smaller than the propagation distance, Equations (21) and (28) tell us that there is an upper limit also for the relaxation time and for the distance travelled by wave-packets during the propagation of the thermal signal, or, which is the same, for the maximum length of the tunnel, or, alternatively, for the maximum number of
liquid particles with which a
lattice particle may interact before being definitively damped (remember that in Equation (11), it holds that <
ϑ> =
n<
τ> with
n ≥ 1). This offers us the possibility to illustrate the dynamics occurring in a liquid during the thermal transient. When an external temperature gradient is applied, the thermal content obtained by Equation (4) increases, determining an imbalance of the phonon flux, so that there will be an excess of interactions as well of the energy transferred from the thermal current to the
liquid particles through events such as those of
Figure 1a (see Equation (9)). Let us start at
z =
z0. Each interaction lasts <
τ> = <
τp> + <
τR>, the time interval during which the energy disappears as liquid free energy to become an iceberg’s internal and kinetic energy, and the
liquid particle moves by <Λ> = <Λ
p> + <Λ
R> forward; after that, the emerging wave packet has lost part of its initial polarization. Depending on its residual energy and momentum, it may interact with another liquid particle <
τwp> seconds later, and the above process is replicated, say,
n times. The overall duration of the randomization process lasts <
ϑ> =
n<
τ>, during which the particle, and the thermometric front, will have advanced by
, determining a temperature increase by ∆
T over <Λ
C>. At the end of <
ϑ>, a liquid warmer both in its molecular and gas of excitation components will be in contact with the still unperturbed medium laying beyond
z =
z0 + <Λ
C>, setting the stage for a replica of the events. At
z =
z0, instead, in absence of a new advancing front, the process of heat transport after <
ϑ> seconds reaches the steady state, the propagation of thermal excitations becoming at this point purely diffusive.
In [
21], the authors highlight that the
k-gap sets three distinct intervals for the propagating modes, namely (i) non-propagating shear modes, (ii) damped oscillatory shear modes and (iii) purely elastic non-dissipative shear modes. The authors recognize the presence of solid-like structures in liquids for distances where purely elastic non-dissipative modes are allowed, a picture absolutely similar to that of the DML. Comparing then <
ϑ>
M and <Λ
C>
M with <
τ> and <Λ> of Equations (5) and (6), respectively, (or with their multiples, <
ϑ> =
n<
τ> and <Λ
C> =
n<Λ>, with
n ≥ 1), we may envisage the following correspondences: (i) the momentum carried by wave packets is too low to interact with
liquid particles, and there are no propagating modes (
n = 0); (ii) the momentum is large enough to allow the wave packet to interact with several
liquid particles, thus obtaining damped oscillating modes and
n ≥ 1; (iii) this is what happens inside a single
liquid particle, a solid-like structure with the dispersionless propagation of elastic perturbations. In this last case, one experiences the propagation velocity of elastic waves similar to that of the corresponding solid [
17,
46,
47,
48,
49,
50,
51,
52,
53,
54,
55,
56,
57,
58,
59,
60,
61]. These limitations are therefore an indirect evidence of the presence of pseudo-crystalline structures in liquids.
It is interesting, if not mandatory, to numerically evaluate the values of phonon mean free path <Λ
0> and lifetime <
τ0> [
17] within a liquid particle (see
Figure 2) that are connected with <Λ
C> and <
ϑ>. They can be deduced from the experimental values obtained in light scattering experiments for the wave-vector
k. Indeed, <Λ
0> will be a multiple of the phonon wavelength
λ0, <Λ
0> =
aλ0, and <
τ0> that of
τ = 1/
ν0, <
τ0> =
a/
ν0, with
a > 1. Using the data for water of [
58,
60], typical values for the parameters characterizing a phonon (variation range is function of temperature, pressure and
k orientation) are (central) frequency
n/<
τ0> = <
ν0> ≈ 0.95 ÷ 2.5 THz, wave-length <Λ
0>/
n = <
λ0> ≈ 1 ÷ 3 nm and velocity <Λ
0>/<
τ0> = <
λ0>·<
ν0> = <
u0> ≈ 3.1 ÷ 3.4·10
3 m/s. Interestingly, this last value is in very good agreement with the experimental data obtained for the propagation velocity of thermal waves in water [
46] of 3.2·10
3 m/s (see also Figure 5 in [
17]).
It is worth noting that the finite extension of the <Λ
C>-gap is a direct consequence of the presence of dissipation that takes place during <
ϑ>. The absence of dissipation would imply an infinite propagation range, as it happens in perfect ideal crystals and as is described by the classical Fourier law. Because of the relevance of these aspects, they will be carefully dealt with in a separate paper [
62], being outside the main topic of the present one. However, it is worth anticipating some additional comments regarding the presence of
k-gap [
19,
20,
21,
22,
23]. Because the
k-gap in liquids is present only in the transverse spectrum, while the longitudinal one remains gapless, it is reasonable to assume the
k-gap in liquids to be related to a finite propagation length of shear waves. For the
k-gap to emerge in the wave spectrum, two essential ingredients are mandatory. The first is to obtain a wave-like component enabling wave propagation; this is represented in the DML by the wave packets that in turn allow for propagation of the thermal (and generally of the elastic) signal through progressive waves. The second consists in producing a dissipative effect that disrupts the wave continuity and dissipates it over a given distance, thus destroying waves and giving origin to the
k-gap. The latter is represented by the wave-packet ↔
liquid particle interaction, which works by moving the wave packets from where they are absorbed by the
liquid particle to where they return to the system energy pool, like in a tunnel effect. If <
ϑ> is the time during which the shear stress relaxes, then
represents the shear wave propagation length (or liquid elasticity length).
Which is the physical interpretation of the behaviour described above in the frame of DML? The additional time derivative of the flow of wave packets,
, is intrinsically negative because it represents that part of the energy flow that is subtracted during the phonon propagation and sequestered into internal DoF of the icebergs. We may imagine that thermal (and elastic) energy does not propagate continuously, but step-by-step, as originally supposed by Frenkel (see also Figure 1 and Figure 2 in [
17]). The energy remains “trapped” in the internal DoF for a certain time <
τ>, at the end of which the particle relaxes the stored energy, subtracted to the pool a mean free path <Λ> before. This behaviour is fundamental for energy balance purposes only in the transient phase. In fact, once this is finished, globally, there will be no more effects due to the energy removed from the flow, because the phenomenon at the steady state is present in all the medium crossed by the heat flow, and therefore it will no longer give any contribution to the overall system budget. This is the physical explanation of why Cattaneo’s equation gives way to the Fourier equation once the transient phase has elapsed. Incidentally, the presence of a maximum value for the relaxation time, <
ϑ>
M, also has an influence on the additional (negative) term
characteristic of the Cattaneo equation, this being limited by the upper limit for <
ϑ>
M.
In strict connection to the duality of the system and to the energy conservation it is very instructive to recover the approach used by Baggioli et al. [
17,
19,
20,
21,
22] to build up the Lagrangian describing systems (exhibiting
k-gap) constituted by two mutually interacting sub-systems that we identify in the DML with the
lattice particles and the
liquid particles. They introduce a two-field potential representing displacements and velocities,
ϕ1 and
ϕ2, respectively. Neglecting the details of the mathematical formalism, what matters is that the equations of motion for the two scalar fields decouple, leading to two separate Cattaneo-like equations for
ϕ1 and
ϕ2, whose solutions are the following:
Some consequences of this approach for the DML have been extensively discussed in [
17]. In the following, we want to highlight only those relevant for the topic dealt with in this paper. In particular, the interaction potential related to the Lagrangian is an oscillating function (see Figure 5 in [
19] and Figure 2 in [
21]), i.e.,
ϕ1 and
ϕ2 reduce and grow over time <
τ>, respectively (as electrical current and voltage do for an inductance); this implies that the two interacting sub-systems, represented by the two scalar fields, exchange energy and momentum, like wave-packets and
liquid particles do. Therefore, we may hypothesize that the interaction between the population of wave packets and that of
liquid particles is described by such couple of mutually interacting potentials. In addition, because the total scalar field is the product of
ϕ1 and
ϕ2, the total energy of the whole system does not vary with time, i.e., it is a constant of motion, as expected in the DML for systems constituted by the two populations of mutually interacting sub-systems (as in an electrical circuitry without sources or sinks). Finally, the motion is dissipative and hydrodynamic, and could represent a possible microscopic origin for the viscosity. Theories in which the system interacts with its environment have been used to explain important effects involving dissipation [
19,
23].
As pointed out by many authors [
66,
67,
68], complex systems such as liquids exhibit a distribution of relaxation times rather than a single one. This may be also correlated with the fact that in the DML [
17,
18], the propagation of energy (and momentum) can take place either as foreseen by the classical theory, that is, by means of collisions between single molecules, or by means of interactions between the
lattice particles and the
liquid particles. In this second case, the propagation occurs through inelastic collisions between the wave packets and the molecule clusters, the ubiquitous presence of which in turn involves that of wave-packets, or
lattice particles, by means of which the largest part of, if not quite all, the elastic energy and momentum are carried through and in between the icebergs. In addition, and this is also important to the validity of the model, the number of
lattice particles has been shown to be comparable to that of the liquid molecules [
17]. In [
18], it has also been shown that the Equation (13) for the specific heat
in DML as function of the collective DoF, is in line with the experimental results, and its relevance with respect to the total specific heat,
, i.e.,
, has been extensively discussed. The classical treatment of heat propagation has always been applied to the molecular part alone, that is, the one described by the mutual interactions among the molecules of the liquid. The various authors have shown that the paradox of infinite propagation speed is resolved by introducing the delay term <
τ> in the diffusion equation, making it a propagation equation. In this work, we have shown that even for the part of energy that propagates by means of the interactions of wave packets with the pseudo-crystalline structures, heat propagation is described by a Cattaneo-like equation with “memory”. While classically it is not possible to provide an explanation of the delay term and mainly of the undulatory behaviour in the transient phase, in the DML, the introduction of the delay term has a clear physical explanation due to the tunnel effect, and the undulatory behavior is made possible by the presence of the phonons as energy carriers. However, a formal generalization of the propagation equation, including either the part related to the wave-packets or the “classical” one related to molecular interactions, may be advanced, namely
each one with own relaxation time and thermal conductivity. Because the internal energy of the system is distributed between the two sub-systems, one should consider an energy balance equation for the whole system. However, what really matters is that the thermal evolution of the system is characterized by two wave equations, each one with its own medium parameters, relaxation time and, of course, wave propagation velocity (Equation (18)). Indeed, because the DML is a Dual System, the situation recalls the one proposed by Landau for the superfluidity of HeII [
40], i.e., that below the λ–point liquid He is composed both of ordinary and superfluid He, each one with its own sound velocity. Equation (31)
mol is associated with the macroscopic sound velocity, while Equation (31)
wp is associated with the hyperfrequency sound velocity detected at mesoscopic scale for the first time by Ruocco and Sette [
46].
Let us now return to the problem of the relaxation times. With reference to Equations (5) and (6) and to
Figure 1a, the energy lost by the wave packet is commuted into kinetic (i.e., translational) and potential (i.e., collective vibrations) energies of the iceberg, a relaxation time being definable for each process. The kinetic part of the particle energy, involving external DoF, will be dissipated against the liquid friction with its own decay time τ
k along the decay process
The part responsible for the excitation of the internal collective vibratory quantized DoF will be relaxed along with the relaxation time(s)
pertaining to the several excited distinct DoF, and following the decay processes [
66]:
This event is repeated many times as in a chain, giving origin to the thermal avalanche. To the purpose of the present paper, however, we still consider here a single relaxation time, <τ> (or <ϑ>), working for our interactions because what is relevant here is not just distinguishing between the several relaxation times one may consider, but rather establishing that there is a delay physically associated to the lattice particle ↔ liquid particle interaction at the origin of <ϑ> in Equation (15). This fact per se represents one of the novelties of this model, because the delay term in the transient phase in the DML represents a physical consequence of the model.
Equation (15) solves the paradox of infinite propagation velocity of a thermal signal; in fact, its solutions predict a phenomenology of the diffusive type for heat transport after an initial short-lived undulatory phase consisting in a wave propagation with velocity
obtained by Equation (18). By comparing Equations (18), (21), (28) and (29), we may easily recover the expressions for some well-known quantities defined in Irreversible Thermodynamics (independently of whether the system is in propagative or diffusive (i.e., steady state) regime, [
22]):
We will show now the conditions under which the picture illustrated above provides the same results as that originally found by Cattaneo, in particular concerning the propagation velocity defined in Equation (34). In the DML, the wave packets carrying thermal energy are seen as a gas of
lattice particles, each of which moves with velocity
uwp (we limit here to consider an idealized dispersionless elastic medium). In an isothermal system, they move in random directions, so that we may consider the following relation holding for
uwp [
40,
64,
65]:
Therefore, the average RMS of the phonon velocity in any direction is
from which we finally obtain
An energy disturbance in the phonon gas is carried through the liquid in the direction of propagation of the disturbance with the same velocity
, which is related to the phonon velocity through Equation (37), in line with the result obtained by Cattaneo [
1].
Many authors have raised a number of objections about the use of a hyperbolic equations to describe the propagation of heat, especially (i) for the physical meaning of the initial condition to be attributed to the temperature gradient, (ii) because the total amount of heat, obtained by Equation (3), is no longer conserved ([
5,
6] and references therein), and (iii) for their compatibility with II Principle. Here, we do not want to engage into these debates, because what is written in other works about the compatibility of hyperbolic equations with heat propagation is also valid in this case. However, we are keen to highlight the following aspects. One is connected to the first point. As widely explained before, in the DML, there is a physical need for a propagative form of thermal energy in a liquid during the transient phase rather than diffusive due to the “tunnel” effect, by means of which energy is shifted from one place in the medium to another,
Figure 1a; for each interaction, the length of the tunnel is <Λ> and the energy takes <
τ> to cross it. Let us then evaluate an expression one may easily deduce for the rate of temperature variation. To do this, we begin with considering the variation of heat flux
associated to wave packets and due to a variation of the boundary conditions of the system. As outlined in
Section 3 and deeply discussed in [
17], the current of wave packets generates a pressure during its propagation that in turn is equal to the amount of heat carried by phonons,
. The overpressure wave ∆
∏wp multiplied by the velocity of advancement of the wave-front,
, provides the power per unit cross-section,
, dissipated by the wave-packets:
where ∆
T is the local temperature increase due to
. Dividing
by <Λ
C>, one obtains the thermal power per unit of volume dissipated by phonons along <Λ
C>:
Finally, dividing
by
CV, one obtains the temperature variation vs. time of the liquid contained in a volume of unitary cross-section and height <Λ
C>:
where Equation (13) for the phonon-specific heat
has been used. Equation (40) shows that the rate of temperature variation does not depend on the external applied temperature gradient, but only on constitutive properties of the medium, in particular on the number of collective DoF excited (through
m).
A second remark concerns the energy conservation principle, that is, of course, not violated in the present approach. In fact, the missing part to the molecular energy content is that temporarily stored into non-propagating DoF of the icebergs during its travel through the tunnel; this missing part is not taken into account in dealing with a system in the classical “single-system” approach. This is another key point of the DML, which makes hyperbolic equations applicable to the energy (and mass) propagation in liquids due to the supposed “duality” of the system.
The final remark concerns the consistency of a propagation equation such as Equation (15) with the II Principle. In addition to what has already been written in support of this by various authors [
12,
28,
30,
33,
67,
69], the compatibility with the II Principle of thermodynamics has been dealt with in [
70], in which an expression derived from a statistical approach is compared with the one obtained from considerations of rational mechanics, where the non-isothermal fluid is considered as continuum. A modified stress tensor containing a term depending on heat flux can be obtained if one considers the system as a thermoelastic fluid, whose internal energy depends also on the heat flux. The insertion of this new independent variable in the energy equation leads to a modified entropy production and, in order for this model to be compatible with the II Principle, a Cattaneo-type equation must be adopted to describe heat propagation.
5. Conclusions
Contrary to its simplicity, the title of this work is by no means trivial; as often happens, the most naïve questions are the most insidious and those requiring more attention. In this paper, we have analyzed for the first time the problem of heat propagation in liquids modeled as Dual Systems, the two interacting subsystems being the population of phonons, or lattice particles, that interact with the population of liquid molecules, aggregates of liquid molecules, whose extension and density depend upon the temperature and pressure of the liquid. The two populations interact by means of fth that allows the propagation not only of energy but also of momentum. The interaction is characterized by a tunnel effect, by means of which the energy subtracted to the phonon pool is sequestered for a time lapse <τ> in a non-propagating form, the internal DoF of the liquid particle. Once <τ> has elapsed, the liquid molecule has travelled through the liquid by <Λ> and in that point the energy emerges from the tunnel and returns to the phonon pool. This interaction has allowed to apply a hyperbolic equation for the first time to describe the heat (or mass) propagation in a liquid, thus solving the dilemma of infinite diffusion velocity which is typical of the Fourier law. The additional term distinguishing the Cattaneo-type equation from the Fourier law is indeed justified from the physical point of view just by the anharmonic interaction liquid particle ↔ lattice particle. Tunneling in DML has various consequences. First, it represents the missing link to justify the use of a hyperbolic equation to describe the propagation of a thermal (and elastic) signal in a liquid. The hyperbolic equation is of course representative of the transient phase, when the effect of the propagation delay is also present at the macroscopic level. At stationary state, the consequences of the tunnel effect are no longer appreciable at the macroscopic level, although still present at the microscopic level but equally distributed throughout the system. The hyperbolic equation reduces to the parabolic Fourier equation once the steady state is reached. Furthermore, the tunnel effect justifies the presence of shear waves on distances of the order of the dimensions of the molecular clusters. The above picture also allows to justify the additional initial condition needed to solve the hyperbolic equation that results to be dependent only upon constitutive properties of the medium. Therefore, another capability of DML is demonstrated.
DML offers, of course, many other perspectives of application to just as many problems in the mesoscopic range of the physics of liquids. Future applications will certainly be addressed to compare our results with those of independent research groups. In particular, it is by far very interesting to determine a way for calculating the values of the relaxation times involved in the heat propagation. Specific calculations are being finalized [
62], although an Order of Magnitude has been already provided in this paper. In this frame, it will be relevant to account for the works already published on this topic [
5,
6,
12]. As is well known, application of a temperature gradient to liquid solutions may reveal interesting phenomena [
9], such as the selective diffusion of their components, the so-called thermo-diffusion. Provided that the system is gravitationally stabilized, the flux of thermal energy separates its components until a dynamic equilibrium is reached, the Soret equilibrium. A similar, in some way opposite, phenomenon is observed if a gradient of concentration is applied; this generates a temperature difference inside the solution, the Dufour effect. Type (b) events of
Figure 1 indeed show the capability of the reversible character of the elementary collisions, the particle that returns a more energetic phonon, undergoes a recoil as a result of the impulse conservation principle. This could explain the Dufour effect at mesoscopic level, i.e., the energy flux due to a mass concentration gradient occurring as a coupled effect of irreversible processes. The above listed phenomena are well known and well described in non-equilibrium phenomenological thermodynamics [
9]. A possible future application for the DML will be to provide a physical description of thermo-diffusion and mechano-thermal effects in terms of phonon ↔
liquid particle inelastic collisions.
It is worth to mention the work by Zhao et al. [
71]. The authors use the expression for
CV deduced in the Phonon Theory of Liquid Thermodynamics [
72,
73], a thermodynamic model of liquids in which these are assumed to be Dual Systems as in the DML. They develop a method to calculate the thermal conductivity of liquids, with the highest agreement with experimental data ever obtained, even if compared with previous models of liquids.
Experiments performed by Noirez and co-workers revealed an “unexpected” thermo-elastic effect in liquids confined at the mesoscopic level [
74,
75,
76,
77]. The mechano-thermal effect consists in the occurrence of a temperature gradient inside a liquid due to the momentum transferred by a moving plate to the liquid; this is confined in between one moving plate and one fixed. Although the thermal behaviour of the liquid in the several cases examined is not exactly the same, the dependence of the intensity of the mechano-thermal phenomenon, in particular of the temperature difference that originates, with respect to the distance between the two plates, remains almost the same. These interesting experiments were already analyzed in a previous paper [
17] and internally discussed with one of the authors [
78]. What matters here is that DML could provide a physical explanation for this “unexpected” phenomenon by means of the elementary wave-packet ↔
liquid particle interaction described in
Figure 1b. The acceleration of the moving plate generates a momentum flux, directed towards the fixed plate, as one may easily deduce from a Rayleigh argument. According to the DML, and also following Rayleigh’s reasoning, the momentum flux, dimensionally a pressure, generates a temperature gradient. The
liquid particles, pushed by the momentum flux, transfer their excess impulse to the phonons, which emerge from each single impact with an increased energy. They are then pushed and collected in proximity of the fixed plate, giving rise to a temperature gradient directed towards the fixed plate. The phenomenon is very rapid because it is determined by a succession of (almost) elastic collisions, which propagate very quickly (the relaxation time is of the order of <
ϑ>). In addition, as explained in [
77], the thermal effect is scale-dependent, in particular it depends on the velocity gradient, and hence on the pressure gradient generated inside the liquid (is inversely proportional to the liquid thickness). It is here important to highlight that the wave-packet ↔
liquid particle collision also explains why a temperature gradient (i.e., a generalized flux force crossed effect) is generated inside the liquid instead of a simple heating due to the energy stored as consequence of the mechanical stress (G′ >> G″), as one would have expected on the basis of a classical interpretation of the elastic modulus. In this framework, it is interesting to look at Equation (40), although written in terms of pressure gradient instead of temperature. Equation (40) tells us that when a temperature (pressure) gradient is applied to a (dual) system, it generates a heat flux, the heat propagation being described by a hyperbolic Equation (15). For such equation to be solved, one needs to specify an additional initial condition on temperature (pressure) variation vs. time, quantitatively described by Equation (40). In the case of the experiments of Noirez, we have to deal with a momentum gradient applied to a (dual) system;
Figure 1b could explain why it generates a temperature gradient as consequence of its propagation through the liquid. An equation similar to Equation (40) could be set up to quantitatively justify the observed phenomena of the mechano-thermal effect. It is worth remembering that in Equation (40), only constitutive properties of the medium appear, in particular the number of collective DoF excited. Because of the complexity of the argument, a dedicated analysis will be conducted in a separate paper [
62].
Trachenko and co-workers [
79] have recently observed that the thermal diffusivity of liquids exhibit a lower bound that is fixed by fundamental physical constants for each system; even more intriguingly, the same value is shared by the kinematic viscosity of liquids. This, in turn, means that energy and momentum diffusion in liquids share the same universal lower bound, and a strict correlation between the two transport mechanisms may be hypothesized. Interestingly, in the DML, energy and momentum are both carried by interactions between the two subsystems constituting the liquids,
liquid particles and
lattice particles.
Performing experiments on the earth to measure conduction in liquids has always been a challenge due to the onset of convection, even when limiting geometric and boundary conditions are adopted. A way to study conduction free from large disturbances due to gravity is that offered today by the microgravitational environment typical of platforms orbiting the earth, where a residual gravity field approximately 10−5–10−6 times that of the earth is present.
On the experimental side, performing experiments in non-stationary temperature gradients may allow to investigate the way in which liquid parameters evolve from equilibrium to non-equilibrium conditions. It could be possible, for instance, to investigate the evolution of correlation lengths, sound velocity, thermal conductivity, etc. A second type of experiments could be aimed at investigating the glassy and liquid-to-solid transitions. The latter could be achieved starting from a stationary temperature gradient applied to a liquid sample and lowering both temperatures in order to also lower the average temperature of the medium until its solidification. Light scattering experiments performed during the non-stationary phase should allow to investigate the dynamics of the system when the glassy and liquid-to-solid transitions are crossed. In particular, the external temperature gradient should orient the local domains along the same direction, thus allowing the increase in the correlation lengths, sound velocity, thermal conductivity, etc., along the preferential direction of the external temperature gradient. The experimental data collected should evidence a difference between the same parameters when measured along the direction of the temperature gradient with respect to those measured along a different direction.
In addition, it could be very interesting to investigate whether a temperature gradient affects the viscous coupling between two adjacent liquids.