Can We Teach Machines to Select Like a Plant Breeder? A Recommender System Approach to Support Early Generation Selection Decisions Based on Breeders’ Preferences

Abstract

Plant breeding is considered to be the science and art of genetically improving plants according to human needs. Breeders in this context oftentimes face the difficult task of selecting among thousands of genotypes for dozens of traits simultaneously. Using a breeder’s selection decisions from a commercial wheat breeding program as a case study, this study investigated the possibility of implementing a recommender system based on the breeder’s preferences to support early-generation selection decisions in plant breeding. The target trait was the retrospective binary classification of selected versus non-selected breeding lines during a period of five years, while the selection decisions of the breeder were predicted by various machine learning models. The explained variance of these selection decisions was of moderate magnitude (${\mathsf{\rho }}_{\mathrm{S}\mathrm{N}\mathrm{P}}^2$ = 0.45), and the models’ precision suggested that the breeder’s selection decisions were to some extent predictable (~20%), especially when some of the pending selection candidates were part of the training population (~30%). Training machine learning algorithms with breeders’ selection decisions can thus aid breeders in their decision-making processes, particularly when integrating human and artificial intelligence in the form a recommender system to potentially reduce a breeder’s effort and the required time to find interesting selection candidates.

1. Introduction

Statistical and machine learning, both fields of study in artificial intelligence, have opened up new avenues for agriculture in recent years, where plant breeders and quantitative genetics have, for example, exploited the power of the methods to optimize and accelerate genetic improvement in various crop species [1,2,3]. Statistical learning methods have thus gained large popularity for phenomics and genomics applications in plant breeding [4,5], giving rise, amongst others, to manifold predictive breeding approaches during the last decade [6,7,8,9]. In particular, the utilization of big data coming from vast multi-environment trials in combination with genome-wide distributed SNP markers to support selection decisions has become a routine procedure in many cereal breeding programs [10,11,12,13]. The foundation for conducting such a genomic selection lies in the quality and comprehensiveness of the underlying dataset, while the model training represents the heart of the genomic selection process [14]. Aside from classical statistical learning methods, Bayesian models or approaches like machine and deep learning algorithms, which are part of the field of artificial intelligence [15], are thereby employed to establish the relationship between genetic markers and phenotypic traits [16]. Regularly updating training populations with selection candidates that are routinely phenotyped across multiple years in multi-location trials in the framework of variety development [17,18,19] or with genotypes that are chosen by dedicated algorithms [20,21,22] is thereby pivotal in order to maintain a high accuracy of these prediction models [23,24]. The resulting genomic estimated breeding values can subsequently be used to guide a breeder’s selection decisions among early-generation non-phenotyped selection candidates, aiding in the selection of individuals with the most desirable genetic profiles [25]. Genomic selection has accordingly been successfully used for targeting major agronomic traits in cereal breeding to improve quantitively inherited traits like grain yield [26,27], baking quality in wheat [28,29], and malting quality in barley [30,31]. In addition to the usage of genomic estimated breeding values on a continuous scale for the mentioned traits, some successes have also been reported for classifying selection candidates by machine learning algorithms [32,33,34], especially for certain characteristics, such as rust resistant versus non-resistant lines in wheat [4,35].

Aside from these data-driven approaches, a breeder’s intuition and knowledge, sometimes referred to as the breeder’s eye, still remains an important aspect of modern plant breeding, as it has been for more than 100 years [36]. Although this breeder’s eye has sometimes been romanticized in the form of a personal relationship between breeders and plants, it is without doubt the habit of successful plant breeders to constantly visit field trials during the season and systematically take note of their germplasm [37]. The breeder’s eye thereby makes use of objective traits like phenology and disease resistance but also considers more subjective traits, like general field impressions, with a certain ideotype in mind [38] as well as breeder’s knowledge of the crop germplasm [36]. Based on their knowledge about the demands of the seed market and sometimes direct interaction with the farmers [37], breeders nowadays possess a strong expertise in integrating both knowledge-driven [39] as well as data-driven inputs based on statistical approaches [40] in their selection decisions in order to develop new and improved crop varieties. These selection decisions are thus oftentimes reached by a breeder after implicitly combining phenotypic observations made in the field, knowledge about the germplasm, and the mentioned data-driven inputs from statistical and machine learning models, such as genomic estimated breeding values. However, this expertise of bridging human and artificial intelligence by breeders has not been adequately taken into consideration by statistical modelling approaches for combining machine learning and expert knowledge in plant breeding.

Nevertheless, machine learning algorithms trained on human decision making are an inherent part of other disciplines, like online commerce and marketing, where they are frequently used in the form of recommender systems on shopping, entertainment, and learning platforms [41]. Although many such platforms are making use of vast amounts of consumer data and highly sophisticated algorithms, the simplest form of recommender system is given by training a simple machine learning model like random forest [42] with the preferences of just one user. The results of applying this so-called content-based approach for implementing a recommender system is the suggestion of personalized items or information based on the characteristics of previously chosen items or information by this user [43]. The merit of a recommender system is accordingly given by the fact that this person does not have to screen all the available content on a platform to find a suitable item or information [41,43]. The usage of such a content-based recommender system has thus the advantage of providing highly personalized recommendations that are most relevant to one particular user [43]. Using such a recommender system in the context of plant breeding might likewise have some potential, since breeders oftentimes have to select among thousands of genotypes for dozens of traits simultaneously during product development. Training a statistical or machine learning model with a breeder’s preferences to obtain recommendations for selection would accordingly allow a breeder to screen the available data more systematically without being overwhelmed by the vast amount of information about a plethora of agronomic traits from all selection candidates at once. Hence, the application of such a recommender system in plant breeding would potentially reduce a breeder’s effort and required time to find the most interesting selection candidates when conducting selection decisions. The derived recommendations would furthermore be highly personalized, reflecting a breeder’s preferences and breeding goals, which might lead to a high acceptance of such a recommender system as an additional selection tool. The aim of this case study was thus to investigate the possibility of predicting selection decisions of a plant breeder by various methods of statistical and machine learning and to assess the potential of implementing a recommender system based on breeders’ preferences as a tool for supporting breeders in their selection decisions.

2. Materials and Methods

2.1. Plant Material, Classification of Breeder’s Decisions, and Genotypic Data

This study focuses on a set of 4674 winter wheat (Triticum aestivum L.) breeding lines from the commercial breeding program of Saatzucht Donau GesmbH & CoKG (Probstdorf, Austria), which were tested in preliminary yield trials between 2015 and 2019 in Austria. The lines were part of five distinct cohorts, each comprising 532–1966 lines that were part of 64–342 different families. The plant material within each cohort was classified into non-selected lines ($\mathrm{s}\mathrm{e}\mathrm{l}=0$) and lines that were selected and advanced to the first year of multi-environment trials ($\mathrm{s}\mathrm{e}\mathrm{l}=1$), based on the decisions by the breeder (Franziska Löschenberger) in the respective preliminary yield trials (Figure 1). These selection decisions served as the target trait in this study, and they were reached by the breeder after implicitly combining phenotypic observations made in the field, knowledge about the germplasm, and data-driven inputs such as genomic estimated breeding values.

All breeding lines were genotyped with the DArTcap targeted genotyping-by-sequencing approach [44]. Alleles of the SNP markers were coded as “−1” for homozygous minor, ”+1” for homozygous major, and “0” for heterozygous. SNP markers with more than 10% missing data were filtered out, as were SNP markers with a minor allele frequency smaller than 5%, which resulted in a final dataset of 2219 SNP markers as predictors for the below-described statistical and machine learning models, i.e., recommender systems, after imputation with the missForest algorithm [45]. A principal component analysis with these SNP markers lines did not reveal a clear population structure in the studied panel of winter wheat breeding lines (Figure S1).

Genomic estimated breeding values for grain yield, protein content, protein yield, extensogram dough energy, and Fusarium head blight (FHB) severity of the 4674 breeding lines additionally served as potential predictors for the recommender systems. These genomic estimated breeding values were available to the breeder and extensively used when conducting selection decisions as part of the routine implementation of genomic selection in the wheat breeding program. Hence, they were chosen as predictors for the target trait, i.e., the breeder’s selection decisions, as they represented the major breeding targets, i.e., yield, quality, and disease resistance in the investigated wheat breeding program. The genomic estimated breeding values were computed based on genomic best linear unbiased prediction (GBLUP) models, which were trained on numerous multi-environment trial series with advanced generation breeding lines, as outlined in previous studies [46,47,48].

2.2. Estimating the Explained Variance of Breeders’ Decisions

Bayesian logistic models were fitted with the BGLR package v1.1.0 [49] for the R statistical environment [50] separately for the individual cohorts as well as for the combination of all five cohorts in order to estimate the variance of the breeder’s selection decisions that can be explained by the different predictor sets. Aside from the SNP markers, the above-mentioned genomic estimated breeding values for the five major agronomic traits served as predictors in these models. The genomic estimated breeding values for grain yield, protein content, protein yield, extensogram dough energy, and FHB severity of each individual cohort were for this purpose standardized by

$${\mathrm{s}}_{{\mathrm{g}\mathrm{e}\mathrm{b}\mathrm{v}}_{\mathrm{i}\mathrm{j}\mathrm{k}}}={\displaystyle \frac{{\mathrm{g}\mathrm{e}\mathrm{b}\mathrm{v}}_{\mathrm{i}\mathrm{j}\mathrm{k}}-{\mathrm{\mu }}_{\mathrm{j}\mathrm{k}}}{{\mathsf{\sigma }}_{\mathrm{j}\mathrm{k}}}}$$

(1)

where ${\mathrm{g}\mathrm{e}\mathrm{b}\mathrm{v}}_{\mathrm{i}\mathrm{j}\mathrm{k}}$ is the genomic estimated breeding value of the ith line for the jth trait in the kth cohort, ${\mathrm{\mu }}_{\mathrm{j}\mathrm{k}}$ is the average of the genomic estimated breeding values for the jth trait in the kth cohort, and ${\mathsf{\sigma }}_{\mathrm{j}\mathrm{k}}$ is the standard deviation of the genomic estimated breeding values for the jth trait in the kth cohort. A Gaussian prior and Gibbs sampler algorithm with a burn-in of 2000 followed by an additional 10,000 MCMC (Markov chain Monte Carlo) samples and a thinning factor of five was used in the model:

$$\mathbf{y}=\mathsf{\mu }+\mathbf{Z}\mathbf{u}+\mathbf{e}$$

(2)

where $\mathbf{y}$ is the vector of labels for the lines classifying them into non-selected ($\mathrm{s}\mathrm{e}\mathrm{l}=0$) or selected ($\mathrm{s}\mathrm{e}\mathrm{l}=1$), $\mathsf{\mu }$ is the grand mean, and $\mathbf{u}$ is the vector of random marker effects with variance ${\mathsf{\sigma }}_{\mathrm{u}}^2$. $\mathbf{Z}$ is the matrix of predictors that either contained the SNP markers or the standardized genomic estimated breeding values, and $\mathbf{e}$ is the vector of residuals. The proportion of the explained variance of this binary classification was estimated as suggested by Nakagawa and Schielzeth (2010), de Villemereuil et al. (2013), and Heuer et al. (2016) [51,52,53]:

$${\mathsf{\rho }}^2={\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{a}}^2}{{\mathsf{\sigma }}_{\mathrm{a}}^2+1+1}}$$

(3)

where the additive genetic variance ${\mathsf{\sigma }}_{\mathrm{a}}^2$ was estimated based on ${\mathsf{\sigma }}_{\mathrm{a}}^2=m{\mathsf{\sigma }}_{\mathrm{u}}^2$, where $m$ is the number of predictors, the first 1 for the probit link variance, and the second 1 for the residual variance ${\mathsf{\sigma }}_{\mathrm{e}}^2$, as implemented in the BGLR package for the probit link function [49].

2.3. Forward Prediction of Breeder’s Decisions by Machine Learning Algorithms

Training populations for fitting machine learning models with predicted breeder’s decisions were built by 50 times repeatedly sampling 400 lines from each individual cohort for 2015–2019. Following the scheme of a multi-stage selection in a line breeding program, 350 of these 400 lines were sampled based on their labelling from the non-selected class ($\mathrm{s}\mathrm{e}\mathrm{l}=0$) and 50 lines from the selected class ($\mathrm{s}\mathrm{e}\mathrm{l}=1$), assuming a selection intensity of 12.5% from preliminary yield trials to multi-environment trials. For the purpose of a forward prediction, validation populations were created by analogously sampling 50 times 80 different lines from each individual cohort in 2017–2019, where 70 lines ($\mathrm{s}\mathrm{e}\mathrm{l}=0$) belonged to the non-selected class and 10 lines to the selected class ($\mathrm{s}\mathrm{e}\mathrm{l}=1$), likewise reflecting a selection intensity of 12.5%. This resampling scheme was implemented in order to equalize the training and validation population sizes when assessing the potential to predict breeder’s decisions in two forward prediction schemes:

(1)

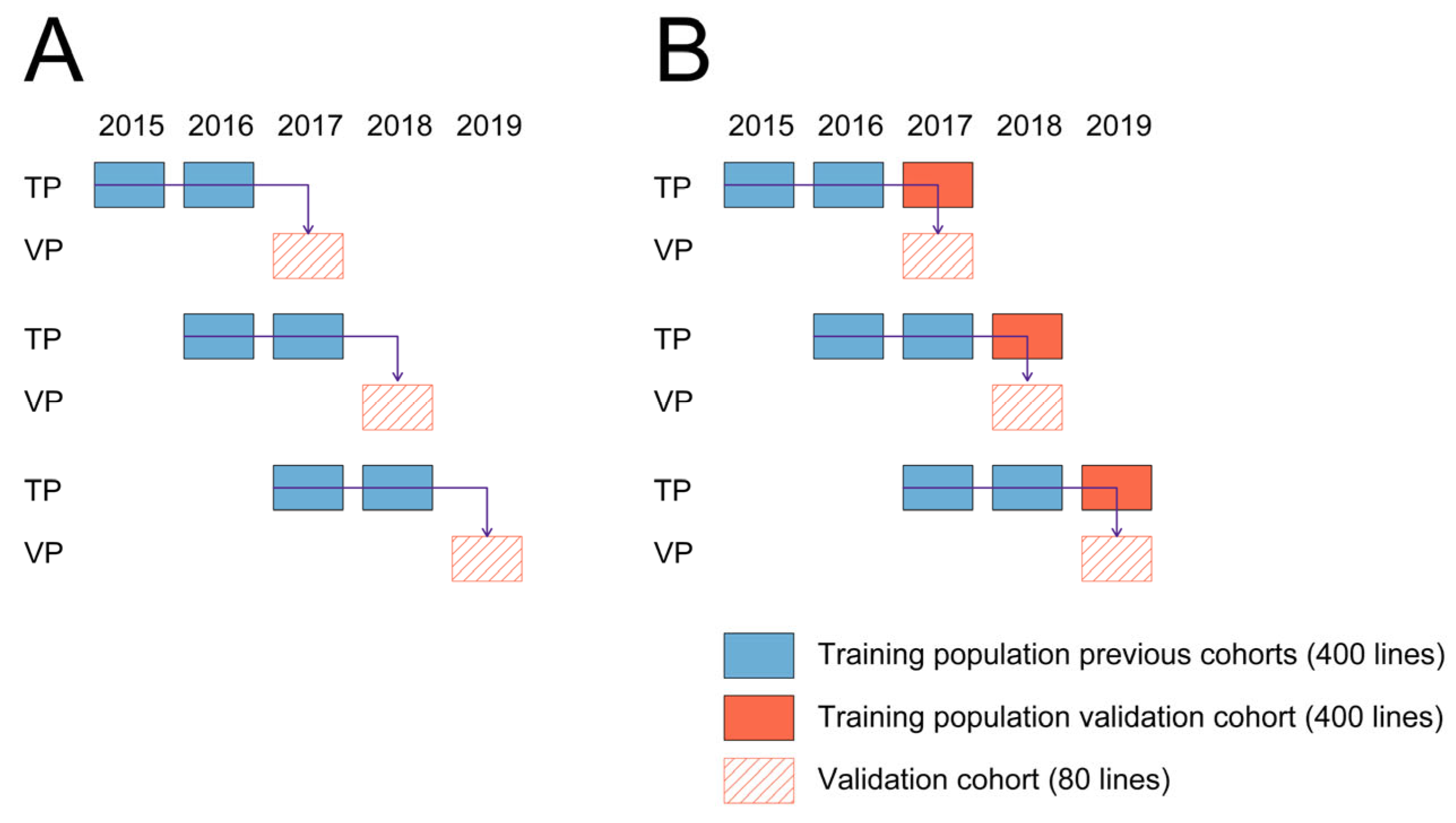
Training populations coming from two cohorts preceding the cohort that was used for validation were used for fitting prediction models (800 lines) (Figure 2A).

(2)

Training populations coming from two cohorts preceding the cohort used for validation were used for fitting prediction models, while this set was augmented by the training population coming from the same cohort that was used for validation (1200 lines) (Figure 2B).

The former scheme thus represented a scenario in which none of the pending selection candidates was labeled, and the latter scheme a scenario where a certain proportion of the pending selection candidates was already pre-labeled by the breeder. The individual validation populations sampled from the cohorts in 2017–2019 served thereby to measure the precision of the predicted classification in both forward prediction schemes. Additionally, the training population size was varied between 400 and 800 lines by equally sampling lines from two cohorts preceding the cohort that was used for validation (Figure 2A) or from three cohorts including the cohort that was used for validation (Figure 2B) in order to investigate if a general larger training population size or, specifically, the inclusion of the lines from the validation cohort would lead to a higher predictive performance of the below-described machine learning models.

For the purpose of obtaining predictions of the breeder’s decisions, both SNP markers as well as the standardized genomic estimated breeding values for grain yield, protein content, protein yield, extensogram dough energy, and FHB severity served again as predictors. Bayesian logistic models were firstly trained with BGLR [49] and a Gibbs sampler algorithm with a burn-in of 2000 followed by an additional 10,000 MCMC samples and a thinning factor of five. A Gaussian prior was used when implementing the Bayesian logistic models, equally shrinking all predictor effects towards zero and assuming purely additive effects of the predictors. Alternatively, the R package glmnet v4.1-6 [54] was used to predict the breeders’ decisions with elastic nets, where a sequence of 1000 values was used to search for an optimum of the penalty parameter $\mathsf{\lambda }$ based on the lowest deviance. The elastic nets also assumed purely additive effects, while the predictor effects $\widehat{\mathbf{u}}$ were estimated by

$$\widehat{\mathbf{u}}=\underset{\mathbf{u}}{\mathrm{argmin}}({‖\mathbf{y}-\mathbf{Z}\mathbf{u}‖}^2+\mathsf{\lambda }[\mathsf{\alpha }{‖\mathbf{u}‖}_1+{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(1-\mathsf{\alpha }\right){‖\mathbf{u}‖}_2^2])$$

(4)

Setting the hyperparameter $\mathsf{\alpha }={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$ ensured an equal weight of the ${\mathrm{L}}_1$ and ${\mathrm{L}}_2$ regularization for combining shrinkage properties and handling multicollinearity with predictor selection properties for reducing the influence of noisy signals. Neural networks were subsequently tested in order to also model interactions between the predictors, i.e., both additive as well as non-additive effects. The R package neuralnet v1.44.2 [55] was used to fit multi-layer perceptrons based on resilient backpropagation with backtracking, one hidden layer, and ${\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}m$ neurons in this hidden layer, where $m$ is the total number of available predictors. Random forest models [42] were finally fitted with the R package randomForest v4.7-1.1 [56], which likewise included modeling additive as well as non-additive effects among the predictors. Half the number of lines in the respective training population were sampled to build 500 classification trees with a minimum size of the terminal nodes of 1, while the number of sampled predictors for building each tree was set to $p=\sqrt{m}$, where $m$ is the total number of available predictors.

The predictions from each of the models were expressed in terms of the probability for each of the 80 breeding lines in the validation population to fall into the class of selected lines ($\mathrm{s}\mathrm{e}\mathrm{l}=1$). Aiming to reflect a recommender system where the most desirable selection candidates are suggested to a breeder, the 10 lines in the validation population with the highest probability were accordingly labeled to fall into the mentioned class of the selected lines ($\mathrm{s}\mathrm{e}\mathrm{l}=1$), and the other 70 lines were labeled to fall into the class of non-selected lines ($\mathrm{s}\mathrm{e}\mathrm{l}=0$). The precision of this classification was estimated by

$$\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}}$$

(5)

where $\mathrm{T}\mathrm{P}$ is the number of true positive and $\mathrm{F}\mathrm{P}$ is the number of false positive classified lines in the validation population based on a confusion matrix. The true positives refer to lines that were predicted as being selected and were actually selected by the breeder, whereas the false positives refer to lines that were wrongly classified by the statistical and machine learning algorithms to fall into the class of selected lines ($\mathrm{s}\mathrm{e}\mathrm{l}=1$). This metric can, in the study at hand, also be interpreted as the percentage overlap between the lines recommended by the different statistical and machine learning algorithms and the actual breeder’s choice. Aside from the precision, the Matthews correlation coefficient $\left(\mathsf{\varphi }\right)$ was chosen as an additional comprehensive measure of model performance and estimated by

$$\mathsf{\varphi }={\displaystyle \frac{\mathrm{T}\mathrm{P}\times \mathrm{T}\mathrm{N}-\mathrm{F}\mathrm{P}\times \mathrm{F}\mathrm{N}}{\sqrt{(\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N})(\mathrm{F}\mathrm{P}+\mathrm{F}\mathrm{N})(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N})(\mathrm{F}\mathrm{P}+\mathrm{T}\mathrm{N})}}}$$

(6)

where $\mathrm{T}\mathrm{P}$ is the number of true positive, $\mathrm{T}\mathrm{N}$ is the number of true negative, $\mathrm{F}\mathrm{P}$ is the number of false positive, and $\mathrm{F}\mathrm{N}$ is the number of false negative classified lines in the validation population based on a confusion matrix. The true positives again refer to lines that were predicted as being selected and were actually selected by the breeder, whereas the true negatives refer to lines that were predicted as being non-selected and were actually not selected by the breeder. The false positives and false negatives refer accordingly to lines that were wrongly classified by the machine algorithms. The Matthews correlation coefficient $\left(\mathsf{\varphi }\right)$ was chosen as an additional metric as it is similar to the Pearson correlation coefficient $\mathsf{\rho }$ in its interpretation, given the case of a binary classification. Notably, it can be shown that $\mathsf{\varphi }$ is identical to $\mathsf{\rho }$ when coding non-selected lines as “0” and selected lines as “1” followed by calculating the Pearson correlation coefficient between the predicted and observed selection decisions.

The precision and Matthews correlation coefficient obtained when training with the different machine learning models and choosing the lines with the highest probability to fall into the class of selected lines ($\mathrm{s}\mathrm{e}\mathrm{l}=1$) was lastly compared to a random choice among the lines in the validation population in the above-outlined forward prediction schemes (Figure 2).

2.4. Retrospective Assessment of the Machine Learning Algorithms’ Recommendations as a Selection Decision Support Tool

The merit of using the recommendations made by the different machine learning models trained with breeder’s preferences as a selection decision support tool was assessed by using a reciprocal fine-tuning algorithm (Figure 3). The algorithm was initiated by obtaining recommendations for the population of selection candidates in 2017, 2018, and 2019 based on model training with the respective two previous years, 2015–2016, 2016–2017, and 2017–2018. Initial training populations of 400 lines were sampled from each of these years, while 350 of these 400 lines were sampled based on their labelling from the non-selected class ($\mathrm{s}\mathrm{e}\mathrm{l}=0$) and 50 lines from the selected class ($\mathrm{s}\mathrm{e}\mathrm{l}=1$). The populations of selection candidates were constructed by sampling 420 lines from the non-selected class ($\mathrm{s}\mathrm{e}\mathrm{l}=0$) and 60 lines from the selected class ($\mathrm{s}\mathrm{e}\mathrm{l}=1$) from each of the validation years, 2017, 2018 and 2019, individually. A retrospective perspective was taken in this study to test the suggested algorithm, where the aim was to identify an as high as possible proportion of ${\mathrm{l}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}=60$ lines that were actually chosen by the breeder among a population of 480 selection candidates:

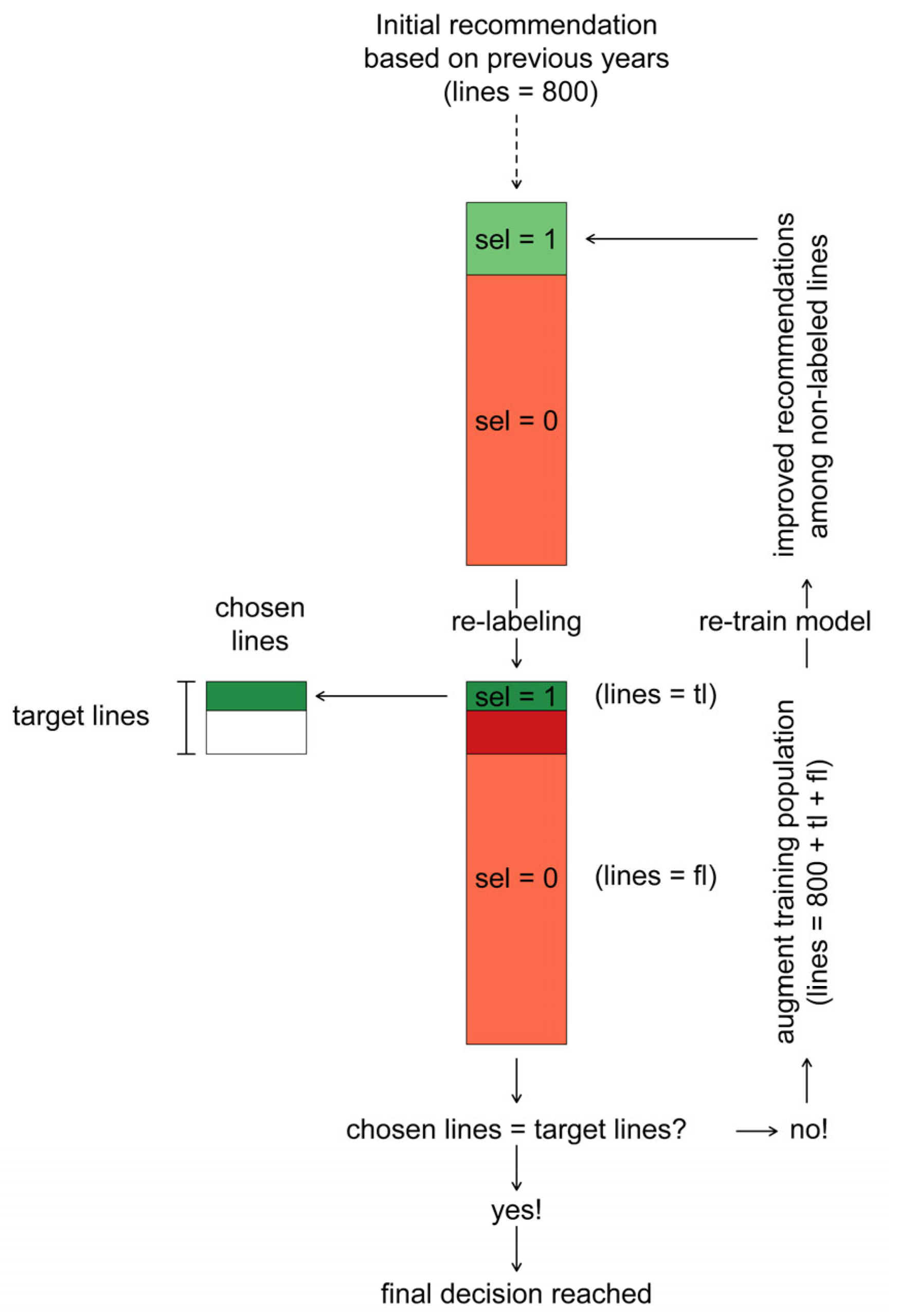
(1)

In the first iteration $(\mathrm{i}=1)$, the ${\mathrm{l}}_{\mathrm{i}=1}=60$ lines with the highest probability of selection were recommended and labeled to fall into the class of selected lines $(\mathrm{s}\mathrm{e}\mathrm{l}=1)$.

(2)

Based on the actual breeder’s choice among these recommended lines, this labeling of $\mathrm{s}\mathrm{e}\mathrm{l}=1$ was retained for a number of ${\mathrm{t}\mathrm{l}}_{\mathrm{i}=1}$ lines corresponding to the true positives, while it was changed to $\mathrm{s}\mathrm{e}\mathrm{l}=0$ for a number of ${\mathrm{f}\mathrm{l}}_{\mathrm{i}=1}$ lines corresponding to the false positives.

(3)

The ${\mathrm{t}\mathrm{l}}_{\mathrm{i}=1}$ true positive lines were then added to the pool of chosen lines (${\mathrm{l}}_{\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{n}})$.

(4)

After (re)-labeling the lines in the population of selection candidates in this way, they were used to augment the initial training population of ${\mathrm{c}}_{\mathrm{i}=1}=800$ lines to a size of ${\mathrm{c}}_{\mathrm{i}=2}={\mathrm{c}}_{\mathrm{i}=1}+{\mathrm{t}\mathrm{l}}_{\mathrm{i}=1}+{\mathrm{f}\mathrm{l}}_{\mathrm{i}=1}$.

(5)

Machine learning models were then re-trained with this augmented training population to obtain recommendations for the remaining not-yet-labeled lines in the population of selection candidates.

(6)

In the second iteration $\left(\mathrm{i}=2\right),$ the ${\mathrm{l}}_{\mathrm{i}=2}={\mathrm{l}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}-{\mathrm{l}}_{\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{n}}$ crosses with the highest probability of selection were recommended and labeled to fall into the class of selected lines $(\mathrm{s}\mathrm{e}\mathrm{l}=1)$, reducing the number of recommended lines to the remaining difference towards the target of ${\mathrm{l}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}=60$ lines.

(7)

Steps (2)–(6) were subsequently repeated for $\mathrm{i}=20$ iterations or until the target number of lines ${\mathrm{l}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}=60$ was reached in the pool of chosen lines ${\mathrm{l}}_{\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{n}}=60$.

The initial recommendations for a population of selection candidates were thus based on model training with previous years, followed by feedback by the breeder and re-training the models with an augmented training population. The performance of the above-outlined machine learning models in this scheme was finally compared to a random choice among the lines in terms of the average percentage of found target lines as well as the average percentage of totally labeled lines in each iteration across 50 repetitions of random sampling of the training populations and the populations of selection candidates. The latter was performed by choosing lines randomly from the selection candidates in each iteration instead of choosing the lines with the highest probability to fall into the class of selected lines ($\mathrm{s}\mathrm{e}\mathrm{l}=1$) based on the recommendations made by the different machine learning models. It should lastly be noticed that the first iteration of the suggested algorithm corresponds to the above-described scenario, where the training populations are coming from two cohorts preceding the cohort that was used for validation, i.e., the cohort that contained the pending selection candidates (Figure 2A). All subsequent iterations, on the other hand, corresponded to the above-described scenario, where this training population is augmented with lines coming from the same cohort that was used for validation (Figure 2B).

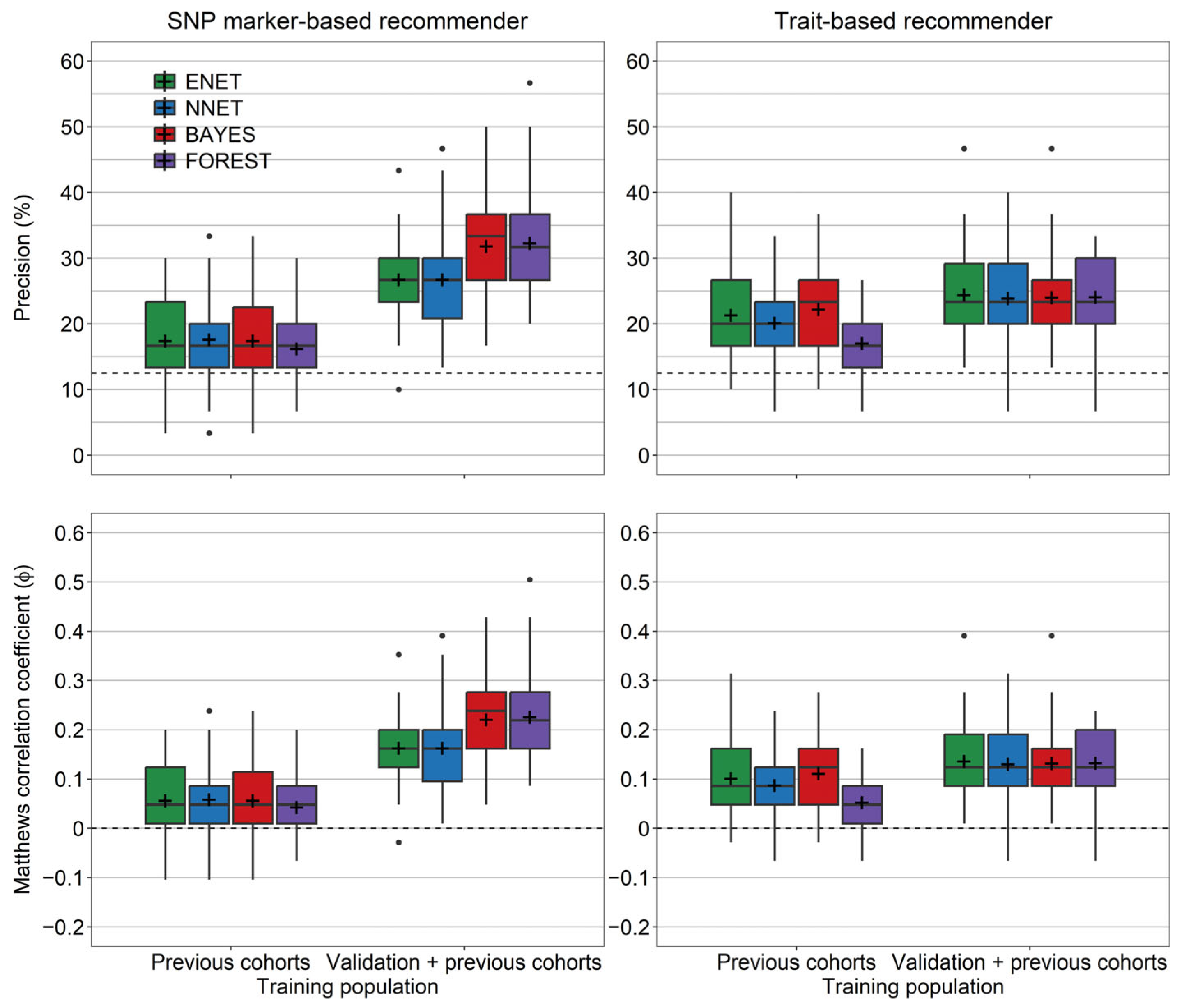
3. Results

The estimated explained variance of breeders’ decisions based on SNP markers with the combination of all five cohorts was of moderate magnitude, with ${\mathsf{\rho }}_{\mathrm{S}\mathrm{N}\mathrm{P}}^2=0.45$, while it was substantially lower when the genomic estimated breeding values of the individual traits served as predictors, with ${\mathsf{\rho }}_{\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{I}\mathrm{T}}^2=0.25$. Similar observations were made when estimating the explained variance of the individual cohorts, suggesting that the SNP markers were able to explain a larger proportion of the breeder’s selection decisions than the genomic estimated breeding values of the employed five agronomic traits (

Table 1. Proportion of the explained variance based either on SNP array data (${\mathsf{\rho }}_{\mathrm{S}\mathrm{N}\mathrm{P}}^2$) or the genomic estimated breeding values of grain yield, protein content, protein yield, extensogram dough energy, and Fusarium head blight severity (${\mathsf{\rho }}_{\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{I}\mathrm{T}}^2)$ for the individual cohorts as well as the combinations among all five cohorts in 2015–2019 for selection decisions made by the breeder in the stage of preliminary yield trials concerning lines that were advanced to the first year of multi-environment trials.

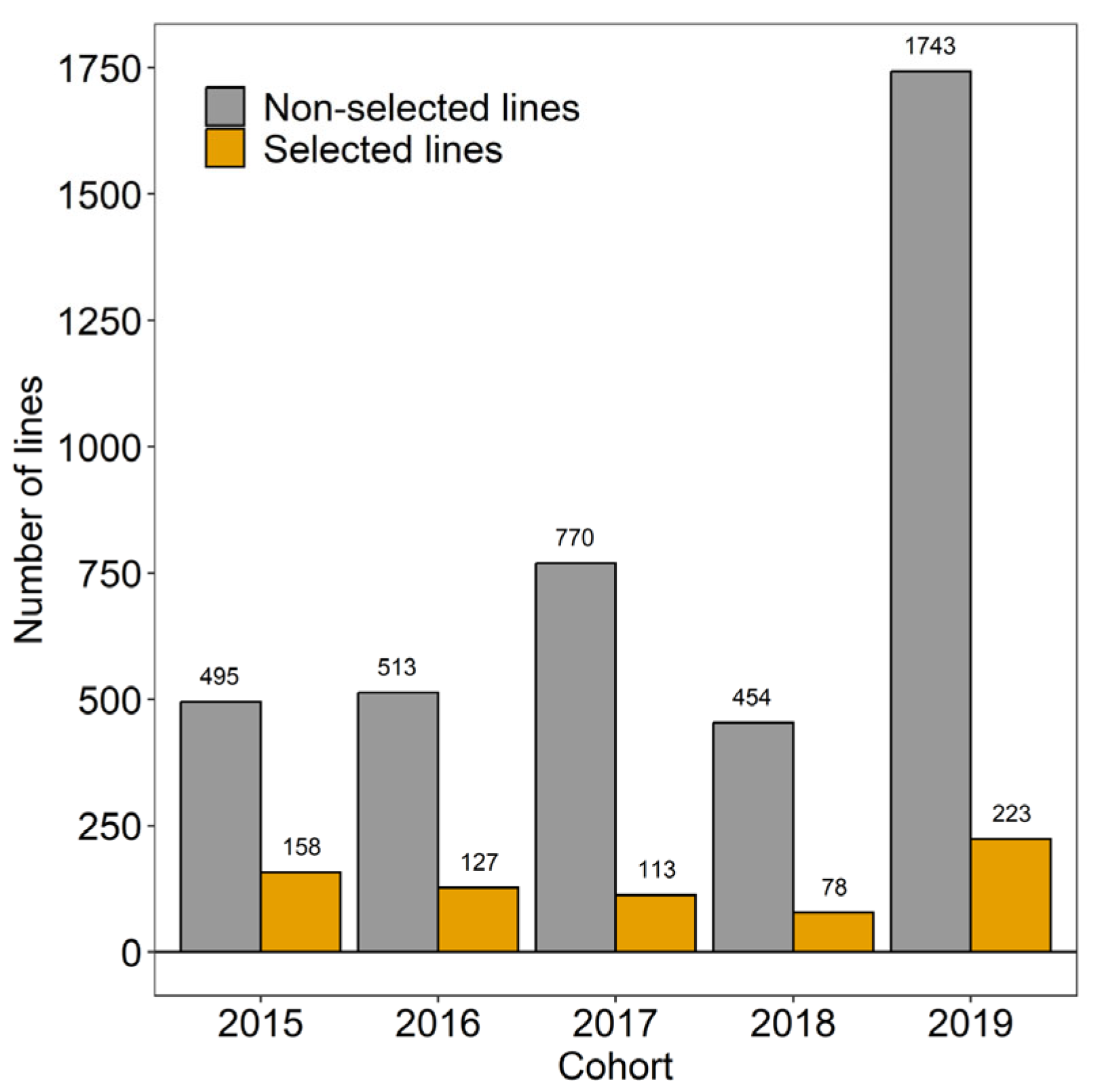
Year	Lines	Non-Selected Lines	Selected Lines	${\mathsf{\rho }}_{\mathbf{S}\mathbf{N}\mathbf{P}}^2$	${\mathsf{\rho }}_{\mathbf{T}\mathbf{R}\mathbf{A}\mathbf{I}\mathbf{T}}^2$
2015	653	495	158	0.77	0.33
2016	640	513	127	0.57	0.32
2017	883	770	113	0.53	0.24
2018	532	454	78	0.55	0.22
2019	1966	1743	223	0.54	0.34
2015–2019	4674	3975	669	0.45	0.25

). The estimated explained variance for the individual cohorts ranged accordingly between ${\mathsf{\rho }}_{\mathrm{S}\mathrm{N}\mathrm{P}}^2=0.53–0.77$ and ${\mathsf{\rho }}_{\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{I}\mathrm{T}}^2=0.22–0.34$ for selection decisions made in the stage of preliminary yield trials concerning lines that were selected for the first year of multi-environment trials. These results thus suggested that the selection decisions taken by the breeder can to some extent be explained by genome-wide distributed SNP markers or genomic estimated breeding values. Hence, in a second step, it was investigated whether these selection decisions are also predictable and can be used in the form of a recommender system.

The usage of SNP markers for model training with the two cohorts preceding the individual cohorts in 2017–2019 that were used for validation resulted in a similar precision of 16.2–17.6% of all four tested statistical and machine learning models (Figure 4), which slightly exceeded the precision of 12.5% that would be expected by a random recommendation of lines for selection. Employing genomic estimated breeding values of the above-mentioned major agronomic traits led to a marked increase in average precisions for the Bayesian logistic models (22.2%), the elastic nets (21.3%), and the neural networks (20.1%) in this scenario (Figure 2A). Augmentation of the training population by lines coming from the same cohort as used for validation (Figure 2B) led to a marked increase in precision both when SNP markers and genomic estimated breeding values were used as predictors (Figure 4). The highest average precision of 32.2% was achieved by random forest models, given that SNP markers were used as predictors in this scenario, while the elastic net performed best when genomic estimated breeding values served as predictors, with a precision of 24.4%. The Matthews correlation coefficient revealed a similar pattern (Figure 4) as the Bayesian logistic models $(\mathsf{\varphi }=0.22)$ and the random forest models $\left(\mathsf{\varphi }=0.23\right),$ showing the best performance, especially when training models with SNP markers and including lines coming from the same cohort as was used for validation.

The retrospective testing of using the recommendations made by the different machine learning models as a selection decision support tool revealed that, on average, a higher percentage of target lines selected by the breeders were found by all models in comparison to a non-systematic random choice among the selection candidates (Figure 5 and Figure S2). The usage of the machine-based recommendations showed, for example, that in most cases more than 60% of the target lines were already identified in the fifth iteration of the reciprocal fine-tuning algorithm, while less than 50% of these lines were found by randomly choosing among the selection candidates. This trend continued in subsequent iterations, and in iteration 15 more than 90% of the target lines were identified on average by using the machine-based recommendations, while only 70% of all lines had to be labeled for this purpose. Using a random selection, 86% of all lines had to labeled to achieve this goal, which corresponded to a relative advantage of 23% and underpinned the merit of the suggested recommender system approach as a selection decision support tool.

4. Discussion

Plant breeding is considered to be the science and art of genetically improving plants according to human needs. Scientific breeding is thereby driven by big data from various omics disciplines, while the art of breeding is determined by breeder’s intuition, experience, and the so-called breeder’s eye [39]. The importance of the art and science aspects therefore changes gradually throughout the multi-stage selection in line breeding programs for crops like bread wheat. A higher weight can probably be ascribed to the art aspect in earlier generations, where selection takes place on a head-row basis, since phenotypic information from precise field trials for agronomic traits such as grain yield is not available. A turning point in this continuum from art to science is certainly the stage of preliminary yield trials and the first assessment of the selection candidates in yield plots, while this is nowadays quite often also the stage in which genotyping data and genomic estimated breeding values are available to breeders [14]. Hence, breeders are usually integrating the science and art aspects when making selection decisions in preliminary yield trials with regard to the material that is advanced to a first year of multi-environment trials.

These selection decisions are inherently complex, and many factors can play a role, for example, field impression, the occurrence of diseases, tackling negative trade-offs such as grain yield and protein content, and the aim to develop potential varieties for specific market segments [37]. Taking the vast additional information coming from genomic estimated breeding values and methods like independent culling with certain thresholds for multiple traits into account renders the final binary classification into selected versus non-selected lines into an array of many small decisions. Notwithstanding, the proportion of explained variance based on genome-wide distributed SNP markers or genomic estimated breeding values of a few major agronomic traits was relatively high, considering the complexity of these selection decisions in the study at hand. Some variation in explained variance was though found when regarding individual cohorts, which might be attributed to some cognitive bias by the breeder, with a certain ideotype in mind when making field observations in early generations, which can be influenced by environmental effects that in this way indirectly introduce a non-genetic trend into the estimation of the explained variance of the selection decisions. However, the medium-scaled proportion of explained variance when using the combination of all five cohorts indicated a common trend during selection decisions in preliminary yield trials, reflecting the fact that the breeder’s selection decision ideally considered both the current as well as future performance of the selection candidates [39].

For the purpose of predicting the complex patterns of these selection decisions during variety development, machine learning algorithms were directly trained with the breeders’ selection decisions. This revealed that the breeder’s selection decisions were to some extent predictable, especially when some lines of the validation cohort, i.e., the cohort containing the pending selection candidates, were included in the training population. Since the increase in training population size from 800 to 1200 lines might have some influence on this observation, it was additionally tested if a larger training population size or specifically the inclusion of the lines from the validation cohort would lead to a higher predictive performance of the machine learning models. Although the predictive performance of the models generally increased when enlarging the training population from 400 to 800 lines, it was evident that the inclusion of lines from the validation cohort resulted in a markedly higher precision and correlation coefficient in comparison to model training based solely on past cohorts at the same training population size (Figures S3 and S4). Although the consensus between the breeders’ selection and machine-based recommendations was only of low to moderate magnitude in the study at hand, it suggested that a breeder can find at least some desired selection candidates among the machine-based recommendations. Hence, one possible strategy to exploit the increase in precision when adding lines from the current cohort to the training population is given by firstly obtaining machine-based recommendations trained with decisions from previous cohorts where, for example, a proportion of the selection candidates are labeled to fall into the classes of the selected genotypes. These recommendations can subsequently be used by breeders for a human analysis and providing feedback to the machine learning algorithm by keeping the selection recommendations for certain lines or by re-labeling recommended lines to fall into the “non-selected” class. The pending selection candidates labeled in this way can then be added to the training population, followed by refitting the prediction model with this extended training population and obtaining updated recommendations for the other pending selection candidates. A final selection decision might, in this way, be reached after several rounds of reciprocal fine-tuning based on the synthesis of artificial and human intelligence [57,58] by repeating this procedure until the desired number of lines is labeled as “select”. Testing such a reciprocal fine-tuning algorithm in a retrospective manner showed that lines preferred by the breeder can be more readily and systematically identified in comparison to a non-systemic approach. Following such a strategy would most likely require the usage of models with a low computational burden to provide rapid results to a breeder and allow the implementation of a flexible feedback system, even when their precision would not be as high in comparison to more sophisticated models and predictor sets. It should, however, also be stressed that the results of the content-based recommender system approach that was employed in the study at hand are specific to the investigated breeding program, while the recommender system methodology itself might generally serve as an interesting selection decision support tool for breeders.

Using such a recommender system would moreover exploit the combined power of machine learning and the human capability of finding solutions in unexpected and changing circumstances, where methods of artificial intelligence are still inferior at the moment [57,59]. Hence, humans can be considered as essential in cases where it is necessary to bridge the gap between science and art in disciplines like plant breeding, while artificial intelligence can be considered as a supporting tool in the decision-making process. Breeders are accordingly able to reach selection decisions that involve thorough considerations about multiple aspects simultaneously, including objective phenotypic data from field trials and more subjective observations like field impressions. It should be noted, however, that a breeder’s selection decisions are not perfect due to the limited information that is available at a certain stage of selection; also, oftentimes the heuristic decision making by breeders might lead to the advancement of some selection candidates through the product development pipeline that do not ultimately fulfill the strict requirements of variety registration trials. Nevertheless, breeders’ selection decisions based on phenotypic observations made in the field, knowledge about the germplasm, and data-driven inputs such as genomic estimated breeding values can still be considered the gold standard for finding genotypes with favorable trait combinations and boosting crop genetic improvement.

Another way to aid breeders in the inherently difficult task of finding such promising genotypes, aside from recommending individual selection candidates by statistical and machine learning algorithms, is given by selection indices that feature continuous scaling. Although selection indices such as grain yield deviations and grain protein deviations, involving the two major agronomic traits grain yield and protein content, have gained popularity, e.g., in wheat breeding [60,61], finding objective weights for selection indices that involve all relevant traits is difficult in plant breeding. Such selection indices might be moreover defined solely based on statistical aspects, leaving out breeders’ preferences, which can lead to a low acceptance of these indices by breeders as a selection tool. Bernardo (1991) [62] suggested a retrospective index based on selection differential applied by a breeder in order to derive index weights. Even though this approach is limited to a certain array of assessed traits, such a retrospective index will clearly reflect a breeder’s preferences, giving it a higher chance to be applied in practice. Extending this approach, a related index can be obtained by training machine learning algorithms with breeders’ selection decisions and deriving the probabilities of new selection candidates to fall into the class of selected genotypes. The continuous scaling of these probabilities as a breeder index would make it possible to rank young selection candidates and ease the identification of genotypes with favorable trait combinations. The most convenient option for implementing such a strategy is probably given by deriving such a breeder index once with a model and predictor set that provides high precision, irrespective of the computational burden. The breeder index might in this way routinely obtain back-to-back genomic estimated breeding values as used in combination with other index selection approaches [60,63,64,65], representing a complement or alternative to the here-suggested recommender system with a binary classification according to selected and non-selected genotypes.

5. Conclusions

This study investigated the possibility of implementing a recommender system based on breeders’ preferences to support early generation selection decisions in plant breeding by using breeders’ selection decisions from a commercial wheat breeding program as a case study. It was found that for the breeder’s selection decisions, the medium-scaled proportion of variance could be explained by genome-wide distributed SNP markers as well as the genomic estimated breeding values of a few major agronomic traits, even when considering the combination of different cohorts from multiple years. Training machine learning algorithms with the selection decisions made by this experienced breeder revealed that they were, to some extent, predictable across and within cohorts. These predictions might accordingly be used in the form of a recommender system, and it is suggested that a final selection decision is reached after several rounds of reciprocal fine-tuning, based on recommendations by a statistical or machine learning algorithm and feedback given to this prediction model by the breeder. Deriving a breeders’ index based on the mentioned algorithms might alternatively be useful both for young and senior breeders for checking up on their breeding goals and potentially as a supporting tool to guide their selection decisions. Training statistical or machine learning algorithms with expert knowledge has great potential to aid breeders in their decision-making processes, especially when integrating human and artificial intelligence in the form a recommender system to reduce a breeder’s effort and required time in finding interesting selection candidates.