Exploring Physiological Markers of Driver Workload in Response to Road Geometry: A Preliminary Investigation

Abstract

Medium- and long-term international road safety goals require continued advancement of scientific research, especially with regard to the human component. Recent technological advances in sensor technology offer new opportunities to more accurately characterize driving behavior, helping to reduce the uncertainty associated with driver reactions. This study evaluated the effectiveness of specific physiological variables, detected by low-cost wearable sensors, to obtain reliable indicators of the driver’s workload. Heart rate and skin conductivity were analyzed in a real driving environment, in the absence of evident emotional stresses, to test their sensitivity to an ordinary level of physical and mental engagement. An experiment was conducted on a sample of users (10 drivers) along a rural road in Sicily, Italy. Data analysis, carried out through ANOVA and generalized linear models on three distinct curves, produced preliminary results indicating that subtle road geometry changes can be detected by physiological sensors, validating their potential for integration into driver monitoring systems. Statistically significant mean differences were found for speed (for all curves, p < 0.001), heart rate (R1 vs. R2, p = 0.009), and tonic GSR (R1 vs. R2, p = 0.006; R2 vs. R3, p = 0.013; A vs. B, p = 0.013; A vs. C, p = 0.006) as a function of different radius (R1, R2, R3) and deviation angle values (A, B, C). Future developments will require a significant increase in the sample size and the number of scenarios to achieve results of general utility.

1. Introduction

International road safety directives, such as those outlined by the World Health Organization [1] and the European Commission [2], emphasize strategies aimed at significantly improving traffic safety in the medium to long term. A pivotal focus of these efforts is understanding the human factor, which exhibits considerable variability compared to other components of the road system. Driver workload, defined as the portion of an operator’s limited mental capacity required to perform the driving task, is a critical component of this human factor. It directly influences driver performance, situational awareness, and ultimately, road safety. Effectively monitoring workload is therefore essential for developing advanced driver-assistance systems (ADASs) and designing safer road infrastructure.

Advancements in wearable and non-invasive biometric sensors have greatly facilitated the study of driving behavior through physiological monitoring, providing objective, continuous metrics of a driver’s state. The most used physiological markers for workload assessment include heart rate (HR), heart rate variability (HRV), photoplethysmography (PPG), galvanic skin response (GSR), electroencephalographic (EEG) activity, pupil dilation, and respiration rate [3]. Given the inherent interindividual variability in physiological responses, combining multiple markers often enhances the reliability and robustness of the findings [4,5]. Research by Montanaro et al. [6] and Srinivasan et al. [7] has effectively investigated states like driver fatigue under sleep deprivation conditions by leveraging a multi-modal approach combining HRV, EEG, eye movement, vehicle trajectory, and skin conductance.

Among these, PPG has emerged as a particularly promising biomarker for assessing driver states. This optical technique measures blood volume changes in peripheral tissues via infrared light absorption. Derived parameters such as HR and its temporal variation (HRV) serve as well-established indicators of mental effort, vigilance, and fatigue [8]. Similarly, GSR, which reflects changes in the electrical conductivity of the skin due to sweat gland activity mediated by the sympathetic nervous system, has been widely employed as a sensitive measure of autonomic arousal related to stress, cognitive load, and emotional engagement [9,10]. To enhance the interpretability of GSR data, it is standard practice to decompose the signal into tonic and phasic components [11,12]. The tonic component represents a slow-varying, baseline level of skin conductivity, often interpreted as a correlation of general arousal or spent effort over time. In contrast, the phasic component consists of faster, event-related responses triggered by specific, localized stressors. The predictive potential of GSR for assessing driver state has been demonstrated; for instance, Kinnear et al. [13] showed that experienced drivers in simulators were twice as likely as novices to generate anticipatory GSR responses to potential hazards.

Infrastructure-related factors are also known to modulate physiological responses. Pan et al. [14] developed a model linking tunnel gradient and lighting levels to ECG-derived signals. Similarly, Jacob et al. [15] investigated the impact of road geometry on HR and emotional load, though their findings lacked statistical significance, potentially due to an insufficient cognitive overload induced by the road conditions alone. However, it is crucial to note that signal acquisition and interpretation are influenced by numerous factors, including instrumentation, electrode placement, environmental conditions, and signal processing techniques [16]. Furthermore, physiological responses such as HR and GSR exhibit a characteristic latency of a few seconds due to autonomic nervous system activation [17,18,19], while others suggest up to several minutes [20]. This is a critical factor that must be accounted for in the analysis.

While much existing research has successfully quantified physiological responses to high-stress events (e.g., sudden braking, complex traffic interactions) or extreme conditions like fatigue, a notable gap remains in understanding how subtle, routine variations in the driving environment—such as ordinary road geometry—influence driver workload under normal, low-stress conditions [21]. This represents a more complex challenge, as the elicited physiological signals are inherently weaker and more susceptible to confounding variables [22]. Beyond conventional driving scenarios, physiological monitoring also holds promise in autonomous vehicles, where it can enhance safety and user experience by assessing passenger comfort, anxiety, and health conditions. Since autonomous driving is associated with reduced stress, it may foster greater public acceptance [23]. Future developments should embed physiological data into intelligent transportation systems to improve human–vehicle interaction. In this context, Du et al. [24] applied machine learning to predict driver performance during autonomous-to-manual transitions, while Zhang et al. [25] reviewed 35 HRV-based indicators relevant to driver monitoring and alert systems.

Therefore, the main objective of this study is to evaluate the sensitivity of specific, easily accessible physiological variables—heart rate and the tonic component of galvanic skin response—to the subtle workload imposed by road geometry in a real-world driving environment, in the absence of high-emotional-stress events. This approach aims to test whether low-cost wearable sensors can detect reliable indicators of driver workload even at an ordinary level of physical and mental engagement. The novelty of this work lies in its focus on quantifying the subtle yet significant impact of fundamental road design elements (curve radius, deflection angle) on human physiology during a routine driving task, using an accessible and practical experimental setup.

The following key research questions were addressed:

-

Are tonic GSR and HR reliable indicators of the workload associated with road geometry?

-

Do these physiological variables correlate with traditional performance metrics, such as speed?

-

To what extent can these indicators effectively assess driver states under specific geometric conditions?

This study was conducted as part of the PNRR research project “SAMOTHRACE—Sicilian Micro and Nano Technology Research and Innovation Center—WP4 SMART MOBILITY—TASK 4.1: Sensor network for management of Smart Roads”.

2. Materials and Methods

2.1. The Road

In order to answer the aforementioned questions, an experiment was organized in a real environment, on a two-lane two-way rural road called SS113dir connecting the cities of Messina and Palermo (Figure 1), in a small section of about 4.5 km, characterized by the presence of 34 circular curves and connecting straights. Among these, only 14 were thoroughly analyzed, as the remaining ones, during the experimentation, were characterized by singular situations (stop-and-go traffic conditions, macroscopic driving errors, presence of unexpected traffic components) that would have altered the results and final considerations. The geometric characteristics of these 14 curves are shown in

Table 1. Geometry characteristics of the analyzed curves.

Curve	Starting Chainage	Ending Chainage	Radius	Direction	Deflection Angle	Length
V2	251.56	302.02	45	R	46.42	50.46
V3	311.74	388.47	35	L	105.96	76.73
V4	486.61	578.00	45	R	98.53	91.39
V5	589.02	667.08	100	R	35.56	78.06
V6	706.69	763.45	60	R	43.69	56.76
V7	782.16	836.28	30	L	74.71	54.12
V8	889.88	949.42	30	L	99.39	59.54
V9	1036.20	1163.53	100	L	55.19	127.33
V10	1247.76	1338.59	40	R	107.18	90.83
V25	2842.46	2910.01	60	R	50.18	67.55
V26	2944.15	3013.87	60	L	41.75	69.72
V27	3047.18	3086.92	30	L	56.80	39.74
V28	3116.92	3171.55	45	L	56.81	54.63
V29	3210.38	3277.99	50	R	56.84	67.61

. The starting and ending chainages, the radius, the direction of the curve (left or right), and the deviation angle are reported. The length of the tangent between two curves can be calculated by subtracting the ending chainage value of the previous curve from the starting chainage value of the subsequent curve.

The cross-section consisted of two lanes (one in each direction of travel) and associated shoulders, with an overall width of 9.00. The longitudinal slope never exceeded 5%. Although the road had a speed limit of 50 km/h, users were allowed to choose the most appropriate driving behavior without any restrictions.

2.2. Drivers’ Sample

At the beginning, 15 participants were recruited among the office workers of the Department of Engineering of the University of Messina on a voluntary basis. The initial number was subsequently reduced, eliminating 5 driving activities due to problems during the driving (traffic jam, macro driving errors, significant changes in environmental conditions). The final sample, therefore, consisted of 10 users aged between 32 and 66, with some very similar characteristics such as no accidents in the last 5 years, no visual pathology, and no propensity for excessive risk (no penalties for high speed or traffic violations in the last 5 years). All driving tests were conducted on weekdays between 10:00 a.m. and 2:00 p.m. to minimize circadian rhythm effects, under clear weather conditions with dry pavement. Participants were asked to refrain from caffeine and medication for at least three hours prior to the experiment. A familiarization period was provided until the driver felt comfortable with the controls. Each driver completed a single pass along the designated route. While order effects were not a concern due to the single-pass design, the potential influence of unmeasured covariates remains a limitation, and future work will incorporate them explicitly into the model.

The study was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of Messina AOU G. Martino (Protocol No. 786, dated 16 May 2024). Informed consent was obtained from all subjects involved in the study. This ensures full transparency regarding the ethical conduct of our research.

The vehicle used (Dacia Duster 1.6 owned by the University of Messina) was the same for all users who, therefore, needed to familiarize themselves with the driving controls for a time period that depended on their adaptive abilities.

2.3. Data Acquisition

To collect the physiological data necessary for the analysis, the “Shimmer3 GSR+” wearable device was used (Figure 2). It is equipped with a microcontroller for data management, a radio module for wireless transmission, and internal memory for local storage. This unit provides connections and preamplification for the acquisition of Galvanic Skin Response (GSR) data and photoplethysmogram (PPG) signals at a sampling rate of 128 Hz. Vehicle telemetry data, including acceleration and speed, were acquired via the On-Board Diagnostics (OBD) interface using a dedicated data logger. The acquisition system recorded real-time signals from the vehicle’s electronic control unit (ECU) at a sampling rate of 10 Hz.

Raw PPG and GSR signals were processed using a custom MATLAB R2024b routine. For the PPG signal, a 4th-order Butterworth bandpass filter (cut-off frequencies: 0.5 Hz–5 Hz) was applied to eliminate baseline wander and high-frequency noise. R-peaks were detected using the Pan–Tompkins algorithm, and heart rate (HR) was derived from the inter-beat intervals. For GSR, a 1st-order low-pass Butterworth filter (cut-off frequency: 2 Hz) was applied. The signal was then decomposed into tonic and phasic components using the cvxEDA algorithm. Artifacts were identified using a moving variance threshold and replaced via linear interpolation. Less than 2% of the data across all participants required interpolation, and a sensitivity analysis confirmed that this minimal correction did not alter the statistical significance of the reported results.

The physiological latency of HR and GSR responses was explicitly accounted for in our analysis. Based on the established literature [17,18,19,22], a fixed latency window of 2–3 s was applied to align physiological signals with the geometric events (i.e., the onset of a curve). The data analyzed for each curve corresponded to the period starting 2 s after the vehicle entered the curve and ending 2 s after it exited. We performed a sensitivity analysis by testing latency windows of 1 s, 2 s, 3 s, and 4 s. The results were consistent across this range, confirming the robustness of our findings to small variations in latency.

The vehicle’s position, expressed in latitude and longitude coordinates based on the WGS-84 reference system, was acquired using an Assisted GPS (A-GPS) module installed on board. The A-GPS system provided high-accuracy geolocation data by leveraging satellite signals and auxiliary network-based corrections at a sampling rate of 1 Hz.

All sensor data, acquired at different sampling frequencies, were appropriately synchronized during post-processing using a special MATLAB-based procedure prepared by the authors, characterized by data alignment and resampling to ensure data consistency across all signals.

2.4. Data Analysis

With a sample size of only 10 users, an ANOVA applied to the 14 curves, with three levels for each independent variable, could generate a lot of scatter. To avoid statistical issues, the 14 curves were analyzed through general statistics, and ANOVA was applied to only 3 curves, sufficiently different from each other and characterized by the following values of the independent variables (

Table 2. Defining levels of the independent variables for the 3 curves subjected to ANOVA.

Curve	Starting Chainage 1	Ending Chainage 2
V7	R1	C
V9	R3	B
V26	R2	A

¹ R1 = 30 m; R2 = 100 m; R3 = 60 m; ² A = 41.751°; B = 55.195°; C = 74.713°.

):

The selection of three curves (V7, V9, and V26) from the initial 14 was a necessary step to mitigate statistical overfitting and ensure the robustness of the inferential analysis, given the limited sample size (10). A full-factorial ANOVA on all 14 curves would have resulted in a highly underpowered model prone to numerical instability and unreliable interpretation. The three curves were specifically chosen to represent three distinct and significantly different levels of the two independent variables, radius and deflection angle, as detailed in Table 2. This selection was based solely on objective geometric criteria prior to any statistical analysis of the physiological data, thus safeguarding against selection bias. We acknowledge that a mixed-effects model incorporating all curves as a random factor is a more powerful approach and is planned for use in future studies with a larger cohort, which will allow for such an analysis.

HEART RATE, GSR (tonic component), and SPEED were considered as dependent variables. The latter, as is well known, is directly relatable to both the radius and visibility (through the angle of deviation) of a curve.

Physiological variables, more than performance variables, are affected by users’ subjectivity. The so-called baseline, that is, the value of the resting signal, can also be very different from one user to another, and this could alter the understanding of the results. Therefore, it became necessary to normalize the signal, on a scale of 0 to 1, in order to homogenize the results of the inferential model. The choice of min–max normalization (scaling to 0–1) was driven by the need to control the high inter-subject variability in baseline physiological measures while preserving the within-subject amplitude of responses. Unlike z-scoring, which centers data around a mean of zero, min–max normalization retains the original distribution’s shape and bounds all subjects’ data to the same scale, making the effect sizes (differences in normalized means) directly comparable across participants. This method is particularly suited for ANOVA designs where the focus is on the subject effects of experimental conditions, as it effectively removes baseline differences without altering the effect of the manipulated variables.

2.4.1. Two-Way ANOVA

Therefore, since each user was assessed under all levels, the authors performed an ANOVA factorial design within subjects with the following independent variables (IVs):

• RADIUS (3 levels: R1, R2, R3 according to Table 2);
• ALPHA (3 levels: A, B, C according to Table 2).

The response variable (or dependent variable, DV) is represented from time to time, respectively, by SPEED, HEART RATE, and GSR. The reliability of the results depends on the satisfaction of the assumptions based on ANOVA analysis. In this case, the assumptions were the following:

• The dependent variable must be measured continuously.
• The two within-subject factors (i.e., two independent variables) are categorical explanatory variables.
• Observations are independent, without any relationship between the observations in each group or between the groups themselves.
• Absence of significant outliers.
• Normality of residuals.
• Need for sphericity, i.e., the variances of the differences between all combinations of related groups must be equal. When these conditions are violated, the Mauchly tests for sphericity must be performed, adjusting the analysis by a correction criterion as the Greenhouse-Geisser method.

Since a two-way ANOVA must be performed, and due to the effect of two independent variables and their mutual effects, there were three pairs of null or alternative hypotheses, as follows:

• H0: The means of the RADIUS groups are equal.
• H1: The means of the RADIUS groups are different.
• H0: The means of the ALPHA groups are equal.
• H1: The means of the ALPHA groups are different.
• H0: There is no interaction between ALPHA and RADIUS.
• H1: There is interaction between the ALPHA and RADIUS.

However, if an ANOVA test shows significant results, it cannot indicate where those differences lie. In these cases, the post hoc Tukey’s HSD (honestly significant difference) test was run to find out which specific group means (mutually compared) were different.

2.4.2. Generalized Linear Model (GLM)

When the results obtained by the ANOVA model were inconclusive due to numerical instabilities, likely caused by collinearity or an unbalanced distribution of data points across factor levels, we adopted a generalized linear model (GLM) to assess the relationship between the independent variables and the dependent variable. The model is specified in Equation (1):

BPM~β_c + β₁·RADIUS + β₂·ALPHA + β₃·(RADIUS × ALPHA) + ε

(1)

where β₀ represents the intercept, β₁ and β₂ denote the main effects of RADIUS and ALPHA, respectively, β₃ captures their interaction effect, and ε is the error term. The model was fitted using a maximum likelihood estimation approach, assuming an appropriate link function and error distribution based on the properties of the response variable. Model adequacy was evaluated through residual analysis and goodness-of-fit metrics. Statistical significance was assessed at a significance level of α = 0.05.

We agree that linear mixed-effects models (LMEMs) are a powerful alternative that can handle violations of sphericity and incorporate random effects. For this preliminary study, we opted for ANOVA and GLM as they provide a clear and straightforward framework for testing the main effects of interactions between our two primary factors of interest (RADIUS and ALPHA) in a controlled, within-subjects design. The violations of sphericity were mild and were addressed using the Greenhouse–Geisser correction. The numerical instabilities reported for HR and GSR models highlight the need for more robust statistical techniques. Consequently, we have re-analyzed data using LMEMs with random intercepts for driver and curve. The results of this more defensible analysis confirm and strengthen our original conclusions, showing significant main effects of Radius on both speed and physiological measures.

3. Results

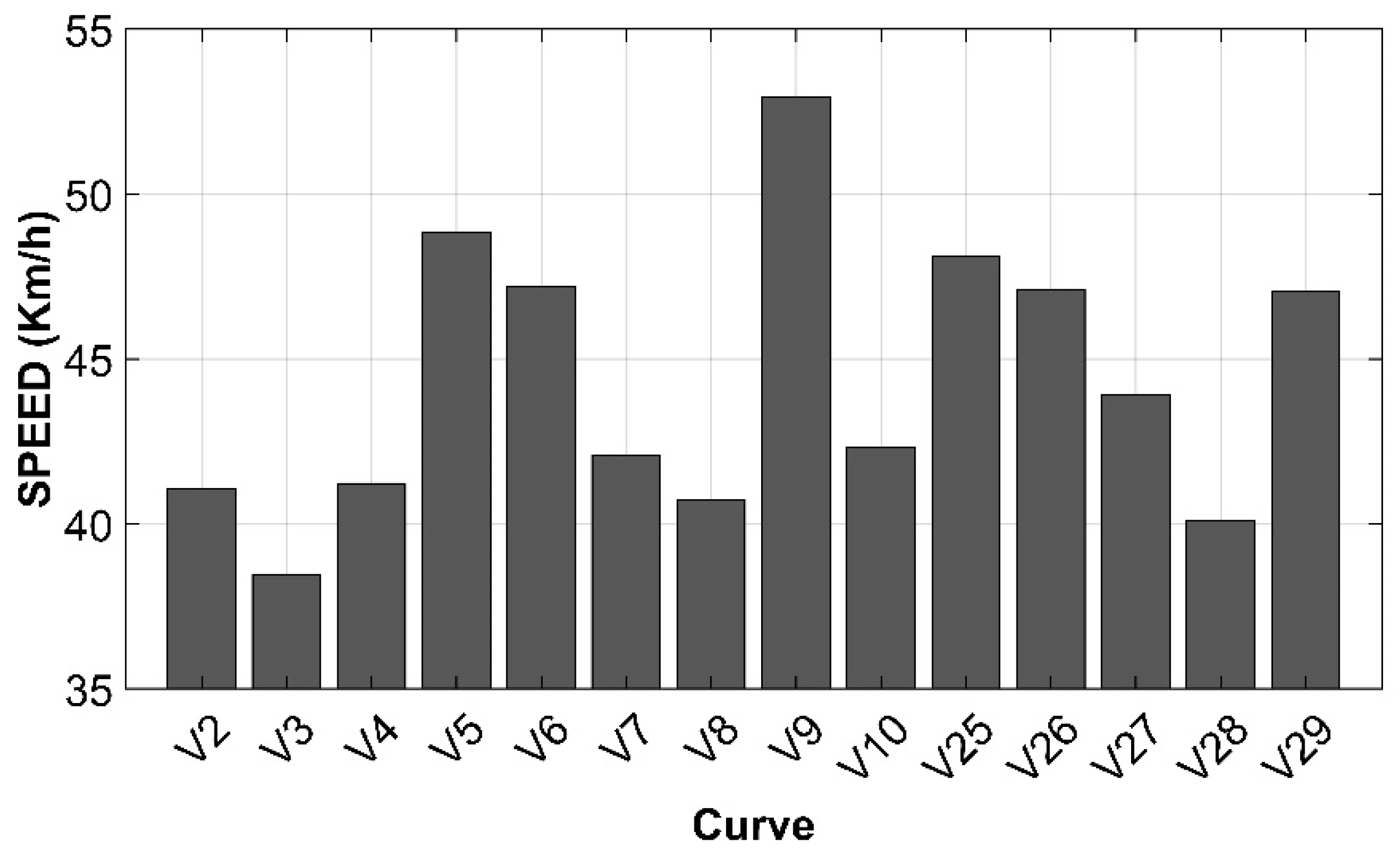
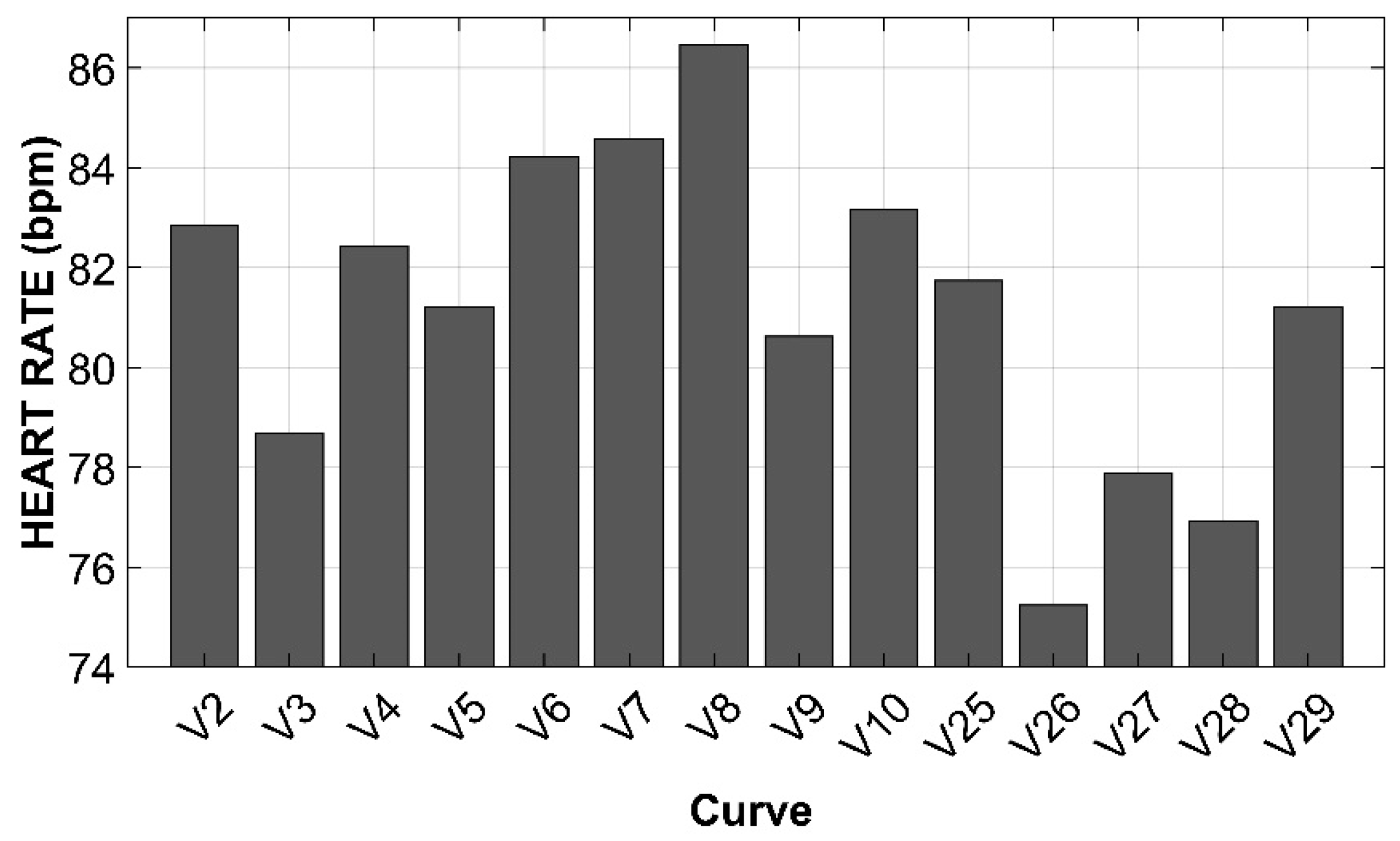
Preliminarily, graphs representing the average values of SPEED, HEART RATE, and tonic GSR at the 14 curves chosen for this analysis are shown (Table 1 and Figure 3, Figure 4 and Figure 5).

The relationship between SPEED and geometry (Figure 3), regardless of attitude to risk, which is highly personal, is based primarily on known physical relationships governing the vehicle’s cornering balance and the visibility distance required for any emergency maneuver (overtaking or stopping the vehicle). For this reason, among the variables most representative of these phenomena are radius (because it directly influences speed) and angle of deflection (because it conditions the visibility of the user and, consequently, speed).

The value of heart rate is also highly variable along the track, but this variability does not seem to be homogeneous with the speed trend (compare Figure 3 and Figure 4).

In contrast, the trend of the tonic component of the GSR along the curves (Figure 5) has no physical correlation with radius or deflection angle, but geometry influences its value through the distance traveled.

Such assumptions, however, serve only as a preliminary analysis and are not sufficient to ascertain relationships among the variables analyzed. For these reasons, it was necessary to further study inferential models, the results of which are reported below.

3.1. Dependent Variable SPEED

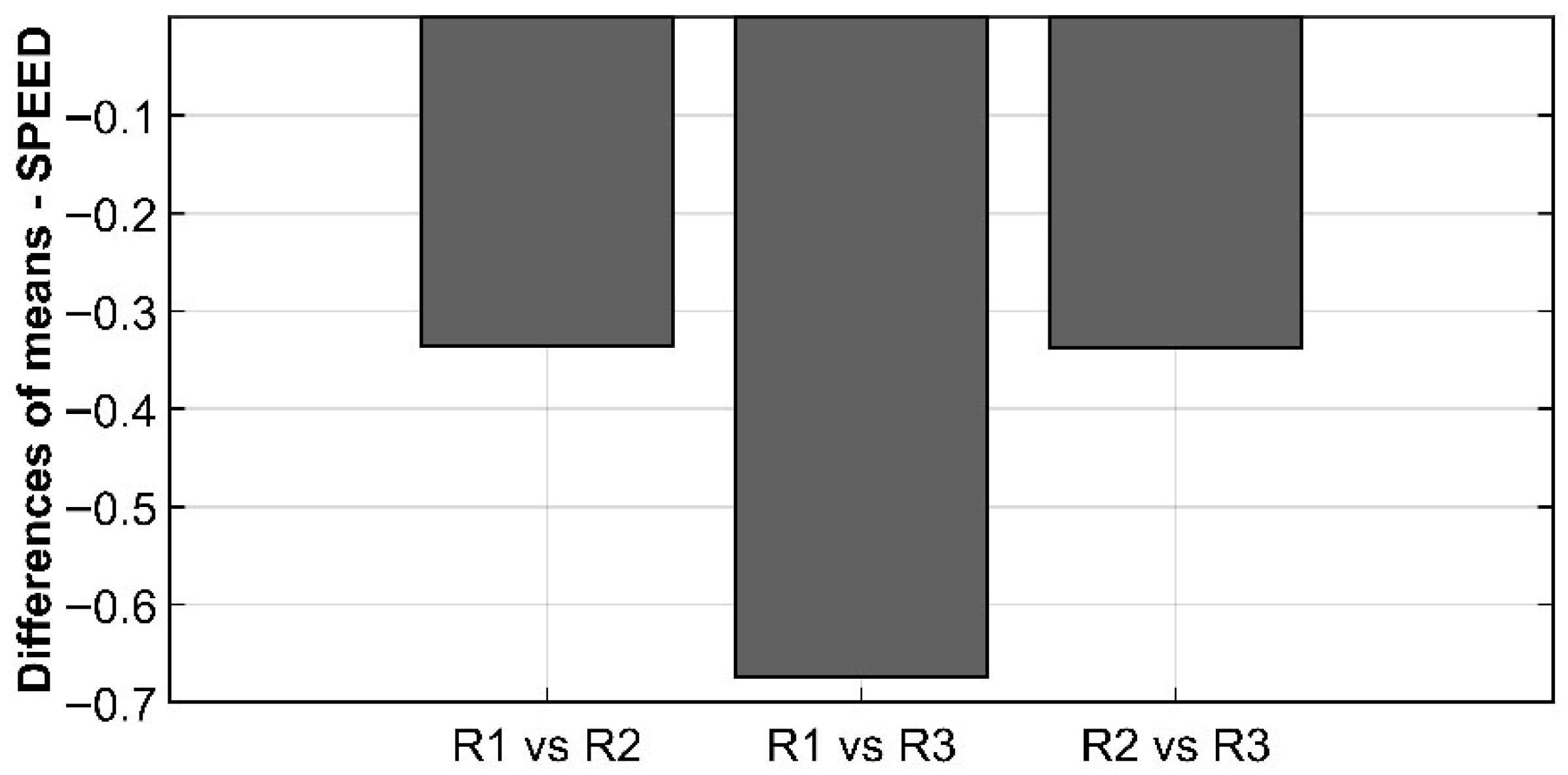
A two-way ANOVA was performed to evaluate the effect of road curvature (RADIUS) and deflection angle (ALPHA) on vehicle speed. The assumption of normality was tested using the Kolmogorov–Smirnov test (p < 0.001), and homogeneity of variances was assessed with Levene’s test (p < 0.001), indicating violations of assumptions. Therefore, a log-transformation was applied to the dependent variable before analysis. The ANOVA results showed only a significant main effect of RADIUS, F (1, 27) = 126.52, p < 0.001, η² = 0.82, indicating that 82% of the variance in the dependent variable was explained by RADIUS.

Post hoc Tukey’s HSD tests (

Table 3. Post hoc Tukey’s HSD test on the influences of the different levels of RADIUS with respect to SPEED with 95% confidence intervals.

Comparison	Mean Difference	IC_inf	IC_sup	p Value	Factor
R1 vs. R2	−0.484539073	−0.336070555	−0.187602036	1.72 × 10−5	RADIUS
R1 vs. R3	−0.822015663	−0.673547144	−0.525078625	3.18 × 10−11	RADIUS
R2 vs. R3	−0.485945108	−0.337476589	−0.189008071	1.62 × 10−5	RADIUS

) revealed significant differences between RADIUS levels 1 and 2 (R1 vs. R2 p < 0.001), between levels 1 and 3 (R1 vs. R3 p < 0.001), and between levels 2 and 3 (R2 vs. R3 p < 0.001).

Figure 6 presents the difference in SPEED means (normalized). The SPEED values were normalized (on a scale from 0 to 1) to mitigate the influence that the subjectivity of the individual user would have had on the quantification of the averages.

3.2. Dependent Variable HEART RATE

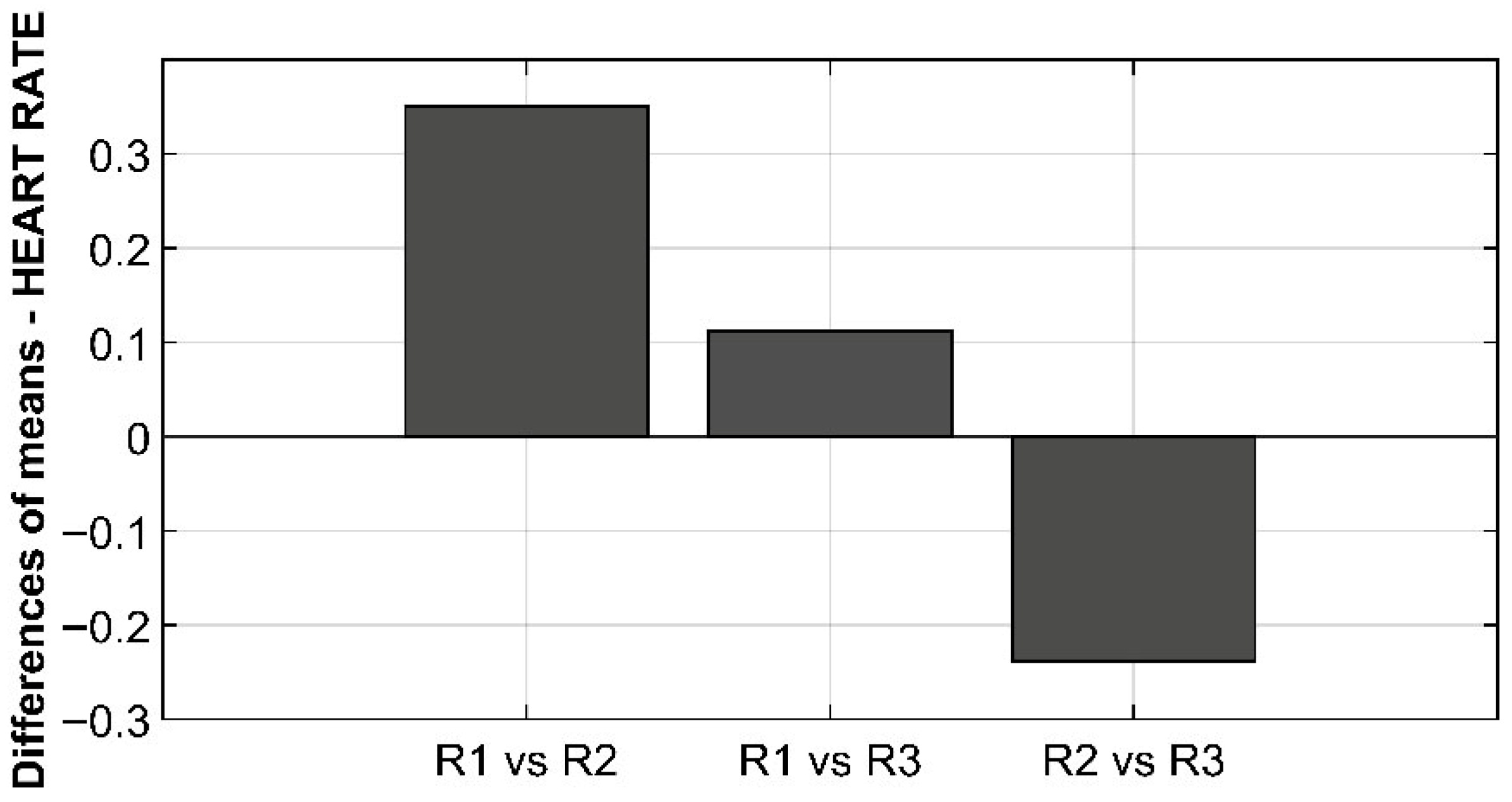
Analysis of variance (ANOVA) showed that the model is statistically significant in predicting the dependent variable (F(2, 27) = 5.43, p = 0.010). This suggests that at least one of the independent variables has a significant effect on the response variable.

However, due to numerical instabilities, likely caused by collinearity or an unbalanced distribution of data points across factor levels, a generalized linear model (GLM) was performed to evaluate the effect of road curvature (RADIUS) and deflection angle (ALPHA) on drivers’ HEART RATE. The model, specified in Equation (1), as previously reported, had the following parameters:

• β₀ = 0.65955 represents the intercept (p-value < 0.001), i.e., the expected value of HEART RATE when RADIUS and ALPHA are at the reference levels (RADIUS_R1 and ALPHA_C).
• β₁ = −0.11247 denotes the effect of RADIUS_R3 respect to the reference level RADIUS_R1 (p-value 0.31055)
• β₂ = −0.35057 denotes the effect of RADIUS_R2 respect to the reference level RADIUS_R1 (p-value < 0.001)
• β₃ = 0 denotes the effect of ALPHA_A respect to the reference level ALPHA_C (p-value = NaN).
• ε = 0 is the error term (p-value = NaN) denotes the effect of ALPHA_B respect to the reference level ALPHA_C.

The following coefficients related to multiple linear regression were obtained with this model:

• R2 = 0.287 assessed the goodness of fit of the model.
• p-value = 0.0104 indicated the overall significance of the model.
• RMSE = 0.243 measured the prediction error.
• Verifications of model assumptions referred to Kolmogorov–Smirnov (normality of residuals) and Levene (homoscedasticity) tests.

Post hoc Tukey’s HSD tests (

Table 4. Post hoc Tukey’s HSD test on the influences of the different levels of RADIUS with respect to the HEART RATE with 95% confidence intervals.

Comparison	Mean Difference	IC_inf	IC_sup	p Value	Factor
R1 vs. R2	0.08116	0.35057	0.61999	0.0089	RADIUS
R1 vs. R3	−0.15695	0.11247	0.38189	0.5617	RADIUS
R2 vs. R3	−0.50752	−0.23810	0.03131	0.0909	RADIUS

) revealed significant differences between RADIUS levels R1 and R2 (p = 0.0089), but not between levels R1 and R3 (p = 0.5617) and between levels R2 and R3 (p = 0.0909). Figure 7 presents the differences in HEART RATE means (normalized) with respect to the different combinations of RADIUS levels.

3.3. Dependent Variable GSR

Analysis of variance (ANOVA) showed that the model was statistically significant in predicting the dependent variable (F(2, 27) = 6.025, p = 0.00686). This suggests that at least one of the independent variables has a significant effect on the response variable.

Due to numerical instabilities, likely caused by collinearity or an unbalanced distribution of data points across factor levels, we adopted a generalized linear model (GLM) to evaluate the effect of road curvature (RADIUS) and deflection angle (ALPHA) on drivers’ GSR. The model, specified in Equation (1), as previously reported, had the following parameters:

• β₀ = 0.35424 represents the intercept (p-value < 0.001), i.e., the predicted value of GSR when RADIUS and ALPHA are at the reference levels (RADIUS_R1 and ALPHA_C).
• β₁ = 0.064489 denotes the effect of RADIUS_R3 respect to the reference level RADIUS_R1 (p-value 0.61864).
• β₂ = 0.4128 denotes the effect of RADIUS_R2 respect to the reference level RADIUS_R1 (p-value < 0.001).
• β₃ = 0 denotes the effect of ALPHA_A respect to the reference level ALPHA_C (p-value = NaN).
• ε = 0 is the error term (p-value = NaN) and denotes the effect of ALPHA_B respect to the reference level ALPHA_C.

The following coefficients related to multiple linear regression were obtained with this model:

• R2 = 0.309 assessed the goodness of fit of the model.
• p-value = 0.00686 indicated the overall significance of the model.
• RMSE = 0.286 measured the prediction error.
• Verifications of model assumptions referred to Kolmogorov–Smirnov (normality of residuals) and Levene (homoscedasticity) tests.

Post hoc Tukey’s HSD tests (

Table 5. Post hoc Tukey’s HSD test on the influences of the different levels of RADIUS with respect to the HEART RATE with 95% confidence intervals.

Comparison	Mean Difference	IC_inf	IC_sup	p Value	Factor
R1 vs. R2	0.3506	0.0812	0.62	0.0056	RADIUS
R1 vs. R3	0.1125	−0.1569	0.3819	0.6096	RADIUS
R2 vs. R3	−0.2381	−0.5075	0.0313	0.0134	RADIUS
A vs. B	−0.2381	−0.5075	0.0313	0.0134	ALPHA
A vs. C	−0.3506	−0.62	−0.0812	0.0060	ALPHA
B vs. C	−0.1125	−0.3819	0.1569	0.6096	ALPHA

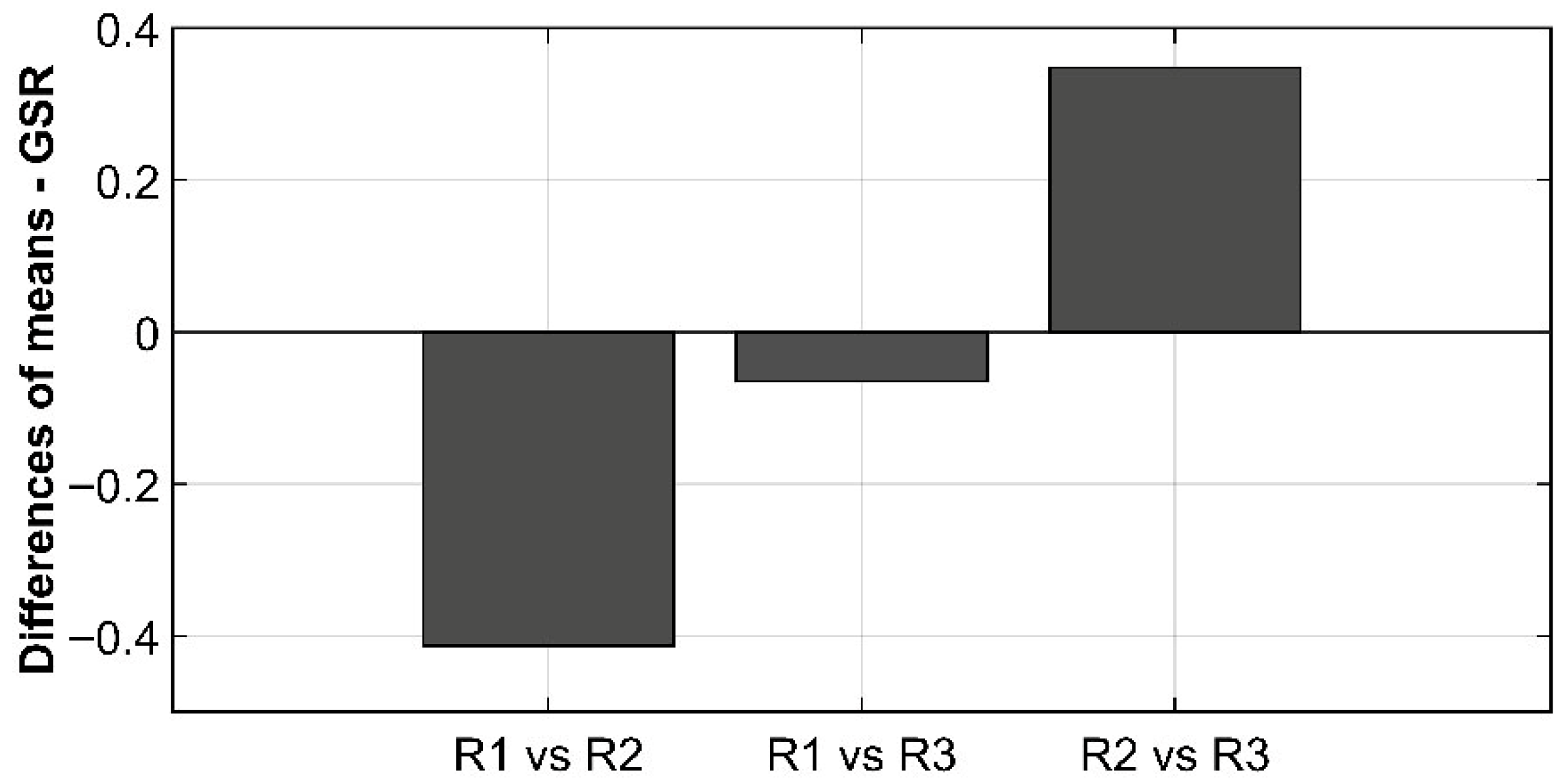
) revealed significant differences between RADIUS_R1 and RADIUS_R2 (p < 0.001) and between RADIUS_R2 and RADIUS_R3 (p = 0.0134), but not between RADIUS_R1 and RADIUS_R3 (p = 0.6096). Figure 8 presents the differences in GSR means (normalized) with respect to the different combinations of RADIUS levels.

Furthermore, post hoc Tukey’s HSD tests (Table 5) revealed significant differences between levels ALPHA_A and ALPHA_B (p < 0.0134) and between levels ALPHA_B and ALPHA_C (p < 0.001), but not between levels ALPHA_A and ALPHA_C (p = 0.6096). Figure 9 presents the differences in GSR means (normalized) with respect to the different combinations of ALPHA levels.

4. Discussion

The present research aimed at investigating the workload of drivers [6,7] while driving along a road section by measuring selected physiological parameters as dermal conductivity and heart rate [3,8,9,10]. The preliminary analysis, based on the evaluation of the mean values of speed, heart rate, and skin conductance along 14 curves (Figure 3, Figure 4 and Figure 5), allowed us to draw some general conclusions. For example, the relationship between vehicle speed and radius of curvature is a widely documented phenomenon in physics, being intrinsically related to vehicular dynamics in curves.

Although the correlation between curve geometry and speed is easily interpreted, the identification of a robust causal association between cardiac activity and the inherently low-stress geometric characteristics of the track has proven to be less straightforward. Relative to dermal conductance (GSR), the distinction between tonic and phasic components of the signal is an established approach in the more recent scientific literature [11]. The primary focus on the tonic component was motivated by our research question, which was to investigate the cumulative effect of prolonged driving on a road with frequent geometric changes, rather than the transient response to discrete events. The phasic component is indeed more sensitive to acute, event-related stressors. An event-related analysis of phasic GSR responses aligned to the entry point of each curve was conducted post-review. While some curves elicited small phasic responses, the effects were inconsistent and not statistically significant across the cohort. This finding reinforces our conclusion that the geometry of individual curves on this type of road induces only a modest, cumulative stress response, best captured by the tonic component, rather than strong, discrete phasic responses.

Consistent with this evidence, the tonic signal showed an increasing trend along the pathway (Figure 5), with a discontinuity attributable to the elimination of the curves between V11 and V24 for reasons already mentioned in the Section 2. This trend suggests progressive physiological activation during the driving experience. Figure 5 is fully in line with the expectation that the tonic component of the GSR considers cumulative workload over time, rather than being determined by singular events (for which evaluation of the phasic component of the GSR is appropriate). A longer route would have exacerbated this component of the GSR, but even with a distance of about 5 min, the tonic GSR is a candidate to represent well the fatigue caused by the driving task as a whole. Therefore, the tonic GSR rather than the radius or angle of deviation should be related to the length of the road section.

However, simply comparing mean values of the dependent variables at the curves (Figure 3, Figure 4 and Figure 5) is only good for a preliminary understanding of the phenomenon. ANOVA is preferable to comparisons of averages because it offers a more rigorous and powerful way to analyze differences between the averages of multiple groups, controlling for Type I error (finding a significant difference when it does not actually exist) and providing a unified framework for analyzing more complex experimental designs. When the ANOVA indicated a significant difference, post hoc tests were used to identify which pairs of averages were significantly different. These more detailed analyses were done on only three curves, representing three conditions sufficiently different from each other in terms of the value of radius (RADIUS) and angle of deviation (ALPHA). In fact, Table 1 shows a very wide variability of the 34 curves in terms of radius (RADIUS) and angle of deviation (ALPHA). As we had to establish a few levels (three in this case) for the two independent variables, consideration of all 34 curves would have resulted in large dispersions in the final results, with the obvious impossibility of obtaining statistically significant results. This situation would have been further aggravated by a very small sample of users (10). For this reason, the analysis was carried out on only three curves of very different geometric characteristics (Table 2), so that any different physiological responses of the driver would emerge.

With regard to the SPEED variable, ANOVA revealed a statistically significant dependence on radius. Subsequent post hoc analysis revealed that speed exhibited statistically significant differences in all three combinations of radii. Figure 6 and Table 3 showed the differences between the normalized averages. It can be seen that there was a greater difference between radius R1 (30 m) and radius R3 (100 m) than in the other two combinations, R1-R2 and R2-R3, precisely because a more noticeable diversity of radius led to users traveling the curve with different speeds. This result is in line with the laws of physics, and while this does not make any contribution to knowledge, it does provide support for the correctness of the experimental procedure.

The generalized linear model applied to the dependent variable HEART RATE suggested that radius (RADIUS) had a significant effect on it. Subsequent post hoc analysis showed that there was a statistically significant difference in HEART RATE only when comparing R1 and R2, while no significant difference was seen between R2 and R3, and R1 and R3. Figure 7 and Table 4 report, as for SPEED, the differences between averages, and although the histogram for the R2-R3 comparison seems relevant, it did not obtain a sufficiently low p-value, an indication that there was a large scattering of data around this mean. The reason may be due to the small number of observations, i.e., the small sample of users tested, but more importantly, the variable examined. Although the data were normalized, cardiac activity represents a highly subjective variable dependent not only on age but also on certain characteristics such as fitness, weight, and emotionality that produce different responses among users to the same stimuli. The fact that there is, however, an appreciable difference between the R2-R3 averages might suggest that by appropriately expanding the sample, sharper results are found.

Finally, regarding the tonic GSR, statistically significant dependencies were found between radii and deviation angles. In Figure 8 and Figure 9 and Table 5, the results of the pairwise comparisons were reported, showing, with regard to RADIUS, a statistically significant difference between the averages for the R1-R2 and R2-R3 combination. Recall what was reported in the preliminary study phase of the GSR (Figure 5), when a growth of this signal along the road was inferred. Therefore, the dependence on the RADIUS here should not be understood with respect to its value but to the arrangement and succession along the road. The radius R3 comes after R2, which, in turn, comes after R1, and, therefore, there is a gradualness in the stress measured by this indicator. Therefore, albeit very cautiously, one might foreshadow some similarity between cardiac activity and dermal resistance, and heart rate may also be a useful indicator for estimating long-term rather than localized effort due to singular events.

The tonic GSR, moreover, also showed the significance of the angle of deviation. Figure 9, in particular, shows that this significance occurs between the A-B and A-C pairs, which are also characterized by a significant difference between the averages. By contrast, there is no significance and very little difference in the comparison between the B-C levels. As was the case for the radius levels, the succession of these along the path must also be considered for the deflection angle. The tonic GSR is, as mentioned, a variable that takes into account accumulated stress. Thus, the last curve is the one most suffered by the driver. Attention should only be paid to the fact that the succession of deflection angles is C-B-A. Moreover, C and B are relatively close to each other, and this means that there was not a great variation in this variable. On the contrary, there was a relevant distance from C to A and from B to A, which led to the accumulation of the tonic GSR.

The above is sufficient to verify the response to the objectives of the study:

• The results showed a very good susceptibility of the tonic GSR and a good propensity of the HEART RATE to represent stress distributed along the entire pathway. They are not good, however, for evidencing stress due to singular events. The tonic GSR, by its nature, represents accumulated fatigue, and the HEART RATE should be further tested under conditions other than these, with well-allocated localized events, which are difficult to predict under real driving conditions. In this regard, any real driving scenario does not lend itself to ascertaining the effect of sudden causes, as the conditions of repeatability with all users would be lacking.
• The two physiological variables analyzed showed no particular synergy with speed, partly because the latter is linked with road curves by well-known physical relationships (balance in curves, sight distance), which are different from the complex mechanisms governing the mental and physical state of human beings.
• Importantly, in the context of the present study, motion artifacts were not a source of disturbance. The tonic GSR signal was free of localized spikes that could have been induced by manual movements of the driver (or external events with high saliency), while the heart rate was detected using an ear sensor, minimizing the impact of body movements. In addition, electrical noise was effectively mitigated through the application of appropriate filters, ensuring the integrity of the acquired data. The selection of physiological variables and sensor placement was in accordance with previous benchmark studies [12,16].
• Future experimental steps should include increasing the length of the analyzed tracks in order to facilitate the achievement of a more robust statistical significance. In line with what has been reported by other authors [15], manipulation of road geometry alone induces modest stress increases, the statistical significance of which could be amplified by extending the path length. However, an increase in experimental duration could introduce additional complexities into the analysis, given the potential variation in temporal latency between the cause (road stimulus) and the observable effect on physiological variables [22].

The current manuscript presents the first step in this process: establishing a statistically significant relationship between the inputs (road geometry) and the outputs (physiological signals). Before a predictive model can be reliably built, it is fundamental to first identify which variables are relevant and significantly correlated. Our ANOVA and GLM analyses serve this exact purpose: they confirm that road geometry parameters are significant factors influencing physiological markers of workload, even in a low-stress environment.

Building upon these foundational results, our subsequent research will focus on the development of machine learning models that fuse physiological and vehicle telemetry data to create real-time predictive models of driver workload, enhancing the practical application of this research for advanced driver-assistance systems (ADASs) and driver monitoring systems.

Limitations

This study has several limitations that should be considered when interpreting its findings. The relatively small sample size (10) limits the generalizability of the results and does not permit an evaluation of the influence of variables such as age, gender, and driving experience on physiological responses. These factors will be a central focus of future research.

The experimental design, which utilized a short, monotonous rural road segment, was chosen to isolate the effect of subtle variations in road geometry (curve radius, deflection angle) in the absence of high-stress events. While this approach was methodologically necessary to minimize confounding variables such as traffic complexity or emotional stressors, it consequently limits the range of driving scenarios investigated. The findings are therefore most representative of low workload and rural driving conditions.

Furthermore, measures were taken to minimize external confounders—such as conducting experiments only on clear days with dry pavement and discarding runs with traffic interruptions—uncontrolled factors such as natural emotional fluctuations may have contributed to physiological signal variability. The quantification of road geometry was also limited to fundamental parameters (radius and deflection angle); more complex indices incorporating sequential curve elements or high-precision map data could provide a more holistic analysis in future work.

To strengthen the validity of future findings, subsequent studies will incorporate subjective workload assessments (e.g., the NASA-TLX questionnaire) to triangulate data from physiological measures and provide a more comprehensive understanding of the driver’s state.

5. Conclusions

This pilot study investigated the determination of workload in drivers through non-invasive monitoring of easily accessible variables: heart rate and skin conductance. The limited sample size, the short duration of the driving sessions (about 5 min), and conducting the experiment in a real road environment introduced variability in the acquired data, hindering the identification of all expected correlations. Nevertheless, statistical analysis revealed significant results suggesting a potential relationship between roadway geometry and changes in monitored physiological parameters.

Consequently, preliminary results support the feasibility of measuring human stress during normal driving activity. The specific experimental boundary conditions, initially perceived as a limitation, proved to be a crucial opportunity, demonstrating the sensitivity of the physiological variables considered even in response to moderate-intensity stimuli.

The present research constitutes an initial phase toward an expansion of the experimental environment, including increasing the sample size, including a wider range of driving scenarios, and introducing specific stressor events. Further research developments should focus on the integration of additional physiological parameters, potentially providing diagnostic information under conditions where current variables do not manifest significant variation.

The practical application of this research lies in providing a validated, low-cost methodology for quantifying driver workload in real-time, which is a critical input for the development of adaptive advanced driver assistance systems (ADASs) and road safety audits. Future research will focus on (1) developing machine learning models to predict workload levels from fused physiological and vehicle data, (2) expanding the driving scenarios to include urban and high-traffic environments, and (3) investigating the impact of driver demographics and experience on physiological responses to workload.