1. Introduction
This paper represents an initial step of a longer research program. The goal of the research is to investigate the transferability and scalability of activity-based models and their calibration supported by opportunistic/big data.
In the long term, our research aims to identify which sub-models can be directly transferred without calibration and which require calibration, and to develop a dedicated calibration framework for each sub-model requiring it. The frameworks will leverage crowd-sourced or opportunistically collected data, thereby avoiding the need for dedicated surveys.
The focus of this paper is on the calibration of destination choice models embedded in an activity-based model through external opportunistic data.
In our study, we use an observed matrix hypothetically estimated by any means based on data collected from cell phones, calls, and/or data collected from apps installed on smartphones. Through the processing of this data, it is possible to derive OD trip matrices marked by a good level of temporal and spatial characterization.
However, we develop a calibration framework by assuming the availability of an observed OD trip matrix.
The analysis of different possible sources of data opportunistic/big data to derive the performance measures (based on the observed OD trip matrix) is not addressed in this paper. Many articles can be found in the technical literature which propose different methodologies for the utilization of opportunistic sources of data.
Some relevant references are provided in
Section 2.
We acknowledge that real-world opportunistic data often presents imperfections that can influence model calibration outcomes. Common issues include sampling bias, where certain user groups or travel behaviors are over- or under-represented; missing trips due to incomplete detection or coverage gaps; and temporal sparsity, where data availability is uneven across time periods. Such imperfections can lead to biased parameter estimates or the reduced robustness of the calibrated model. In practice, these challenges could be mitigated through preprocessing steps such as bias correction, data imputation, or weighting schemes, as well as by incorporating multiple complementary data sources.
A literature review on the calibration of transport demand models reveals that most existing approaches rely primarily on link-based performance measures, such as vehicle or passenger counts. Only a limited number of studies propose more comprehensive calibration frameworks that incorporate elements of the supply model. However, link flows, or observed counts, are ultimately the outcome of the interaction between demand and supply components. This highlights the need to explore alternative performance measures that enable a more coherent formulation of the calibration problem, one that aligns demand model calibration with demand-observed data and demand-related performance indicators.
Furthermore, comparative analyses of different optimization algorithms within this context are scarce, as are investigations into the most suitable goodness-of-fit measures to adopt.
The present research advances the development of a comprehensive calibration framework that leverages crowd-sourced individual mobility data, or more broadly, opportunistic and big data sources.
Finally, this work seeks to explore the applicability of the ADAM optimizer—a widely used algorithm in neural network training—which has not yet been applied in the context of transport demand model calibration. Introducing and testing ADAM as an alternative optimizer for calibration is a primary methodological contribution.
To guide the reader, the structure of the paper is summarized as follows.
Section 2 presents a literature review focusing on two main topics: the calibration of demand models and the use of mobile phone data in the context of transport demand estimation.
Section 3 outlines the proposed methodology and provides a detailed description of the data employed in the study.
Section 4 illustrates the experimental design and reports the results of the experiment, followed by a comprehensive analysis of the findings.
Section 5 discusses the key aspects of the results, including the algorithm setup and performance, the main insights derived from the study, and their practical implications. Additionally, directions for future research are proposed. Finally,
Section 6 summarizes the authors’ conclusions.
2. Literature Review
The calibration of complex models often necessitates iterative, trial-and-error procedures that cannot be fully captured by formal optimization frameworks. As a result, the calibration of such models typically incorporates substantial heuristic elements [
1].
This situation applies to transport simulation models, which involve conducting an explicit run of the transport simulation models. In applied engineering contexts, established guidelines mandate that transport network calibration follows a structured set of procedures to ensure that the model output is consistent with observed data as well as the physical and logical properties of the system [
2].
This also applies to four-stage transport models, where feedback from lower-level to upper-level components is typically limited, and the individual stages are often calibrated independently [
3].
In general, excluding the cases in which the model output is linked to the input through a direct and explicit formulation of mathematical functions, the calibration of transportation simulation models is only one specific case of the broader problem of simulation optimization.
In recent decades, simulation optimization has received considerable attention from both researchers and practitioners. Simulation optimization is the process of finding the best values of some decision variables for a system whose performance is evaluated using the output of a simulation model [
4].
In the calibration process, the decision variables are the parameters of the model to be calibrated while the performance to be evaluated is the model’s ability to reproduce reality. In simulation model optimization, the best possible values of a set of decision variables of a system are sought for which the performance functions are evaluated using a simulation model.
A robust statistical framework for integrating traffic counts with additional data sources was developed by [
5], who extended the standard origin–destination (OD) matrix estimation approach to address the broader problem of parameter estimation in pre-specified, aggregated travel demand models.
The widespread adoption of ICT devices and communication protocols along with Intelligent Transportation Systems (ITS) has introduced new sources of mobility data and generated an unprecedented volume of information on transport system performance, thereby offering significant opportunities for the development of more advanced calibration methodologies. Examples of different developed approaches can be found in [
6,
7,
8,
9].
Due to privacy constraints, these datasets exclude personal user attributes, making the disaggregate calibration of behavioral models impractical. Consequently, calibration must be performed at an aggregate level. In the existing literature, the majority of such applications rely on metaheuristic optimization techniques.
Predominantly, approaches in the literature aim to identify model coefficient values that best reproduce observed traffic or passenger flow counts. However, some studies extend this framework by incorporating multiple data sources such as link-level traffic counts and point-to-point travel times into the calibration process. Examples of extended approaches are in [
10,
11,
12].
In the literature, most applications are based on the Stochastic Approximation Method, especially Simultaneous Perturbation Stochastic Approximation (SPSA).
In [
7] the authors present the use of the Simultaneous Perturbation Stochastic Approximation (SPSA) algorithm for calibrating large-scale transportation simulation models, demonstrating its effectiveness in optimizing model parameters under noisy and high-dimensional conditions
The objective function used in their SPSA-based calibration is formulated as a weighted sum of squared deviations between the simulated and field-observed traffic measurements—primarily link counts, speeds, and travel times.
Ref. [
13] apply the Simultaneous Perturbation Stochastic Approximation (SPSA) algorithm to the calibration of traffic simulation models, emphasizing its efficiency and robustness in handling high-dimensional, noisy, and computationally expensive calibration problems.
The authors introduce the Weighted Simultaneous Perturbation Stochastic Approximation (W–SPSA) algorithm—an enhanced version of SPSA—which incorporates a weight matrix to account for spatial and temporal correlations among traffic network variables, thereby improving gradient approximation, robustness, and convergence for large-scale traffic simulation calibration. The objective functions used are RMSE and RMSNE.
Ref. [
14] leverage the Simultaneous Perturbation Stochastic Approximation (SPSA) algorithm to efficiently calibrate parameters in an activity–travel model—specifically tuning transition probabilities and duration distributions—to align simulated schedules with observed time use survey data.
The study minimizes a marginal fitting error, expressed through two Mean Absolute Percentage Error (MAPE) metrics across activity types and durations.
Ref. [
15] formulate the calibration of a boundedly rational activity–travel assignment (BR–ATA) model—integrating both activity choices and traffic assignment within a multi-state super-network—as an optimization problem and employ the Simultaneous Perturbation Stochastic Approximation (SPSA) algorithm to efficiently estimate model parameters across spatial and temporal dimensions.
The objective function is formulated as an SE, subject to linear constraints on the parameters’ vector.
A second family of optimization approaches is based on metaheuristic methods like genetic algorithms and Particle Swarm Optimization.
Ref. [
16] employ Particle Swarm Optimization (PSO) alongside automatic differentiation and backpropagation techniques to calibrate the second-order METANET macroscopic traffic flow model, optimizing fundamental diagram and density–speed parameters for the accurate reproduction of real-world motorway traffic dynamics.
They define the calibration objective as the time-averaged mean squared error MSE between the simulated and observed space mean speeds from roadway loop detectors.
Ref. [
17] presents an automated method to calibrate and validate a transit assignment model using a Particle Swarm Optimization algorithm. It minimizes an error term based on root mean square error and mean absolute percent error, capturing deviations at both segment and mode levels, and is suitable for large-scale networks. The observations are based on smartcard data.
Ref. [
18] presents a general methodology for the aggregate calibration of transport system models that exploit data collected in mobility jointly with other data sources within a multi-step optimization procedure based on metaheuristic algorithms. The authors address the calibration of national four-step model parameters through Floating Car Data (FCD) data, given train matrix, and air flow counts, by employing a PSO algorithm.
Among the many electronic devices, mobile phones have the highest penetration rate. While conventional mobile phones typically exchange information with cell towers only sporadically, the widespread use of smartphones offers new and promising opportunities for mobility studies. Most of the studies available in the literature regarding the use of mobile network data in mobility models rely on Call Detail Records (CDRs), which represent a subset of mobile network data but also include event-triggered updates. Mobile phone traces are used as large-scale sensors of individual mobility.
Some studies on mobile data utilization in transport modeling are reported below.
Ref. [
19] utilize mobile phone data to estimate origin–destination (OD) flows in the Paris region, aiming to infer transportation modes such as metro usage through an individual-based analysis of spatiotemporal trajectories, building a data-driven, microscopic travel behavior model.
In [
20] the authors leverage mobile phone data collected from the two largest cellular providers in Israel over a two-year period for modeling national travel demand.
They develop algorithms to extract trip generation, distribution, and mode choice information from anonymized mobile phone records. They integrate this data into travel demand models that traditionally rely on surveys and census data.
Ref. [
21] presents a comprehensive review of mobile phone data sources and their applications in transportation studies. The study explores various data types, including Call Detail Records (CDRs) and synthetic CDRs, discussing their strengths and limitations. It delves into methodologies for estimating travel demand, generating origin–destination (OD) matrices, and conducting mode-specific OD estimation. The paper highlights the reliability of CDR data for trip purpose estimation, while noting challenges in accurately predicting travel modes. It concludes with recommendations for enhancing synthetic CDR data and expanding its use in mobility studies.
A thematic synthesis of the reviewed papers is reported below.
The calibration of transportation models is typically conducted at either aggregate or disaggregate levels, depending on data availability and model complexity. Aggregate calibration dominates the literature due to privacy constraints and the widespread use of traffic counts, link flows, travel times, or OD matrices as calibration targets [
5,
6,
7,
8,
18]. Such approaches scale well to large networks and allow the integration of multi-source mobility data [
18,
20], but they may mask behavioral heterogeneity and introduce aggregation biases [
19,
20]. Disaggregate calibration, on the other hand, leverages detailed individual-level data, such as mobile phone records or enriched activity–travel schedules [
14,
19], capturing traveler heterogeneity at the cost of increased data and computational requirements.
Methodologically, calibration techniques range from heuristic and iterative adjustments [
1,
2], to statistical estimation methods such as Maximum Likelihood, GLS, or Bayesian approaches [
5,
22], which provide rigorous frameworks for parameter estimation but can be computationally demanding. Stochastic approximation methods, particularly Simultaneous Perturbation Stochastic Approximation (SPSA) and its weighted variant W-SPSA [
7,
11,
13,
14,
15], have emerged as efficient gradient-free approaches for high-dimensional, noisy simulation environments. Metaheuristic methods, including genetic algorithms and Particle Swarm Optimization [
1,
6,
16,
17,
18], offer flexibility for multi-objective, nonlinear calibration problems but can be computationally intensive and sensitive to objective weighting. Deterministic or solver-based approaches are applied in specific contexts such as boundedly rational activity–travel assignments [
15] or quasi-dynamic traffic assignment [
8], providing theoretically grounded solutions but sometimes lacking scalability or robustness to stochastic simulation noise.
Calibration objectives and performance metrics typically involve minimizing the deviations between simulated and observed flows, speeds, or travel times, often using multi-objective formulations such as sums of squared errors SE or a weighted variant, RMSE, RMSNE, or MAPE [
1,
6,
13,
16,
17]. Evaluation may also incorporate distributional comparisons, such as the Kolmogorov–Smirnov tests, for probabilistic travel time models [
12]. Emerging trends emphasize the integration of diverse data sources, high-dimensional optimization techniques, and enhanced behavioral realism through activity-based or boundedly rational models [
14,
15,
18,
20]. Hybrid approaches that combine stochastic approximation with metaheuristics or statistical estimation with simulation optimization can be explored to overcome the limitations of individual methods and improve calibration accuracy, efficiency, and scalability.
3. Methodology
3.1. Data Used
The model used in this research is the built-in simplified activity-based model (ABM) provided in PTV Visum 2024 [
23], known as the “ABM Nested Demand” model. This model provides a streamlined approach to simulating individual activity-based travel behavior through agents.
The key features of the Simplified ABM in Visum 2024 are reported below.
Synthetic Population Generation: The model utilizes a synthetic population, representing individuals with specific socio-demographic attributes. This population is generated exogenously, based on statistical data, and can be imported into Visum, enabling detailed person-level analysis.
Activity and Tour Modeling: Each individual in the synthetic population is assigned a sequence of activities (e.g., home, work, and shopping) and corresponding tours. These sequences are structured to reflect realistic daily schedules, capturing the temporal and spatial aspects of travel behavior. The activities and tours, which represent the daily schedules of individuals, are fixed and linked to people. They are therefore generated during the phase of population synthesis.
Nested Choice Modeling: As specified above, the participation in activities and related duration, and time-of-day preferences, are exogenous inputs derived from the daily schedule of each individual entered into the model via the synthetic population. However, the model employs nested logit structures to simulate decision making processes, such as destination choice and mode choice. This allows for a more nuanced representation of traveler behavior compared with traditional aggregate models.
The demand model is a nested demand destination mode choice for which the following applies.
where
D = Destination.
M = Mode.
Vdm = Base utility.
= Destination choice Lambda.
= Mode choice Lambda.
= Attraction factor of destination d.
= Inclusive value (logsum) summarizing expected utility of mode choice within destination.
= Marginal probability of choosing destination.
= Conditional probability of choosing mode m, given destination d.
The formulation implemented in Visum and reported above follows the formulation in [
23].
3.2. Characteristics of the Test Network Used
The model represents a neighborhood of 0.8 km2 subdivided into 49 zones and includes a synthetic population which encompasses 33,090 households and 68,731 persons.
The private and public transport networks are represented through 647 nodes, 1404 links, 3414 turns, 103 stop points, and 28 line routes. Also, the network is characterized by 1053 point of interest and 1355 locations.
Figure 1 below, illustrates the road network and the points of interest of the test model used.
3.3. Formalization of the Calibration Model
The observed performance measures, M
obs, are defined as the relative attractiveness of each zone by time slot determined through sample OD matrices derived from phone call, apps, and social media data analysis.
where
= Observed attractiveness of zone j in the time slot p.
= Number of trips estimated from apps and social media data, from zone o to zone d, regardless of mode m in the time slot p.
The simulated performance measures, M
sim, are defined as the relative attractiveness of each zone by time slot determined by model output matrices.
where
m = Generic mode of transport.
M = Number of transport modes considered.
p = Generic time slot.
o = Generic origin zone.
d = Generic destination zone.
Z = Total number of zones.
= Simulated attractiveness of zone j in the temporal slot p.
= Number of trips estimated by the model from zone o to zone d by mode m in the time slot p. The estimated number of trips is a function of the set of parameters , .
In the current study, intraday dynamics—variations in travel behavior and transport system performance within a single day—are not taken into account. Instead, both the observed and simulated measures used for calibration and validation are aggregated at the daily level. This means that the analysis assumes a consistent pattern throughout the day and does not capture time-dependent fluctuations such as peak and off-peak variations.
While this simplification helps reduce model complexity and computational effort, it may limit the model’s ability to reflect the more granular temporal dynamics that are often important in urban transport systems. Future research will enhance the model accuracy by incorporating time-of-day variations into the calibration process.
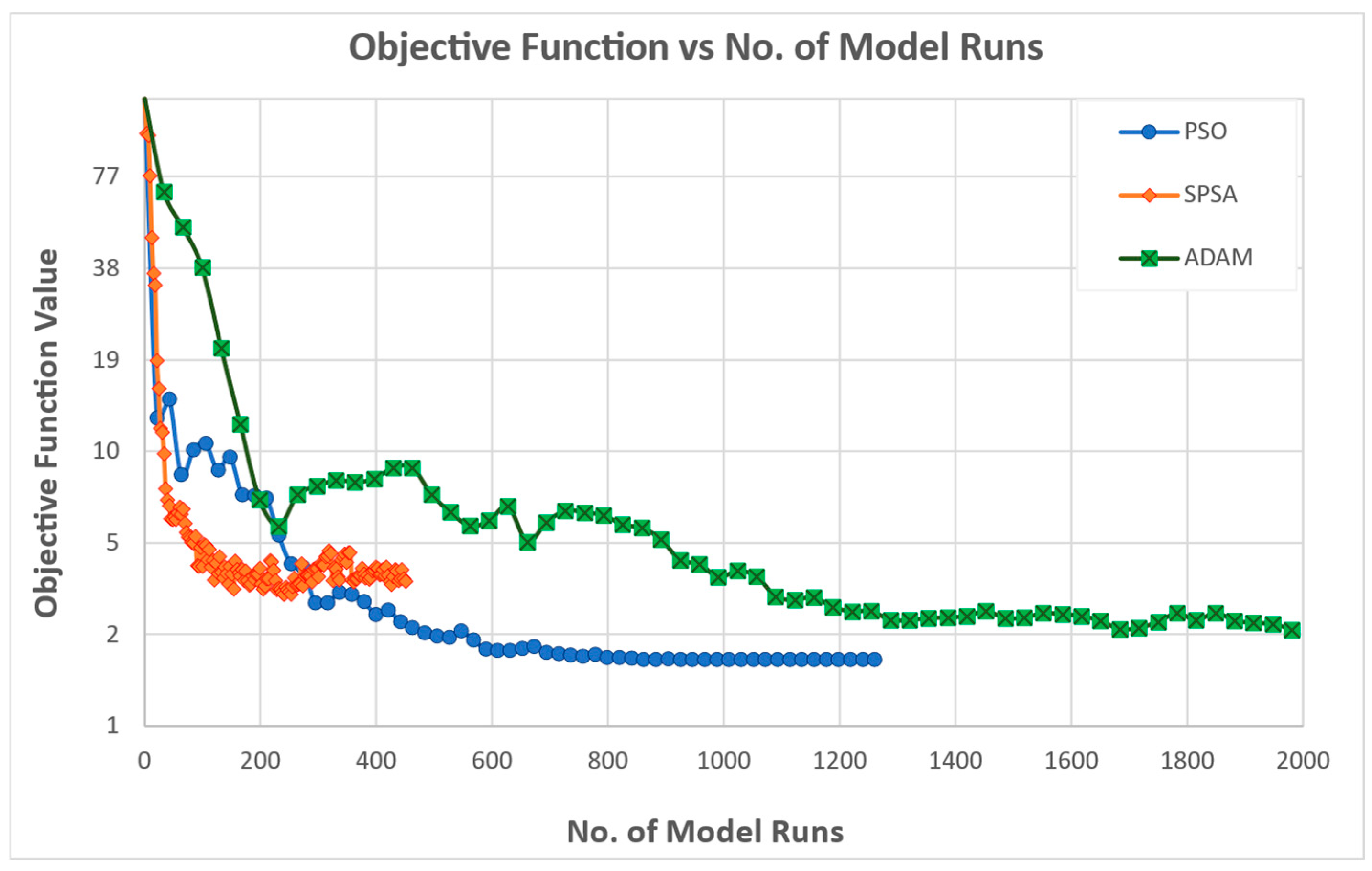
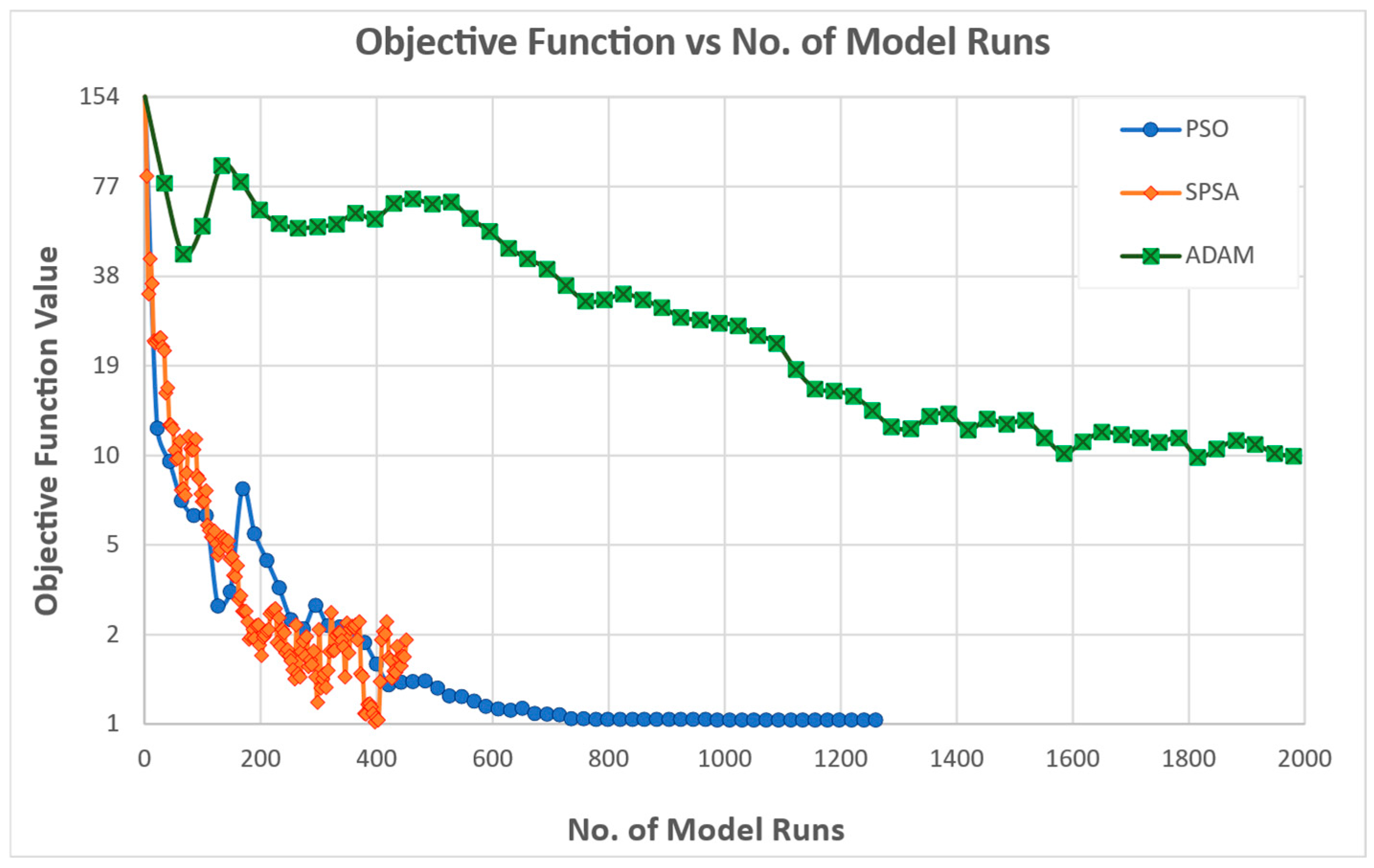
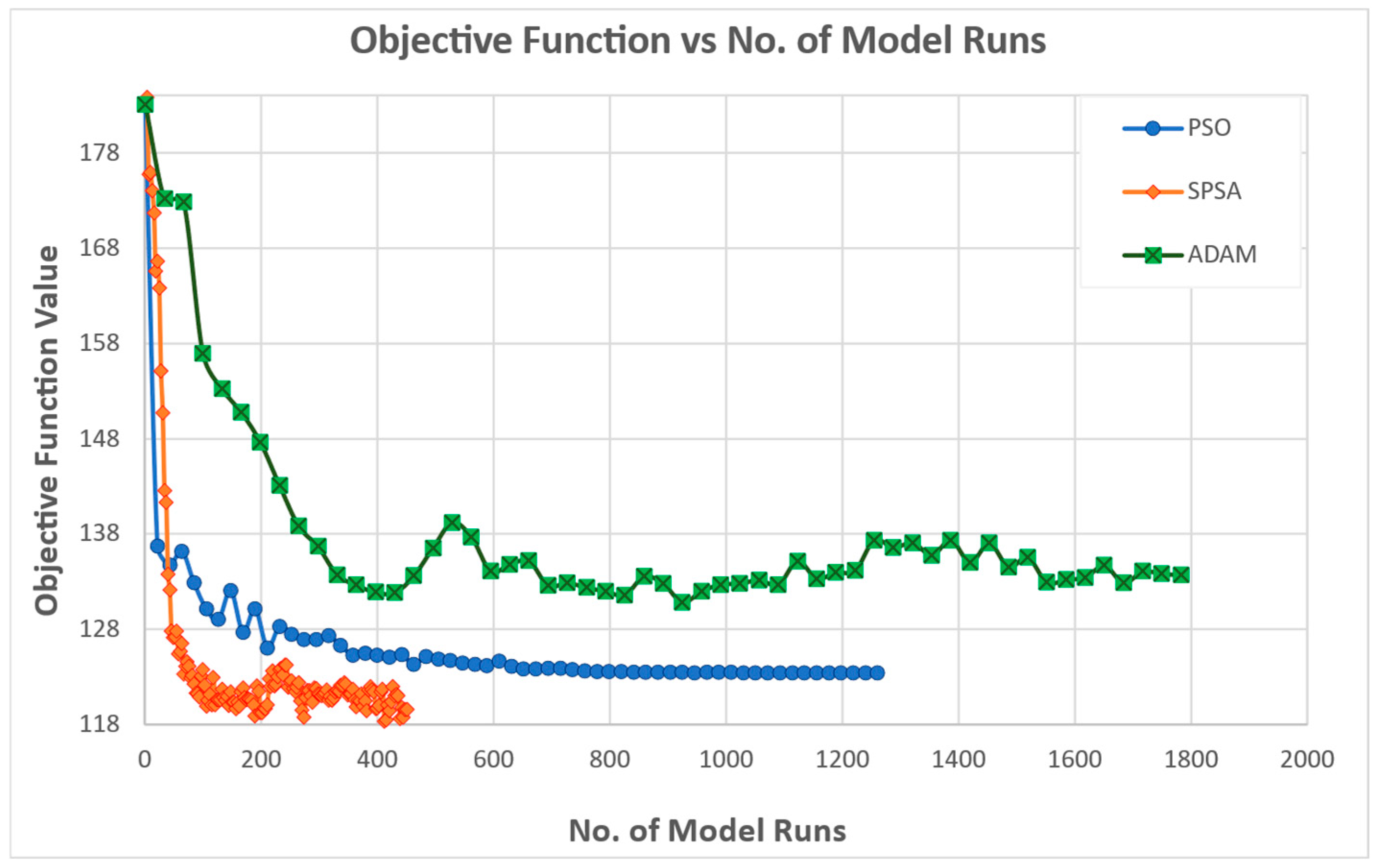
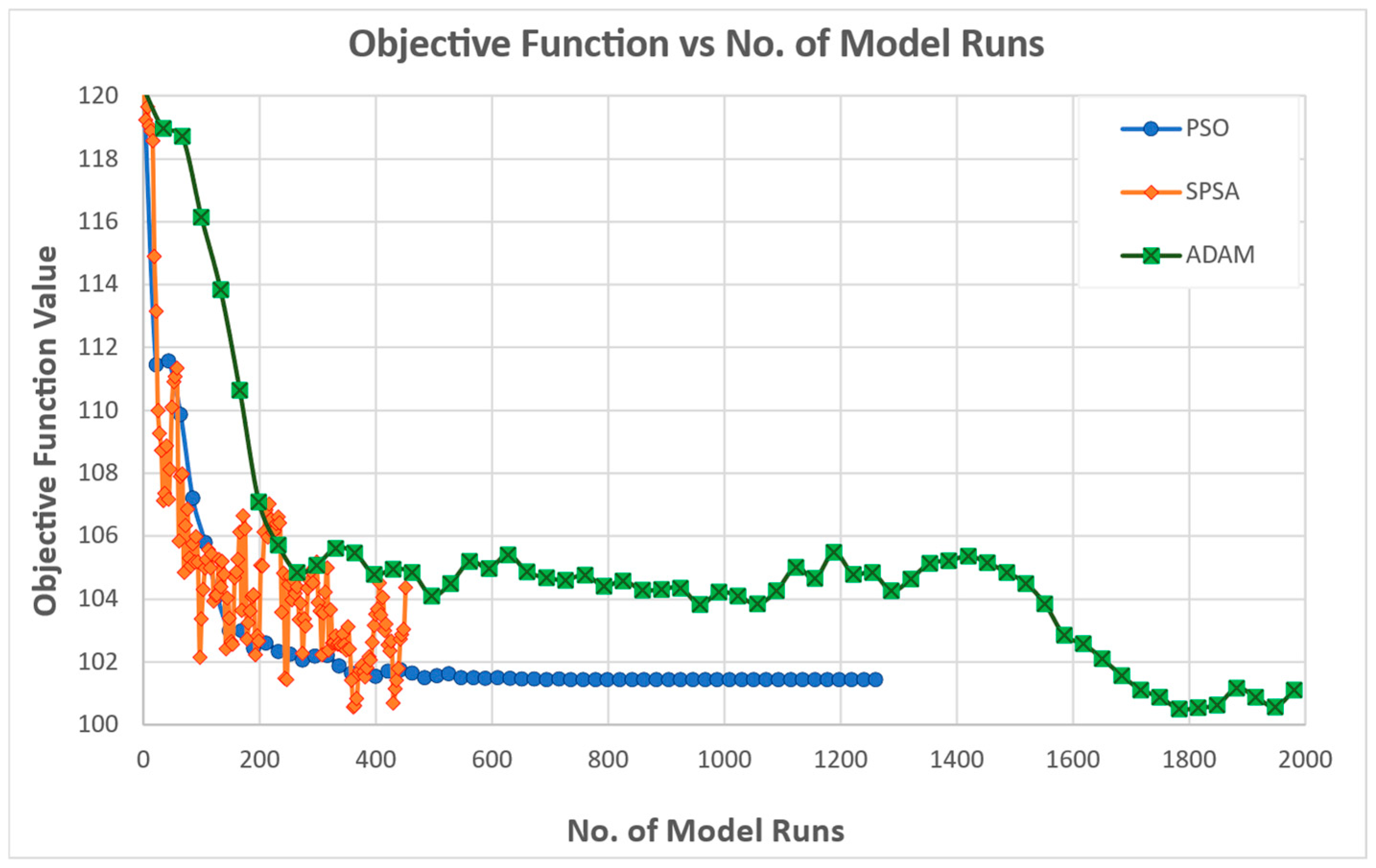
The goodness-of-fit adopted as the objective function is the SE squared error, i.e., the sum of the squared errors of the simulated and observed attractiveness, summed over all zones considered in the calibration and summed over all time frames.
Having defined the above measures of performance and goodness-of-fit, the mathematical formulation of the problem is as follows:
where
j = generic zone.
K = scaling factor to be calibrated based on the initial value assumed by the objective function.
βi = generic parameter in the distribution model to be calibrated.
λi = generic parameter in the nested model to be calibrated.
M = total number of βi parameters.
m = total number of λi parameters.
The calibration model has been formally integrated into the transport simulation by applying parameter multipliers. Within the Visum model, each Beta and Lambda parameter is associated with a corresponding multiplier. This setup allows the demand model to function using the product of the original parameters and their respective multipliers. The calibration process itself operates externally from the model, optimizing these multipliers and feeding the updated values back into the Visum model.
3.4. Selection of Optimization Algorithm
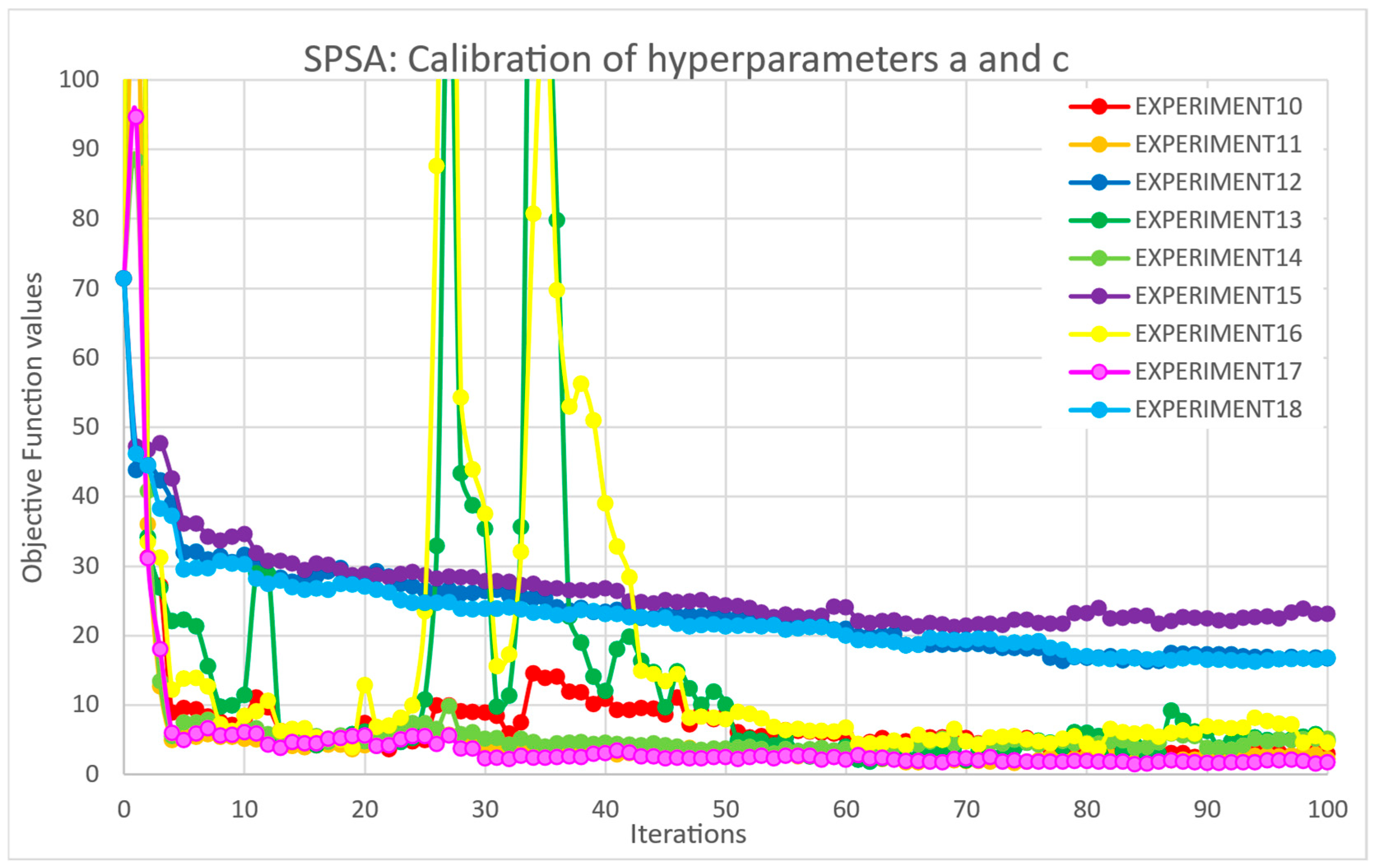
Calibrating travel demand models involves adjusting the model parameters to closely replicate observed travel patterns, a process that typically requires solving complex, nonlinear, and often stochastic optimization problems. Given the high dimensionality and potential non-convexity of the parameter space, the choice of optimization algorithms is critical to achieving reliable and efficient calibration results. In this context, three algorithms were selected for their complementary strengths: Simultaneous Perturbation Stochastic Approximation (SPSA), Particle Swarm Optimization (PSO), and Adaptive Moment Estimation (ADAM).
SPSA, introduced in [
24], is particularly well suited for high-dimensional optimization problems where the objective function is noisy or expensive to evaluate. Its ability to approximate gradients with minimal function evaluations makes it an efficient choice for calibrating travel demand models, where simulation outputs can be computationally intensive. Moreover, SPSA’s stochastic nature helps it avoid local minima, enhancing the robustness of the calibration process.
The hyperparameters values adopted as the starting point are listed below:
a = 0.1 (initial step size).
c = 0.1 (perturbation size).
alpha = 0.602 (learning rate decay exponent).
gamma = 0.101 (perturbation decay exponent).
A = 10 (stability constant for learning rate).
Max No. iter = 100–200 (maximum number of iterations).
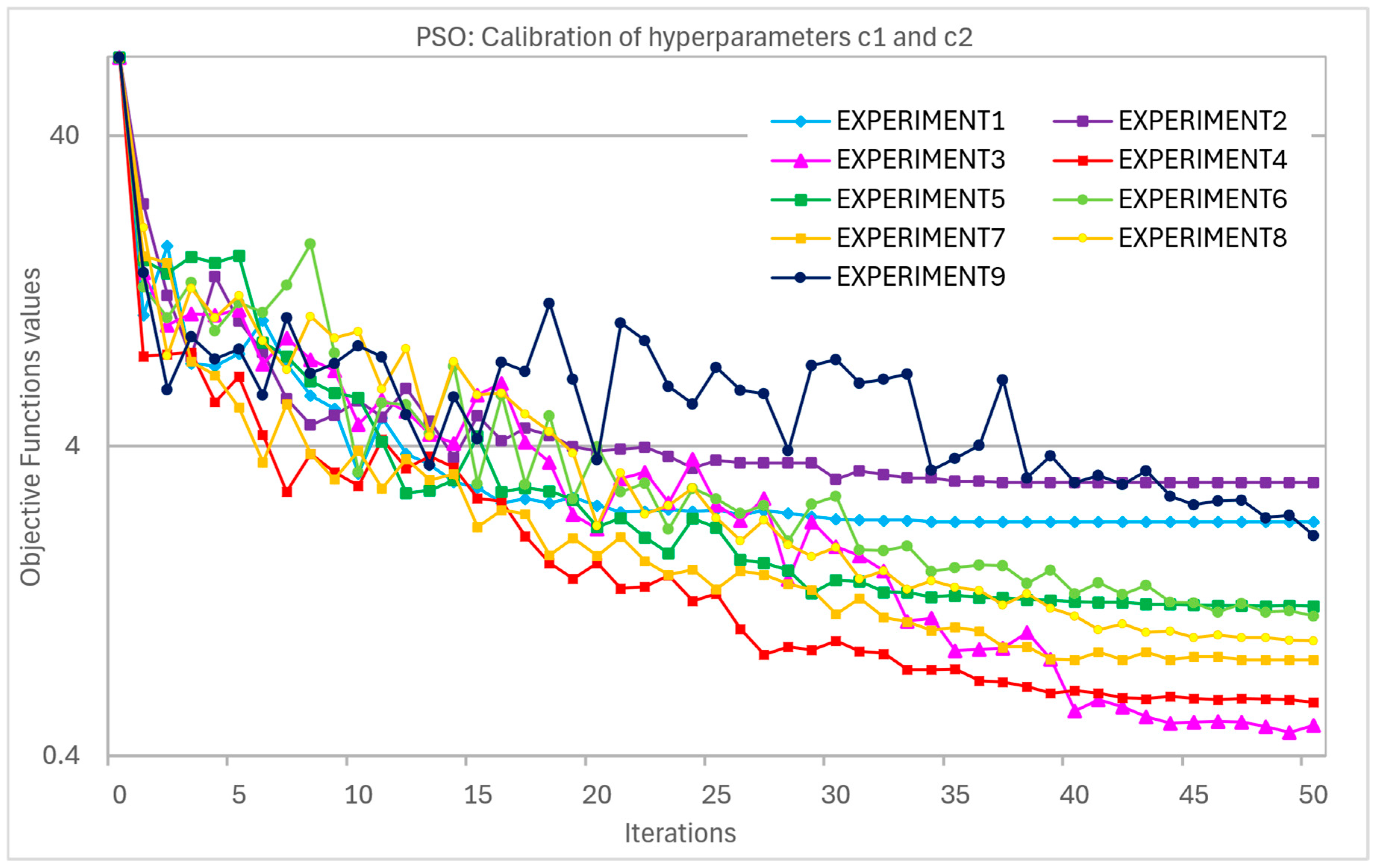
PSO, introduced in [
25], inspired by the social behavior of biological swarms, offers a population-based, heuristic approach to exploring the parameter space. Its global search capability and simplicity in implementation make it effective in navigating complex, multimodal landscapes that are typical in travel demand calibration. PSO’s adaptability and parallel evaluation potential further support efficient convergence toward high-quality solutions.
The hyperparameters values adopted as the starting point are listed below:
No. particles = 20 (number of particles).
V = −0.1–0.1 (velocity).
w_max = 1 (initial inertia weight).
w_min = 0.005 (final inertia weight).
c1 = 0.5–2.5 (cognitive coefficient).
c2 = 0.5–2.5 (social coefficient).
Max No. iter = 50–100 (maximum number of iterations).
ADAM, introduced in [
26], originally developed for training deep neural networks, combines the advantages of adaptive learning rates with momentum-based gradient descent. Its ability to dynamically adjust step sizes based on past gradients facilitates stable and rapid convergence, which is particularly useful in the context of gradient-based calibration tasks. ADAM’s efficiency and effectiveness in handling noisy gradients align well with the stochastic nature of travel demand model outputs.
The hyperparameters values adopted as the starting point are listed below:
α = 0.001 (learning rate).
β1 = 0.9 (first moment decay rate).
β2 = 0.999 (second moment decay rate).
epsilon = 10−8 (numerical stability term).
epsilon_grad = 10−2 (perturbation for numerical gradient estimation).
Max n. iter = 50–100 (maximum number of iterations).
All three algorithms discussed above—Simultaneous Perturbation Stochastic Approximation (SPSA), Particle Swarm Optimization (PSO), and Adaptive Moment Estimation (ADAM)—have been implemented with explicit consideration for variable constraints. To ensure that the solutions remain within the defined bounds, constraint handling is performed by clipping the candidate solutions at each iteration. This approach enforces the limits by adjusting any out-of-bound values back to the nearest permissible value, thereby maintaining feasibility throughout the optimization process.
Although various convergence criteria have been explored and implemented, the termination of the optimization algorithms was governed solely by the maximum number of iterations, irrespective of the values achieved by other convergence criteria. Convergence was monitored during the hyperparameter calibration experiments; however, some results from the regular experiments suggest that the convergence behavior warrants further investigation.
The three algorithms leverage their diverse methodological approaches, stochastic approximation, population-based search, and adaptive gradient optimization, to address the multifaceted challenges of travel demand model calibration. This selection aims to understand the different behaviors of the tested algorithms; indeed, each one presents a different balance between exploration and exploitation in the parameter space, different convergence speed, and different accuracy of solutions.
Before applying the three optimization algorithms, each underwent a dedicated calibration process to fine-tune their hyperparameters and ensure stable and efficient performance. The details of this calibration procedure, including parameter selection strategies and evaluation criteria, are provided in
Appendix A.1.
5. Discussion
5.1. Algorithm Setups, Hardware, and Performances
The algorithm configurations used in this study are based on those determined during the hyperparameter calibration phase, with the exception of the maximum number of iterations, which was increased for the experimental runs.
The stopping criteria were set as follows: parameter variation lower than 1 × 10−3 or objective function variation lower than 1 × 10−5 with respect to the previous iteration. These criteria were met during the hyperparameters’ calibration, leading to the setting of the maximum number of iterations.
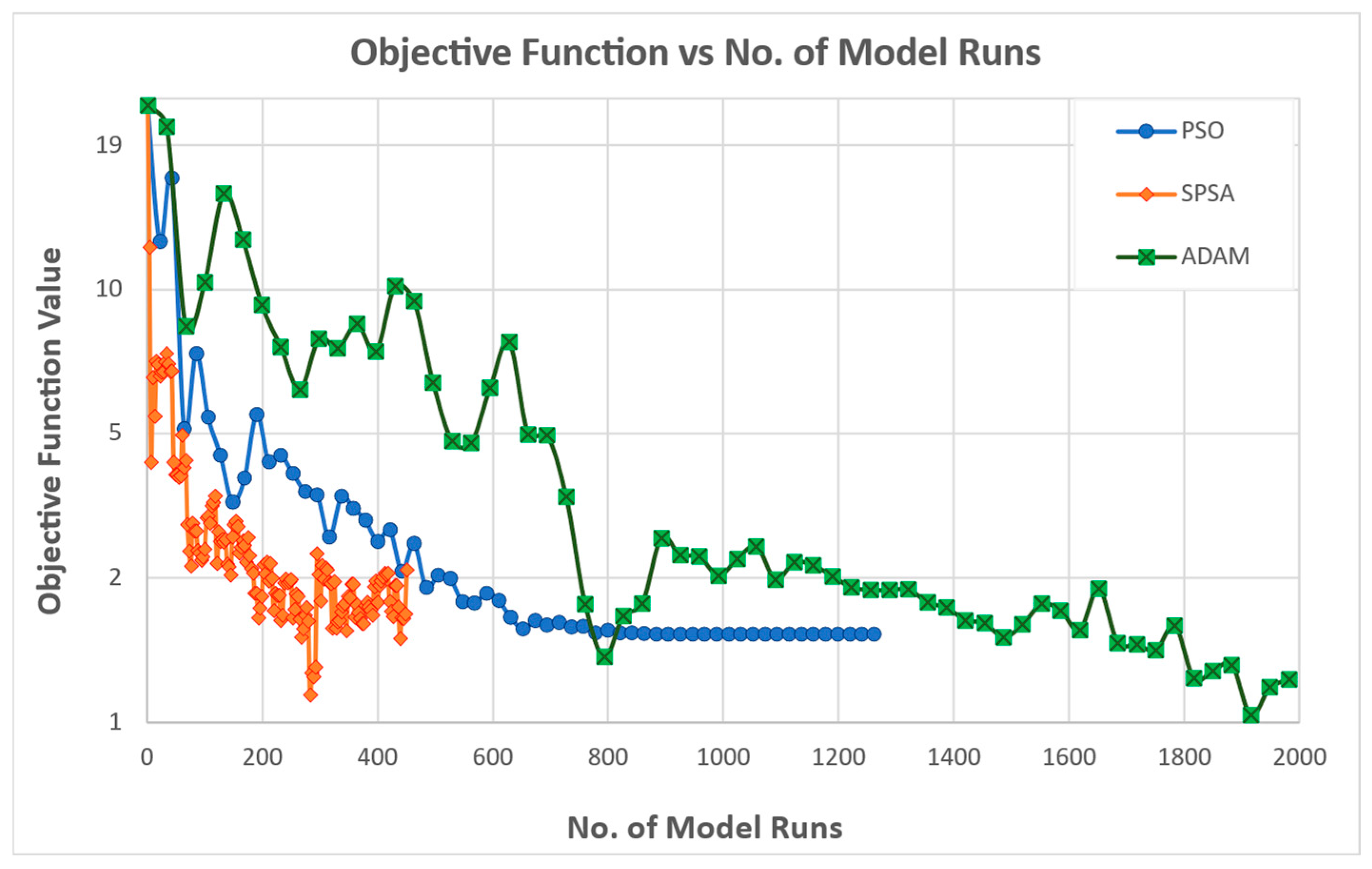
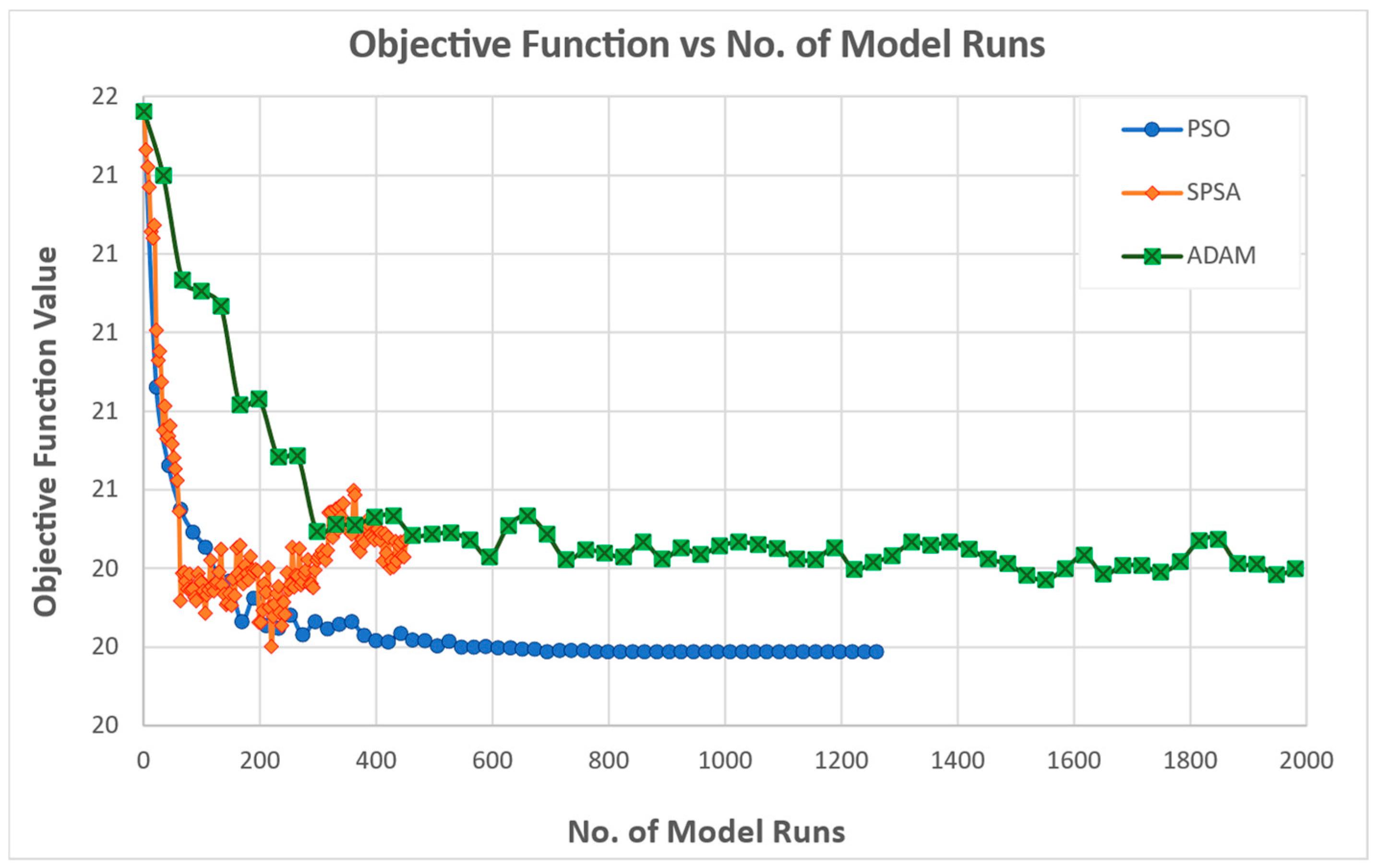
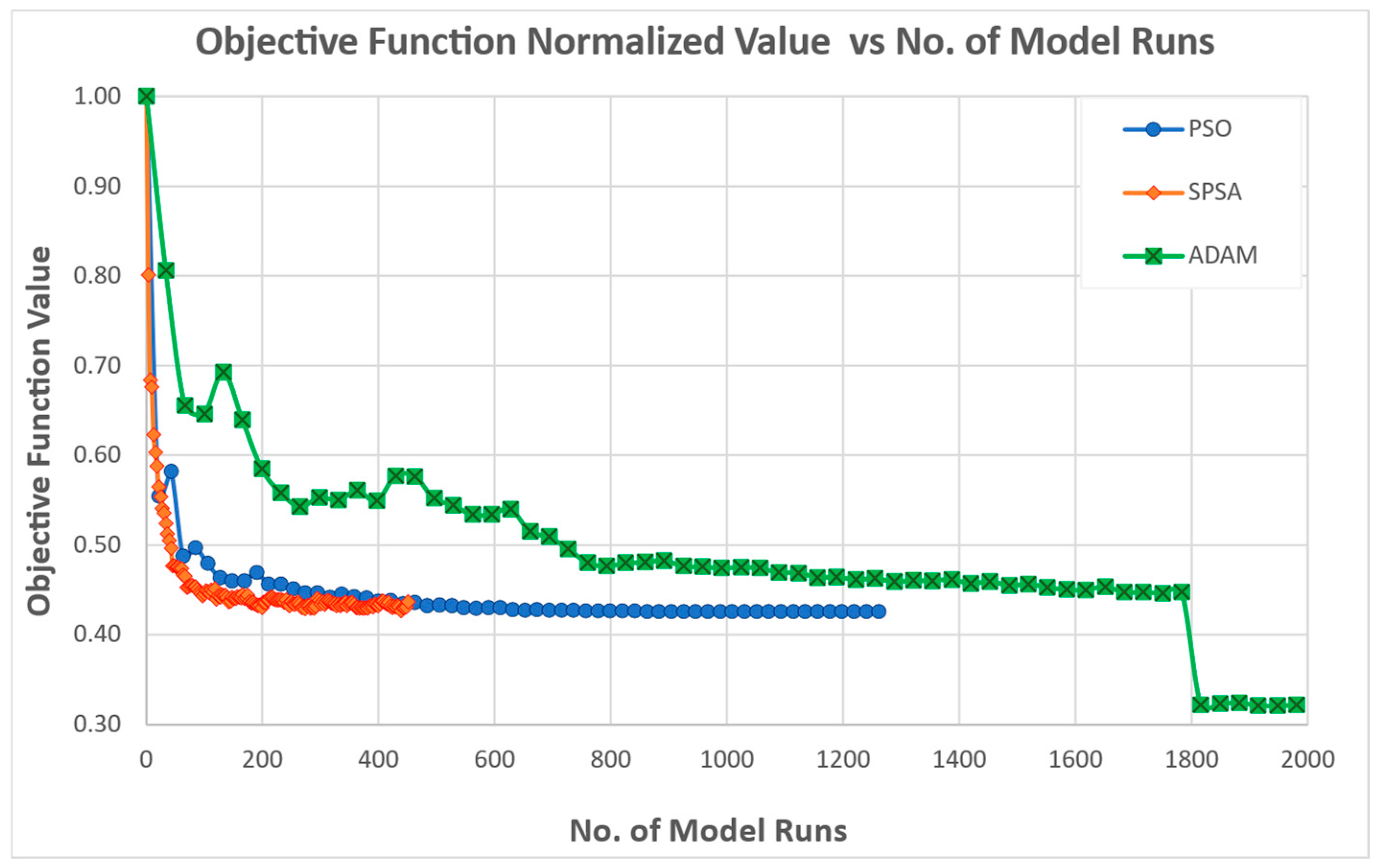
During the experiments’ execution, the maximum number of iterations was raised from 100 to 150 for SPSA, and from 50 to 60 for both PSO and ADAM. This adjustment was necessary due to the initial objective function values being higher than those observed during calibration. Nevertheless, despite the increased iteration limits, the solutions produced by all three algorithms remain significantly distant from the true optimal solutions.
This suggests that future experiments should consider further increasing the maximum number of iterations.
All experiments were conducted on a machine equipped with an Intel® Core™ Ultra 9 Processor 285 K (36 M Cache, up to 5.70 GHz) and 64 GB of RAM. On this hardware, a single model evaluation requires approximately one minute. Taking into account both the calibration and experimental phases, the total computational time amounts to roughly 1000 h.
It is also worth noting that, at the current stage of the research, the use of a kriging surrogate meta-model for approximating the objective function has not been pursued. While surrogate modeling—particularly kriging—can significantly reduce computational costs by approximating the objective function based on a limited number of model evaluations, it introduces an additional layer of modeling complexity and potential approximation error. In this study, the focus has been placed on assessing the optimization algorithms in their direct application to the true, high-fidelity model, without the influence of surrogate-induced biases. This choice allows for a more transparent evaluation of the algorithms’ behavior and performance characteristics in solving the original problem. Nonetheless, incorporating surrogate models such as kriging remains a promising avenue for future work, especially in contexts where computational demands become prohibitive.
Across the six calibration experiments, distinct patterns emerge in the behavior and performance of the three optimizers, reflecting inherent trade-offs between convergence speed, stability, and final accuracy.
5.2. Practical Implications
Trade-off between speed and precision: PSO’s swift, low-noise descent makes it ideal for time-constrained calibrations requiring a good—but not necessarily the best—fit.
Noisy but flexible: SPSA can be leveraged when alternative goodness-of-fit measures are prioritized, though it demands careful tuning to mitigate variability.
Long-run accuracy: ADAM is preferable when the computational budget allows for many iterations and when minimizing squared errors and recovering true parameters are critical. Introducing and testing ADAM as an alternative optimizer for calibration is a primary methodological contribution.
5.3. Findings
The calibration experiments reveal that no single optimizer uniformly dominates across all criteria; instead, each offers strengths tailored to specific calibration priorities:
PSO provides the most reliable and rapid convergence to low objective values with minimal noise, making it well suited for scenarios requiring consistent, fast calibration.
SPSA delivers competitive early improvements and excels in some metrics, but demands tighter perturbation control to achieve stability and precision.
ADAM is the method of choice for achieving the lowest squared error objectives and the superior recovery of true parameter vectors when ample iterations are available.
Ultimately, the selection of an optimization algorithm should align with the calibration goals—whether that is maximizing overall accuracy, ensuring stability under tight iteration budgets, or targeting specific distributional fit measures.
Under the conditions of limited computational resources or strict time constraints, SPSA is preferable, as it delivers faster initial performance gains.
It should also be noted that certain model parameters cannot be reliably identified given the selected calibration targets. For instance, in experiment 1.1, all three algorithms consistently underestimated the BETA_TRANSFER parameter, likely because the zonal attractiveness indicator contains insufficient information to capture transfer penalties. Similarly, parameters such as the LAMBDA values for demand segments related to education activities are difficult to identify, owing to the limited contribution of these segments to the overall demand and, consequently, to the zones’ attractiveness.
Some limitations stem from the model’s original formulation. At the outset of the study, we chose to use the ABM supplied by PTV as an example, rather than investing time in developing a more specific and detailed model.
This decision was guided by two main considerations. First, using the PTV model facilitates reproducibility, as it is a widely accessible platform. Second, it supports a broader research objective: developing a calibration procedure that can be applied to models transferred from other contexts. In such situations, modifying the transferred model is often impractical; our aim is therefore to enable calibration even when the underlying model is simplistic or sub-optimally specified.
5.4. Future Research Directions
Further research is recommended across several key areas, with the aim of enhancing both the travel demand modeling aspects and the calibration and optimization frameworks employed in this study.
Enhancements to the travel demand model:
Incorporation of a higher temporal resolution: Future work should explore the integration of performance measures at a finer temporal granularity—such as by specific time slots or periods within the day. This would allow for a more accurate representation of travel behavior and model sensitivity to temporal variations in demand.
Extension to additional demand sub-models: The calibration framework could be extended to encompass other components of the demand model, starting with the mode choice sub-model. This is particularly relevant in the context of the agent-based model (ABM) used in this research, where destination and mode choices are modeled together in a nested structure. A more comprehensive calibration approach could lead to improved consistency and predictive power across interrelated sub-models.
Advancements in the calibration framework:
Utilization of emerging mobility data sources: Future studies should investigate the integration of alternative data sources—including crowd-sourced mobility data and opportunistically collected individual movement traces—as inputs for generating more robust and diverse performance measures. These data could help capture a wider range of travel behaviors and increase the realism of calibration scenarios.
Development of novel goodness-of-fit metrics: There is also scope for defining new formulations of goodness-of-fit indicators or the definition of multi-objective functions that better reflect the complexity of model behavior and user interactions in ABMs. These metrics should aim to balance statistical rigor with computational efficiency, while being sensitive to spatial and temporal heterogeneity in observed patterns.
Improvements in the optimization process:
Assessment of convergence behavior: Further exploration is needed to understand the ability of optimization algorithms to identify global optima as the maximum number of iterations is increased. Based on these insights, appropriate convergence criteria can be defined to ensure reliable termination conditions.
Algorithmic enhancements: Lastly, future research should consider possible enhancements or adaptations of the employed optimization algorithms to improve performance, scalability, and robustness. This may involve hybrid approaches, adaptive parameter tuning, or incorporating problem-specific heuristics to accelerate convergence and improve solution quality.
Testing the framework on a real-world larger network:
Challenges: Increasing the size and complexity of the agent-based model (ABM) would substantially raise the computational burden for each simulation run. This, in turn, would extend the total execution time required for the calibration process, as a larger number of parameter combinations must be evaluated. In practical terms, this means that scaling up to more detailed or larger-scale ABMs could result in calibration procedures that take days or even weeks to complete, depending on the available computational resources. Moreover, the real-world applications may present data quality issues (e.g., missing or noisy connections, the over- or under-representation of some specific users’ segments).
The possible solutions to be investigated to overcome the computational challenges are the algorithmic enhancements mentioned above, including approximation techniques, employing heuristic approaches to approximate key metrics without requiring full-scale computation on the entire network, distributed computing, adapting the framework for a high-performance computing environment, and domain-specific constraints, incorporating prior knowledge about parameter values to limit the search space and computational load.
Possible solutions to be investigated to overcome the data quality include the following: robust data preprocessing pipelines, integrating multiple data sources to improve completeness and accuracy, and applying noise reduction or filtering techniques to mitigate measurement errors.
6. Conclusions
This paper has presented a general methodology for the aggregate calibration of transport models applied to the case of destination choice models, embedded in an activity-based model. Using a test network, this paper utilizes processed data collected from cell phone calls and/or data collected from apps installed on smartphones. Although the characterization of trips with regard to the trip purpose and mode of transport is still controversial, the processing of this data provides OD trip matrices marked by a good level of temporal and spatial characterization.
The calibration task is approached as a simulation optimization process, which aims to minimize the deviations between the model simulation output and the observed data, which have been hypothesized.
Three different types of algorithms have been used, evaluated, and compared: Simultaneous Perturbation Stochastic Approximation (SPSA), Particle Swarm Optimization (PSO), and Adaptive Moment Estimation (ADAM).
Based on the literature reviewed, the use of the ADAM optimizer in this specific calibration context appears to be novel, as no prior studies were identified that have explored its application for this purpose. Introducing and systematically testing ADAM as an alternative to more conventional optimization algorithms represents a primary methodological contribution of this study, which is centered on calibration methodology rather than on the development of a new demand model. Introducing ADAM not only broadens the set of available tools for model calibration but also provides an initial benchmark for evaluating the potential advantages and limitations of adaptive gradient methods in this domain.
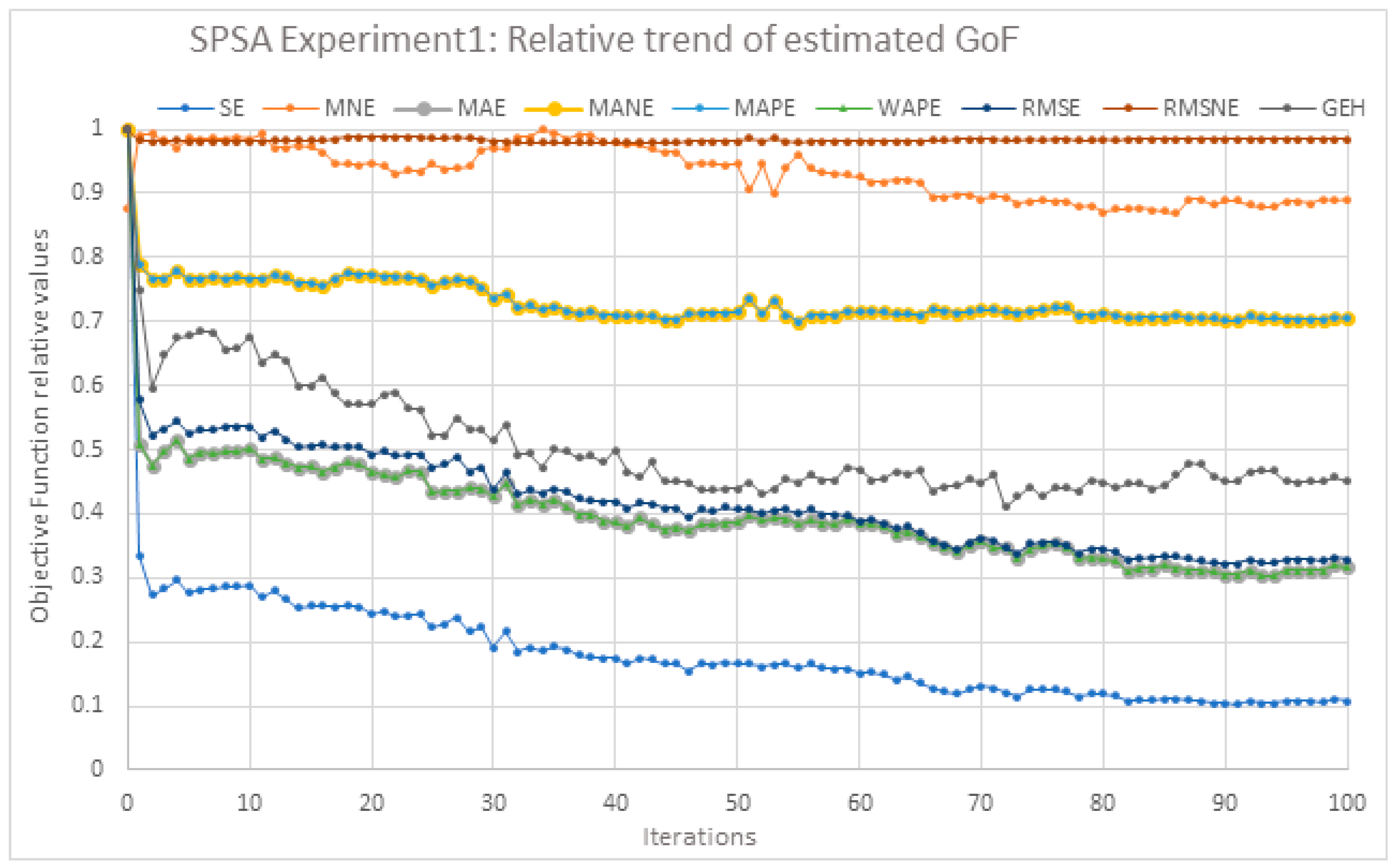
Also, tests were performed to calibrate the three optimization algorithms’ hyperparameters; the squared error and several goodness-of fit values have been calculated.
The following deductions were made on the latter. The MNE can also present a negative correlation with the distance (between the solutions and the true solution), indicating that MNE is not suitable to be used as a GoF. The RMSNE and SE present the worst performances. Different GoF tests perform differently with different algorithms, such as GEH and the correlation coefficient. MAE, MANE, MAPE, and WAPE rank in the middle to highly. The RMSE always shows a strong correlation with the distance between the computed solutions and the true solution.
The calibration experiments reveal that no single optimizer uniformly dominates across all criteria; instead, each offers strengths tailored to specific calibration priorities. It is interesting to note that ADAM is preferable when the computational budget allows for many iterations (and model runs) since it presents the ability to ensure long-term objective function improvements.
On the practical side, the approach presented here allows an efficient calibration of destination choice model parameters by using cheap and readily available data. Given the limited data with which travel models are often estimated in practice, the proposed framework appears to be valuable.
The method can easily be extended to use other sources of available opportunistic data to calibrate other sub-models’ parameters.
The proposed methodology for aggregate model calibration has wide-ranging applications, suitable for various types of models regardless of their specific structure or scale. Crowd-sourced individual mobility data has become a valuable resource for updating or calibrating transport system models. These technological developments further expand the potential for applying aggregate calibration using crowd-sourced mobility data.
A key limitation of the proposed calibration approach lies in the inherent characteristics of simulation optimization. This typically requires numerous evaluations of the objective function, each requiring a full execution of the transport model. When applied to real-world networks with a large size, this process can become computationally intensive and time-consuming. As the size and complexity of the network increase, so does the computational burden, potentially limiting the practicality of the method for large-scale applications without significant strategies to increase the algorithms’ performances.
However, the approach developed here is not only more rigorous but also more efficient than the manual trial and error procedures. Also, the result is the first to develop a wider framework for the aggregate calibration of a full transport simulation model that is less costly and more accurate, using crowd-sourced individual and/or opportunistic mobility data.