Analysis of Resampling Methods for the Red Edge Band of MSI/Sentinel-2A for Coffee Cultivation Monitoring
Abstract
1. Introduction
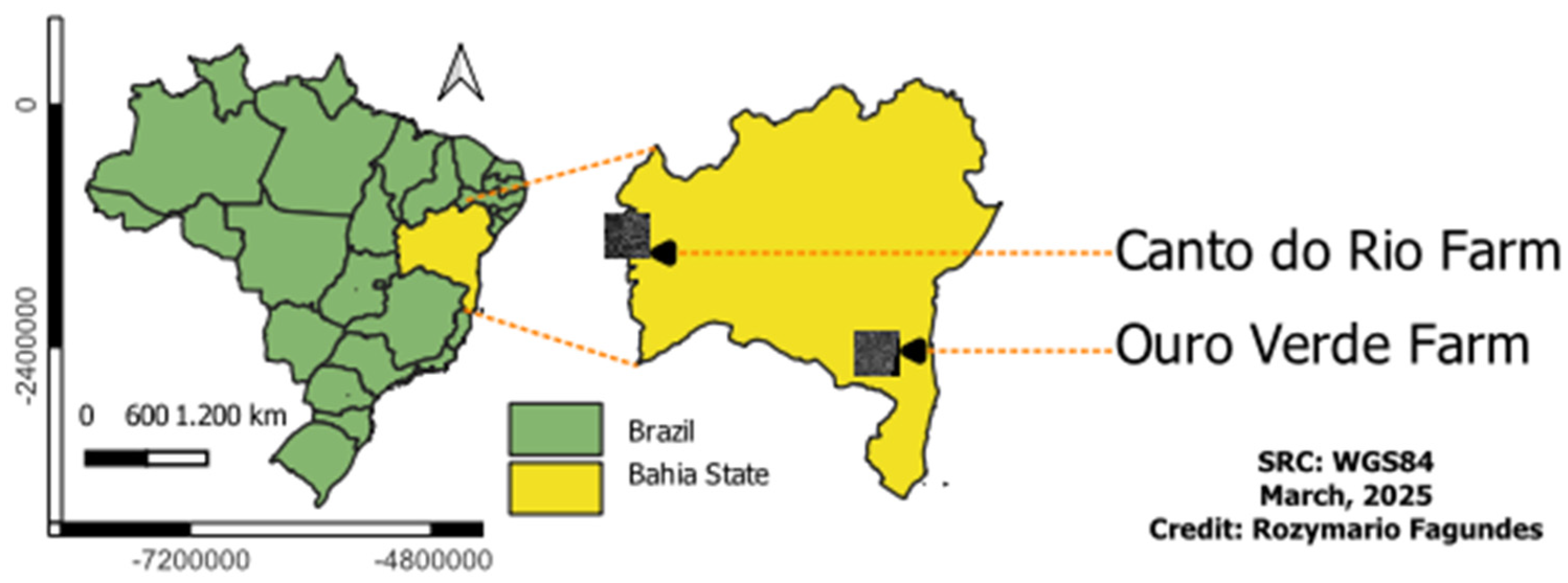
2. Materials and Methods
- (1)
- Initial division into 70% for training and 30% for testing, applied to the normalized data set extracted from the sample points. This stage aimed to simulate a real prediction scenario, using a fraction of the data not observed in the training.
- (2)
- K-fold cross-validation (k = 5, with 5 repetitions), applied only to the training subset. This approach allowed for the adjustment and validation of the linear regression models with greater statistical robustness, minimizing the effect of random partitioning. The final results refer exclusively to the performance obtained on the test set (30%).
3. Results
3.1. Results of the Family Health Program (FHP) Evaluation
3.1.1. “Ouro Verde” Farm
3.1.2. “Canto do Rio” Farm
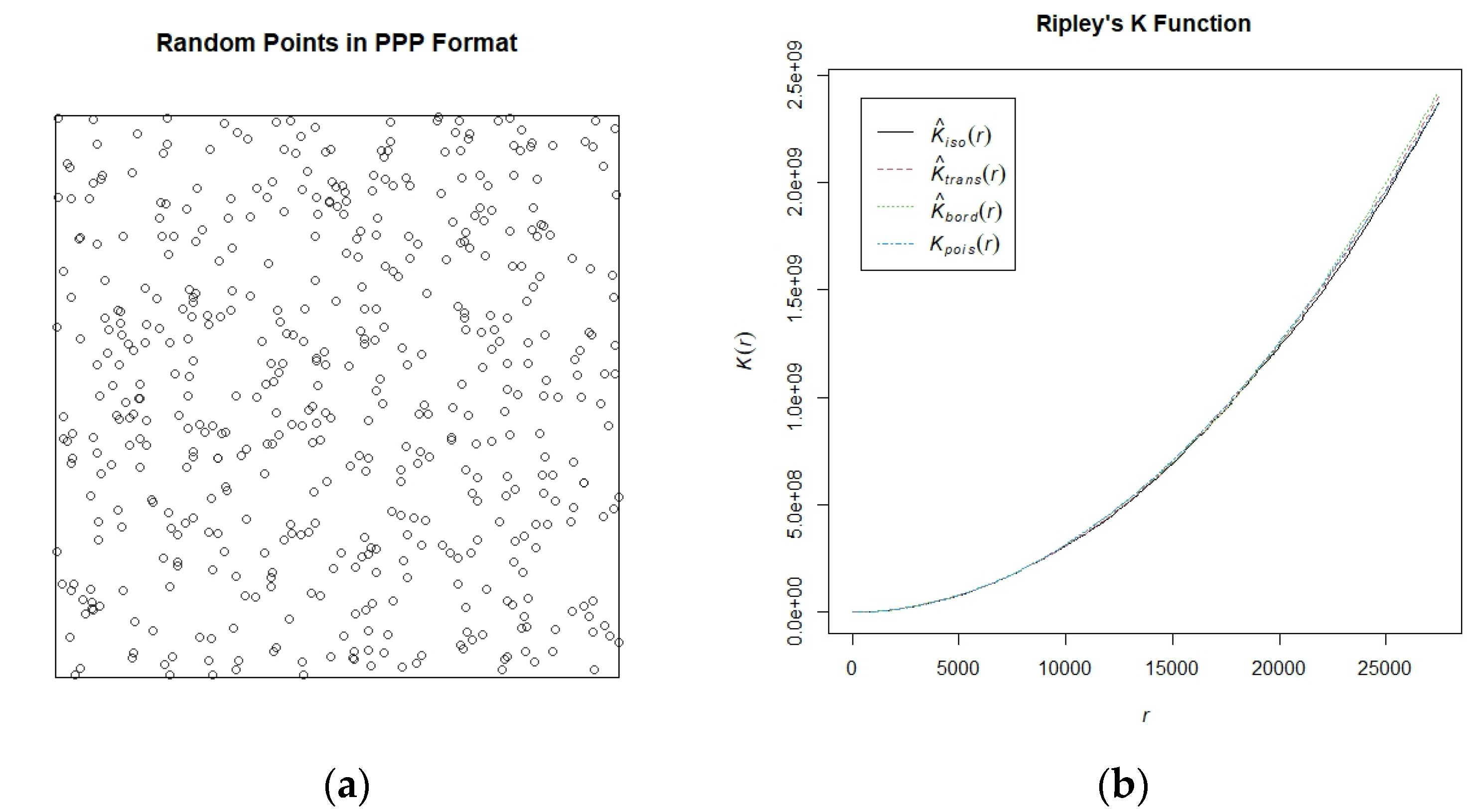
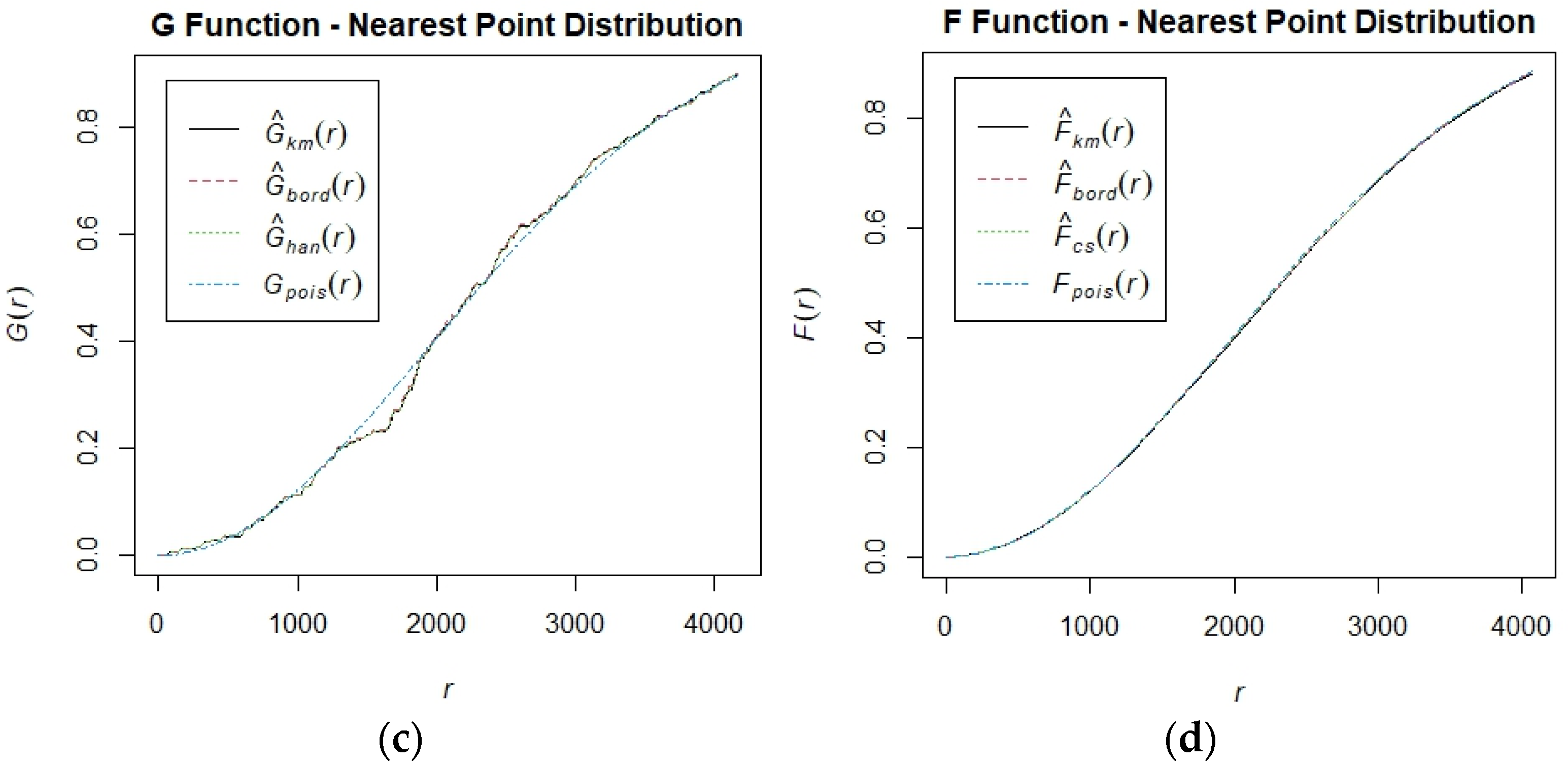
3.2. Cross-Validation Results and Metrics Evaluation
3.2.1. “Ouro Verde” Farm
3.2.2. “Canto do Rio” Farm
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Castro, G.D.M.; Vilela, E.F.; de Faria, A.L.R.; Silva, R.A.; Ferreira, W.P.M. New vegetation index for monitoring coffee rust using sentinel-2 multispectral imagery. Coffee Sci. 2023, 18, e182170. [Google Scholar] [CrossRef]
- Dias, G. Riscos Climáticos e Produtividade do Coffea Arabica L. Para as Principais Regiões Cafeeiras do BRASIL: Clima Presente e Futuro. Doctoral Thesis, Federal University of Itajubá, Itajubá, Brazil, 5 April 2024. [Google Scholar]
- CONAB—Companhia Nacional de Abastecimento. Acompanhamento da Safra Brasileira de Café, v. 11 – Safra 2024, n.4- Quarto levantamento, Brasília, p. 1-53, Janeiro 2025. Available online: https://www.gov.br/conab/pt-br/atuacao/informacoes-agropecuarias/safras/safra-de-cafe/4o-levantamento-de-cafe-safra-2024/4o-levantamento-de-cafe-safra-2024 (accessed on 16 February 2025).
- Campo e N. Anuário de Café 2021, 12th ed.; Editora Gazeta: Uberlândia, Brazil, 2021; ISSN 2316-6290. [Google Scholar]
- Silva, F.M.; Alves, M.C. Cafeicultura de Precisão; Editora UFLA: Lavras, Brazil, 2013. [Google Scholar]
- Ferraz, G.A.S. Cafeicultura de Precisão: Malhas Amostrais Para o Mapeamento de Atributos do Solo, da Planta e Recomendações. Ph.D. Thesis, Federal University of Lavras, Lavras, Brazil, 2012. [Google Scholar]
- Santana, L.S.; Ferraz, G.A.S.; Santos, S.A.d.o.s.; Dias, J.E.L. Precision coffee growing: A review. Coffee Sci. 2022, 17, e172007. [Google Scholar] [CrossRef]
- Melos, N.D. Uso de Análise Multivariada Para Identificação de Zonas de Potenciais Produtivos Agrícolas. Master’s Thesis, University of Santa Maria, Santa Maria, Brazil, 9 March 2023. [Google Scholar]
- Barnes, E.M.; Clarke, T.R.; Richards, S.E.; Colaizzi, P.D.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T.; et al. Coincident detection of crop water stress, nitrogen status and canopy density using ground-based multispectral data. In Proceedings of the 5th International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Chemura, A.; Mutanga, O.; Odindi, J.; Kutywayo, D. Mapping spatial variability of foliar nitrogen in coffee (Coffea arabica L.) plantations with multispectral Sentinel-2 MSI data. ISPRS J. Photogramm. Remote Sens. 2018, 138, 1–11. [Google Scholar] [CrossRef]
- Nogueira, M.R.; de Carvalho Pinto, F.d.A.; Marçal de Queiroz, D.; Magalhães Valente, D.S.; Fim Rosas, J.T. A Novel Vegetation Index for Coffee Ripeness Monitoring Using Aerial Imagery. Remote Sens. 2021, 13, 263. [Google Scholar] [CrossRef]
- ESA-Europe Spatial Agence. Sentinel Online. Available online: https://sentinels.copernicus.eu/web/sentinel/home (accessed on 12 December 2024).
- Kai, P.M.; de Oliveira, B.M.; Vieira, G.S.; Soares, F.; Costa, R.M. Effects of resampling image methods in sugarcane classification and the potential use of vegetation indices related to chlorophyll. In Proceedings of the 2021 IEEE 45th Annual Computers, Software, and Applications Conference (COMPSAC), Madrid, Spain, 12–16 July 2021; pp. 1526–1531. [Google Scholar] [CrossRef]
- Richards, J.A.; Richards, J. Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 1999; Volume 3. [Google Scholar]
- Rodrigues, S.A.; Cortez, J.W.; Henriques, H.J.R. Efeito da chuva de granizo em variedades do café arábica por meio de índices de vegetação. Agrarian 2021, 14, 433–441. [Google Scholar] [CrossRef]
- Feio, S. Análise Multitemporal de Imagens de Satélite Sentinel-2 Como Suporte à Elegibilidade das Ajudas Comunitárias Agrícolas. Master’s Dissertation, University of Lisbon, Lisbon, Portugal, 2017. [Google Scholar]
- Mookambiga, A.; Gomathi, V. Comprehensive review on fusion techniques for spatial information enhancement in hyperspectral imagery. Multidimens. Syst. Signal Process. 2016, 27, 863–889. [Google Scholar] [CrossRef]
- Sadeghi, S.; Guo, L.; Toliyat, H.A.; Parsa, L. Wide Operational Speed Range of Five-Phase Permanent Magnet Machines by Using Different Stator Winding Configurations. IEEE Trans. Ind. Electron. 2012, 59, 2621–2631. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Wahba, G. Spline Models for Observational Data; SIAM: Pennsylvania, PA, USA, 1990. [Google Scholar]
- Oliver, M.A.; Webster, R. Kriging: A Method of Interpolation for Geographical Information Systems. Int. J. Geogr. Inf. Syst. 2014, 4, 313–332. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Boggione, G.A.; Costa, D.D. Reamostragem em imagens de sensoriamento remoto: Uma abordagem sob o ponto de vista do maup. In Proceedings of the IV Simpósio Brasileiro de Geomática–SBG2017 I I, Presidente Prudente, São Paulo, Brazil, 24–26 July 2017; pp. 315–322, ISSN 1981-6251. [Google Scholar]
- Porwal, S.; Katiyar, S.K. Performance Evaluation of Various Resampling Techniques on IRS Imagery. In Proceedings of the 2014 Seventh International Conference on Contemporary Computing (IC3), Noida, India, 9 August 2014. [Google Scholar] [CrossRef]
- Lezine, E.M.D.; Kyzivat, E.D.; Smith, L.C. Super-Resolution Surface Water Mapping on the Canadian Shield Using Planet CubeSat Images and a Generative Adversarial Network. Can. J. Remote Sens. 2021, 47, 261–275. [Google Scholar] [CrossRef]
- Ceccato, G.Z.; Das, N.; José, M.G.; Cesar, J. Avaliação dos valores de erro do modelo linear de mistura espectral em imagens etm+/landsat 7 a partir de reamostragens pelo vizinho mais próximo e convolução cúbica. Geociências 2021, 40, 795–810. [Google Scholar] [CrossRef]
- Guo, L.; Shi, T.; Linderman, M.; Chen, Y.; Zhang, H.; Fu, P. Exploring the Influence of Spatial Resolution on the Digital Mapping of Soil Organic Carbon by Airborne Hyperspectral VNIR Imaging. Remote Sens. 2019, 11, 1032. [Google Scholar] [CrossRef]
- Madhukar, B.N.; Narendra, R. Lanczos Resampling for the Digital Processing of Remotely Sensed Images. Lect. Notes Electr. Eng. 2013, 258, 403–411. [Google Scholar] [CrossRef]







| Band Number | Spectral Band | Wavelength (nm) | Spatial Resolution (m) |
|---|---|---|---|
| B01 | Costal aerosol | 443 | 60 |
| B02 | Blue | 490 | 10 |
| B03 | Green | 560 | 10 |
| B04 | Red | 665 | 10 |
| B05 | Red Edge 1 | 705 | 20 |
| B06 | Red Edge 2 | 740 | 20 |
| B07 | Red Edge 3 | 783 | 20 |
| B08 | NIR | 842 | 10 |
| B8A | NIR narrow | 865 | 20 |
| B09 | Water vapor | 945 | 60 |
| B10 | Cirrus | 1380 | 60 |
| B11 | SWIR 1 | 1910 | 60 |
| B12 | SWIR 2 | 2190 | 20 |
| Resampling Methods | Characteristics |
|---|---|
| Nearest Neighbor | Assigns the value of a pixel based on the nearest neighboring pixel, thereby preserving the original image data. However, this approach can lead to duplication of values, potential loss of fine details, and slight spatial misalignment, requiring careful application depending on the study’s objectives. |
| Bilinear | Determines a new pixel value by interpolating between the four nearest points, using a weighted averaging approach. This method provides smoother transitions between pixels but may introduce slight blurring effects. |
| Cubic | Computes the value of a new pixel by considering the 16 nearest neighbors, applying weighted averaging. This approach enhances image smoothness and reduces pixelation, albeit at a higher computational cost. |
| Lanczos | Uses a high-quality Lanczos kernel to interpolate signal values, effectively preserving image details while reducing aliasing effects. Although this method requires increased processing time, it generally yields superior visual and spectral quality in resampled images. |
| r | Theo | Border | Trans | iso | |
|---|---|---|---|---|---|
| Min. | 0 | 0 × 100 | 0 × 100 | 0 × 100 | 0 × 100 |
| 1st Qu | 6.862 × 103 | 1.48 × 1011 | 1.47 × 1011 | 1.46 × 1011 | 1.46 × 1011 |
| Median | 1.3725 × 104 | 5.92 × 1011 | 6.01 × 1011 | 6.00 × 1011 | 5.98 × 1011 |
| Mean | 1.3725 × 104 | 7.90 × 1011 | 7.86 × 1011 | 7.90 × 1011 | 7.87 × 1011 |
| 3rd Qu | 2.0588 × 104 | 1.33 × 1012 | 1.33 × 1012 | 1.33 × 1012 | 1.32 × 1012 |
| Max | 2.745 × 104 | 2.37 × 1012 | 2.33 × 1012 | 2.37 × 1012 | 2.36 × 1012 |
| r | Theo | Han | rs | km | Hazard | Theohaz | |
|---|---|---|---|---|---|---|---|
| Min. | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000000 | 0.0000000 |
| 1st Qu | 2350 | 0.5130 | 0.5175 | 0.5131 | 0.5134 | 0.0000000 | 0.0006124 |
| Median | 4700 | 0.9438 | 0.9353 | 0.9357 | 0.9300 | 0.0000000 | 0.0012248 |
| Mean | 4700 | 0.7383 | 0.7290 | 0.7278 | 0.7267 | 0.0006211 | 0.0012248 |
| 3rd Qu | 7050 | 0.9985 | 10.000 | 10.000 | 10.000 | 0.0004483 | 0.0018371 |
| Max | 9400 | 10.000 | 10.000 | 10.000 | 10.000 | 0.0377538 | 0.0024495 |
| r | Theo | cs | Rs | km | Hazard | Theohaz | |
|---|---|---|---|---|---|---|---|
| Min. | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000000 | 0.0000000 |
| 1st Qu | 2359 | 0.5157 | 0.5254 | 0.5244 | 0.5226 | 0.0003114 | 0.0006147 |
| Median | 4718 | 0.9450 | 0.9542 | 0.9548 | 0.9541 | 0.0009524 | 0.0012294 |
| Mean | 4718 | 0.7345 | 0.7387 | 0.7390 | 0.7382 | 0.0009808 | 0.0012294 |
| 3rd Qu | 7077 | 0.9985 | 0.9977 | 0.9978 | 0.9978 | 0.0012554 | 0.0018441 |
| Max | 9436 | 10.000 | 10.000 | 10.000 | 10.000 | 0.0064643 | 0.0024588 |
| r | Theo | Border | Trans | iso | |
|---|---|---|---|---|---|
| Min. | 0 | 0 | 0 | 0 | 0 |
| 1st Qu | 6862 | 1.48 × 1011 | 1.47 × 1011 | 1.48 × 1011 | 1.48 × 1011 |
| Median | 13,725 | 5.92 × 1011 | 5.92 × 1011 | 5.88 × 1011 | 5.85 × 1011 |
| Mean | 13,725 | 7.90 × 1011 | 7.90 × 1011 | 7.89 × 1011 | 7.83 × 1011 |
| 3rd Qu | 20,588 | 1.33 × 1012 | 1.33 × 1012 | 1.33 × 1012 | 1.32 × 1012 |
| Max | 27,450 | 2.37 × 1012 | 2.36 × 1012 | 2.38 × 1012 | 2.37 × 1012 |
| r | Theo | Han | rs | km | Hazard | Theohaz | |
|---|---|---|---|---|---|---|---|
| Min. | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000000 | 0.0000000 |
| 1st Qu | 2350 | 0.5130 | 0.5088 | 0.5000 | 0.5003 | 0.0000000 | 0.0006124 |
| Median | 4700 | 0.9438 | 0.9451 | 0.9447 | 0.9412 | 0.0000000 | 0.0012248 |
| Mean | 4700 | 0.7383 | 0.7382 | 0.7368 | 0.7355 | 0.0006246 | 0.0012248 |
| 3rd Qu | 7050 | 0.9985 | 10.000 | 10.000 | 10.000 | 0.0004799 | 0.0018371 |
| Max | 9400 | 10.000 | 10.000 | 10.000 | 10.000 | 0.0377538 | 0.0024495 |
| r | Theo | cs | rs | km | Hazard | Theohaz | |
|---|---|---|---|---|---|---|---|
| Min. | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.000 | 0.0000000 |
| 1st Qu | 2359 | 0.5157 | 0.5224 | 0.5197 | 0.5180 | 2.25 × 10−2 | 0.0006147 |
| Median | 4718 | 0.9450 | 0.9496 | 0.9469 | 0.9461 | 6.14 × 10−1 | 0.0012294 |
| Mean | 4718 | 0.7345 | 0.7363 | 0.7353 | 0.7344 | 8.43 × 10−1 | 0.0012294 |
| 3rd Qu | 7077 | 0.9985 | 0.9998 | 0.9997 | 0.9994 | 1.15 | 0.0018441 |
| Max | 9436 | 10.000 | 10.000 | 10.000 | 0.9997 | 3.78 | 0.0024588 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fagundes, R.; Kayser, L.P.; de Paula Amaral, L.; Benedetti, A.C.; Bolfe, É.L.; Parreiras, T.C.; Ramos-Ospina, M.; Marulanda-Tobón, A. Analysis of Resampling Methods for the Red Edge Band of MSI/Sentinel-2A for Coffee Cultivation Monitoring. Geomatics 2025, 5, 19. https://doi.org/10.3390/geomatics5020019
Fagundes R, Kayser LP, de Paula Amaral L, Benedetti AC, Bolfe ÉL, Parreiras TC, Ramos-Ospina M, Marulanda-Tobón A. Analysis of Resampling Methods for the Red Edge Band of MSI/Sentinel-2A for Coffee Cultivation Monitoring. Geomatics. 2025; 5(2):19. https://doi.org/10.3390/geomatics5020019
Chicago/Turabian StyleFagundes, Rozymario, Luiz Patric Kayser, Lúcio de Paula Amaral, Ana Caroline Benedetti, Édson Luis Bolfe, Taya Cristo Parreiras, Manuela Ramos-Ospina, and Alejandro Marulanda-Tobón. 2025. "Analysis of Resampling Methods for the Red Edge Band of MSI/Sentinel-2A for Coffee Cultivation Monitoring" Geomatics 5, no. 2: 19. https://doi.org/10.3390/geomatics5020019
APA StyleFagundes, R., Kayser, L. P., de Paula Amaral, L., Benedetti, A. C., Bolfe, É. L., Parreiras, T. C., Ramos-Ospina, M., & Marulanda-Tobón, A. (2025). Analysis of Resampling Methods for the Red Edge Band of MSI/Sentinel-2A for Coffee Cultivation Monitoring. Geomatics, 5(2), 19. https://doi.org/10.3390/geomatics5020019








