Bathymetric Survey for Enhancing the Volumetric Capacity of Tagwai Dam in Nigeria via Leapfrogging Approach
Abstract
1. Introduction
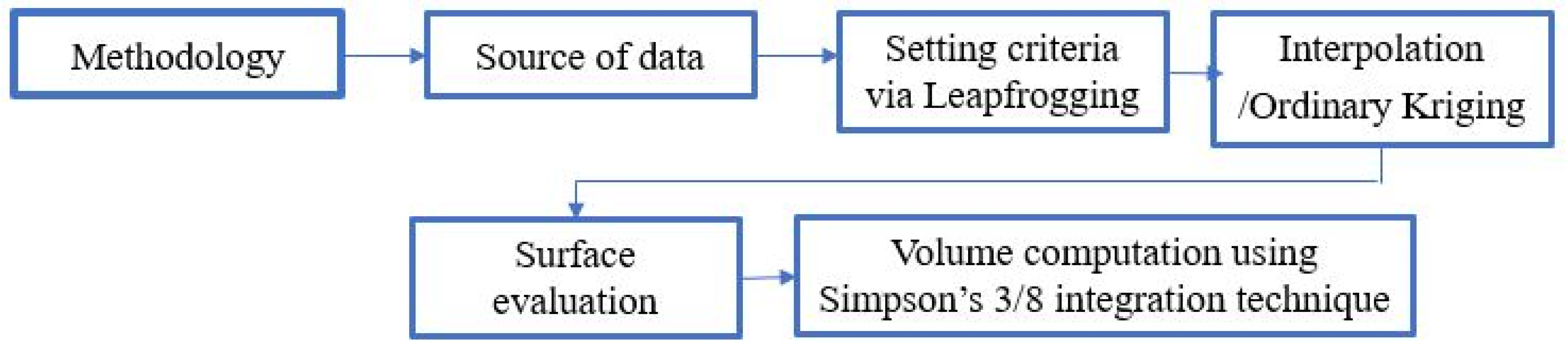
2. Material and Method
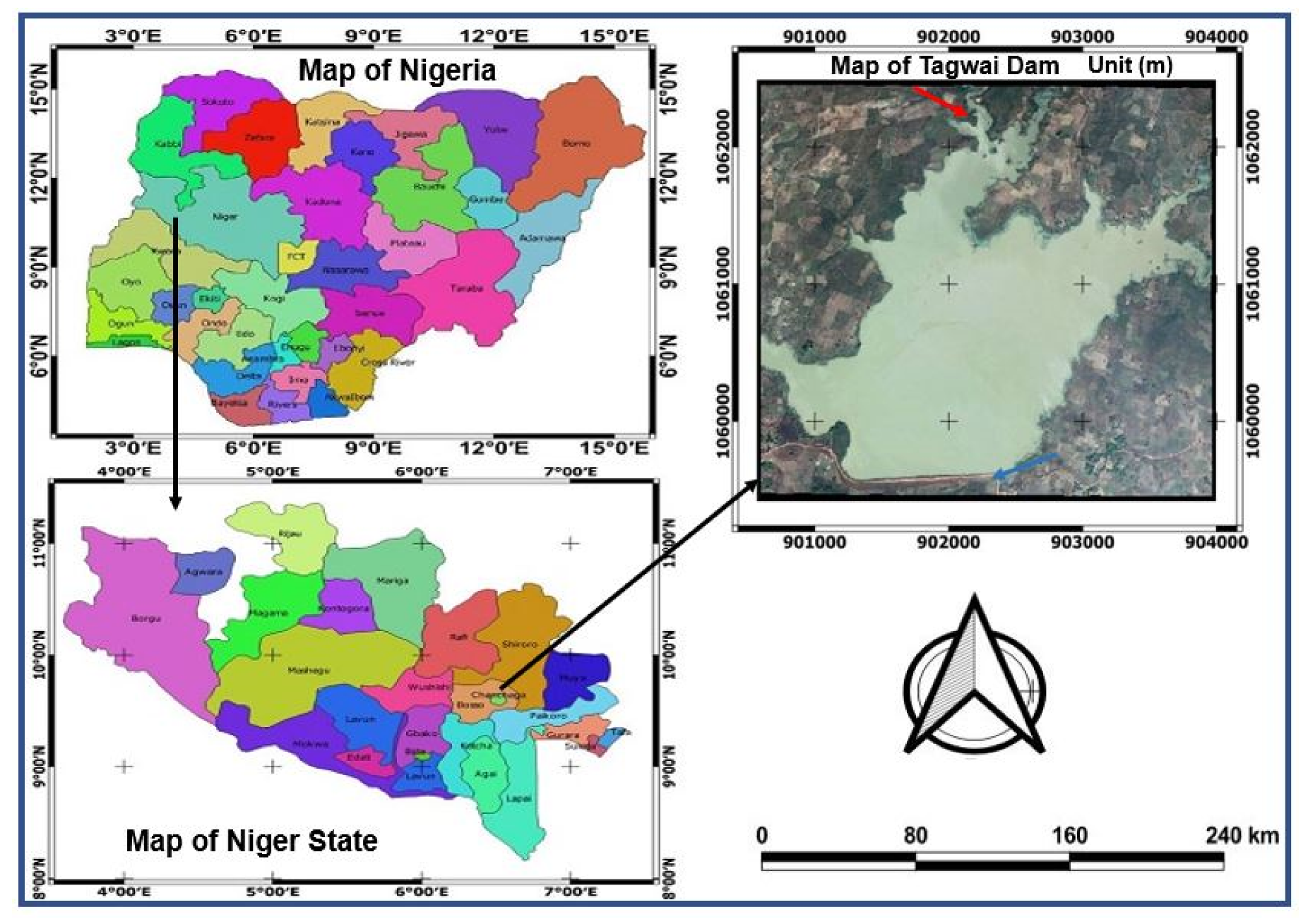
2.1. Study Area
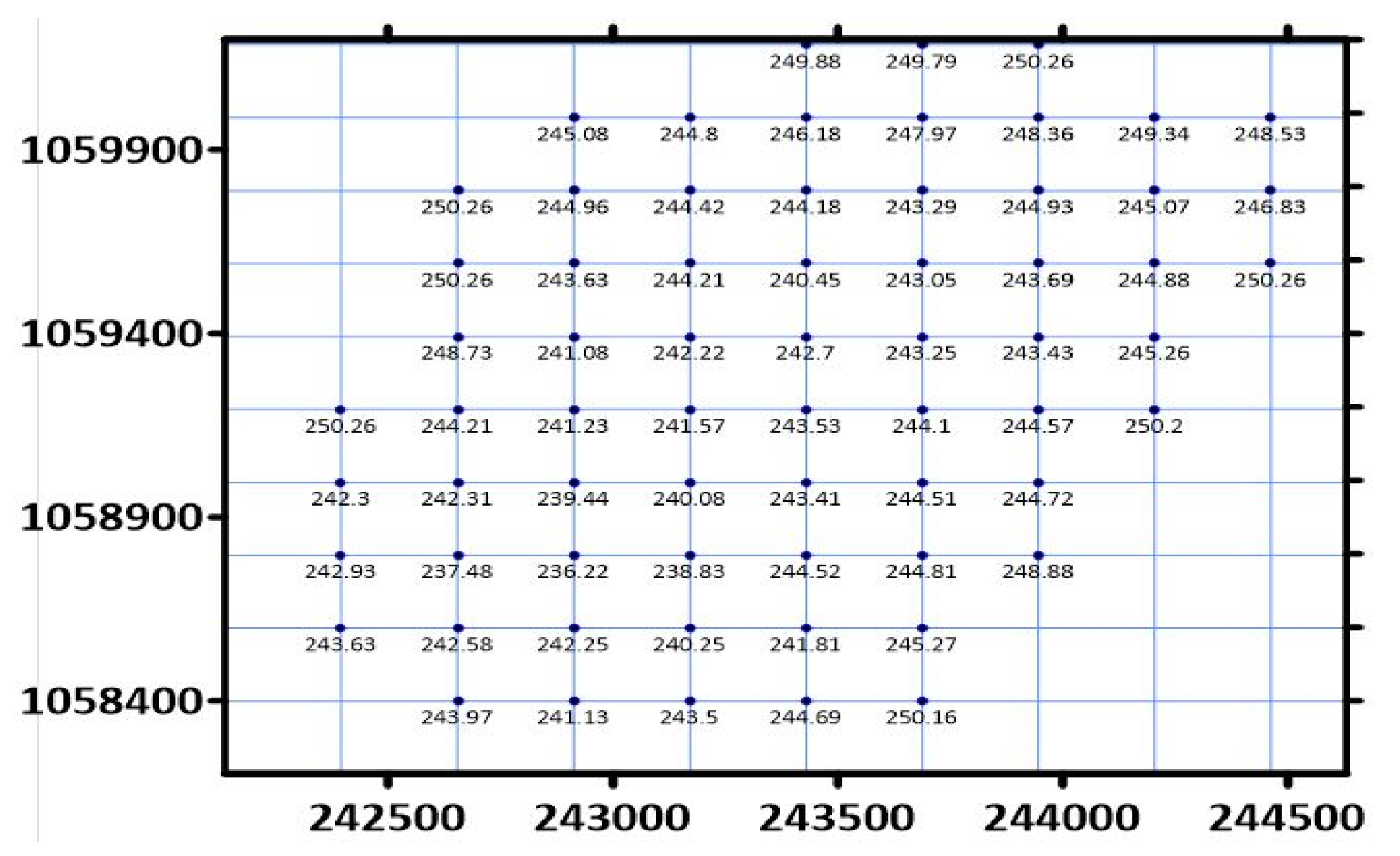
2.2. Source of Data
2.3. Setting Criteria and Scenario via Leapfrogging
2.4. Interpolation and Kriging
2.5. Ordinary Kriging Interpolation Experiment
2.6. Evaluation of Interpolation Surface
2.7. Volume Computation via Simpson 3/8 Integration Techniques
3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- David, D.; Hart, N.; Leroy, P. A Special Section on Dam Removal and River Restoration. BioScience 2002, 52, 653–655. [Google Scholar] [CrossRef]
- Ajith, A.V. Bathymetric Survey to Study the Sediment Deposit in Reservoir of Peechi Dam. IOSR J. Mech. Civ. Eng. 2016, 12, 34–38. [Google Scholar] [CrossRef]
- Amano, K. Water Quality Enhancement Techniques in Dam Reservoirs. J. Soc. Mech. Eng. 2003, 106, 454–455. [Google Scholar] [CrossRef]
- Girish, G.; Ashitha, M.K.; Jayakumar, K.V. Sedimentation assessment in a multipurpose reservoir in Central Kerala, India. Environ. Earth Sci. 2014, 72, 4441–4449. [Google Scholar] [CrossRef]
- Estigoni, M.; Matos, A.; Mauad, F. Assessment of the accuracy of different standard methods for determining reservoir capacity and sedimentation. J. Soils Sediments 2014, 14, 1224–1234. [Google Scholar] [CrossRef]
- Hart, D.D.; Johnson, T.E.; Bushaw-Newton, K.L.; Horwitz, R.J.; Bednarek, A.T.; Charles, D.F.; Kreeger, D.A.; Velinsky, D.J. Dam Removal: Challenges and Opportunities for Ecological Research and River Restoration. BioScience 2002, 52, 669–682. [Google Scholar] [CrossRef]
- Badejo, O.T.; Adewuyi, K.G. Bathymetric Survey and Topography Changes Investigation of Part of Badagry Creek and Yewa River, Lagos State, Southwest Nigeria. J. Geogr. Environ. Earth Sci. Int. 2019, 22, 1–16. [Google Scholar] [CrossRef]
- Khattab, M.F.; Abo, R.K.; Al-Muqdadi, S.W.; Merkel, B.J. Generate Reservoir Depths Mapping by Using Digital Elevation Model: A Case Study of Mosul Dam Lake, Northern Iraq. Adv. Remote Sens. 2017, 6, 161–174. [Google Scholar] [CrossRef]
- Morris, L.M.; Fan, J. Reservoir Sedimentation Handbook: Design and Management of Dams, Reservoirs, and Watersheds for Sustainable Use; McGraw-Hill: New York, NY, USA, 1998; p. 4.17. [Google Scholar]
- Lampe, D.C.; Morlock, S.E. Collection of bathymetric data along two reaches of the Lost River within Bluespring Cavern near Bedford, Lawrence County, Indiana. Sci. Investig. Rep. 2007, 142, 2008–5023. Available online: http://pubs.water.usgs.gov/sir (accessed on 15 August 2020).
- Silveira, D.T.; Portugal, J.L.; de Oliveira Vital, S.R. Análise estatística espacial aplicada a construção de superfícies batimétricas. Geociências 2014, 33, 596–615. [Google Scholar]
- Farrira, I.O.; Dalto, D.R.; Gérson, R.S.; Lidiane, M.F. In Bathymetric Surfaces: IDW Or Kriging. Bol. Ciênc. Geod. 2017, 23, 493–508. [Google Scholar] [CrossRef]
- McIntire, J.P.; Webber, F.C.; Nguyen, D.K.; Li, Y.; Foong, S.H.; Schafer, K.; Chue, W.Y.; Ang, K.; Vinande, E.T. LeapFrogging: A technique for accurate long-distance ground navigation and positioning without GPS. J. Inst. Navig. 2018, 65, 35–47. [Google Scholar] [CrossRef]
- Fudenberg, D.; Gilbert, R.; Stiglitz, J.; Tirole, J. Preemption, Leapfrogging, and Competition in Patent Races. Eur. Econ. Rev. 1983, 22, 3–31. [Google Scholar] [CrossRef]
- Brezis, E.; Krugman, P.; Tsiddon, D. Leapfrogging: A Theory of Cycles in National Technological Leadership. Am. Econ. Rev. 1993, 1211–1219. [Google Scholar] [CrossRef]
- Brezis, E.S.; Krugman, P. Technology and Life Cycle of Cities. J. Econ. Growth 1997, 2, 369–383. [Google Scholar] [CrossRef]
- Munasinghe, M. Is environmental degradation an inevitable consequence of economic growth: Tunneling through the environmental Kuznets curve. Ecol. Econ. 1999, 29, 89–109. [Google Scholar] [CrossRef]
- Barro, R.; Sala-i-Martin, X. Economic Growth; MIT Press: Cambridge, MA, USA, 2003; p. 375. ISBN 9780262025539. [Google Scholar]
- Arseni, M.; Voiculescu, M.; Georgescu, L.P.; Iticescu, C.; Rosu, A. Testing Different Interpolation Methods Based on Single Beam Echosounder River Surveying. Case Study: Siret River. Int. J. Geo-Inf. 2019, 8, 507. [Google Scholar] [CrossRef]
- Parente, C.; Vallario, A. Interpolation of Single Beam Echo Sounder Data for 3D Bathymetric Model. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 6–13. [Google Scholar] [CrossRef]
- IHO Manual on Hydrography. International Hydrographic Organization Publication C-13; International Hydrographic Bureal: Monaco City, Monaco, 2011. [Google Scholar]
- Hare, R.; Eakins, B.; Amante, C. Modelling Bathymetric Uncertainty. Int. Hydrogr. Rev. 2011, 6, 31–42. Available online: https://coast.noaa.gov/data/digitalcoast/pdf/topo-bathy-data-considerations.pdf (accessed on 15 August 2020).
- Williams, C.K.I. Prediction with Gaussian Processes: From Linear Regression to Linear Prediction and Beyond. Learn. Graph. Models 1998, 599–621. [Google Scholar] [CrossRef]
- Marcelo, C.; Joaquim, L.; Igor, O.; Joao, L.; Jose, S. Assessment of Spatial Interpolation Methods to Map Bathymetry of an Amazonian Hydroelectric reservoir to Aid in decision marking for water Management. ISPRS Int. J. Geo-Inform. 2015, 4, 220–235. [Google Scholar] [CrossRef]
- Ferreira, I.O.; Domingos, R.D.; Santos, G.R. Coleta, Processamento e Análise de Dados Batimétricos; Novas Edições Acadêmicas: do Paraná, Brazil, 2015. [Google Scholar]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Wu, C.; Joann, M.; Liang, M.; Mohammad, A. Comparison of different spatial interpolation methods for historical hydrographic data of the lowermost Mississippi River. Ann. GIS 2019, 25, 133–151. [Google Scholar] [CrossRef]
- Santos, G.R.; Oliveira, M.S.; Louzada, J.M.; Santos, A.M.R.T. Krigagem simples versus krigagem universal: Qual o preditor mais precison. Energy Agric. 2011, 26, 49–55. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M. Geostatistics for Environmental Scientists; John Wiley & Sons, Ltd.: Chichester, UK, 2001; p. 271. [Google Scholar]
- Eriksson, M.; Siska, P.P. Understanding Anisotropy Computations. Math. Geol. 2000, 32, 683–700. [Google Scholar] [CrossRef]
- Merwade, V.M.; Maidment, D.R.; Goff, J.A. Anisotropic considerations while interpolating river channel bathymetry. J. Hydrol. 2006, 331, 731–741. [Google Scholar] [CrossRef]
- Canadian Hydrographic Service (CHS). CHS Standards for Hydrographic Surveys, 1st ed.; Fisheries and Oceans: Ottawa, ON, Canada, 2005. [Google Scholar]
- Hernandez-Stefanoni, J.L.; Ponce-Hernandez, R. Mapping the spatial variability of plant diversity in a tropical forest: Comparison of spatial interpolation methods. Environ. Monit. Assess. 2006, 117, 307–334. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989; p. 561. [Google Scholar]
- Nalder, I.A.; Wein, R.W. Spatial interpolation of climatic Normals: Test of a new method in the Canadian boreal forest. Agric. For. Meteorol. 1998, 92, 211–225. [Google Scholar] [CrossRef]
- Ahmed, S.; De Marsily, G. Comparison of geostatistical methods for estimating transmissivity using data on transmissivity and specific capacity. Water Resour. Res. 1987, 23, 1717–1737. [Google Scholar] [CrossRef]
- Burrough, P.A.; McDonnell, R.A. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 1998; p. 333. [Google Scholar]
- Hu, K.; Li, B.; Lu, Y.; Zhang, F. Comparison of various spatial interpolation methods for non-stationary regional soil mercury content. Environ. Sci. 2004, 25, 132–137. [Google Scholar]
- Vicente-Serrano, S.M.; Saz-Sánchez, M.A.; Cuadrat, J.M. Comparative analysis of interpolation methods in the middle Ebro Valley (Spain): Application to annual precipitation and temperature. Clim. Res. 2003, 24, 161–180. [Google Scholar] [CrossRef]

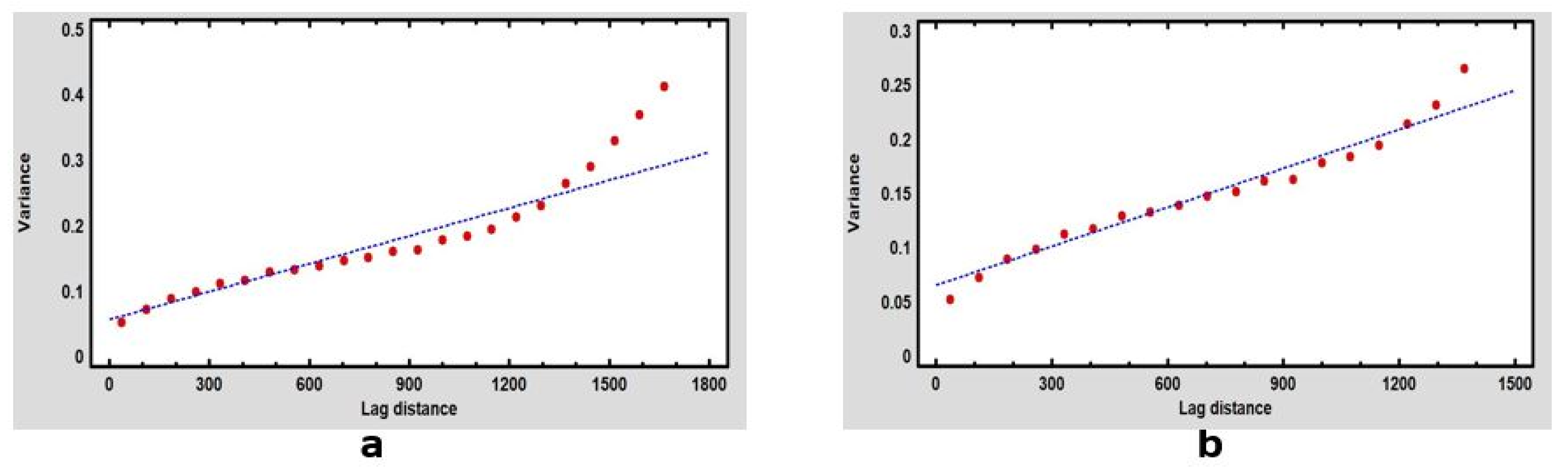
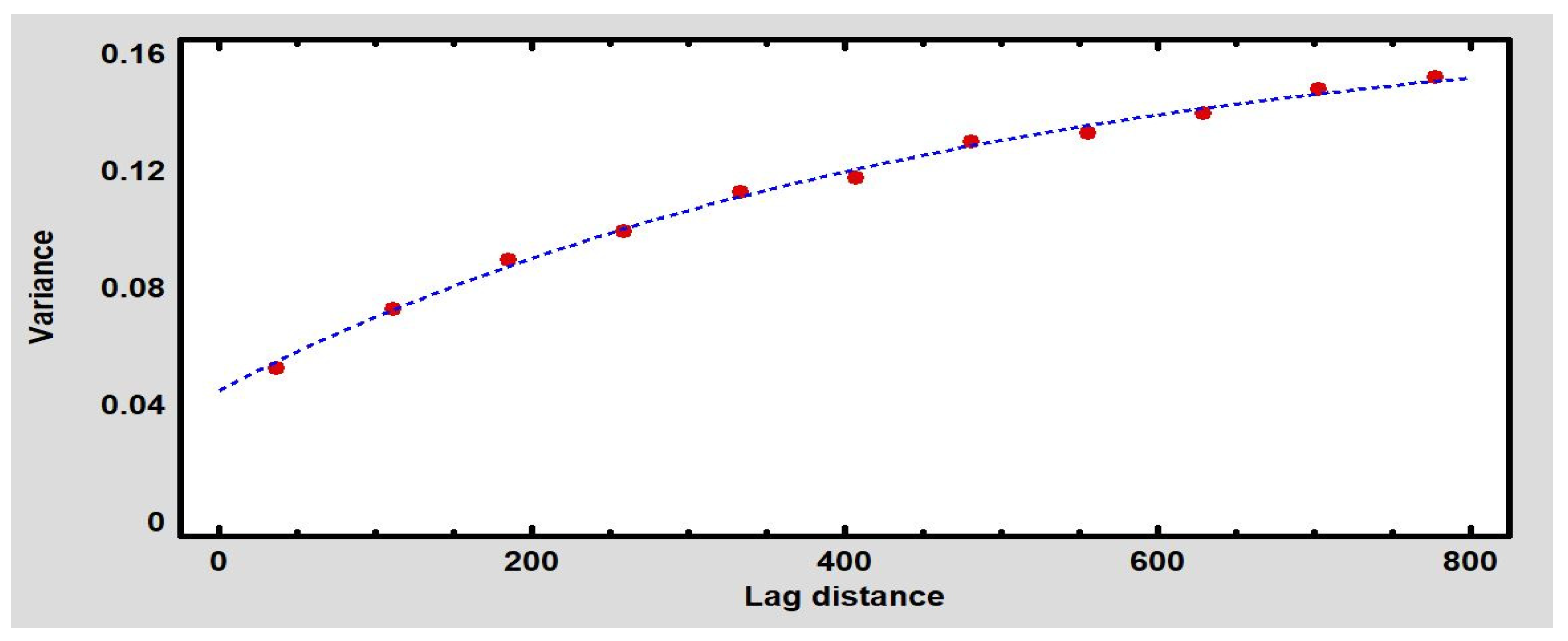
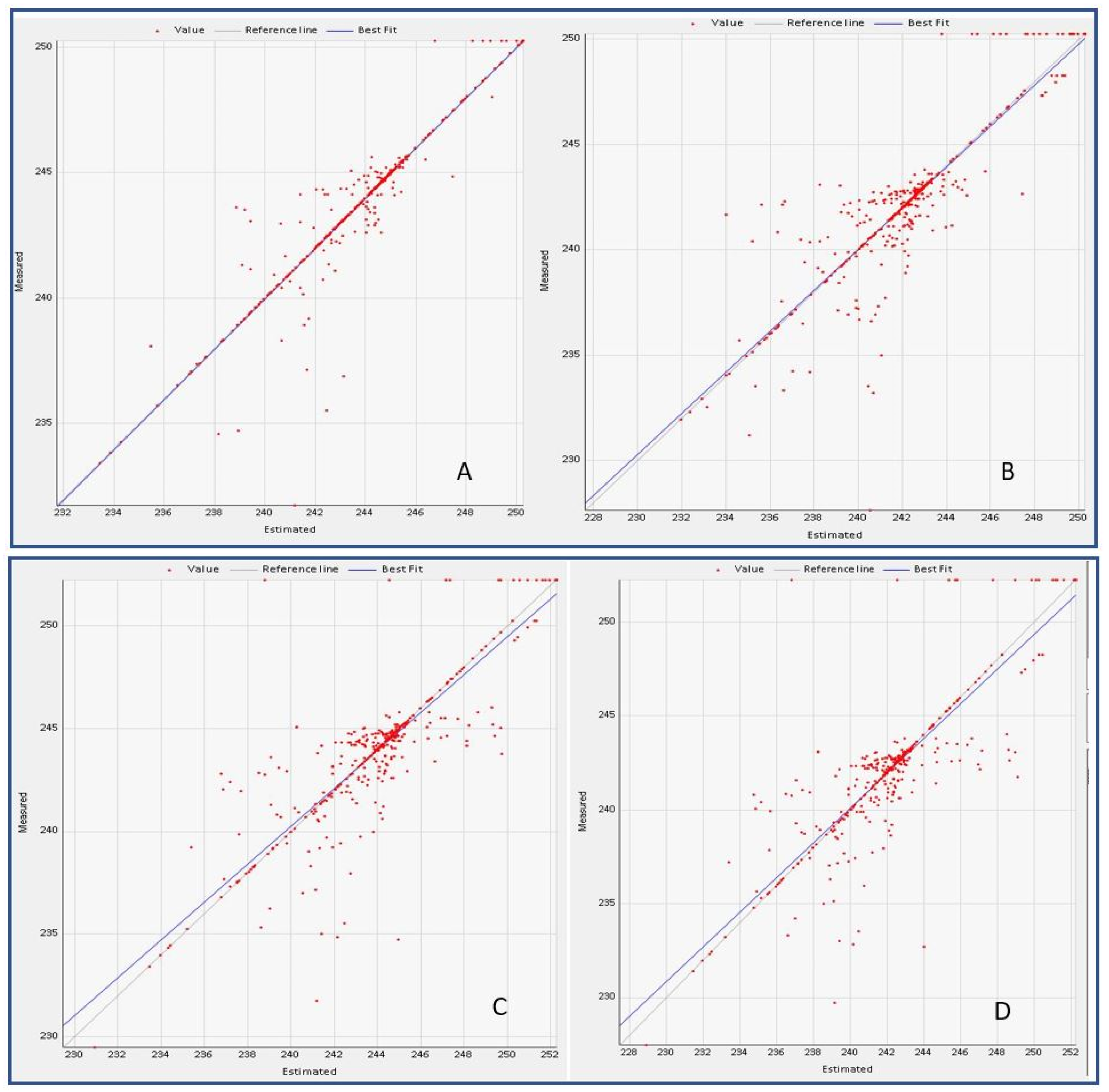
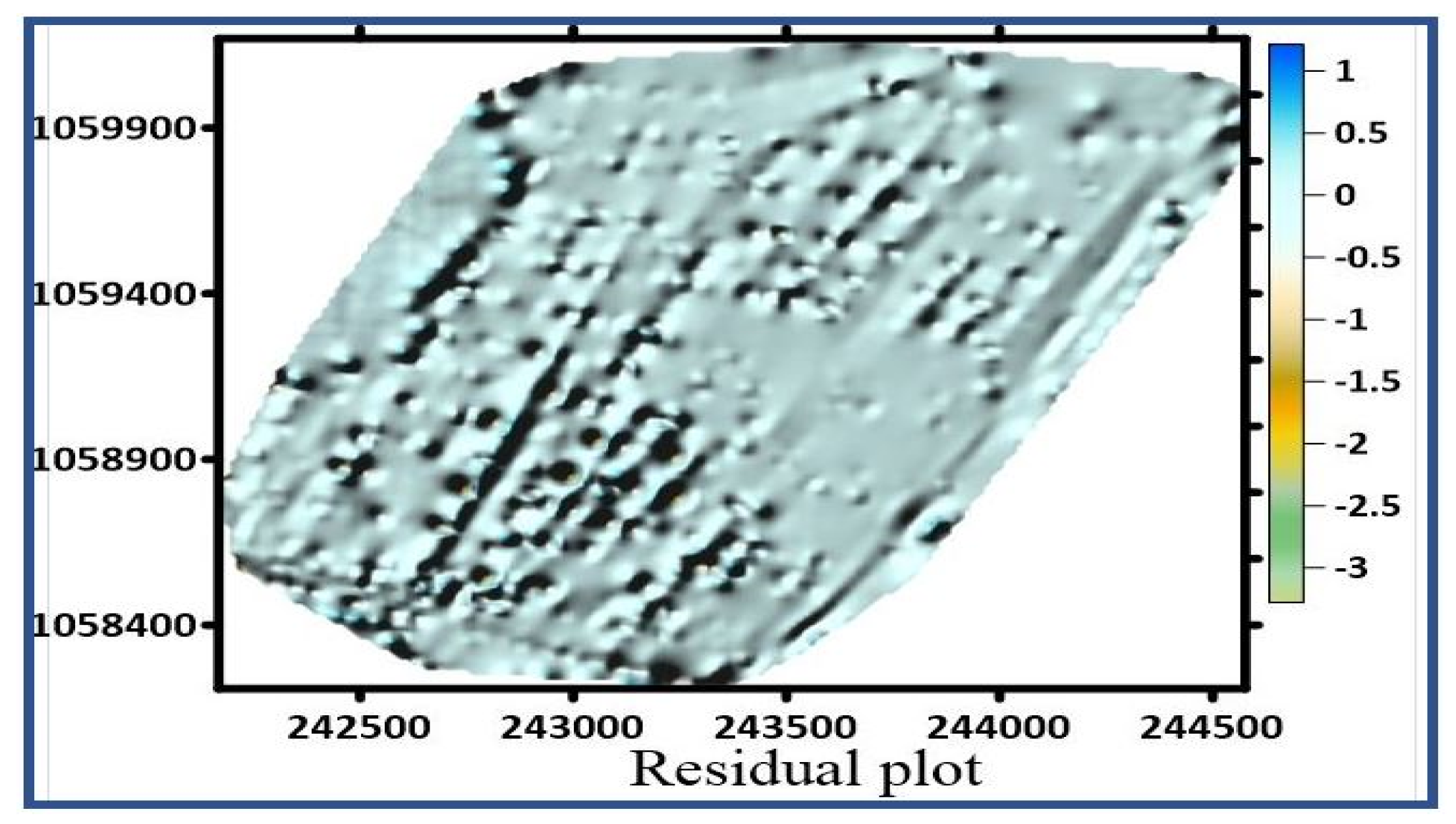

| Model | Nugget | Sill | Range | R-Squared | RMSE | |
|---|---|---|---|---|---|---|
| Figure 5a | Exponential | 0.075 | 0.421 | 1702.12 | 91.01% | 0.165 |
| Figure 5b | - | 0.062 | 0.253 | 1425.20 | 92.63% | 0.065 |
| Figure 6 | - | 0.0451 | 0.157 | 775.21 | 99.58% | 0.006 |
| Scenario | ME | MSE | RMSE | R2 | Coef. of Va. | Volume (m3) | % Volume |
|---|---|---|---|---|---|---|---|
| A | 0.008 | 0.138 | 0.371 | 0.965 | 0.015 | 93,129,808 | 23.79 |
| B | 0.008 | 0.148 | 0.385 | 0.962 | 0.017 | 97,668,974 | 24.95 |
| C | 0.008 | 0.148 | 0.385 | 0.951 | 0.014 | 98,030,602 | 25.04 |
| D | 0.008 | 0.168 | 0.410 | 0.959 | 0.018 | 102,631,952 | 26.22 |
| Easting (m) | Northing (m) | Reduced Depth (m) | Residuals (m) |
|---|---|---|---|
| 242,502.387 | 1,058,741.722 | 242.414 | 0.006 |
| 243,107.042 | 1,058,271.965 | 244.086 | −0.130 |
| 244,246.156 | 1,059,864.163 | 244.877 | −0.004 |
| 242,885.429 | 1,059,116.951 | 236.219 | 0.207 |
| 243,209.73 | 1,059,435.427 | 242.708 | −0.012 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, P.O.; Sternberg, H. Bathymetric Survey for Enhancing the Volumetric Capacity of Tagwai Dam in Nigeria via Leapfrogging Approach. Geomatics 2021, 1, 246-257. https://doi.org/10.3390/geomatics1020014
Ibrahim PO, Sternberg H. Bathymetric Survey for Enhancing the Volumetric Capacity of Tagwai Dam in Nigeria via Leapfrogging Approach. Geomatics. 2021; 1(2):246-257. https://doi.org/10.3390/geomatics1020014
Chicago/Turabian StyleIbrahim, Pius Onoja, and Harald Sternberg. 2021. "Bathymetric Survey for Enhancing the Volumetric Capacity of Tagwai Dam in Nigeria via Leapfrogging Approach" Geomatics 1, no. 2: 246-257. https://doi.org/10.3390/geomatics1020014
APA StyleIbrahim, P. O., & Sternberg, H. (2021). Bathymetric Survey for Enhancing the Volumetric Capacity of Tagwai Dam in Nigeria via Leapfrogging Approach. Geomatics, 1(2), 246-257. https://doi.org/10.3390/geomatics1020014







