Influence of Motive Nozzle Supersonic Part Profiling on the Effectiveness of the Vaporization Process: Experimental Results

Abstract

This article presents experimental results for motive nozzles with profiled supersonic parts of parabolic, hyperbolic, and elliptical shapes, compared to conical nozzles with unprofiled supersonic parts. This study examined the effect of nozzle geometry and profile on thermodynamic and flow parameters of the vaporization process. The measured parameters included outlet pressure, flow velocity, and mass vapor content, along with dimensionless efficiency indicators, such as relative outflow velocity and the velocity coefficient. Graphical dependencies of these parameters on the relative initial underheating, (1 − ε_s0), were obtained. This parameter represents the ratio of the pressure difference between inlet and saturation conditions (at inlet temperature) to the inlet pressure. The results show that profiled nozzles operate effectively over a wider range of (1 − ε_s0) = 0.20–0.45, compared to conical unprofiled nozzles. The vaporization constant for profiled nozzles remained at b_n ≈ (2/3)^0.5 along their length. The velocity coefficients for profiled designs were 4–6% higher, and the volumetric vapor content at the outlet was also greater, indicating a more efficient vaporization process. Overall, the findings demonstrate that profiling the supersonic section of a motive nozzle improves the operating range, flow characteristics, and vaporization quality compared to conventional conical designs.

1. Introduction

In the context of the ongoing war in Ukraine, the issue of protecting critical infrastructure—particularly heat and power generation facilities—has become increasingly urgent. According to the Distributed Generation Development Strategy through 2035, a key research priority is the development of mini-CHP (combined heat and power) plants, which would enable the creation of a decentralized network of thermal and electric generation capacities [1,2,3,4]. This approach would mitigate the impact of enemy attacks on critical infrastructure, as the systems would be numerous and low-capacity (serving individual neighborhoods or even single buildings). In addition, it would provide flexibility in regulating both heat and electricity consumption.

The core component of such systems is the liquid-vapor jet apparatus (LVJA), which operates on the principle of jet thermocompression. It has replaced outdated and inefficient steam turbines and internal combustion engines that were commonly used in similar systems throughout the previous century [5,6]. Two-phase jet devices are successfully used in technological systems, including refrigeration machines, thermal transformers, and heat pump systems. Their use allows for significantly increasing the efficiency of such systems, and the use of water as a working fluid allows for reducing the costs of the refrigerant. Considering the similarity of operating parameters in the above systems, the authors consider their use in mini-CHPs to be appropriate.

The need for a deeper understanding of its working processes, in particular, improving vaporization processes occurring in the motive nozzle—in order to improve the efficiency of heat and power generation units based on this technology—is what motivated the authors to carry out the present study.

1.1. Literature Review and Problem Statement

Research conducted by both domestic and international scientists has shown that one of the key factors influencing the efficiency of two-phase jet devices is the degree of completion of the vaporization process within the motive nozzle [7,8,9]. These studies indicate that the efficiency of steam generation in expanding channels with variable geometry directly depends on the outflow velocity of the boiling subcooled liquid.

The authors of works [10,11,12,13] carried out theoretical and experimental studies that revealed the influence of both the operating and geometric parameters of a working jet at the nozzle outlet on the performance of two-phase jet devices. These studies examined the velocity characteristics of the boiling flow and the duration of the vaporization process, during which structural reorganization occurs within the motive nozzle.

In works [14,15,16,17], it is noted that the efficiency of the vaporization process is directly influenced by the position of the nozzle outlet—that is, the length of its supersonic section. This factor determines the shape of the primary flow, whose energy is then used to eject the secondary flow and subsequently mix with it.

The sources analyzed above describe the results of theoretical and experimental studies on expanding channels with variable geometries, in which the subcooled working fluid flows through the motive nozzle and undergoes a phase transition (vaporization) in the supersonic section. However, these studies do not account for the profile of the channel itself, which also affects the efficiency of the process.

The need for profiling expanding channels was first mentioned in research related to centrifugal compressors [18,19,20]. In that context, profiling the flow path of diffusers was necessary to prevent flow separation from the channel walls. Thus, it became essential to shape the flow path in such a way that it ensures the desired flow structure while minimizing energy losses.

Profiling of elements in two-phase jet devices—particularly motive nozzles—has not yet become widespread. The efficiency of vaporization processes has so far been achieved primarily through the above-mentioned factors and has reached a relatively high level [21,22,23]. For instance, the velocity coefficient of unprofiled conical nozzles is in the range of 0.92–0.97. Nevertheless, the issue of achieving the desired jet structure at the nozzle outlet and avoiding flow separation from the walls of the supersonic section remains relevant [24,25,26].

Attempts to profile the supersonic parts of Laval nozzles in two-phase jet devices in recent years have been considered by the authors of works [27,28,29,30] as a secondary measure aimed at studying the position of the nozzle outlet section, in which the flow separation from the channel walls occurs. The shape of the supersonic part in these works is studied by CFD modeling methods, as a result of which the channel shape remains close to conical. Studies on the profiling of motive nozzles are further widespread in works [31,32,33], in which numerical modeling was supplemented by experimental studies, as a result of which the authors note a relatively insignificant increase in the efficiency of two-phase jet devices with profiled supersonic parts of the motive nozzles.

In works [34,35,36,37], the authors conducted studies, as a result of which they concluded that by achieving the appropriate regimes of boiling liquid movement in the supersonic parts of motive nozzles with a nonprofiled shape, it is possible to obtain the same values of their efficiency indicators as in nozzles with the profiled shape. However, these regimes can be achieved in a narrow range of operating parameters and for certain types of active flow liquids.

In works [38,39], the prospects of profiling propulsion nozzles from the point of view of influencing the time during which the vaporization process will occur in these nozzles are noted. The studies conducted by the authors of these works showed a positive effect of profiling on the value of the vapor content and the degree of completion of the vaporization process in the nozzles with the profiled shape. This allows us to draw conclusions about the feasibility of profiling of active flow nozzles.

The necessity of profiling the supersonic part of the nozzle was raised by the authors of works [40,41], driven not only by the aim to improve the efficiency of vaporization but also to enhance the structural reorganization during the boiling process. In those studies, the authors performed numerical calculations and modeling of the working process inside a motive nozzle.

For this reason, there arose a need for experimental validation of the mathematical model developed by the authors—a task that forms the basis of the present article.

1.2. The Aim and Objective of This Research

The aim of this article is to experimentally investigate a liquid-vapor jet apparatus equipped with motive nozzles featuring profiled supersonic sections, in order to determine the effective operating ranges of each nozzle type.

To achieve this aim, the following objectives were formulated and require resolution:

(a)

To design and construct an experimental setup for studying the vaporization process in nozzles with profiled supersonic sections;

(b)

To conduct experimental studies of vaporization in nozzles with profiled supersonic sections;

(c)

To experimentally determine the influence of the geometric shape of the supersonic section of the motive nozzle on the thermodynamic and operating parameters at the outlet;

(d)

To experimentally determine the influence of the geometric shape of the supersonic section of the motive nozzle on the achievable efficiency indicators of the vaporization process;

(e)

To compare the obtained experimental results with those derived from calculations and numerical modeling.

2. Materials and Methods

2.1. Initial Data

This section describes the selection of operational and geometric parameters for the experimental investigation of motive nozzles with profiled supersonic sections.

Theoretical studies previously conducted by the authors on motive nozzles with profiled supersonic sections are described in [41]. Based on the results of that work, experimental studies were carried out on nozzles with parabolic, hyperbolic, and elliptical shapes of the supersonic section, since nozzles with supersonic sections designed using the Vitoshinsky formula demonstrate rather low efficiency indicators compared to the above-mentioned shapes and even compared to an unprofiled conical nozzle with straight walls.

The operating conditions under which the experiment was conducted are presented in

Table 1. Operation conditions for the experimental studies.

Type of Nozzle	Parameters
	p01, bar	t01, °C	pa, bar	(1 − εs0)
Unprofiled (conical supersonic section)	20	200	1	0.15–0.5
	10	170	0.6
	8	165	0.3
Profiled (parabolic supersonic section)	20	200	1	0.15–0.5
	10	170	0.6
	8	165	0.3
Profiled (hyperbolic supersonic section)	20	200	1	0.15–0.5
	10	170	0.6
	8	165	0.3
Profiled (elliptical supersonic section)	20	200	1	0.15–0.5
	10	170	0.6
	8	165	0.3

.

The physical content of the relative initial underheating (1 − ε_s0) value means the percentage of underheated value of the primary flow to the state of saturation, complicated by formula:

$$\left(1-{\epsilon }_{s0}\right)=1-{\displaystyle \frac{p_{01}}{p_{s0}}},$$

(1)

where $p_{01}$—the pressure value of the primary flow in the inlet of the motive nozzle, Pa;

• $p_{s0}$—the pressure value of the primary flow in the state of saturation, Pa.

The range of change in the relative initial underheating value is within 0.15–0.5. It was obtained from the results of a numerical simulation conducted by the authors in [41] and based on the results of an experimental study on nozzles with an unprofiled supersonic part.

The vaporization constant $b_n$ is determined from the vaporization equation, which is

$$dx=b_n·f·{\displaystyle \frac{{{\upsilon }_0}^{\prime }}{{\upsilon }_v\left(t_{liq}\right)}}·{\displaystyle \frac{\sqrt{{\upsilon }_{liq}\left(t_{liq}\right)·\left[p_s\left(t_{liq}\right)-p\right]}}{w_f}}·d\overline{z},$$

(2)

where $f$—nozzle area in a specific cross-section;

• ${{\upsilon }_0}^{\prime }$—specific volume in the state of saturation;
• ${\upsilon }_v\left(t_{liq}\right)$—specific volume of vapor in the state of liquid;
• ${\upsilon }_{liq}\left(t_{liq}\right)$—specific volume of liquid in the state of liquid;
• $\left[p_s\left(t_{liq}\right)-p\right]$—determines the pressure difference between the vapor in the bubble and the environment;
• $w_f$—velocity of primary flow in critical section of the nozzle.

The average value of the vaporization constant during spontaneous boiling for the same range of relative initial underheating values approximately coincides with the value for a single bubble and is equal $b_n=\sqrt{2/3}$.

To address the set objectives, experimental studies were conducted on a test bench to examine the formation of the primary flow and the characteristics of its structure during the outflow of a metastable underheated liquid from the nozzle, under known and constant ambient conditions (pressure and temperature), and a specified pressure level in the heating chamber for the working fluid supplied to the nozzle:

(a)

The pressure and temperature of the working fluid at the nozzle inlet of the primary flow, the pressure at the nozzle outlet, and the jet reaction force were measured within a range of pressures in the heating reservoir used to heat the working fluid supplied to the nozzle at different heating levels;

(b)

The temperatures at the inlet and outlet of the cooling water passing through the heat exchanger (used to heat the working fluid supplied to the motive nozzle) were measured at various values of the relative initial underheating of the working fluid.

2.2. Equations for Processing the Experimental Data

In accordance with the objectives of the experimental study, after conducting the experiments, the processing of their results was carried out according to the methodology developed by the authors. According to this methodology, the processing of the results was carried out according to the following formulas:

(a)

The impulse (momentum) of the working fluid jet, N/m:

$$i_a={\displaystyle \frac{9.81·R_a}{0.7854·d_f}},$$

(3)

where R_a—reaction force of the working fluid jet, N;

• d_f—diameter of the nozzle at the critical cross-section, m.

(b)

Mass flow rate of the working fluid passing through the motive nozzle, kg/s:

$${\dot{m}}_a={\displaystyle \frac{w_f·F_f}{{{\nu }_0}^{\prime }}},$$

(4)

where w_f—average velocity of the working fluid of the primary flow at the critical cross-section of the nozzle, m/s, calculated as:

$$w_f={\mu }_0·{\nu }_f·\sqrt{2·{10}^5·\left(P_0-P_{s0}\right)·{{\nu }_0}^{\prime }},$$

(5)

where F_f—area of the nozzle at the critical cross-section, m².

(c)

Velocity coefficient of the motive nozzle:

$${\phi }_a={\displaystyle \frac{{\gamma }_a}{{\gamma }_{as}}},$$

(6)

where γ_a—relative velocity of the fluid in the outlet of the nozzle and γ_as—relative adiabatic velocity of the fluid in the outlet of the nozzle.

As a result of processing the experimental data using this method, it was possible to determine the efficiency of the vaporization process in motive nozzles with various shapes of the supersonic part. The factor determining this efficiency is the velocity coefficient, which is determined by Formula (6).

2.3. Experimental Stand

The experimental stand for studying nozzles with a profiled supersonic section is a modernized test stand developed by the authors, with its design described in detail in [42]. The upgraded stand features a transparent section located downstream of the motive nozzle, with a length equal to ten outlet diameters of the nozzle. This allows for visual observation of the primary flow jet’s shape at the outlet of the nozzle and enables us to determine whether jet separation (choking) occurs.

Figure 1 shows a photograph of the experimental stand, while Figure 2 presents images of motive nozzles with various geometric shapes of the supersonic section.

The design of the motive nozzle allows for the replacement of its supersonic section. The supersonic parts of the nozzles are 3D-printed and engineered to withstand the corresponding temperature conditions during the operation of the LVJA.

2.4. Uncertainty Analysis

During the experimental study, multiple measurements of the controlled variables were taken. Then, the arithmetic mean value was calculated—for example, the temperature or the velocity coefficient of the motive nozzle of the LVJA was calculated as follows:

$${\phi }_a={\displaystyle \frac{{\gamma }_a}{{\gamma }_{as}}}={\displaystyle \frac{\frac{w_a}{w_f}}{\frac{w_{as}}{w_f}}}={\displaystyle \frac{w_a}{w_f}}·{\displaystyle \frac{w_f}{w_{as}}}={\displaystyle \frac{w_a}{w_{as}}},$$

(7)

$${\phi }_a={\displaystyle \frac{\frac{9.81·R_a·{\upsilon }_0^{\prime }}{F_f·w_f}}{\sqrt{2·{10}^3·\left[h_0-h_n^{\prime }-\left(s_0-s_n^{\prime }\right)·T_n\right]}}},$$

(8)

$${\phi }_a={\displaystyle \frac{\frac{39.24·R_a·{\upsilon }_0^{\prime }}{\pi ·d_f^2·{\mu }_0·{\nu }_f·\sqrt{2·{10}^5·\left(P_0-P_{s0}\right)·{\upsilon }_0^{\prime }}}}{\sqrt{2·{10}^3·\left[h_0-h_n^{\prime }-\left(s_0-s_n^{\prime }\right)·T_n\right]}}},$$

(9)

$${\phi }_a={\displaystyle \frac{R_a·{\upsilon }_0^{\prime }}{1.962·{10}^5·\pi ·d_f^2·w_f·\sqrt{\left(P_0-P_{s0}\right)·{\upsilon }_0^{\prime }·\left[h_0-h_n^{\prime }-\left(s_0-s_n^{\prime }\right)·T_n\right]}}}.$$

(10)

The relative error in determining the velocity coefficient of the motive nozzle was calculated using the formula:

$${\delta \phi }_a=b·\sqrt{{\left({\displaystyle \frac{∆R_a}{R_a}}\right)}^2+{\left({\displaystyle \frac{∆P_0}{P_0}}\right)}^2+{\left({\displaystyle \frac{∆P_{s0}}{P_{s0}}}\right)}^2+{\left({\displaystyle \frac{∆{v`}_0}{{v`}_0}}\right)}^2+{\left({\displaystyle \frac{∆h_0}{h_0}}\right)}^2+{\left({\displaystyle \frac{∆{h`}_{\prod }}{{h`}_{\prod }}}\right)}^2+{\left({\displaystyle \frac{∆s_0}{s_0}}\right)}^2+{\left({\displaystyle \frac{∆{s`}_{\prod }}{{s`}_{\prod }}}\right)}^2+{\left({\displaystyle \frac{∆T_{\prod }}{T_{\prod }}}\right)}^2}.$$

(11)

Table 2. Values of errors for measured and calculated quantities.

Parameter	Type of Measurement/Calculation	Error in Determination
Pressure, MPa	Direct measurements using standard manometers and vacuum gauges	0.1–0.5%
Temperature, °C	Direct measurements using thermocouples and multimeters	1.2%
Enthalpy, J/kg	Tabulated values	0.005%
Entropy, J/(kg K)	Tabulated values	0.00005%
Specific volume, m3/kg	Tabulated values	0.005%
Velocity, m/s	Estimated value, depends on the flow rates of primary and secondary flows	Does not exceed 1.6%
Jet reaction force, N	Direct measurements using electronic scales	Does not exceed 2%

presents the parameters required to calculate the error of the velocity coefficient of the motive nozzle, the methods used for their measurement or determination, and the corresponding measurement or calculation errors.

The calculations show that the average systematic error in determining the velocity coefficient of the motive nozzle does not exceed 2.6%.

Thus, as a result of our LVJA study, the operational and geometric characteristics of the apparatus were obtained, as well as the distribution of pressures and temperatures in the flow path, with a measurement error not exceeding 5% at a confidence level of 0.95. This confidence interval was confirmed by repeatedly conducting the experiment with the same parameters, as well as relying on previous research by the authors, which correlates well with the mathematical model.

3. Results

As a result of the experimental studies on motive nozzles with profiled supersonic sections, as shown in Figure 2, conducted under the operating conditions listed in Table 1, graphical dependencies were obtained, which are presented in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7.

The most important factor determining the completeness of the vaporization process in the motive nozzle is the vaporization constant. For a conical nozzle with straight walls, it was experimentally proven in [41] that its average value is b_n ≈ $\sqrt{2/3}$ for values of relative initial underheating (1 − ε_s0) < 0.7. Figure 3 shows the dependencies of the vaporization constant on the relative initial underheating for unprofiled conical nozzles with straight walls and for nozzles with profiled supersonic sections, according to the operating modes under which the experiments were conducted (see Table 1).

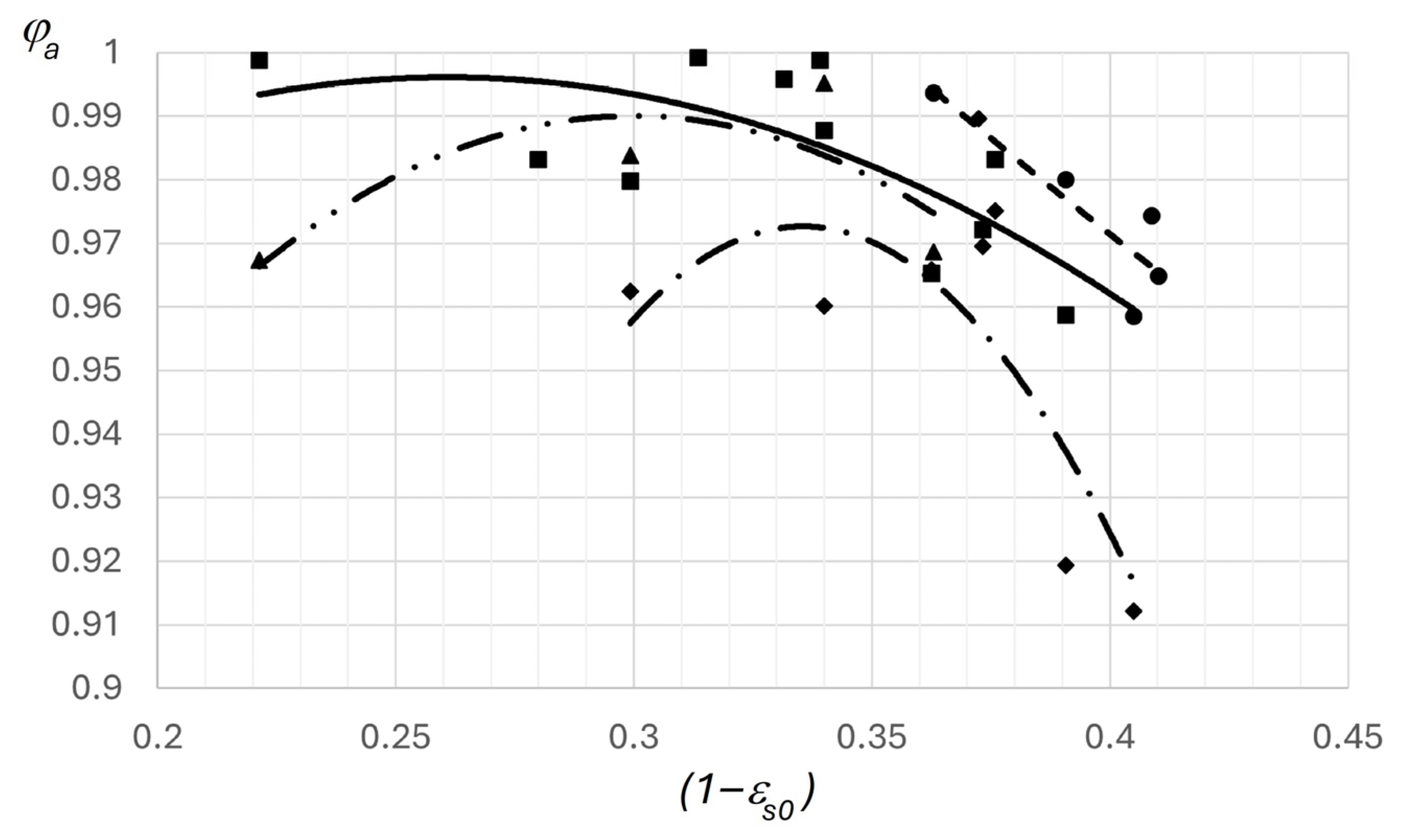
As Figure 3 shows, the most optimal nozzle shape is the parabolic form, since the vaporization constant remains nearly constant across the entire range of relative initial underheating values. This is especially evident at the first operating mode. The least efficient is the elliptical shape, as this nozzle operates effectively only within a narrow range of relative initial underheating values across all three operating modes.

To evaluate the completeness of the vaporization process at the nozzle outlet, we constructed graphs showing the dependence of the vaporization constant on the relative initial underheating at the outlet of the nozzle (Figure 4).

Figure 4 shows that the highest degree of completeness in the vaporization process occurs in nozzles with parabolic and hyperbolic shapes. For these nozzles, the vaporization constant reaches approximately 99.7% for the first and second operating modes (see Table 1). This indicates an almost complete phase transition of the primary flow from a liquid state to a gaseous state within the nozzles with this supersonic section geometry. In the vacuum operating mode (mode 3), the highest efficiency is observed in nozzles with conical and elliptical shapes, although not across the entire range of relative initial underheating values (1 − ε_s0) = 0.2–0.45.

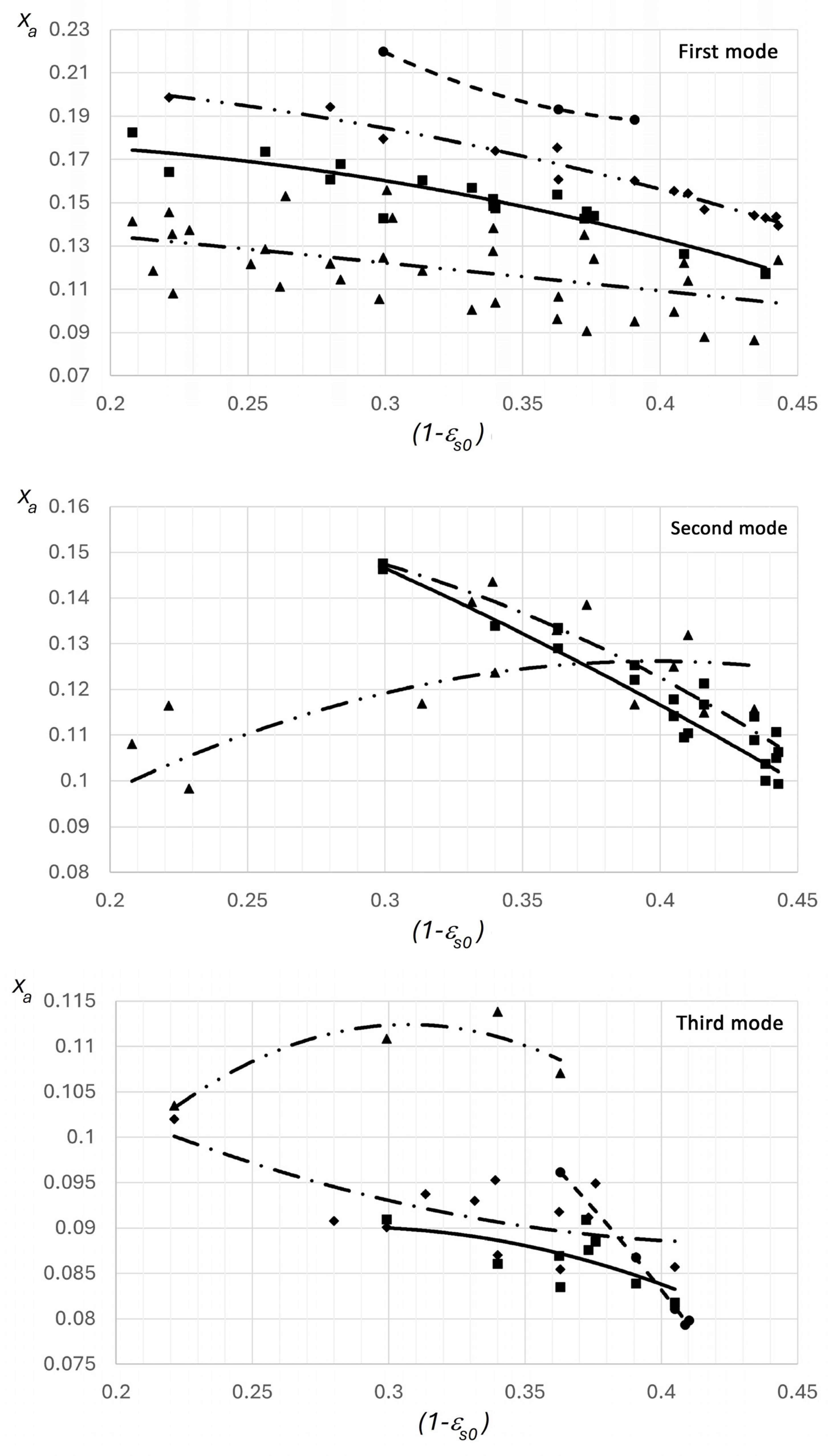
Figure 5 presents the results showing the effect of the geometric shape of motive nozzles on the mass vapor content at the outlet cross-section of the motive nozzle.

Figure 5 shows that nozzles with parabolic and hyperbolic shapes have mass vapor content values in the range of 0.1–0.2 kg/kg, which is higher than that of conical nozzles with straight walls. This indicates a greater degree of completeness in vaporization and the effectiveness of profiling the supersonic section of the nozzles. The nozzle with an elliptical supersonic section has mass vapor content values ranging from 0.18 to 0.22 kg/kg, but only for relative initial underheating values (1 − ε_s0) = 0.3–0.4. In the vacuum operating mode (mode 3), similar to the vaporization constant, higher mass vapor content values are observed for conical and elliptical nozzles but only within a narrow range, which reduces their overall efficiency.

To evaluate the efficiency of LVJA motive nozzles with profiled supersonic sections, experimental studies were conducted to examine the influence of geometry on the outlet velocity, relative velocity of outflow, and velocity coefficient of the nozzle. The results of these studies are presented in Figure 6 and Figure 7.

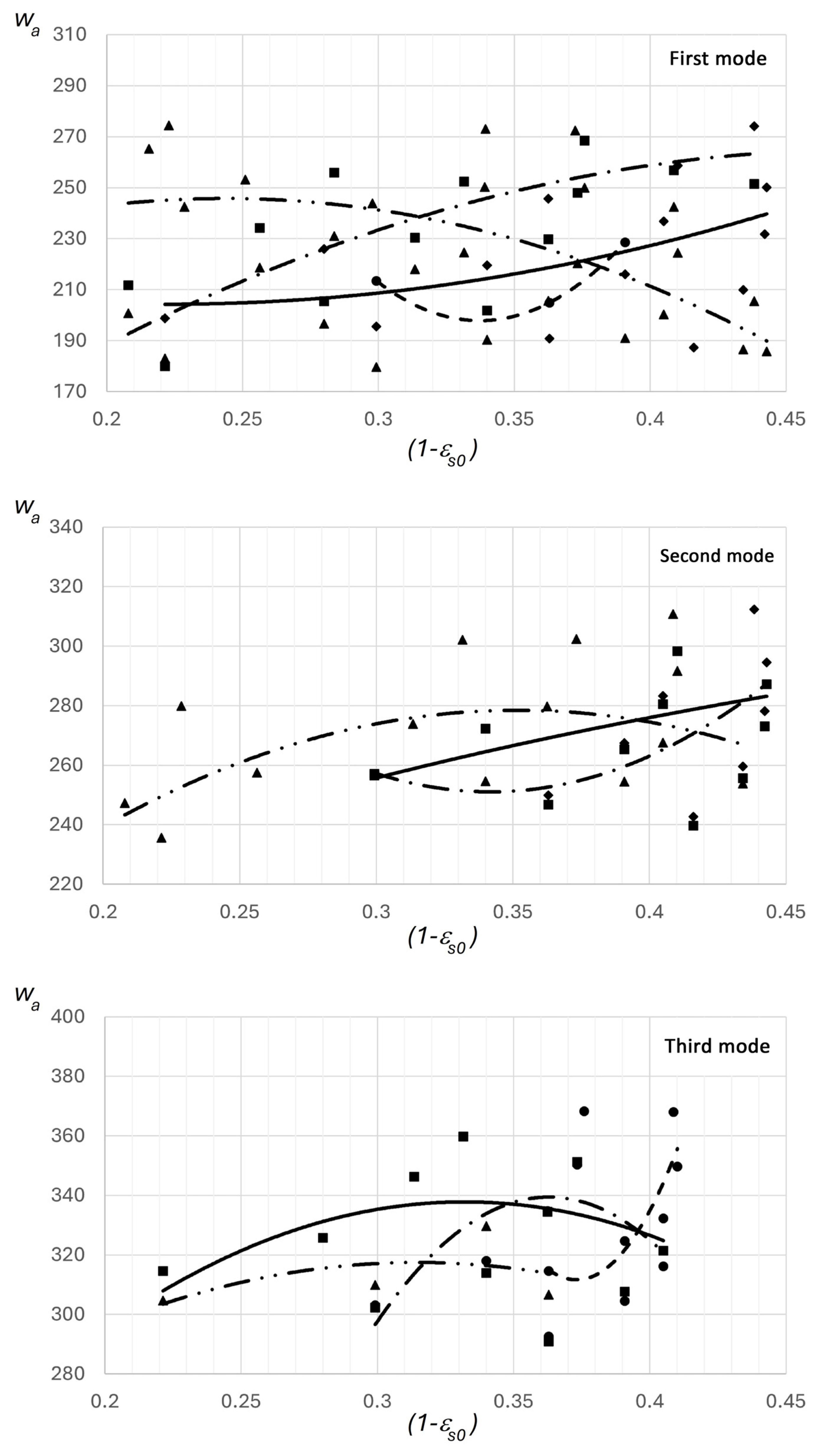
Figure 6 shows experimental data on the effect of the supersonic section geometry of the motive nozzle on the outlet velocity.

Figure 6 shows that the lower the outlet velocity from the motive nozzle, the longer the vaporization process takes. This positively affects the completeness of the mixing process. Thus, nozzles with a parabolic shape have outlet velocities 30–40 m/s lower than conical and elliptical nozzles, which positively influences the vaporization process in the working fluid of the primary flow.

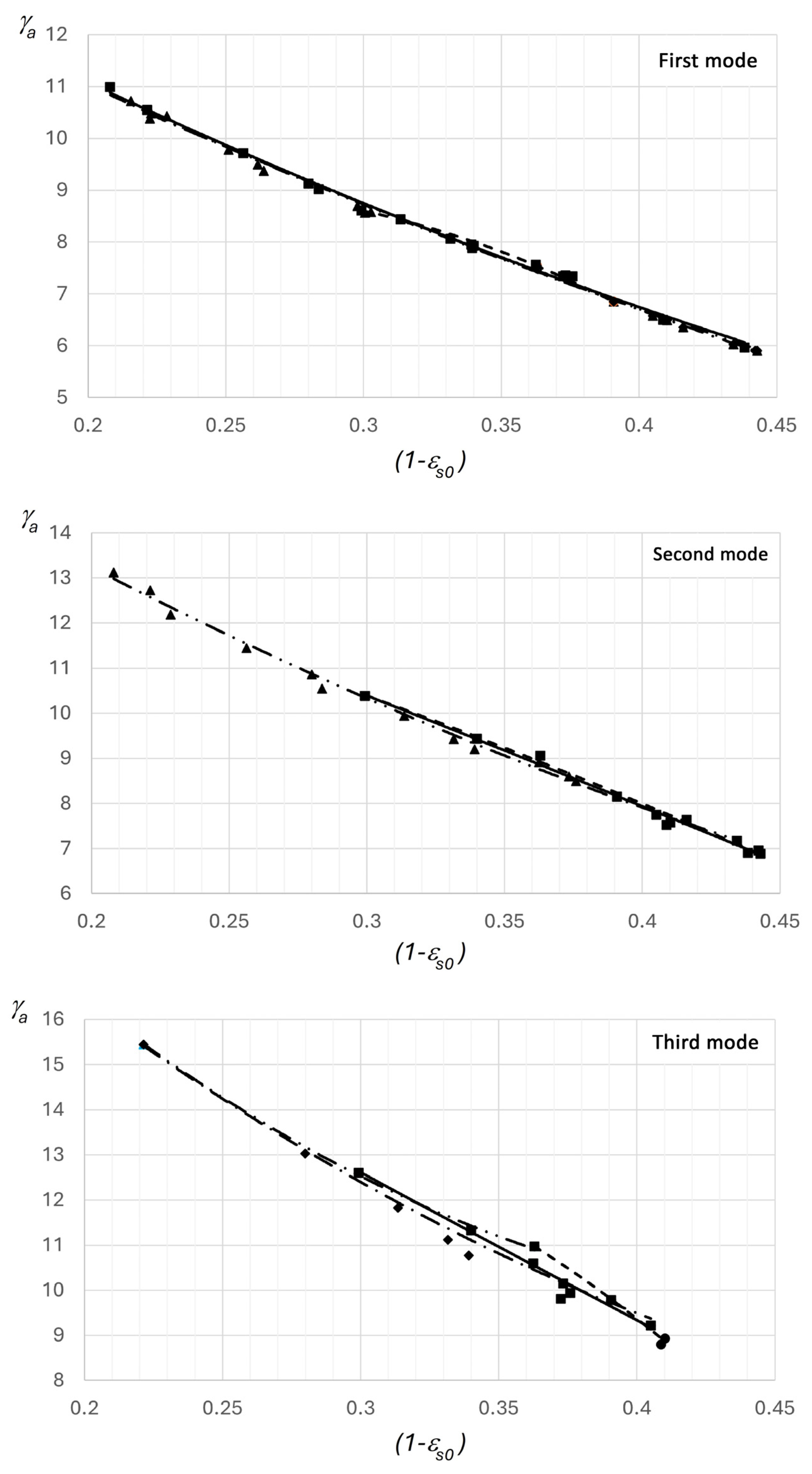
Figure 7 presents the results of experimental studies on the influence of the supersonic section geometry of the motive nozzle on the relative velocity of outflow.

Figure 7 shows that for certain operating modes, the values of the relative outflow velocity are very close to each other; however, as the modes shift toward the vacuum mode (see Table 1), these values increase. This is explained by the difference in initial parameters and changes in the thermodynamic characteristics under vacuum operating conditions [4].

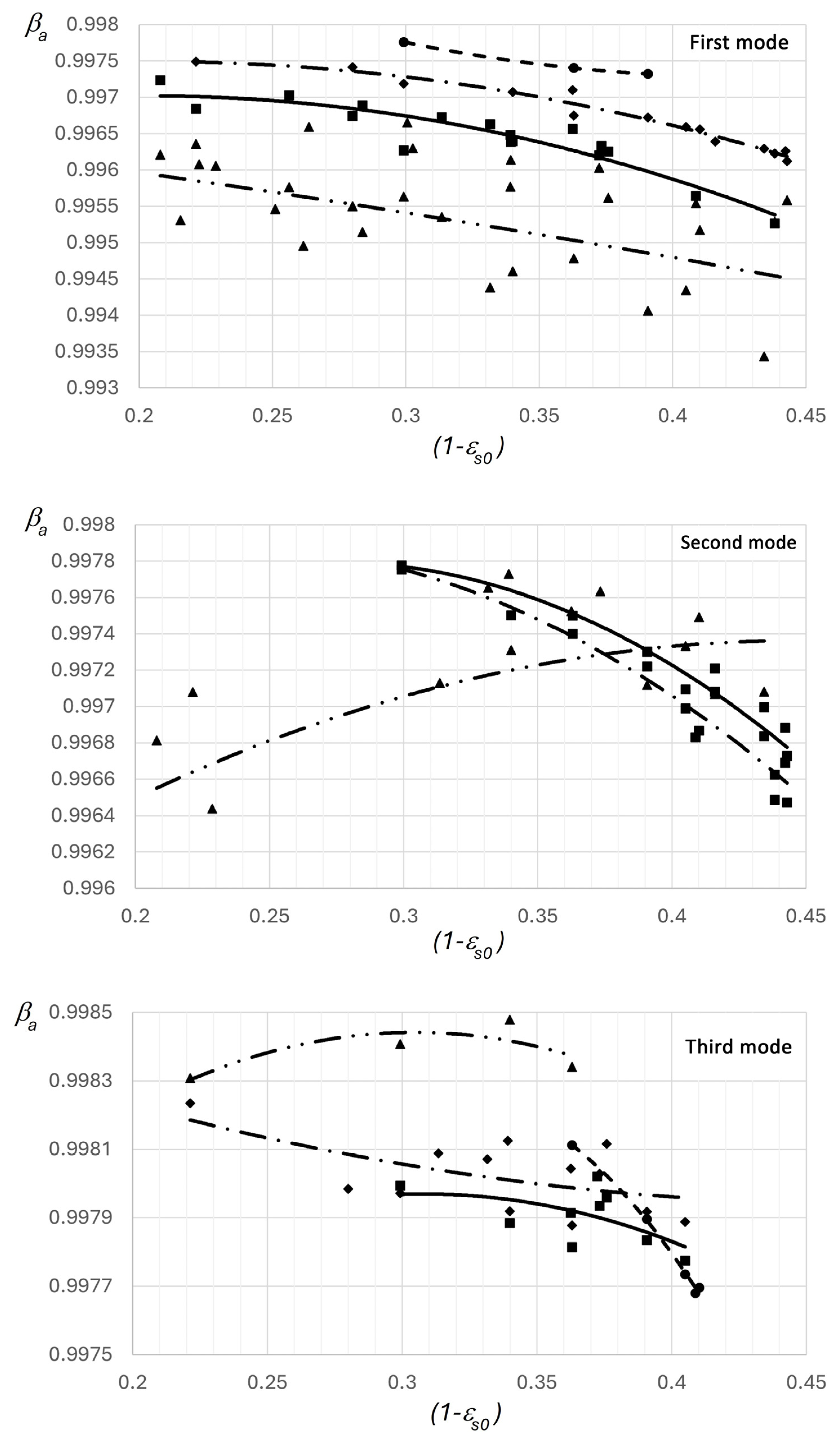
Figure 8 presents a summary characteristic of nozzle efficiency across the three operating modes.

Figure 8 shows that the highest efficiency is observed in nozzles with a parabolic supersonic section, with a velocity coefficient ${\phi }_a$ = 0.96–0.995. In nozzles with this section, the efficiency is higher across the entire range of research. In particular, a nozzle of this section allows for the formation of primary flow in the initial section and prevents its separation from the channel walls, as in elliptical nozzles. Also, due to the speed values, it is possible to achieve the optimal time of the vaporization process and the formation of a flow of the required structure in the outlet of the nozzle.

4. Discussion

The experimental studies conducted by the authors address all the unresolved issues in previous research. Among these, the main challenges are the formation of a working steam jet with specified parameters at the outlet cross-section of the motive nozzle, ensuring optimal velocity coefficient values, and achieving an optimal degree of completion of the vaporization process.

The authors of works [3,4,8] performed theoretical and experimental studies of two-phase jet apparatuses and considered the issue of forming a two-phase steam-droplet flow at the outlet of the motive nozzle, with a maximum value of the volumetric steam content in which the liquid and vapor phases are evenly distributed. However, they solved this problem by changing the diffuser angle and the length of its supersonic section. This approach only partially solves the problem because there are limit operating and geometric parameters beyond which flow separation from the channel walls and nozzle choking occur. Profiling the supersonic section of the nozzles allows for solving this problem over a wider range and enables determining the position of the nozzle outlet cross-section where flow separation occurs, thus optimizing the working parameters of the vaporization process.

The influence of the primary flow working fluid parameters at the nozzle outlet cross-section on the efficiency of the vaporization process remains insufficiently studied. Many authors investigated this from the perspective of determining the effect of thermodynamic and operating parameters of a working jet at the nozzle outlet on the initial parameters of the passive flow in the receiving chamber [5,6,7]. However, the value of the nozzle velocity coefficient significantly affects the vaporization process that occurs in its supersonic section. This coefficient determines the injection coefficient value and thus the mass flow rate of the passive flow, which influences the geometric parameters of the mixing chamber. Profiling the supersonic section of the motive nozzle allows for maintaining optimal velocity coefficient values over a wider range of working parameters of the motive nozzle.

The degree of completion of the vaporization process in the supersonic section of the motive nozzle is one of the main factors that affects the velocity coefficient and is the central focus of the studies presented in works [9,11,15,16]. Changing the diffuser angle of the nozzles only partially addresses this issue since such a change is possible within a narrow range from 8° to 12°. Profiling the supersonic section of the nozzles allows for altering the velocity of the outflow process from the expanding channels of boiling, underheated to saturation, liquid primary flow, and, consequently, the time during which the vaporization process takes place. Each profile ensures the maximum efficiency of the motive nozzle’s working process depending on the operating mode and type of working fluid.

The limitations encountered by the authors of this article when conducting experimental studies of nozzles with a profiled supersonic part are related to the method of CFD modeling and the choice of the optimal geometric shape. This means setting the initial geometric shape. The authors relied on the results of their own previous studies and the conclusions made by the authors of the works [43,44,45]. That is why such profiles of the supersonic part of the nozzles were chosen. However, further research by the authors will aim to solve the inverse problem and automate the process of rationally selecting the geometric shape of the supersonic part of the nozzle based on the flow parameters at the inlet and outlet. That is why the results of the experimental studies conducted in this article will be used with the additional application of variational calculations and methods for identifying the parameters of the developed mathematical model.

Difficulties that arose during the experimental research include the instability of the vaporization process when the stand enters the operating mode. This design of the stand does not allow us to clearly determine the boundary of this transition. Therefore, when processing the experimental data, the authors took into account only those results that were obtained after the flow parameters at the outlet of the nozzle stopped changing. However, conducting research on a transparent model would help to more accurately determine the time when the experimental installation enters the operating parameters and conduct further studies at the limit modes of its operation.

The advantages of this study are that it allows us to determine the most optimal geometric shapes of the supersonic part with the highest efficiency indicators, even at the stage of numerical calculation and modeling. Thus, the authors conducted a numerical study on nozzles with a shape calculated using the Vitoshinsky formula, but the results showed that such a nozzle has significantly lower efficiency indicators compared to the studied shapes. The authors of works [46,47] reached the same conclusions, which indicates the correctness of the obtained calculations and their reliability. At the same time, such a shape can be successfully applied to the conical part of mixing chambers, as evidenced by the results presented in works [48,49]. However, such an assumption requires further experimental verification.

Regarding the practical significance of this research, it can be noted that a greater completeness of the vapor generation process in nozzles with a profiled supersonic part will allow for increasing the efficiency of mini-CHPs based on them, namely, it will significantly reduce the consumption of boiler steam for heating the working fluid of the primary flow and industrial water necessary to maintain a constant flow rate of the primary and secondary flows.

Thus, the studies conducted by the authors in this work confirm the advisability of profiling the supersonic section of a motive nozzle and represent a new stage in the study of two-phase jet apparatuses aimed at improving the efficiency of their working process.

5. Conclusions

The analysis of our experimental results confirmed the influence of the geometric parameters of the motive nozzle on the efficiency indicators of the vaporization process of the working jet, specifically the shape of its supersonic section. This allowed for identifying the operating ranges of the motive nozzle with maximum efficiency for each profile.

The experimental studies were performed following the methodology developed by the authors, which allows for calculating different profiles of the supersonic parts of motive nozzles. However, this methodology only solves the direct problem of profiling. This limitation represents an uncertainty in the method and defines further directions for its improvement.

As a result of the conducted experimental study on motive nozzles with a profiled supersonic section, several limitations can be identified. These include the thermodynamic properties of water and the steam derived from it, which is used as the primary flow in the LVJA. Additionally, certain limitations are imposed by the structural features of the apparatus’s flow section and, consequently, by the amount of pressure increase in the passive flow that can be generated in a single stage of the LVJA.

Since the experimental study was conducted on unprofiled nozzles with a conical supersonic section and profiled nozzles with parabolic, elliptical, and hyperbolic shapes, further research directions will focus on solving the inverse problem and automating the process of rationally selecting the geometric shape of a nozzle’s supersonic section based on flow parameters at the inlet and outlet. This will be carried out using modern software packages such as Ansys CFX 2004 R1 (ANSYS, Inc., Canonsburg, PA, USA).

The practical significance of the obtained experimental results lies in their potential use for improving existing technological schemes and designing new energy-efficient equipment employing two-phase jet apparatuses.

The most promising profile for the supersonic part of motive nozzles is parabolic, since such a nozzle has the highest velocity coefficient in the entire range of relative initial underheating.