Mixed Thermal and Renewable Energy Generation Optimization in Non-Interconnected Regions via Boolean Mapping

Abstract

Global efforts aiming to shift towards renewable energy and smart grid configurations require accurate unit commitment schedules to guarantee power balance and ensure feasible operation under different complex constraints. Intelligent systems utilizing hybrid and high-level techniques have arisen as promising solutions to provide optimum exploration–exploitation trade-offs at the expense of computational complexity. To ameliorate this requirement, which is extremely expensive in non-interconnected renewable systems, radically different approaches based on enhanced priority schemes and Boolean encoding/decoding have to take place. This compilation encompasses various mappings that convert multi-valued clausal forms into Boolean expressions with equivalent satisfiability. Avoiding any need to introduce prior parameter settings, the solution utilizes state-of-the-art advancements in the field of artificial intelligence models, namely Boolean mapping. It allows for the efficient identification of the optimal configuration of a non-convex system with binary and discontinuous dynamics in the fewest possible trials, providing impressive performance. In this way, Boolean mapping becomes capable of providing global optimum solutions to unit commitment utilizing fully tractable procedures without deteriorating the computational time. The results, considering a non-interconnected power system, show that the proposed model based on artificial intelligence presents advantageous performance in terms of generating cost and complexity. This is particularly important in isolated networks, where even a-not-so great deviation between production and consumption may reflect as a major disturbance in terms of frequency and voltage.

1. Introduction

Optimizing the scheduling of electricity generation is essential for the smooth integration of renewable resources, responsive appliances, plug-in electric vehicles, and weather-dependent devices, which is a pivotal strategy for achieving future low-carbon energy solutions [1]. One of the primary challenges in global energy planning is the temporal mismatch between energy supply and demand, posing a significant obstacle to the integration of renewable energy sources (RESs). Therefore, power system decision-makers must develop robust and effective flexibility strategies to ensure power balance and economical operation across various time horizons while meeting different technical, environmental, and geographical constraints [2]. These limitations are generally addressed through unit commitment (UC) models, which define both the on/off status and the economic dispatch of different generators. Nevertheless, this iterative process involves an enormous number of combinations, rendering complete enumeration impractical, even for short-term scheduling periods (hours, days, or weeks) and medium-scale systems [3].

The UC problem is typically viewed as a mixed-integer, multivariate, non-convex, and non-linear optimization challenge, characterized by a large number of complex constraints. Distinguished into mathematical, heuristic, meta-heuristic, and hybrid, the various approaches used broadly aim at converging to high-quality solutions with optimum exploration–exploitation trade-offs. Mathematical optimization offers a more flexible approach, enabling the constraints to easily be added. It is represented by exact methods for achieving convergence, with inherent transitions reliant on gradient information about the objective function. To broaden the exploration space and reach a global optimum, numerous heuristic alternatives have emerged. These approaches are generally categorized as population-based mechanisms and, depending on the task they mimic, are classified into physics-inspired, evolution-inspired, and swarm-inspired techniques [4]. The primary merits of these methods lie in their flexibility in terms of incorporating practical operating constraints, and their moderate computational memory and execution time requirements. However, heuristic approaches tend to be very problem-dependent and they often reach a solution based on priority assumptions.

To employ more rigorous mechanisms and develop independent solutions, meta-heuristic approaches have been introduced. These high-level techniques, although computationally intensive, can be applied to a wider range of problems. Unlike deterministic mathematical methods, both heuristic and meta-heuristic approaches involve randomness and use a stochastic process to move within independent solutions. Consequently, the extent of their sub-optimality and their overall ‘problem dimensionality’ cannot be precisely calculated [5].

To address these limitations and lead to acceptable solutions in terms of convergence time and costs, several researchers have turned to hybrid methods. By leveraging the strengths of both heuristic and mathematical techniques, these solutions strive to balance exploration and exploitation effectively. Specifically, to prevent premature convergence to local optima and to enhance solving accuracy with reasonable computational efforts, these approaches exploit the stochastic nature of heuristics to iteratively balance some penalty/reward signals, improving the generation output [6]. To tackle the mixed-integer non-linear unit commitment task, further repair procedures have been presented, utilizing de-commitment heuristics for generators and operating reserves [7]. Notable hybrid methods combine binary components to determine the state values (0 or 1) and satisfy all system-wide constraints by using exact methods, whereas the discontinuous unit-specific constraints are addressed by making use of search mechanisms [8,9].

Despite these advancements, there is still no analytical method capable of guaranteeing a global solution without requiring parameter tuning to match the model characteristics of a given non-interconnected power system. Dynamic programming remains the only accurate way to achieve a global solution, albeit with significant dimensionality challenges due to exhaustive enumeration. Mixed-integer linear programming (MILP) continues to be the state-of-the-art solution due to its effectiveness in overcoming the difficulties posed by non-convexity and non-linearity in large-scale systems. Embedding this framework to their software, some well-known solvers, referred to as CPLEX, GUROBI, Xpress and GAMS, can solve this type of UC problem in a very computationally efficient fashion. In this work, a radically different approach is proposed to ensure optimality in the fewest possible trials through a tractable process. The aim is to provide an embedded system that can be easily utilized without requiring expert programming knowledge, can automatically adapt to each power system configuration without needing additional parameter adjustments, and can reduce the dependence on the number of participating generators of the overall problem dimensionality.

The solution is based on the Boolean mapping (BM) framework, comprising a set of mappings that convert multi-valued clausal forms into Boolean expressions with equivalent satisfiability [10]. This artificial intelligence tool models hard combinatorial problems as instances of the propositional satisfiability problem. It can be integrated with higher-level techniques to facilitate optimization through consecutive encoding and decoding, while maintaining observability, resilience, and reliability in solutions. By leveraging these advancements to create a BM object based on enhanced priority lists, the mapping to a convex optimization problem can be accomplished using modified neural networks (NNs) to achieve the global optimum solution.

The rest of the paper is organized in a theoretical and an experimental part. Section 2 defines the unit commitment problem and outlines the main constraints that must always be satisfied. Section 3 details the Boolean Mapping framework and the modified neural network model used for inference. In Section 4, the proposed novel methodology is applied to achieve optimal UC in non-interconnected regions under real-world scenarios. Finally, the conclusions are presented in Section 5.

2. Thermal Unit Commitment Problem Formulation

The cost-effective operation and planning of electric power generation systems have always been paramount in the electric power industry. A crucial aspect of the economic operation challenge is understanding the input–output characteristics of a thermal power generation unit. The standard setup of a boiler–turbine–generator unit, depicted in Figure 1, demonstrates the concepts of gross and net output.

As illustrated, each chain set’s electrical output is linked not only to the main power grid but also to an auxiliary power system that uses a portion of the gross output for various auxiliary functions such as boiler feed pumps, fans, and condenser circulating water pumps. Gross input is represented by the heat rate (H) or cost rate (F), typically measured in million Btu per hour (MBtu/h) or dollars per hour (USD/h), respectively. The auxiliary equipment of a boiler–turbine–generator unit in a conventional power plant includes water feed pumps, air preheaters, and condensers to support the steam cycle. Additionally, systems like fuel handling, ash removal, and cooling towers are used for the efficient operation and overall energy management.

In contrast, net output refers to the electrical power available to the utility system (P), measured in megawatts (MW). These values can be derived from design calculations or heat rate tests. Figure 2a depicts the input–output characteristics of a generating unit. Minimum load constraints usually stem from fuel combustion stability and inherent design limitations. The collected data can be approximated using polynomial curves. In economic dispatching, a common metric is the incremental heat or cost rate relative to input. The heat rate function can be converted into a cost function (F) by multiplying it by the fuel cost (f_c) in USD/Btu. The slope (or derivative) of this curve (ΔF/ΔP) represents the incremental cost.

Another key characteristic of a thermal unit is the unit net heat rate, calculated by dividing H by P. This rate is inversely proportional to efficiency and indicates the amount of heat input required per kilowatt-hour of output. Figure 2b shows the net heat rate of H/P as a function of P for a steam turbine generator.

In most power system optimization tasks, strategies typically require the model to function consistently across different types of thermal generating units, including steam generators, gas turbines, combined cycle systems, and internal combustion engines. A steam turbine, based on the Rankine cycle, consists of: (1) the boiler, where water is heated to produce steam; (2) the turbine, which is driven by the steam that is subsequently condensed; and (3) the condenser, which returns the hot water to the boiler for reheating and vaporization. On the contrary, a gas turbine includes a burner where combustion occurs, and the resulting exhaust gasses drive the turbine. After driving the turbine, the superheated gasses are expelled into the atmosphere, completing the Brayton cycle.

A combination of Rankine and Brayton cycles can improve overall thermal-to-electrical efficiency by making use of configurations like those depicted in Figure 3.

Combined cycle generating units, however, must account for the heat rate curves of both the individual gas turbines and the boiler, depending on the operational configuration (e.g., 1 + 1, 2 + 1, …, N + 1). This arrangement is depicted in the figure, which illustrates a 4 + 4 + 1 configuration. Here, G/T represents the gas turbines, HRSG denotes each heat-recovery steam generator, and T signifies the steam turbine of the plant. It is clear that the efficiency characteristics of the plant are influenced by the number of gas turbines in operation.

The unit commitment problem is formulated to minimize the total operating costs while adhering to both unit-specific and system-complicating constraints. The unit commitment model uses the generator’s characteristics and residual load demand as input data to determine the commitment status and generation dispatch for the available generating units.

2.1. Objective Function

In most basic approaches, the total production cost of a power system consisting of N thermal units is mainly represented by the cost of fuel and start-up cost (SU) during a specified period T as follows:

$$f\left({x_i^t,G}_i^t\right)=\sum _{t=1}^T\sum _{i=1}^N\left[F_i\left(G_i^t\right)+\left(1-x_i^{t-1}\right){SU}_i\right]G_i^t$$

(1)

$x_i^t$ defines the on/off status of generators, while the thermal generating cost is determined by $F_i\left(G_i^t\right)$. This cost is dependent on the production level $G_i^t$ of each generator i and the fuel cost coefficients a_i, b_i, and c_i, which are derived from the convolution of the specific fuel cost and heat rate curves, as described in Equation (2) [12].

$$F_i\left(G_i^t\right)=a_i+b_i·G_i^t+c_i.{\left(G_i^t\right)}^2$$

(2)

Based on this formulation, the total production cost of a power system consisting of N conventional generating units derives from the overall cost of each generator during the time horizon T. This accounts for their respective power output derived from the economic dispatch decision (which in turn takes the fuel cost coefficients into account) and the duration that each unit operates ($G_i^t=1$). The optimal UC is obtained by making use of binary combinations which progressively lead to better outcomes. Consequently, economic dispatch forms a sub-problem in UC tasks and optimization algorithms are requested to iteratively lower the overall costs whilst satisfying all imposed constraints.

2.2. Constraints

The key constraints that must be met during the optimization process are categorized into three types: (a) unit-specific, (b) plant-wide, and (c) system-wide. Unit-specific constraints pertain to the power limits (Equation (5)), ramping capabilities (Equations (8) and (9)), minimum state-change times (Equations (6) and (7)), and operational status restrictions (Equation (10)) for each individual generator involved, while the system-wide limitations concern the system power balance (Equation (3)) and spinning reserve (Equation (4)) [13]. The plant-wide constraint (Equation (11)) accounts for the available actions within a whole plant and is known as the crew constraint.

$$\sum _{i=1}^N{x_i^t·G}_i^t=D_{net}^t$$

(3)

$$\sum _{i=1}^N{x_i^t·G}_{i,\mathrm{m}\mathrm{a}\mathrm{x}\_cap}^t\ge D_{net}^t+{SR}^t$$

(4)

$${x_i^t·G}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}^t\le G_i^t\le {x_i^t·G}_{i,\mathrm{m}\mathrm{a}\mathrm{x}}^t$$

(5)

$${\Delta x}_i=1if\sum _{t=td}^{t-1}\left(1-x_i^t\right)\ge {MD}_i$$

(6)

$${\Delta x}_i=-1if\sum _{t=tu}^{t-1}{x}_i^t\ge {MU}_i$$

(7)

$${\Delta G}_i\le {RU}_i,if{\Delta G}_i>0$$

(8)

$${\Delta G}_i\ge -{RD}_i,if{\Delta G}_i<0$$

(9)

$$\forall t\in \mathcal{T}\left\{\begin{array}{c}{x}_j^t=1,if{j}^{th}unitmustrun\\ x_j^t=0,if{j}^{th}unitmustout\\ G_j^t=\left\{\begin{array}{c}0,if{x}_j^t=0\\ c_j,if{x}_j^t=1\end{array}\right.,if{j}^{th}atfixedoutput\end{array}\right.$$

(10)

$$\sum _{i=1}^N{x}_i^t\left(1-x_i^{t-1}\right)+x_i^{t-1}\left(1-x_i^t\right)\le c_r$$

(11)

2.3. Solution Methodology

Denoting the generator’s status by x, the problem of finding the global minimizer $x_{*}$ of the scalar objective function $f\left(x\right)$ over some bounded domain, typically $\mathrm{X}\subset {\mathbb{R}}^D$, subject to a set of $K=7$ constraints $c_1,\dots ,c_K$, can be defined as:

$$x_{*}=\underset{x\in X}{\mathrm{argmin}}f\left(x\right)s·t·c_1\left(x\right)\le 0,\dots ,c_7\left(x\right)\le 0$$

(12)

This problem represents a non-convex and NP-hard combinatorial optimization challenge. Given the presence of discontinuous binary and dynamic continuous constraints, finding the global optimum requires exhaustive enumeration. The vast number of combinations, estimated as ${\left(2^N-1\right)}^T$, imposes significant capacity constraints for generating solutions, even for day-ahead schedules in medium-scale power systems. Consequently, the time required to derive the final solution through dynamic programming often exceeds the optimization horizon. For example, exploring the combinations generated for a power system consisting of N generating units, one can observe that each time generator j starts up the combinations are doubled so that the total function evaluations are 2 × (j − 1).

A clear representation of a small system that consists of only four generators is included in Figure 4. Based on this dynamic exploration, the produced combinations with respect to each committed generating unit are given in

Table 1. Added combinations and function evaluations per committed unit.

Committed Unit	Rest Unit Status	Binary Combinations	Function Evaluations
	U1→10 = off	1	1
U1 = on	U2→10 = off	1	2
U2 = on	U3→10 = off	2	4
U3 = on	U4→10 = off	4	8
U4 = on	U5→10 = off	8	16
U5 = on	U6→10 = off	16	32
U6 = on	U7→10 = off	34	64
U7 = on	U8→10 = off	64	128
U8 = on	U9→10 = off	128	256
U9 = on	U10 = off	256	512
U10 = on		512	1024

, for a paradigm of 10 generators.

Initially, x denotes the binary status of a generator, where a value of 0 indicates that the generator is off, and a value of 1 signifies that the unit is online so that $x\in \left\{0,1\right\}$. By using Boolean expressions, the problem of the feasible binary combinations $x:X\to \mathbb{R}$ is mapped to an integer domain which reads as $\tilde{x}:X\to {\mathbb{N}}^{+}$. This approach reduces the dimensionality by a factor of N, as the vector needed to represent an Nx1 binary combination is now expressed as a single integer value. Using the BM framework, a CxT matrix can be constructed to tabulate all possible solutions, C, over the time horizon T. To develop an automated procedure that aims to minimize costs, the sum of the T inputs is taken into account. Each value is taken individually from the T (Cx1) vectors so that:

$$f\left(\tilde{x}\right)=\sum _{t=1}^T{\tilde{x}}_t$$

(13)

To guarantee optimality, it must be ensured that the lowest $\tilde{x}$ value corresponds to those combinations which undoubtedly give the lowest cost binary combination. Prior to the transformation, an optimal rearrangement of the generators is created relying on enhanced priority lists. Then, the ordinally valued states $\overrightarrow{x}$ are arranged in descending order, ensuring that the most economical combinations correspond to smaller decimal values, while less economical combinations result in larger decimal values.

3. Mathematical Framework

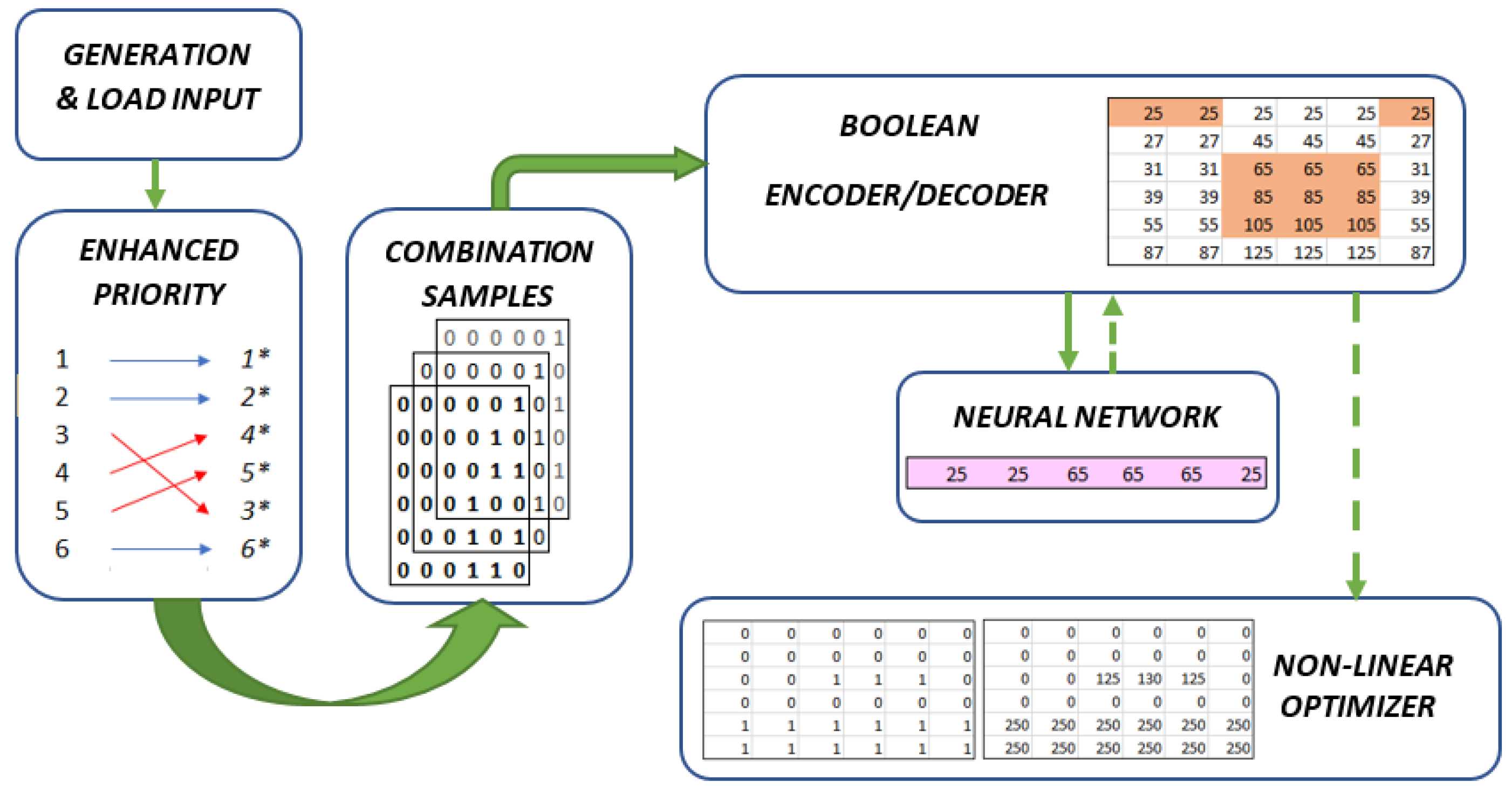
The embedded, step-by-step process is divided into three main stages, each addressing different constraints to ensure that all are effectively satisfied by the end of the process. Initially, enhanced priority list schemes are constructed before the BM is performed. The descending order considers the must-run units, and once the appropriate priority is assigned to each generating unit, all feasible combinations are generated while ensuring load balance and spinning reserve requirements are met. Subsequently, the problem is converted into a convex minimum-sum problem, as outlined in Equation (13), using Boolean coding.

In an additional stage, a mechanism is employed to iteratively select the next minimum candidate $\tilde{x}$. During this phase, Boolean decoding is applied to each recommendation, and state constraints, including MU, MD, and Cr, are verified. If the candidate meets these constraints, non-linear programming is conducted to ensure that the ramping capabilities satisfy system-wide constraints and that the optimal power contribution is achieved at the minimum cost. Once the first acceptable solution for the objective (13) is identified, the model ceases to be updated and the algorithm makes the final recommendation ${\overrightarrow{x}}_{*}$, presenting the global optimum estimated by the algorithm. The textual representation respecting the proposed optimization process is summarized in

Table 2. Textual representation of the proposed algorithm process.

Algorithm Process	Process Details
Initialization	Initialize the system parameters, including the number of generating units, their characteristics, and the forecasted load demand.
Boolean Mapping	Represent the binary decision variables traditionally used in UC problems as Boolean variables, introducing a more flexible and granular approach to UC decisions.
Objective Function Formulation	Formulate the objective function, integrating Boolean variables to reflect the cost minimization or economic objective while considering the dynamic constraints of the isolated power system. At this stage, all system-wide constraints are simultaneously qualified.
Constraints Integration	Integrate the system constraints, such as unit operating limits, ramping constraints, and minimum up time/down time requirements, into the Boolean mapping framework. During this stage, all unit-specific constraints are satisfied.
Optimization Algorithm Application	Employ advanced optimization algorithms that leverage Boolean mapping to efficiently search the solution space. Boolean variables enable a more direct and agile representation of UC decisions. The minimum-cost recommendation takes place by applying economic dispatch, considering the ramping constraints.
Convergence Analysis	Monitor the convergence of the optimization algorithm using Boolean mapping, ensuring that the UC solution stabilizes within acceptable tolerance levels.
Solution Validation	Validate the obtained solution against the system constraints and operational requirements to ensure its feasibility and adherence to the specified UC objectives. The recommended solution takes into account the satisfaction of the plant-wide constraints.
Output Generation	Generate the optimal UC schedule based on the Boolean mapping strategy, providing detailed information on the status of each generating unit over the scheduling horizon.

. Figure 5 demonstrates the comprehensive flow diagram of this paradigm.

3.1. Enhanced Formulation of Priority List Schemes

Priority list schemes based on incremental generation costs offer key advantages compared to traditional mathematical methods. Unlike common priority-based approaches, which rely solely on single-factor reordering, the proposed model incorporates additional factors such as start-up costs, minimum up times, and maximum power ratings. Dealing with a minimization problem, the first factor ($F_i^1$) considers the derivative of the cost function. In an attempt to avoid frequent start-ups that add considerable costs to the overall expenditures, the remaining three factors, $F_i^2$, $F_i^3$, and $F_i^4$, ensure that the generators with the highest capacity, minimum up times and start-up cost, respectively, will shut down last. This comprehensive approach provides a more nuanced prioritization, expressed as:

$$F_i^{\left(1\right)}=\left.{\displaystyle \frac{d\left(F\left(P_i\right)\right)}{d{P}_i}}\right|{\displaystyle \genfrac{}{}{0pt}{}{i\ne j}{P_i=P_{mean}}},F_i^{\left(2\right)}=P_{i,max},F_i^{\left(3\right)}={MU}_i,F_i^{\left(4\right)}={SU}_i$$

(14)

The enhanced approach is based on the key assumption that the new configuration is established according to the descending order of the developed list, taking into account the available units and potentially excluding the must-run units j. The optimal priority is assigned using the normalization function specified in Equation (15).

$$F_i^{*}={\displaystyle \frac{F_i^{\left(1\right)}}{min\left(F_i^{\left(1\right)}\right)}}+{\displaystyle \frac{1}{\left(\frac{F_i^{\left(2\right)}}{min\left(F_i^{\left(2\right)}\right)}\right)}}+{\displaystyle \frac{1}{\left(\frac{F_i^{\left(3\right)}}{min\left(F_i^{\left(3\right)}\right)}\right)}}+{\displaystyle \frac{1}{\left(\frac{F_i^{\left(4\right)}}{min\left(F_i^{\left(4\right)}\right)}\right)}}$$

(15)

Considering the contribution of must-run generators, a binary generator is used to produce the feasible combinations relying on the rearrangement so that $\overrightarrow{x}=R\left(F_i^{*}\right)$. Equation (16) dictates a typical example distinguishing the must-run units ($j=2$) with bold values.

$$\overrightarrow{x}={\left[\begin{array}{ccc}\begin{array}{c}\begin{array}{c}\begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}\\ ⋮\end{array}\\ \begin{array}{cc}0& 1\end{array}\end{array}& \cdots & \begin{array}{c}\begin{array}{c}\begin{array}{cc}\begin{array}{cc}\begin{array}{c}0\\ 1\end{array}& \begin{array}{c}\mathbf{1}\\ \mathbf{1}\end{array}\end{array}& \begin{array}{c}\mathbf{1}\\ \mathbf{1}\end{array}\end{array}\\ ⋮\end{array}\\ \begin{array}{ccc}1& \mathbf{1}& \mathbf{1}\end{array}\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}1& 1\end{array}& \cdots & \begin{array}{cc}1& \begin{array}{cc} \mathbf{1}& \mathbf{1}\end{array}\end{array}\end{array}\right]}_{CxN}$$

(16)

3.2. Boolean Mapping—Encoding/Decoding

Boolean mapping has a range of applications in computer-aided design. However, its practical utility is often limited by the size of the Boolean functions that can be transformed [14]. Despite this, BM serves as a cost-effective means to guide transformation algorithms toward convex and explicitly managed objectives. Its implementation relies on an effective procedure capable of mapping large binary matrices into integer vectors. For encoding, it employs q-base expansion equations determined by the following function.

$$\tilde{x}=\sum _{i=0}^{N-1}{\overrightarrow{x}}_{N-i}·q^i$$

(17)

The binary expression refers to base-2 system ($q=2$). To this end, the set $D_N=\{{\overrightarrow{x}}_N,{\overrightarrow{x}}_{N-1},\dots ,{\overrightarrow{x}}_1\}$, which shows a possible combination of $C^t$ at t, can be represented by ${\tilde{x}}^t$. Likewise, the set of natural numbers determining the feasible combinations n during the assessed time frame T is represented by T (nx1) vectors. For a 10-generating unit system, the respective decimals per committed generator are listed in

Table 3. Boolean decimals generated per committed unit.

Committed Unit	U10	U9	U8	U7	U6	U5	U4	U3	U2	U1	Boolean Decimal
U1	0	0	0	0	0	0	0	0	0	1	1
U2	0	0	0	0	0	0	0	0	1	x	2–3
U3	0	0	0	0	0	0	0	1	x	x	4–7
U4	0	0	0	0	0	0	1	x	x	x	8–15
U5	0	0	0	0	0	1	X	x	x	x	16–31
U6	0	0	0	0	1	x	X	x	x	x	32–63
U7	0	0	0	1	x	x	X	x	x	x	64–127
U8	0	0	1	x	x	x	X	x	x	x	128–255
U9	0	1	x	x	x	x	x	x	x	x	256–511
U10	1	x	x	x	x	x	x	x	x	x	512–1023

.

For any $\overrightarrow{x}$, the value $f\left(\overrightarrow{x}\right)$ is a lower bound on the optimal objective function value $f\left({\tilde{x}}_{*}\right)$ of the original problem. As a result, the optimal solution $f\left(\tilde{x}\right)$ forms a lower bound to $f\left({\tilde{x}}_{*}\right)$ such that [15]:

$$f\left({\tilde{x}}_{*}\right)=\underset{\tilde{x}}{\max }f\left(\tilde{x}\right)$$

(18)

The reversible transformation process (Boolean decoding) extracts the binary states ${\overrightarrow{x}}_i$ from the positive value $\tilde{x}$ according to the q-base deduction equations as:

$$d_i=⌈{\displaystyle \frac{\tilde{x}}{q^{N-i}}}⌉$$

(19)

$${\overrightarrow{x}}_i=\left\{\begin{array}{c}\tilde{x}-q·d_{i-1},ifi=N\\ d_{i+1}-q·d_i,elsewhere\end{array}\right.$$

(20)

3.3. Conceptual Convex Optimization

Up to this point, the highly non-convex and non-linear combinatorial task has been transformed into a convex optimization task, namely integer minimization. Consequently, the desired minimizer ${\tilde{x}}_{*}$ can now be expressed as follows

$${\tilde{x}}_{*}=\underset{\tilde{x}\in X}{\mathrm{argmin}}f\left(\tilde{x}\right)$$

(21)

subject to the constraints $c_4$ and $c_7$. To enable the transitions towards the most promising regions—that is, the next minimum valued $\tilde{x}$—non-linear regression mechanisms are evolved. By making use of an appropriate activation function feed-forward neural networks can be modified to deal with integers [16]. At each interval t, the temporal solution is treated as the target data. The goal is to effectively minimize the error between this target outcome and the progressively obtained solution patterns.

4. Experimental Evaluation

The assessed power system considers an islanded network (such as that in Cyprus) which is supplied by utilizing 10 conventional generators and domestic RESs including biomass, solar PV, and wind. To gain an overview of the system’s electricity demand, Figure 6 demonstrates the typical MW demand by season during a minimum contribution by RESs. The biomass is treated as a firm input providing a predictable electricity production with eliminated forecast deviations. Conversely, wind is considered a stochastic import [17]. However, due to its centralized nature, it can easily be curtailed as necessary upon an independent Transmission System Operator order.

Instead, the production derived from PVs forms a critical challenge. As the installation of PV parks is given priority, especially in the Mediterranean region due to the increased sunshine hours, the process of predicting their considerably distributed nature becomes extremely difficult. Even in small areas, factors like altitude, terrain morphology, climatic conditions, ambient temperature, air quality, and technical aspects of the installation’s features, can deteriorate the accurate prognosis of aggregated PV production [18,19]. As a result, during the early morning and late evening, where the rate of change in PV power output becomes superior and inferior, respectively, the conventional power generators are unable to follow the residual load demand [20].

The conditions are drastically worsened during the spring and autumn months where the load demand during the aforementioned hours is relatively decreased. A daily representation can be seen in Figure 7. Low, medium, and high season loads, along with the corresponding PV generation, were analyzed to evaluate the robustness of the algorithm and its performance under varying load and PV profiles. Then, the residual load is retrieved by considering domestic models for PV and battery-integrated PV household systems found in refs [21,22].

All necessary properties of a power system consisting of 10 generating units are summarized in

Table 4. Characteristics of the thermal generating units (* unit 1 forced into must-run operation) [23].

Unit i	a (USD/MW2h)	b (USD/MWh)	c (USD/h)	SU (USD)	Pmin (MW)	Pmax (MW)	RU and RD (MW/h)	MU and MD (h)
1 *	0.00048	16.19	1000	4500	225	682.5	405	8
2	0.00031	17.26	970	5000	225	682.5	405	8
3	0.00200	16.60	700	550	30	195	54	5
4	0.00211	16.50	680	560	30	195	54	5
5	0.00398	19.70	450	900	37.5	243	67.5	6
6	0.00712	22.26	370	170	30	120	54	3
7	0.00079	27.74	480	260	37.5	127.5	67.5	3
8	0.00413	25.92	660	30	15	82.5	27	1
9	0.00222	27.27	665	30	15	82.5	27	1
10	0.00173	27.79	670	30	15	82.5	27	1

.

Figure 8 offers the annual electricity requirements by month in terms of a minimum (or base load), maximum (or peak load), and RES contribution. The variable input of net load power demand is presented over a daily horizon of 24 hourly intervals, as listed in

Table 5. Net load power demand (MW) for 24 h [23].

Hour	Load	Hour	Load	Hour	Load
1	700	9	1300	17	1000
2	750	10	1400	18	1100
3	800	11	1450	19	1200
4	850	12	1500	20	1400
5	950	13	1400	21	1300
6	1000	14	1300	22	1100
7	1150	15	1200	23	900
8	1200	16	1050	24	800

[24], while the required spinning reserve is 50 MW $\forall t\in T$.

A plausible implementation can be observed in Figure 9. Using this configuration, all feasible combinations C are generated, considering system adequacy, namely power balance and spinning reserve sufficiency. The Boolean mapping procedure is then applied to create a convex C×T-dimensional object. In this format, the modified neural network can process the values using T independent inputs, effectively directing the optimization process toward achieving the minimum cost.

Based on the performed simulations, a global optimum solution is achieved, offering a unit commitment schedule at the minimum total production cost (TPC) of USD 504803.4. This is certified by the dynamic programming method which converges to the same result.

The minimum cost function output from the modified NN is 476 and the obtained unit commitment and power dispatch results are included in Figure 10. Finally,

Table 6. Comparative results relating to the 10-unit power system.

Method	Number of Trials	Execution Time (s)	Minimum TPC (USD)
Boolean Mapping	8.9 × 103	1064	504,803.4
Dynamic Programming	1.7259 × 1072	131,400	504,803.4

lists the comparisons between the proposed Boolean mapping and dynamic programming methods. The proposed method based on BM also appears very promising for large-scale power systems through enhanced computational efficiency, scalability, and solution accuracy. By decoupling the complexity from the number of generators, usually presented in large-scale networks, it reduces the solution time significantly compared to traditional methods, while improving the quality of the optimal generation scheduling. Its ability to handle large datasets and complex constraints makes it particularly effective in addressing the challenges posed by modern power grids, leading to more reliable and cost-effective operations.

Inaccurate assumptions or estimations of fuel cost uncertainties may result in suboptimal scheduling decisions, potentially increasing operational costs or reducing system reliability. The aspect of treating uncertainties in fuel cost during the solution of UC causes increased complexity in modeling and solving the problem, which can lead to a higher computational burden. To overcome this weakness, more stochastic mechanisms can take place as pre-process tasks, relying on fuzzy logic.

5. Conclusions

A novel mechanism for addressing a unit commitment task based on a Boolean mapping paradigm has been proposed. The primary motivations for this work were twofold: (1) to eliminate the reliance on stochastic search methods by providing a solution that optimally balances exploration and exploitation and (2) to achieve convergence with minimal function evaluations, thereby decoupling the overall computational complexity from the total number of generating units.

The proposed approach leverages advanced priority list schemes and a robust coding/decoding algorithm to facilitate the Boolean inference of the underlying cost function in its decimal form. Additionally, it employs a cutting-edge feed-forward neural network to efficiently select subsequent function evaluations. By following a three-stage procedure, this method systematically addresses constraints, effectively separating complex binary constraints from discontinuous dynamic restrictions. It is interesting to note that the findings of the research support the theoretical section regarding the effectiveness of the Boolean mapping method in solving the non-convexity problem, which can be a challenging unit commitment task in renewable energy systems. Providing impressive performance in terms of global optimum solution and minimum convergence times, this framework can consolidate further constraints transforming the cost function into a multi-objective optimization task. In this way, the DC problem of unit commitment that takes into account only the active power balance can also satisfy the reactive power requirements (AC-UC) and even the thermal demand. It could even be used in greenhouse gas emission minimization tasks by making use either of emission–cost coefficients or exploiting simple weighted sum methods.

The future directions for research in this area suggest incorporating stochastic or fuzzy formulations to account for the uncertainty of renewable generation in the objective. Additionally, extending the research to include multiple-bus formulations that consider actual power network constraints and the inclusion of energy storage could further enhance the optimization performance of the Boolean mapping method. By increasing the complexity of the formulation, it is anticipated that novel Boolean mapping approaches may achieve even better optimization results.