Next Article in Journal
Metallic Nanoparticles for Surface-Enhanced Raman Scattering Based Biosensing Applications
Previous Article in Journal
Cyanobacterial Pigments as Natural Photosensitizers for Dye-Sensitized Solar Cells
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photochem
Volume 4
Issue 4
10.3390/photochem4040025
photochem-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Ultrafast Excited State Dynamics of a Verdazyl Diradical System

by
Caitlyn Clark
1,
Filip Pawłowski
1,
David J. R. Brook
2 and
Christopher Grieco
1,*
1
Department of Chemistry and Biochemistry, Auburn University, Auburn, AL 36849, USA
2
Department of Chemistry, San Jose State University, San Jose, CA 95192, USA
*
Author to whom correspondence should be addressed.
Photochem 2024, 4(4), 404-416; https://doi.org/10.3390/photochem4040025
Submission received: 9 August 2024 / Revised: 14 September 2024 / Accepted: 19 September 2024 / Published: 24 September 2024
Browse Figures
Versions Notes

Abstract

While the photophysics of closed-shell organic molecules is well established, much less is known about open-shell systems containing interacting radical pairs. In this work, we investigate the ultrafast excited state dynamics of a singlet verdazyl diradical system in solution using transient absorption (TA) spectroscopy for the first time. Following 510 nm excitation of the excitonic S0 → S1 transition, we detected TA signals in the 530–950 nm region from the S1 population that decayed exponentially within a few picoseconds to form a vibrationally hot S0* population via internal conversion. The dependence of the S1 decay rate on solvent and radical–radical distance revealed that the excited state possesses charge-transfer character and likely accesses the S0 state via torsional motion. The ultrafast internal conversion decay mechanism at play in our open-shell verdazyl diradicals is in stark contrast with other closed-shell, carbonyl-containing organic chromophores, which exhibit ultrafast intersystem crossing to produce long-lived triplet states as the major S1 decay pathway.

Graphical Abstract

1. Introduction

Verdazyl diradicals are open-shell molecules with tunable intramolecular electronic and spin interactions, which determine the governing properties of organic solids used in a variety of fields, including redox batteries and redox active polymer systems [1,2,3,4], magneto-optics [5,6,7,8], spintronics [9,10], quantum information science [11,12,13], and sensing applications [14,15,16]. Verdazyl diradicals are particularly unique molecular building blocks in this space due to their stability and synthetic versatility in ambient conditions in a variety of different solvents [17]. Their ground state energies and multiplicities may be manipulated by replacing their substituents or by tuning the covalent linkers between the two verdazyl units, which dramatically affect their spin delocalization and electron coupling [18]. Building our knowledge of how the through-space (TS) and through-bond (TB) electronic interactions [19] between the radical–radical centers control their optical and magnetic properties is an important step for the development of diradical building blocks for stable open-shell π-conjugated low- and high-spin molecules.
Ultrafast transient absorption (TA) spectroscopy is an effective technique for probing structure–function relationships in electronically interacting (excitonically coupled) organic chromophores [20,21,22,23]. While models for electronic interactions and photophysical pathways in closed-shell [24,25,26], monoradical [27,28], and ionic [13,29] organic systems have been well established, very little is known about these behaviors and how they may differ in open-shell molecules [30]. Due to the characteristically small S0-T1 energy gaps in open-shell molecules [18], we anticipate that their excited state dynamics may not follow photophysical models established for closed-shell systems, warranting further study.
Here, we use ultrafast TA spectroscopy to investigate the photophysical pathways in two open-shell π-conjugated verdazyl diradical model systems with different radical–radical distances, which are based on compounds previously developed by Brook and coworkers [17,31,32]. In Figure 1a,b, M1 and M2 are both singlet ground-state verdazyl diradicals and are the focus of this study. While M1 has not been published in the literature before, its properties are inferred from its extensively characterized counterpart, M1b [32], which only differs in the type of alkyl substituents. We chose to study M1 over M1b because the isopropyl groups increase the stability of the diradical in its powder form. M1b and M2 are singlet ground-state verdazyl diradicals with a S0-T1 splitting of ~760 cm−1 [32] and 150 cm−1 [17], respectively. The verdazyl ring has a bond length comparable to other 6-oxoverdazyls and is relatively planar [31]. Although M2 is linked by a methylene bridged spacer, there is still a relatively strong radical–radical interaction between the radical centers compared to the directly linked compounds (M1 and M1b), which experience greater repulsion due to the proximity of their radical centers. Unlike other singlet diradical systems [33], we found that M1 and M2 are stable in solution at ambient conditions in light and dark, enabling time-resolved spectroscopic investigation using TA spectroscopy.
In this study, we use a combination of steady-state and ultrafast visible/near-infrared (Vis-NIR) absorption spectroscopies to study the low-energy S0 → S1 transition and the resulting S1 excited-state dynamics of the two verdazyl diradicals (M1 and M2) in polar and nonpolar solvents. Consistent with a previous study [17], the ground-state absorption spectrum was found to be sensitive to both solvent polarity and intramolecular radical-radical geometry, which reflects the excitonic, charge-transfer character of the S0 → S1 transition. Following photoexcitation of the S0 → S1 transition at 510 nm, we observed ultrafast S1 relaxation during the early picosecond timescale in all cases, with a single exponential time constant that is sensitive to both solvent environment and bridging unit. Spectral analysis revealed the subsequent formation of a vibrationally hot electronic ground state (S0*) and without population of a T1 state intermediate, indicating nonradiative deactivation of the S1 state via internal conversion. Altogether, the results provide evidence for an S1/S0 conical intersection, which explains the remarkable photostability of the M1 and M2 diradicals in solution.

2. Materials and Methods

2.1. Materials

Butanol (≥99.4%, BeanTown Chemical, Hudson, NH, USA) and hexane (>99%, Thermo Scientific, Lenexa, KS, USA) were used to make 2.0 mM and 2.4 mM solutions of M1 and M2, respectively, for all spectroscopic measurements. The concentration of M1 and M2 were kept close to achieve similar absorbance.

2.2. Synthesis

M1 was synthesized as detailed below, and M2 was synthesized as previously reported [17].
3,3′-bis-(1,5-diisopropyl-6-oxo-tetrazane). Glyoxal sodium bisulfite addition compound hydrate, (0.28 g, 1 mmol), 2,4-diisopropylcarbonohydrazide bis hydrochloride (0.5 g, 2 mmol) and sodium acetate trihydrate (0.41 g, 4 mmol) were combined in 5 mL water and the solution heated on a hot plate for 10 min. When precipitation started, the solution was removed from the heat and allowed to cool overnight. Filtration of the white crystalline solid gave 3,3′-bis-(1,5-diisopropyl-6-oxo-tetrazane), 196 mg (53%). 1H NMR (CDCl3) d 4.46 (4H septet J = 6.6), 3.94 (m, 6H, CH, NH) 1.12 (d, 12 H), 1.09 (d, 12H) 13C NMR 159.9, 70.0, 47.2, 19.5, 18.7; IR (ATR) 3261 (NH), 1650 (C=O), EIMS m/z (relative abundance): 370 (4), 185 (20), 160 (19), 142 (32), 99 (45), 70 (100).
3,3′-bis-(1,5-diisopropyl-6-oxoverdazyl) (M1). 3,3′-bis-(1,5-diisopropyl-6-oxo-tetrazane) (60 mg, 0.16 mmol) was dissolved in 5 mL toluene along with 35 mg benzoquinone (0.5 mmol, 3 equiv). The solution was heated under reflux for 2 h during which it changed from yellow to dark brown. Upon cooling an off-white crystalline precipitate of hydroquinone was deposited and removed by filtration. The remaining solution was evaporated and the resulting brown solid was triturated with water and filtered. The collected dark brown solid was redissolved in hexanes, filtered, and the solution evaporated to leave dark brown rhombs, 15 mg (25%). IR (ATR) 1685 (C=O); EIMS m/z (relative abundance) 364 (98), 322 (25), 280 (75) 238 (100) 196 (77), 125 (30).

2.3. Spectroscopy Methods

The ground-state absorption spectra of M1 and M2 were recorded from 300 to 1100 nm at 0.9 nm resolution using a Hewlett Packard 8453 UV-VIS spectrophotometer in a 1 mm glass cuvette (CV1G035AE, Thorlabs, Newton, NJ, USA). Temperature-dependent UV-VIS spectra from 300 to 1000 nm at 0.1 nm resolution of M1 (2.0 mM) and M2 (2.4 mM) in butanol were recorded using a dual beam constant-temperature cell holder (P/N 202-30858-44, Shimadzu, Columbia, MD, USA) in a Shimadzu UV-2450 UV-VIS spectrophotometer in 1 cm path length quartz cuvettes (21FLUV10, Firefly Sci, Ottawa, ON, USA) at room temperature (RT), 40, 60, and 80 °C. The temperature was controlled by a 9500 Isotemp Refrigerated Circulator (907997, Fisher Scientific, Pittsburgh, PA, USA) temperature controller, and the temperatures were verified using a thermal camera (FLIR E50bx, Teledyne FLIR, Wilsonville, OR, USA) after equilibrating the reference and sample cells for 10 min.
To perform broadband transient absorption (TA) spectroscopy, a homebuilt ultrafast pump-probe spectrometer with spectral sensitivity in the visible/near-IR region (~500–1000 nm) was used. The instrument setup is extensively detailed in our previous reports [34,35]. TA spectra were recorded for M1 (2.0 mM) and M2 (2.4 mM) in both butanol and hexane in a 1 mm glass cuvette (CV1G035AE, Firefly Sci, Ottawa, ON, USA). Each molecule was optically excited using 510 nm at a 0.5 kHz laser repetition rate with excitation fluences at approximately 300 µJ/cm2. Fluence dependence studies of each molecule in each solvent can be found in the Supplementary Materials (Figures S2.1 and S2.2). The TA signals were detected at the magic angle pump/probe geometry. Absorbance spectra of M1 and M2 recorded before and after 510 nm laser irradiation in the transient absorption measurements did not exhibit any changes, indicating a lack of photodegradation. Due to the photostability of these diradicals, we found that a flow cell setup was not necessary.

2.4. Computational Methods

All calculations were carried out with the Gaussian 16 [36] quantum-chemistry software. Equilibrium geometries for the ground-state triplet and open-shell singlet of the M1 and M2 molecules were obtained using the density functional theory (DFT) with unrestricted B3LYP [37,38,39,40] functional and the 6-311++G(d,p) basis set, i.e., the 6-311G basis [41,42] augmented with the single set of first polarization functions on both the heavy atoms and the hydrogen atoms (d,p) and diffuse functions [43] on both atom types (++). The geometry optimizations and harmonic frequency calculations were carried out in the 1-butanol solvent, employing the implicit solvation, polarizable continuum model (PCM) with the integral equation formalism (IEFPCM) [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59].
The optimized ground-state equilibrium structures were used to calculate vertical, ground-to-excited-state excitation energies and corresponding oscillator strengths. To this end, the long-range-corrected version of the B3LYP functional using Coulomb attenuation, CAM-B3LYP [60] was employed, within the time-dependent DFT, along with the same 6-311++G(d,p) basis set that was used for ground-state geometry optimizations. Thirty singlet and thirty triplet transitions were requested for open-shell singlet ground state, and 50 excitation energies were calculated out of the triplet ground state. The inclusion of solvent (1-butanol) for the vertical excitation-energy calculations was realized with the default Gaussian 16 behavior, i.e., employing a linear response formalism in combination with PCM [61,62]. The resulting excitation energies and oscillator strengths were used to plot the computed spectra with a MATLAB (2022a) script.
Orbital initial guesses for the open-shell singlet species were obtained by assigning atomic centers to different fragments and then setting appropriate spin for an unpaired electron in those fragments. Visualization of molecular structures, orbitals, and spin densities was performed using the GaussView software (version 6.0.16) [63]. A more in-depth analysis is discussed in Section S1, Figure S1.1–S1.9.

3. Results

3.1. Steady-State Absorption Spectroscopy

Figure 2 shows the steady-state absorption spectra of M1 and M2 in butanol and hexane. In each spectrum, three absorption bands are seen that vary in position and relative intensity depending on the chemical structure and solvent. The band at ~450 nm, which is also seen in the 1,5-diisopropyl-3-methyl-6-oxoverdazyl monoradical [17], is assigned to local excitation of the verdazyl unit. Unlike in the monoradical, additional higher and lower energy bands are seen at ~370 nm and ~510 nm for both M1 and M2 diradicals, which arise from symmetric and antisymmetric combinations of the Singly Occupied Molecule Orbitals (SOMOs) of each radical unit [17]. These bands are relatively more intense in M1, pointing to larger excitonic interactions (greater SOMO overlap) between the verdazyl radical groups, which is expected due to their ~0.7 Å shorter distance [17] compared to those in M2. Sharpening of the vibronic structure in all three bands occurs when M1 and M2 are dissolved in the nonpolar solvent, hexane. Concentration-dependent UV-VIS spectra of M1 and M2 in butanol suggest that the molecules do not aggregate (see Figure S3.1).

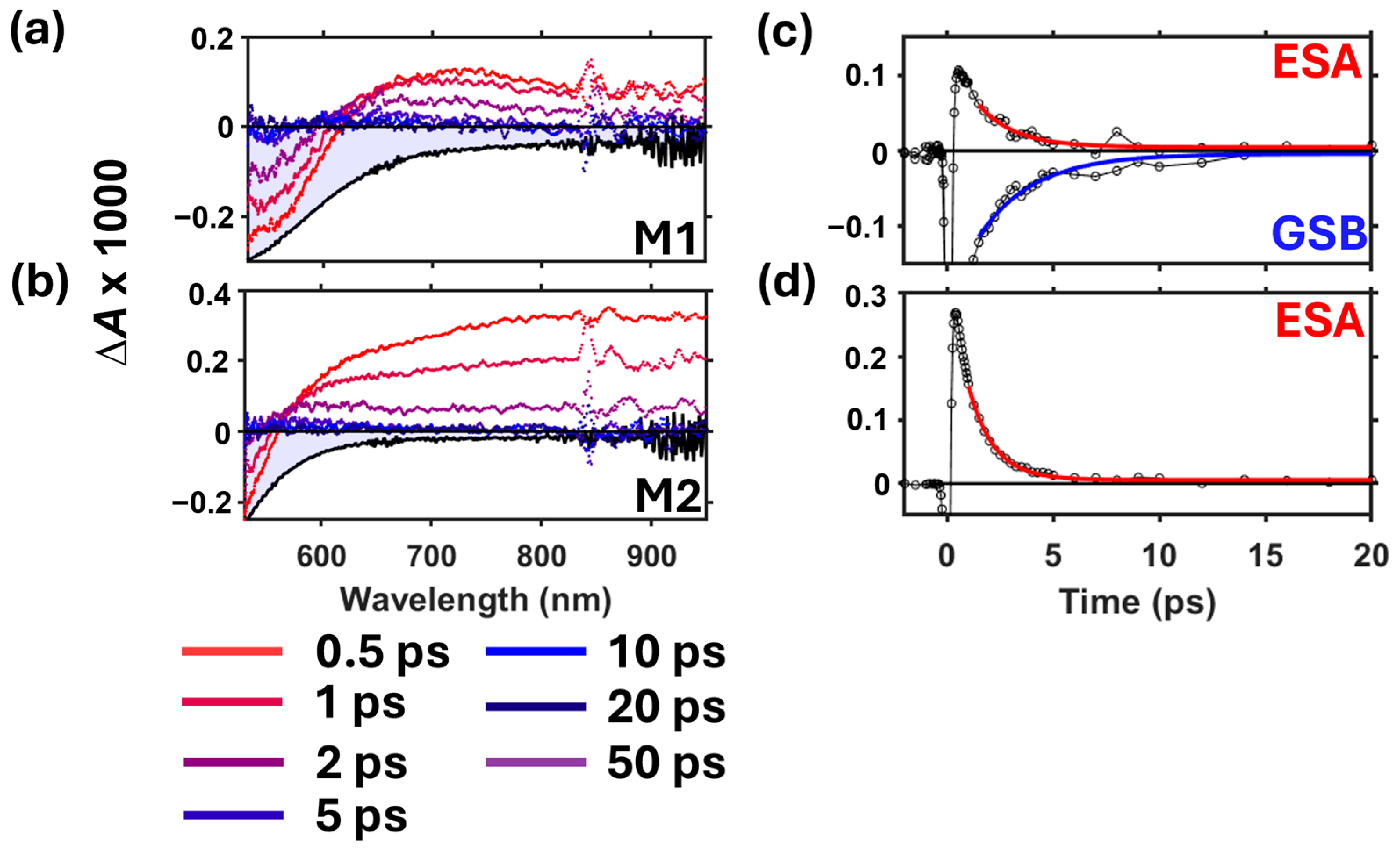
3.2. Broadband Transient Absorption Spectroscopy

In this first investigation into the excited state pathways of verdazyl diradicals, we focus on exciting the lowest energy S0 → S1 excitonic transition. Ultrafast transient absorption (TA) spectra following 510 nm excitation of M1 and M2 in butanol are shown in Figure 3a,b. At the earliest time delays, both diradicals exhibit a ground-state bleach (GSB) signal at wavelengths below 600 nm and an excited-state absorption (ESA) band that spans the ~600–950 nm range. These signals decay together within a few picoseconds, after which small residual signals are seen that persist on the tens of picoseconds that are assigned to the vibrationally hot electronic ground state (see below). M1 has a redshifted GSB compared to M2, which tracks with the respective ground state absorption spectra (see filled gray spectra in Figure 3a,b and Figure 4a,b). Similar results were observed for M1 and M2 in hexane, except with slight differences in peak shape and position (Figure 4a,b).
The TA spectra for M1 and M2 in either solvent did not exhibit nonlinear effects at 0.5 ps and later time delays (see power-dependent measurements in Figures S2.1 and S2.2). Solvent-only signals were observed near the time origin and are attributed to coherent artifacts due to the moderately high fluence (~300 μJ cm−2) used, which interferes with the sample signals (see Figures S2.1 and S2.2).
To study the excited-state dynamics of the diradicals, TA decay kinetics of the ESA and/or GSB signals are displayed in Figure 3c,d and Figure 4c,d. To obtain the kinetics, the ESA signals for M1 and M2 in butanol were averaged over 700–900 nm and 600–800 nm, respectively, while the ESA signal for both diradicals in hexane were averaged over 700–900 nm. Additional normalized ESA kinetic data of M1 and M2 in each solvent can be found in Figure S2.4. The GSB kinetics for M1 were taken at 550 nm for both solvents. Due to time-dependent overlap of positive and negative signals at the red edge of the GSB signal of M2, these kinetics were more complicated and are thus omitted for clarity.
Kinetic analysis points to exponential relaxation of a single excited-state population in both M1 and M2 solutions. Each ESA and GSB kinetic trace was fit using a single exponential decay model offset by a small constant following Equation (1) below:
∆ A ( t ) = N e − t / τ + c
where N is a scaling factor, τ is the time constant, and c is a constant. Note the sign of N is negative for GSB kinetics and positive for ESA kinetics. The data were fit at 1 ps and longer time delays due to interference of the TA signals near the time origin by coherent artifacts. The best fit parameters are summarized in Table 1, which shows that longer time constants are observed for M1 and M2 as the solvent polarity decreases but with overall shorter lifetimes for M2.
To highlight the differences in single exponential decay rates as a function of both chemical structure and solvent, the ESA kinetics are directly compared in Figure 5, along with the best-fit lifetime values. Considering M1 first, there is an obvious difference in the decay time constant between solvents, where its value changes from 1.7 ± 0.1 ps (butanol) to 4.06 ± 0.05 ps (hexane) as solvent polarity decreases. Unlike M1, M2 shows similar decay constants for both solvents, with a slight increase in time constant from 1.18 ± 0.02 ps to 1.56 ± 0.02 ps for butanol and hexane, respectively. The matching time constants for the ESA and GSB kinetics of M1 provides further evidence that a single excited state is populated during the early picosecond timescale.
To understand the differences in the TA decay kinetics, we considered the nature of the excited state population. We first considered whether the photogenerated S1 state rapidly intersystem crosses to the T1 state on the sub-picosecond timescale prior to ground state recovery. In this case, the ESA signal observed in Figure 3a,b and Figure 4a,b would arise from T1 → Tn excitation. Given the small S0-T1 energy gaps in M1 and M2, we used temperature-dependent absorption spectroscopy to independently measure the absorbance of the thermally populated T1 state in the 530–950 nm spectral window for comparison to the TA spectra.
The temperature-dependent absorption spectra of M1 and M2 were recorded over the 25 to 80 °C range in butanol due to its higher boiling point compared to hexane (Figure S3.2), and the data were corrected for solvent expansion as described in Section S3.2. To visualize the small changes in the spectrum resulting from heating, Figure 6 shows the difference between the absorbance measured at temperature, T, and that measured at room temperature (25 °C). As temperature increases, a GSB signal near 530 nm develops for each molecule, indicating thermal depopulation of the singlet ground state (S0). However, no corresponding ESA signals are produced, suggesting that the T1 state does not absorb in this spectral window. Our quantum chemical calculations (see below) confirm that the T1 state also does not absorb in the region of the S0 GSB. Therefore, the T1 state is not likely populated during excited state relaxation, but some other population is responsible for the ESA signal shown in the TA spectra in Figure 3 and Figure 4.
Note that the absorption spectrum for M1 and M2 did not change before and after heating (see the roughly flat blue traces in Figure 6a,b), which suggests that the observed absorbance signals are reversible and that neither M1 nor M2 degraded during the experiments. Additionally, unlike the data in Figure 6, simulated absorption difference spectra show thermally induced absorbance in the 530–950 nm spectral window (see Figure S4.3). This mismatch confirms that the signals in Figure 6 do not arise from thermal population of low-frequency vibrational modes in the S0 state.
Next, we considered the possibility that the TA signals observed in Figure 3a,b and Figure 4a,b arise from a vibrationally hot ground electronic state (S0*), which forms via sub-picosecond nonradiative deactivation of S1. Weinert et al. reported a similar mechanism in a transient absorption study of a verdazyl monoradical in solution, where the photoexcited doublet state (D1) was found to internally convert within a few hundred femtoseconds to form a highly vibrationally excited ground electronic state (D0*) that then undergoes vibrational cooling within a few picoseconds [27]. Following the procedure reported in that work, we used the Sulzer-Wieland (S-W) model [64,65,66] to simulate the temperature-dependent absorption spectrum of M1 and M2 in each solvent, as detailed in the Supplementary Materials (see also Figures S4.1–S4.3). While the simulated thermal absorption difference spectra did not match the corresponding TA spectra at early time delays, the TA spectra at late time delays could be produced using this model (see Figure S4.4). Figure 7 highlights the results of this analysis, showing that the S-W model effectively describes the TA spectra at late time delays for M1 and M2 in each solvent. Therefore, we conclude that the excited state of each diradical relaxes nonradiatively within a few picoseconds to form a vibrationally hot ground electronic state.
Due to the low S0-T1 energy gaps in M1 and M2, we last considered whether the steady-state population of ground-state triplets (T1) could be excited by the 510 nm pump pulse in our TA experiments. The excitation energies obtained from quantum chemical calculations of the optimized singlet and triplet ground states of M1 and M2 are displayed in Figure 8, along with their simulated absorption spectra. The calculations predict the lowest energy singlet transition (S0 → S1) in the visible spectrum near 550 nm for both M1 and M2, while no triplet excitations were found in this spectral region. These results suggest that the lowest energy bands seen in the experimental spectra near 510 nm (Figure 2) correspond specifically to a singlet–singlet transition with charge-transfer character (see Figure S5.1). We therefore conclude that 510 nm selectively excites the ground state singlet population in the TA experiments. A similar observation of a spin-specific lowest energy transition was recently reported by Shimizu et al. for a benzotriazinyl diradical compound [30].
Based on the TA spectroscopy and computational results, we conclude that the early picosecond signals in the TA spectra of M1 and M2 arise from the S1 excited state. Altogether, the TA results reveal the following model for the excited-state decay pathways in the verdazyl diradicals:
S 1 → ~ 1   p s   S 0 ∗ → > 10   p s S 0
where the S1 population relaxes exponentially within a few picoseconds to produce a vibrationally hot singlet ground state, which vibrationally cools on the tens of picoseconds timescale. Global analysis of the TA data using a two-state sequential model provides further support for this model (see Section S6 and Figure S6.1).

4. Discussion

The solvent-dependent TA spectroscopy results suggest that the S1 state in M1 and M2 has charge-transfer (CT) character. Previous studies showed that polar solvents can lower the CT state energy, resulting in a faster relaxation to the ground state [29,30]. Shimizu et al. reported this effect in a benzotriazinyl diradical system, where the excited state lifetime decreased from 1.6 ps to 0.35 ps when increasing solvent polarity from toluene to acetone [30]. Table 1 and Figure 5 show similar decreases in S1 lifetime in M1 and M2 when switching the solvent from hexane to butanol, suggesting that the S1 state in the verdazyl diradicals also possess CT character. This observation is also supported by previous work suggesting that the S1 state in verdazyl diradicals is ionic due to charge transfer between the radical–radical centers [17]. Our molecular orbital analysis further supports the assignment of S0 → S1 to a charge-transfer transition for both M1 and M2 (see Figure S5.1). Furthermore, considering the chemical similarities between the benzotriazinyl diradical system and our verdazyl diradicals (M1 and M2), along with their analogous S1 excited-state behavior, we propose that symmetry-breaking intramolecular charge transfer (SBCT), as discussed by Shimizu et al. [30], may be a characteristic pathway of symmetrical diradical systems.
The drastic difference in the relaxation time for M1 in butanol (1.7 ps) and hexane (4.84 ps), compared to the modest change seen for M2 (1.18 ps to 1.56 ps), can be understood by considering differences in their intramolecular geometries. The large difference in lifetime for M1 suggests that excited-state solvation plays a critical role in CT state relaxation in this compound. On the other hand, M2 shows a short CT state lifetime irrespective of solvent polarity, indicating that when the verdazyl units are separated by a methylene bridge, some other factor plays a greater role in excited state relaxation. The additional flexibility in the angle between verdazyl groups in M2 suggests that torsional motion may facilitate access to the S0 state in this compound more than CT state stabilization. These observations altogether suggest the presence of an S1/S0 conical intersection that mediates ultrafast internal conversion in our verdazyl diradicals. Although excited-state deactivation via CI is typically barrierless, geometry and solvent dependence are known to hinder the rate of crossing through the CI [29].
Lastly, we highlight the remarkably different deactivation pathways of our singlet open-shell diradical molecules compared to those established in other carbonyl-containing singlet closed-shell organic molecules, such as xanthone, benzophenone, and thioxanthone [24,25,26,67,68]. Unlike the single exponential decay seen for internal conversion of the S1 population in M1 and M2 presented in our results, closed-shell ketone-containing compounds typically exhibit biexponential kinetics reflecting ultrafast intersystem crossing, in accordance with the well-established El-Sayed rules [69]. We propose that in singlet diradicals, the excitonic nature of the S0 → S1 transition, in addition to the large S1–T1 energy gap, explains a different paradigm for the photophysical pathways in such open-shell systems.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/photochem4040025/s1, Figure S1.1: M1, open-shell singlet ground-state equilibrium structure; Figure S1.2: M2, open-shell singlet ground-state equilibrium structure; Figure S1.3: M1, triplet ground-state equilibrium structure; Figure S1.4: M2, triplet ground-state equilibrium structure; Figure S1.5: Initial guess for open-shell singlet M1 molecule; Figure S1.6: Initial guess for open-shell singlet M2 molecule; Figure S1.7: Spin density for the initial guess for the open-shell singlet M1 molecule; Figure S1.8: Spin density for the initial guess for the open-shell singlet M2 molecule; Figure S1.9: Spin density for verdazyl; Figure S2.1: Power dependent TA spectra of M1 and M2 in butanol; Figure S2.2: Power dependent TA spectra of M1 and M2 in hexane; Figure S2.3: TA spectra of M2 in hexane shown using more time delays; Figure S2.4: Normalized ESA kinetic data of M1 and M2; Figure S3.1: Concentration-dependent absorption spectra of M1 and M2; Figure S3.2: Temperature-dependent absorption spectra of M1 and M2 in butanol; Figure S4.1: Simulated linear absorption spectra at 300 K of M1 and M2; Figure S4.2: Simulated temperature-dependent linear absorption spectra of M1 and M2; Figure S4.3: Simulated linear absorption difference spectra of M1 and M2; Figure S4.4: Comparison of simulated linear absorption difference spectra with TA spectra of M1 and M2; Figure S5.1: Molecular orbital analysis of the lowest energy singlet–singlet transitions in M1 and M2; Figure S6.1: Global analysis of the TA data using a 2-state sequential model for M1 and M2; Table S4.1: Best-fit parameters for the simulated linear absorption spectra at 300 K; Table S6.1: Lifetimes from global analysis of the TA data for M1 and M2.

Author Contributions

Conceptualization, C.C. and C.G.; investigation, C.C., F.P. and D.J.R.B.; formal analysis, C.C., F.P. and C.G.; resources, D.J.R.B., F.P. and C.G.; software, C.G.; writing—original draft preparation, C.C.; writing—reviewing and editing, C.C., F.P., D.J.R.B. and C.G.; supervision, C.G. All authors have read and agreed to the published version of the manuscript.

Funding

The chemical synthesis in this study was financially supported by a grant from the National Science Foundation (NSF-CHE-1900491).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon request.

Acknowledgments

C.C. and C.G. thank Auburn University for supporting this work through startup funding. C.C., F.P. and C.G. thank the Alabama Supercomputer Center for computing resources.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Magnan, F.; Dhindsa, J.S.; Anghel, M.; Bazylewski, P.; Fanchini, G.; Gilroy, J.B. A Divergent Strategy for the Synthesis of Redox-Active Verdazyl Radical Polymers. Polym. Chem. 2021, 12, 2786–2797. [Google Scholar] [CrossRef]
  2. McKinnon, S.D.J.; Patrick, B.O.; Lever, A.B.P.; Hicks, R.G. Verdazyl Radicals as Redox-Active, Non-Innocent, Ligands: Contrasting Electronic Structures as a Function of Electron-Poor and Electron-Rich Ruthenium Bis(β-Diketonate) Co-Ligands. Chem. Commun. 2010, 46, 773–775. [Google Scholar] [CrossRef] [PubMed]
  3. Kumar, V.J.; Wu, J.-Z.; Judd, M.; Rousset, E.; Korb, M.; Moggach, S.A.; Cox, N.; Low, P.J. The Syntheses, Structures and Spectroelectrochemical Properties of 6-Oxo-Verdazyl Derivatives Bearing Surface Anchoring Groups. J. Mater. Chem. C 2022, 10, 1896–1915. [Google Scholar] [CrossRef]
  4. Kunz, S.; Bui, T.T.; Emmel, D.; Janek, J.; Henkensmeier, D.; Schröder, D. Aqueous Redox Flow Cells Utilizing Verdazyl Cations Enabled by Polybenzimidazole Membranes. ChemSusChem 2024. [Google Scholar] [CrossRef]
  5. Shil, S.; Bhattacharya, D.; Misra, A.; Bytautas, L. Antiaromatic Molecules as Magnetic Couplers: A Computational Quest. J. Phys. Chem. A 2024, 128, 815–828. [Google Scholar] [CrossRef] [PubMed]
  6. Ratera, I.; Veciana, J. Playing with Organic Radicals as Building Blocks for Functional Molecular Materials. Chem. Soc. Rev. 2012, 41, 303–349. [Google Scholar] [CrossRef]
  7. Polo, V.; Alberola, A.; Andres, J.; Anthony, J.; Pilkington, M. Towards Understanding of Magnetic Interactions within a Series of Tetrathiafulvalene–π Conjugated-Verdazyl Diradical Cation System: A Density Functional Theory Study. Phys. Chem. Chem. Phys. 2008, 10, 857–864. [Google Scholar] [CrossRef]
  8. Bodzioch, A.; Obijalska, E.; Jakubowski, R.; Celeda, M.; Gardias, A.; Trzybiński, D.; Tokarz, P.; Szczytko, J.; Woźniak, K.; Kaszyński, P. Electronic and Magnetic Interactions in 6-Oxoverdazyl Diradicals: Connection through N(1) vs. C(3) Revisited. J. Org. Chem. 2024, 89, 6306–6321. [Google Scholar] [CrossRef]
  9. Yeo, H.; Debnath, S.; Krishnan, B.P.; W. Boudouris, B. Radical Polymers in Optoelectronic and Spintronic Applications. RSC Appl. Polym. 2024, 2, 7–25. [Google Scholar] [CrossRef]
  10. Brook, D.J.R.; Lynch, V.; Conklin, B.; Fox, M.A. Spin Delocalization in the Copper(I) Complexes of Bis (Verdazyl) Diradicals. J. Am. Chem. Soc. 1997, 119, 5155–5162. [Google Scholar] [CrossRef]
  11. Poh, Y.R.; Morozov, D.; Kazmierczak, N.P.; Hadt, R.G.; Groenhof, G.; Yuen-Zhou, J. Alternant Hydrocarbon Diradicals as Optically Addressable Molecular Qubits. J. Am. Chem. Soc. 2024, 146, 15549–15561. [Google Scholar] [CrossRef] [PubMed]
  12. Wright, N.D.; Huff, J.S.; Barclay, M.S.; Wilson, C.K.; Barcenas, G.; Duncan, K.M.; Ketteridge, M.; Obukhova, O.M.; Krivoshey, A.I.; Tatarets, A.L.; et al. Intramolecular Charge Transfer and Ultrafast Nonradiative Decay in DNA-Tethered Asymmetric Nitro- and Dimethylamino-Substituted Squaraines. J. Phys. Chem. A 2023, 127, 1141–1157. [Google Scholar] [CrossRef] [PubMed]
  13. Choppella, S.; Paramasivam, G.; Sambasivam, S.; Ravva, M.K. Understanding the Stability of π-Conjugated Diradicaloid Organic Molecules. J. Electron. Mater. 2023, 52, 1681–1690. [Google Scholar] [CrossRef]
  14. Koivisto, B.D.; Hicks, R.G. The Magnetochemistry of Verdazyl Radical-Based Materials. Coord. Chem. Rev. 2005, 249, 2612–2630. [Google Scholar] [CrossRef]
  15. Rota, J.-B.; Le Guennic, B.; Robert, V. Toward Verdazyl Radical-Based Materials: Ab Initio Inspection of Potential Organic Candidates for Spin-Crossover Phenomenon. Inorg. Chem. 2010, 49, 1230–1237. [Google Scholar] [CrossRef]
  16. Haller, B.C.; Chambers, D.; Cheng, R.; Chemistruck, V.; Hom, T.F.; Li, Z.; Nguyen, J.; Ichimura, A.; Brook, D.J.R. Oxidation of Electron Donor-Substituted Verdazyls: Building Blocks for Molecular Switches. J. Phys. Chem. A 2015, 119, 10750–10760. [Google Scholar] [CrossRef]
  17. Brook, D.J.R.; Yee, G.T. Radical–Radical Interaction through a Saturated Link: Methylenebis-6-Oxoverdazyl. J. Org. Chem. 2006, 71, 4889–4895. [Google Scholar] [CrossRef]
  18. Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar] [CrossRef]
  19. Buchwalter, S.L.; Closs, G.L. Electron Spin Resonance and CIDNP Studies on 1,3-Cyclopentadiyls. A Localized 1,3 Carbon Biradical System with a Triplet Ground State. Tunneling in Carbon-Carbon Bond Formation. J. Am. Chem. Soc. 1979, 101, 4688–4694. [Google Scholar] [CrossRef]
  20. Alam, M.M.; Sato, M.; Watanabe, A.; Akasaka, T.; Ito, O. Photochemical Reactions between C60 and Aromatic Thiols. Protonation of C60 via Photoinduced Electron Transfer. J. Phys. Chem. A 1998, 102, 7447–7451. [Google Scholar] [CrossRef]
  21. Baldovi, H.G.; Krüger, M.; Reinsch, H.; Alvaro, M.; Stock, N.; Garcia, H. Transient Absorption Spectroscopy and Photochemical Reactivity of CAU-8. J. Mater. Chem. C 2015, 3, 3607–3613. [Google Scholar] [CrossRef]
  22. Son, M.; Park, K.H.; Shao, C.; Würthner, F.; Kim, D. Spectroscopic Demonstration of Exciton Dynamics and Excimer Formation in a Sterically Controlled Perylene Bisimide Dimer Aggregate. J. Phys. Chem. Lett. 2014, 5, 3601–3607. [Google Scholar] [CrossRef] [PubMed]
  23. Sebastian, E.; Sunny, J.; Hariharan, M. Excimer Evolution Hampers Symmetry-Broken Charge-Separated States. Chem. Sci. 2022, 13, 10824–10835. [Google Scholar] [CrossRef] [PubMed]
  24. Alías-Rodríguez, M.; De Graaf, C.; Huix-Rotllant, M. Ultrafast Intersystem Crossing in Xanthone from Wavepacket Dynamics. J. Am. Chem. Soc. 2021, 143, 21474–21477. [Google Scholar] [CrossRef]
  25. Mundt, R.; Villnow, T.; Ziegenbein, C.T.; Gilch, P.; Marian, C.; Rai-Constapel, V. Thioxanthone in Apolar Solvents: Ultrafast Internal Conversion Precedes Fast Intersystem Crossing. Phys. Chem. Chem. Phys. 2016, 18, 6637–6647. [Google Scholar] [CrossRef]
  26. Aloïse, S.; Ruckebusch, C.; Blanchet, L.; Réhault, J.; Buntinx, G.; Huvenne, J.-P. The Benzophenone S1(n,Π*) → T1(n,Π*) States Intersystem Crossing Reinvestigated by Ultrafast Absorption Spectroscopy and Multivariate Curve Resolution. J. Phys. Chem. A 2008, 112, 224–231. [Google Scholar] [CrossRef]
  27. Weinert, C.; Wezisla, B.; Lindner, J.; Vöhringer, P. Ultrafast Primary Processes of the Stable Neutral Organic Radical, 1,3,5-Triphenylverdazyl, in Liquid Solution. Phys. Chem. Chem. Phys. 2015, 17, 13659–13671. [Google Scholar] [CrossRef]
  28. Sadhukhan, T.; Datta, A.; Datta, S.N. Quantum Chemical Investigation of Light-Activated Spin State Change in Pyrene Coupled to Oxoverdazyl Radical Center. J. Phys. Chem. A 2015, 119, 9414–9424. [Google Scholar] [CrossRef]
  29. Kumpulainen, T.; Lang, B.; Rosspeintner, A.; Vauthey, E. Ultrafast Elementary Photochemical Processes of Organic Molecules in Liquid Solution. Chem. Rev. 2017, 117, 10826–10939. [Google Scholar] [CrossRef]
  30. Shimizu, D.; Sotome, H.; Miyasaka, H.; Matsuda, K. Optically Distinguishable Electronic Spin-Isomers of a Stable Organic Diradical. ACS Cent. Sci. 2024, 10, 890–898. [Google Scholar] [CrossRef]
  31. Brook, D.J.R. Coordination Chemistry of Verdazyl Radicals. Comments Inorg. Chem. 2015, 35, 1–17. [Google Scholar] [CrossRef]
  32. Brook, D.J.R.; Fox, H.H.; Lynch, V.; Fox, M.A. Structural Indicators of Electronic Interaction in the 1,1’,5,5’-Tetramethyl-6,6’-Dioxo-3,3’-Biverdazyl Diradical. J. Phys. Chem. 1996, 100, 2066–2071. [Google Scholar] [CrossRef]
  33. Günaydın-Şen, Ö.; Chen, P.; Fosso-Tande, J.; Allen, T.L.; Cherian, J.; Tokumoto, T.; Lahti, P.M.; McGill, S.; Harrison, R.J.; Musfeldt, J.L. Magnetoelectric Coupling in 4,4′-Stilbenedinitrene. J. Chem. Phys. 2013, 138, 204716. [Google Scholar] [CrossRef]
  34. Dorris, A.L.; Umar, A.R.; Grieco, C. Ultrabroadband Near-Infrared Transient Absorption Spectrometer with Simultaneous 900–2350 Nm Detection. Appl. Spectrosc. 2024. [Google Scholar] [CrossRef]
  35. Umar, A.R.; Dorris, A.L.; Kotadiya, N.B.; Giebink, N.C.; Collier, G.S.; Grieco, C. Probing Polaron Environment in a Doped Polymer via the Photoinduced Stark Effect. J. Phys. Chem. C 2023, 127, 9498–9508. [Google Scholar] [CrossRef]
  36. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
  37. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  38. Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  39. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
  40. Vosko, S.H.; Wilk, L.; Nusair, M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
  41. McLean, A.D.; Chandler, G.S. Contracted Gaussian Basis Sets for Molecular Calculations. I. Second Row Atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
  42. Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
  43. Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21 + G Basis Set for First-Row Elements, Li–F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
  44. Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic Interaction of a Solute with a Continuum. A Direct Utilizaion of AB Initio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
  45. Miertus, S.; Tomasi, J. Approximate Evaluations of the Electrostatic Free Energy and Internal Energy Changes in Solution Processes. Chem. Phys. 1982, 65, 239–245. [Google Scholar] [CrossRef]
  46. Pascual-ahuir, J.L.; Silla, E.; Tuñon, I. GEPOL: An improved description of molecular surfaces. III. A new algorithm for the computation of a solvent-excluding surface. J. Comput. Chem. 1994, 15, 1127–1138. [Google Scholar] [CrossRef]
  47. Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab Initio Study of Solvated Molecules: A New Implementation of the Polarizable Continuum Model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
  48. Barone, V.; Cossi, M.; Tomasi, J. A New Definition of Cavities for the Computation of Solvation Free Energies by the Polarizable Continuum Model. J. Chem. Phys. 1997, 107, 3210–3221. [Google Scholar] [CrossRef]
  49. Cancès, E.; Mennucci, B.; Tomasi, J. A New Integral Equation Formalism for the Polarizable Continuum Model: Theoretical Background and Applications to Isotropic and Anisotropic Dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
  50. Mennucci, B.; Tomasi, J. Continuum Solvation Models: A New Approach to the Problem of Solute’s Charge Distribution and Cavity Boundaries. J. Chem. Phys. 1997, 106, 5151–5158. [Google Scholar] [CrossRef]
  51. Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
  52. Cammi, R.; Mennucci, B.; Tomasi, J. Second-Order Møller—Plesset Analytical Derivatives for the Polarizable Continuum Model Using the Relaxed Density Approach. J. Phys. Chem. A 1999, 103, 9100–9108. [Google Scholar] [CrossRef]
  53. Tomasi, J.; Mennucci, B.; Cancès, E. The IEF Version of the PCM Solvation Method: An Overview of a New Method Addressed to Study Molecular Solutes at the QM Ab Initio Level. J. Mol. Struct. THEOCHEM 1999, 464, 211–226. [Google Scholar] [CrossRef]
  54. Mennucci, B.; Cancès, E.; Tomasi, J. Evaluation of Solvent Effects in Isotropic and Anisotropic Dielectrics and in Ionic Solutions with a Unified Integral Equation Method:  Theoretical Bases, Computational Implementation, and Numerical Applications. J. Phys. Chem. B 1997, 101, 10506–10517. [Google Scholar] [CrossRef]
  55. Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef] [PubMed]
  56. Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
  57. Lipparini, F.; Scalmani, G.; Mennucci, B.; Cancès, E.; Caricato, M.; Frisch, M.J. A Variational Formulation of the Polarizable Continuum Model. J. Chem. Phys. 2010, 133, 014106. [Google Scholar] [CrossRef]
  58. Scalmani, G.; Frisch, M.J. Continuous Surface Charge Polarizable Continuum Models of Solvation. I. General Formalism. J. Chem. Phys. 2010, 132, 114110. [Google Scholar] [CrossRef]
  59. Caricato, M. Absorption and Emission Spectra of Solvated Molecules with the EOM–CCSD–PCM Method. J. Chem. Theory Comput. 2012, 8, 4494–4502. [Google Scholar] [CrossRef]
  60. Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
  61. Cammi, R.; Mennucci, B.; Tomasi, J. Fast Evaluation of Geometries and Properties of Excited Molecules in Solution:  A Tamm-Dancoff Model with Application to 4-Dimethylaminobenzonitrile. J. Phys. Chem. A 2000, 104, 5631–5637. [Google Scholar] [CrossRef]
  62. Cossi, M.; Barone, V. Time-Dependent Density Functional Theory for Molecules in Liquid Solutions. J. Chem. Phys. 2001, 115, 4708–4717. [Google Scholar] [CrossRef]
  63. Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, version 6.0.16; Semichem Inc.: Shawnee Mission, KS, USA, 2019. [Google Scholar]
  64. Sulzer, P. Intensitätsverteilung eines Kontinuierlichen Absorptionsspektrums in Abhängigkeit von Wellenzahl und Temperatur. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 1952. [Google Scholar]
  65. Schalk, O.; Yang, J.-P.; Hertwig, A.; Hippler, H.; Unterreiner, A.N. Vibrational Cooling in the Liquid Phase Studied by Ultrafast Investigations of Cycloheptatriene. Mol. Phys. 2009, 107, 2159–2167. [Google Scholar] [CrossRef]
  66. Beckwith, J.S.; Rumble, C.A.; Vauthey, E. Data Analysis in Transient Electronic Spectroscopy—An Experimentalist’s View. Int. Rev. Phys. Chem. 2020, 39, 135–216. [Google Scholar] [CrossRef]
  67. Marazzi, M.; Mai, S.; Roca-Sanjuán, D.; Delcey, M.G.; Lindh, R.; González, L.; Monari, A. Benzophenone Ultrafast Triplet Population: Revisiting the Kinetic Model by Surface-Hopping Dynamics. J. Phys. Chem. Lett. 2016, 7, 622–626. [Google Scholar] [CrossRef] [PubMed]
  68. Ley, C.; Morlet-Savary, F.; Jacques, P.; Fouassier, J.P. Solvent Dependence of the Intersystem Crossing Kinetics of Thioxanthone. Chem. Phys. 2000, 255, 335–346. [Google Scholar] [CrossRef]
  69. El-Sayed, M.A. Triplet State. Its Radiative and Nonradiative Properties. Acc. Chem. Res. 1968, 1, 8–16. [Google Scholar] [CrossRef]
Photochem 04 00025 g001
Figure 1. Chemical structure of verdazyl diradicals (a) 3,3′-bis-(1,5-diisopropyl-6-oxoverdazyl) (M1) and 1,1′,5,5′-tetramethyl-6,6′-dioxo-3,3′-biverdazyl (M1b) and (b) Methylene Bis(1,5-diisopropyl-6-oxoverdazyl) (M2).
Figure 1. Chemical structure of verdazyl diradicals (a) 3,3′-bis-(1,5-diisopropyl-6-oxoverdazyl) (M1) and 1,1′,5,5′-tetramethyl-6,6′-dioxo-3,3′-biverdazyl (M1b) and (b) Methylene Bis(1,5-diisopropyl-6-oxoverdazyl) (M2).
Photochem 04 00025 g001
Photochem 04 00025 g002
Figure 2. Steady-state absorption spectra of M1 (2.0 mM) and M2 (2.4 mM) in (a) butanol and (b) hexane with 1 mm pathlength.
Figure 2. Steady-state absorption spectra of M1 (2.0 mM) and M2 (2.4 mM) in (a) butanol and (b) hexane with 1 mm pathlength.
Photochem 04 00025 g002
Photochem 04 00025 g003
Figure 3. TA spectra from 530 to 950 nm of (a) M1 and (b) M2 in butanol with their corresponding inverted ground state absorption spectra for reference. Exponential kinetic fits (red and blue lines) and kinetic data (black markers) of (c) M1 ESA (700–900 nm) and inverted GSB (550 nm) and (d) M2 ESA (600–800 nm). Due to intense coherent artifacts present near the time origin, the plots (c,d) are scaled to better visualize the signals from M1 and M2.
Figure 3. TA spectra from 530 to 950 nm of (a) M1 and (b) M2 in butanol with their corresponding inverted ground state absorption spectra for reference. Exponential kinetic fits (red and blue lines) and kinetic data (black markers) of (c) M1 ESA (700–900 nm) and inverted GSB (550 nm) and (d) M2 ESA (600–800 nm). Due to intense coherent artifacts present near the time origin, the plots (c,d) are scaled to better visualize the signals from M1 and M2.
Photochem 04 00025 g003
Photochem 04 00025 g004
Figure 4. TA spectra from 530 to 950 nm of (a) M1 and (b) M2 in hexane with their coordinating inverted ground state absorption spectra, respectively. To take into consideration the differences in the spectral evolution of M1 and M2 in hexane, a partner graph to Figure 4b is plotted in Figure S2.3 to show the spectral evolution of the M2 chromophore at different delay times. Exponential kinetic fits (red and blue lines) and kinetic data (black markers) of (c) M1 ESA (700–900 nm) and inverted GSB (550 nm) and (d) M2 ESA (700–900 nm). Due to intense coherent artifacts present near the time origin, the plots (c,d) are scaled to better visualize the signals from M1 and M2.
Figure 4. TA spectra from 530 to 950 nm of (a) M1 and (b) M2 in hexane with their coordinating inverted ground state absorption spectra, respectively. To take into consideration the differences in the spectral evolution of M1 and M2 in hexane, a partner graph to Figure 4b is plotted in Figure S2.3 to show the spectral evolution of the M2 chromophore at different delay times. Exponential kinetic fits (red and blue lines) and kinetic data (black markers) of (c) M1 ESA (700–900 nm) and inverted GSB (550 nm) and (d) M2 ESA (700–900 nm). Due to intense coherent artifacts present near the time origin, the plots (c,d) are scaled to better visualize the signals from M1 and M2.
Photochem 04 00025 g004
Photochem 04 00025 g005
Figure 5. Solvent comparison of exponential kinetic fits (red and blue lines) and kinetic data (black markers) of M1 and M2 ESA. The data were fit at 1 ps and longer time delays due to exclude artifacts near the time origin.
Figure 5. Solvent comparison of exponential kinetic fits (red and blue lines) and kinetic data (black markers) of M1 and M2 ESA. The data were fit at 1 ps and longer time delays due to exclude artifacts near the time origin.
Photochem 04 00025 g005
Photochem 04 00025 g006
Figure 6. Temperature-dependent absorption difference spectra for T = 25 °C, 45 °C, 60 °C, and 80 °C, where ∆A = A(T) − A(25 °C), of (a) M1 (2.0 mM) and (b) M2 (2.4 mM) in butanol with 1 cm path length in the 530 to 950 nm spectral window. A concentration-independent y-axis is utilized.
Figure 6. Temperature-dependent absorption difference spectra for T = 25 °C, 45 °C, 60 °C, and 80 °C, where ∆A = A(T) − A(25 °C), of (a) M1 (2.0 mM) and (b) M2 (2.4 mM) in butanol with 1 cm path length in the 530 to 950 nm spectral window. A concentration-independent y-axis is utilized.
Photochem 04 00025 g006
Photochem 04 00025 g007
Figure 7. Comparison of TA spectra at early and late time delays with simulated thermal absorption difference spectra calculated using the Sulzer–Wieland model for (a) M1 and (b) M2 in butanol and (c) M1 and (d) M2 in hexane. Each TA spectrum was obtained by averaging over the indicated time delays.
Figure 7. Comparison of TA spectra at early and late time delays with simulated thermal absorption difference spectra calculated using the Sulzer–Wieland model for (a) M1 and (b) M2 in butanol and (c) M1 and (d) M2 in hexane. Each TA spectrum was obtained by averaging over the indicated time delays.
Photochem 04 00025 g007
Photochem 04 00025 g008
Figure 8. Theoretical UV-VIS spectra from 100 to 1000 nm in 1-butanol of the singlet ground state and triplet ground state of (a,b) M1 and (c,d) M2, respectively. The inset graphs show a closer view of their corresponding absorbance spectra. The absorbance bands were simulated using Gaussian functions with 0.8 eV full width at half maxima (FWHM).
Figure 8. Theoretical UV-VIS spectra from 100 to 1000 nm in 1-butanol of the singlet ground state and triplet ground state of (a,b) M1 and (c,d) M2, respectively. The inset graphs show a closer view of their corresponding absorbance spectra. The absorbance bands were simulated using Gaussian functions with 0.8 eV full width at half maxima (FWHM).
Photochem 04 00025 g008
Table 1. Comparison of best fit parameters 1 from kinetic modeling of the transient absorption data for M1 and M2.
Table 1. Comparison of best fit parameters 1 from kinetic modeling of the transient absorption data for M1 and M2.
Sample/SolventN/103τ (ps)c/103 (Offset)
M1/butanol0.13 ± 0.01 (ESA) 2
−0.037 ± 0.007 (GSB) 3		1.7 ± 0.1 (ESA)
1.7 ± 0.3 (GSB)		0.0047 ± 0.0008 (ESA)
0.0028 ± 0.0008 (GSB)
M1/hexane0.154 ± 0.001 (ESA)
−0.367 ± 0.003 (GSB)		4.06 ± 0.05 (ESA)
4.84 ± 0.06 (GSB)		0.0070 ± 0.0003 (ESA)
0.0024 ± 0.0008 (GSB)
M2/butanol0.345 ± 0.006 (ESA)1.18 ± 0.02 (ESA)0.0057 ± 0.0004 (ESA)
M2/hexane0.591 ± 0.008 (ESA)1.56 ± 0.02 (ESA)0.0027 ± 0.0004 (ESA)
1 Uncertainties were taken as the 95% confidence intervals from the nonlinear regression fits. 2 ESA: Excited-state absorption. 3 GSB: Ground-state bleach.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Clark, C.; Pawłowski, F.; Brook, D.J.R.; Grieco, C. Ultrafast Excited State Dynamics of a Verdazyl Diradical System. Photochem 2024, 4, 404-416. https://doi.org/10.3390/photochem4040025

AMA Style

Clark C, Pawłowski F, Brook DJR, Grieco C. Ultrafast Excited State Dynamics of a Verdazyl Diradical System. Photochem. 2024; 4(4):404-416. https://doi.org/10.3390/photochem4040025

Chicago/Turabian Style

Clark, Caitlyn, Filip Pawłowski, David J. R. Brook, and Christopher Grieco. 2024. "Ultrafast Excited State Dynamics of a Verdazyl Diradical System" Photochem 4, no. 4: 404-416. https://doi.org/10.3390/photochem4040025

APA Style

Clark, C., Pawłowski, F., Brook, D. J. R., & Grieco, C. (2024). Ultrafast Excited State Dynamics of a Verdazyl Diradical System. Photochem, 4(4), 404-416. https://doi.org/10.3390/photochem4040025

Article Metrics

Back to TopTop