Abstract
Singlet fission is a desired process in photovoltaics since it enhances photoelectric conversion efficiency. Intramolecular singlet fission is of special interest as the fission efficiency can be improved through tuning configurations between chromophore units that are covalently connected. However, intramolecular singlet fission chromophores feature a large tetraradical character, and may tend to dissatisfy the criterion for all singlet fission chromophores, intramolecular or not. We performed spin-flip time-dependent density functional theory calculations for a collection of representative intramolecular singlet fission chromophores to show that this is indeed the case.
1. Introduction
When one chromophore absorbs a photon and becomes excited to a singlet excited state, it may quickly relax to the lowest singlet state (), share the excitation energy with another chromophore in ground state (), and generate a pair of lowest triplet states on the two chromophores. Such a singlet fission (SF) process generates two long-lived triplet excitons on the absorption of one photon [1,2,3]. The number doubling and lifetime elongation of the excitons lead to a higher photoelectric conversion efficiency. SF has the potential to increase the photoelectric conversion efficiency to exceed the Shockley-Queisser limit [4] of ∼30% of a single-junction photovoltaic device and reach ∼45% [5,6].
SF was first observed and most intensely investigated in crystals of chromophore molecules [7,8,9,10,11]. When the two chromophore units are covalently connected, i.e., SF occurs within one molecule, the multi-exciton generation is called intramolecular singlet fission (iSF), and the molecule that contains several chromophore units is called an iSF chromophore. The efficiency of SF is highly dependent on the configuration between the chromophore units that participate in the process. ISF is of special interest since there are more chemical handles to effectively tune the inter-chromophore configuration when the chromophore units are covalently connected. Research in iSF has thrived for more than a decade [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43].
In general, SF chromophores, intramolecular or not, are anticipated to satisfy three criteria for the energies of their low-lying excited states:
Throughout this work, all excitation energies are minimum-to-minimum excitation energies, unless further specified. Equation (1) guarantees a thermodynamically favorable SF, Equation (2) implies a thermodynamically unfavorable triplet fusion (TF), and Equation (3) implies a thermodynamically unfavorable triplet-pair concentration (TC) from residing on two chromophores to residing on the same chromophore in the lowest quintet state (). The three inequalities correspond to the three total spins of singlet, triplet, and quintet that a pair of triplets can be coupled to, and the total spin multiplicities are denoted by the superscripts addressed to the triplet-pair states, while the electronic spin of chromophore monomers are indicated by the , , and labels of their states, with n indicating the energy ordering. is used only for the ground state. The SF, TF, and TC are formally internal conversions that conserve the total electronic spins. After SF, ideally, the state undergoes spin decoherence to generate two uncoupled triplet excitons that are spatially separated [44]. When the free triplet excitons encounter, they may undergo TC and TF. TC is detrimental since it reduces the mobility of the triplet excitons, although it does not annihilate them. TF is even more detrimental since it halves the number of triplet excitons. The fusion is formally an internal conversion within the triplet spin manifold. The spin conservation implies that it can occur efficiently, especially when there is a thermodynamics driving force. The fusions may also occur. However, with the non-conservation of the total electronic spin, they are supposed to occur less efficiently. Therefore, throughout this work, “triplet fusion” and its abbreviation“TF” are reserved for the spin-conserved fusion, unless further specified.
For most realistic molecules, we can safely assume that they satisfy Equation (3). This is because often involves simultaneous HOMO-to-LUMO and HOMO-to-LUMO spin-flipped excitations, while is usually dominated by HOMO-to-LUMO spin-flipped excitation. The larger HOMO-to-LUMO energy gap vs. the HOMO-to-LUMO gap suggests , i.e., the satisfaction of Equation (3). The satisfaction of Equation (1) is determined by the diradical character of a molecule [45,46,47,48,49,50,51,52,53,54,55,56]. is the lowest-energy diradical state of a chromophore, while usually consists of a mixture of closed-shell character and singlet open-shell diradical character. The larger the diradical character, the less alternation of the electronic structure to reach the purely diradical state, and thus the lower . The satisfaction of Equation (2) is determined by the tetraradical character of a molecule. A large tetraradical character implies that the state features substantial simultaneous contributions from two diradical valence bond structures [57], thus the easiness to alternate the electronic structure to reach the second-lowest-lying pure diradical state , thus a low , and thus the dissatisfaction of Equation (2). Therefore, SF chromophores shall feature large diradical character to satisfy Equation (1) and low tetraradical character to satisfy Equation (2). These selective requirements on polyradical characters make the searches/designs of SF chromophores a task of finding needles in a haystack [58].
The requirement of low tetraradical character, however, appears to be unsatisfiable to iSF chromophores. With the SF occurs within one molecule, the of an iSF chromophore shall contain a pair of triplet states, one on each of the covalently connected chromophore units, i.e., a pure tetraradical . Only with a large tetraradical character in its can a molecule have a pure tetraradical . In other words, each of the covalently connected chromophore units shall feature a large diradical character so that iSF is thermodynamically favorable. Consequently, an iSF chromophore with two such diradicaloid chromophore units must feature a significant tetraradical character. If the two chromophore units are symmetrically connected, one of the and states of an iSF chromophore shall be a symmetric combination of the two states on the two chromophoric units, while the other is an antisymmetric combination. The combination with a bonding interaction gives while the other with an antibonding interaction gives . Such an inter-chromophoric-units interaction cannot be large; otherwise, it impairs the diradical character of each of the chromophoric units and hence impairs the tetraradical character in of the iSF chromophore, and lessens the thermodynamics favorability for iSF. Therefore, for an iSF chromophore, the – gap shall be small, so that Equation (2) is not satisfied, and when two iSF chromophores, each of which bears a exciton, collide, the triplet fusion is thermodynamically viable.
Overall, there is an intrinsic incompatibility between the requirement of large tetraradical character and the requirement of satisfying Equation (2) for iSF chromophores. Such an incompatibility, despite the straightforward argument above to reach it, has rarely been mentioned in the literature. This fact motivated the present survey study: we calculated s and s for a collection of representative iSF chromophores, and show that they all fail to satisfy Equation (2).
2. Computational Details
ISF chromophores that have been experimentally investigated are summarized in a recent review article by Koroniva et al. [59]. This work is referred to as “the review article” henceforth. We selected a bunch of pentacene-based chromophores listed in Table 1 of the review article to calculate their s and s. All the iSF chromophores consist of two pentacene-based chromophore units that are symmetrically connected, either directly or through a linker. They all have or symmetry, under which and transform as A or B, or or irreducible representations (IRREPs). For each iSF chromophore, five calculations were performed: (1)–(3) structural optimizations for , , and preserving the symmetry of the chromophore; (4) structural optimization for without symmetry constraint; (5) calculation of non-adiabatic coupling matrix element (NACME) between and at the -optimized structure. Energies of the optimized structures are used to calculate the excitation energies. The anticipated close-lying and are expected to induce a substantial pseudo-Jahn–Teller (pJT) interaction [60,61], which distorts the structure to symmetry (i.e., no symmetry) and localizes the exciton on one chromophoric unit. The difference between s obtained in symmetry-constrained and symmetry-broken optimizations, i.e., the reorganization energy due to symmetry breaking, indicates the strength of the pJT interaction. The pJT interaction on the other hand results in a minimum of the potential energy surface that preserves the symmetry, and a delocalized of an antibonding combination of the excitons localized on the two chromophoric units. The absolute value of the calculated NACME indicates the propensity for the -to- non-adiabatic transition, i.e., whether can stably exist. We do not need to consider , since of an iSF chromophore is a triplet-pair state, just like . Therefore, is also a TC process, without annihilating a triplet exciton. Other triplet states () shall have high enough energies to satisfy and are hence not considered.
All calculations were performed at the regular density functional theory (DFT) level, and all and calculations were performed at the spin-flip time-dependent density functional theory (SF-TDDFT) level, [62] using the BHHLYP functional [63,64] and the cc-pVDZ basis set [65,66]. In the SF-TDDFT calculations of and , the same reference state was used, so that the two triplet states are treated on the same footing. The values were monitored in all our SF-TDDFT and calculations, and they are all less than 2.3, close to the ideal value of 2, i.e., the SF-TDDFT calculations did not suffer substantial spin contamination. Since the calculation of NACME requires a better description of wave functions of the coupled states, the more accurate cc-pVTZ basis set [65,66] was used. All calculations were performed using the 5.0.1 version of the ORCA program package [67].
3. Results and Discussion
The following 19 iSF chromophores in Table 1 of the review article were considered in the present work: 1a, 1b, 1c (abbreviated as 1a–c), 2a–c, 3d–h, 4a, 5a,d, 6a, 8a, and 9a,b. In all the iSF chromophores in Table 1 of the review, the pentacene chromophoric units are spatially separated and are unlikely to have through-space coupling. Therefore, we preferably selected those that are more likely to have through-bond interaction between the two chromophore units, and are hence more likely to have larger – gaps. Still, as the results shown below, the gaps are all close to zero.
The structures of 1a–c, 2a–c, and their calculated results are summarized in Figure 1. Throughout this work, structure labels with the same numeric index indicate structures that share the same chromophoric units, while the letter indices indicate different linkers or different connections to the same linker. All groups connected to Si were simplified by H atoms to reduce computational costs. Those groups were introduced in experiments to increase solubility of the chromophores in organic solvents. They are spatially far from the pentacene framework and therefore, the simplification shall not lower the accuracy in simulating the triplet states that mainly consist of excitons on the pentacene frameworks. With this simplification, the chromophore units in the chromophores with numeric indices 1 and 2 are identical, and so are those with the numeric indices 3, 5, 6, 8, and 9. Following the same logic, the CH group on the N atoms in 2c are also simplified as H atoms. , , etc., those addressed with irreducible representations, are the energies of the triplet states obtained with symmetry-constrained optimizations. As mentioned above, these structures are minima on the potential energy surfaces and the etc. are used to calculate . On the other hand, these high-symmetry structures are saddle points on the potential energy surfaces. indicates the energy of the minimum obtained without symmetry constraint. This without irreducible representations is used to calculate . The further lowering of from , etc., enhances the propensity to satisfy .
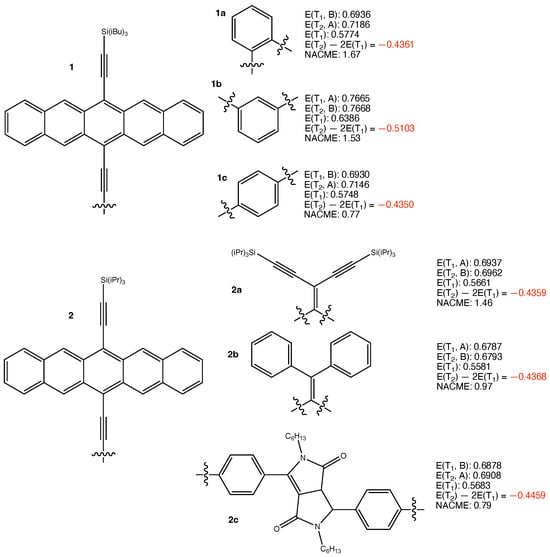
Figure 1.
Structures of 1a–c, 2a–c, and their calculated results. The energy quantities are given in eV. The absolute values of non-adiabatic coupling matrix elements (NACME) are given in atomic unit.
The calculated results summarized in Figure 1 clearly show that all the six iSF chromophores based on chromophoric units 1 and 2 feature negative values. and are almost degenerate if their respective optimizations were performed under symmetry constraints. We have to keep four digits after the decimal point for those and values to show their differences. The weak couplings between the excitons on the two chromophoric units in each of the iSF chromophores are evident. The pseudo-degeneracy between and at high symmetry results in substantial pJT interactions for all the chromophores, leading to ∼0.15 eV energy lowering of when the symmetry constraints are alleviated. Structural optimizations for without symmetry constraints led to the same high symmetry configurations, confirming that the structures obtained with symmetry constraints are true minima of the potential energy surfaces. Even with the ∼0.15 eV lowering of , all the six iSF chromophores in Figure 1 feature substantially negative values, which are highlighted in red.
The small – gaps at the optimized structures of the chromophores suggest substantial non-adiabatic couplings between the two triplet states. We calculated the non-adiabatic coupling matrix elements between and at the -optimized structures of the six chromophores. The absolute values of those vectors are presented in Figure 1. They are all substantial, ranging from 0.77 to 1.67 atomic units (a.u.). The calculated results of 1a–c and 2a–c clearly indicate the thermodynamic driving force for their triplet fusions, and the likelihood of the subsequent rapid decays. The net outcome of the two subsequent processes is the annihilation of one exciton.
The structures of the other considered iSF chromophores and their calculated results are presented in Figure 2 and Figure 3. The results are qualitatively similar to those in Figure 1. This is reasonable since the same logic applies. We do not need to discuss the results of those iSF chromophores one by one. The least negative eV is obtained for 3h. It arises from the largest pJT-induced reorganization of 0.2761 eV among all investigated chromophores. Overall, the results are as expected.
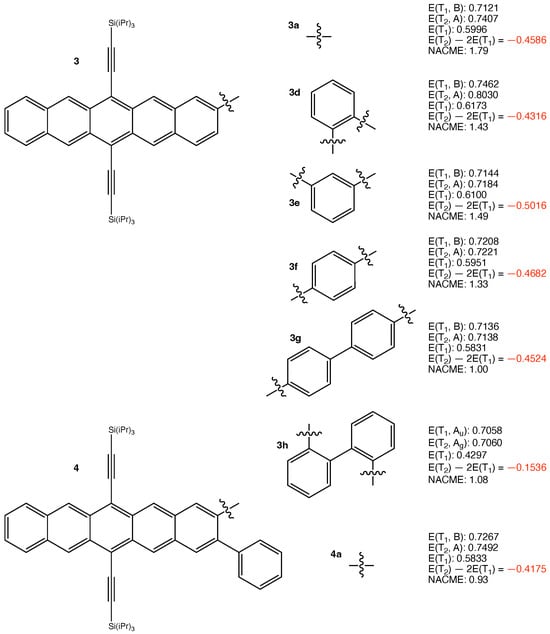
Figure 2.
Structures of 3a,d–h, 4a, and their calculated results. The energy quantities are given in eV. The absolute values of non-adiabatic coupling matrix elements (NACME) are given in atomic unit.
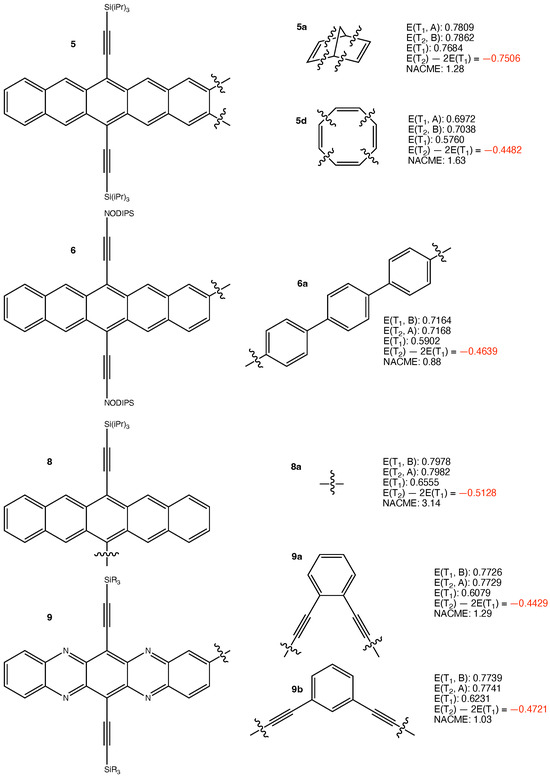
Figure 3.
Structures of 5a,d, 6a, 8a, 9a,b, and their calculated results. The energy quantities are given in eV. The absolute values of non-adiabatic coupling matrix elements (NACME) are given in atomic unit.
Despite the thermodynamics driving force, the fusion may not occur efficiently due to kinetics hindrance. The first atomistic quantum dynamics simulation for TF has been recently reported [68]. This study clearly showed that, under its veil of internal conversion, the fusion essentially consists of a intersystem crossing and a concerted internal conversion. The hidden intersystem crossing occurs slowly when the chromophore does not contain heavy elements that lead to substantial spin–orbit coupling [69,70,71,72,73,74,75,76,77], and/or when the relevant excited states only involve excitations, so that intersystem crossing is quenched by El Sayed’s Rule [78,79,80]. Most organic iSF chromophores indeed have these two features, and therefore, TF should not occur rapidly. Actually, realizing the hidden intersystem crossing in TF, the authors of [68] pointed out that TF should occur with a similar time scale as the decay, and therefore, we may not need to worry about TF for two reasons: (1) if the decay occurs efficiently, then there will be no excitons to undergo TF; (2) if the decay occurs slowly, then the TF also occurs slowly. A main conclusion in [68] is that the criterion in Equation (2) shall not be viewed as likewise important as the criterion in Equation (1). More efforts shall be dedicated to harvest the SF-generated triplet excitons before they decay to ground state, instead of preventing their fusion within the triplet manifold of the total electronic spin. Also, the same intersystem crossing is hidden in fusions. Therefore, we shall not think of the fusion occurring faster than the other two.
4. Conclusions
In this work, we performed spin-flip time-dependent density functional theory calculations for 19 representative intramolecular singlet fission chromophores to evaluate their and energies. The results show that all the chromophores dissatisfy . Considering the representativity of the sampled chromophores, we can safely concluded that all intramolecular singlet fission chromophores fail to satisfy , which is a thermodynamic requirement imposed onto all singlet fission chromophores, intra- or intermolecular. The reason underlying the relation for intramolecular singlet fission chromophores is straightforward to understand, and is presented in the Introduction section: there is an intrinsic incompatibility between the high tetraradical character of intramolecular singlet fission chromophores and the satisfaction of . This computational chemistry study provides the first comprehensive survey that confirms this general relation between and of intramolecular singlet fission chromophores. We hope that this relation and the intrinsic incompatibility will be widely recognized in the field of singlet fission research. Such a wide recognition is certainly not the case yet. It should be emphasized that while the triplet fusion is thermodynamically favorable for all intramolecular singlet fission chromophores, the fusion may be kinetically hindered. For more discussion of the kinetic hindrance, we refer the readers to a recent paper [68], which is dedicated to this subject.
Author Contributions
Conceptualization, T.Z.; model construction, G.Y.; calculations, G.Y.; results analysis, G.Y. and T.Z.; writing: G.Y., Z.Y. and T.Z.; supervision, Z.Y. and T.Z.; project administration, T.Z.; funding acquisition, Z.Y., G.Y. and T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Sciences and Engineering Research Council (NSERC) of Canada (RGPIN-2016-06276), York University (481333), and China Scholarship Council (202206380126).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
This research was supported by the Digital Research Alliance of Canada. We thank the Neese group at the University of Bonn for their continuous development of the ORCA program package.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SF | Singlet fission |
| iSF | Intramolecular singlet fission |
| TF | Triplet fusion |
| TC | Triplet-pair concentration |
| SF-TDDFT | Spin-flip time-dependent density functional theory |
References
- Smith, M.B.; Michl, J. Singlet Fission. Chem. Rev. 2010, 110, 6891–6936. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.B.; Michl, J. Recent Advances in Singlet Fission. Annu. Rev. Phys. Chem. 2013, 64, 361–386. [Google Scholar] [CrossRef]
- Michl, J. Unconventional Solar Energy: Singlet Fission. Mol. Front. J. 2019, 3, 84–91. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of P-N Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Hanna, M.C.; Nozik, A.J. Solar Conversion Efficiency of Photovoltaic and Photoelectrolysis Cells with Carrier Multiplication Absorbers. J. Appl. Phys. 2006, 100, 074510. [Google Scholar] [CrossRef]
- Tayebjee, M.J.Y.; McCamey, D.R.; Schmidt, T.W. Beyond Shockley–Queisser: Molecular Approaches to High-Efficiency Photovoltaics. J. Phys. Chem. Lett. 2015, 6, 2367–2378. [Google Scholar] [CrossRef]
- Singh, S.; Jones, W.J.; Siebrand, W.; Stoicheff, B.P.; Schneider, W.G. Laser generation of excitons and fluorescence in anthracene crystals. J. Chem. Phys. 1965, 42, 330–342. [Google Scholar] [CrossRef]
- Merrifield, R.E. Theory of magnetic field effects on the mutual annihilation of triplet excitons. J. Chem. Phys. 1968, 48, 4318. [Google Scholar] [CrossRef]
- Swenberg, C.E.; Stacy, W.T. Bimolecular radiationless transitions in crystalline tetracene. Chem. Phys. Lett. 1968, 2, 327–328. [Google Scholar] [CrossRef]
- Groff, R.P.; Avakian, P.; Merrifield, R.E. Coexistence of exciton fission and fusion in tetracene crystals. Phys. Rev. B 1970, 1, 815–817. [Google Scholar] [CrossRef]
- Johnson, R.; Merrifield, R. Effects of magnetic fields on the mutual annihilation of triplet excitons in anthracene crystals. Phys. Rev. B 1970, 1, 896–902. [Google Scholar] [CrossRef]
- Paci, I.; Johnson, J.C.; Chen, X.D.; Rana, G.; Popović, D.; David, D.E.; Nozik, A.J.; Ratner, M.A.; Michl, J. Singlet Fission for Dye-Sensitizerd Solar Cells: Can a Suitable Sensitizer be Found? J. Am. Chem. Soc. 2006, 128, 16546–16553. [Google Scholar] [CrossRef] [PubMed]
- Schwerin, A.F.; Johnson, J.C.; Smith, M.B.; Sreearunothai, P.; Popović, D.; Černý, J.; Havlas, Z.; Paci, I.; Akdag, A.; MacLeod, M.K.; et al. Toward Designed Singlet Fission: Electronic States and Photophysics of 1,3-Diphenylisobenzofuran. J. Phys. Chem. A 2010, 114, 1457–1473. [Google Scholar] [CrossRef] [PubMed]
- Greyson, E.C.; Stepp, B.R.; Chen, X.; Schwerin, A.F.; Paci, I.; Smith, M.B.; Akdag, A.; Johnson, J.C.; Nozik, A.J.; Michl, J.; et al. Singlet Exciton Fission for Solar Cell Applications: Energy Aspects of Interchromophore Coupling. J. Phys. Chem. B 2010, 114, 14223–14232. [Google Scholar] [CrossRef] [PubMed]
- Zirzlmeier, J.; Lehnherr, D.; Coto, P.B.; Chernick, E.T.; Casillas, R.; Basel, B.S.; Thoss, M.; Tykwinski, R.R.; Guldi, D.M. Singlet Fission in Pentacene Dimers. Proc. Natl. Acad. Sci. USA 2015, 112, 5325–5330. [Google Scholar] [CrossRef]
- Zirzlmeier, J.; Casillas, R.; Reddy, S.R.; Coto, P.B.; Lehnherr, D.; Chernick, E.T.; Papadopoulos, I.; Thoss, M.; Tykwinski, R.R.; Guldi, D.M. Solution-Based Intramolecular Singlet Fission in Cross-Conjugated Pentacene Dimers. Nanoscale 2016, 8, 10113–10123. [Google Scholar] [CrossRef]
- Hertzer, C.; Basel, B.S.; Kopp, S.M.; Hampel, F.; White, F.J.; Clark, T.; Guldi, D.M.; Tykwinski, R.R. Chromophore Multiplication to enable exciton delocalization and triplet diffusion following singlet fission in tetrameric pentacene. Angew. Chem. Int. Ed. 2019, 58, 115263–115267. [Google Scholar]
- Chien, A.D.; Molina, A.R.; Abeyasinghe, N.; Varnavski, O.P.; Goodson, T.; Zimmerman, P.M. Structure and Dynamics fo the 1(TT) State in a Quinoidal Bithiophene: Characterizing a Promising Intramolecular Singlet Fission Candidate. J. Phys. Chem. C 2015, 119, 28258–28268. [Google Scholar] [CrossRef]
- Basel, B.S.; Young, R.M.; Krzyaniak, M.D.; Papadopoulos, L.; Hetzer, C.; Gao, Y.; La Porte, N.T.; Phelan, B.T.; Clark, T.; Tykwinski, R.R.; et al. Influence of the Heavy-Atom Effect on Singlet Fission: A Study of Platinum-Bridged Pentacene Dimers. Chem. Sci. 2019, 10, 11130–11140. [Google Scholar] [CrossRef]
- Huang, Z.; Fujihashi, Y.; Zhao, Y. Effects of Off-Diagonal Exciton-Phonon Coupling on Intramolecular Singlet Fission. J. Phys. Chem. Lett. 2017, 8, 3306–3312. [Google Scholar] [CrossRef]
- Pradhan, E.; Zeng, T. Triplet Separation after the Fastest Intramolecular Singlet Fission in the Smallest Chromophore. J. Chem. Theory Comput. 2023, 19, 2092–2101. [Google Scholar] [CrossRef]
- Pradhan, E.; Zeng, T. Design of the Smallest Intramolecular Singlet Fission Chromophore with the Fastest Singlet Fission. J. Phys. Chem. Lett. 2022, 13, 11076–11085. [Google Scholar] [CrossRef]
- Zeng, T.; Goel, P. Design of Small Intramolecular Singlet Fission Chromophores: An Azaborine Candidate and General Small Size Effects. J. Phys. Chem. Lett. 2016, 7, 1351–1358. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wang, Y.; Chen, J.; Zhang, G.; Yao, J.; Zhang, D.; Fu, H. Intramolecular Singlet Fission in an Antiaromatic Polycyclic Hydrocarbon. Angew. Chem. Int. Ed. 2017, 56, 9400–9404. [Google Scholar] [CrossRef] [PubMed]
- Varnavski, O.; Abeyasinghe, N.; Aragó, J.; Serrano-Pérez, J.J.; Ortí, E.; López Navarrete, J.T.; Takimiya, K.; Casanova, D.; Casado, J.; Goodson, T. High Yield Ultrafast Intramolecular Singlet Exciton Fission in a Quinoidal Bithiiophene. J. Phys. Chem. Lett. 2015, 6, 1375–1384. [Google Scholar] [CrossRef] [PubMed]
- Zeng, T. Through-Linker Intramolecular Singlet Fission: General Mechanism and Designing Small Chromophores. J. Phys. Chem. Lett. 2016, 7, 4405–4412. [Google Scholar] [CrossRef] [PubMed]
- Reddy, S.R.; Coto, P.B.; Thoss, M. Intramolecular Singlet Fission: Insights from Quantum Dynamical Simulations. J. Phys. Chem. Lett. 2018, 9, 5979–5986. [Google Scholar] [CrossRef]
- Sanders, S.N.; Kumarasamy, E.; Pun, A.B.; Appavoo, K.; Steigerwald, M.L.; Campos, L.M.; Sfeir, M.Y. Exciton Correlations in Intramolecular Singlet Fission. J. Am. Chem. Soc. 2016, 138, 7289–7297. [Google Scholar] [CrossRef]
- Sanders, S.N.; Kumarasamy, E.; Pun, A.B.; Trinh, M.T.; Choi, B.; Xia, J.; Taffet, E.J.; Low, J.Z.; Miller, J.R.; Roy, X.; et al. Quantitative Intramolecular Singlet Fission in Bipentacene. J. Am. Chem. Soc. 2015, 137, 8965–8972. [Google Scholar] [CrossRef]
- Pun, A.B.; Asadpoordarvish, A.; Kumarasamy, E.; Tayebjee, M.J.Y.; Niesner, D.; McCamey, D.R.; Sanders, S.N.; Campos, L.M.; Sfeir, M.Y. Ultra-fast intramolecular singlet fission to persistent multiexcitons by molecular design. Nat. Chem. 2019, 11, 821–828. [Google Scholar] [CrossRef]
- Ito, S.; Nagami, T.; Nakano, M. Design Principles of Electronic Couplings for Intramolecular Singlet Fission in Covalently Linked Systems. J. Phys. Chem. A 2016, 120, 6236–6241. [Google Scholar] [CrossRef] [PubMed]
- Momenti, M.R. Intramolecular Singlet Fission in Quinoidal Bi- and Tetrathiophenes: A Comparative Study of Low-Lying Excited Electronic States and Potential Energy Surfaces. J. Chem. Theory Comput. 2016, 12, 5067–5075. [Google Scholar] [CrossRef]
- Margulies, E.A.; Miller, C.E.; Wu, Y.; Ma, L.; Schatz, G.C.; Young, R.M.; Wasielewski, M.R. Enabling Singlet Fission by Controlling Intramolecular Charge Transfer in π-Stacked Covalent Terrylenediimide Dimers. Nat. Chem. 2016, 8, 1120–1125. [Google Scholar] [CrossRef]
- Basel, B.S.; Zirzlmeier, J.; Hetzer, C.; Phelan, B.T.; Krzyaniak, M.D.; Reddy, S.R.; Coto, P.B.; Horwitz, N.E.; Young, R.M.; White, F.J.; et al. Unified Model for Singlet Fission within a Non-Conjugated Covalent Pentacene Dimer. Nat. Commun. 2017, 8, 15171. [Google Scholar] [CrossRef] [PubMed]
- Krishnapriya, K.C.; Musser, A.J.; Patil, S. Molecular Design Strategies for Efficient Intramolecular Singlet Exciton Fission. ACS Energy Lett. 2019, 4, 192–202. [Google Scholar] [CrossRef]
- Hasobe, T.; Nakamura, S.; Tkachenko, N.V.; Kobori, Y. Molecular design strategy for high-yield and long-lived individual doubled triplet excitons through intramolecular singlet fission. ACS Energy Lett. 2022, 7, 390–400. [Google Scholar] [CrossRef]
- Lin, H.H.; Kue, K.Y.; Claudio, G.C.; Hsu, C.P. First Principle Prediction of Intramolecular Singlet Fission and Triplet Triplet Annihilation Rates. J. Chem. Theory Comput. 2019, 15, 2246–2253. [Google Scholar] [CrossRef]
- Fuemmeler, E.G.; Sanders, S.N.; Pun, A.B.; Kumarasamy, E.; Zeng, T.; Miyata, K.; Steigerwald, M.L.; Zhu, X.Y.; Sfeir, M.Y.; Campos, L.M.; et al. A Direct Mechanism of Ultrafast Intramolecular Singlet Fission in Pentacene Dimers. ACS Cent. Sci. 2016, 2, 316–324. [Google Scholar] [CrossRef]
- Busby, E.; Xia, J.; Wu, Q.; Low, J.Z.; Song, R.; Miller, J.R.; Zhu, X.Y.; Campos, L.M.; Sfeir, M.Y. A Design Strategy for Intramolecular Singlet Fission Mediated by Charge-Transfer States in Donor–Acceptor Organic Materials. Nat. Mater. 2015, 14, 426–433. [Google Scholar] [CrossRef]
- Kefer, O.; Ahrens, L.; Han, J.; Wollscheid, N.; Misselwitz, E.; Rominger, F.; Freudenberg, J.; Dreuw, A.; Bunz, U.H.F.; Buckup, T. Efficient Intramolecular Singlet Fission in Spiro-Linked Heterodimers. J. Am. Chem. Soc. 2023, 145, 17965–17974. [Google Scholar] [CrossRef]
- James, D.; Pradhan, E.; Zeng, T. Design of Singlet Fission Chromophores by the Introduction of N-Oxyl Fragments. J. Chem. Phys. 2022, 156, 034303. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulos, I.; Reddy, S.R.; Coto, P.B.; Lehnherr, D.; Thiel, D.; Thoss, M.; Tykwinski, R.R.; Guldi, D.M. Parallel versus Twisted Pentacenes: Conformational Impact on Singlet Fission. J. Phys. Chem. Lett. 2022, 13, 5094–5100. [Google Scholar] [CrossRef] [PubMed]
- Tayebjee, M.J.Y.; Sanders, S.N.; Kumarasamy, E.; Campos, L.M.; Sfeir, M.Y.; McCamey, D.R. Quintet Multiexciton Dynamics in Singlet Fission. Nat. Phys. 2017, 13, 182–188. [Google Scholar] [CrossRef]
- Scholes, G.D. Correlated Pair States Formed by Singlet Fission and Exciton–Exciton Annihilation. J. Phys. Chem. A 2015, 119, 12699–12705. [Google Scholar] [CrossRef]
- Minami, T.; Ito, S.; Nakano, M. Theoretical Study of Singlet Fission in Oligorylenes. J. Phys. Chem. Lett. 2012, 3, 2719–2723. [Google Scholar] [CrossRef] [PubMed]
- Ito, S.; Minami, T.; Nakano, M. Diradical Character Based Design for Singlet Fission of Condensed-Ring Systems with 4nπ Electrons. J. Phys. Chem. C 2012, 116, 19729–19736. [Google Scholar] [CrossRef]
- Minami, T.; Nakano, M. Diradical Character View of Singlet Fission. J. Phys. Chem. Lett. 2012, 3, 145–150. [Google Scholar] [CrossRef]
- Minami, T.; Ito, S.; Nakano, M. Fundamental of Diradical-Character-Based Molecular Design for Singlet Fission. J. Phys. Chem. Lett. 2013, 4, 2133–2137. [Google Scholar] [CrossRef]
- Zeng, T.; Hoffmann, R.; Ananth, N. The Low-Lying Electronic States of Pentacene and Their Roles in Singlet Fission. J. Am. Chem. Soc. 2014, 136, 5755–5764. [Google Scholar] [CrossRef]
- Zeng, T.; Ananth, N.; Hoffmann, R. Seeking Small Molecules for Singlet Fission: A Heteroatom Substitution Strategy. J. Am. Chem. Soc. 2014, 136, 12638–12647. [Google Scholar] [CrossRef]
- Japahuge, A.; Zeng, T. Theoretical Studies of Singlet Fission: Searching for Materials and Exploring Mechanisms. ChemPlusChem 2018, 83, 146–182. [Google Scholar] [CrossRef] [PubMed]
- Zeng, T.; Mellerup, S.K.; Yang, D.; Wang, X.; Wang, S.; Stamplecoskie, K. Identifying (BN)2-pyrenes as a New Class of Singlet Fission Chromophores: Significance of Azaborine Substitution. J. Phys. Chem. Lett. 2018, 9, 2919–2927. [Google Scholar] [CrossRef] [PubMed]
- Japahuge, A.; Lee, S.; Choi, C.H.; Zeng, T. Design of Singlet Fission Chromophores with Cyclic (Alkyl)(Amino) Carbene Building Blocks. J. Chem. Phys. 2019, 150, 234306. [Google Scholar] [CrossRef]
- Pradhan, E.; Bentley, J.N.; Caputo, C.B.; Zeng, T. Designs of Singlet Fission Chromophores with a Diazadiborinine Framework. ChemPhotoChem 2020, 4, 5279–5287. [Google Scholar] [CrossRef]
- Pradhan, E.; Lee, S.; Choi, C.H.; Zeng, T. Diboron- and Diaza-Doped Anthracenes and Phenanthrenes: Their Electronic Structures for Being Singlet Fission Chromophores. J. Phys. Chem. A 2020, 124, 8159–8172. [Google Scholar] [CrossRef]
- James, D.; Pradhan, E.; Lee, S.; Choi, C.H.; Zeng, T. Dicarbonyl Anthracenes and Phenanthrenes as Singlet Fission Chromophores. Can. J. Chem. 2022, 100, 520–529. [Google Scholar] [CrossRef]
- Shaik, S.; Hiberty, P.C. A Chemist’s Guide to Valence Bond Theory; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Padula, D.; Omar, Ö.H.; Nematiaram, T.; Troisi, A. Singlet Fission Molecules among Known Compounds: Finding a Few Needles in a Hay Stack. Energy Environ. Sci. 2019, 12, 2412–2416. [Google Scholar] [CrossRef]
- Korovina, N.V.; Pompetti, N.F.; Johnson, J.C. Lessons from Intramolecular Singlet Fission with Covalently Bound Chromophores. J. Chem. Phys. 2020, 152, 040904. [Google Scholar] [CrossRef]
- Bersuker, I.B. The Jahn-Teller Effect; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Brown, J.; Lang, R.A.; Zeng, T. Unified Hamiltonian formalism of Jahn-Teller and pseudo-Jahn-Teller problems in axial symmetries. J. Chem. Theory Comput. 2021, 17, 4392–4402. [Google Scholar] [CrossRef]
- Shao, Y.; Head-Gordon, M.; Krylov, A.I. The Spin–Flip Approach within Time-Dependent density Functional Theory: Theory and Applications to Diradicals. J. Chem. Phys. 2023, 118, 4807–4818. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. 1. The Effect of the Exchange-Only Gradient Correction. J. Chem. Phys. 1992, 96, 2155–2160. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. WIRES Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Pradhan, E.; Zeng, T. The Lack of Triplet Fusion for an Intramolecular Singlet Fission Chromophore: The Expected, the Unexpected, and a Reconciliation. J. Phys. Chem. Lett. 2024, 15, 43–50. [Google Scholar] [CrossRef]
- Pyykkö, P. Relativistic Effects in Chemistry: More Common Than You Thought. Annu. Rev. Phys. Chem. 2012, 63, 45–64. [Google Scholar] [CrossRef] [PubMed]
- Pyykkö, P. Relativistic effects in structural chemistry. Chem. Rev. 1988, 88, 563–594. [Google Scholar] [CrossRef]
- Marian, C.M. Spin-Orbit Coupling in Molecules. In Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; WILEY-VCH: New York, NY, USA, 2001; Volume 17, pp. 99–204. [Google Scholar]
- Penfold, T.J.; Gindensperger, E.; Daniel, C.; Marian, C.M. Spin-Vibronic Mechanism for Intersystem Crossing. Chem. Rev. 2018, 118, 6975–7025. [Google Scholar] [CrossRef]
- Zeng, T.; Fedorov, D.G.; Klobukowski, M. Model core potentials for studies of scalar relativistic effects and spin–orbit coupling at Douglas-Kroll level. I. Theory and applications to Pb and Bi. J. Chem. Phys. 2009, 131, 124109. [Google Scholar] [CrossRef]
- Zeng, T.; Fedorov, D.G.; Klobukowski, M. Performance of Dynamically Weighted Multiconfiguration Self-Consistent Field and Spin-Orbit Coupling Calculations of Diatomic Molecules of Group 14 Elements. J. Chem. Phys. 2011, 134, 024108. [Google Scholar] [CrossRef] [PubMed]
- Zeng, T.; Fedorov, D.G.; Schmidt, M.W.; Klobukowski, M. Two-component natural spinors from two-step spin–orbit coupled wave functions. J. Chem. Phys. 2011, 134, 214107. [Google Scholar] [CrossRef]
- Zeng, T.; Fedorov, D.G.; Schmidt, M.W.; Klobukowski, M. Effects of spin–orbit coupling on covalent bonding and the Jahn-Teller e ect are revealed with the natural language of spinors. J. Chem. Theory Comput. 2011, 7, 2864–2875. [Google Scholar] [CrossRef] [PubMed]
- Zeng, T.; Fedorov, D.G.; Schmidt, M.W.; Klobukowski, M. Nautral spinors reveal how the spin–orbit coupling affects the Jahn-Teller distortions in the hexafluorotungstate(V) anion. J. Chem. Theory Comput. 2012, 8, 3061–3071. [Google Scholar] [CrossRef] [PubMed]
- Lower, S.K.; El-Sayed, M.A. The Triplet State and Molecular Electronic Processes in Organic Molecules. Chem. Rev. 1966, 66, 199–241. [Google Scholar] [CrossRef]
- El-Sayed, M.A. Triplet state. Its radiative and nonradiative properties. Acc. Chem. Res. 1968, 1, 8–16. [Google Scholar] [CrossRef]
- Pokhilko, P.; Krylov, A.I. Quantitative El-Sayed Rules for Many-Body Wave Functions from Spinless Transition Density Matrices. J. Phys. Chem. Lett. 2019, 10, 4857–4862. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).