Meso-Macro Simulations of the Forming of 3D Non-Crimp Woven Fabrics
Abstract
:1. Introduction
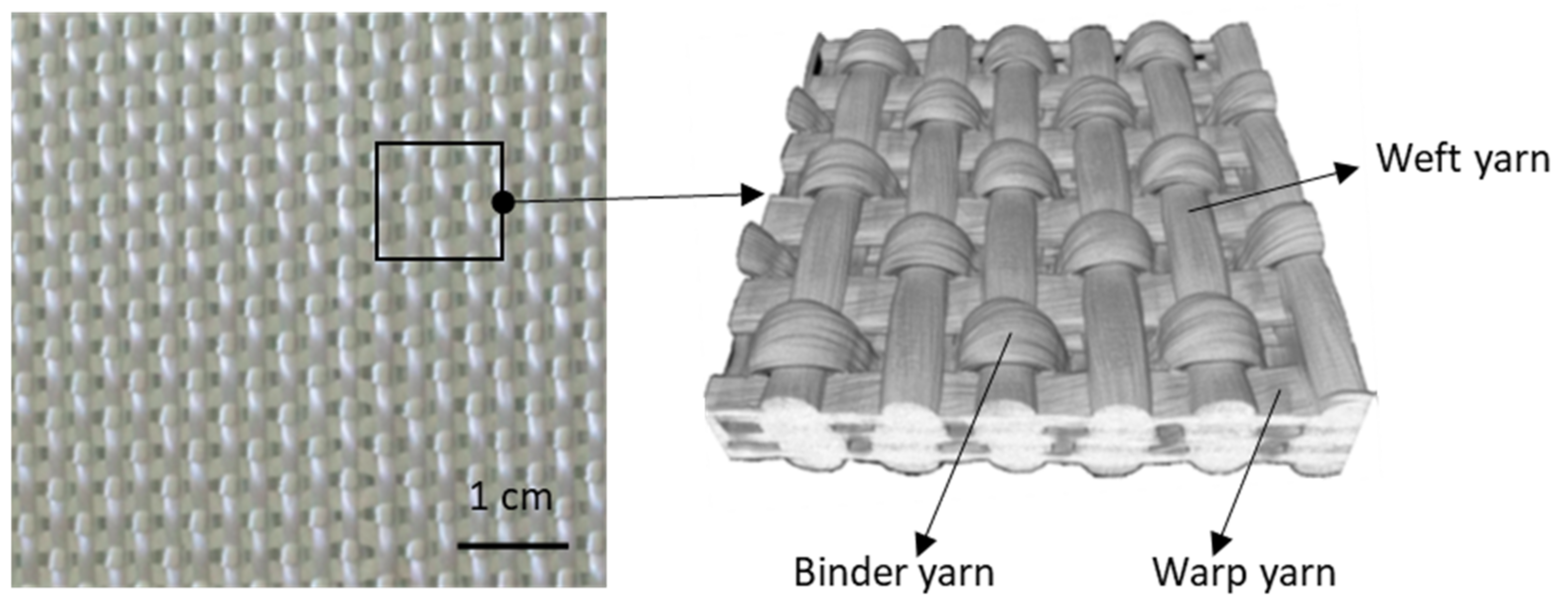
2. Macroscopic Analysis of Woven Reinforcements
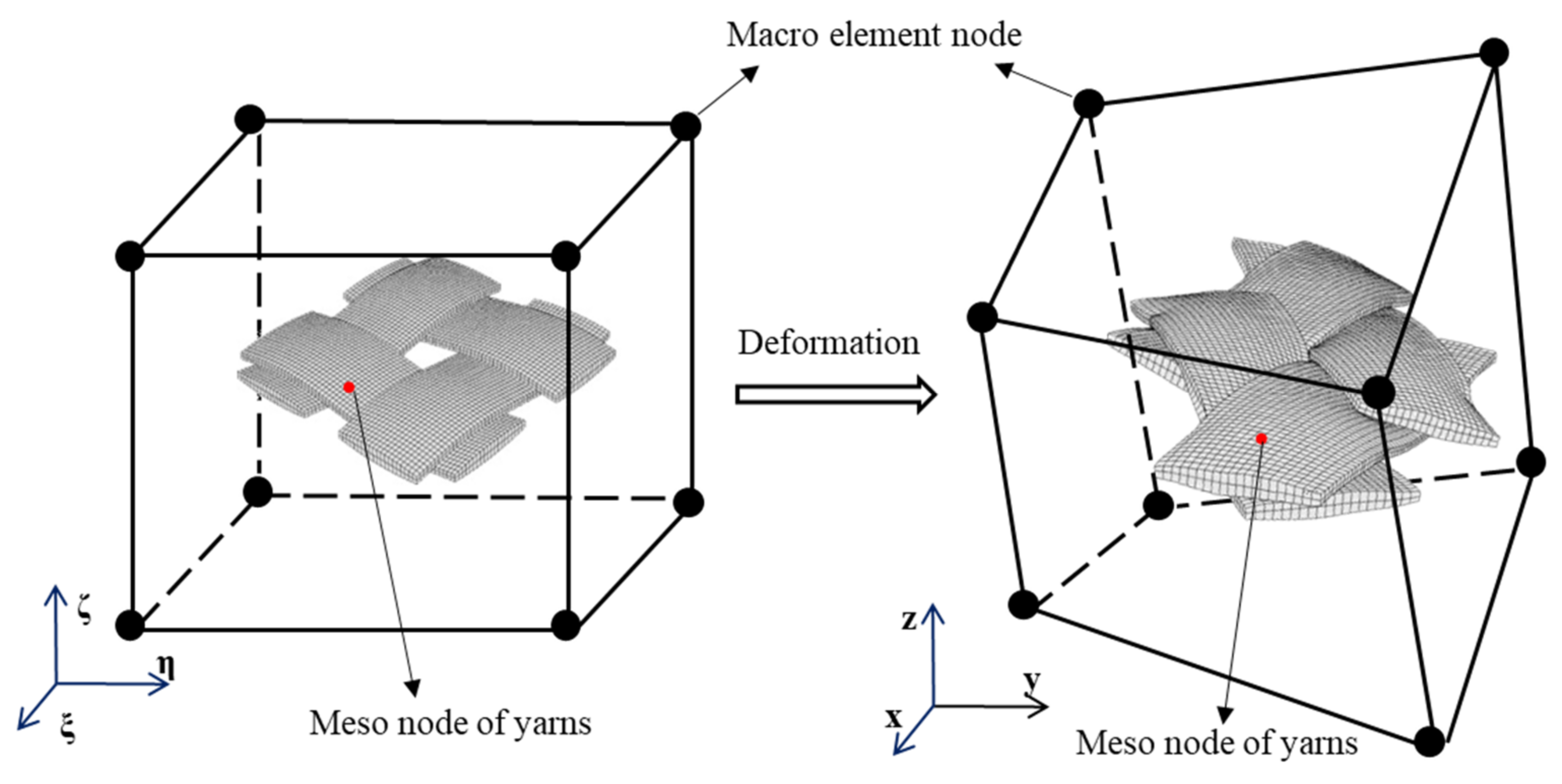
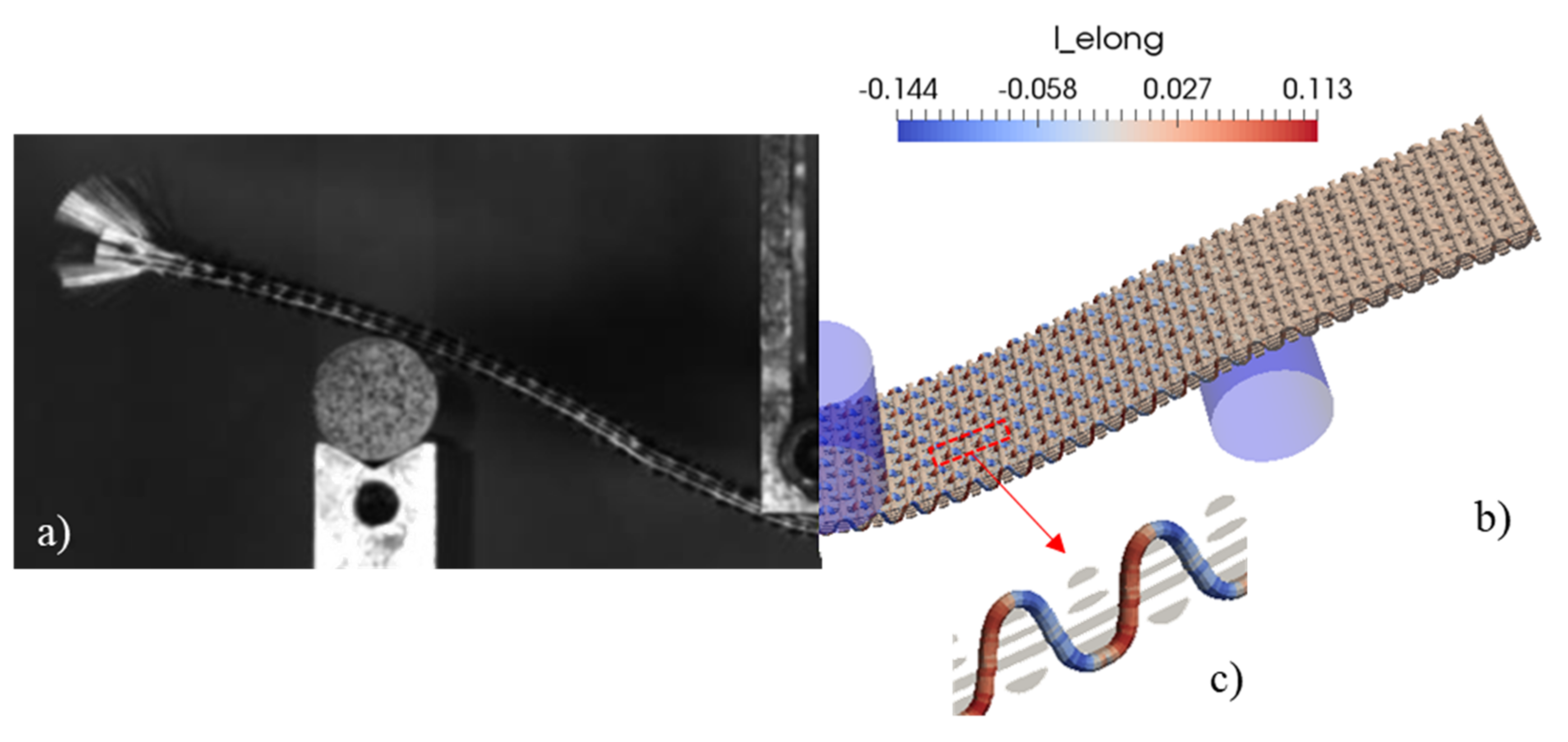
3. Mesoscopic Analysis by Macro-Meso Embedded Approach
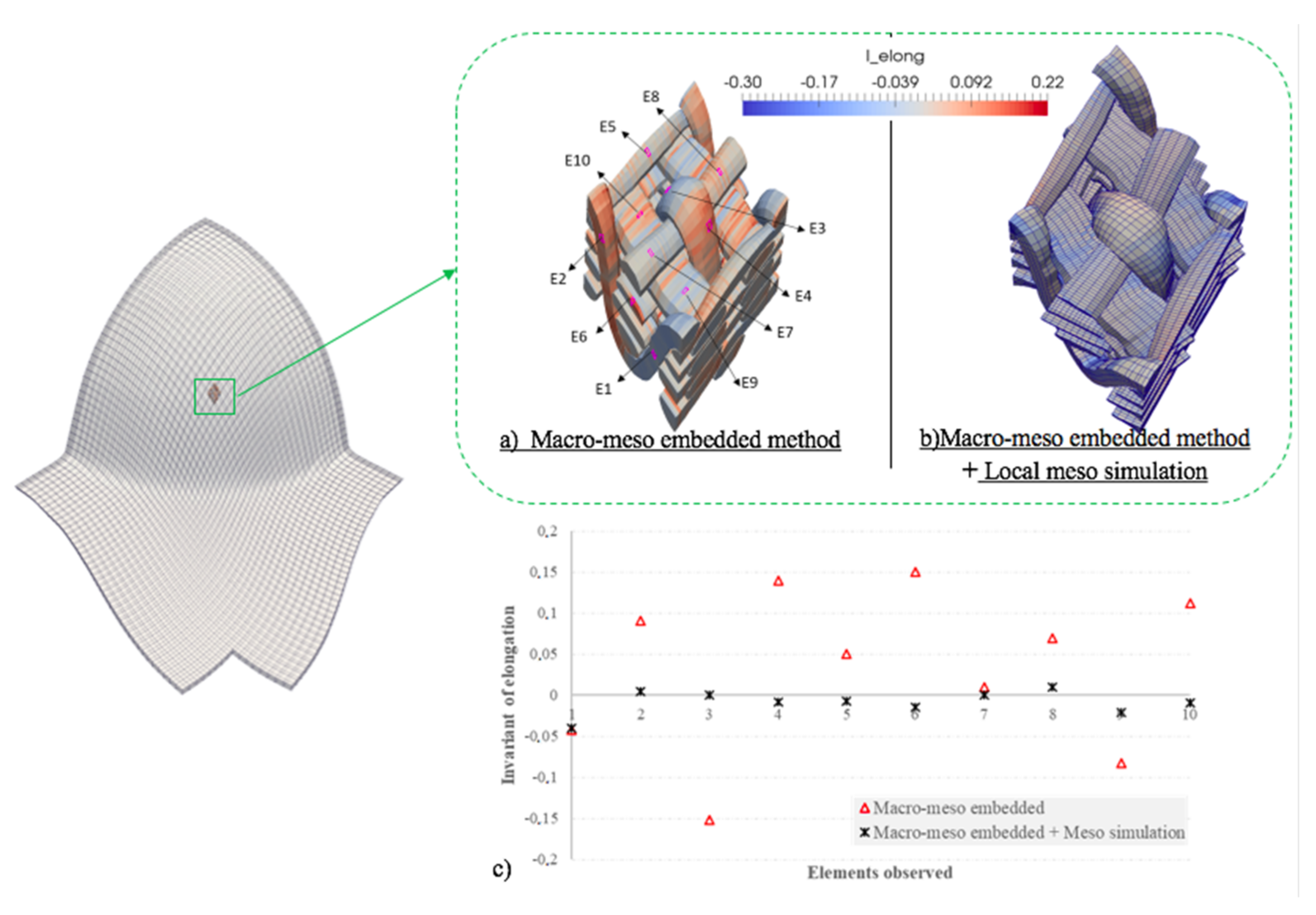
4. Mesoscopic Analysis Enriched by Local Mesoscopic Simulation
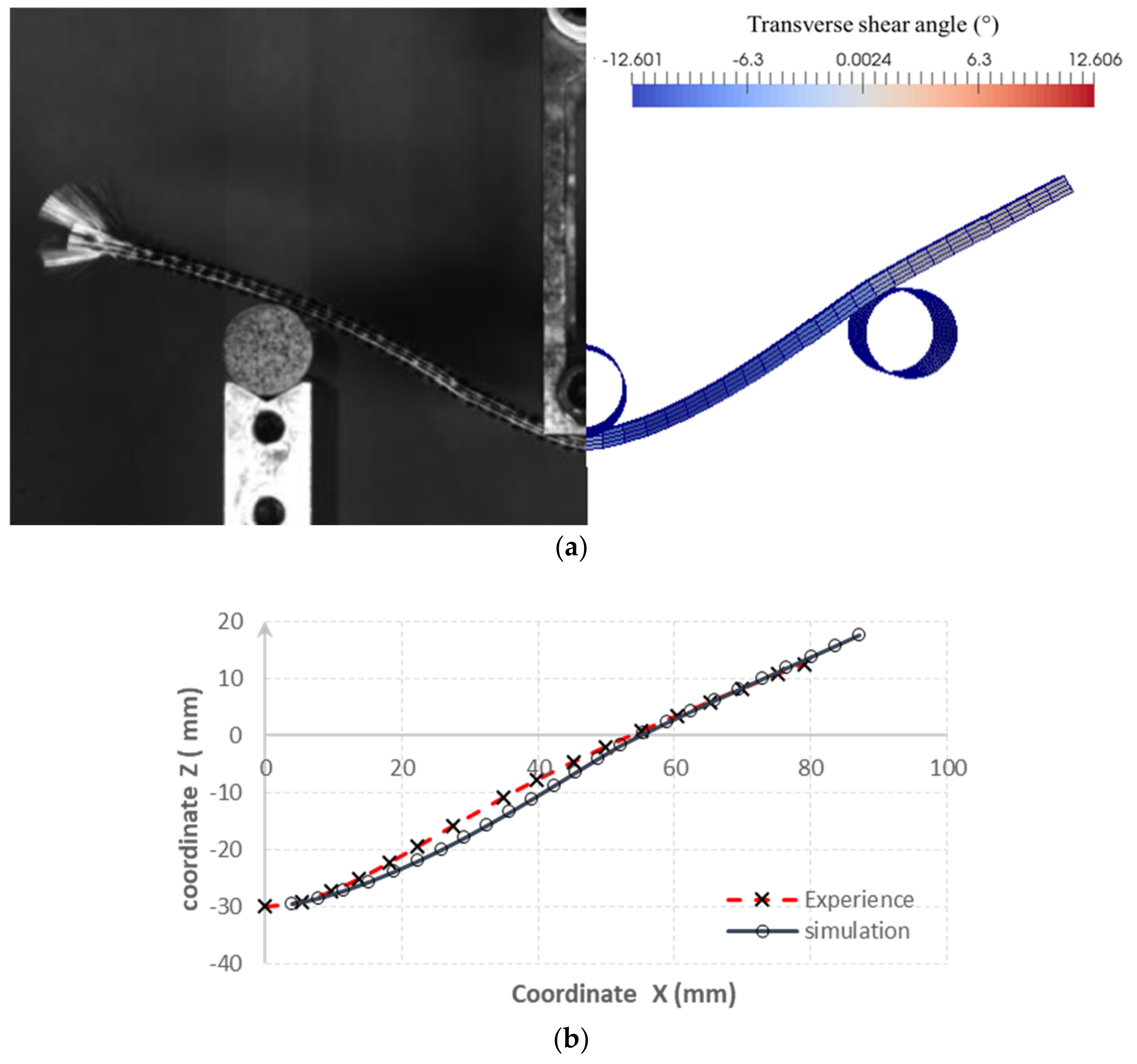
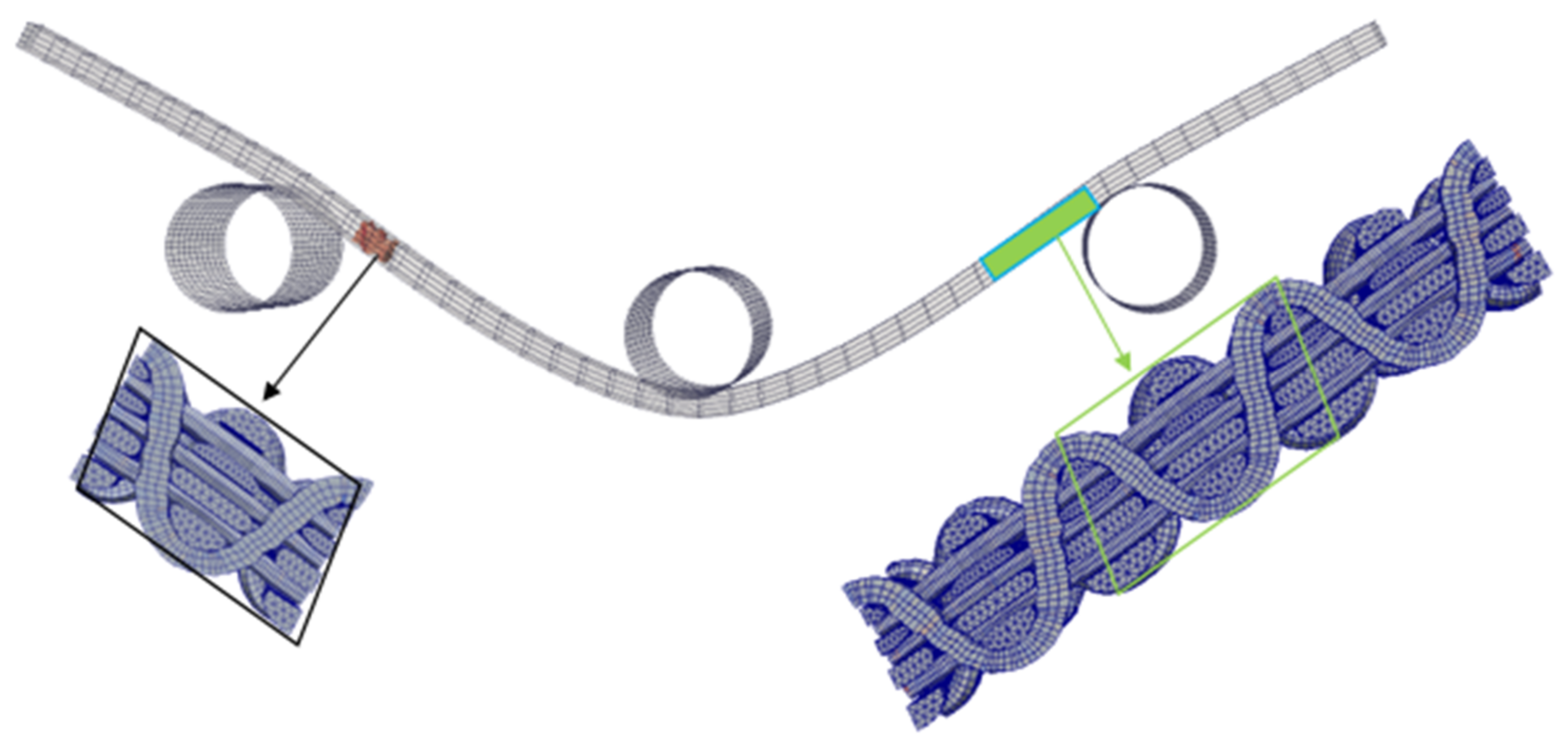
4.1. Local Mesoscopic Simulation
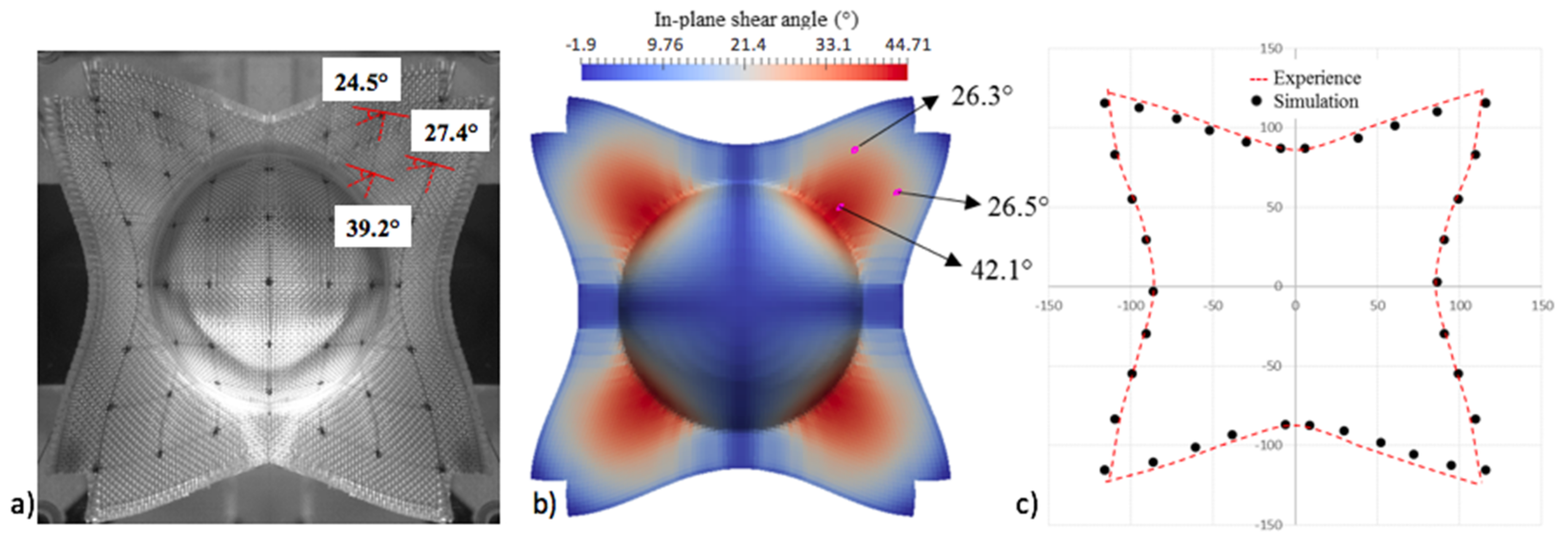
4.2. Comparison with Experimental Results
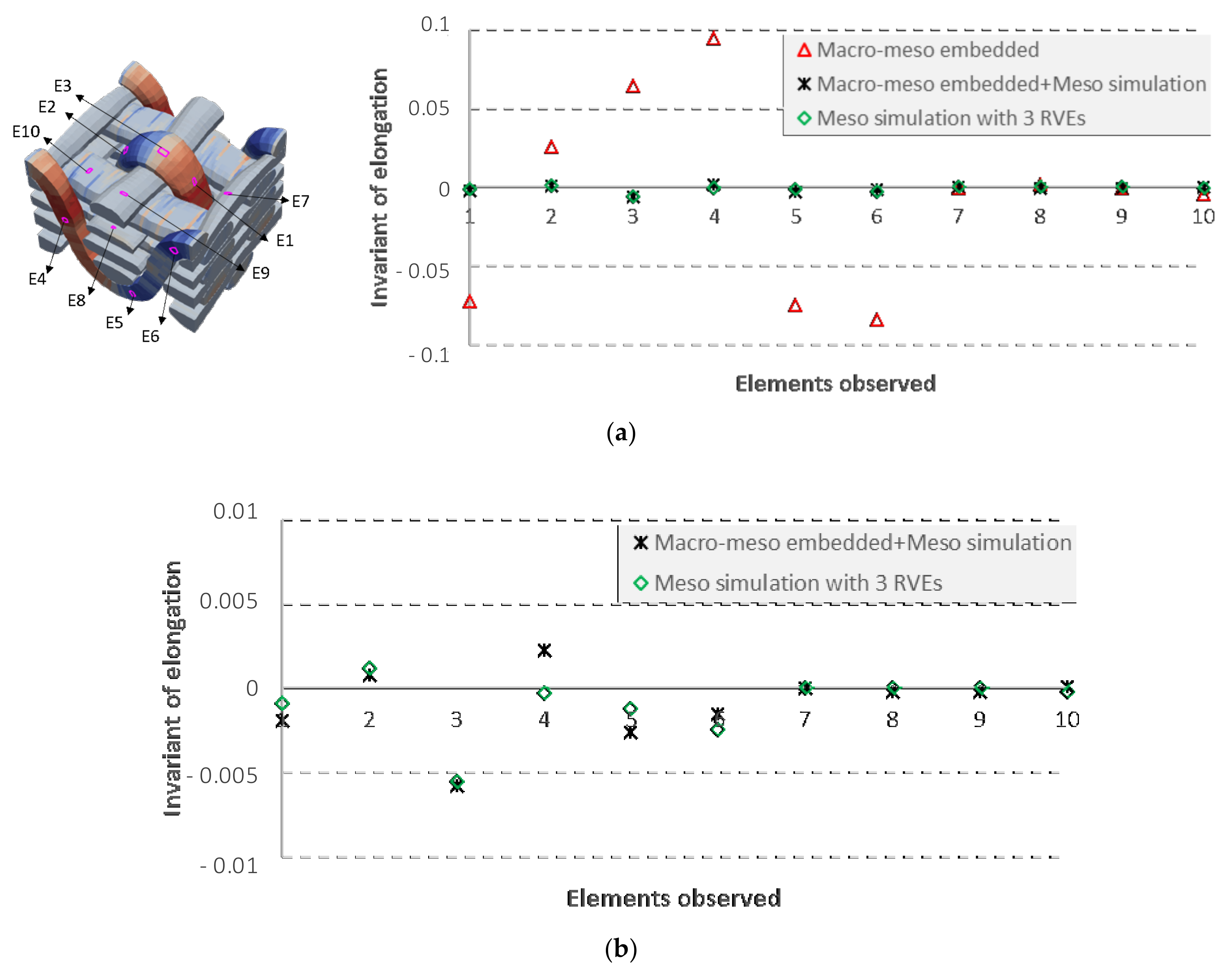
4.3. Influence of the Number of RVEs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| welong1/2 | k1 | k2 | k3 | k4 | k5 | k6 |
| 8.692 | 4816 | −1.002 × 106 | 8.275 × 107 | −2.419 × 109 | 2.442 × 1010 | |
| k7 | k8 | k9 | k10 | k11 | k12 | |
| 8.692 | −505.6 | 1.073 × 105 | −2.687 × 106 | 0 | 0 | |
| wcomp | k1/k7 | k2/k8 | k3/k9 | k4/k10 | k5/k11 | k6/k12 |
| 9.69 × 10−2 | 0.7009 | 6.426 × 10−2 | −1.339 | 0.8777 | 2.855 × 10−2 | |
| wsh | k1/k7 | k2/k8 | k3/k9 | k4/k10 | k5/k11 | k6/k12 |
| 0.3441 | −2.019 | 7.416 | −14.01 | 14.01 | −5.444 | |
| wshT1 | k1/k7 | k2/k8 | k3/k9 | k4/k10 | k5/k11 | k6/k12 |
| 3.721 × 10−2 | 3.844 × 10−2 | −0.521 | 1.877 | −2.78 | 1.572 | |
| wshT2 | k1/k7 | k2/k8 | k3/k9 | k4/k10 | k5/k11 | k6/k12 |
| 347.3 | −5.674 × 10−2 | −1.46 × 10−2 | 0.5835 | −1.201 | 0.8084 | |
| D0 (warp) | D1 (warp) | D0 (weft) | D1 (weft) | |||
| 3.6 | 117.9 | 3.748 | 123.6 |
Appendix B
| E | EA_Elongation | EA_Compression | GA | |
|---|---|---|---|---|
| 3200 | 45,516 | 100 | 0 | 1600 |
References
- Ten Thije, R.H.W.; Akkerman, R.; Huétink, J. Large deformation simulation of anisotropic material using an updated Lagrangian finite element method. Comput. Methods Appl. Mech. Eng. 2007, 196, 3141–3150. [Google Scholar] [CrossRef]
- Boisse, P. Finite element analysis of composite forming. In Composites Forming Technologies; Woodhead Publishing: Cambridge, UK, 2007; pp. 46–79. [Google Scholar]
- Gereke, T.; Döbrich, O.; Hübner, M.; Cherif, C. Experimental and computational composite textile reinforcement forming: A review. Compos. A Appl. Sci. Manuf. 2013, 46, 1–10. [Google Scholar] [CrossRef]
- Bussetta, P.; Correia, N. Numerical forming of continuous fibre reinforced composite material: A review. Compos. A Appl. Sci Manuf. 2018, 113, 12–31. [Google Scholar] [CrossRef]
- Boisse, P.; Hamila, N.; Vidal-Sallé, E.; Dumont, F. Simulation of wrinkling during textile composite reinforcement forming. Influence of tensile, in-plane shear and bending stiffnesses. Compos. Sci. Technol. 2011, 71, 683–692. [Google Scholar] [CrossRef] [Green Version]
- Dangora, L.M.; Mitchell, C.J.; Sherwood, J.A. Predictive model for the detection of out- of-plane defects formed during textile-composite manufacture. Compos. A Appl. Sci. Manuf. 2015, 78, 102–112. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, F.; Wells, G. An analytical model for ballistic impact on textile based body armour. Compos. Part B Eng. 2013, 45, 1508–1514. [Google Scholar] [CrossRef]
- Gatouillat, S.; Bareggi, A.; Vidal-Sallé, E.; Boisse, P. Meso modelling for composite preform shaping–simulation of the loss of cohesion of the woven fibre network. Compos. A Appl. Sci. Manuf. 2013, 54, 135–144. [Google Scholar] [CrossRef]
- Allaoui, S.; Hivet, G.; Soulat, D.; Wendling, A.; Ouagne, P.; Chatel, S. Experimental preforming of highly double curved shapes with a case corner using an interlock reinforcement. Int. J. Mater. Form. 2014, 7, 155–165. [Google Scholar] [CrossRef]
- Schirmaier, F.J.; Dörr, D.; Henning, F.; Kärger, L. A macroscopic approach to simulate the forming behaviour of stitched unidirectional non-crimp fabrics (UD-NCF). Compos. A Appl. Sci. Manuf. 2017, 102, 322–335. [Google Scholar] [CrossRef]
- Schirmaier, F.J.; Weidenmann, K.A.; Kärger, L.; Henning, F. Characterisation of the draping behaviour of unidirectional non-crimp fabrics (UD-NCF). Compos. A Appl. Sci. Manuf. 2016, 80, 28–38. [Google Scholar] [CrossRef]
- Bréard, J.; Henzel, Y.; Trochu, F.; Gauvin, R. Analysis of dynamic flows through porous media. Part I: Comparison between saturated and unsaturated flows in fibrous reinforcements. Polym. Compos. 2003, 24, 391–408. [Google Scholar] [CrossRef]
- Loix, F.; Badel, P.; Orgéas, L.; Geindreau, C.; Boisse, P. Woven fabric permeability: From textile deformation to fluid flow mesoscale simulations. Compos. Sci. Technol. 2008, 68, 1624–1630. [Google Scholar] [CrossRef]
- Tran, T.; Comas-Cardona, S.; Abriak, N.E.; Binetruy, C. Unified microporomechanical approach for mechanical behavior and permeability of misaligned unidirectional fiber reinforcement. Compos. Sci. Technol. 2010, 70, 1410–1418. [Google Scholar] [CrossRef] [Green Version]
- Llorca, J.; Gonzalez, C.; Molina-Aldaregui, J.M.; Segurado, J.; Seltzer, R.; Sket, F. Multiscale modelling of composite materials: A road map towards virtual testing. Adv. Mater. 2011, 23, 5130–5147. [Google Scholar] [CrossRef]
- Iwata, A.; Inoue, T.; Naouar, N.; Boisse, P.; Lomov, S.V. Coupled meso-macro simulation of woven fabric local deformation during draping. Compos. A Appl. Sci. Manuf. 2019, 118, 267–280. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Hamila, N.; Boisse, P. Mesoscopic analyses of the draping of 3D woven composite reinforcements based on macroscopic simulations. Compos. Struct. 2020, 250, 112602. [Google Scholar] [CrossRef]
- Whitcomb, J.; Srirengan, K.; Chapman, C. Evaluation of homogenization for global/local stress analysis of textile composites. Compos. Struct. 1995, 31, 137–149. [Google Scholar] [CrossRef]
- Carvelli, V.; Poggi, C. A homogenization procedure for the numerical analysis of woven fabric composites. Compos. A Appl. Sci Manuf. 2001, 32, 1425–1432. [Google Scholar] [CrossRef]
- Lomov, S.V.; Ivanov, D.S.; Verpoest, I.; Zako, M.; Kurashiki, T.; Nakai, H.; Hirosawa, S. Meso-FE modelling of textile composites: Road map, data flow and algorithms. Compos. Sci. Technol. 2007, 67, 1870–1891. [Google Scholar] [CrossRef]
- Chen, X. (Ed.) Advances in 3D Textiles; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Software PLASFIB. Inter Deposit Certification; Agence Pour la Protection des Programmes: Paris, France, 2015. [Google Scholar]
- Boisse, P.; Aimène, Y.; Dogui, A.; Dridi, S.; Gatouillat, S.; Hamila, N.; Vidal-Sallé, E. Hypoelastic, hyperelastic, discrete and semi-discrete approaches for textile composite reinforcement forming. Int. J. Mater. Form. 2010, 3, 1229–1240. [Google Scholar] [CrossRef]
- Charmetant, A.; Orliac, J.G.; Vidal-Sallé, E.; Boisse, P. Hyperelastic model for large deformation analyses of 3D interlock composite preforms. Compos. Sci. Technol. 2012, 72, 1352–1360. [Google Scholar] [CrossRef]
- Mathieu, S.; Hamila, N.; Bouillon, F.; Boisse, P. Enhanced modeling of 3D composite preform deformations taking into account local fiber bending stiffness. Compos. Sci. Technol. 2015, 117, 322–333. [Google Scholar] [CrossRef]
- Creech, G.; Pickett, A.K. Meso-modelling of non-crimp fabric composites for coupled drape and failure analysis. J. Mater. Sci. 2006, 41, 6725–6736. [Google Scholar] [CrossRef]
- Naouar, N.; Vidal-Salle, E.; Schneider, J.; Maire, E.; Boisse, P. 3D composite reinforcement meso FE analyses based on X-ray computed tomography. Compos. Struct. 2015, 132, 1094–1104. [Google Scholar] [CrossRef]
- Bonet, J.; Burton, A.J. A simple orthotropic, transversely isotropic hyperelastic constitutive equation for large strain computations. Comput. Methods Appl. Mech. Eng. 1998, 162, 151–164. [Google Scholar] [CrossRef]
- Florimond, C. Contribution à la Modélisation Mécanique du Comportement de Mèches de Renforts Tissés à L’Aide d’un Schéma Éléments Finis Implicite. Ph.D. Thesis, INSA Lyon, Lyon, France, 2015. [Google Scholar]



| Size of Model RVE: 4.78 × 4.64 × 3.25 mm3 | Number of Elements (RVE: 39,888 Elements) | Calculation Time | |||
|---|---|---|---|---|---|
| Macro Simulation | Macro-Meso Embedded Analysis | Meso Local Simulation | |||
| Three-point bending | 41 RVEs | 1.6 millions | 6 h | 15 min | 30 min |
| Hemispherical forming | 625 RVEs | 25 millions | 1 day | 1 h | 2 h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, P.; Hamila, N.; Boisse, P. Meso-Macro Simulations of the Forming of 3D Non-Crimp Woven Fabrics. Textiles 2022, 2, 112-123. https://doi.org/10.3390/textiles2010006
Wang J, Wang P, Hamila N, Boisse P. Meso-Macro Simulations of the Forming of 3D Non-Crimp Woven Fabrics. Textiles. 2022; 2(1):112-123. https://doi.org/10.3390/textiles2010006
Chicago/Turabian StyleWang, Jie, Peng Wang, Nahiene Hamila, and Philippe Boisse. 2022. "Meso-Macro Simulations of the Forming of 3D Non-Crimp Woven Fabrics" Textiles 2, no. 1: 112-123. https://doi.org/10.3390/textiles2010006
APA StyleWang, J., Wang, P., Hamila, N., & Boisse, P. (2022). Meso-Macro Simulations of the Forming of 3D Non-Crimp Woven Fabrics. Textiles, 2(1), 112-123. https://doi.org/10.3390/textiles2010006








