Quantum Transport Behavior in Quasi-One-Dimensional Topological Matter Bi4X4 (X = Br, I)
Abstract
1. Introduction
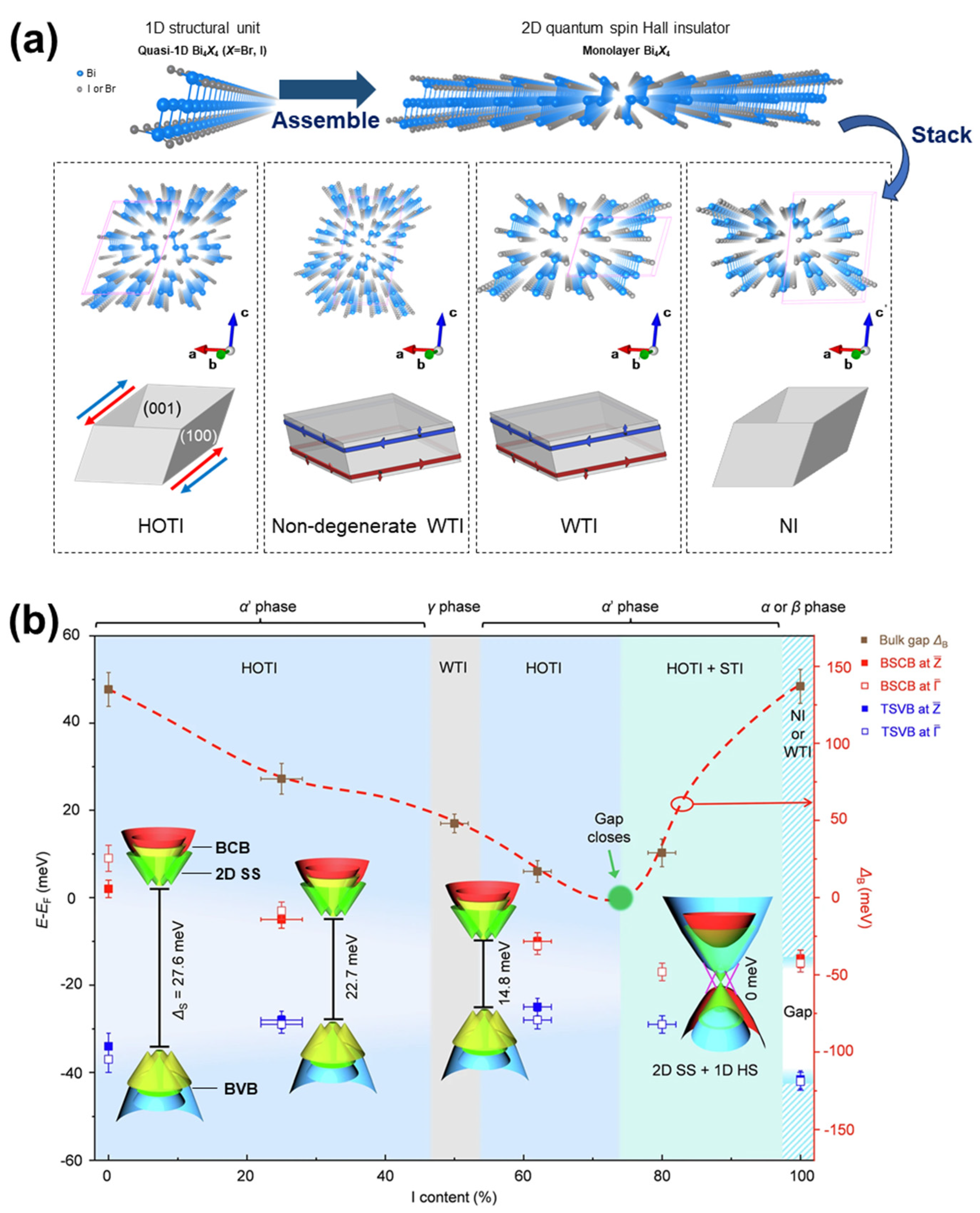
2. Crystal Structure of Bi4X4
3. Quantum Transport Behavior
3.1. Three-Dimensional Transport Behavior
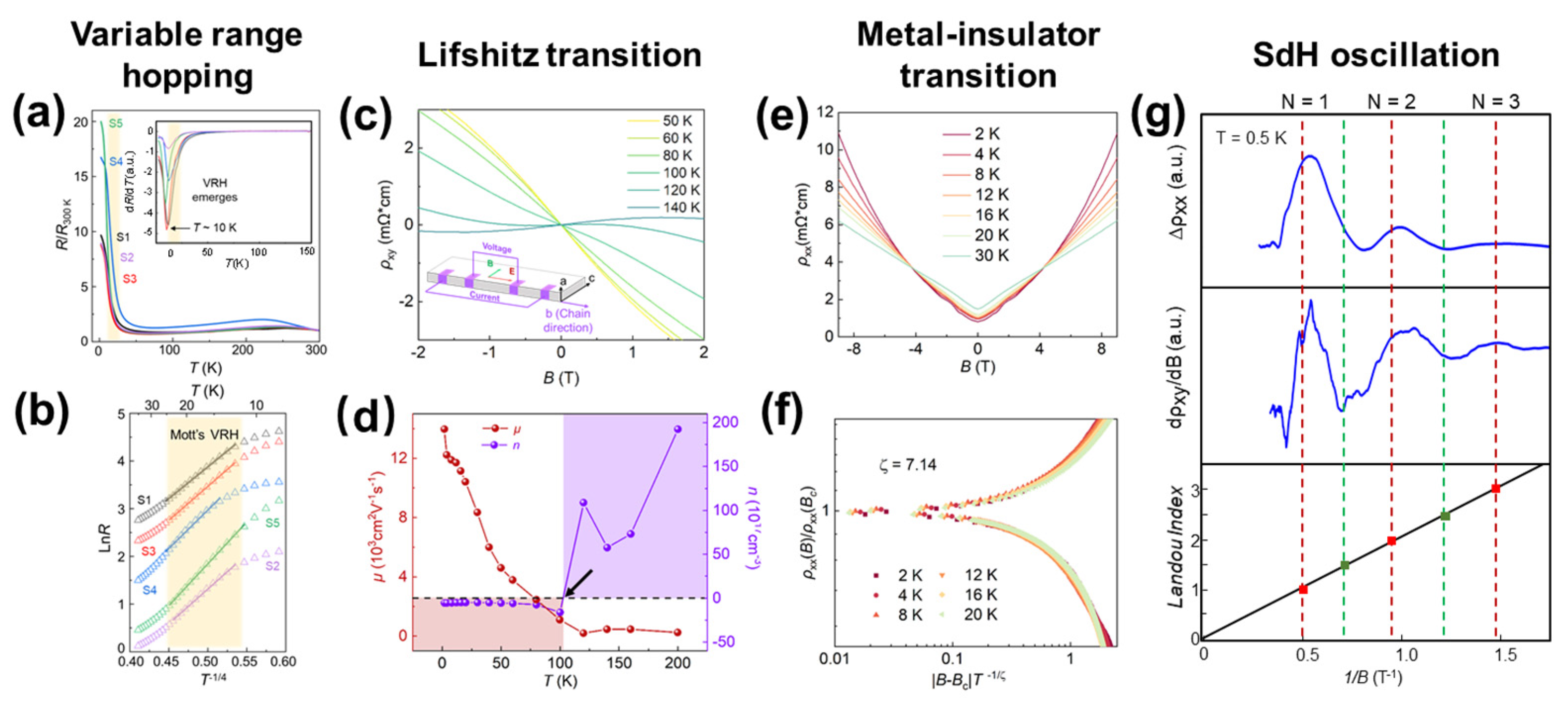
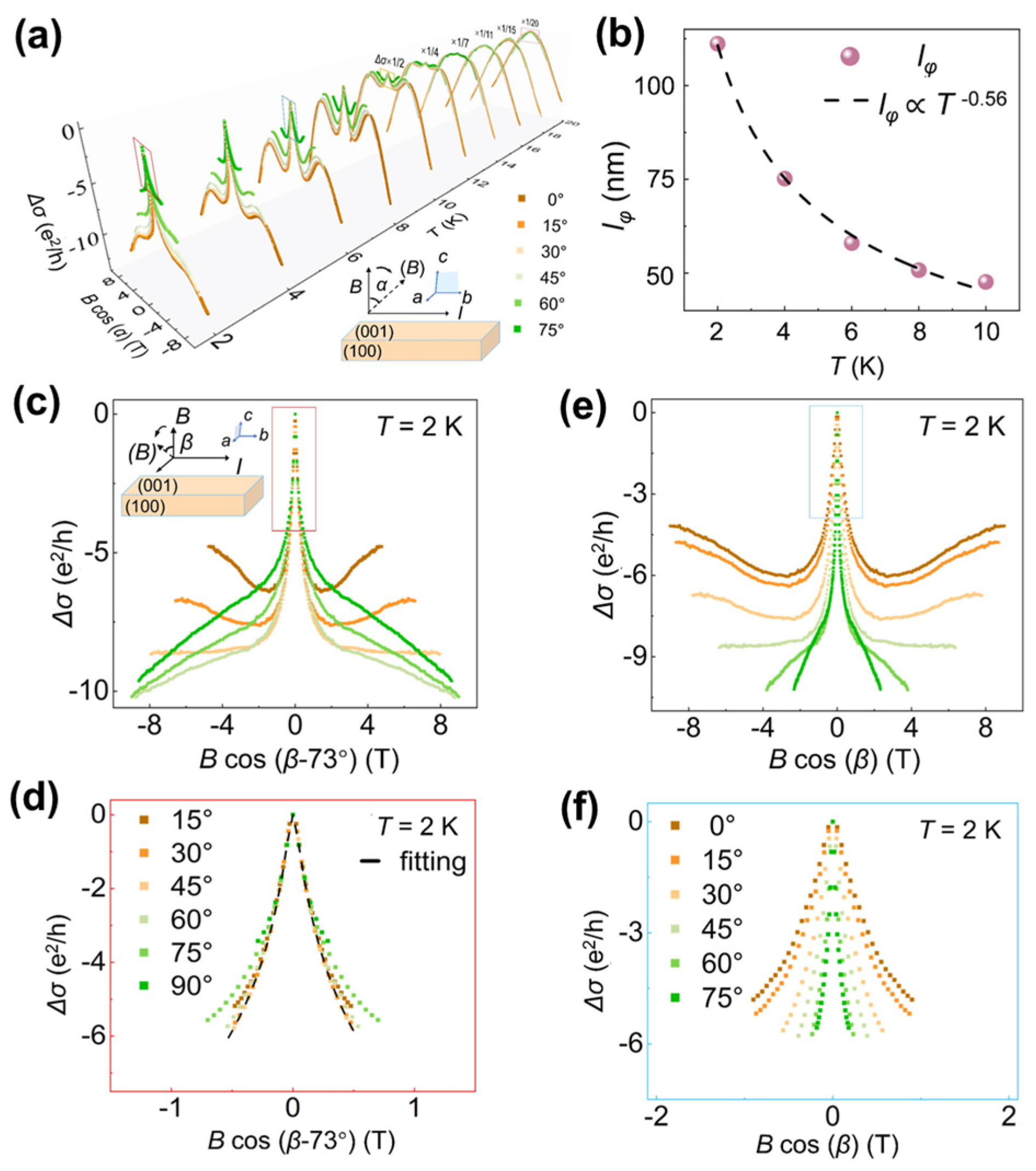
3.2. Two-Dimensional Transport Behavior
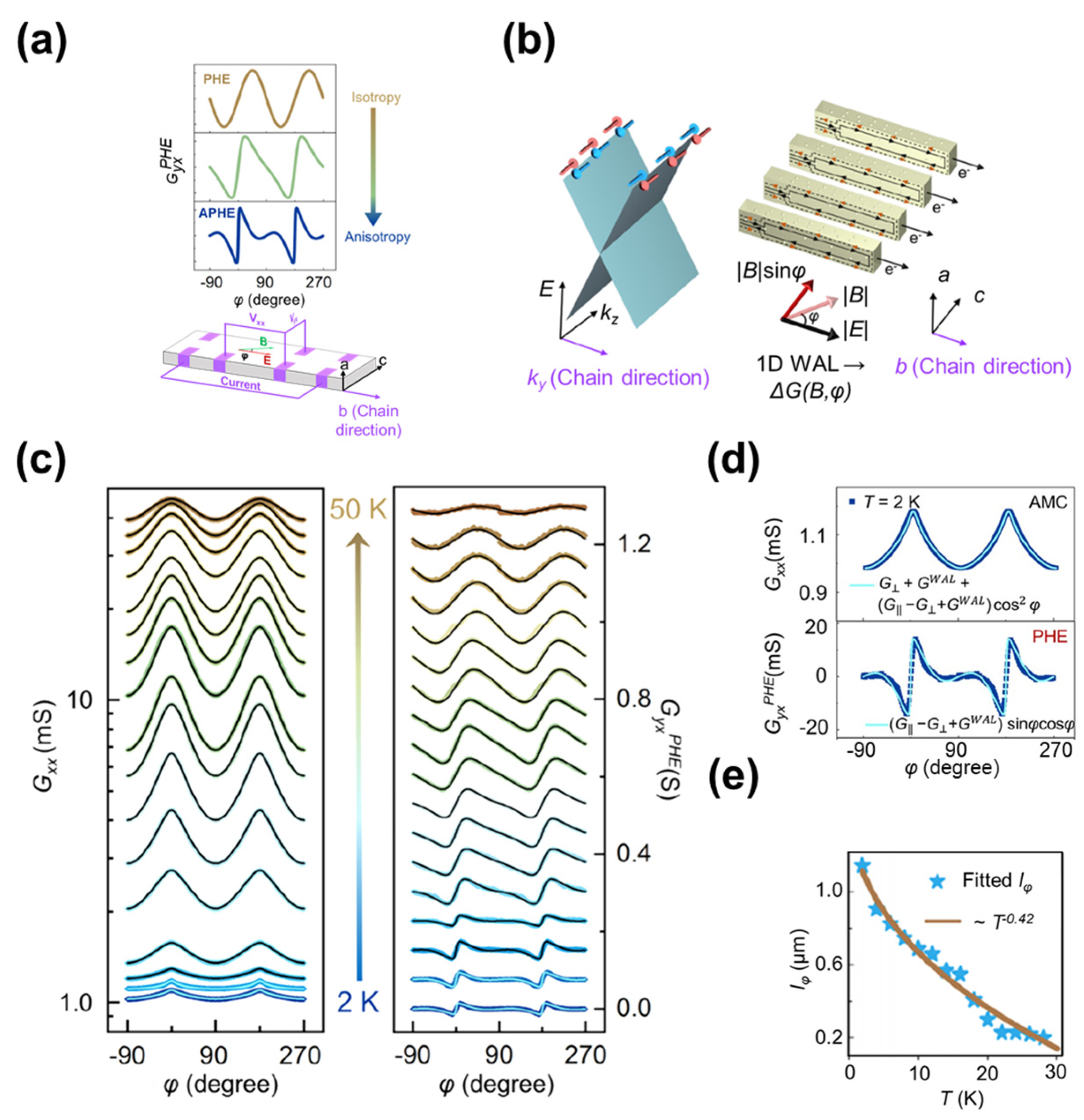
3.3. One-Dimensional Transport Behavior
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, K.-S.; Palumbo, G.; Guo, Z.; Hwang, Y.; Blackburn, J.; Shoemaker, D.P.; Mahmood, F.; Wang, Z.; Fiete, G.A.; Wieder, B.J.; et al. Spin-resolved topology and partial axion angles in three-dimensional insulators. Nat. Commun. 2024, 15, 550. [Google Scholar] [CrossRef]
- Xu, L.; Niu, H.; Bai, Y.; Zhu, H.; Yuan, S.; He, X.; Han, Y.; Zhao, L.; Yang, Y.; Xia, Z.; et al. Shubnikov–de Haas oscillations and nontrivial topological states in Weyl semimetal candidate SmAlSi. J. Phys. Condens. Matter 2022, 34, 485701. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Topological insulators with inversion symmetry. Phys. Rev. B 2007, 76, 045302. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological insulators in three dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef] [PubMed]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.-L.; Zhang, S.-C. Quantum spin Hall insulator state in HgTe quantum wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Xia, Y.; Qian, D.; Wray, L.; Dil, J.H.; Meier, F.; Osterwalder, J.; Patthey, L.; Checkelsky, J.G.; Ong, N.P.; et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 2009, 460, 1101–1105. [Google Scholar] [CrossRef]
- Bradlyn, B.; Elcoro, L.; Cano, J.; Vergniory, M.G.; Wang, Z.; Felser, C.; Aroyo, M.I.; Bernevig, B.A. Topological quantum chemistry. Nature 2017, 547, 298–305. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, J.; Xiao, D.; Yao, Y. Tunable Intrinsic Plasmons due to Band Inversion in Topological Materials. Phys. Rev. Lett. 2017, 119, 266804. [Google Scholar] [CrossRef]
- Jiang, X.; Kang, L.; Wang, J.; Huang, B. Giant Bulk Electrophotovoltaic Effect in Heteronodal-Line Systems. Phys. Rev. Lett. 2023, 130, 256902. [Google Scholar] [CrossRef]
- Yang, L.; Li, L.; Yu, Z.-M.; Wu, M.; Yao, Y. Two-Dimensional Topological Ferroelectric Metal with Giant Shift Current. Phys. Rev. Lett. 2024, 133, 186801. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Huang, J.; Nie, S.; Liu, G.; Liang, A.; Zhang, Y.; Shen, B.; Liu, J.; Hu, C.; et al. Observation of Fermi Arc and Its Connection with Bulk States in the Candidate Type-II Weyl Semimetal WTe2. Phys. Rev. B 2016, 94, 241119. [Google Scholar] [CrossRef]
- Wu, Y.; Mou, D.; Jo, N.H.; Sun, K.; Huang, L.; Bud’ko, S.L.; Canfield, P.C.; Kaminski, A. Observation of Fermi Arcs in the Type-II Weyl Semimetal Candidate WTe2. Phys. Rev. B 2016, 94, 121113. [Google Scholar] [CrossRef]
- Li, P.; Wen, Y.; He, X.; Zhang, Q.; Xia, C.; Yu, Z.-M.; Yang, S.A.; Zhu, Z.; Alshareef, H.N.; Zhang, X.-X. Evidence for Topological Type-II Weyl Semimetal WTe2. Nat. Commun. 2017, 8, 2150. [Google Scholar] [CrossRef] [PubMed]
- Fei, Z.; Zhao, W.; Palomaki, T.A.; Sun, B.; Miller, M.K.; Zhao, Z.; Yan, J.; Xu, X.; Cobden, D.H. Ferroelectric Switching of a Two-Dimensional Metal. Nature 2018, 560, 336–339. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Charles, L.K. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Chang, C.; Liu, C.; MacDonald, A.H. Colloquium: Quantum anomalous hall effect. Rev. Mod. Phys. 2023, 95, 011002. [Google Scholar] [CrossRef]
- Jacak, J.E. Topological approach to electron correlations at fractional quantum Hall effect. Ann. Phys. 2021, 430, 168493. [Google Scholar] [CrossRef]
- Jacak, J.E. Explanation of puzzling FQHE at the filling fraction 3/4 in a band-hole 2D system in GaAs. J. Phys. Condens. Matter 2024, 36, 505601. [Google Scholar] [CrossRef]
- Slager, R.-J.; Mesaros, A.; Juričić, V.; Zaanen, J. The space group classification of topological band-insulators. Nat. Phys. 2013, 9, 98–102. [Google Scholar] [CrossRef]
- Maczewsky, L.J.; Höckendorf, B.; Kremer, M.; Biesenthal, T.; Heinrich, M.; Alvermann, A.; Fehske, H.; Szameit, A. Fermionic time-reversal symmetry in a photonic topological insulator. Nat. Mater. 2020, 19, 855–860. [Google Scholar] [CrossRef]
- Schindler, F.; Cook, A.M.; Vergniory, M.G.; Wang, Z.; Parkin, S.S.P.; Bernevig, B.A.; Neupert, T. Higher-order topological insulators. Sci. Adv. 2018, 4, eaat0346. [Google Scholar] [CrossRef] [PubMed]
- Tan, L.Z.; Rappe, A.M. Enhancement of the Bulk Photovoltaic Effect in Topological Insulators. Phys. Rev. Lett. 2016, 116, 237402. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Li, L.; Sun, S.; Liu, G.; Zhao, H.; Chen, Z.; Yan, X.; Lv, Y.; Yang, Y.; Yao, S.; et al. Probing anisotropic quasiparticle dynamics and topological phase transitions in quasi-1D topological insulator ZrTe5. Adv. Sci. 2025, 12, e04798. [Google Scholar] [CrossRef]
- Youn, S.; Kim, J.; Lee, H.; Kim, D.H.; Bang, J.; Lee, W. Strong anisotropic transport properties of quasi-one-dimensional ZrTe3 nanoribbons. Nano Energy 2024, 127, 109771. [Google Scholar] [CrossRef]
- Xing, J.; Blawat, J.; Speer, S.; Saleheen, A.I.U.; Singleton, J.; Jin, R. Manipulation of the magnetoresistance by strain in topological TaSe3. Quantum Technol. 2022, 5, 2200094. [Google Scholar] [CrossRef]
- Liu, C.C.; Zhou, J.J.; Yao, Y.; Zhang, F. Weak topological insulators and composite Weyl semimetals: β-Bi4X4 (X=Br, I). Phys. Rev. Lett. 2016, 116, 066801. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, R.; Zhang, Z.; Bockrath, M.; Lau, C.N.; Zhou, Y.-F.; Yoon, C.; Li, S.; Liu, X.; Dhale, N.; et al. Gate-tunable transport in quasi-one-dimensional α-Bi4I4 field-effect transistors. Nano Lett. 2022, 22, 1151–1158. [Google Scholar] [CrossRef]
- Zhuang, J.; Li, J.; Liu, Y.; Mu, D.; Yang, M.; Liu, Y.; Zhou, W.; Hao, W.; Zhong, J.; Du, Y. Epitaxial growth of quasi-one-dimensional bismuth-halide chains with atomically sharp topological non-trivial edge states. ACS Nano 2022, 16, 14850–14857. [Google Scholar] [CrossRef]
- Filatova, T.G.; Gurin, P.V.; Kloo, L.; Kulbachinskii, V.A.; Kuznetsov, A.N.; Kytin, V.G.; Lindsjo, M.; Popovkin, B.A. Electronic Structure, Galvanomagnetic and Magnetic Properties of the Bismuth Subhalides Bi4I4 and Bi4Br4. J. Solid State Chem. 2007, 180, 1103–1109. [Google Scholar] [CrossRef]
- Zhang, X.; Xing, X.; Li, J.; Peng, X.; Qiao, L.; Liu, Y.; Xiong, X.; Han, J.; Liu, W.; Xiao, W.; et al. Controllable Epitaxy of Quasi-One-Dimensional Topological Insulator α-Bi4Br4 for the Application of Saturable Absorber. Appl. Phys. Lett. 2022, 120, 171102. [Google Scholar] [CrossRef]
- Autès, G.; Isaeva, A.; Moreschini, L.; Johannsen, J.C.; Pisoni, A.; Mori, R.; Zhang, W.; Filatova, T.G.; Kuznetsov, A.N.; Forró, L.; et al. A novel quasi-one-dimensional topological insulator in bismuth iodide β-Bi4I4. Nat. Mater. 2016, 15, 154–158. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Duan, W. Quasi-1D topological insulators. Nat. Mater. 2016, 15, 129–130. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, R.; Takahashi, T.; Kuroda, K.; Ochi, M.; Shirasawa, T.; Sakano, M.; Bareille, C.; Nakayama, M.; Watson, M.D.; Yaji, K.; et al. A weak topological insulator state in quasi-one-dimensional bismuth iodide. Nature 2019, 566, 518–522. [Google Scholar] [CrossRef]
- Noguchi, R.; Kobayashi, M.; Jiang, Z.Z.; Kuroda, K.; Takahashi, T.; Xu, Z.F.; Lee, D.; Hirayama, M.; Ochi, M.; Shirasawa, T.; et al. Evidence for a higher-order topological insulator in a three-dimensional material built from van der Waals stacking of bismuth-halide chains. Nat. Mater. 2021, 20, 473–479. [Google Scholar] [CrossRef]
- Huang, J.W.; Li, S.; Yoon, C.; Oh, J.S.; Wu, H.; Liu, X.Y.; Dhale, N.; Zhou, Y.F.; Guo, Y.C.; Zhang, Y.C.; et al. Room-temperature topological phase transition in quasi-one-dimensional material Bi4I4. Phys. Rev. B 2021, 106, 031042. [Google Scholar] [CrossRef]
- Zhao, W.X.; Yang, M.; Xu, R.Z.; Du, X.; Li, Y.D.; Zhai, K.Y.; Peng, C.; Pei, D.; Gao, H.; Li, Y.W.; et al. Topological electronic structure and spin texture of quasi-one-dimensional higher-order topological insulator Bi4Br4. Nat. Commun. 2023, 14, 8089. [Google Scholar] [CrossRef]
- Noguchi, R.; Kobayashi, M.; Kawaguchi, K.; Yamamori, W.; Aido, K.; Lin, C.; Tanaka, H.; Kuroda, K.; Harasawa, A.; Kandyba, V.; et al. Robust weak topological insulator in the bismuth halide Bi4Br2I2. Phys. Rev. Lett. 2024, 133, 086602. [Google Scholar] [CrossRef]
- Zhao, W.X.; Yang, M.; Du, X.; Li, Y.D.; Zhai, K.Y.; Hu, Y.Q.; Han, J.F.; Huang, Y.; Liu, Z.K.; Yao, Y.G.; et al. Topological phase transition in quasi-one-dimensional bismuth iodide Bi4I4. npj Quantum Mater. 2024, 9, 103. [Google Scholar] [CrossRef]
- Zhong, J.; Yang, M.; Zhao, W.; Zhai, K.; Zhen, X.; Zhang, L.; Mu, D.; Liu, Y.; Shi, Z.; Cheng, N.; et al. Coalescence of multiple topological orders in quasi-one-dimensional bismuth halide chains. Nat. Commun. 2025, 16, 1163. [Google Scholar] [CrossRef]
- Oh, J.S.; Xu, T.; Dhale, N.; Li, S.; Lei, C.; Yoon, C.; Liu, W.; Huang, J.; Wu, H.; Hashimoto, M.; et al. Ideal Weak Topological Insulator and Protected Helical Saddle Points. Phys. Rev. B 2023, 108, L201104. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Feng, W.; Liu, C.-C.; Guan, S.; Yao, Y. Large-gap quantum spin Hall insulator in single layer bismuth monobromide Bi4Br4. Nano Lett. 2014, 14, 4767–4771. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Liu, Y.; Zhou, W.; Liu, C.; Mu, D.; Liu, Y.; Wang, J.; Hao, W.; Li, J.; Zhong, J.; et al. Large-Gap Quantum Spin Hall State and Temperature-Induced Lifshitz Transition in Bi4Br4. ACS Nano 2022, 16, 3036–3044. [Google Scholar] [CrossRef] [PubMed]
- Shumiya, N.; Hossain, M.S.; Yin, J.-X.; Wang, Z.; Litskevich, M.; Yoon, C.; Li, Y.; Yang, Y.; Jiang, Y.-X.; Cheng, G.; et al. Evidence of a room-temperature quantum spin Hall edge state in a higher-order topological insulator. Nat. Mater. 2022, 21, 1111–1115. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, W.; Mu, D.; Shi, Z.; Zhong, J.; Li, Y.; Liu, Y.; Zhong, J.; Cheng, N.; Zhou, W.; et al. Mass acquisition of Dirac fermions in Bi4I4 by spontaneous symmetry breaking. Phys. Rev. Lett. 2024, 133, 256601. [Google Scholar] [CrossRef]
- Zhong, J.; Yang, M.; Shi, Z.; Li, Y.; Mu, D.; Liu, Y.; Cheng, N.; Zhao, W.; Hao, W.; Wang, J.; et al. Towards layer-selective quantum spin Hall channels in weak topological insulator Bi4Br2I2. Nat. Commun. 2023, 14, 4964. [Google Scholar] [CrossRef]
- Zhong, J.; Yang, M.; Ye, F.; Liu, C.; Wang, J.; Wang, J.; Hao, W.; Zhuang, J.; Du, Y. Facet-dependent electronic quantum diffusion in the high-order topological insulator Bi4Br4. Phys. Rev. Appl. 2022, 17, 064017. [Google Scholar] [CrossRef]
- Zhong, J.; Yang, M.; Wang, J.; Li, Y.; Liu, C.; Mu, D.; Liu, Y.; Cheng, N.; Shi, Z.; Yang, L.; et al. Observation of anomalous planar Hall effect induced by one-dimensional weak antilocalization. ACS Nano 2024, 18, 4343–4351. [Google Scholar] [CrossRef]
- Hossain, M.S.; Zhang, Q.; Wang, Z.; Dhale, N.; Liu, W.; Litskevich, M.; Casas, B.; Shumiya, N.; Yin, J.-X.; Cochran, T.A.; et al. Quantum transport response of topological hinge modes. Nat. Phys. 2024, 20, 776–782. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Feng, W.; Liu, G.-B.; Yao, Y. Topological Edge States in Single- and Multi-Layer Bi4Br4. New J. Phys. 2015, 17, 015004. [Google Scholar] [CrossRef]
- Gong, Z.; Lai, X.; Miao, W.; Zhong, J.; Shi, Z.; Shen, H.; Liu, X.; Li, Q.; Yang, M.; Zhuang, J.; et al. Br-vacancies induced variable ranging hopping conduction in high-order topological insulator Bi4Br4. Small Methods 2024, 8, 2400517. [Google Scholar] [CrossRef]
- Mu, D.; Zhou, W.; Liu, Y.; Li, J.; Yang, M.; Zhuang, J.; Du, Y.; Zhong, J. Resolving the intrinsic bandgap and edge effect of BiI3 film epitaxially grown on graphene. Mater. Today Phys. 2021, 20, 100454. [Google Scholar] [CrossRef]
- Cassemiro, G.H.; Hinostroza, C.D.; de Faria, L.R.; Mayoh, D.A.; Liu, J.; Aguiar, M.C.O.; Lees, M.R.; Balakrishnan, G.; Larrea Jiménez, J.; da Silva Machado, A.J.; et al. Role of native point defects and Hg impurities in the electronic properties of Bi4I4. Phys. Rev. B 2024, 110, 224113. [Google Scholar] [CrossRef]
- Hinostroza, C.D.; de Faria, L.R.; Cassemiro, G.H.; Larrea Jiménez, J.; da Silva Machado, A.J.; Brito, W.H.; Martelli, V. Structural investigation of the quasi-one-dimensional topological insulator Bi4I4. Phys. Rev. B 2024, 109, 174105. [Google Scholar] [CrossRef]
- Mott, N.F. Conduction in glasses containing transition metal ions. J. Non-Cryst. Solids 1968, 1, 1. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, O.; Levy, M.; Sarachik, M.P. Probind the coulomb gap in insulating n-type CdSe. Phys. Rev. Lett. 1990, 64, 2687. [Google Scholar] [CrossRef]
- Shlimak, I.; Kaveh, M.; Yosefin, M.; Lea, M.; Fozooni, P. Crossover phenomenon for hopping conduction in strong magnetic fields. Phys. Rev. Lett. 1992, 68, 3076. [Google Scholar] [CrossRef]
- Li, X.; Chen, D.; Jin, M.; Ma, D.; Ge, Y.; Sun, J.; Guo, W.; Sun, H.; Han, J.; Xiao, W.; et al. Pressure-induced phase transitions and superconductivity in a quasi–1-dimensional topological crystalline insulator α-Bi4Br4. Proc. Natl. Acad. Sci. USA 2019, 116, 17696–17700. [Google Scholar] [CrossRef]
- Pisoni, A.; Gaál, R.; Zeugner, A.; Falkowski, V.; Isaeva, A.; Huppertz, H.; Autès, G.; Yazyev, O.V.; Forró, L. Pressure Effect and Superconductivity in the β-Bi4I4 Topological Insulator. Phys. Rev. B 2017, 95, 235149. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.; Wang, J.; Chen, T.; Gao, H.; Lu, P.; Chen, Q.; Ding, C.; Wen, J.; Sun, J. Pressure-Induced Structural and Electronic Transitions in Bismuth Iodide. Phys. Rev. B 2018, 98, 174112. [Google Scholar] [CrossRef]
- Qi, Y.; Shi, W.; Werner, P.; Naumov, P.G.; Schnelle, W.; Wang, L.; Rana, K.G.; Parkin, S.; Medvedev, S.A.; Yan, B.; et al. Pressure-Induced Superconductivity and Topological Quantum Phase Transitions in a Quasi-One-Dimensional Topological Insulator: Bi4I4. npj Quantum Mater. 2018, 3, 4. [Google Scholar] [CrossRef]
- Chen, D.-Y.; Ma, D.; Duan, J.; Chen, D.; Liu, H.; Han, J.; Yao, Y. Quantum transport evidence of boundary states and Lifshitz transition in Bi4Br4. Phys. Rev. B 2022, 106, 075206. [Google Scholar] [CrossRef]
- Wang, P.; Tang, F.; Wang, P.; Zhu, H.; Cho, C.-W.; Wang, J.; Du, X.; Shao, Y.; Zhang, L. Quantum transport properties of β-Bi4I4 near and well beyond the extreme quantum limit. Phys. Rev. B 2021, 103, 155201. [Google Scholar] [CrossRef]
- Gvozdikov, V.M. The Landau band effects in the quantum magnetic oscillations and the deviations from the quasiclassical Lifshitz–Kosevich theory in quasi-two-dimensional conductors. Low Temp. Phys. 2011, 37, 964–974. [Google Scholar] [CrossRef]
- Gong, Z.; Zhong, J.; Li, Q.; Shen, H.; Zhuang, J.; Du, Y. Identification of Lifshitz transition, quantum oscillations, and metal-insulator transition in a composite topological matter Bi4(Br0.2I0.8)4. Sustain. Mater. Technol. 2025, 45, e01438. [Google Scholar] [CrossRef]
- Chen, D.-Y.; Ma, D.-S.; Li, Y.; Du, Z.Z.; Xiong, X.; He, Y.; Duan, J.; Han, J.; Chen, D.; Xiao, W.; et al. Quantum Transport Properties in Single Crystals of α-Bi4I4. Phys. Rev. Mater. 2018, 2, 114408. [Google Scholar] [CrossRef]
- Wang, J.; Yang, H.; Ding, L.; You, W.; Xi, C.; Cheng, J.; Shi, Z.; Cao, C.; Luo, Y.; Zhu, Z.; et al. Angle-dependent magnetoresistance and its implications for Lifshitz transition in W2As3. npj Quantum Mater. 2019, 4, 58. [Google Scholar] [CrossRef]
- Sharma, M.M.; Chhetri, S.K.; Acharya, G.; Graf, D.; Upreti, D.; Dahal, S.; Nabi, M.R.U.; Rahman, S.; Sakon, J.; Churchill, H.O.H.; et al. Quantum oscillation studies of the nodal line semimetal Ni3In2S2−xSex. Acta Mater. 2025, 289, 120884. [Google Scholar] [CrossRef]
- Wu, S.; Ren, Z.; Zhang, Y.; Li, Y.; Han, J.; Duan, J.; Wang, Z.; Li, C.; Yao, Y. Gate-tunable transport in van der Waals topological insulator Bi4Br4 nanobelts. J. Phys. Condens. Matter 2023, 35, 234001. [Google Scholar] [CrossRef]
- Akiyama, R.; Fujisawa, K.; Yamaguchi, T.; Ishikawa, R.; Kuroda, S. Two-dimensional quantum transport of multivalley (111) surface state in topological crystalline insulator SnTe thin films. Nano Res. 2016, 9, 490–498. [Google Scholar] [CrossRef]
- Liu, M.; Chang, C.Z.; Zhang, Z.; Zhang, Y.; Ruan, W.; He, K.; Wang, L.L.; Chen, X.; Jia, J.F.; Zhang, S.C.; et al. Electron interaction-driven insulating ground state in Bi2Se3 topological insulators in the two-dimensional limit. Phys. Rev. B 2011, 83, 165440. [Google Scholar] [CrossRef]
- Checkelsky, J.G.; Hor, Y.S.; Cava, R.J.; Ong, N.P. Bulk band gap and surface state conduction observed in voltage-tuned crystals of the topological insulator Bi2Se3. Phys. Rev. Lett. 2011, 106, 196801. [Google Scholar] [CrossRef] [PubMed]
- Shekhar, C.; Nayak, A.K.; Sun, Y.; Schmidt, M.; Nicklas, M.; Leermakers, I.; Zeitler, U.; Skourski, Y.; Wosnitza, J.; Liu, Z.; et al. Extremely large nonsaturating magnetoresistance and ultrahigh mobility due to topological surface states in the metallic Bi2Te3 topological insulator. Phys. Rev. B 2017, 95, 195113. [Google Scholar]
- Lu, H.-Z.; Shen, S.-Q. Weak localization of bulk channels in topological insulator thin films. Phys. Rev. B. 2011, 84, 125138. [Google Scholar] [CrossRef]
- Hsu, Y.-W.; Chiu, S.-P.; Lien, A.-S.; Lin, J.-J. Long electron dephasing length and disorder-induced spin-orbit coupling in indium tin oxide nanowires. Phy. Rev. B 2010, 82, 195429. [Google Scholar] [CrossRef]
- Hikami, S.; Larkin, A.I.; Nagaoka, Y. Spin-orbit interaction and magnetoresistance in the two-dimensional random system. Prog. Theor. Phys. 1980, 63, 707. [Google Scholar] [CrossRef]
- Sharma, M.M.; Rani, P.; Awana, V.P.S. Probing the topological surface states in superconducting Sn4Au single crystal: A magneto transport study. J. Phys. Condens. Matter 2022, 34, 415701. [Google Scholar] [CrossRef]
- Lee, P.A.; Ramakrishnan, T.V. Disordered electronic systems. Rev. Mod. Phys. 1985, 57, 287. [Google Scholar] [CrossRef]
- Thouless, D.J. Maximum metallic resistance in thin wires. Phys. Rev. Lett. 1977, 39, 1167. [Google Scholar] [CrossRef]
- Kazakov, A.; Brzezicki, W.; Hyart, T.; Turowski, B.; Polaczyński, J.; Adamus, Z.; Aleszkiewicz, M.; Wojciechowski, T.; Domagala, J.Z.; Caha, O.; et al. Signatures of dephasing by mirror-symmetry breaking in weak-antilocalization magnetoresistance across the topological transition in Pb1−xSnxSe. Phys. Rev. B 2021, 103, 245307. [Google Scholar] [CrossRef]
- Nandy, S.; Sharma, G.; Taraphder, A.; Tewari, S. Chiral Anomaly as the Origin of the Planar Hall Effect in Weyl Semimetals. Phys. Rev. Lett. 2017, 119, 176804. [Google Scholar] [CrossRef]
- Taskin, A.A.; Legg, H.F.; Yang, F.; Sasaki, S.; Kanai, Y.; Matsumoto, K.; Rosch, A.; Ando, Y. Planar Hall effect from the surface of topological insulators. Nat. Commun. 2017, 8, 1340. [Google Scholar] [CrossRef]
- Kumar, N.; Guin, S.N.; Felser, C.; Shekhar, C. Planar Hall effect in the Weyl semimetal GdPtBi. Phys. Rev. B 2018, 98, 041103. [Google Scholar] [CrossRef]
- Li, H.; Wang, H.; He, H.; Wang, J.; Shen, S. Giant anisotropic magnetoresistance and planar Hall effect in the Dirac semimetal Cd3As2. Phys. Rev. B 2018, 97, 201110. [Google Scholar] [CrossRef]
- Li, P.; Zhang, C.; Zhang, J.; Wen, Y.; Zhang, X. Giant planar Hall effect in the Dirac semimetal ZrTe5-δ. Phys. Rev. B 2018, 98, 121108. [Google Scholar] [CrossRef]
- Wu, M.; Zheng, G.; Chu, W.; Liu, Y.; Gao, W.; Zhang, H.; Lu, J.; Han, Y.; Zhou, J.; Ning, W.; et al. Probing the chiral anomaly by planar Hall effect in Dirac semimetal Cd3As2 nanoplates. Phys. Rev. B 2018, 98, 161110. [Google Scholar] [CrossRef]
- Liu, Q.; Fei, F.; Chen, B.; Bo, X.; Wei, B.; Zhang, S.; Zhang, M.; Xie, F.; Naveed, M.; Wan, X.; et al. Nontopological origin of the planar Hall effect in the type-II Dirac semimetal NiTe2. Phys. Rev. B 2019, 99, 155119. [Google Scholar] [CrossRef]
- Burkov, A.A. Giant planar Hall effect in topological metals. Phys. Rev. B 2017, 96, 041110. [Google Scholar] [CrossRef]
- Liu, J.Y.; Hu, J.; Graf, D.; Zou, T.; Zhu, M.; Shi, Y.; Che, S.; Radmanesh, S.M.A.; Lau, C.N.; Spinu, L.; et al. Unusual interlayer quantum transport behavior caused by the zeroth Landau level in YbMnBi2. Nat. Commun. 2017, 8, 646. [Google Scholar] [CrossRef]
- Liang, D.; Sakr, M.R.; Gao, X. One-Dimensional Weak Localization of Electrons in a Single InAs Nanowire. Nano Lett. 2009, 9, 1709–1712. [Google Scholar] [CrossRef]
- Beenakker, C.W.J.; van Houten, H. Boundary scattering and weak localization of electrons in a magnetic field. Phys. Rev. B 1988, 38, 3232–3240. [Google Scholar] [CrossRef]
- Karn, N.K.; Sharma, M.M.; Awana, V.P.S. Weak antilocalization and topological edge states in PdSn4. J. Appl. Phys. 2023, 133, 17. [Google Scholar] [CrossRef]
- Okamoto, M.; Takane, Y.; Imura, K.I. One-dimensional topological insulator: A model for studying finite-size effects in topological insulator thin films. Phys. Rev. B 2024, 89, 125425. [Google Scholar] [CrossRef]
- Guo, H. A brief review on one-dimensional topological insulators and superconductors. Sci. China Phys. Mech. Astron. 2016, 59, 637401. [Google Scholar] [CrossRef]
- Yu, S.; Deng, J.; Liu, W.; Zhang, Y.; Sun, Y.; Dhale, N.; Li, S.; Ma, W.; Wang, Z.; Wu, P.; et al. Observation of robust one-dimensional edge channels in a three-dimensional quantum spin Hall insulator. Phys. Rev. X 2024, 14, 041048. [Google Scholar] [CrossRef]
- Amet, F.; Ke, C.T.; Borzenets, I.V.; Wang, J.; Watanabe, K.; Taniguchi, T.; Deacon, R.S.; Yamamoto, M.; Bomze, Y.; Tarucha, S.; et al. Supercurrent in the quantum Hall regime. Science 2016, 352, 966–969. [Google Scholar] [CrossRef]
- Calado, V.E.; Goswami, S.; Nanda, G.; Diez, M.; Akhmerov, A.R.; Watanabe, K.; Taniguchi, T.; Klapwijk, T.M.; Vandersypen, L.M.K. Ballistic Josephson junctions in edge-contacted graphene. Nat. Nanotechnol. 2015, 10, 761–764. [Google Scholar] [CrossRef]
- Shalom, M.B.; Zhu, M.J.; Fal’ko, V.I.; Mishchenko, A.; Kretinin, A.V.; Novoselov, K.S.; Woods, C.R.; Watanabe, K.; Taniguchi, T.; Geim, A.K.; et al. Quantum oscillations of the critical current and high-field superconducting proximity in ballistic graphene. Nat. Phys. 2016, 12, 318–322. [Google Scholar] [CrossRef]
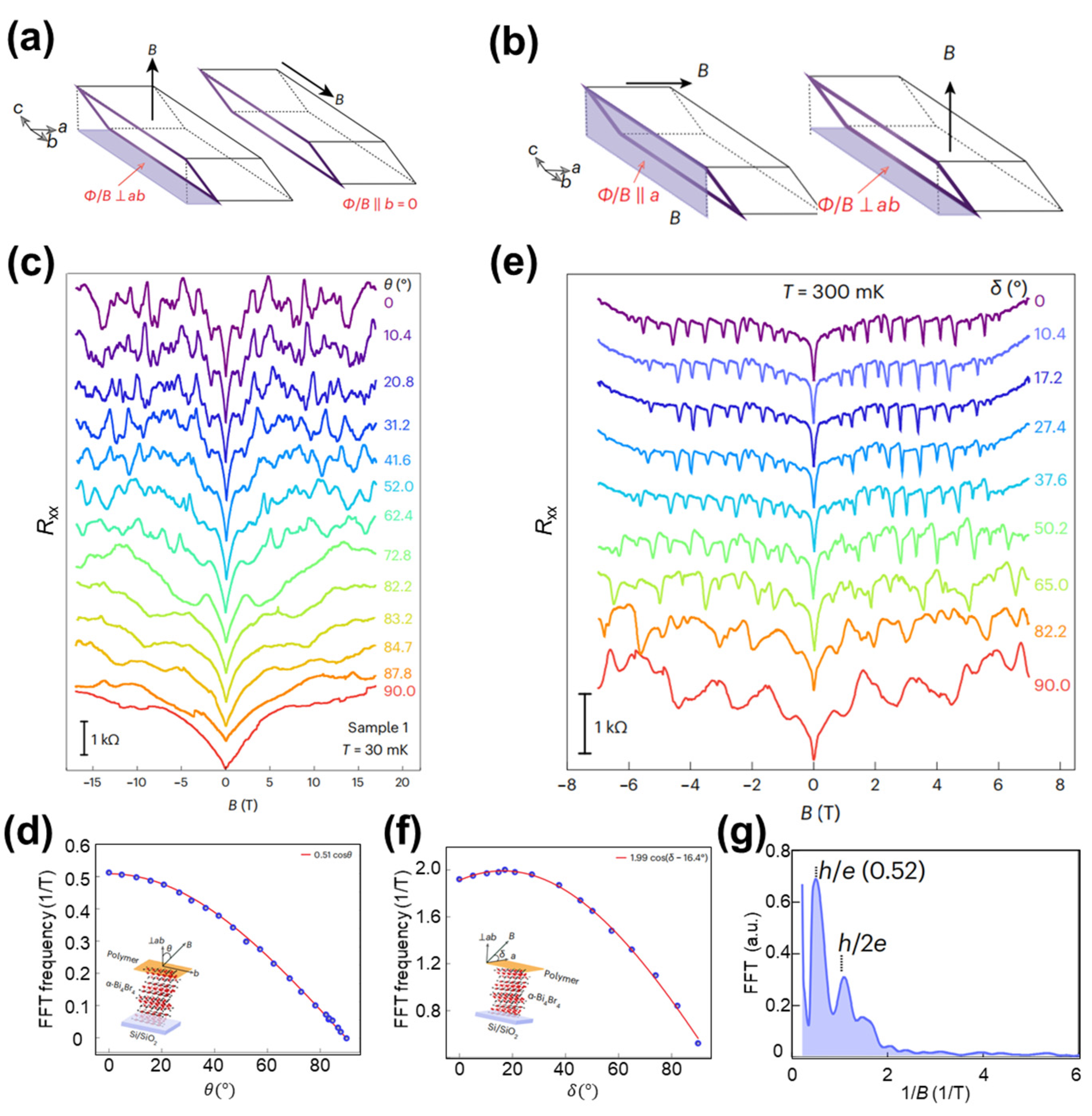
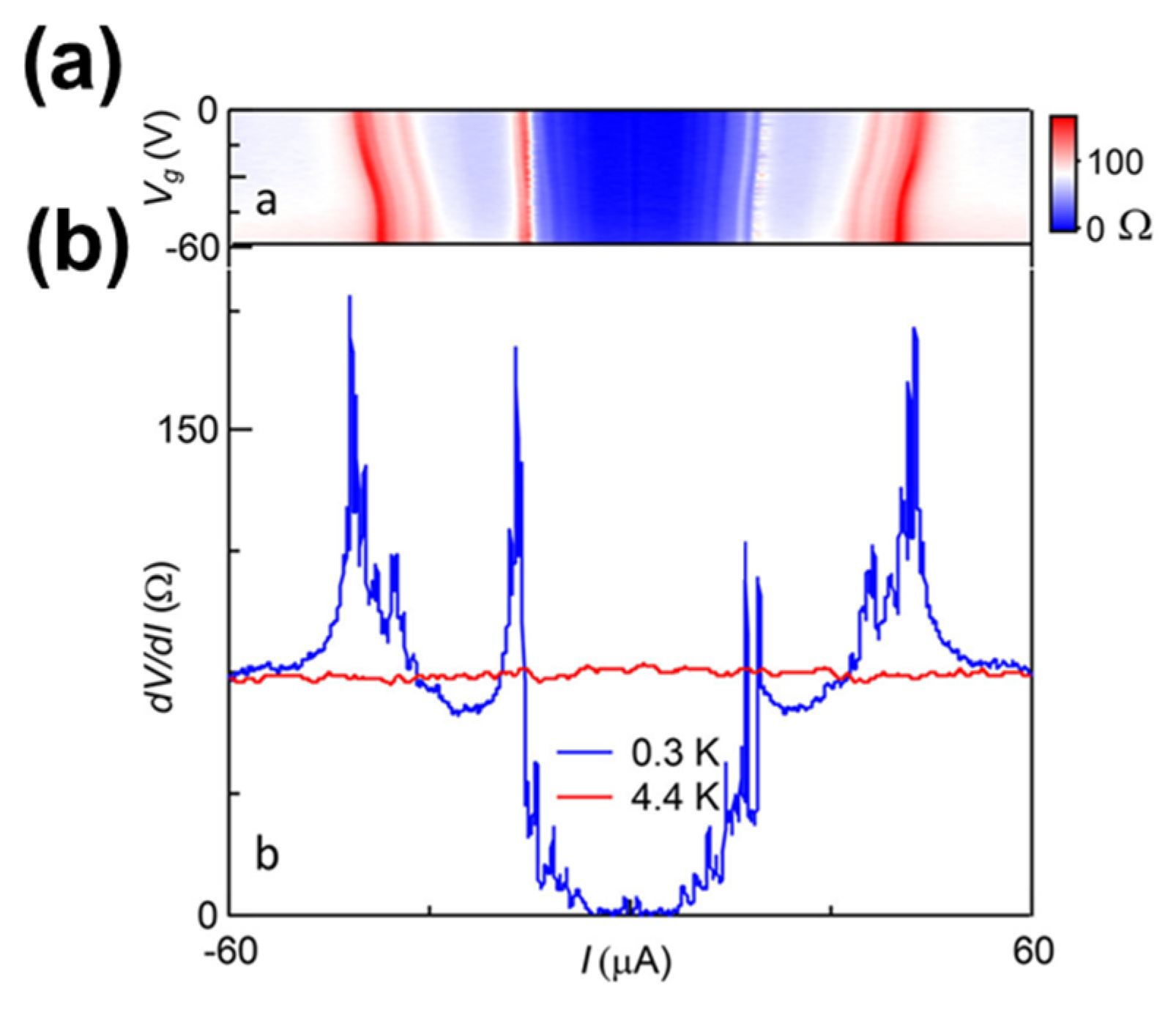
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Z.; Zhong, J.; Li, Q.; Shen, H.; Zhuang, J.; Du, Y. Quantum Transport Behavior in Quasi-One-Dimensional Topological Matter Bi4X4 (X = Br, I). Physchem 2025, 5, 47. https://doi.org/10.3390/physchem5040047
Gong Z, Zhong J, Li Q, Shen H, Zhuang J, Du Y. Quantum Transport Behavior in Quasi-One-Dimensional Topological Matter Bi4X4 (X = Br, I). Physchem. 2025; 5(4):47. https://doi.org/10.3390/physchem5040047
Chicago/Turabian StyleGong, Zixin, Jingyuan Zhong, Qiyi Li, Huayi Shen, Jincheng Zhuang, and Yi Du. 2025. "Quantum Transport Behavior in Quasi-One-Dimensional Topological Matter Bi4X4 (X = Br, I)" Physchem 5, no. 4: 47. https://doi.org/10.3390/physchem5040047
APA StyleGong, Z., Zhong, J., Li, Q., Shen, H., Zhuang, J., & Du, Y. (2025). Quantum Transport Behavior in Quasi-One-Dimensional Topological Matter Bi4X4 (X = Br, I). Physchem, 5(4), 47. https://doi.org/10.3390/physchem5040047





