Figure 1.
A graphene lattice showing the unit cell and primitive lattice vectors.
Figure 1.
A graphene lattice showing the unit cell and primitive lattice vectors.
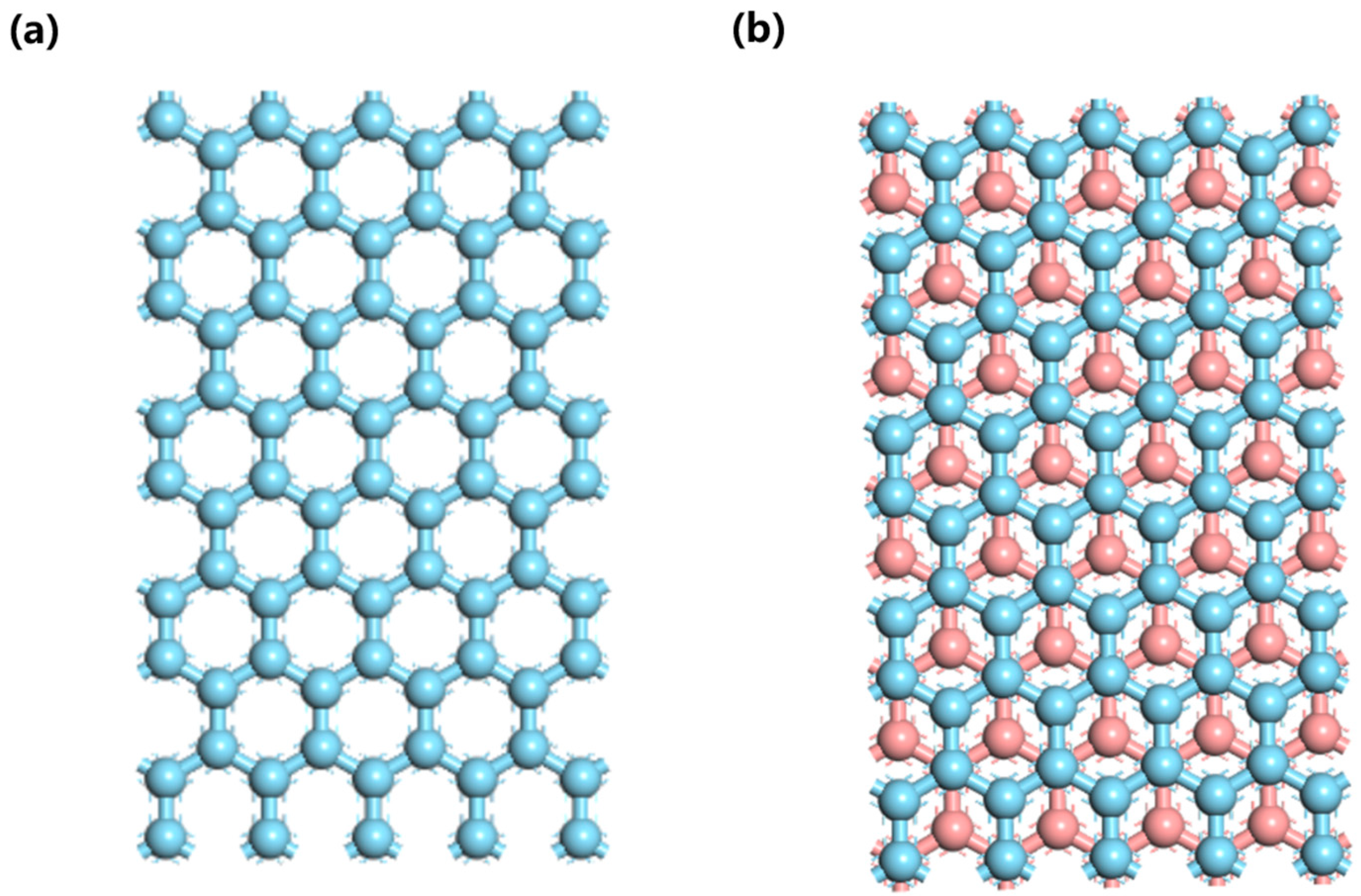
Figure 2.
The graphene model, constructed by Materials Studio, displays the hexagonal lattice of graphene. The blue and red atoms are represented as C atoms. (a) A top view of a single layer of graphene is shown here. (b) The figure above depicts a top view of an AB stacked bilayer of graphite. In this configuration, the second layer is shifted by one bond length with respect to the first layer along one of the basis vectors of the honeycomb lattice.
Figure 2.
The graphene model, constructed by Materials Studio, displays the hexagonal lattice of graphene. The blue and red atoms are represented as C atoms. (a) A top view of a single layer of graphene is shown here. (b) The figure above depicts a top view of an AB stacked bilayer of graphite. In this configuration, the second layer is shifted by one bond length with respect to the first layer along one of the basis vectors of the honeycomb lattice.
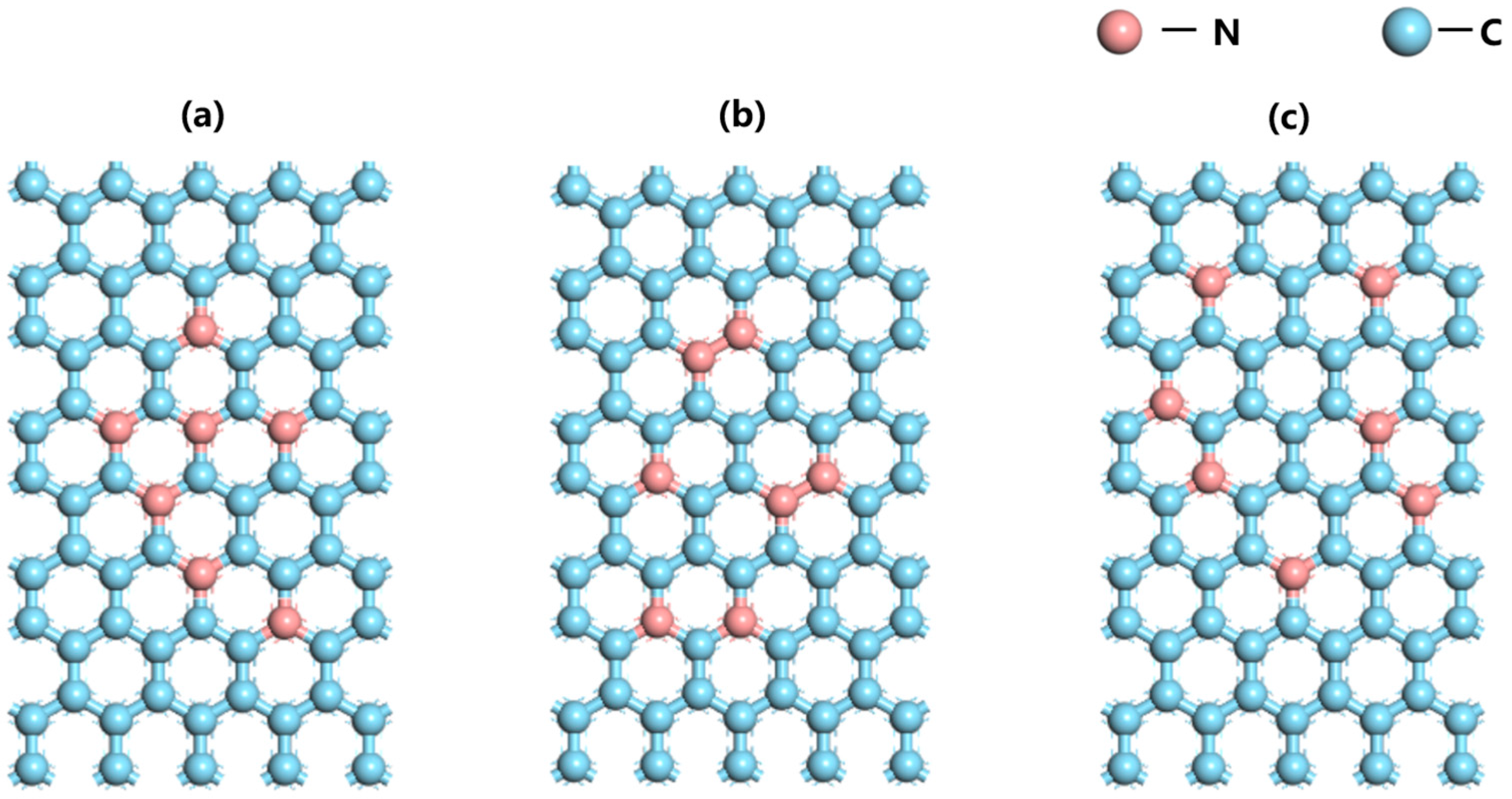
Figure 3.
(a–c) represent three random structures of graphene with a 5.2% N doping rate, respectively, with random N doping positions. The crystal structure was constructed using Materials Studio, where the red atoms are N atoms and the blue atoms are C atoms.
Figure 3.
(a–c) represent three random structures of graphene with a 5.2% N doping rate, respectively, with random N doping positions. The crystal structure was constructed using Materials Studio, where the red atoms are N atoms and the blue atoms are C atoms.
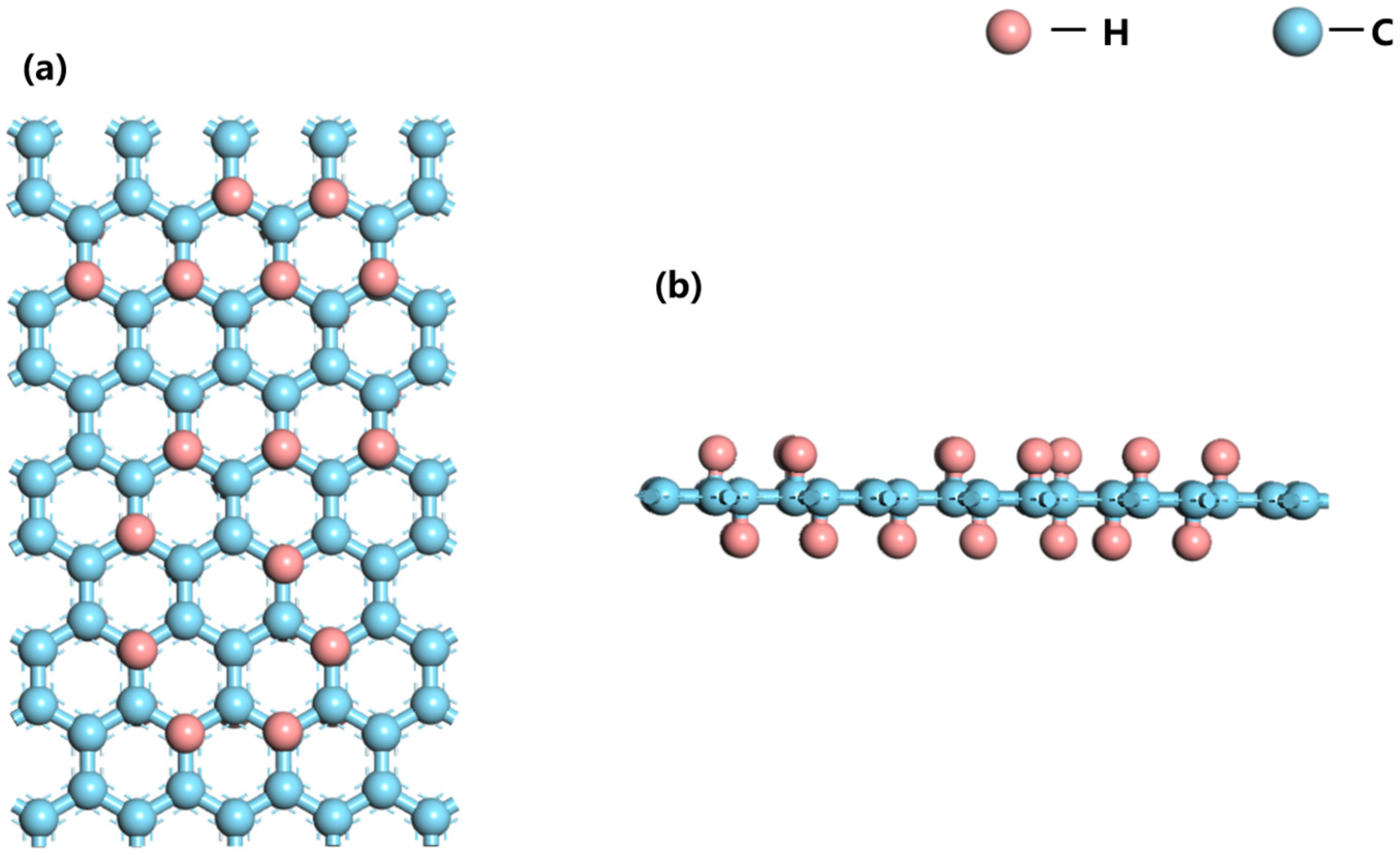
Figure 4.
Chair conformation of partially hydrogenated graphene with 39% hydrogen absorption, model constructed by Materials studio, can be observed as a hexagonal lattice of graphene sp3-hybridized, where the red atoms are the H atoms and the blue atoms are the C atoms: (a) top view (b) side view.
Figure 4.
Chair conformation of partially hydrogenated graphene with 39% hydrogen absorption, model constructed by Materials studio, can be observed as a hexagonal lattice of graphene sp3-hybridized, where the red atoms are the H atoms and the blue atoms are the C atoms: (a) top view (b) side view.
Figure 5.
(a–c) illustrate the training set data distributions for graphene with an external electric field, N-doped graphene, and H-adsorbed graphene, respectively, when the number of bins is 10. (d–f) illustrate the data distributions when the number of bins is 12. The vertical axis of the graph represents the number of data samples in each interval.
Figure 5.
(a–c) illustrate the training set data distributions for graphene with an external electric field, N-doped graphene, and H-adsorbed graphene, respectively, when the number of bins is 10. (d–f) illustrate the data distributions when the number of bins is 12. The vertical axis of the graph represents the number of data samples in each interval.
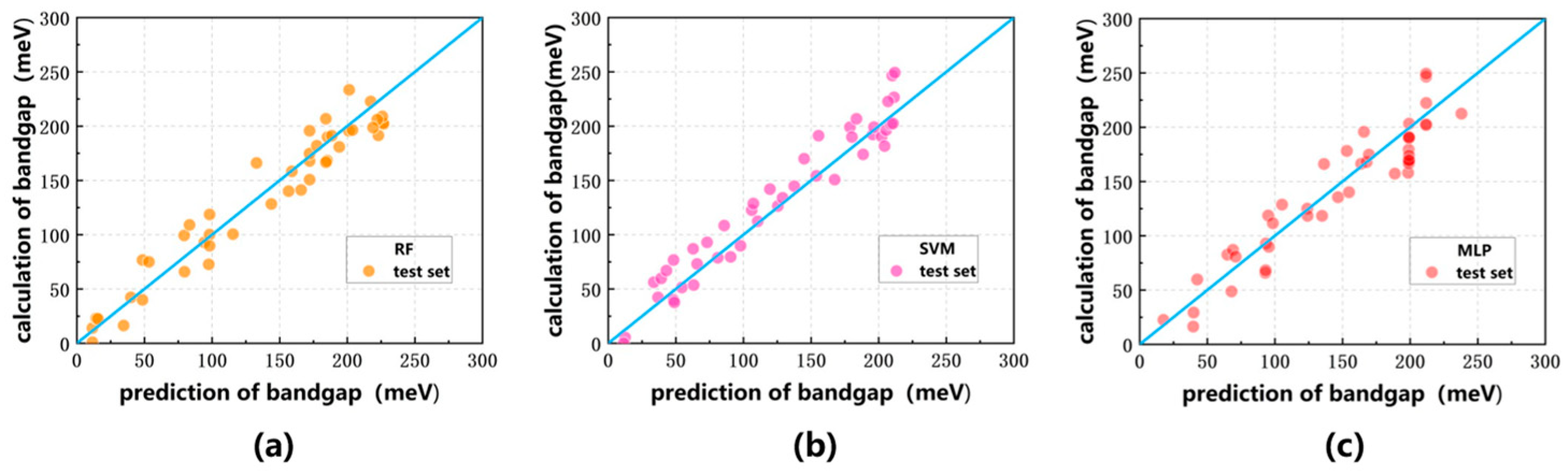
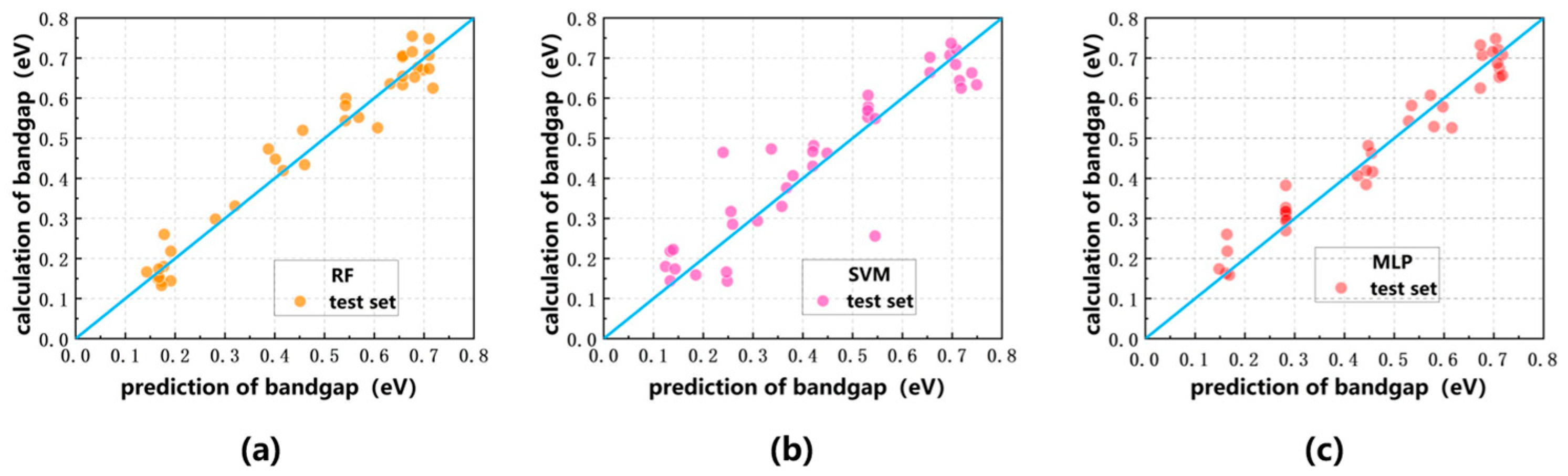
Figure 6.
Vertical external electric field and graphene band gap prediction results on the test set. In the three plots, the blue curves all indicate the y = x function curves, and the values predicted by the RF model, the SVM model, and the MLP model are labeled in yellow, pink, and red: (a) RF model (b) SVM model (c) MLP model.
Figure 6.
Vertical external electric field and graphene band gap prediction results on the test set. In the three plots, the blue curves all indicate the y = x function curves, and the values predicted by the RF model, the SVM model, and the MLP model are labeled in yellow, pink, and red: (a) RF model (b) SVM model (c) MLP model.
Figure 7.
N-doping and graphene bandgap prediction results on the test set. In all three plots, the blue curves indicate the y = x function curves, and the values predicted by the RF model, the SVM model, and the MLP model are labeled in yellow, pink, and red: (a) RF model (b) SVM model (c) MLP model.
Figure 7.
N-doping and graphene bandgap prediction results on the test set. In all three plots, the blue curves indicate the y = x function curves, and the values predicted by the RF model, the SVM model, and the MLP model are labeled in yellow, pink, and red: (a) RF model (b) SVM model (c) MLP model.
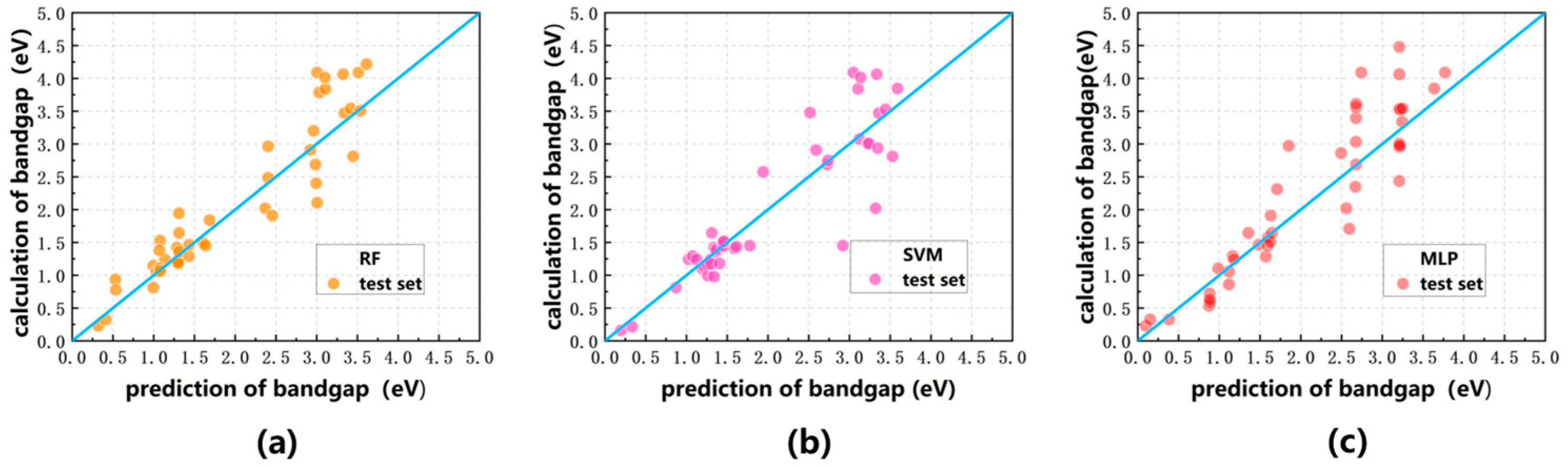
Figure 8.
H adsorption rate and graphene band gap prediction results on the test set. In all three plots, the blue curves indicate the y = x function curves, and the values predicted by the RF model, the SVM model, and the MLP model are labeled in yellow, pink, and red: (a) RF model (b) SVM model (c) MLP model.
Figure 8.
H adsorption rate and graphene band gap prediction results on the test set. In all three plots, the blue curves indicate the y = x function curves, and the values predicted by the RF model, the SVM model, and the MLP model are labeled in yellow, pink, and red: (a) RF model (b) SVM model (c) MLP model.
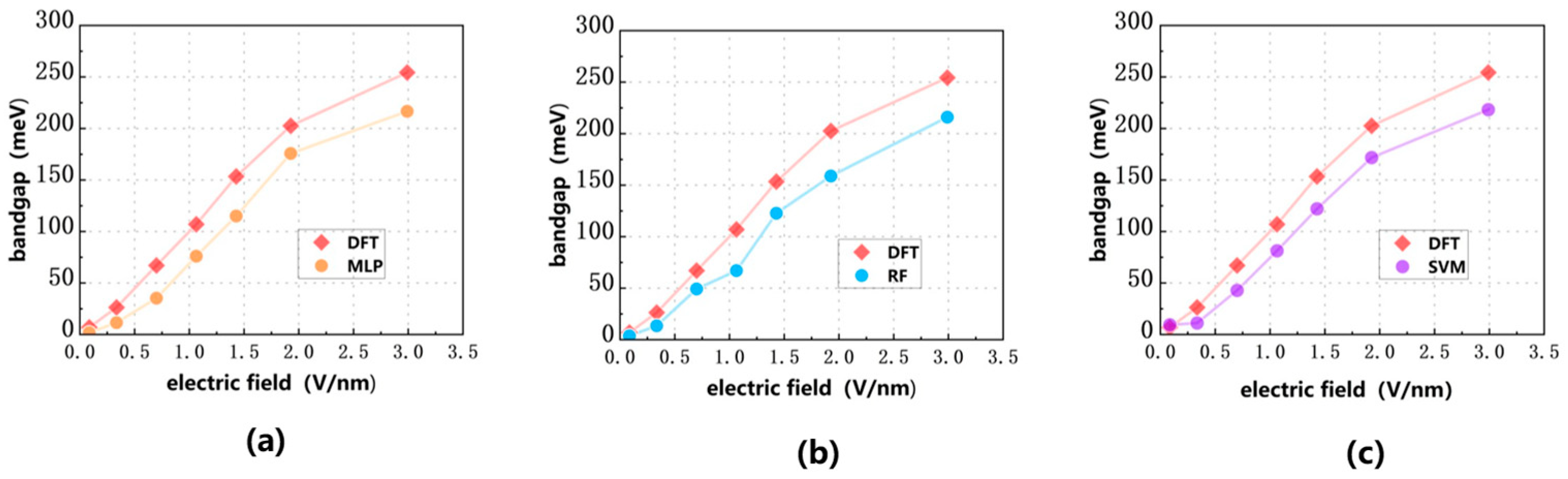
Figure 9.
Evaluation of AB stacked bilayer graphene bandgap validation set under the influence of vertical external electric field, the red folded line is the result of DFT calculation in the validation set, and the prediction results of RF, SVM, and MLP models are marked by blue, purple, and yellow curves: (a) RF model (b) SVM model (c) MLP model.
Figure 9.
Evaluation of AB stacked bilayer graphene bandgap validation set under the influence of vertical external electric field, the red folded line is the result of DFT calculation in the validation set, and the prediction results of RF, SVM, and MLP models are marked by blue, purple, and yellow curves: (a) RF model (b) SVM model (c) MLP model.
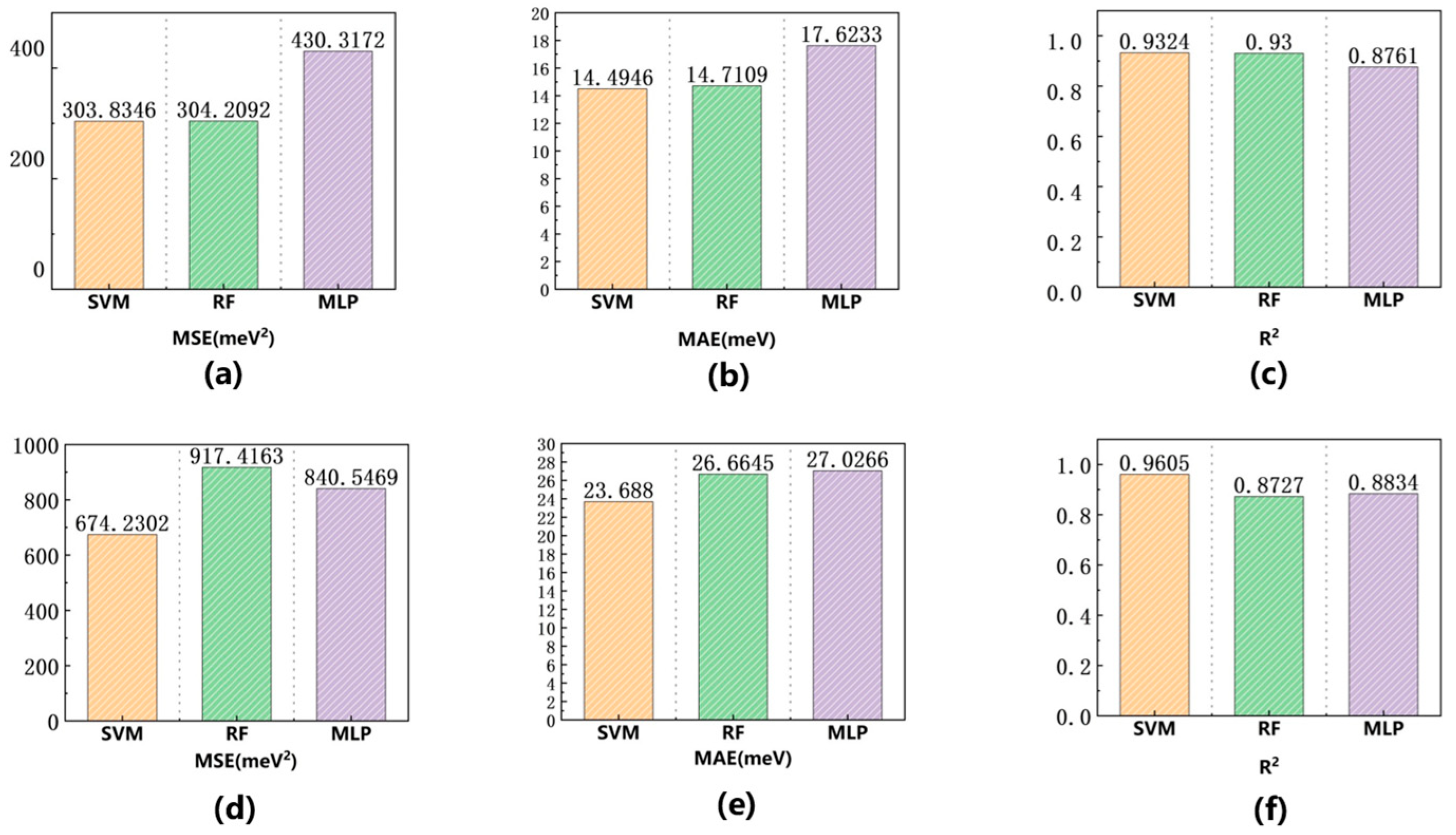
Figure 10.
Vertical external electric field with AB stacked bilayer graphene machine learning model evaluation, metrics for SVM model, RF model, and MLP model are shown as yellow, green, and purple bars: (a) Test set MSE, (b) Test set MAE, (c) Test set R2, (d) Validation set MSE, (e) Validation set MAE, (f) Validation set R2.
Figure 10.
Vertical external electric field with AB stacked bilayer graphene machine learning model evaluation, metrics for SVM model, RF model, and MLP model are shown as yellow, green, and purple bars: (a) Test set MSE, (b) Test set MAE, (c) Test set R2, (d) Validation set MSE, (e) Validation set MAE, (f) Validation set R2.
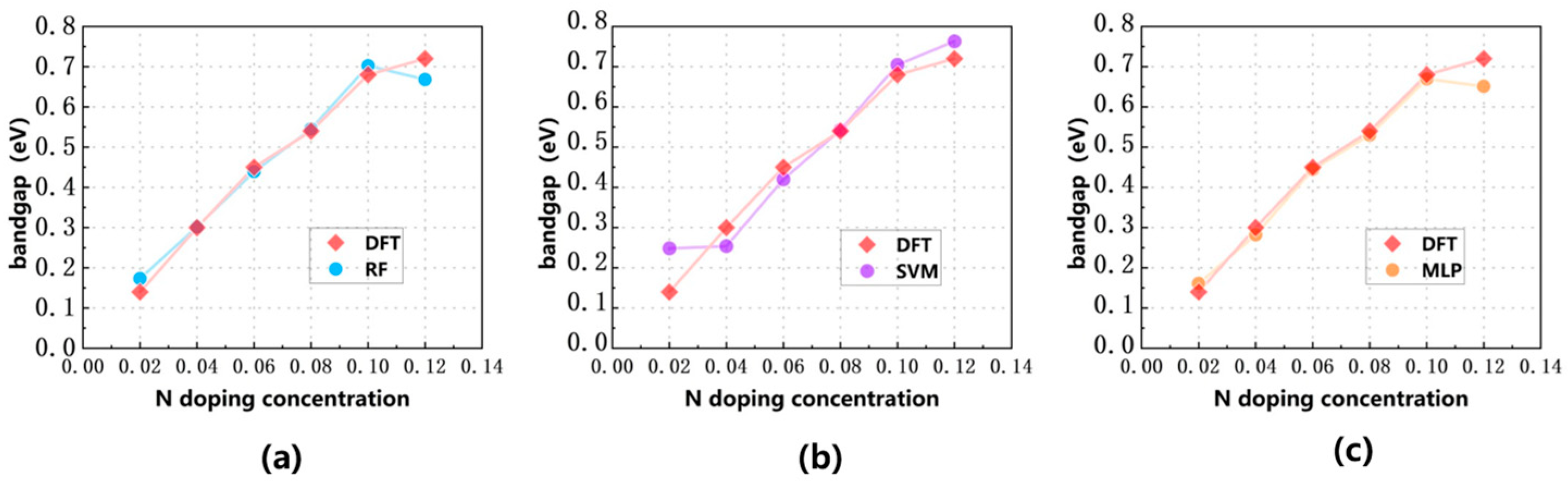
Figure 11.
Evaluation of N-doped graphene bandgap in the validation set, the red folded line is the result of DFT calculation in the validation set, and the prediction results of RF, SVM, and MLP models are marked by blue, purple, and yellow curves: (a) RF model, (b) SVM model, (c) MLP model.
Figure 11.
Evaluation of N-doped graphene bandgap in the validation set, the red folded line is the result of DFT calculation in the validation set, and the prediction results of RF, SVM, and MLP models are marked by blue, purple, and yellow curves: (a) RF model, (b) SVM model, (c) MLP model.
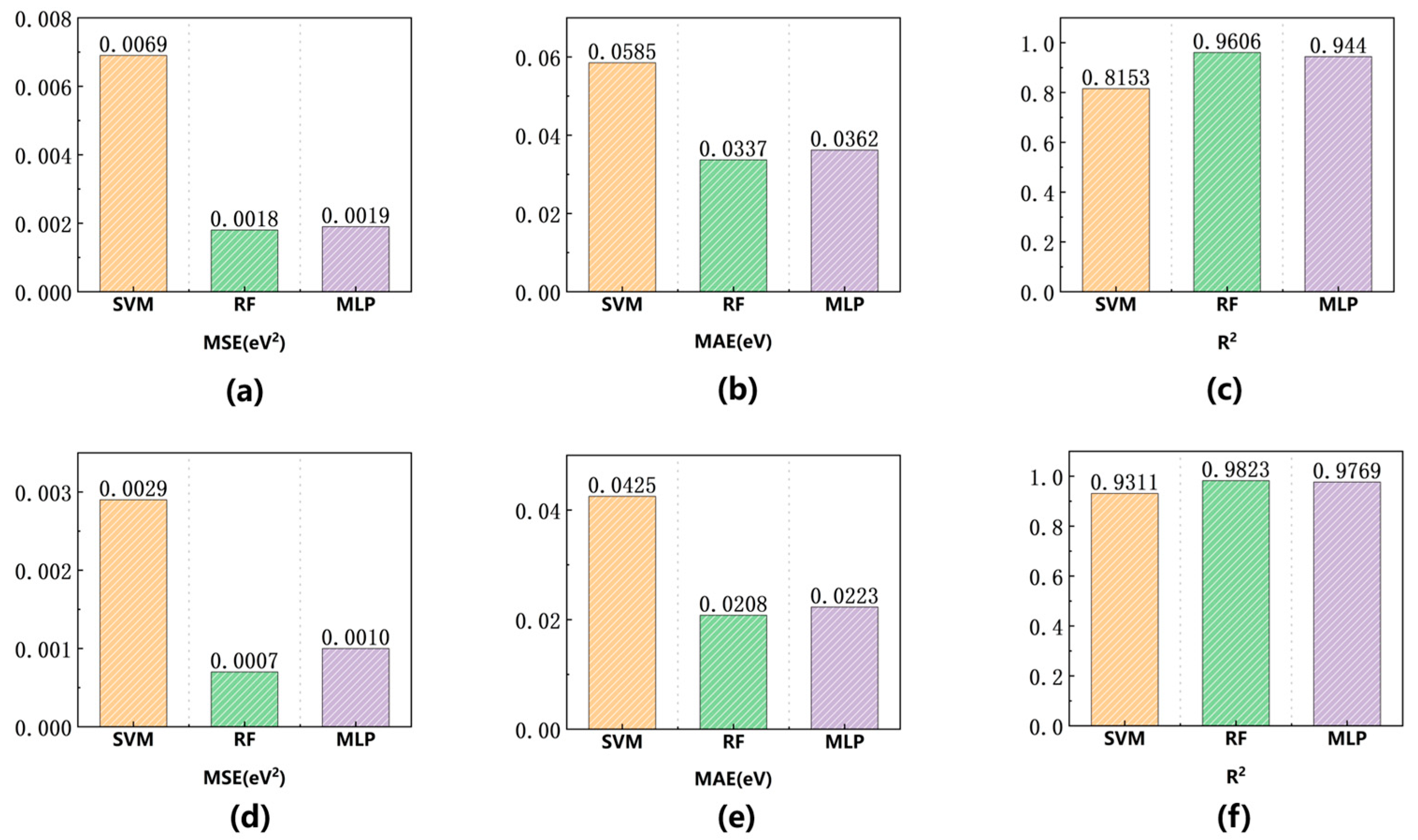
Figure 12.
N-doped graphene machine learning model evaluation, metrics for SVM model, RF model, and MLP model are shown as yellow, green, and purple bars: (a) test set MSE, (b) test set MAE, (c) test set R2, (d) validation set MSE, (e) validation set MAE, (f) validation set R2.
Figure 12.
N-doped graphene machine learning model evaluation, metrics for SVM model, RF model, and MLP model are shown as yellow, green, and purple bars: (a) test set MSE, (b) test set MAE, (c) test set R2, (d) validation set MSE, (e) validation set MAE, (f) validation set R2.
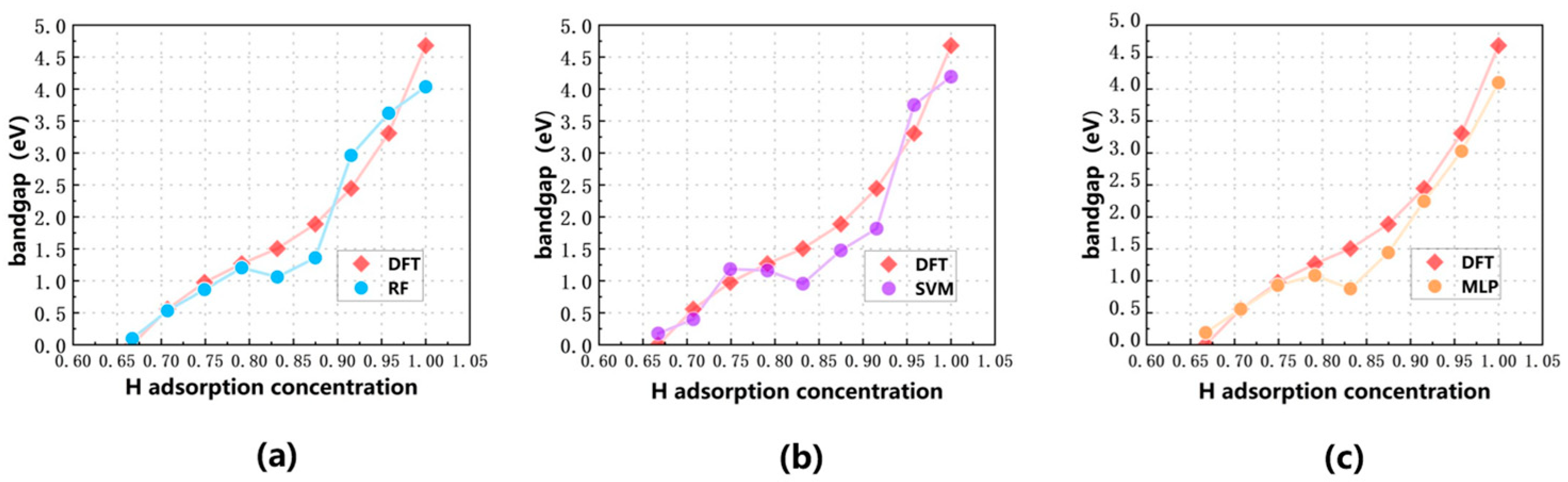
Figure 13.
Evaluation of H-adsorbed graphene bandgap in the validation set, the red folded line is the result of DFT calculation in the validation set, and the prediction results of RF, SVM, and MLP models are marked by blue, purple, and yellow curves: (a) RF model, (b) SVM model, (c) MLP model.
Figure 13.
Evaluation of H-adsorbed graphene bandgap in the validation set, the red folded line is the result of DFT calculation in the validation set, and the prediction results of RF, SVM, and MLP models are marked by blue, purple, and yellow curves: (a) RF model, (b) SVM model, (c) MLP model.
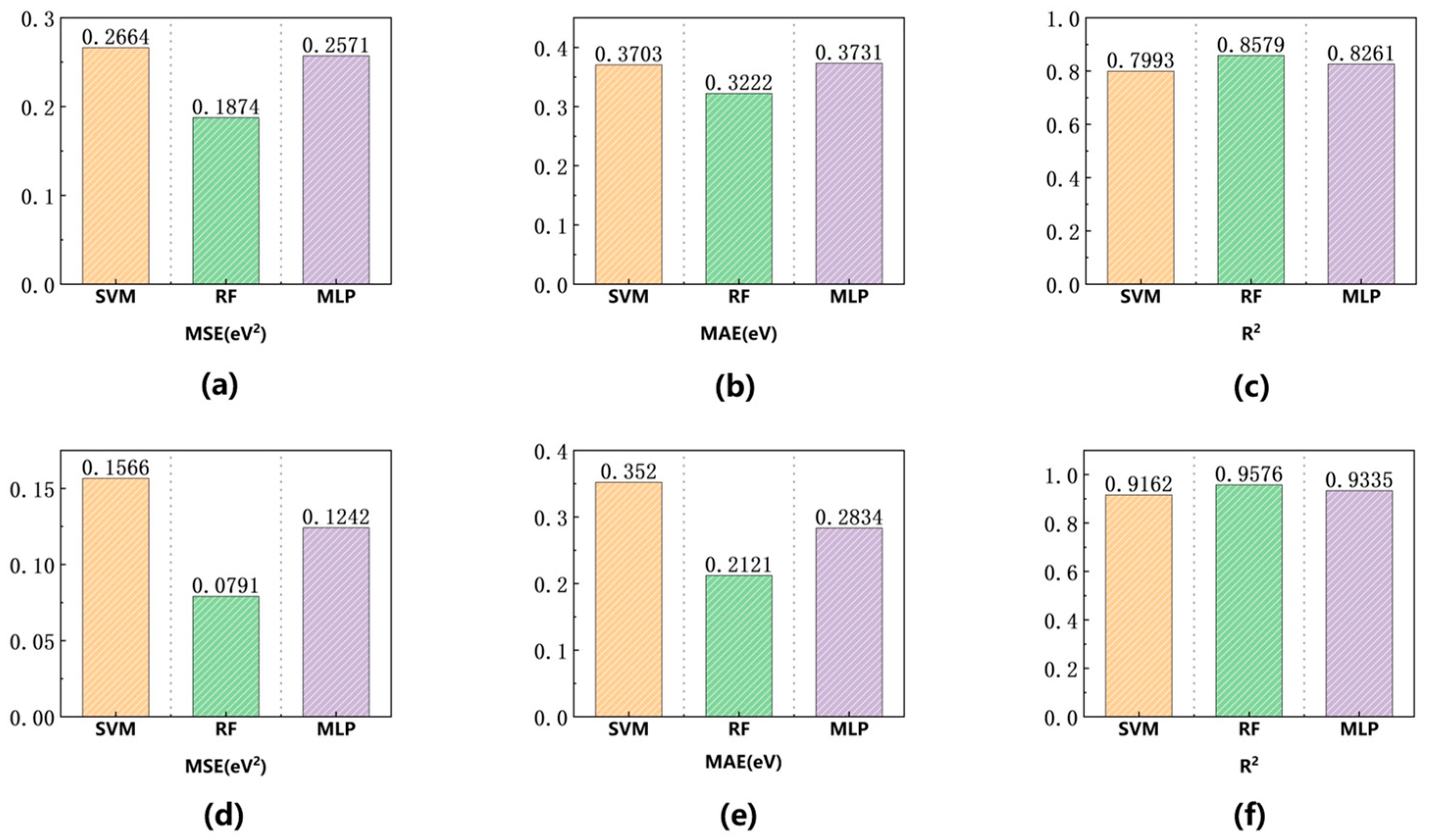
Figure 14.
H adsorption graphene machine learning model evaluation, metrics for SVM model, RF model, and MLP model are shown as yellow, green, and purple bars: (a) test set MSE, (b) test set MAE, (c) test set R2 (d) validation set MSE, (e) validation set MAE, (f) validation set R2.
Figure 14.
H adsorption graphene machine learning model evaluation, metrics for SVM model, RF model, and MLP model are shown as yellow, green, and purple bars: (a) test set MSE, (b) test set MAE, (c) test set R2 (d) validation set MSE, (e) validation set MAE, (f) validation set R2.
Table 1.
Graphene structural parameters.
Table 1.
Graphene structural parameters.
| Structure | Methods/Å | Calculated/Å | Experimental/Å |
|---|
| Graphene | a | 2.456 | [18]
|
| | b | 2.456 | [18]
|
| AB-stacked | spacings | 3.40 | [19]
|
Table 2.
Random Forest Regression Algorithm Machine Learning Model Parameter Settings.
Table 2.
Random Forest Regression Algorithm Machine Learning Model Parameter Settings.
| Hyperparameters | Values |
|---|
| Number of decision trees | 50 |
| Number of minimum leaf node samples | 1 |
| Number of feature samples | 1 |
| MaxNumSplits | 5 |
Table 3.
Support Vector Machine Regression Algorithm Machine Learning Model Parameter Settings.
Table 3.
Support Vector Machine Regression Algorithm Machine Learning Model Parameter Settings.
| Hyperparameters | Values |
|---|
| Regularization parameter C | 400 |
| Kernel function | Gaussian |
| Insensitive bandwidth | 0.001 |
Table 4.
Multilayer perceptron regression algorithm machine learning model parameterization.
Table 4.
Multilayer perceptron regression algorithm machine learning model parameterization.
| Hyperparameters | Values |
|---|
| Maximum number of training rounds | 500 |
| Learning rate | 0.01 |
| Minimum gradient threshold | 1 × 10−6 |
| Hidden Layer Size | 10 |
Table 5.
Comparison of graphene bandgap under the influence of vertical electric field in the validation set predicted by SVM model, RF model, MLP model with DFT calculation.
Table 5.
Comparison of graphene bandgap under the influence of vertical electric field in the validation set predicted by SVM model, RF model, MLP model with DFT calculation.
| Model | 0.0862 (V/nm) | 0.335 | 0.700 | 1.064 | 1.428 | 1.927 | 2.990 |
|---|
| DFT | 6.853 (meV) | 26.269 | 67.005 | 106.980 | 153.426 | 202.538 | 254.315 |
| SVM | 9.319 | 11.154 | 42.763 | 81.262 | 121.990 | 171.764 | 218.249 |
| RF | 3.748 | 13.401 | 49.148 | 66.949 | 122.670 | 158.825 | 215.992 |
| MLP | 1.786 | 11.477 | 35.200 | 75.980 | 114.983 | 175.30 | 216.615 |
Table 6.
Comparison of the performance of SVM model, RF model, and MLP model for predicting graphene bandgap under vertical electric field in the validation set.
Table 6.
Comparison of the performance of SVM model, RF model, and MLP model for predicting graphene bandgap under vertical electric field in the validation set.
| Model | MSE (eV2) | MAE (eV) | R2 | Test Point Error |
|---|
| SVM | 674.2302 | 23.688 | 0.9605 | 13.4% |
| RF | 917.4163 | 26.6645 | 0.8727 | 13.6% |
| MLP | 840.5469 | 27.0266 | 0.8834 | 12.7% |
Table 7.
Comparison of N-doped graphene bandgap in the validation set predicted by SVM model, RF model, MLP model with DFT calculation.
Table 7.
Comparison of N-doped graphene bandgap in the validation set predicted by SVM model, RF model, MLP model with DFT calculation.
| Model | 2% | 4% | 6% | 8% | 10% | 12% |
|---|
| DFT | 0.14 | 0.3 | 0.45 | 0.54 | 0.68 | 0.72 |
| SVM | 0.24824 | 0.25365 | 0.42019 | 0.54272 | 0.70462 | 0.76299 |
| RF | 0.17399 | 0.30171 | 0.43926 | 0.54484 | 0.70234 | 0.66835 |
| MLP | 0.16117 | 0.28199 | 0.44465 | 0.53021 | 0.66951 | 0.66501 |
Table 8.
Comparison of the performance of SVM model, RF model, and MLP model for predicting N-doped graphene bandgap in the validation set.
Table 8.
Comparison of the performance of SVM model, RF model, and MLP model for predicting N-doped graphene bandgap in the validation set.
| Model | MSE (eV2) | MAE (eV) | R2 | Test Point Error |
|---|
| SVM | 0.0029 | 0.0425 | 0.9311 | 6% |
| RF | 0.0004 | 0.0208 | 0.9823 | 7.2% |
| MLP | 0.001 | 0.0223 | 0.9769 | 9.6% |
Table 9.
Comparison of H-adsorbed graphene bandgap in the validation set predicted by SVM model, RF model, MLP model with DFT calculation.
Table 9.
Comparison of H-adsorbed graphene bandgap in the validation set predicted by SVM model, RF model, MLP model with DFT calculation.
| Model | 66.723% | 70.716% | 74.905% | 79.133% | 83.166% | 87.472% | 91.544% | 95.811% | 100% |
|---|
| DFT | 0 | 0.5571 | 0.97493 | 1.26741 | 1.50418 | 1.88719 | 2.44429 | 3.3078 | 4.67976 |
| SVM | 0.17622 | 0.39923 | 1.18484 | 1.16102 | 0.95467 | 1.47579 | 1.81633 | 3.75084 | 4.19398 |
| RF | 0.09636 | 0.53222 | 0.86319 | 1.20472 | 1.06 | 1.35905 | 2.96153 | 3.62186 | 4.03528 |
| MLP | 0.18945 | 0.55735 | 0.93019 | 1.08532 | 0.87621 | 1.44179 | 2.24336 | 3.02714 | 4.10075 |
Table 10.
Comparison of the performance of SVM model, RF model, and MLP model for predicting H-adsorbed graphene bandgap in the validation set.
Table 10.
Comparison of the performance of SVM model, RF model, and MLP model for predicting H-adsorbed graphene bandgap in the validation set.
| Model | MSE (eV2) | MAE (eV) | R2 | Test Point Error |
|---|
| SVM | 0.1556 | 0.352 | 0.9162 | 10.1% |
| RF | 0.0791 | 0.2121 | 0.9576 | 13.5% |
| MLP | 0.1242 | 0.2834 | 0.9335 | 12% |