Improving Methanol Production from Carbon Dioxide Through Electrochemical Processes with Draining System

Abstract

The paper describes the conversion of carbon dioxide into methanol in a chemical reactor under standard operating conditions. Electro-analytical techniques, cyclic voltammetry, and chrono-amperometry characterize the process. The electrochemical redox reaction develops using various catalyzers to evaluate the performance of the carbon dioxide conversion into methanol process under variable chemical conditions. The results of the applied technique showed an incomplete redox reaction with an electronic change of z = 2.84 on average, below the ideal number, z = 6, that may be due to methanol decomposition (reverse reaction) because the system operates with a reaction constant above the equilibrium value. The methanol production may improve by draining the methanol/water solution from the chemical reactor to reduce the methanol concentration in the electrochemical cell, shifting the forward reaction towards the formation of methanol, increasing the electron change number, which approaches the ideal value, and improving the methanol production efficiency. The draining process shows a significant increase in methanol formation, which depends on the draining flow rate and the catalyzer type. A simulation process shows that if we operate in optimum conditions, with no methanol decomposition through a reverse reaction, the redox reaction fulfills the ideal condition of maximum electronic change. The experimental tests validate the simulation results, showing a relevant increase in the electron change number with values up to z = 4.2 for optimum draining flow rate conditions (0.2 L/s). The experimental results show a relative increase factor of 4.7 in methanol production, meaning we can produce more than four times more methanol compared with no draining techniques. The data analysis shows that the draining flow rate has a threshold of 0.2 L/s, beyond which the extent of the reaction reverses, reducing the methanol formation due to a chemical reaction disequilibrium. The paper concludes that using the draining method, the methanol production mass rate increases significantly from an average value of 20.9 kg/h for non-draining use, considering all catalyzer types, to a range between 91.9 kg/h and 104.3 kg/h, depending on the flow rate. Averaging all values for different flow rates and comparing with the non-draining case, we obtain an absolute methanol production mass rate of 77 kg/h, meaning an incremental percentage of 469.1%, more than four times the initial production. Although the proposed methodology looks promising, applying this procedure on an industrial scale may suffer from restrictions since the chemical reactions intervening in the methanol formation do not perform linearly. According to experimental tests, the best option among the six catalyzers used for methanol production is the plain copper, with copper oxides (Cu₂O, CuO) and copper Sulphur (CuS) as feasible alternatives.

1. Introduction

Global warming has become more of a social concern in recent decades than a scientific topic. Governments, private companies, social organizations, and people are concerned by climate change and the natural disasters caused by global warming. Anthropogenic emissions of greenhouse gases (GHGs) since the preindustrial era have caused an increase of 1 °C in global average temperature. The Intergovernmental Panel on Climate Change (IPCC) has concluded that global warming will increase by up to 1.5 °C between 2030 and 2050 if the current rate of GHG emissions continues. Within the GHGs, carbon dioxide, or CO_2, is the most notorious gas, accounting for 78% of total emissions in 1970–2010. The Intergovernmental Panel on Climate Change (IPCC) published a report showing an average 1 °C temperature increase on Earth due to anthropogenic emissions of greenhouse gases (GHGs) growing from the pre-industrial era until the present. The report concludes that demographic and economic growth is responsible for global warming within a probable range of 0.8 °C to 1.2 °C [1]. Additional studies, based on the IPCC report, analyze the global warming consequences, including the summary for policymakers, and evaluate the measurements society should apply to revert the phenomenon [2,3,4]. The principal conclusion is an expected 1.5 °C temperature increase on Earth in 2030–2050 if GHG emissions continue to rise.

Figure 1 shows the reported temperature evolution and the predicted values from the developed models of the stylized trajectories of anthropogenic emissions and forcing. The European Council approved in October 2014 the energy and climatic policy framework for 2030, including the political goals for the European Union in the 2021–2030 decade [5]. Among the EU Council decisions, we can highlight a minimum 40% reduction in GHG emissions for 2030 compared to GHG emissions in 1990, the achievement of 32% of energy consumption in the EU by 2030 being supplied by renewable energies, with 74% of electric generation from renewable sources, and a 32.5% energy efficiency improvement in the mentioned period. The economic consequences of this resolution would have a high impact [6,7,8].

Carbon dioxide (CO₂) is, among the GHGs, the most relevant component of pollutant emissions, representing 78% of global warming in the 1970–2010 decades [9]. Burning fossil fuels like coal, petrol, and gas is the principal source of carbon dioxide emissions, equivalent to 56.6% of global emissions [10,11], requiring political decisions [12].

Among the procedures to reduce and mitigate carbon dioxide emissions, the conversion into valuable chemical products is the most relevant pathway for researchers and technicians. The conversion of carbon dioxide into methanol appears to be a good solution due to its relatively high energy density (20.1 kJ/g), around half that of gasoline (44.3 kJ/g), and its stability at ambient temperature, making it a good candidate for storage [13]. Besides, methanol is produced in many places around the world due to its application in industrial processes like olefins, gasoline, ether dimethyl, acetic and formic acids, and hydrogen production [14,15,16,17,18,19]. On the other hand, bio-methanol represents a challenge in the search for less pollutant fuels [20,21,22].

Methanol has become one of the most interesting chemical products for industry because of its many applications, such as fuel for the future, chemical synthesis, green energy storage, automotive manufacturing, biodegradable solvents, and hydrogen production [23]. In fuel applications, methanol exhibits a pristine and efficient use, especially in replacing fossil fuels or as an additive to minimize the greenhouse effects caused by fossil fuel combustion [24,25,26,27,28]. Among other methanol applications, we can mention its use in fuel cells to generate electricity [29,30,31], a practical application in the automotive industry [32,33,34], or in portable devices [35,36].

In this paper, we propose a technique for methanol production from carbon dioxide electro-reduction by using captured carbon dioxide from combustion processes, where electroanalytical techniques are applied, and the methanol produced is quantified. A previous study deals with the effect of methanol production and application in internal combustion engines on emissions in the context of carbon neutrality [37]. The paper also proposes improvements in the applied technique to increase methanol production and optimize carbon dioxide concentration for optimum redox reaction and its conversion into methanol.

The principal goal of this paper is to produce methanol from carbon dioxide through electrochemical conversion. The process reduces the atmospheric CO₂ content, generates a product applicable to different industrial processes, and produces an automotive fuel.

2. Materials and Methods

2.1. Fundamentals

2.1.1. Carbon Dioxide Electrochemical Reduction

Carbon dioxide electrochemical reduction involves an anodic semi-reaction for water oxidation and a cathodic semi-reaction for carbon dioxide reduction, as in Equation (1).

$$\begin{array}{l}3H_{2}O\rightleftharpoons \left(3/2\right)O_2+6H^{+}+6e^{-}\hspace{1em}\hspace{1em}\hspace{1em}(Anodic\hspace{0.33em}reaction)\\ C{O}_2+6H^{+}+6e^{-}\rightleftharpoons C{H}_{3}OH+H_{2}O\hspace{1em}(Cathodic\hspace{0.33em}reaction)\\ C{O}_2+3H_{2}O\rightleftharpoons C{H}_{3}OH+H_{2}O\hspace{1em}\hspace{1em}\hspace{1em}(Global\hspace{0.33em}reaction)\end{array}$$

(1)

The global reaction in Equation (1) develops under specific conditions since the carbon dioxide conversion may produce other chemical components, as shown below (

Table 1. Chemical reactions (anodic, cathodic, and global) for CO₂ conversion.

Cathodic Semi-Reaction	Anodic Semi-Reaction	Global Reaction
CO2 (g) → HCOOH (aq)	H2O → 2H+ + 2e− + (1/2)O2	CO2 + 2H+ + 2e− → HCOOH
CO2 (g) → CO (g)	H2O → 2H+ + 2e− + (1/2)O2	CO2 + 2H+ + 2e− → CO+ H2O
CO2 (g) → HCHO (g)	2H2O → 4H+ + 4e− + O2	CO2 + 4H+ + 4e− → HCHO+ H2O
CO2 (g) → CH3OH (aq)	3H2O → 6H+ + 6e− + (3/2)O2	CO2 + 6H+ + 6e− → CH3OH + H2O
CO2 (g) → CH4 (g)	H2O → 8H+ + 8e− + 2O2	CO2 + 8H+ + 8e− → CH4 + 2H2O

) [38].

The above reactions group shows the simplified anodic semi-reaction for methanol production, corresponding to the complete semi-reaction shown in Equation (1).

Analyzing the above reactions, we notice that carbon dioxide electro-reduction produces different chemical species depending on the atomic hydrogen formation (H⁺). On the other hand, every reaction requires a reduction potential, as shown in

Table 2. Reduction potential of chemical component production from CO₂ [39].

Global Reaction	Eo (V)
CO2 + 2H+ + 2e− → HCOOH	−0.665
CO2 + 2H+ + 2e− → CO+ H2O	−0.521
CO2 + 4H+ + 4e− → HCHO+ H2O	−0.554
CO2 + 6H+ + 6e− → CH3OH + H2O	−0.399
CO2 + 8H+ + 8e− → CH4 + 2H2O	−0.249

.

Therefore, by controlling the formation of atomic hydrogen and limiting the reduction potential, we may control the production of methanol and prevent the formation of other chemical species.

2.1.2. Electroanalytical Techniques

According to the applied perturbation input, voltage, or current, the system reacts, providing an output signal from which we obtain the necessary information to characterize the molecules, electrode chemical reactions, and the transformation process characteristics. We use transient electrochemical processes at controlled potential where the electric current is a time function, the potentiostat method, characterized by a natural diffusion mass transport to the electrode. The applied methodologies are cyclic voltammetry and chrono-amperometry.

Cyclic voltammetry is one of the most widely used techniques to characterize redox reactions, supplying information about the chemical species and thermodynamic parameters. The sweep voltage derives from a triangular potential variation whose slope absolute value matches the sweep velocity (Figure 2). According to the setup sweep voltage, we obtain a voltammogram for every recorded current peak (Randles–Sevcik equation) [40].

The Randles–Sevcik equation relates the sweep voltage and the current peak, anodic or cathodic. Applying the equation for this last case and drawing the peak current versus the sweep velocity root square, we determine one of the unknown parameters: oxidant agent diffusion coefficient, oxidant agent concentration, electrons transfer number, or working electrode area, provided all other parameters are known. If we deal with a reversible reaction, the Randles–Sevcik equation becomes the following:

$$I_{pc}=-0.4463\sqrt{{\displaystyle \frac{F^{3}D}{RT}}}{z}^{3/2}Ac{v}^{1/2}$$

(2)

I_pc is the peak current, F is the Faraday number, D is the diffusion coefficient, T is the Kelvin temperature, z is the electrons transfer number, A is the electrode area, c is the oxidant agent concentration, and v is the sweep velocity.

Table 3. Voltammogram parameter values.

F (C/mole)	R (J/mole·K)	T (K)	z	A (cm2)	D (cm2/s)
96,485	8.314	298	6	22.5	1.77 × 10−5

shows the values used for the parameters in Equation (2).

For an irreversible redox reaction, Equation (2) transforms into the following:

$$I_{pc}=-2.99\times {10}^{-5}{\alpha }^{1/2}zA{D}^{1/2}c{v}^{1/2}$$

(3)

α is the electron transfer coefficient, given as follows:

$$\alpha ={\displaystyle \frac{1.857RT}{\left|E_{pc}-E_{pc/2}\right|zF}}$$

(4)

E_pc and E_pc/2 represent the potential at the peak and half the height of the cathodic peak.

A diffusion flow from the bulk solution to the electrode interphase starts if the potential pulse is high enough to reduce the oxidant agent concentration to a value near zero in the electrode vicinity, and the current through the electrode is given by the Cotrell equation [41].

$$I(t)={\displaystyle \frac{zFAc\sqrt{D/\pi }}{t^{1/2}}}=K{t}^{-1/2}\to K={\displaystyle \frac{zFA}{{\pi }^{1/2}}}c{D}^{1/2}$$

(5)

2.2. Experimental Device

The electrolytic cell is a closed cylinder of 8.56 cm diameter and 10.77 cm height with four openings on the upper side for the three electrodes and the carbon dioxide injection (Figure 3).

The red, green, and blue cylinders on left side of Figure 3 correspond to the working, reference, and counter-electrode, respectively.

Figure 4 shows the schematic view of the analytical cell electric circuit.

We used copper (Cu), copper sulfur (CuS), cupric copper oxide (CuO), cuprous copper oxide (Cu₂O), aluminum (Al), and zinc (Zn) as working electrodes (catalyzers). Single metal electrodes (Cu, Al, Zn) were purchased from the electrode manufacturer [42]. Copper oxide and sulfur electrodes were manufactured at the lab, applying electrodeposition techniques. We generated the copper oxidation process on the copper film using a graphite bar as counter-electrode, and a KHCO₃ and NaHCO₃ aqueous solution for the CuO and Cu₂O formation. We avoided the corrosion process on the working electrode (catalyzer) (CuO, Cu₂O) by exposing the oxidized electrode to the ambient environment once the oxidation process had finished.

We produced a copper sulfur electrode using saturated aqueous micronized Sulphur as an electrolyte. In such conditions, the following chemical reactions develop:

$$\begin{array}{l}2HCl+S\rightleftharpoons C{l}_2+H_{2}S\\ H_{2}S+H_{2}O\rightleftharpoons H_3{O}^{+}+H{S}^{-}\\ H{S}^{-}+H_{2}O\rightleftharpoons H_3{O}^{+}+S^{2-}\\ S^{2-}+C{u}^{2+}\rightleftharpoons CuS\end{array}$$

(6)

The anodization and cathodization processes last for 60 and 1 min.

The reference (Ag/AgCl) and counter-electrode (Pt) are commercial products supplied by the same company [42].

We used a potentiostat model NEV 3.2 from Nanoelectra, controlled by software supplied by the manufacturing company [43]. Figure 5 shows the potentiostat and the software control screen.

2.3. Experimental Procedure

Gas chromatography is the technique applied for methanol identification. We use an inert gaseous flow that drags the generated sample through a heated chamber at a setup temperature. We can identify the sample type by determining the drag volatile component velocity, since in the steady state, the chamber retains the analytes, releasing them at variable velocity depending on their composition [44,45]. Figure 6 shows the schematic view of the process.

3. Results

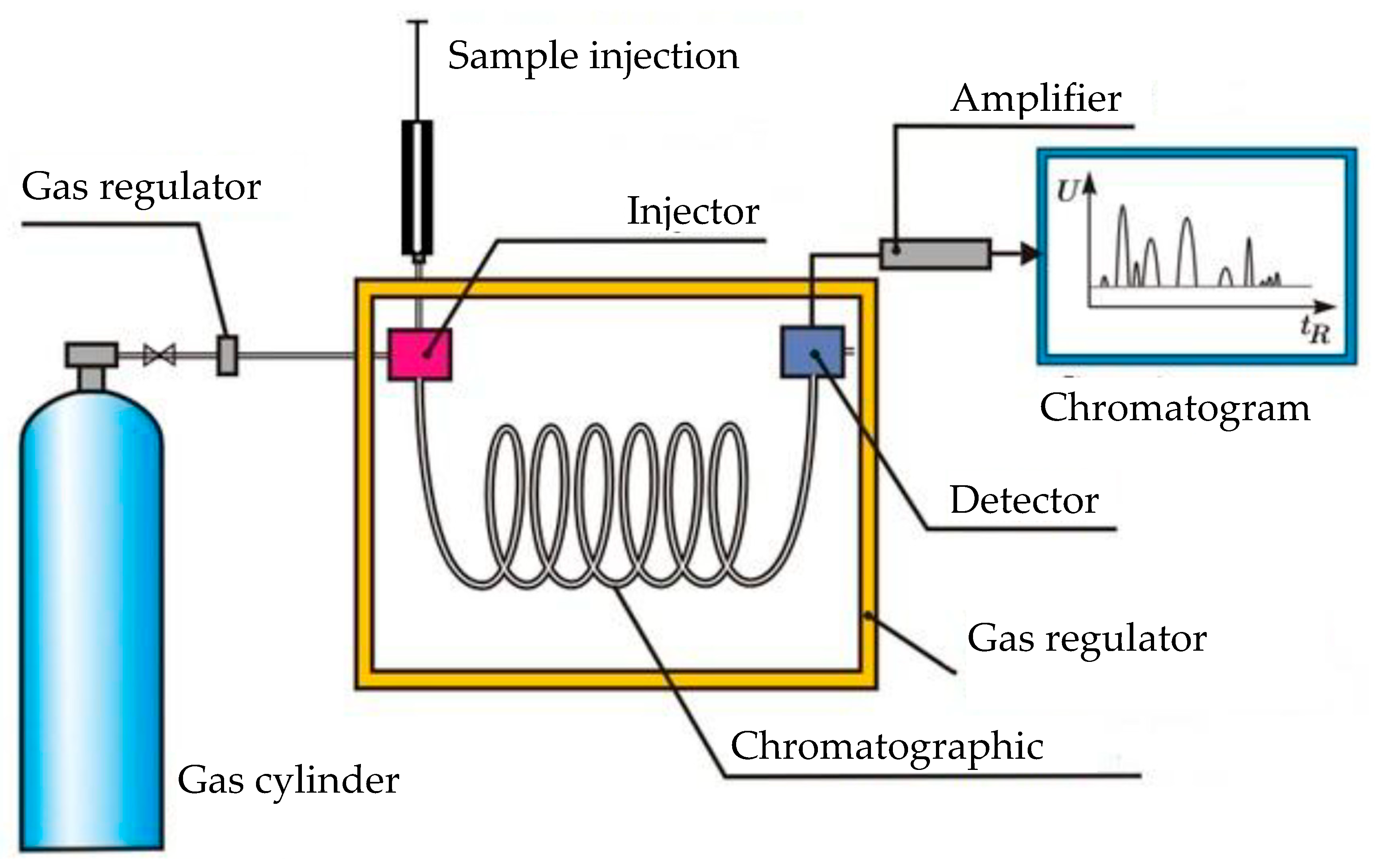
3.1. Experimental Results

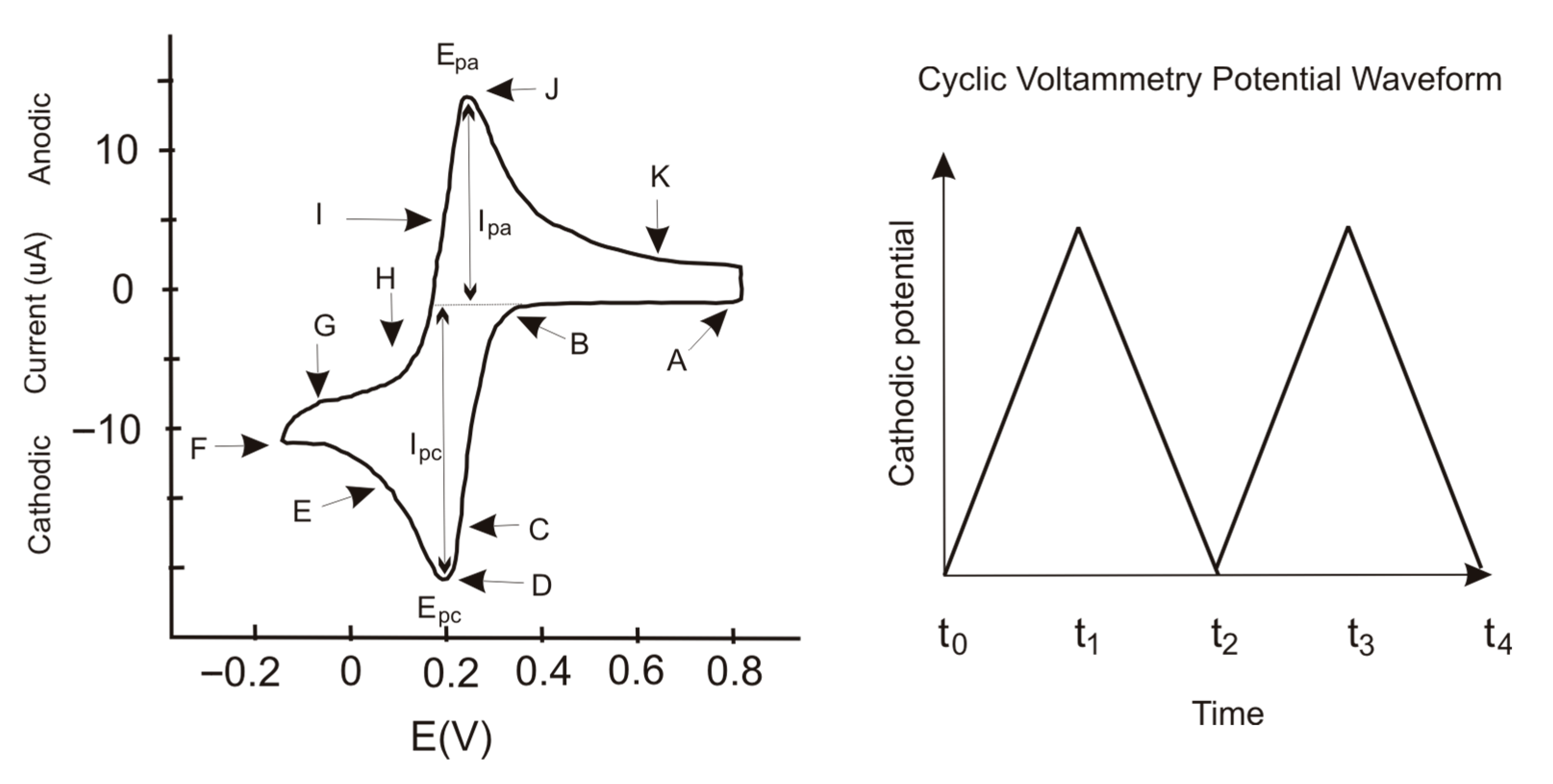
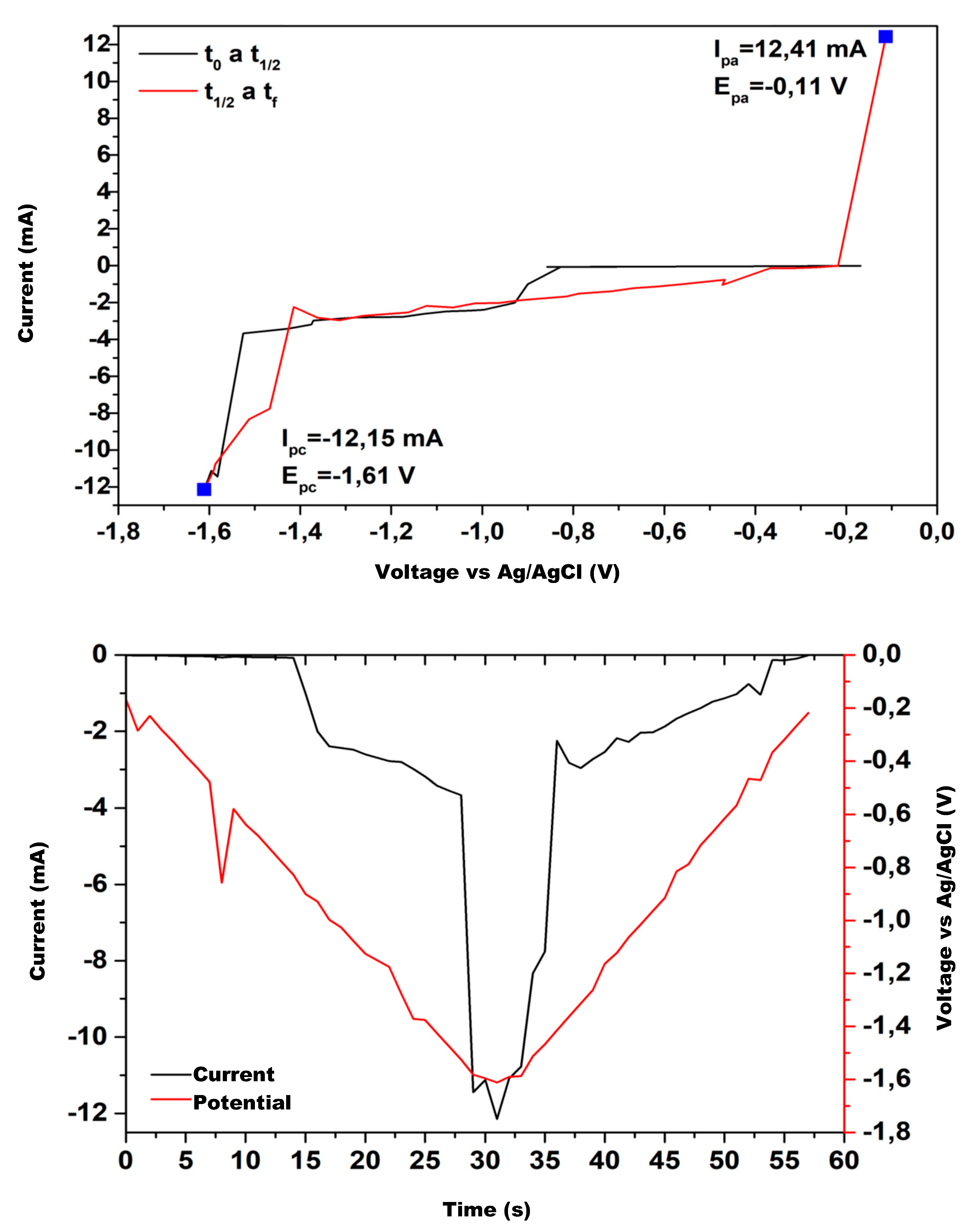
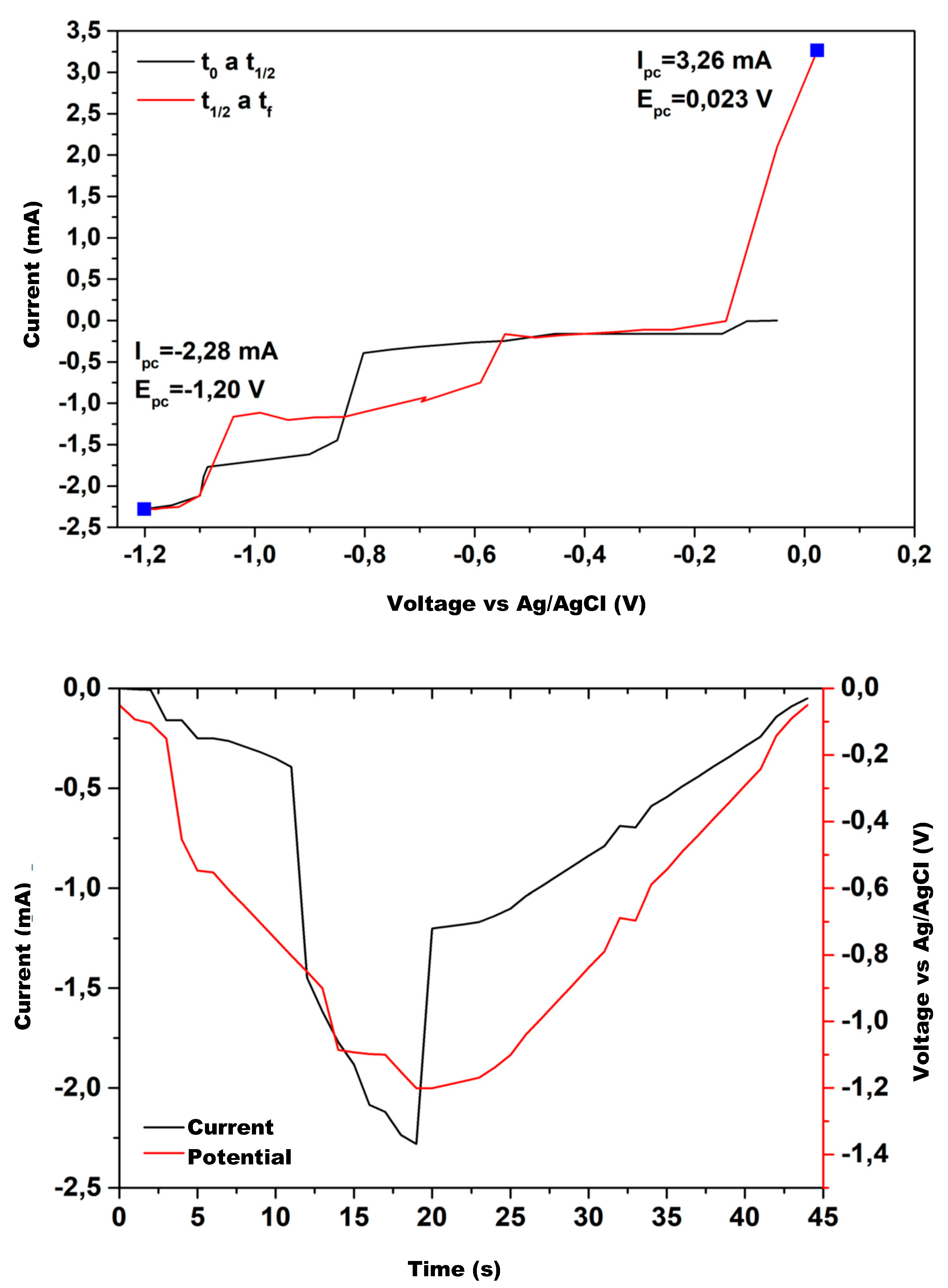
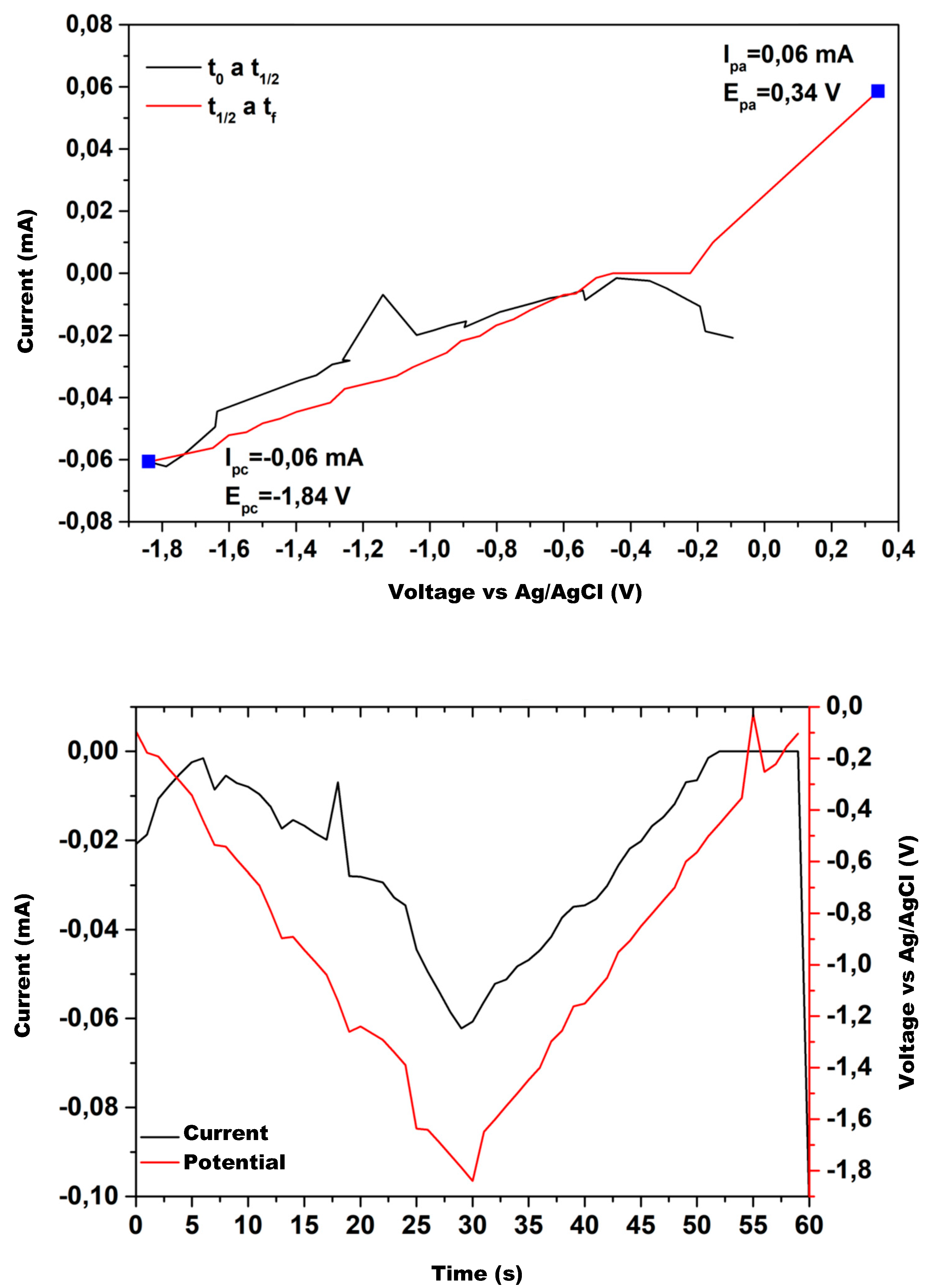
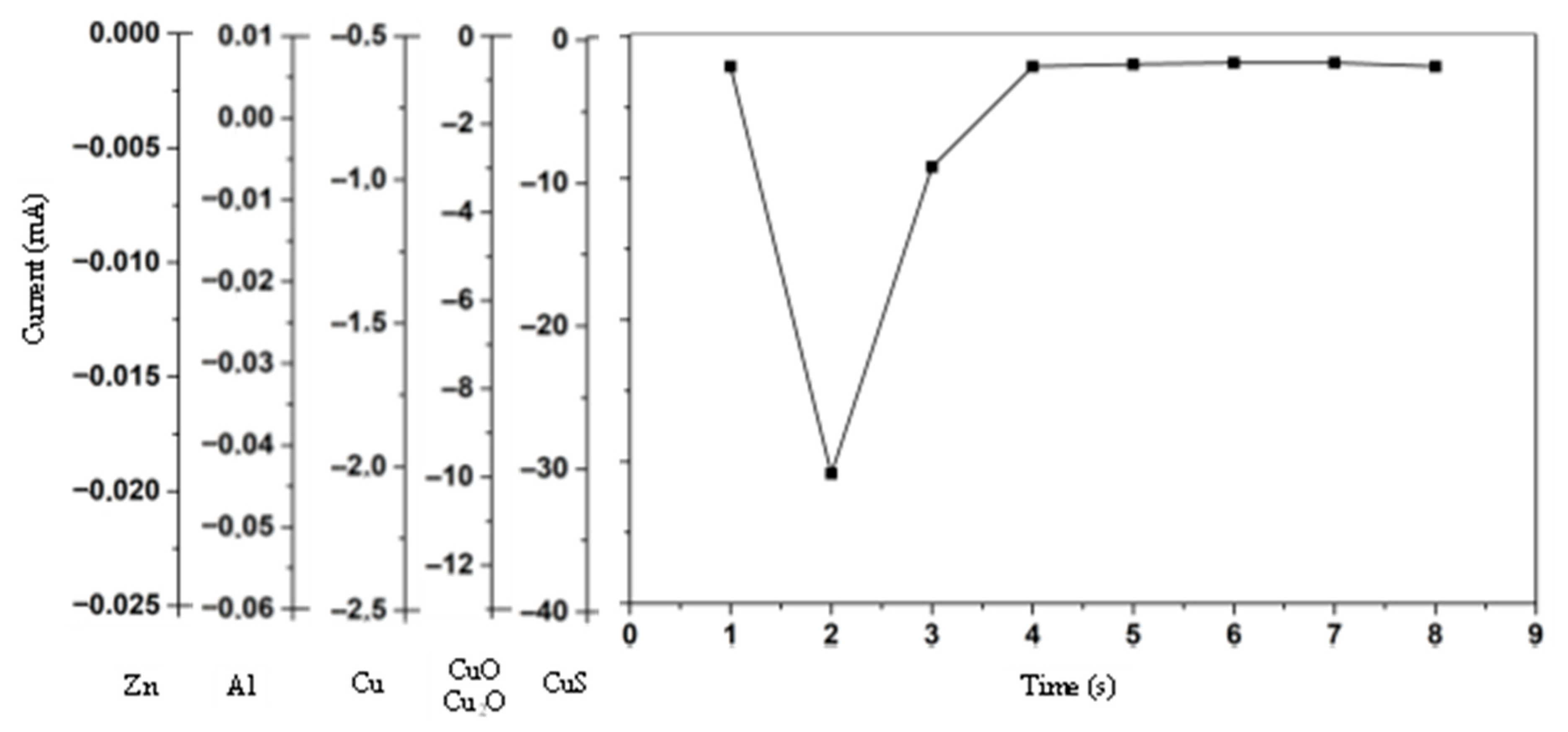
Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 show the cyclic voltammetry for the various catalysts used in the experimental tests. The graph on the upper side corresponds to I–V curve, while the one on the lower shows the current and potential time evolution.

Table 4. Average standard deviation for experimental tests (Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12).

Figure 7 Top	Figure 7 Bottom	Figure 8 Top	Figure 8 Bottom	Figure 9 Top	Figure 9 Bottom	Figure 10 Top	Figure 10 Bottom	Figure 11 Top	Figure 11 Bottom	Figure 12 Top	Figure 12 Bottom
5.05	2.42	1.01	1.01	1.01	3.03	2.02	1.72	0.05	0.09	0.03	0.40

shows the average standard deviation for experimental tests shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12.

The upper hand side of Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 shows the electroanalytical response to a programmed voltage evolution regarding the reference electrode (Ag/AgCl). The current evolution is the result of the electrochemical reaction, with a first step representing the concentration gradient effect and a second step where the concentration stabilizes, maintaining a constant density current. If the current continues changing over the entire voltage range, the concentration gradient remains, and the system does not reach a steady state. Low variations in the stabilized current value are acceptable because the system’s redox reactions may provoke slight changes in the concentration at the double layer zone when ions exchange charge with the electrode.

Analyzing Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, the obtained results show that the current evolution with time is similar for all electrode types when the process starts, with a gray line corresponding to the time interval and slight differences for the Al electrode where the plateau never appears. The plateau means that the current remains constant from a voltage threshold, whose value depends on the electrode type (

Table 5. Voltage threshold for the plateau current onset in cyclic voltammetry.

Working Electrode	Voltage (V)
CuS	−1.168
Cu2O	−1.532
CuO	−1.173
Cu	−0.817
Al	none
Zn	−1660

).

Aluminum working electrode does not show a plateau (Figure 11); therefore, no value is included in Table 5 for this electrode.

Therefore, we realize that the Cu electrode requires a lower voltage to reach the plateau, while the Zn and Cu₂O electrodes require nearly double the voltage. CuS and CuO electrodes require an intermediate voltage threshold for the onset value.

According to the voltage threshold data in Table 3, when starting the process, the Cu electrode is the most suitable because it requires a lower voltage to reach the zero current value; however, Zn and Cu₂O are not recommended.

As the process evolves, as shown by the red line, the obtained results show that the copper mixture electrodes, CuS, Cu₂O, and CuO, maintain the current values for the same voltage range. The pure copper electrodes tend to reproduce the current evolution but show noticeable differences in the first half of the voltage range. The Zn electrode exhibits a significant difference, and Al does not maintain a constant current at any voltage value.

The current evolution over the entire time-lapse shows that electrodes with a copper mixture have a higher performance; therefore, they are more suitable for methanol production.

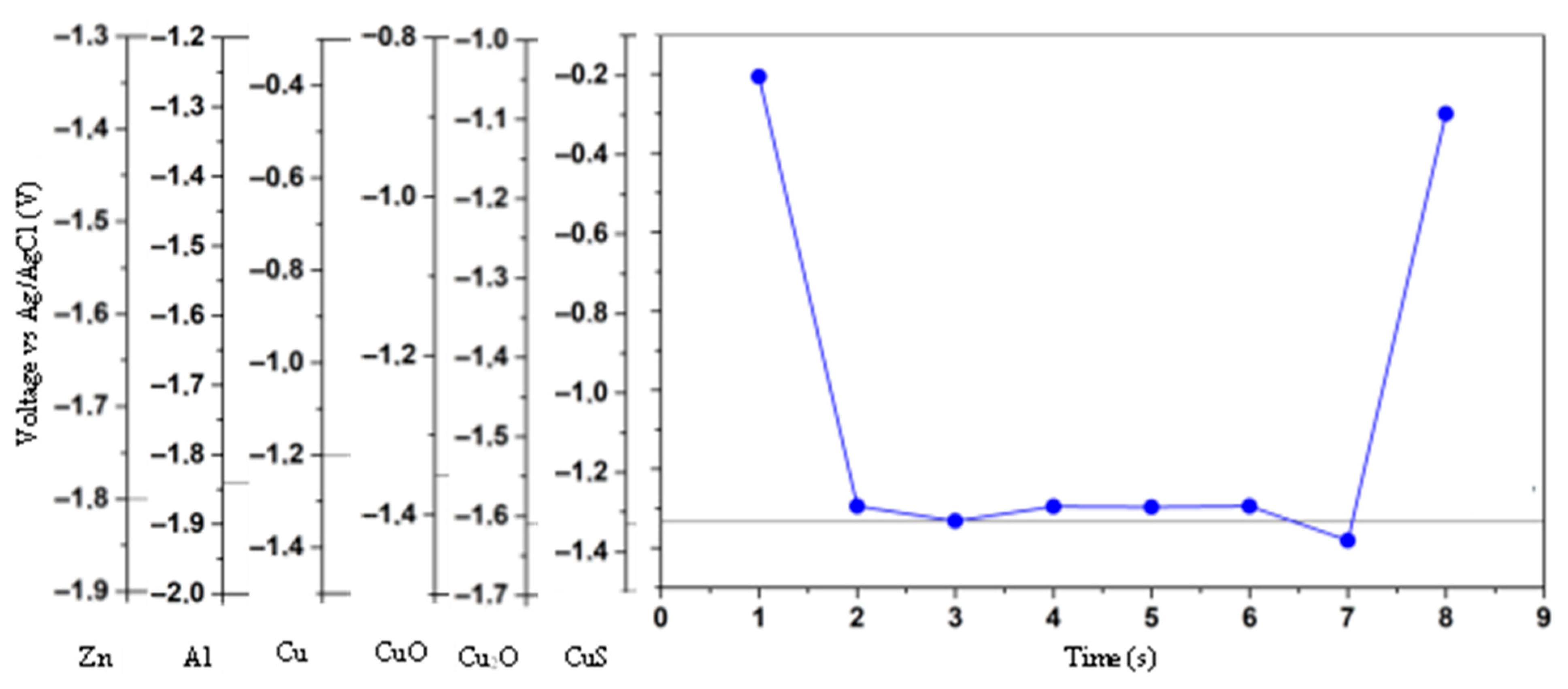
On the other hand, the right side of Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 shows the electric potential well due to the potential barrier in the double layer, generated by the concentration gradient in that area. The potential well peak occurs at a similar time for each electrode, with a slight difference between them. The current time evolution shows a similar behavior because of the electrical relations between current and voltage.

Comparing the performance of the electrodes used, we find that for plain copper or a copper–copper mixture, the current behaves close to the potential, with the peak value close to the one for the potential, indicating that these electrodes are suitable for methanol production; however, for Al and Zn electrodes, the current does not reach the peak of the well, reinforcing the assertion that these electrodes are not suitable for methanol production under current operating conditions.

Table 6. Relevant parameter values for the experimental tests.

Working Electrode	Cathodic Peak Current (mA)	Cathodic Potential vs. Ag/AgCl Reference Electrode (V) [46,47]	Sweep Velocity (mV/s)
CuS	−29.89	−1.33	61.7 ± 1.4
Cu2O	−12.15	−1.61	49.7 ± 1.3
CuO	−12.14	−1.35	57.5 ± 1.2
Cu	−2.28	−1.20	62.5 ± 3.1
Al	−0.06	−1.84	59.1 ± 0.4
Zn	−0.023	−1.80	49.5 ± 3.5

shows the relevant parameter values for the experimental tests.

Now, representing the chrono-amperometry for the different working electrodes, we have (Figure 13 and Figure 14):

Table 7. Average standard deviation for Figure 13 and Figure 14.

CuS	Cu2O	CuO	Cu	Al	Zn
Figure 13	Figure 13	Figure 13	Figure 13	Figure 13	Figure 13
5.0	8.0	1.0	1.0	0.04	0.01
Figure 14	Figure 14	Figure 14	Figure 14	Figure 14	Figure 14
0.15	0.17	0.14	0.14	0.2	0.15

shows the average standard deviation for test values in Figure 13 and Figure 14.

Y-axis scale in Figure 13 and Figure 14 corresponds to the working electrode shown at the bottom.

The obtained results show that in the experimental tests, the current shows a common trend, with a lowering peak at 2 s, then recovering to the previous value at 4 s, and maintaining this value for the rest of the test. Concerning the related applied voltage jump, the trend is also common, lowering from the initial value to the minimum at t = 2 s, maintaining this minimum value for 5 s, and recovering back to the initial value at the time equal to 8 s.

The carbon dioxide in the bulk solution arrives at the electrode surface by natural diffusion at a potential value of E_pc. The kinetics of the reduction reaction exceed the mass contribution by diffusion, causing a decrease in the CO₂ concentration at the catalytic surface and, therefore, a decrease in the current passing through the working electrode. However, the decrease is not immediate but progressive. The diffusion-limited regions, where the diffusion rate is still higher than the kinetics of the reduction reaction, are located from the maximum cathodic current until the current reaches a lower and stable value.

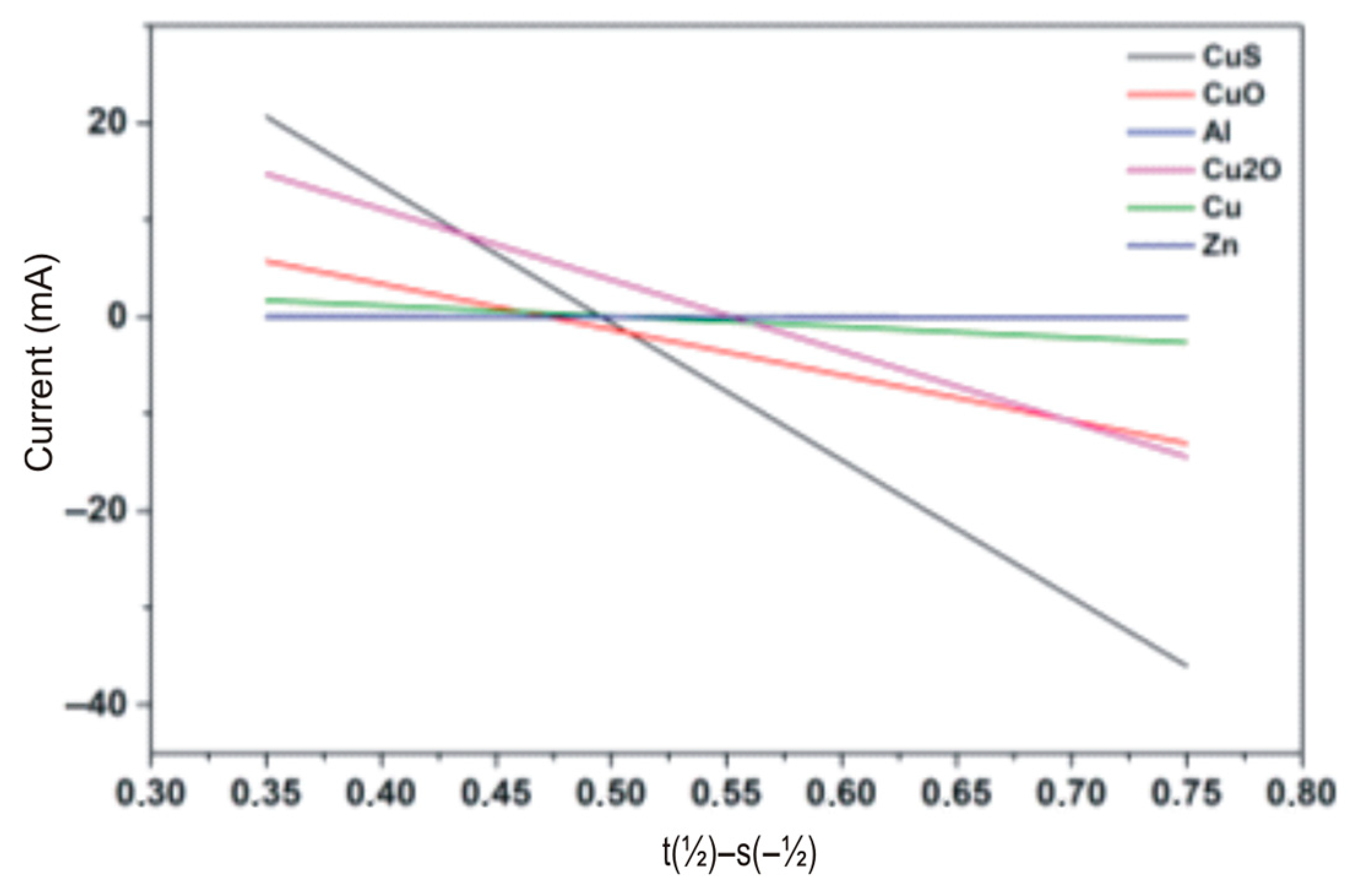
At t = 2 s, the carbon dioxide concentration becomes null, represented by the current drop in Figure 13. This phenomenon is in close agreement with the applied potential jump drop shown in Figure 14. We can model the diffusion current using the Cotrell equation; therefore, representing the recorded current as a function of time, we have the linear correlation (Figure 15).

The slope of the curve corresponds to the K-coefficient in Equation (5).

Table 8. K-coefficient values for the linear correlation between current and time square root for the different working electrodes in the experimental tests.

Electrode	CuS	Cu2O	CuO	Cu	Al	Zn
K (mA·s1/2)	−141.668	−73.019	−47.422	−10.946	−0.247	−0.125

shows the K-values for the different working electrodes.

Because the electrolytic cell sample contains methanol and water, following the chronoamperometry tests, we submitted the sample to a 35 min distillation process to obtain water and methanol separately due to their different vapor pressure and evaporation temperatures.

Table 9. Distilled water and methanol percentage from the electrolytic cell sample for various working electrodes (catalyzer) (p = 1 atm; T = 65 °C).

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
Methanol (CH3OH)	4.9	5.9	4.3	4.9	4.3	3.2
Water (H2O)	0.9	1.1	0.8	0.9	0.8	0.6

shows the water and methanol percentages after distillation for the various working electrodes.

We notice that the distilled methanol percentage is low, below 6% in all cases, indicating that the carbon dioxide conversion into methanol is not highly efficient.

Repeating the distillation process at the same time as for the electrolytic cell sample for a pure water and methanol solution, in separated processes, at a temperature equal to the methanol evaporation temperature at ambient pressure, corresponding to the electrolytic cell sample distillation, we obtained the following (

Table 10. Percentage of distilled water process at ambient pressure and 65 º C temperature.

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
Water (H2O)	2.49	2.00	1.80	1.54	1.44	1.44

):

The water percentage obtained from the distillation process in the electrolytic cell sample differs from the values in the pure water distillation at equivalent pressure and temperature conditions, showing that the chemical reaction for carbon dioxide conversion into methanol develops at partial electron transfer, resulting in a lower efficiency with a reduced methanol production level.

Table 11. Methanol production efficiency for various working electrodes.

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
Efficiency (%)	36.1	55.0	44.5	58.3	55.5	41.6

shows the efficiency ratio in methanol production, using the distilled water as a reference parameter.

The lower distilled water percentage obtained in the electrolytic cell sample distillation indicates that the carbon dioxide conversion produces hydrocarbons other than the type C_xH_z−2nO_2x−n, corresponding to methanol with x = 1, z = 6, and n = 1, with subscript z accounting for the maximum electron transfer number.

Indeed, if the chemical reaction for carbon dioxide conversion into methanol develops at incomplete electron transfer, the resulting product is not methanol but an alternative hydrocarbon; therefore, the methanol percentage obtained in the process is lower than the maximum expected value.

Regarding the Randles–Sevcik and Cotrell equations:

$$z={\left({\displaystyle \frac{I_{pc}}{v^{1/2}K}}\right)}^2{\displaystyle \frac{RT}{{\left(-0.4463\right)}^2\pi F}}$$

(7)

Equation (7) provides a method to determine the adequate number of electrons transferred during carbon dioxide conversion. On the other hand, by using Equation (5) and clearing the electron transfer number, n, we obtain the electron transfer number’s theoretical value:

$$z={\displaystyle \frac{{\pi }^{1/2}K}{FAc{D}^{1/2}}}$$

(8)

Applying data from our experimental tests, we have (

Table 12. Electron transfer number in CO₂ to CH₃OH conversion for various catalyzers.

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
z (th)	2.16	3.35	2.68	3.51	3.30	2.48
z (exp)	2.15	3.22	2.63	3.36	3.28	2.40
Deviation (%)	0.85	3.95	1.87	4.54	0.69	3.46

):

We should note the close agreement between theoretical and experimental values, proving the validity of the developed method for calculating the electron transfer number.

Table 11 shows the deficit in the electron transfer number regarding the optimum, z = 6, proving that the carbon dioxide conversion into methanol develops at incomplete chemical redox reaction, generating a deficit in the methanol production, as shown by the low efficiency values.

Since the process efficiency in converting carbon dioxide into methanol is closely related to the electron transfer number, we calculate the ratio between these two parameters, obtaining the following results (

Table 13. Ratio of electron transfer number to efficiency in converting CO₂ into CH₃OH.

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
n/η (th)	6.00	6.00	6.00	6.00	6.00	6.00
n/η (exp)	5.94	5.85	5.92	5.76	5.91	5.77
Deviation (%)	0.9	2.5	1.4	4.1	1.5	4.1

):

Theoretical predictions and experimental values indicate that the expected methanol production increases if the redox reaction develops at optimum conditions, with the electron transfer number matching the maximum (z = 6). Applying these conditions, we hope to reach a 100% methanol percentage production if operating at optimum conditions (complete redox reaction).

3.2. Energy Balance and Thermodynamic Reversibility

The energy balance analysis for methanol production is critical to evaluating the methodology’s feasibility. A highly negative value discourages the development of the process because of the energy losses compared to the methanol combustion power and the required energy to produce the burnt methanol. To this goal, we evaluate the methanol energy formation and the power generation when burning the produced methanol. Experimental data applies to the calculation.

Table 14. Energy balance for the methanol formation and combustion (incomplete redox reaction).

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
Formation energy (kJ)	60.1	110.1	65.7	95.5	82.3	46.9
Global energy (kJ)	164.1	199.5	146.0	164.2	149.0	111.8
Energy deviation (kJ)	104.0	89.4	80.3	68.6	66.8	64.8
Conversion energy ratio	0.366	0.552	0.450	0.582	0.552	0.420
Electron change ratio	0.367	0.550	0.450	0.583	0.550	0.417
Combustion power (kJ)	59.8	109.7	65.2	93.6	81.2	44.6
Energy balance (kJ)	−0.3	−0.5	−0.5	−1.9	−1.0	−2.4

shows the calculation results.

The explanation of the data in Table 9 is as follows:

• Formation energy corresponds to the energy used in generating the methanol according to the experimental results;
• Global energy is the energy used in the experimental process;
• Energy deviation corresponds to the difference between formation and global energy;
• The energy ratio is the quotient between formation and global energy;
• The electron ratio is the relation between the experimental and theoretical electron change number;
• Combustion power corresponds to the energy produced by burning the generated methanol;
• Energy balance is the difference between combustion and formation power.

The obtained results show that the energy balance is slightly negative for all catalyzers, showing that the methanol formation requires more energy than recovered when burning.

The energy ratio shows the approach coefficient to the ideal redox reaction; the closer this parameter is to unity, the higher the ideality in carbon dioxide conversion into methanol through redox reaction.

The electron change ratio indicates the reversibility coefficient of the methanol formation process; the higher the ratio, the higher the reversibility coefficient. An electron ratio equal to 1.0 means a perfect reversible process.

Comparing data for the energy and electron change ratio, we observe a close agreement between the two parameters, with 99.8% accuracy, on average. This high accuracy proves that the experimental energy involved in the carbon dioxide conversion into methanol matches the theoretical prediction of the electron change number, allowing accurate correspondence between the energy fraction devoted to the carbon dioxide conversion and the electron change ratio.

3.3. Chemical Reaction Balance

Data from Table 9 show that we operate far from the ideal conditions, with an incomplete redox reaction meaning a lower than ideal methanol formation. Indeed, the methanol formation reaction from carbon dioxide develops in both senses due to the intermediate formation of a weak acid, the formic acid, as shown in Equation (9) [48].

$$C{O}_2+3H_{2}O⥂HCOOH+{\displaystyle \frac{1}{2}}{O}_2+2H_{2}O⥂C{H}_{3}OH+H_{2}O+\left(3/2\right)O_2$$

(9)

Because formic is a weak acid, it decomposes in carbon dioxide and water quickly, reverting the equation toward the left, limiting the progress of the global reaction. In such a situation, the overall reaction balance is the result of methanol formation (→) and decomposition (←). If the carbon dioxide molecular concentration is higher than that of methanol, which is the current situation at the methanol formation process, the global reaction progresses to the right but at a limited speed, resulting in an incomplete redox reaction, producing an electron change number lower than the optimum.

We can improve the methanol formation by reducing the methanol concentration, generating a disequilibrium in the global reaction, and accelerating methanol formation, thus increasing the reaction progress and the electron change number. To do so, we can drain the methanol/water solution in the electrolytic cell, carrying it to a distiller where we separate methanol and water through a distillation process.

On the other hand, if we raise the carbon dioxide concentration by increasing the CO₂ pressure, the global reaction tends to displace to the right, accelerating methanol formation and improving the efficiency of the process.

3.4. Simulation

We run a simulation to evaluate the system capacity of achieving the optimum conditions; i.e., an electron change number equal to ideal value (z = 6). To this goal, we apply the correspondence between energy and electron change ratio, using data from Table 12 and Table 13, and repeating the calculation for a complete redox reaction, thus obtaining the following (

Table 15. Energy balance for methanol formation and combustion (complete redox reaction).

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
Formation energy (kJ)	164.1	199.5	146.0	164.2	149.0	111.8
Global energy (kJ)	167.4	204.9	149.9	168.0	153.0	114.5
Energy deviation (kJ)	3.3	5.4	3.9	3.9	3.9	2.7
Conversion energy ratio	0.980	0.974	0.974	0.977	0.974	0.976
Electron change ratio	0.997	0.976	0.947	0.961	0.985	0.961
Combustion power (kJ)	167.2	204.3	148.6	167.2	148.6	111.5
Energy balance (kJ)	−0.2	−0.6	−1.3	−0.8	−4.4	−3.1

):

As in the former case, the energy balance is negative, meaning we cannot recover all the energy invested in the formation process, no matter which catalyzer we use. The negative energy balance, however, is low, showing a developed process close to the optimum performance.

We determine the energy balance considering half of the error band, adding the value to the formation energy, and subtracting it from the combustion power. Since the calculation corresponds to ideal conditions, the energy balance should be null because the cyclic transformation matches a thermodynamic cycle where enthalpy variation is null. The deviation from the null value, shown in Table 15, corresponds to irreversibilities in the process. Considering the energy balance to combustion power ratio as the irreversibility index, we obtain an average value of 1.2%, which is acceptable for a quasi-reversible process. The low deviation shown in the reversibility index value proves the proposed methodology feasibility.

The proven method feasibility encourages the development of a protocol in which we drain the methanol/water solution generated at the chemical reactor as soon as it is produced, with water obtained after the distillation process re-injected into the chemical reactor to compensate for water loss during the chemical reaction. Figure 16 shows the schematic view of the process.

Table 15 data from the simulation corresponds to an ideal process where the redox reaction completely displaces to the right with no reverse methanol decomposition. This situation never happens since we cannot achieve an infinite carbon dioxide or null methanol concentration. In the current procedure, we reduce the methanol concentration by draining the methanol/water solution from the reactor.

Provided we operate at constant pressure, the concentration equilibrium constant depends on the elements intervening in the chemical reaction, as in the following [49,50]:

$$K_c={\displaystyle \frac{\left[C{H}_{3}OH\right]}{\left[C{O}_2\right]{\left[H_{2}O\right]}^2}}$$

(10)

Considering the carbon dioxide concentration to be constant, since the CO₂ flow to the reactor remains unchanged, and the water concentration is constant too, as the reaction progresses, the methanol concentration increases, generating a disequilibrium in the response and increasing K_c. Therefore, because the chemical reaction tends to the equilibrium, it reacts by decomposing methanol in water and carbon dioxide, lowering the Kc until it is back to the equilibrium value, K_c^o. This situation generates an effective reduction in the electron change number [51].

Considering the equilibrium and disequilibrium concentration constants as K_c^o and K_c, we have the following:

$$K_c={\displaystyle \frac{{\left[C{H}_{3}OH\right]}^{1+x}}{\left[C{O}_2\right]{\left[H_{2}O\right]}^2}}\hspace{0.33em};\hspace{0.33em}{K}_c^o={\displaystyle \frac{\left[C{H}_{3}OH\right]}{\left[C{O}_2\right]{\left[H_{2}O\right]}^2}}$$

(11)

The x-parameter represents the incremental fraction of methanol concentration, which is directly related to the degree of chemical reaction progress.

Operating in Equation (11), for the [CO₂] and [H₂O] constants, we have the following:

$$K_c=K_c^o{\left({\left[C{H}_{3}OH\right]}_{eq}\right)}^x$$

(12)

According to the setup chemical reaction for methanol production, the pressure equilibrium constant, K_p, is expressed in terms of the concentration equilibrium constant, K_c, and the variation of the mole number, Δn (Equation (13)) [52].

$$K_p=K_{c}RT\Delta n$$

(13)

We can express the variation in the mole number as follows:

$$\Delta n=n_{C{H}_{3}OH}-n_{C{O}_2}-n_{H_{2}O}$$

(14)

Combining Equations (12)–(14):

$$n_{C{H}_{3}OH}={\displaystyle \frac{K_p}{K_c^o{\left({\left[C{H}_{3}OH\right]}_{eq}\right)}^{x}RT}}+n_{C{O}_2}+n_{H_{2}O}$$

(15)

If the methanol concentration increases due to the redox reaction while the carbon dioxide supply stays constant, provided the water content in the electrolytic solution, the initial concentration, and the working pressure remain unchanged, all factors on the right side of Equation (15) will be constant except for the incremental fraction of methanol concentration, x, producing a decrease in the methanol number of moles, and creating a reverse flow as per Equation (9). Consequently, this decrease reduces the net electron transfer number and leads to an incomplete redox reaction if we do not drain the produced methanol.

On the other hand, if we control the methanol concentration in the electrolytic solution, the methanol mole number on the left side of Equation (15) increases, and the redox reaction moves toward a complete chemical reaction, approaching the electron change number to the ideal value z = 6.

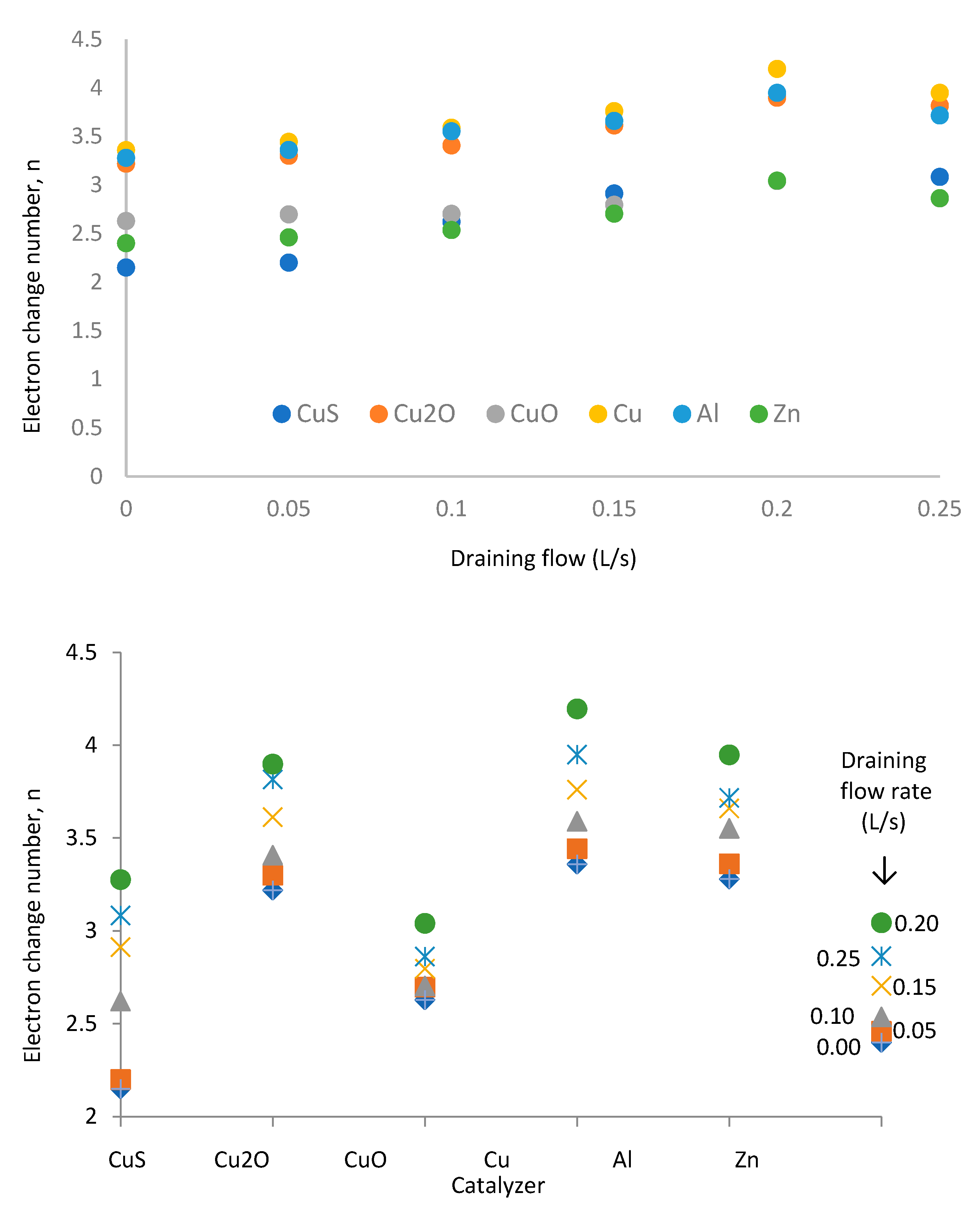
A new simulation process shows the chemical reaction and the development of the electron change number with the methanol/water solution draining (Figure 17).

We notice that the electron change number increases with the methanol draining flow until it reaches the 0.2 L/s value. The electron change number decreases for higher rates. The draining flow rate of 0.2 L/s represents the optimum operation conditions, showing a maximum electron change number of 4.2 for the copper as the catalyzer. This simulation shows that we cannot achieve the ideal condition of z = 6 independently of the methanol/water solution draining flow.

The simulation results are coherent with theoretical behavior of redox chemical reaction. Operating in Equation (11), and clearing the methanol and water concentration terms, we have the following:

$$K_c\left[C{O}_2\right]={\displaystyle \frac{{\left[C{H}_{3}OH\right]}^{1+x}}{{\left[H_{2}O\right]}^2}}$$

(16)

Since carbon dioxide concentration and K_c remain constant, applying equilibrium conditions, the first derivative of Equation (16) should be zero; therefore:

$${\displaystyle \frac{d}{dt}}\left(K_c\left[C{O}_2\right]\right)={\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{{\left[C{H}_{3}OH\right]}^{1+x}}{{\left[H_{2}O\right]}^2}}\right)=0$$

(17)

Operating in Equation (17):

$${\displaystyle \frac{{\left[C{H}_{3}OH\right]}^{1+x}}{{\left[H_{2}O\right]}^2}}\ln \left({\displaystyle \frac{\left[C{H}_{3}OH\right]}{{\left[H_{2}O\right]}^2}}\right)=0$$

(18)

Since the methanol concentration never becomes null and the water concentration does not achieve the infinitum at any time:

$$\ln \left({\displaystyle \frac{\left[C{H}_{3}OH\right]}{{\left[H_{2}O\right]}^2}}\right)=0$$

(19)

Applying the values for methanol and water concentration, the results are as follows.

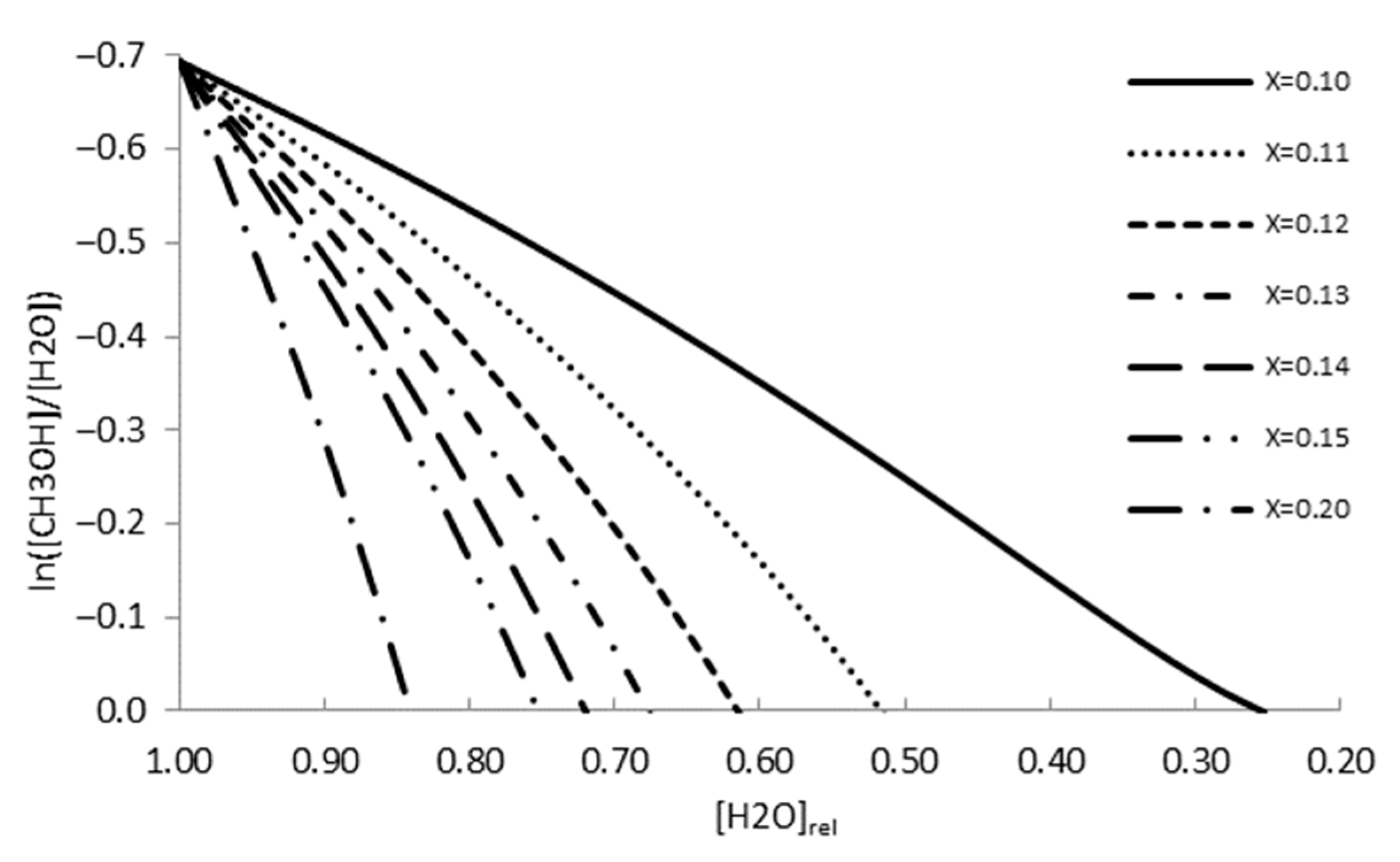
Analyzing Figure 18, the obtained results show that the chemical reaction disequilibrium of methanol formation tends to zero as the relative water concentration diminishes. Below the value where the function crosses the X-axis, the reaction reverses, and the electron change number reduces. The relative water concentration at which the redox reaction reverses depends on the incremental fraction of the methanol concentration, x, as shown in

Table 16. Relative water concentration for the redox reaction reversing point as a function of the incremental fraction of the methanol concentration (x).

x	0.10	0.11	0.12	0.13	0.14	0.15	0.20
[H2O]rel	0.253	0.518	0.622	0.685	0.725	0.753	0.844

.

The relative water concentration relates to the initial value in the electrolytic cell.

The simulation shows that for x-values below 0.1, the redox reaction never reverses, meaning that methanol concentration in the electrolytic cell is not high enough to stop the reaction progress.

3.5. Experimental Tests

We run experimental tests to validate the simulation results. To this goal, we proceed to inject carbon dioxide at atmospheric pressure and the ambient temperature inside the electrolytic cell to produce methanol, according to Equation (1). We calculate the methanol concentration by determining the pH evolution in the electrolytic cell solution. Figure 19 shows the evolution of the methanol concentration with time.

Table 17. Average standard deviation for Figure 19.

Catalyzer
CuS	Cu2O	CuO	Cu	Al	Zn
0.26	0.08	0.32	0.16	0.60	0.46

shows the average standard deviation for values in Figure 19.

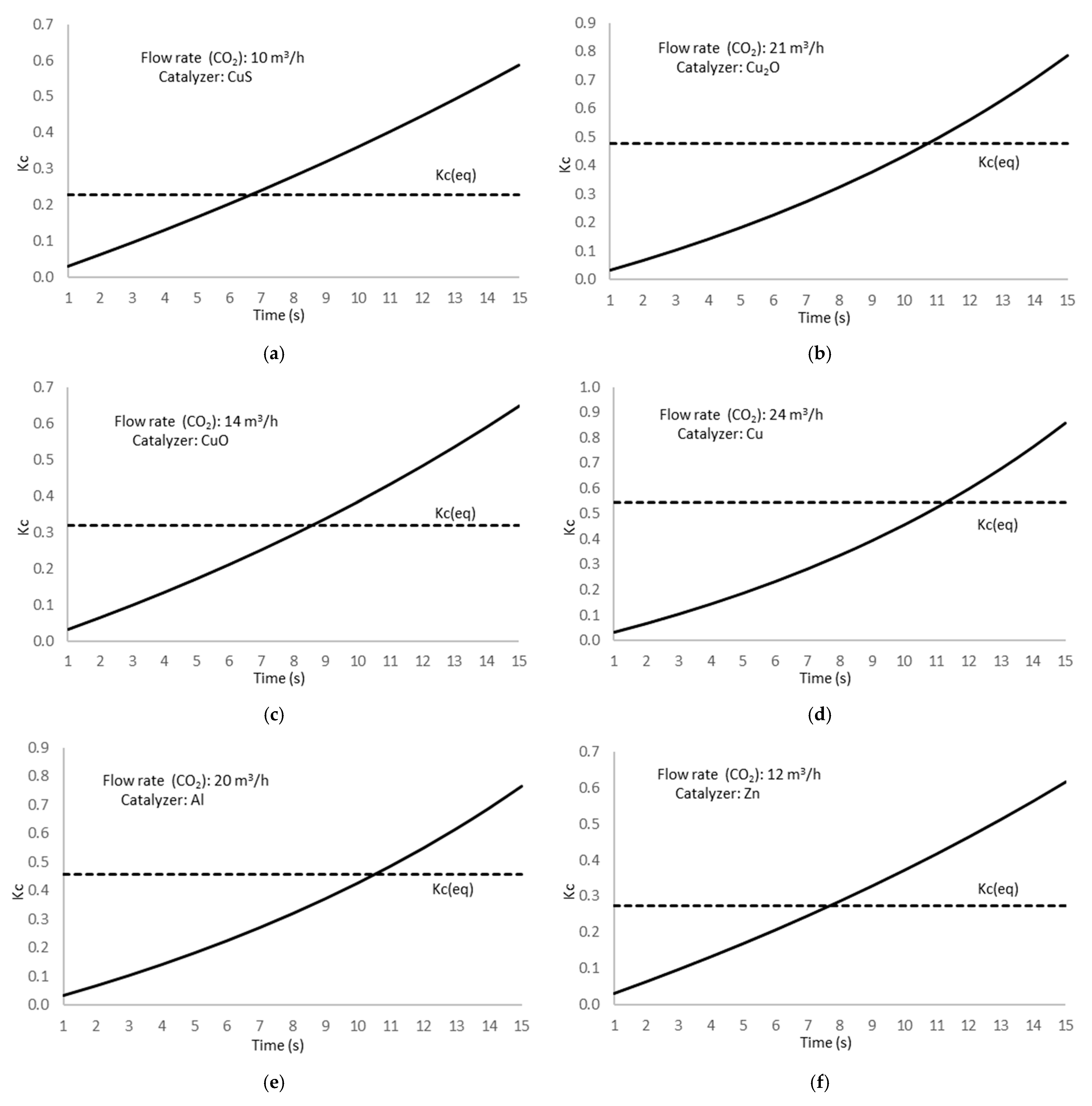
The next step in the experimental tests is determining the time evolution of the methanol concentration with the chemical reaction progress. To this goal, we calculate the K_c value using Equation (11) since the carbon dioxide and water concentrations are known. Figure 20 shows the results of the experimental tests.

Table 18. Average standard deviation for Figure 20.

Catalyzer
CuS	Cu2O	CuO	Cu	Al	Zn
0.40	0.50	0.62	0.25	0.39	0.55

shows the average standard deviation for values in Figure 20.

The dashed line corresponds to the K_c value at the equilibrium state.

The experimental running time corresponds to where the electron change number from running tests matches the calculated value using data from Figure 20 and applying Equation (13).

Analyzing data from Figure 20, the obtained results show that the experimental value for the K_c constant overpasses the equilibrium at a specific time, depending on the catalyzer used in the electrochemical reaction, showing that a reverse process starts from this time to maintain the equilibrium in the methanol formation chemical reaction. This result is consistent with a lower electron change number because of the reverse chemical process to return to the equilibrium state and maintain the K_c constant.

Table 19. Time for methanol decomposition reverse reaction starting.

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
Time (s)	6.01	10.53	8.05	10.94	10.16	7.06

shows the time at which the experimental concentration constant matches the equilibrium value; therefore, the time from which the methanol decomposition reverse reaction starts.

The carbon dioxide injection flow corresponds to the required value to match the equilibrium value.

From the data in Table 19, we notice that the methanol decomposition reverse reaction occurs quickly from the beginning of the process. This proves that the redox reaction develops in an incomplete form and results in a lower electron change number than the ideal.

If we use the same carbon dioxide injection flow for all catalyzers, taking the value for the CuS catalyzer, 10 m³/h, as a reference, the time at which the experimental concentration constant matches the equilibrium value is different, as shown in

Table 20. Time for methanol decomposition reverse reaction starting using the same carbon dioxide injection flow (10 m³/h).

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
Time (s)	6.0	6.0	6.0	6.0	6.0	6.0

.

On the other hand, the time at which the calculated value for the electron change number, using the K_c values and applying Equation (13), matches the data from the experimental tests is as follows (

Table 21. Running time to match the calculated value and experimental data for the electron change number for the catalyzers used in experimental tests.

Catalyzer	CuS	Cu2O	CuO	Cu	Al	Zn
Time (s)	15.0	10.3	12.5	9.9	10.5	13.4

):

3.6. Results Analysis

Analyzing the results obtained from the experimental tests, if we intend to match the experimental data with the calculated value for the methanol formation electrochemical reaction electron change number simultaneously for all chemical processes, we notice that the carbon dioxide injection flow changes depending on the catalyzer used. Data from Figure 20 shows that for a 15 s running time, the CuS catalyzer requires the lowest carbon dioxide injection flow, while the copper catalyzer requires the highest. The obtained results show that the catalyzers used can be grouped into two categories: CuS, CuO, and Zn, requiring low carbon dioxide injection flow, around 12 m³/h on average; and Cu₂O, CuO, and Al, requiring nearly double the injection flow, 22 m³/h.

On the other hand, the time the methanol decomposition reverse reaction starts depends on the catalyzer type; the CuS catalyzer shows the quickest starting time and the copper catalyzer the lowest. Regarding the reverse reaction starting time, we can group the catalyzers into two categories, CuS, CuO, and Zn, showing a relatively short starting time for the reverse reaction, 7.04 s on average; and Cu₂O, CuO, and Al, with a longer starting time, 10.54 s on average. These values indicate that the reverse reaction begins at 47% of the total methanol formation process time for the first catalyzers group, CuS, CuO, and Zn, and at 70% for the second group, Cu₂O, CuO, and Al, meaning that this latter group is more suitable for methanol formation in the operating conditions.

Applying a constant carbon dioxide injection flow, 10 m³/h, the obtained results show that the reverse reaction starting time is identical for all cases, showing independence from the catalyzer type. Nevertheless, for a constant carbon dioxide injection flow, the time at which the experimental data and calculated value for the electron change number match in the methanol formation electrochemical reaction depends on the catalyzer, with the lowest value for the copper and the highest for the CuS. The analysis of all starting times shows a low standard deviation, σ = 0.759, around the average value of 11.9 s.

3.7. Draining Methodology

Draining the methanol/water solution in the electrolytic cell reduces the methanol concentration and favors the reaction progress to produce methanol from carbon dioxide. The analysis developed in a previous section shows (Figure 17) that draining increases the electron change number, bringing the methanol formation process closer to ideality.

To this goal, we ran experimental tests draining the methanol/water solution at the flow rate shown in Figure 17, except for the case of 0.25 L/s, since we proved that the reaction progress degree reduces from the optimum flow rate of 0.2 L/s. The experimental tests corresponded to the methanol concentration and reaction constant evolution with time for the same time range used for previous tests without draining. 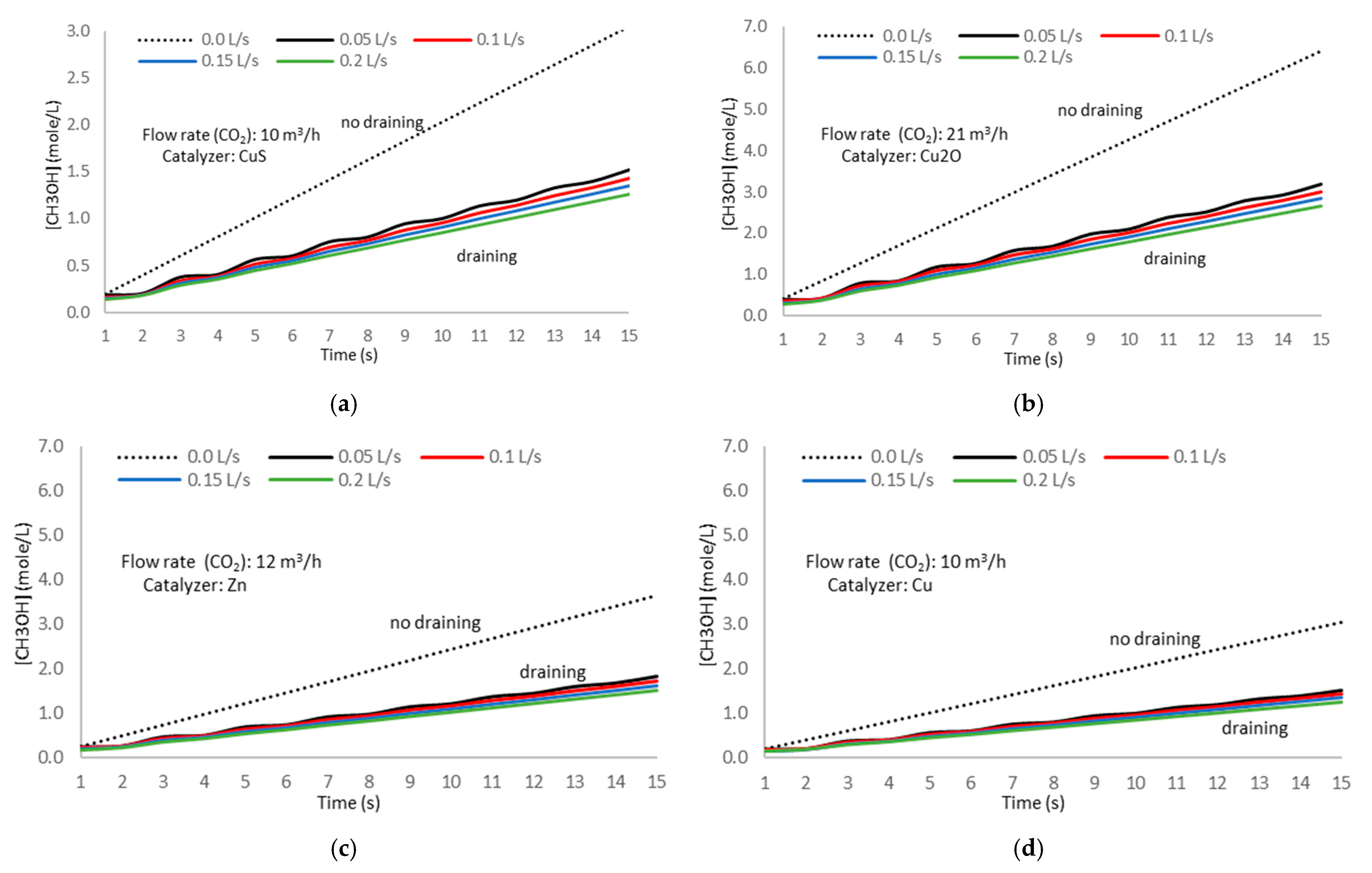Figure 21 and Figure 22 show the experimental results.

Comparing the time evolution of the methanol concentration under current conditions and using the draining methodology, we notice that this last procedure shows a significant reduction in the methanol concentration in the electrolytic cell solution. This process favors the direct reaction progress and continuous methanol formation and tends to achieve the maximum electron change number and the optimum performance. This situation occurs in all cases with slight differences between the catalyzer types.

Analyzing the experiment results, we also noticed no significant differences in the time evolution of methanol concentration between the different catalyzer types when applying the draining methodology. Applying statistical methods, we determined the average ratio of the time evolution of methanol formation with and without draining, obtaining a value of 0.513 with a standard deviation of 0.008, proving the high accuracy in the ratio determination and the consistency of the obtained value.

Table 22. Average standard deviation for Figure 21.

CuS	Cu2O	Cu	Zn
0.11	0.56	0.61	0.16

shows the average standard deviation for testing values in Figure 21.

The colored lines in Figure 21 correspond to the draining flow labels shown on the upper side of the figure. The dashed line represents the time evolution of methanol formation without draining.

The data analysis from the experiment results in Figure 21 shows that the draining flow is not critical to reducing the methanol formation; therefore, we can use the lower draining value, saving energy in pumping the methanol/water solution from the reactor to the distiller.

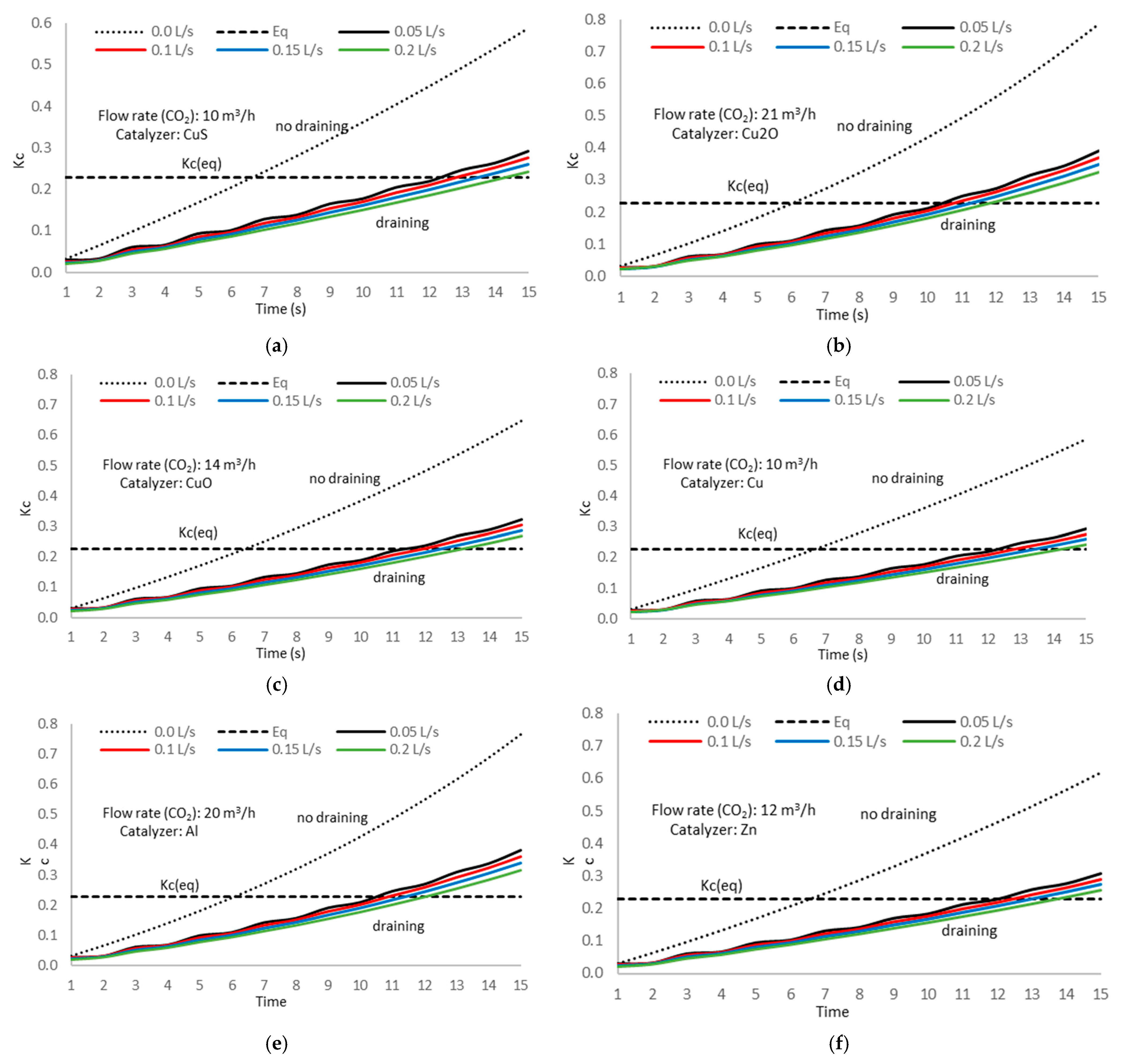
A second step in the experimental tests using the draining methodology is evaluating the time evolution of the concentration constant when we drain the electrolytic cell solution. Figure 22 shows the experiment results.

As expected, the reaction constant in the methanol formation shows the same reduction ratio as for the methanol concentration, with an identical value of 0.513 and a standard deviation of 0.008, proving the accuracy in the value determination.

We also notice no significant difference in the Kc performance between different catalyzers, with a slight gap from one to another. Table 15 shows the time the reaction constant, Kc, matches the equilibrium value for the non-draining and draining cases with the different catalyzers. This value represents the point where the methanol decomposition reverse reaction starts. Table 21 also shows the time fraction where the reverse reaction begins, regarding the total time of the process.

Regarding the data in

Table 23. Methanol decomposition reverse reaction starting time and fraction time regarding the global process.

Starting Time (s)	Catalyzer
Flow Rate (L/s)	CuS	Cu2O	CuO	Cu	Al	Zn
0.00	5.631	4.984	5.386	5.631	4.999	5.449
0.05	11.399	9.379	10.324	11.263	9.484	10.834
0.10	11.781	9.720	10.882	11.703	9.822	11.318
0.15	12.441	10.253	11.420	12.360	10.353	11.913
0.20	13.253	10.719	12.182	13.201	10.912	12.642
Fraction Time	Catalyzer
Flow Rate (L/s)	CuS	Cu2O	CuO	Cu	Al	Zn
0.00	0.375	0.332	0.359	0.375	0.333	0.363
0.05	0.760	0.625	0.688	0.751	0.632	0.722
0.10	0.785	0.648	0.725	0.780	0.655	0.755
0.15	0.829	0.684	0.761	0.824	0.690	0.794
0.20	0.884	0.715	0.812	0.880	0.727	0.843

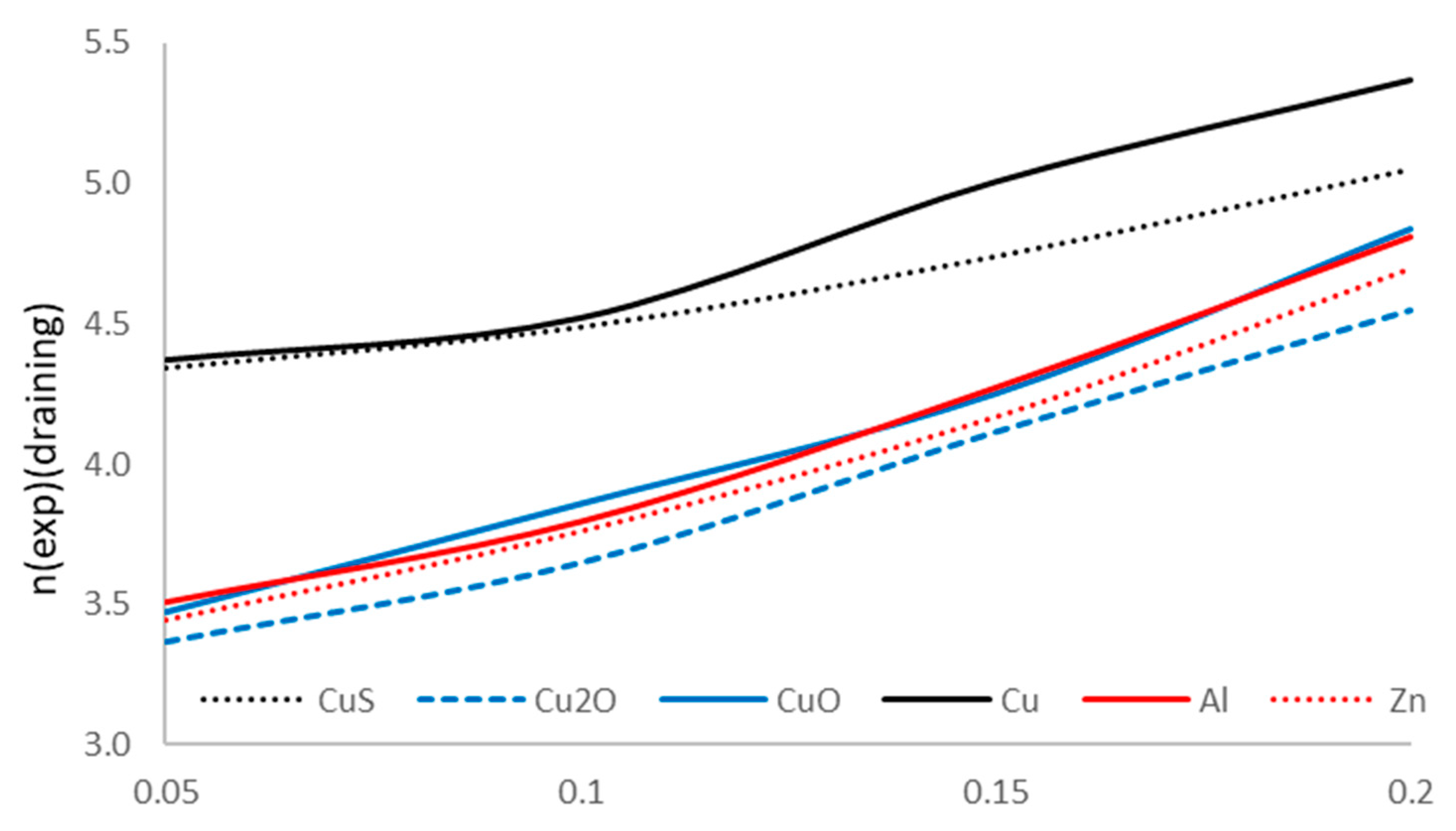
, we notice that the draining process extends the reverse reaction starting time, improving the methanol formation performance. On the other hand, the electronic change is modified when using the draining process; Figure 23 shows the evolution of the experimental n-value for the various flow rates and catalyzer types.

Table 24. Average standard deviation for Figure 22.

Catalyzer
CuS	Cu2O	CuO	Cu	Al	Zn
0.30	0.45	0.42	0.32	0.40	0.44

shows the average standard deviation for testing values in Figure 22.

The obtained results show that the improvement in the methanol formation process, with the electron change number in the redox reaction approaching to the ideal value z = 6. The experiment results using the draining methodology prove the profitability of the technique used.

3.8. Methanol Production

Using data from experimental tests, we determine the absolute methanol production, in number of moles, for the running time. Figure 24 shows the evolution of methanol production with draining flow for the different catalyzers used in the tests.

Table 25. Average standard deviation for Figure 24.

Catalyzer
CuS	Cu2O	CuO	Cu	Al	Zn
0.62	0.99	0.78	0.39	0.75	0.73

shows the average standard deviation for testing values in Figure 24.

The obtained results show a fast increase in methanol formation when applying the draining process. Nevertheless, the flow rate does not significantly increase methanol production, as shown in the near horizontal section of methanol formation for the draining process.

Comparing data from methanol production with and without draining, we obtain a ratio between 4.39 and 4.98, depending on the flow rate, representing a significant increase in methanol production. In absolute terms, the methanol production increase varies from a minimum of 6.523 moles for the copper catalyzer to a maximum of 14.643 for the copper oxide (Cu₂O).

Considering the running time for the methanol formation, the production increase rate is 0.435 moles/s for the copper catalyzer and 0.976 moles/s for the copper oxide.

Table 26. Methanol production for variable draining flow rate and catalyzer type.

		Catalyzer
Flow Rate (L/s)		CuS	Cu2O	CuO	Cu	Al	Zn
Mass rate (kg/h)	0.00	14.4	30.2	20.2	14.4	28.8	17.3
	0.05	63.7	134.0	89.3	60.5	127.6	76.5
	0.10	66.3	139.4	92.9	63.0	132.8	79.6
	0.15	69.2	145.4	96.9	65.7	138.5	83.0
	0.20	72.3	152.0	101.2	68.7	144.7	86.8

summarizes all results for methanol production.

4. Conclusions

The redox chemical reaction for methanol production using carbon dioxide as primary matter proves that the process efficiency depends on the catalyzer used, with noticeable differences in the degree of reaction progress. The six catalyzers used for methanol formation show variable numbers in the electron change number for the redox reaction, ranging from a minimum of z = 2.15 for CuS as a catalyzer to a maximum of 3.36 for copper. These values are far from the ideal number, z = 6, meaning that the methanol decomposition reverse reaction occurs during the methanol formation process due to surpassing the equilibrium value of the reaction constant, Kc, limiting the methanol production and reducing the process efficiency.

According to experimental tests, the best option among the six catalyzers used for methanol production is plain copper, with copper oxides (Cu₂O, CuO) and copper Sulphur (CuS) as feasible alternatives.

Because an excess in the methanol concentration regarding the chemical equilibrium seems to be the principal cause of the reverse reaction, we used a draining process to evacuate the methanol/water solution and to reduce the methanol concentration in the reactor. This procedure improves the methanol production efficiency by delaying the time at which the chemical reaction constant surpasses the equilibrium value, thus delaying methanol decomposition through the reverse reaction. The experimental tests carried out using the draining technique showed an improvement in methanol production, increasing with the draining flow rate from a minimum factor of 4.43 for 0.05 L/s to a maximum of 5.03 for 0.2 L/s. The ratio in increasing the methanol production does not depend on the catalyzer type, with almost identical values for a specific draining flow rate.

Concerning the methanol production, we conclude that using the draining method, the mass rate increases significantly from an average value of 20.9 kg/h for non-draining use, considering all catalyzer types, to a range between 91.9 kg/h and 104.3 kg/h, depending on the flow rate. Averaging all values for different flow rates and comparing with the non-draining case, we obtain an absolute methanol production mass rate of 77 kg/h, meaning an incremental percentage of 469.1%, more than four times the initial production.

The results obtained from the analysis of methanol formation and experimental production prove the validity of the applied draining methodology. Nevertheless, the methanol production increase with a rising draining flow rate shows a limit beyond which the methanol formation decreases due to the imbalance in the chemical reaction; in our case, the optimum flow rate is 0.2 L/s, representing one third of the electrolytic cell volume.

Data provided by the methanol formation process used and the experimental test results represent a base for application to methanol production at a larger scale; however, extrapolating the values to a larger scale may not result in a linear increase since the developed chemical reactions do not perform identically when applied to the industrial scale range. To achieve this goal, we propose applying the proposed methodology to larger prototypes, even on a small industrial scale, and evaluating the influence of the scale factor on the system’s performance. This evaluation will lead to a correlation function that allows for the prediction of results within an industrial scale range.